Introduction

Nonlinear phenomena in fiber optics have many attractive features and have a great potential for a possible all optical communication system. Optical fiber material shows nonlinear response to strong elecric fields [1]. Normally the responses are detrimental to the signal transmission but the same can also lead to a number of favourable results. Optical soliton is one such application in which the nonlinear effect counterbalances the chromatic dispersion to generate a stable pulse [2, 3].

Pulse propagation in a single mode fiber is described by the nonlinear Schrödinger equation [1]:

$$ i \textbf{q}_{x} - \frac{\beta_{2}}{2} \textbf{q}_{tt} + \gamma |\textbf{q}|^{2} \textbf{q} = 0 $$
(1)

where q(x, t) is a slowly varying pulse envelope in a reference frame, moving with the group velocity of the pulse, β 2 is the group velocity dispersion(GVD) (β 2 > 0 for fiber with normal dispersion and β 2 < 0 for fiber with anomalous dispersion), \(\gamma = \frac {2 \pi n_{2}}{\lambda A_{eff}} \) is the Kerr non-linearity coefficient, n 2 the Kerr (index) coefficient, λ the central wavelength of the pulse and A e f f the effective core area of the fiber. Equation (1) is exactly integrable by the inverse scattering method [4]. The simplified fundamental soliton solutions of (1) for (β 2 = ±1) respectively are:

$$ \textbf{q}= \frac{\eta}{\sqrt{\gamma}}Tanh (\eta (t - t_{s} )e^{i \eta^{2} x + i\phi} $$
(2)
$$= \frac{\eta}{\sqrt{\gamma}}Sech (\eta (t - t_{s}))e^{i \frac{\eta^{2} x}{2} + i\phi} $$
(3)

where η, ϕ, t s are the fundamental soliton parameters representing the pulse amplitude (also the width-inverse), phase and the position of the soliton respectively [1].

In deriving NLS equation (1) properties such as polarization of light is neglected. In practice however even a single mode fiber support two orthogonally polarized light. In an elliptically birefringent fiber the propagation of optical pulses is governed by the following two coupled nonlinear Schrödinger equation [1]

$$\begin{array}{@{}rcl@{}} i \textbf{q}_{1_{x}} - \frac{\beta_{2}}{2} \textbf{q}_{1_{tt}} + \gamma (|\textbf{q}_{1}|^{2} +|\textbf{q}_{2}|^{2})\textbf{q}_{1} &=& 0\\ i \textbf{q}_{2_{x}} - \frac{\beta_{2}}{2} \textbf{q}_{2_{tt}} + \gamma (|\textbf{q}_{1}|^{2}+|\textbf{q}_{2}|^{2})\textbf{q}_{2} &=& 0 \end{array} $$
(4)

where q 1 and q 2 are the two polarization components. The pair of equations are frequently referred to as the Manakov system and has exact analytic solution [1, 5].

The i th component fundamental soliton solutions of (4) for (β 2 = ±1) respectively are:

$$ \textbf{q}_{\textbf{i}}= \frac{\alpha_{i}\eta}{\sqrt{\gamma}}Tanh (\eta t)e^{i \eta^{2} x} $$
(5)
$$= \frac{\alpha_{i}\eta}{\sqrt{\gamma}}Sech (\eta t)e^{i \frac{\eta^{2} x}{2}} $$
(6)

where α i in the amplitude is the state of polarization for each component [1].

Adomian method is a useful technique to find the approximate solutions of nonlinear differential equations [11–14, 17]. The uniqueness of this method is that the solution is obtained in the form of a fast converging series [11], such that first few terms of the series are sufficient to give an insight into the character and behaviour of the solution. For nonlinear problems unlike many other methods this method does not require linearization and it does not make smallness assumptions or physically unrealistic white noise assumption [11].

ADM method being a semi-analytical method is often compared with other semi-analytical methods and numerical methods. Several authors in their work showed the effectiveness and advantage of Adomian method over other such type of methods. In [15] auther has shown that compared to other series method it is easier to program the decomposition method in nonlinear problems, and it provides immediate and visible solution terms without linearization and discretization. The adantage of this method over another successive approximation method, namely the Picard’s method is shown in [16], that the later method works only if the equation satisfies the Lipschitz condition and no such condition is imposed on the Adomian method. In [18] author showed that although both the Taylor series method and Adomian method provides the same answer the Adomian method minimizes the computational difficulties of the Taylor series and determines the components of the solution elegantly by using simple integrals.

In optics the method has been applied earlier to wave-guide problem [19], beam propagation in saturable absorber [21] and problem of tracing rays through graded index (GRIN) media, where the authors also showed the superiority of Adomian method over the Runge-Kutta method [20]. In nonlinear optics also the use of decomposition method is reported in [22, 25], where the shape preserving S e c h type solitary wave solution is discussed for continuous and discrete NLS equation. To the authors knowledge however, there is no report of a decomposition method giving both the dark and bright solitary wave solutions. Moreover the application of the method to coupled-NLS equation (4) also remained unexplored.

Since there are already some analytical methods available, such as Inverse scattering transform (IST) method, Darbaux transformation method and Hirota bilinear formalism which solve the NLS problem analytically, it is natural to compare the Adomian method with these methods. In Inverse scattering method the problem is solved indirectly by transforming the nonlinear problem into a pair of linear problems and the linear problems provides the solution of the original problem though inverse transformation [4, 6]. In Darbaux transformation method the problem is solved through simultaneous mapping between solutions and coefficients of a pair of equations of the same form [10]. In Hirota bilinear formalism the original problem is transformed to a set bilinear equations and the solution is obtained by solving the bilinear equations [7–9]. Although these methods are elegant and do not require initial or boundary conditions but each of them require involved calculations and are not always easy to use. The Adomian method on the other hand require initial or boundary conditions, but the method attacks any problem directly, which minimizes the volume of computation and the successive solutions are determined elegantly by using simple integrals only.

In this paper we show that within the framework of a more general decomposition algorithm the critical pulse shape of fundamental dark (β 2 = 1) and bright (β 2 = −1) soliton can be generated with a suitable initial condition and without using the precondition of a definite pulse shape. Subsequently we have proposed a generalized decomposition algorithm for the coupled nonlinear schrödinger (CNLS) equation and obtained soliton like solutions using the method. In Section “Decomposition method for NLS equation”. we present an overview of the decomposition method for the NLS equation. The section also contains the results. In Section “Decomposition method for coupled NLS equation”. we present the application of the method to the coupled NLS equation together with results. Section “Discussion”. is devoted to general discussions. Section “Conclusion”. contains the conclusion.

Decomposition method for NLS equation

In the operator form NLS equation (1) can be written as

$$ i L_{x} \textbf{q} = \beta_{2} \frac{1}{2}L_{t} \textbf{q} -\gamma N \textbf{q} $$
(7)

where \(L_{x}=\frac {\partial }{\partial x}\), \(L_{t}=\frac {\partial ^{2}}{\partial t^{2}}\) and N q = |q|2 q. Then \(L_{x}^{-1}= {{\int }_{0}^{x}} dx\) and \(L_{t}^{-1}= {{\int }_{0}^{t}}dt {{\int }_{0}^{t}}dt \). Solving alternately for operators L x and L t ,

$$ L_{x} \textbf{q} = - i \beta_{2} \frac{1}{2}L_{t} \textbf{q} + i \gamma N \textbf{q} $$
(8)
$$ L_{t} \textbf{q} = i \frac{2}{\beta_{2}} L_{x} \textbf{q} + \frac{2}{\beta_{2}} \gamma N \textbf{q} $$
(9)

operating (8) with \(L_{x}^{-1}\) results the equations [22]

$$ \textbf{q} = \textbf{q}(0, t) - i \beta_{2} {{\int}_{0}^{x}} \frac{1}{2}L_{t} \textbf{q} dx + i {{\int}_{0}^{x}} \gamma N \textbf{q}dx $$
(10)

similarly operating (9) with \(L_{t}^{-1}\) results another equation,

$$ \textbf{q} = \textbf{q}(x, 0) + \frac{\partial \textbf{q}(x,t)}{\partial t}{\displaystyle |_{t=0}} t + i \frac{2}{\beta_{2}} {{\int}_{0}^{t}} {{\int}_{0}^{t}} L_{x} \textbf{q}dt dt + \frac{2} {\beta_{2}} {{\int}_{0}^{t}} {{\int}_{0}^{t}}\gamma N \textbf{q}dt dt $$
(11)

adding (10) and (11) we get

$$\begin{array}{@{}rcl@{}} \textbf{q} &= & \frac{1}{2}[\textbf{q}(0, t)+\textbf{q}(x, 0)+\frac{\partial \textbf{q}(x,t)}{\partial t}{\displaystyle |_{t=0}} t ] + \frac{1}{2}[- i \beta_{2} {{\int}_{0}^{x}} \frac{1}{2}L_{t} \textbf{q} dx \\ & &+ i {{\int}_{0}^{x}} \gamma N \textbf{q}dx + i \frac{2}{\beta_{2}} {{\int}_{0}^{t}} {{\int}_{0}^{t}} L_{t} \textbf{q}dt dt + \frac{2}{ \beta_{2}} {{\int}_{0}^{t}} {{\int}_{0}^{t}}\gamma N \textbf{q}dt dt ] \end{array} $$
(12)

Each of the equations (10, 11, 12), with proper boundary condition gives a solution of (7)

Let us assume a solution in the form of a series,

$$ \textbf{q}=\sum\limits_{i=0}^{\infty} q_{i} $$
(13)

with its first term obtained from the boundary condition, for example, q 0 = q(0, t) for equation (10) and \(q_{0}=\textbf {q}(x, 0) + \frac {\partial \textbf {q}(x,t)}{\partial t}{\displaystyle |_{t=0}} \) for equation (11). The nonlinear term N q is defined as,

$$ N \textbf{q} = \sum\limits_{n=0}^{\infty} A_{n}(q_{0}, q_{1},q_{2},......., q_{n}, q_{0}^{\ast}, q_{1}^{\ast},q_{2}^{\ast}.........q_{n}^{\ast}) $$
(14)

where A n is the Adomian polynomial and is defined as

$$ A_{n} = \sum\limits_{i=0}^{n}\sum\limits_{j=0}^{i}\sum\limits_{k=0}^{i} q_{i-j-k} q_{j} q_{k}^{*} $$
(15)

where n = 0, 1, 2, 3, ... .∞. The simple rule here is (i + j + k = n). For example, first few Adomian polynomials are:

$$\begin{array}{@{}rcl@{}} A_{0} &=& |q_{0}|^{2} q_{0} \\ A_{1} &=& 2 |q_{0}|^{2} q_{1} + {q_{0}^{2}} q_{1}^{*} \\ A_{2} &=& 2 |q_{0}|^{2} q_{2} +2 |q_{1}|^{2} q_{0} + {q_{1}^{2}} q_{0}^{*} + {q_{0}^{2}} q_{2}^{*} \\ A_{3} &=& 2 |q_{0}|^{2} q_{3} + 2 q_{1} q_{2} q_{0}^{*} + 2 q_{2} q_{0} q_{1}^{*} + 2 q_{1} q_{0} q_{2}^{*} + |q_{1}|^{2} q_{1} + {q_{0}^{2}} q_{3} \end{array} $$

The polynomials can also be constructed alternatively by the methd given in [26, 27]. We thus have the n-term approximate solution, where the first term is given by the boundary condition of the given problem. By using different boundary conditions a number of solutions are possible as shown:

Example 1

Consider

$$q_{0}=q(0,t)=\eta \qquad (constant)$$

Then using (10, 13, 14) the subsequent terms q 1, q 2, q 3, ⋯ can be calculated and we get

$$\textbf{q}= \sum\limits_{i=0}^{\infty} q_{i}=q_{0} \eta e^{i \gamma |\eta|^{2} x} $$

Example 2

Consider

$$q_{0}=q(0,t)= e^{ikt}$$

Similarly using (10, 13, 14) we get

$$\textbf{q}= \eta e^{i (kt +({\displaystyle \beta_{2} \frac{k^{2}}{2} + \gamma}) x)} $$

Dark solitary wave solution

Soliton solution in nonlinear optics however, is one of the most important aspects. Next we would obtain the dark soliton solution of equation (1) (with β 2 = 1). For that let us consider a T a n h type boundary condition such as,

$$ q_{0}= \frac{\eta}{\sqrt{\gamma}} Tanh[\eta t - \tau_{s}] $$
(16)

where τ s is the position of the pulse. Then using (16) in (10) q 1, q 2, q 3, ⋯ can be calculated [29] and the solution therefore is,

$$ q_{0}= \frac{\eta}{\sqrt{\gamma}} Tanh(\eta t - \tau_{s})(1 + i \eta^{2} x- \frac{\eta^{4} x^{2}}{2} + i\frac{\eta^{6} x^{4}}{4!} {\cdots} ) $$
(17)

Notice that the bracketed terms approximates to the the exponential series \( e^{i \eta ^{2} x}\). Thus the iteration finally leads to the fundamental soliton solution (2) with an amplitude η, position t s , phase ϕ 0 = 0, and zero frequency shift.

Alternately we may also proceed with equation (11). Let we consider a simple initial pulse profile,

$$q_{0}= \frac{\partial \textbf{q}(x,t)}{\partial t}{\displaystyle |_{t=0}} t = \frac{\eta}{\sqrt{\gamma}}e^{i\eta^{2} x} \eta t $$

where we have assumed q(x, 0) = 0

Then using (11) and (14) we get,

$$\begin{array}{@{}rcl@{}} q_{1} &=& - q_{0}\frac{\eta^{2} t^{2}}{3!} \\ q_{2} &=& q_{0}\frac{2 \eta^{4} t^{4}}{15} \\ q_{3} &=& -q_{0}\frac{17\eta^{6} t^{6}}{315}\\ {\vdots} & & \qquad {\vdots} \qquad \end{array} $$

Thus the approximate dark soliton solution is

$$ \textbf{q} = \frac{q_{0}}{\eta t} (\eta t - \frac{\eta^{3} t^{3}}{3!} + q_{0}\frac{2 \eta^{5} t^{5}}{15} - q_{0}\frac{17\eta^{7} t^{7}}{315} {\cdots} \cdots) $$
(18)

It is important to notice that the terms within the bracket in (18) are the first few terms of the standard T a n h(η t) series, which shows that the series obtained is a converging one and approaches the soliton solution (2) with position τ s = 0 and phase ϕ 0 = 0.

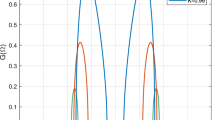
The results are plotted using Mathematica software. In Fig. 1a, decomposition solutions, with first four terms and first eight terms are plotted together with exact solution of NLS equation (2) for η = 0.5, τ s = 0 and phase ϕ 0 = 0. It shows that for a smaller range of ’t’ the decomposition solution coincide with the exact solution, however, with increase in ’t’, more components of the decomposition are required for a better match. Figure 1b shows the same comparison but with ’ η = 1’. A comparison of these figures shows that for a higher value of ’ η’ (smaller pulse width ) more components are required for a better match with the exact solution.

Fig. 1
figure 1

Plot of exact dark soliton(red), 4-terms Adomian solution (green) and 8-terms Adomian solution (blue) for (a) η = 0.5 and (b) η = 1

Full size image

Thus by choosing an appropriate boundary condition we can recover the well known shape preserving form of the solitary wave solution for (7). Two soliton solution, it is often stated in the literature [5, 23] that the solution is too complicated to analyze. However, combining a pair of one-soliton solutions, as stated in [24] it should be possible to obtain two-soliton solution also, which will be our future work.

Bright solitary wave solution

Consider Equation (10) (with β 2 = −1) and assume a shape preserving form (as considered in [22]) at position τ s :

$$q_{0}= q(0,t)=\frac{\eta}{\sqrt{\gamma}}Sech (\eta t - \tau_{s} ) $$

then q 1, q 2 and q 3,⋯ can be calculated as [22, 29]

$$\begin{array}{@{}rcl@{}} q_{1} &=& q_{0} (i \eta^{2} x) \\ q_{2} &=& q_{0} (-\frac{\eta^{4} x^{2}}{2!})\\ q_{3} &=& q_{0} (-i \frac{\eta^{6} x^{3}}{3!})\\ {\cdots} \qquad {\cdots} \qquad \cdots \end{array} $$

and the solution approaches (3), with amplitude η, position t s , phase ϕ 0 = 0 and zero frequency shift [22].

Alternately we proceed with equation (11) and consider a simple boundary condition. Let us assume that \( \frac {\partial \textbf {q}(x,t)}{\partial t}{\displaystyle |_{t=0}} = 0 \) and the first component of the decomposition be

$$q_{0}= q(x,0)=\frac{\eta}{\sqrt{\gamma}}e^{\displaystyle i \frac{\eta^{2}}{2} x} $$

The successive components of the decomposition (13) are obtained using (11) and (14). First few components are

$$\begin{array}{@{}rcl@{}} q_{1} &=& - q_{0}\frac{\eta^{2} t^{2}}{2} \\ q_{2} &=& q_{0}\frac{5 \eta^{4} t^{4}}{24}\\ q_{3} &=& -q_{0}\frac{61 \eta^{6} t^{6}}{720} \end{array} $$

Thus the approximate solitary wave solution is

$$ \textbf{q} = q_{0}(1 - \frac{\eta^{2} t^{2}}{2} + \frac{5 \eta^{4} t^{4}}{24} - \frac{61 \eta^{6} t^{6}}{720} {\cdots} \cdots) $$
(19)

The terms within the bracket in (19) are the first few terms of standard S e c h(η t) series, which shows that the series is convergent and approaches the soliton solution 3.

The Adomian solution (19) is compared with the single soliton solution (3) with τ s = 0 and phase ϕ 0 = 0 by using Mathematica. In Fig. 2a,b decomposition solutions, with first four terms and first eight terms are plotted together with single bright soliton solution of NLS equation for η = 0.5 and η = 1 respectively. The figures show that for a smaller range of ’t’and ’ η’ the decomposition solution coincide with the single soliton solution, however, with increase in ’t’ and η more components of the decomposition are required for a better match.

Fig. 2
figure 2

Plot of exact bright soliton (red), 4-terms Adomian solution (green) and 8-term Adomian solution (blue) for (a) η = 0.5 and (b) η = 1

Full size image

Decomposition method for coupled NLS equation

In this section we present a generalized the decomposition method for the coupled NLS equation (4). In the operator form the equations in (4) are rewritten as:

$$ i L_{x} \textbf{q}_{\textbf{1}} = \beta_{2} \frac{1}{2}L_{t} \textbf{q}_{\textbf{1}} -\gamma N \textbf{q}_{\textbf{1}} $$
(20)
$$ i L_{x} \textbf{q}_{\textbf{2}} = \beta_{2} \frac{1}{2}L_{t} \textbf{q}_{\textbf{2}} -\gamma N \textbf{q}_{\textbf{2}} $$
(21)

where \( N={\sum \limits _{k=1}^{2} |\textbf {q}_{\textbf {k}}|^{2}}\).

Solving for each component, k(=1, 2)

$$ L_{x} \textbf{q}_{\textbf{k}} = i \beta_{2} \frac{1}{2}L_{t} \textbf{q}_{\textbf{k}} + i \gamma N \textbf{q}_{\textbf{k}} $$
(22)
$$\begin{array}{@{}rcl@{}} L_{t} \textbf{q}_{\textbf{k}} &=& i \frac{2}{\beta_{2}} L_{x} \textbf{q}_{\textbf{k}} + \frac{2}{\beta_{2}} \gamma N \textbf{q}_{\textbf{k}} \end{array} $$
(23)

operating (22) with \(L_{x}^{-1}\) we get

$$ \textbf{q}_{\textbf{k}} = \textbf{q}_{\textbf{k}}(0, t) + i \beta_{2} {{\int}_{0}^{x}} \frac{1}{2}L_{t}\textbf{q}_{\textbf{k}} dx + i {{\int}_{0}^{x}} \gamma N \textbf{q}_{\textbf{k}}dx $$
(24)

similarly operating (23) with \(L_{t}^{-1}\) we get

$$\begin{array}{@{}rcl@{}} \textbf{q}_{k} &=& \textbf{q}_{\textbf{k}}(x, 0) + \frac{\partial \textbf{q}_{\textbf{k}}(x,t)}{\partial t}{\displaystyle |_{t=0}} t + i \frac{2}{\beta_{2}} {{\int}_{0}^{t}} {{\int}_{0}^{t}} L_{x} \textbf{q}_{\textbf{k}} dt dt \\ &&+ \frac{2}{\beta_{2}}{{\int}_{0}^{t}} {{\int}_{0}^{t}} \gamma N \textbf{q}_{\textbf{i}} dt dt \end{array} $$
(25)

adding (24) and (25) we get

$$\begin{array}{@{}rcl@{}} \textbf{q}_{\textbf{k}} &=& \frac{1}{2}[\textbf{q}_{\textbf{k}}(0, t)+\textbf{q}_{\textbf{k}}(x, 0)+\frac{\partial \textbf{q}_{\textbf{k}}(x,t)}{\partial t} \vert_{t=0} t ] \\ &&{\kern5pt}+ \frac{1}{2}[ i \beta_{2} {{\int}_{0}^{x}} \frac{1}{2}L_{t} \textbf{q}_{\textbf{k}} dx + i {{\int}_{0}^{x}} \gamma N \textbf{q}_{\textbf{k}}dx \\ & & i \frac{2}{\beta_{2}} {{\int}_{0}^{t}} {{\int}_{0}^{t}} L_{x} \textbf{q}_{\textbf{k}}dt dt + \frac{2}{\beta_{2}}{{\int}_{0}^{t}} {{\int}_{0}^{t}} \gamma N \textbf{q}_{\textbf{k}}dt dt] \end{array} $$
(26)

The decomposition and the Adomian polynomials respectively are,

$$ \textbf{q}_{\textbf{k}}=\sum\limits_{i=0}^{\infty} \textbf{q}_{\textbf{k}_{i}} $$
(27)
$$ A_{k_{n}}= N \textbf{q}_{\textbf{k}}= \sum\limits_{p=1}^{2} \sum\limits_{i=0}^{n}\sum\limits_{j=0}^{i}\sum\limits_{l=0}^{i}\textbf{q}_{\textbf{p}_{i-j-l}}\textbf{q}_{\textbf{p}^{*}_{j}}\textbf{q}_{k_{l}} $$
(28)

Dark solitary wave solution

Following (24) (with β 2 = 1) let

$$\textbf{q}_{\textbf{k}_{0}}= q_{k}(0,t)=\frac{C_{k} \eta}{\sqrt{\gamma}}Tanh(\eta t + \phi_{0}) $$

Then \(\textbf {q}_{\textbf {k}_{1}}, \textbf {q}_{\textbf {k}_{2}}, \textbf {q}_{\textbf {k}_{3}} {\cdots } \) can be calculated using (27), (24) and therefore the solution is,

$$\begin{array}{@{}rcl@{}} \textbf{q}_{\textbf{k}_{1}} &=& q_{0}(i \eta^{2} t) \\ \textbf{q}_{\textbf{k}_{2}} &=& - q_{0}\frac{\eta^{4} t^{2}}{2}\\ \textbf{q}_{\textbf{k}_{3}} &=& -q_{0}\frac{i \eta^{6} t^{4}}{4!}\\ {\vdots} & & {\vdots} \qquad \vdots \end{array} $$
$$ \textbf{q}_{\textbf{k}} = \textbf{q}_{\textbf{k}_{0}}(1 + i \eta^{2} x- \frac{\eta^{4} x^{2}}{2} - i\frac{\eta^{6} x^{4}}{4!} {\cdots} ) $$
(29)

Alternately following (25), we consider (q k (x, 0) = 0) and let the first term of the decomposition for each of the components be

$$\begin{array}{@{}rcl@{}} \textbf{q}_{1_{0}} &=& \frac{C_{1} \eta}{\sqrt{|C_{1}|^{2}+|C_{2}|^{2}}}e^{\frac{i\eta^{2} t}{2}} \eta t \end{array} $$
(30)
$$\begin{array}{@{}rcl@{}} \textbf{q}_{2_{0}} &=& \frac{C_{2} \eta}{\sqrt{|C_{1}|^{2}+|C_{2}|^{2}}}e^{\frac{i\eta^{2} t}{2}} \eta t \end{array} $$
(31)

by using (27) and (25) we get the higher components, which are:

$$\begin{array}{@{}rcl@{}} \textbf{q}_{\textbf{k}_{1}} &=& -\textbf{q}_{\textbf{k}_{0}}(\frac{\eta^{2} t^{2}}{3!})\\ \textbf{q}_{\textbf{k}_{2}} &=& \textbf{q}_{\textbf{k}_{0}}(\frac{2 \eta^{4} t^{4}}{15} )\\ \textbf{q}_{\textbf{k}_{3}} &=& -\textbf{q}_{\textbf{k}_{0}}(\frac{17\eta^{6} t^{6}}{315} ) \end{array} $$

The solution thus obtained is:

$$ \textbf{q}_{\textbf{k}}= \frac{\textbf{q}_{\textbf{k}_{0}}}{\eta t} (\eta t - \frac{\eta^{3} t^{3}}{3!}+\frac{2 \eta^{5} t^{5}}{15} -\frac{17\eta^{7} t^{7}}{315}+ \cdots) $$
(32)

It is important to note that the convergence property of the series (32) is same as (16).

Bright solitary wave solution

Following in (24) with β 2 = −1 let us assume that the first term of the decomposition be:

$${q_{k}}_{0}= q(0,t)=\frac{C_{k} \eta}{\sqrt{\gamma}}Sech (\eta t)$$

where γ = |C 1|2 + |C 2|2. Then we get \( \textbf {q}_{\textbf {k}_{1}}, \textbf {q}_{\textbf {k}_{2}}, \textbf {q}_{\textbf {k}_{3}} {\cdots } \)

$$\begin{array}{@{}rcl@{}} \textbf{q}_{\textbf{k}_{1}} &=& \textbf{q}_{\textbf{k}_{0}} (i \frac{\eta^{2}}{2} x) \\ \textbf{q}_{\textbf{k}_{2}} &=& \textbf{q}_{\textbf{k}_{0}} (- \frac{\frac{\eta^{4}}{4} x^{2}}{2!})\\ \textbf{q}_{\textbf{k}_{3}} &=& \textbf{q}_{\textbf{k}_{0}} (- i \frac{\frac{\eta^{6}}{8} x^{3}}{3!}) \end{array} $$

Therefore the solution is

$$\textbf{q}_{\textbf{k}} = \textbf{q}_{\textbf{k}_{0}}(1 + i \frac{\eta^{2}}{2} x - \frac{\frac{\eta^{4}}{4} x^{2}}{2!} - i \frac{\frac{\eta^{6}}{8} x^{3}}{3!}\cdots) $$

Alternately we may proceed with equation (25) and consider (\(\frac {\partial \textbf {q}_{\textbf {k}}(x,t)}{\partial {t}}{|_{t=0}=0}\)) and the first term of the decomposition for each of the components are

$$\begin{array}{@{}rcl@{}} \textbf{q}_{\textbf{1}_{0}} &=& \frac{C_{1} \eta}{\sqrt{|C_{1}|^{2}+|C_{2}|^{2}}}e^{\frac{i(\eta^{2} x + \phi_{1})}{2}}\\ \textbf{q}_{\textbf{2}_{0}} &=& \frac{C_{2} \eta}{\sqrt{|C_{1}|^{2}+|C_{2}|^{2}}}e^{\frac{i(\eta^{2} x + \phi_{2})}{2}} \end{array} $$

where C 1 and C 2 are complex constants and ϕ 1 and ϕ 2 are real constants describing the polarization. By using (25), (27) and (β 2 = −1) we get the higher components,

$$\begin{array}{@{}rcl@{}} q_{k_{1}} &=& - \textbf{q}_{\textbf{k}_{0}}\frac{\eta^{2} t^{2}}{2} \\ q_{k_{2}} &=& \textbf{q}_{\textbf{k}_{0}}\frac{5 \eta^{4} t^{4}}{4!}\\ q_{k_{3}} &=& -\textbf{q}_{\textbf{k}_{0}}\frac{61 \eta^{6} t^{6}}{6!} \end{array} $$

Thus the solution obtained by the decomposition method is:

$$ \textbf{q}_{\textbf{k}}= \textbf{q}_{\textbf{k}_{0}}(1-\frac{ \eta^{2} t^{2}}{2} + \frac{5 \eta^{4} t^{4}}{4!} +\frac{61 \eta^{6} t^{6}}{6!}+ {\cdots} ) $$
(33)

It is important to note that convergence property of (33) is similar to that of (19). It is straightforward to extend the methodology for the n-coupled NLS equation by considering k = 1, 2, ⋯n.

Discussion

To understand the results explicitly let us analyze the Adomian solution on the basis of Taylor series. Notice that the Adomian solutions (18, 19, 32, 33) are infinite series, which are similar to the Taylor Series of a function Q(x, t) (say) about the point t 0 = 0. The Taylor series expansion of the function Q(x, t) about the point t 0 is

$$ Q(x, t)=\sum\limits^{\infty}_{n=0} Q^{(n)}(x,t_{0})\frac{(t-t_{0})^{n}}{n!} $$
(34)

Following the Taylor series the Adomian solution can be written as

$$ q(x,t )= \sum\limits^{\infty}_{n=0}q_{n}(x, t)= \sum\limits^{N-1}_{n=0}q^{(n)}(x,0)\frac{t^{n}}{n!} - R_{N-1} $$
(35)

where the first term on the right hand side of (35) is the N-term Adomian solution and the term R N−1 is the known as the Lagrange reminder, which gives the estimate of error and is given by,

$$ R_{N-1} = \frac{t^{N}}{N!}q^{(N)}(t^{\ast})\qquad t^{\ast} \in [0,t]; N \geq 1 $$
(36)

The value of R N−1 can be calculated by using the mean value theorem [28]. From (36) it is evident that for the values of |t| nearing zero the adomian solution coincides with the exact result, as |t| moves further and further from zero error becomes greater and greater. Then the number of iterations (N) should be increased for better approximation. Figure 1. and Fig. 2., which compare the exact result with Adomian solutions reflect the similar fact.

The method described in this paper is also applicable to other cases of NLS equation. For example, in [29] the present authors have shown another application of Adomian method considering one particular case of HNLS equation, namely the Hirota equation and have shown that with a suitable initial condition ADM method generates a series which converges to the actual solution of the equation after infinite iteration.

Inspite of the fact that adomian method can generate solitary wave solution as other methods and more efficient than other series methods and numerical methods still it is not a substitute of analytical methods such as IST method, Darbaux Transform method or Hirota bilinear method, specially the N-soliton solution is not very simple to find using the Adomian method, in this area the method needs further improvement.

Conclusion

In this paper we have presented a general decomposition algorithm for the NLS equation giving both dark and bright solitary wave solutions. We show that the critical pulse shape of fundamental dark (β 2 = 1) and bright (β 2 = −1) soliton can be generated following decomposition method with a suitable initial or boundary condition. We have also proposed a generalized decomposition method for the coupled nonlinear schrödinger (CNLS) equation and obtained soliton like solutions. The results obtained here demonstrate the reliability of the method and suggests a wider applicability of the method to a class of nonlinear models in optics.