Abstract
Finding the number of limit cycles, as described by Poincaré (Memoire sur les coubes definies par une equation differentielle, Editions Jacques Gabay, Sceaux, 1993), is one of the main problems in the qualitative theory of real planar differential systems. In general, studying limit cycles is a very challenging problem that is frequently difficult to solve. In this paper, we are interested in finding an upper bound for the maximum number of limit cycles bifurcating from the periodic orbits of a given discontinuous piecewise differential system when it is perturbed inside a class of polynomial differential systems of the same degree, by using the averaging method up to third order. We prove that the discontinuous piecewise differential systems formed by a linear focus or center and a cubic weak focus or center separated by one straight line \( y=0\) can have at most 7 limit cycles.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In this paper, we deal with polynomial differential systems in \(\mathbb {R}^2\) of the form
where the degree of the systems is the maximum degree of P and Q. The second part of the 16th Hilbert problem [7, 9] proposes to find an upper bound for the maximum number of limit cycles and relative configurations for the differential system (1). We recall that a limit cycle of the differential system (1) is an isolated periodic orbit in the set of all periodic orbits of the system.
The study of the limit cycles of piecewise differential systems has recently gained much attention in the qualitative theory of differential equations. The 16th Hilbert problem, which many writers have studied, involves determining the maximum number of limit cycles that a polynomial differentiation system of a specific order can have. See for example [8].
To study the periodic solutions of differential systems, the averaging theory is a useful tool; see for instance the books of Sanders, Verhulst, and Murdock [18] and Llibre Moeckel-Simó [15]. This method has a long history, dating back to the classical works of Lagrange and Laplace, who intuitively justified the process. In 1928, Fatou [4] formalized this theory. Significant practical and theoretical contributions to the averaging method were made in 1930s by Bogoliubov-Krylov [3] and in 1945 by Bogoliubov. This technique, originally created for smooth systems, has recently been applied to research on limit cycle of discontinuous piecewise smooth systems, see [14, 19]. The authors of the articles [6, 13] developed the averaging method for discontinuous piecewise differential systems and showed a relationship between the number of limit cycles of the corresponding differential system and the zeros of the averaged functions of periodic differential equations, see for instance [5, 11]. In 2022 Baymout and Benterki [1] proved that five is the maximum number of limit cycles that can bifurcate from the discontinuous piecewise differential systems formed by an arbitrary linear focus or center and an arbitrary cubic uniform isochronous center separated by a straight line, by using the averaging theory up to seven-order.
The objective of this paper is to study the limit cycles that can bifurcate from the discontinuous piecewise differential systems separated by the straight line \(y=0\) and formed by a linear differential system having a center or focus of the form
defined in the half-plane \(y \ge 0\), where \(\alpha \), \(\beta \), \(\gamma \), and \(\delta \in \mathbb {R}\), and by an arbitrary cubic weak focus or center located at the origin given by
defined in the half-plane \(y \le 0\), where all the parameters of the system are real.
The averaging theory described in "Third Order Averaging Theory for Computing Limit Cycles" section allows to study analytically the existence of limit cycles of a non-autonomous differential system, by studying the simple zeros of the averaged function. Here we shall use the averaging theory up to the third order for studying the number of limit cycles that can bifurcate from the discontinuous piecewise differential systems formed by (2) for \(y\ge 0\), when we perturb it inside the class of all polynomial differential systems of degree 1 as follows
and by the differential system (3) for \(y\le 0\) when we perturb it inside the class of all polynomial differential systems of degree 3 as follows
Here \(\varepsilon >0\) is a small parameter, \(i=1,\dots ,3\), \(P_{1i}\) and \(Q_{1i}\), are real polynomials of degree 1 in the variables x and y, and \(P_{3i}\), \(Q_{3i}\) are real polynomials of degree 3 in the variables x and y.
The main result of our paper focuses on determining the maximum number of limit cycles using the averaging theory up to third order, which is presented in the following Theorem.
Theorem 1
For \(|\varepsilon | \ne 0\) sufficiently small and by using the averaging theory up to third order the maximum number of limit cycles of the discontinuous piecewise differential systems formed by linear differential focus or center (2) and the cubic weak focus or center (3) is at most seven. There are examples with exactly seven limit cycles bifurcating from the periodic orbits of these systems.
Third Order Averaging Theory for Computing Limit Cycles
In this section we summarise the basic results of the classical averaging theory that we will use to study the number of limit cycles of discontinuous piecewise differential systems, for more details see [10].
We consider the following discontinuous differential system
where \( F^\pm (\theta ,r,\varepsilon )= \sum _{i=0} ^3 \varepsilon ^i F_i ^\pm (\theta ,r) + \varepsilon ^4 R^\pm (\theta ,r,\varepsilon )\), \(\theta \in \mathcal {S}^1 \) and \(r\in D\) where D is an open interval of \(\mathbb {R}^+.\)
A fundamental inquiry in the investigation of discontinuous differential systems (6) revolves around comprehending which periodic orbits of the unperturbed system \( \dot{r}(\theta )=F^\pm (\theta ,r)\) persists for \(|\varepsilon |\ne 0\) sufficiently small. To address this, we introduce a set of functions \(f_i: D \longrightarrow \mathbb {R}\), for \(i = 1, 2, \dots , k,\) called averaged functions, such that their simple zeros provide the existence of isolated periodic solutions of the differential equation (6). In [12] it was proved that these averaged functions are given by \(f_i=\dfrac{y_i(2\pi ,r)}{i!}\) where \(y_i: \mathbb {R} \times D \rightarrow \mathbb {R}\), are defined by the following integrals
Also, we have the functions
For more details see [10].
The averaged function of order k is the function \(f_k(r) =f_k^{+}(r)+f_k^{-}(r)\). The simple positive real roots of the functions \(f_{l+1}(r)\) which satisfy \(f_l(r) = 0\) for \(l \in \{1, 2\}\) but \(f_{l+1}(r)\ne 0\), provide limit cycles of the piecewise differential system (6).
We need to state the following lemma and Descartes Theorem in order to demonstrate our results regarding the number of zeros in a real polynomial.
Lemma 2
Consider \(p + 1\) linearly independent functions \(f_i: U \subset \mathbb {R} \rightarrow \mathbb {R},\) \(i = 0, 1, \dots , p\)
-
(i)
Given p arbitrary values \(x_i \in U,\) \(i = 1,\dots , p\) there exist \(p + 1\) constants \(C_i,\) \(i = 0, 1,\dots , p\) such that
$$\begin{aligned} f (x):= \sum _{i=0}^{p} C_i f_i(x) \end{aligned}$$(7)is not the zero function and \(f (x_i) = 0\) for \(i = 0,\) \(1,\dots , p.\)
-
(ii)
Furthermore, if all \(f_i\) are analytical functions on U and it exists \(j \in \lbrace 1,\dots , p\rbrace \) such that \(f_j|U\) has constant sign, it is possible to get an f given by (7), such that it has at least p simple zeroes in U.
For a proof, see Proposition 1 of [16].
Theorem 3
(Descartes Theorem) Consider the real polynomial \(r(x)=a_{i_1}x^{i_1}+a_{i_2}x^{i_2}+\ldots +a_{i_r}x^{i_r}\) with \(0=i_1<i_2<\ldots <i_r\) and \(a_{i_j}\ne 0\) real constant for \(j\in \{ 1,\ldots ,r\}\). When \(a_{i_j}a_{i_{j+1}<0}\), we say that \(a_{i_j}\) and \(a_{i_{j+1}}\) have a variation of the sign. If the number of variations of signs is m, then r(x) has at most m positive real roots. Moreover, it is always possible to choose the coefficients of r(x) in such a way that r(x) has exactly \(r -1\) positive real roots.
For more details see [2].
Proof of Theorem 1
In order to apply the averaging method for studying the limit cycles for \(\varepsilon \) sufficiently small, we need to write systems in the standard form. So we have developed the parameters of the differential systems until the third order in \(\varepsilon \). To ensure that the origin of system (2) is a center, we must add \(-1\) with regard to the growth of \(\beta \). Then in \(y\ge 0\) we have the following system
with \( \begin{array}{llll} \alpha =\alpha _1 \varepsilon +\alpha _2 \varepsilon ^2+\alpha _3 \varepsilon ^3, \qquad \beta =-1+\beta _1 \varepsilon +\beta _2 \varepsilon ^2+\beta _3 \varepsilon ^3,\\ \gamma =\gamma _1 \varepsilon +\gamma _2 \varepsilon ^2+\gamma _3 \varepsilon ^3, \quad \,\, \quad \delta =\delta _1 \varepsilon +\delta _2 \varepsilon ^2+\delta _3 \varepsilon ^3.\\ \end{array} \)
Then the perturbed system of system (2) is given by
According to system (4) we know that \(\begin{array}{ll} P_{1 1}(x,y)=\alpha _1 x +\beta _1 y+\gamma _1, \hspace{0.2cm} P_{1 2}(x,y)=\alpha _2 x +\beta _2 y+\gamma _2, \hspace{0.2cm} P_{1 3}(x,y)=\alpha _3 x +\beta _3 y+\gamma _3,\\ Q_{1 1}(x,y)=-\beta _1 x+\alpha _1 y+\delta _1,\hspace{0.12cm} Q_{1 2}(x,y)= -\beta _2 x+\alpha _2 y+\delta _2, \hspace{0.12cm} Q_{1 3}(x,y)= -\beta _3 x+\alpha _3 y+\delta _3. \end{array}\)
In \(y\le 0\) we have the differential system
Where \(\begin{array}{ll} a=a_1 \varepsilon +a_2 \varepsilon ^2+a_3 \varepsilon ^3, \qquad c=c_1 \varepsilon +c_2 \varepsilon ^2+c_3 \varepsilon ^3, \qquad p=p_1 \varepsilon +p_2 \varepsilon ^2+p_3 \varepsilon ^3,\\ z=z_1 \varepsilon +z_2 \varepsilon ^2+z_3 \varepsilon ^3, \qquad k=k_1 \varepsilon +k_2 \varepsilon ^2+k_3 \varepsilon ^3,\qquad m=m_1 \varepsilon +m_2 \varepsilon ^2+m_3 \varepsilon ^3,\\ h=h_1 \varepsilon +h_2 \varepsilon ^2+h_3 \varepsilon ^3, \qquad g=g_1 \varepsilon +g_2 \varepsilon ^2+g_3 \varepsilon ^3,\qquad d=d_1 \varepsilon +d_2 \varepsilon ^2+d_3 \varepsilon ^3,\\ b=b_1 \varepsilon +b_2 \varepsilon ^2+b_3 \varepsilon ^3,\qquad w=w_1 \varepsilon +w_2 \varepsilon ^2+w_3 \varepsilon ^3,\qquad q=q_1 \varepsilon +q_2 \varepsilon ^2+q_3 \varepsilon ^3,\\ n=n_1 \varepsilon +n_2 \varepsilon ^2+n_3 \varepsilon ^3,\qquad l=l_1 \varepsilon +l_2 \varepsilon ^2+l_3 \varepsilon ^3,\qquad \end{array}\)
Then the perturbed system of system (3) is given by
According to system (5) we know that \(\begin{array}{ll} P_{3 1}(x,y)= -a_1 x^2 -c_1 x y-z_1 y^2-k_1 x^3-m_1 x^2 y-p_1 x y^2-h_1 y^3,\\ P_{3 2}(x,y)=-a_2 x^2 -c_2 x y-z_2 y^2-k_2 x^3-m_2 x^2 y-p_2 x y^2-h_2 y^3,\\ P_{3 3}(x,y)=-a_3 x^2 -c_3 x y-z_3 y^2-k_3 x^3-m_3 x^2 y-p_3 x y^2-h_3 y^3,\\ Q_{3 1}(x,y)=b_1 y^2+d_1 x y+g_1 x^2+l_1 y^3+n_1x y^2+q_1 x^2 y+w_1 x^3,\\ Q_{3 2}(x,y)=b_2 y^2+d_2 x y+g_2 x^2+l_2 y^3+n_2 x y^2+q_2 x^2y+w_2 x^3,\\ Q_{3 3}(x,y)=b_3 y^2+d_3 x y+g_3 x^2+l_3 y^3+n_3 x y^2+q_3 x^2 y+w_3 x^3. \end{array}\)
We compute the averaged function \(f_i(r)\), for \(i = 1\) we get
By using Descartes Theorem we know that the polynomial \(f_1(r)\) can have at most three positive real roots, which provide three limit cycles for the discontinuous piecewise differential system (2)-(3).
In order to apply the averaging theory of second order we need that \(f_1(r) \equiv 0\). So we must take \(c_1=2 b_1+g_1\), \(p_1=-3 k_1+3 l_1+q_1\), \(\delta _1=0\), \(\alpha _1=0\). Computing the function \(f_2(r)\) we get \(\begin{array}{ll} f_2(r)=&{}\dfrac{1}{16} \pi r^5(h_1 (q_1-3 k_1)+k_1 (-m_1+n_1+3 w_1)+2 l_1 m_1-2 l_1 n_1+m_1 q_1-n_1 q_1\\ &{}-q_1 w_1)+\dfrac{2}{15} r^4 (a_1 (3 k_1-4 l_1-3 q_1)-4 b_1 m_1+4 b_1 n_1-3 d_1 k_1+2 d_1 l_1+2 d_1 q_1\\ &{}+g_1 (-2 h_1-3 m_1+2 n_1+3 w_1)+6 k_1 z_1-2 q_1 z_1)+\dfrac{1}{8} \pi r^3 (2 a_1 b_1+3 a_1 g_1-b_1 d_1\\ &{}-d_1 g_1+g_1 z_1-3 k_2+3 l_2-p_2+q_2)-\dfrac{2}{3} r^2 (2 b_2-c_2+g_2)+\pi \alpha _2 r+2 \delta _2. \end{array}\)
This polynomial can have at most five positive real roots, which provide at most five limit cycles for the discontinuous piecewise differential system (2)-(3).
In order to apply the averaging theory of third order we need to have \(f_2(r) \equiv 0\), for that we must take \(\begin{array}{ll} w_1=&{}- \dfrac{1}{g_1 (3 k_1-q_1)} \Big ((3 k_1-q_1) (a_1 (3 k_1-4 l_1-3 q_1)-4 b_1 m_1+4 b_1 n_1+d_1 (2 (l_1+q_1)\\ {} &{}-3 k_1)-3 g_1 m_1 +2 g_1 n_1+6 k_1 z_1-2 q_1 z_1)+2 g_1(m_1-n_1) (k_1-2 l_1-q_1)\Big ), \\ c_2=&{} 2 b_2+g_2, p_2=a_1 (2 b_1+3 g_1)-d_1 \left( b_1+g_1\right) +g_1 z_1-3 k_2+3 l_2+q_2, \alpha _2=0, \\ h_1=&{}-\dfrac{1}{g_1 (3 k_1-q_1)}\Big (a_1 (3 k_1 -q_1)(3 k_1-4 l_1-3 q_1)-12 b_1 k_1 m_1+12 b_1 k_1 n_1\\ {} &{}+4 b_1 m_1 q_1 -4 b_1 n_1 q_1-d_1 (3 k_1-q_1) (3 k_1-2 (l_1+q_1))-6 g_1 k_1 m_1+3 g_1 k_1 n_1\\ {} &{}-6 g_1 l_1 m_1+6 g_1 l_1 n_1+g_1 n_1 q_1+2 z_1 (q_1-3 k_1){}^2\Big ), \delta _2=0. \end{array}\)
For \(w_1\) and \(h_1\) we considered four cases \(g_1 (3k_1-q_1) \ne 0\), \(g_1=0 \) and \(3k_1-q_1\ne 0\), \(g_1\ne 0\) and \(3k_1-q_1= 0\) or \(g_1=0\) and \(3k_1-q_1= 0\). We start with the first case \(g_1 (3k_1-q_1)\ne 0\).
Case 1. \(g_1 (3k_1-q_1)\ne 0\). Computing the function \(f_3(r)\) we obtain
Where \(\begin{array}{ll} A_1=&{}\dfrac{1}{64 g_1 \left( 3 k_1-q_1\right) }\Big (\pi (k_1-5 l_1-2 q_1) ((3 k_1-q_1) (m_1-n_1) (a_1 (3 k_1-4 l_1-3 q_1)\\ {} &{}-4 b_1 m_1 +4 b_1 n_1+d_1 (-3 k_1+2 l_1+2 q_1)+6 k_1 z_1-2 q_1 z_1)+g_1 (k_1 (6 l_1 q_1+12 m_1 n_1\\ {} &{}-6 m_1^2-6 n_1^2+q_1^2)-3 k_1^2 (3 l_1+2 q_1)+9 k_1^3-l_1 (-8 m_1 n_1+4 m_1^2+4 n_1^2+q_1^2)))\Big ),\\ A_2=&{}\dfrac{1}{105 g_1 \left( q_1-3 k_1\right) {}^2}\Big (2 ((297 k_1^4-36 (9 l_1+7 q_1) k_1^3+3 (72 l_1^2+132 q_1 l_1-32 m_1^2-32 n_1^2\\ &{}+23 q_1^2+64 m_1 n_1) k_1^2-6 (24 q_1 l_1^2+2 (4 m_1^2-8 n_1 m_1+4 n_1^2+13 q_1^2) l_1+q_1 (-8 m_1^2\\ &{}+16 n_1 m_1-8 n_1^2+q_1^2)) k_1+4 l_1 (6 l_1 (2 m_1^2-4 n_1 m_1+2 n_1^2+q_1^2)+q_1 (12 m_1^2-24 n_1 m_1\\ &{}+12 n_1^2+5 q_1^2))) g_1^2+4 (m_1-n_1) (3 k_1-q_1) (d_1 (-15 k_1^2+33 l_1 k_1+24 q_1 k_1-6 q_1^2\\ &{}-10 l_1 q_1)+a_1 (12 k_1^2-3 (13 l_1+8 q_1) k_1+q_1 (11 l_1+6 q_1))+2 (3 k_1-q_1) (3 k_1-4 l_1\\ \end{array}\) \(\begin{array}{ll} &{}-3 q_1) z_1) g_1-48 b_1^2 (m_1-n_1){}^2 (q_1-3 k_1){}^2+2 (q_1-3 k_1){}^2 (2 (3 l_1+q_1)(3 k_1-4 l_1-3 q_1)\\ &{}a_1^2+((3 k_1-q_1)(3 k_1+8 l_1+q_1) z_1-d_1 (9 k_1-8 l_1-7 q_1) (3 l_1+q_1)) a_1+2 (q_1-3 k_1){}^2 \\ &{}z_1^2+d_1^2 (3 l_1+q_1)(3 k_1-2 (l_1+q_1))-d_1 (3 k_1+4 l_1) (3 k_1-q_1) z_1)+2 b_1 (q_1-3 k_1){}^2 (g_1 \\ &{}(27 k_1^2-3 (12 l_1+5 q_1) k_1+2 (-12 m_1^2+24 n_1 m_1-12 n_1^2+q_1^2+6 l_1 q_1))+2 (m_1-n_1) \\ {} &{}(-9 d_1 k_1+12 z_1 k_1+12 d_1 l_1+8 d_1 q_1+a_1 (9 k_1-24 l_1-13 q_1)-4 q_1 z_1)))\Big ),\\ \end{array}\) \(\begin{array}{ll} A_3=&{}\dfrac{1}{16 g_1 \left( 3 k_1-q_1\right) }\Big (\pi (2 (3 k_1-q_1) (b_1 (3 k_1-4 l_1-3 q_1)+g_1 (8 k_1-11 l_1-8 q_1)) a_1^2\\ {} &{}+(-8(m_1-n_1) (3 k_1-q_1) b_1^2+(4 (z_1 (q_1-3 k_1){}^2+g_1 (-20 k_1 m_1-2 l_1 m_1+6 q_1 m_1\\ &{}+17 k_1 n_1+2 l_1 n_1-5 n_1 q_1))-d_1 (9 k_1-8 l_1-7 q_1) (3 k_1-q_1)) b_1+g_1(-d_1 (3 k_1-q_1)\\ &{}(21 k_1-17 l_1-15 q_1)+g_1 (-37 k_1 m_1-16 l_1 m_1+7 q_1 m_1+19 k_1 n_1+16 l_1 n_1-n_1 q_1)\\ &{}+(3 k_1-q_1)(39 k_1-10 l_1-17 q_1) z_1)) a_1+b_1^2 (3 k_1-q_1) (3 g_1 k_1+4 d_1 m_1-4 d_1 n_1\\ &{}-g_1 q_1)+g_1 ((3 k_1 -q_1) (5 k_1-3 (l_1+q_1)) d_1^2+(g_1 (6 l_1 (m_1-n_1)+k_1 (9 m_1-3 n_1)\\ &{}-(m_1+n_1) q_1)-(18 k_1-5 l_1-8 q_1) (3 k_1-q_1) z_1) d_1-9 h_2 k_1^2-h_2 q_1^2-m_2 q_1^2+n_2 q_1^2\\ &{}+45 k_1^2 z_1^2+5 q_1^2 z_1^2-30 k_1 q_1 z_1^2-6 k_2 l_1 m_1+6 k_1 l_2 m_1-3 k_1^2 m_2+6 k_1 l_1 m_2+6 k_2 l_1 n_1\\ &{}-6 k_1 l_2 n_1+3 k_1^2 n_2-6 k_1 l_1 n_2-2 g_1^2(k_1+l_1) (3 k_1-q_1)+6 h_2 k_1 q_1-2 k_2 m_1 q_1-2 l_2 m_1 q_1\\ &{}+4 k_1 m_2 q_1-2 l_1 m_2 q_1+2 k_2 n_1 q_1+2 l_2 n_1 q_1-4 k_1 n_2 q_1+2 l_1 n_2 q_1+2 k_1 m_1 q_2+2 l_1 m_1 q_2\\ &{}-2 k_1 n_1 q_2-2 l_1 n_1 q_2+9 k_1^2 w_2+q_1^2 w_2-6 k_1 q_1 w_2+g_1 (-10 l_1 (m_1-n_1)+k_1 (7 n_1\\ {} &{} -13 m_1)+(m_1+n_1) q_1) z_1)+b_1 ((3 k_1-q_1) (3 k_1-2 (l_1+q_1)) d_1^2+(g_1 (25 k_1 m_1+4 l_1 m_1\\ &{}-7 q_1 m_1-19 k_1 n_1-4 l_1 n_1+5 n_1 q_1)-2 (q_1-3 k_1){}^2z_1) d_1+g_1 (3 k_1-q_1) (g_1 (3 k_1-5 l_1\\ &{}-2 q_1)+10 (n_1-m_1) z_1)))\Big ),\\ \end{array}\) \(\begin{array}{ll} A_4=&{}\dfrac{1}{15g_1}\Big (2 (a_1 (4 b_1 d_1 g_1+6 d_1 g_1^2+3 g_1 k_2-3 g_2 k_1-4 g_1 l_2+4 g_2 l_1-3 g_1 q_2+3 g_2 q_1\\ {} &{}-6 g_1^2 z_1)+3 a_2 g_1 k_1-4 a_2 g_1 l_1-3 a_2 g_1 q_1-3 a_1^2 g_1^2+b_1 (4 (-g_1 m_2+g_2 m_1+g_1 n_2\\ {} &{}-g_2 n_1+g_1^3)-2 d_1^2 g_1)-4 b_2 g_1 m_1+4 b_2 g_1 n_1+4 b_1^2 g_1^2-3 d_2 g_1 k_1-3 d_1 g_1 k_2\\ {} &{}+3 d_1 g_2 k_1+2 d_2 g_1 l_1+2 d_1 g_1 l_2-2 d_1 g_2 l_1+2 d_2 g_1 q_1+2 d_1 g_1 q_2-2 d_1 g_2 q_1\\ {} &{}+2 d_1 g_1^2 z_1-2 d_1^2 g_1^2-2 g_1^2 h_2+6 g_1 k_2 z_1+6 g_1 k_1 z_2-6 g_2 k_1 z_1-3 g_1^2 m_2+2 g_1^2 n_2\\ {} &{}-2 g_1 q_2 z_1-2 g_1 q_1 z_2+2 g_2 q_1 z_1+3 g_1^2 w_2)\Big ),\\ A_5=&{}\dfrac{\pi }{8}\Big (2 a_2 b_1+2 a_1 b_2+3 a_2 g_1+3 a_1 g_2-b_1 d_2-b_2 d_1-d_2 g_1-d_1 g_2+g_2 z_1+g_1 z_2\\ {} &{}-3 k_3+3 l_3-p_3+q_3\Big ). \end{array}\)
Since the rank of the Jacobian matrix of the function \(\mathcal {A} = (A_1,\dots A_5, -\dfrac{2}{3}\left( 2 b_3-c_3+g_3\right) , \pi \alpha _3,2\delta _3 )\) with respect to its parameters which appear in their expressions is maximal, i.e. it is 8. In view of Lemma 2, we conclude that the maximum number of real solutions of the equation \(f_3(r) = 0\) is at most seven. Now by using Descartes Theorem we conclude that the function \(f_3(r) = 0\) can have at most seven positive solutions. Therefore the averaging theory up to third order can provide at most seven limit cycles for the discontinuous piecewise differential system (2)-(3).
Now we consider the second case.
Case 2. \(g_1 =0\) and \(q_1\ne 3k_1\). Computing the function \(f_2(r)\) we obtain
So the polynomial \(f_2(r)\) can have at most five positive real roots and produce at most five limit cycles for the discontinuous piecewise differential system (2)-(3) when \(\varepsilon \) is sufficiently small. In order to apply the averaging theory of third order we put \(f_2(r) \equiv 0\). So we need to consider \(\begin{array}{ll} c_2=&{} 2 b_2+g_2, p_2=a_1 c_1-b_1 d_1-3 k_2+3 l_2+q_2, \alpha _2=0, \delta _2=0,\\ w_1=&{}\dfrac{1}{4 b_1 (3 k_1-q_1)} \Big ((k_1-2 l_1-q_1) (a_1 (3 k_1-4 l_1-3 q_1)+d_1 (2 (l_1+q_1)-3 k_1)+6 k_1 z_1\\ &{}-2 q_1 z_1)+4 b_1 h_1 (3 k_1-q_1)\Big ),\\ m_1= &{}\dfrac{1}{4 b_1}\Big (a_1 (3 k_1-4 l_1-3 q_1)+4 b_1 n_1+d_1 (2 (l_1+q_1)-3 k_1)+6 k_1 z_1-2 q_1 z_1\Big ). \end{array}\)
From the expression of \(f_2(r)\) we distinguish immediately two subcases \(b_1\ne 0\) or \(b_1=0\).
Subcase 2.1. \(b_1\ne 0\). Computing \(f_3(r)\) we get
Where \(\begin{array}{ll} B_1=&{} \dfrac{\pi }{512 b_1^2 \left( 3 k_1-q_1\right) }(k_1-5 l_1-2 q_1) (-2 a_1 (3 k_1-4 l_1-3 q_1) (b_1 (h_1-n_1) (3 k_1\\ &{}-q_1)+l_1 (d_1 (3 k_1-2 (l_1+q_1)t)+2 z_1 (q_1-3 k_1)))+a_1^2 l_1 (-3 k_1+4 l_1+3 q_1)^2\\ &{}+8 b_1^2 (k_1-l_1)(q_1-3 k_1){}^2+c_1 h_1-n_1) (3 k_1-q_1) d_1 (3 k_1-2 l_1+q_1))+2 z_1 q_1\\ &{}-3 k_1))+l_1 (d_1 (2 (l_1+q_1)-3 k_1)+6 k_1 z_1-2 q_1 z_1){}^2),\\ B_2=&{}\dfrac{1}{105 b_1 (3 k_1-q_1)} \Big (-2 a_1 (b_1 (h_1-n_1) (-24 k_1 q_1+27 k_1^2+5 q_1^2)+d_1 (3 k_1^2 (8 l_1\\ {} &{}+q_1)-3 k_1 (15 l_1 q_1+5 l_1^2+3 q_1^2)+q_1 (29 l_1 q_1+25 l_1^2+6 q_1^2))+z_1 (3 k_1-q_1)\\ &{}(-33 k_1 l_1-9 k_1 q_1+3 k_1^2+29 l_1 q_1+16 l_1^2+6 q_1^2))+a_1^2 (k_1^2 (75 l_1+36 q_1)-3 k_1\\ {} &{}(50 l_1 q_1+28 l_1^2+15 q_1^2)-9 k_1^3+q_1 (75 l_1 q_1+68 l_1^2+18 q_1^2))+4 b_1^2 (q_1-3 k_1){}^2\\ \end{array}\) \(\begin{array}{ll} &{}(9 k_1-2 (6 l_1+q_1))+c_1 (h_1-n_1) (3 k_1-q_1) (d_1 (9 k_1-4 q_1)+8 z_1 (q_1-3 k_1))\\ &{}+90 d_1 k_1 l_1 q_1 z_1+6 d_1^2 k_1 l_1 q_1-54 d_1 k_1^2 l_1 z_1+48 d_1 k_1 l_1^2 z_1-15 d_1^2 k_1^2 l_1+6 d_1^2 k_1 l_1^2\\ &{}+42 d_1 k_1^2 q_1 z_1-12 d_1 k_1 q_1^2 z_1-24 d_1^2 k_1^2 q_1+12 d_1^2 k_1 q_1^2-18 d_1 k_1^3 z_1+9 d_1^2 k_1^3\\ &{}-24 d_1 l_1 q_1^2 z_1-16 d_1 l_1^2 q_1 z_1+8 d_1^2 l_1 q_1^2+8 d_1^2 l_1^2 q_1-96 k_1 l_1 q_1 z_1^2+144 k_1^2 l_1 z_1^2\\ &{}+16 l_1 q_1^2 z_1^2\Big ),\\ B_3=&{}\dfrac{-\pi }{64 b_1 (3 k_1-q_1)}\Big ( a_1 (b_1 (2 z_1 (3 k_1-q_1) (5 k_1-4 l_1-5 q_1)-d_1 (-26 k_1 l_1\\ &{}-22 k_1 q_1+9 k_1^2+22 l_1 q_1+16 l_1^2+9 q_1^2))+8 b_1^2 (h_1+n_1) (3 k_1-q_1)-2 (3 k_1\\ &{}-4 l_1-3 q_1) (-k_2 (3 l_1+q_1)+3 k_1 l_2+k_1 q_2-l_2 q_1+l_1 q_2))+4 a_1^2 b_1 (-5 k_1 (l_1\\ &{}+q_1)+3 k_1^2+5 l_1 q_1+4 l_1^2+2 q_1^2)+b_1 (2 d_1 z_1 (3 k_1-q_1) (2 k_1+2 l_1+q_1)\\ &{}+d_1^2 (-8 k_1 l_1-3 k_1 q_1-3 k_1^2+6 l_1 q_1+4 l_1^2+2 q_1^2)+4 (3 k_1-q_1) (3 h_2 k_1\\ &{}-h_2 q_1+k_1 m_2-k_1 n_2-3 k_1 w_2-2 l_1 m_2+2 l_1 n_2-m_2 q_1+n_2 q_1+q_1 w_2))\\ &{}-4 b_1^2 d_1 (h_1+n_1) (3 k_1-q_1)-4 b_1^3 (q_1-3 k_1){}^2+2 (k_2 (3 l_1+q_1)-k_1 (3 l_2\\ &{}+q_2)+l_2 q_1-l_1 q_2) (d_1 (2 (l_1+q_1)-3 k_1)+6 k_1 z_1-2 q_1 z_1)\Big ),\\ \end{array}\) \(\begin{array}{ll} B_4=&{}\dfrac{1}{15 b_1 (3 k_1-q_1)}\Big (a_1 (8 b_1^2 d_1 (3 k_1-q_1)+(3 k_1-4 l_1-3 q_1) (-b_2 (6 k_1-2 q_1)\\ &{}-3 g_2 (k_1+l_1))+c_1 (3 k_1-q_1) (3 k_2-4 l_2-3 q_2))+c_1 (3 k_1-q_1) (a_2 (3 k_2\\ &{}-4 l_1-3 q_1)-3 d_1 k_2+2 d_1 l_2+2 d_1 q_2-3 d_2k_1+2 d_2 l_1+2 d_2 q_1+g_2 h_1\\ \end{array}\) \(\begin{array}{ll} \hspace{0.9cm} &{}-n_1)+6 k_1 z_2+6 k_2z_1-2 q_1 z_2-2 q_2z_1)+(b_2 (6 k_1-2 q_1)+3 g_2 (k_1+l_1)) \\ &{}(d_1 (3 k_1-2 (l_1+q_1))+2 z_1 (q_1-3 k_1))-4 b_1^2 (3 k_1-q_1) (d_1^2+2 m_2-2 n_2)\Big ) ,\\ \end{array}\) \(\begin{array}{ll}B_5=&\dfrac{\pi }{8}(2 a_1 b_2+3 a_1 g_2+a_2 c_1-b_2 d_1-b_1 d_2-d_1 g_2+g_2 z_1-3 k_3+3 l_3-p_3+q_3). \end{array}\)
In the similar way in the proof of Case 1 and according to Descartes Theorem, we know that the function \(f_3(r)\) can have at most seven positive real roots, which provide at most seven limit cycles.
Subcase 2.2. If \(b_1=0\) the polynomial function \(f_2(r)\) becomes
This function can have at most five positive real roots. We should have \(f_2(r) \equiv 0\) to apply the averaging theory of the third order. So we need to take \(\begin{array}{ll} z_1=&{}\dfrac{a_1 \left( -3 k_1+4 l_1+3 q_1\right) +d_1 \left( 3 k_1-2 \left( l_1+q_1\right) \right) }{6 k_1-2 q_1}, \alpha _2=0, \delta _2=0,\\ \end{array}\) \(\begin{array}{ll} c_2=&2 b_2+g_2, p_2=-3 k_2+3 l_2+q_2, w_1=h_1+\dfrac{2 \left( k_1+l_1\right) \left( m_1-n_1\right) }{q_1-3 k_1}+m_1-n_1. \end{array}\)
Computing \(f_3(r)\) we get
Where \(\begin{array}{ll} C_1=&{} \dfrac{1}{64 \left( 3 k_1-q_1\right) }\Big (\pi (k_1-5 l_1-2 q_1) (k_1 (-3 h_1 m_1+3 h_1 n_1+6 l_1 q_1+3 m_1 n_1-3 n_1^2+q_1^2)\\ {} &{}+q_1 (h_1-n_1) (m_1-n_1)-3 k_1^2 (3 l_1+2 q_1)+9 k_1^3+l_1 (-4 m_1 n_1+2 m_1^2+2 n_1^2-q_1^2))\Big ),\\ \end{array}\) \(\begin{array}{ll} C_2=&{}\dfrac{1}{105 \left( 3 k_1-q_1\right) }\Big ( 2 (a_1 (h_1 (3 k_1-q_1) (3 k_1-16 l_1-7 q_1)+6 k_1 (3 l_1 m_1+5 l_1 n_1+3 m_1 q_1\\ {} &{}+n_1 q_1)-3 k_1^2 (2 m_1+n_1)-10 l_1 m_1 q_1+32 l_1^2 m_1-6 l_1 n_1 q_1-32 l_1^2 n_1-12 m_1 q_1^2\\ {} &{}+5 n_1 q_1^2)+d_1 (-h_1 (3 k_1-q_1) (3 k_1-4 (2 l_1+q_1))+3 k_1 (10 l_1 m_1-18 l_1 n_1+4 m_1 q_1\\ {} &{}-9 n_1 q_1)+k_1^2 (15 n_1-6 m_1)-4 (2 l_1+q_1) (2 l_1 m_1-2 l_1 n_1-n_1 q_1)))\Big ), \end{array}\) \(\begin{array}{ll} C_3=&{}-\dfrac{1}{64 \left( 3 k_1-q_1\right) }\Big (\pi (-2 a_1 d_1 (3 k_1 l_1+q_1 (3 l_1+2 q_1))+a_1^2 (k_1-q_1) (3 k_1-12 l_1-7 q_1)\\ {} &{}+d_1^2 k_1 (-3 k_1+6 l_1+4 q_1)-4 (h_2 (q_1-3 k_1){}^2+2 k_2 (3 l_1+q_1) (m_1-n_1)-6 k_1 l_2 m_1 \\ {} &{}-6 k_1 l_1 m_2+6 k_1 l_2 n_1+6 k_1 l_1 n_2-4 k_1 m_2 q_1-2 k_1 m_1 q_2+3 k_1^2 m_2+4 k_1 n_2 q_1+2 k_1 n_1 q_2\\ &{}-3 k_1^2 n_2+6 k_1 q_1 w_2-9 k_1^2 w_2+2 l_2 m_1 q_1+2 l_1 m_2 q_1-2 l_1 m_1 q_2-2 l_2 n_1 q_1-2 l_1 n_2 q_1\\ {} &{}+2 l_1 n_1 q_2+m_2 q_1^2-n_2 q_1^2-q_1^2 w_2))\Big ),\\ C_4=&{}-\dfrac{1}{(45 k_1-15 q_1)}\Big (2 (-a_2 (3 k_1-q_1) (3 k_1-4 l_1-3 q_1)+12 a_1 k_1 l_2-12 a_1 k_2 l_1+6 a_1 k_1 q_2\\ {} &{}-6 a_1 k_2 q_1-4 a_1 l_2 q_1+4 a_1 l_1 q_2+12 b_2 k_1 m_1-12 b_2 k_1 n_1-4 b_2 m_1 q_1+4 b_2 n_1 q_1\\ {} &{}-6 d_2 k_1 l_1-6 d_1 k_1 l_2+6 d_1 k_2 l_1-9 d_2 k_1 q_1-3 d_1 k_1 q_2+3 d_1 k_2 q_1+9 d_2 k_1^2+2 d_2 l_1 q_1\\ {} &{}+2 d_1 l_2 q_1-2 d_1 l_1 q_2+2 d_2 q_1^2+g_2 (h_1 (q_1-3 k_1)+6 k_1 m_1-3 k_1 n_1+6 l_1 m_1-6 l_1 n_1\\ {} &{}-n_1 q_1)+12 k_1 q_1 z_2-18 k_1^2 z_2-2 q_1^2 z_2)\Big ),\\ C_5=&{}\dfrac{1}{(48 k_1-16 q_1)}\Big (\pi (a_1 (12 b_2 k_1-4 b_2 q_1+15 g_2 k_1+4 g_2 l_1-3 g_2 q_1)+2 b_2 d_1 (q_1-3 k_1)\\ {} &{}-3 d_1 g_2 k_1-2 d_1 g_2 l_1+18 k_1 l_3-6 k_1 p_3+6 k_1 q_3+6 k_3 q_1-18 k_3 k_1-6 l_3 q_1+2 p_3 q_1\\ {} &{}-2 q_1 q_3)\Big ). \end{array}\)
The polynomial \(f_3(r)\) can have at most seven positive real roots, and generate when \(\varepsilon \) is sufficiently small at most seven limit cycles for the discontinuous piecewise differential system (2)-(3).
Case 3. \(g_1\ne 0\) and \(q_1=3k_1\). The polynomial \(f_2(r)\) is written as
This polynomial can have at most five positive real roots. In order to apply the averaging theory of third order we must have \(f_2(r)\equiv 0\), and in order to eliminate the coefficient of \(r^5\) we need to have \(m_1=n_1\) or \(k_1=-l_1\). Here also we have two subcases.
Subcase 3.1. We consider \(\begin{array}{ll} z_1=&{} \dfrac{-a_1 \left( 2 b_1+3 g_1\right) +d_1 \left( b_1+g_1\right) +3 k_2-3 l_2+p_2-q_2}{g_1}, \alpha _2=0, \delta _2=0, \\ w_1=&{}\dfrac{\left( 2 a_1-d_1\right) \left( 3 k_1+2 l_1\right) +g_1 \left( 2 h_1+n_1\right) }{3 g_1}, k_1\ne -l_1, m_1=n_1, c_2=2 b_2+g_2.\\ \end{array}\)
Computing \(f_3(r)\) we get
Where \(\begin{array}{ll} D_1=&{}\dfrac{1}{315g_1}\Big (2 (-2 g_1 (2 a_1-d_1) (h_1-m_1) (15 k_1+8 l_1)-10 l_1 (d_1-2 a_1){}^2 (2 l_1+q_1)+g_1^2\\ {} &{}(-8 h_1 m_1+4 h_1^2+72 k_1 l_1+45 k_1^2+72 l_1^2+4 m_1^2))\Big ),\ \end{array}\) \(\begin{array}{ll} D_2=&{}-\dfrac{1}{48g_1} \Big (\pi (a_1 (6 b_1 (2 d_1 l_1+g_1 (m_1-h_1))+d_1 g_1 (2 l_1-15 k_1)-7 g_1^2 (h_1-m_1)\\ &{}+2 (9 k_2 l_1-9 k_1 l_2+5 l_1 p_2-3 l_1 q_2-15 l_2 l_1+p_2 q_1))+2 a_1^2 (-6 b_1 l_1+15 g_1 k_1\\ &{}+2 g_1 l_1)-3 b_1 (d_1 g_1 (m_1-h_1t)+d_1^2 l_1-g_1^2 (5 l_1+q_1))+2 d_1 g_1^2 h_1-2 d_1^2 g_1 l_1\\ &{}-9 d_1 k_2 l_1+9 d_1 k_1 l_2-3 d_1 k_1 p_2-5 d_1 l_1 p_2+15 d_1 l_1 l_2+d_1 p_1 q_2+18 g_1 h_1 k_2\\ &{}+5 g_1 h_1 p_2-6 g_1 h_1 q_2-6 g_1 k_1 m_2+6 g_1 k_1 n_2+6 g_1^3 k_1-3 g_1 l_2 m_1-6 g_1 l_1 m_2\\ {} &{} +6 g_1 l_1 n_2+6 g_1^3 l_1+g_1 m_1 p_2-15 g_1 h_1 l_2-2 d_1 g_1^2 m_1)\Big ), \end{array}\) \(\begin{array}{ll} D_3=&{}\dfrac{1}{15g_1}\Big (2 (a_1 (-2 b_1 (3 d_1 g_1+6 k_2-2 q_2)-6 d_1 g_1^2-33 g_1 k_2+6 g_2 k_1+14 g_1 l_2\\ &{}-6 g_1 p_2+9 g_1 q_2)+3 a_1^2 g_1 (4 b_1+5 g_1)-6 a_2 g_1 k_1-4 a_2 g_1 l_1+b_1 (6 d_1 k_2-2 d_1 q_2\\ &{}-4 g_1 m_2+4 g_1 n_2+4 g_1^3)+4 b_1^2 g_1^2-3 d_1 g_2 k_1+9 d_1 g_1 k_2+2 d_2 g_1 l_1-2 d_1 g_2 l_1\\ &{}-4 d_1 g_1 l_2+2 d_1 g_1 p_2-2 d_1 g_1 q_2+d_2 g_1 q_1-2 g_1^2 h_2-3 g_1^2 m_2+2 g_1^2 n_2+3 g_1^2 w_2\\ {} &{}-18 k_2 l_2+6 k_2 p_2-12 k_2 q_2+18 k_2^2+6 l_2 q_2-2 p_2 q_2+2 q_2^2+4 g_2 l_1)\Big ),\\ \end{array}\) \( \begin{array}{ll} D_4=&{}\dfrac{1}{8g_1}(\pi (2 a_1 b_2 g_1+a_2 g_1 (2 b_1+3 g_1)-2 a_1 b_1 g_2-b_2 d_1 g_1-b_1 d_2 g_1+b_1 d_1 g_2-d_2 g_1^2\\ &{}-3 g_1 k_3+3 g_2 k_2+3 g_1 l_3-3 g_2 l_2-g_1 p_3+g_2 p_2+g_1 q_3-g_2 q_2+g_1^2 z_2)). \end{array}\)
This polynomial can have at most six positive real roots, which provide at most six limit cycles.
Now we analyze the second subcase.
Subcase 3.2. We consider the following values of the parameters of the function \(f_3(r)\) \( \begin{array}{ll} z_1=&{}\dfrac{-a_1 \left( 2 b_1+3 g_1\right) +d_1 \left( b_1+g_1\right) +3 k_2-3 l_2+p_2-q_2}{g_1}, k_1=-l_1, c_2=2 b_2+g_2, \\ w_1=&{}\dfrac{-2 a_1 l_1-2 n_1 \left( 2 b_1+g_1\right) +4 b_1 m_1+d_1 l_1+2 g_1 h_1+3 g_1 m_1}{3 g_1}, \alpha _2=0, \delta _2=0, m_1\ne n_1. \end{array}\) \(f_3(r)\) becomes
Where \(\begin{array}{ll} F_1=&{}\dfrac{\pi l_1}{192 g_1}( \left( m_1-n_1\right) \left( 5 \left( -2 a_1 l_1+4 b_1 m_1-4 b_1 n_1+d_1 l_1\right) +g_1 \left( -5 h_1+12 m_1-7 n_1\right) \right) ),\\ F_2=&{}\dfrac{1}{315g_1}\Big (2 (2 g_1 (2 a_1 l_1 (7 h_1-45 m_1+38 n_1)-8 b_1 (m_1-n_1) (2 h_1+3 m_1-5 n_1)+d_1 l_1 \\ {} &{}(-7 h_1+24 m_1-17 n_1))+2 (-4 a_1 l_1 (17 b_1 (m_1-n_1)+5 d_1 l_1)+20 a_1^2 l_1^2+34 b_1 d_1 l_1 \\ {} &{}(m_1-n_1)-8 (m_1-n_1) (5 b_1^2 (m_1-n_1)-9 k_2 l_1+3 l_1 (3 l_2-p_2+q_2))+5 d_1^2 l_1^2)\\ {} &{}+g_1^2 (-8 h_1 (3 m_1-2 n_1)+4 h_1^2+45 l_1^2+4 n_1 (6 m_1-5 n_1)))\Big ),\\ \end{array}\) \( \begin{array}{ll} F_3=&{}\dfrac{1}{48g_1}\Big (\pi (a_1(-2 b_1 (6 d_1 l_1+g_1 (-3 h_1+2 m_1+n_1))+12 b_1^2 (m_1-n_1)-17 d_1 g_1 l_1+g_1^2\\ {} &{}(7 h_1-12 m_1+5 n_1)+2 l_1 (-9 k_2+6 l_2-2 p_2+3 q_2))+2 a_1^2 l_1 (6 b_1+13 g_1)+b_1 (d_1 g_1\\ {} &{}(-3 h_1-4 m_1+7 n_1)+3 d_1^2 l_1-2 (3 g_1^2 l_1+(m_1-n_1) (9 k_2-15 l_2+5 p_2-3 q_2)))\\ {} &{}+6 b_1^2 d_1 (n_1-m_1)-2 d_1 g_1^2 h_1+2 d_1^2 g_1 l_1+2 d_1 g_1^2 n_1+9 d_1 k_2 l_1+2 d_1 l_1 p_2-3 d_1 l_1 q_2\\ {} &{}-6 d_1 l_1 l_2-18 g_1 h_1 k_2+15 g_1 h_1 l_2-5 g_1 h_1 p_2+6 g_1 h_1 q_2-3 g_1 k_2 m_1+3 g_1 k_2 n_1\\ {} &{}+15 g_1 l_2 m_1-12 g_1 l_2 n_1-3 g_1 m_1 p_2+3 g_1 m_1 q_2+2 g_1 n_1 p_2-3 g_1 n_1 q_2)\Big ), \end{array}\) \( \begin{array}{ll} F_4=&{}\dfrac{1}{15g_1} \Big (2(-a_1 (2 b_1 (3 d_1 g_1+6 k_2-2 q_2)+6 d_1 g_1^2+33 g_1 k_2-14 g_1 l_2+2 g_2 l_1+6 g_1 p_2\\ {} &{}-9 g_1 q_2)+3 a_1^2 g_1 (4 b_1+5 g_1)+2 a_2 g_1 l_1+b_1 (6 d_1 k_2-2 d_1 q_2-4 g_1 m_2+4 g_2 m_1+4 g_1 n_2\\ {} &{}-4 g_2 n_1+4 g_1^3)-4 b_2 g_1 m_1+4 b_2 g_1 n_1+4 b_1^2 g_1^2+9 d_1 g_1 k_2-d_2 g_1 l_1+d_1 g_2 l_1-4 d_1 g_1 l_2\\ {} &{}+2 d_1 g_1 p_2-2 d_1 g_1 q_2-2 g_1^2 h_2-3 g_1^2 m_2+2 g_1^2 n_2+3 g_1^2 w_2-18 k_2 l_2+6 k_2 p_2-12 k_2 q_2\\ {} &{}+18 k_2^2+6 l_2 q_2-2 p_2 q_2+2 q_2^2\Big ),\\ \end{array}\) \(\begin{array}{cc} F_5=&{}\dfrac{1}{8g_1}\Big (\pi (2 a_1 b_2 g_1+a_2 g_1 (2 b_1+3 g_1)-2 a_1 b_1 g_2-b_2 d_1 g_1-b_1 d_2 g_1+b_1 d_1 g_2-d_2 g_1^2\\ {} &{}-3 g_1 k_3+3 g_2 k_2+3 g_1 l_3-3 g_2 l_2-g_1 p_3+g_2 p_2+g_1 q_3-g_2 q_2+g_1^2 z_2\Big ). \end{array}\)
Then the polynomial \(f_3(r)\) can have at most seven positive real roots.
Case 4. \(g_1 =0\) and \(q_1=3k_1\). Computing the function \(f_2(r)\) we obtain
This polynomial can have at most five positive real roots. Now we apply the averaging theory of third order by considering \(f_2(r) \equiv 0\). We see that to remove the coefficient of \(r^5\) we need to have \(k_1 = -l_1\) or \(m_1 = n_1\). Here we also have two subcases.
Subcase 4.1. We consider \(k_1 = -l_1\), \(c_2=2 b_2+g\), \(q_2=-2 a_1 b_1+b_1 d_1+3 k_2-3 l_2+p_2\), \(m_1=\dfrac{l_1 \left( 2 a_1-d_1\right) }{4 b_1}+n_1\), \(\alpha _2=0\), \(\delta _2=0\), \(b_1\ne 0\), \(m_1\ne n_1\), and we distinguish another two subcases \(b_1\ne 0\) or \(b_1=0.\)
Subcase 4.1.1. For \(b_1\ne 0\). Computing \(f_3(r)\) we get
Where
This polynomial can have at most seven positive real roots, consequently at most seven limit cycles for the discontinuous piecewise differential system (2)-(3).
Subcase 4.1.2. If \(b_1=0\) the polynomial \(f_2(r)\) is written as
In this case the function \(f_2(r)\) can have at most five positive real roots. We set \(f_2(r) \equiv 0\), and to delete the coefficients of \(r^4\) we need another two subcases \(3 k_1 + 2 l_1=0\) or \(d_1=2a_1\). We start with the first subcase \(3 k_1 + 2 l_1=0\).
Subcase 4.1.2.1. \(c_2 = 2 b_2 + g_2\), \(p_2 = -3 k_2 + 3 l_2 + q_2\), \(\alpha _2=0\), \(\delta _2=0\), \(l_1=0\), \(k_1=0\) and \(d_1\ne 2a_1\). Computing the function \(f_3(r)\) we obtain
Then the polynomial \(f_3(r)\) can have at most five positive real roots.
Now we compute \(f_3(r)\) for the second case \(d_1=2a_1\).
Subcase 4.1.2.2. \(c_2 = 2 b_2 + g_2\), \(\alpha _2 = 0\), \(c_2 = 2 b_2 + g_2\), \(\delta _2=0\), \(d_1 = 2 a_1\), \(k_1 = -l_1\) and \(3 k_1 + 2 l_1\ne 0\). Computing the function \(f_3(r)\) we obtain \(\begin{array}{ll} f_3(r)=&{}- \dfrac{1}{64} \pi l_1 r^7 (m_1-n_1) (5 h_1+m_1-n_1-5 w_1) -\dfrac{8}{105} l_1 r^6 (3 a_1-4 z_1) (m_1-n_1)+\dfrac{1}{16}\\ &{}\pi r^5 (h_1 (q_2 -3 k_2)+k_2 (-m_1+n_1+3 w_1)+2 l_2 m_1-2 l_2 n_1+m_1 q_2-n_1 q_2-q_2 w_1)\\ &{}-\dfrac{2}{15} r^4 (3 a_1 k_2-2 a_2 l_1-a_1 q_2+4 b_2 m_1-4 b_2 n_1+d_2 l_1+g_2 (2 h_1+3 m_1 -2 n_1-3 w_1)\\ &{}-6 k_2 z_1+2 q_2 z_1)+\dfrac{1}{8} \pi r^3 (a_1 g_2+g_2 z_1-3 k_3+3 l_3-p_3+q_3) -\dfrac{2}{3} r^2 (2 b_3-c_3+g_3)\\ &{}+\pi \alpha _3 r+2 \delta _3. \end{array}\)
This polynomial function can have at most seven positive real roots. Now taking the second subcase \(m_1 = n_1\).
Subcase 4.2. \(m_1 = n_1\), \(c_2 = 2 b_2 + g_2\), \( p_2 = 2 a_1 b_1 - b_1 d_1 - 3 k_2 + 3 l_2 + q_2\), \( \alpha _2 = 0\), \(\delta _2 = 0\) and \(k_1=-\dfrac{2l_1}{3}\). Computing \(f_3(r)\) we get
This polynomial can have at most six positive real roots. In general, in all the cases mentioned above, the polynomials \(f_i(r)\), with \(i=1,2,3\) can have at most 3, 5, 6, and 7 real positive roots. Thus the maximum number of limit cycles that can be obtained via the averaging theory up to third order is seven.
Now we are going to reach our result by giving an example with exactly seven limit cycles.
Example with seven limit cycles.
In the half plane \(y\ge 0\), we consider the linear differential system (8) with the values \(\lbrace \alpha _1, \beta _1,\gamma _1,\delta _1,\alpha _2, \beta _2,\gamma _2,\delta _2, \alpha _3, \beta _3, \gamma _3,\delta _3\rbrace \rightarrow \lbrace 0, 1, 2, 0, 0, 1, 1, 0, 13,068/ \pi , -1, -1, -2520 \rbrace \).
Now in the half plane \(y\le 0\), we consider the cubic weak focus or center (9) with \(\lbrace a_1,b_1,c_1,d_1,g_1,h_1,k_1,l_1,m_1,n_1,p_1,q_1,w_1,z_1,a_2,b_2,c_2,d_2,g_2,h_2,k_2,l_2,m_2,n_2,p_2,q_2,w_2,z_2,\)
\(a_3,b_3,c_3,d_3,g_3,h_3,k_3,l_3,m_3,n_3,p_3,q_3,w_3,z_3\rbrace \rightarrow \lbrace 0,H_1/K_1, H_1/K_1+1, 0, 1, -2 \sqrt{25+\dfrac{64}{\pi }}-9, 2, 0, 1,\)
\(1,(-5 \pi -\sqrt{64 \pi +25 \pi ^2})/ (2 \pi ), (7 \pi -\sqrt{64 \pi +25 \pi ^2})/(2 \pi ),-2 \sqrt{25+\dfrac{64}{\pi }}-9, 2, 0, 1, 1, 1, -1, -1, \)
\(-1302.26, 0, \dfrac{1}{2}, -\dfrac{1}{2}, 3907.78, -1, 163.431, -1, 1, -20, 0, -1, 19,738, -1, 1, 1, -1, -1, -54,152/ \pi ,\)
\(H_2/ K_2, -2,1 \rbrace \), with \(H_1=-23 \sqrt{\pi (64+25 \pi )}-880 \pi -128\), \(K_1=8 (5 \pi +4+\sqrt{\pi (64+25 \pi )})\), \(H_2=9 \left( \sqrt{\pi (64+25 \pi )}-80 \pi \right) \) and \(K_2=8 \left( \sqrt{\pi (64+25 \pi )}+5 \pi +4\right) \).
An exhausting computation shows that \(f_1(r)\equiv f_2(r)\equiv 0\) and
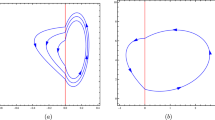
Then for these systems we have seven limit cycles bifurcating from the periodic orbits of the discontinuous piecewise differential system (2)-(3).
Moreover, in polar coordinates \((r, \theta )\) the periodic orbits that bifurcate are \(r = 1, 2, 3,4,5,6,7.\) This completes the proof of the Theorem 1.
Data Availability
The datasets analyzed during the current study are available from the corresponding author on reasonable request.
References
Baymout, L., Benterki, R.: Limit cycles of piecewise differential systems formed by linear center or focus and cubic uniform isochronous center. Mem. Differ. Equ. Math. Phys. Accepted (2023)
Berezin, I., Zhidkov, N.: Computing Methods. Volume II, Oxford, Pergamon Press (1964)
Bogoliubov, N., Krylov, N.: The application of methods of nonlinear mechanics in the theory of stationary oscillations. Publ. 8 of the Ukrainian Acad. Sci. Kiev (1934)
Fatou, P.: Sur le mouvement d’un systéme soumis à des forces à courte période. Bull. Soc. Math. France. 56, 98–139 (1928)
Han, M., Yang, J.: The maximum number of zeros of functions with parameters and application to differential equations. J. Nonlinear Model. Anal. 3, 13–34 (2021)
Han, M.: On the maximum number of periodic solutions of piecewise smooth periodic equations by average method. J. Appl. Anal. Comput. 7(2), 788–794 (2017)
Hilbert, D.: Mathematical problems. Bull. Am. Math. Soc. 8, 437–479 (1902)
Hilbert, D.: Mathematische Probleme (lecture). In. Second Internat. Congress Math, Paris. In: Nach. Ges. Wiss. Gottingen Math-Phys. Kl, 253–297 (1900)
Ilyashenko, Y.S.: Centennial history of Hilbert’s 16th problem. Bull. Am. Math. Soc. 39, 301–354 (2002)
Itikawa, J., Llibre, J., Novaes, D.D.: A new result on averaging theory for a class of discontinuous planar differential systems with applications. Rev. Mat. Iberoam. 33, 1247–1265 (2017)
Llibre, J., Mereu, A.C., Novaes, D.D.: Averaging theory for discontinuous piecewise differential systems. J. Differ. Equ. 258(11), 4007–4032 (2015)
Llibre, J., Novaes, D.D., Teixeira, M.A.: Higher order averaging theory for finding periodic solutions via Brouwer degree. Nonlinearity 27, 563–583
Llibre, J., Novaes, D.D., Teixeira, M.A.: On the birth of limit cycles for non-smooth dynamical systems. Bull. Sci. Math. 139(3), 229–244 (2015)
Llibre, J., Novaes, D.D., Rodrigues, C.A.B.: Averaging theory at any order for computing limit cycles of discontinuous piecewise differential systems with many zones. Phys. D Nonlinear Phenom. 353, 1–10 (2017)
Llibre, J., Moeckel, R., Simó, C.: Central Configurations. Periodic Orbits. and Hamiltonian Systems. Birkhäuser, Basel (2015)
Llibre, J., Swirszcz, G.: On the limit cycles of polynomial vector fields. Dyn. Contin. Discrete Impuls Syst. Ser. A Math. Anal. 18, 203–214 (2011)
Poincaré, M.: Memoire sur les coubes definies par une equation differentielle. Editions Jacques Gabay, Sceaux (1993)
Sanders, J.A., Verhulst, F., Murdock, J.: Averaging Methods in Nonlinear Dynamical Systems. Springer, New York (2007)
Wei, L., Zhang, X.: Averaging theory of arbitrary order for piecewise smooth differential systems and its application. J. Dyn. Differ. Equ. 30, 55–79 (2018)
Acknowledgements
The authors are supported by the Directorate-General for Scientific Research and Technological Development (DGRSDT), Algeria.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Barkat, M., Benterki, R. Limit Cycles of Discontinuous Piecewise Differential Systems Formed by Linear and Cubic Centers via Averaging Theory. Differ Equ Dyn Syst (2024). https://doi.org/10.1007/s12591-023-00671-w
Accepted:
Published:
DOI: https://doi.org/10.1007/s12591-023-00671-w