1 Introduction and statement of the main results

The study of the existence of the so-called limit cycles of a planar differential system, i.e. existence of periodic orbits isolated in the set of all periodic orbits of that system is one of the main difficulties for completely understanding (at least qualitatively) its dynamics. In particular to find a limit cycle of a given class of differential systems is very difficult and to provide an upper bound on the maximum number of them is even harder. When such an upper bound exists, additional difficulties arise when trying to prove that such upper bound is achieved.

In this paper we shall study the limit cycles of a class of piecewise differential systems. These systems have been studied intensively these last decades due to their applications, see for instance the books [1, 4, 20] and the papers [19, 21].

For planar piecewise differential systems with separation curve \(\Sigma =\{h^{-1}(0)\}\) where \(h:{\mathbb {R}}^2\rightarrow {\mathbb {R}}\) (being bi-valuated on the separation curve for the vector fields X and Y) a point \(p=(x,y)\) in \(\Sigma \) is a crossing point if \(Xh(p)\cdot Yh(p)>0,\) where \(\cdot \) denotes the inner product of two vectors, for more details see Filippov [5]. If there exist a periodic orbit of that piecewise differential system such that all the points of the orbit on \(\Sigma \) are crossing points, then we call it a crossing periodic orbit. A crossing limit cycle is an isolated periodic orbit in the set all crossing periodic orbits of the differential system.

The crossing limit cycles of different classes of piecewise differential systems have been studied by many authors during these last years, see for instance [2, 3, 6, 7, 9, 11,12,13,14,15,16,17,18].

In this paper we study the maximum number of crossing limit cycles of the class of planar continuous piecewise differential systems separated by the non-regular line

$$\begin{aligned} \Sigma =\{(x,y)\in {\mathbb {R}}^2: (y=0) \vee (x=0 \wedge y\ge 0)\}. \end{aligned}$$

The three components of \({\mathbb {R}}^2 \setminus \Sigma \) are the positive or first quadrant

$$\begin{aligned} R_1=\{(x,y)\in {\mathbb {R}}^2: x\ge 0 \wedge y\ge 0\}, \end{aligned}$$

the second quadrant

$$\begin{aligned} R_2=\{(x,y)\in {\mathbb {R}}^2: x\le 0 \wedge y\ge 0\}, \end{aligned}$$

and the half-plane

$$\begin{aligned} R_3=\{(x,y)\in {\mathbb {R}}^2: y\le 0\}. \end{aligned}$$

More precisely, in the region \(R_1\) we consider an arbitrary quadratic differential system

$$\begin{aligned} \dot{x}= & {} c_0+c_1 x+c_2 y+c_3 x^2+c_4 x y+c_5 y^2,\nonumber \\ \dot{y}= & {} d_0+d_1 x+d_2 y+d_3 x^2+d_4 x y+d_5 y^2, \end{aligned}$$
(1)

with \(c_i,d_i \in {\mathbb {R}}\) for \(i=0,\ldots , 5.\) In the region \(R_2\) we consider an arbitrary linear center

$$\begin{aligned} \dot{x}= & {} a_0+a_1 x+a_2 y,\nonumber \\ \dot{y}= & {} b_0+b_1 x+b_2 y, \end{aligned}$$
(2)

with \(a_i,b_i \in {\mathbb {R}}\) for \(i=0,1,2,\) and in the region \(R_3\) we consider the linear center

$$\begin{aligned} \dot{x}= & {} -y,\nonumber \\ \dot{y}= & {} x. \end{aligned}$$
(3)

Our main result is the following.

Theorem 1

Any continuous piecewise differential system in the plane formed by systems (1) in \(R_1,\) systems (2) in \(R_2\) and systems (3) in \(R_3\) separated by the non-regular line \(\Sigma \) has at most two crossing limit cycles. Moreover we provide an example of such a system with one crossing limit cycle.

The proof of Theorem 1 is given in Sect. 2. Note that Theorem 1 provides a positive answer to the extension of the 16th Hilbert problem [8] for the class of continuous piecewise differential systems separated by a non-regular line \(\Sigma \) and formed by the above differential systems. Note that although two is the maximum number of crossing limit cycles that the above mentioned system can have, we are only able to find examples of these piecewise differential systems with one crossing limit cycle. So it remains open if the upper bound of two is reached or not.

2 Proof of Theorem 1

Before proving Theorem 1 we recall that a set of functions \(\{f_0, f_1, \ldots ,f_n \}\) is an extended complete Chebyshev system on \({\mathbb {R}}^+\) if and only if the Wronskians

$$\begin{aligned} W(f_0,\ldots ,f_k)(s)=\begin{vmatrix} f_0(s)&f_1(s)&\cdots&f_k(s) \\ f'_0(s)&f'_1(s)&\cdots&f'_k(s) \\ \vdots&\vdots&\ddots&\vdots \\ f_0^k(s)&f_1^k(s)&\cdots&f_k^k(s) \\ \end{vmatrix}\ne 0, \end{aligned}$$

on \({\mathbb {R}}^+\) for \(k=0,1,\ldots ,n.\) Moreover for an extended complete Chebyshev system in \({\mathbb {R}}^+\) we have the following well-known result, for a proof see for instance [10].

Theorem 2

Assume that the functions \(f_0, f_1,\ldots , f_n\) form an extended complete Chebyshev system in \({\mathbb {R}}^+.\) Then the maximum number of zeros of the function

$$\begin{aligned} a_0 f_0(x) + a_1 f_1(x) +\cdots + a_n f_n(x)=0 \end{aligned}$$
(4)

in \({\mathbb {R}}^+\) is n. Furthermore,  if we can choose the coefficients \(a_0, a_1,\ldots ,a_n\) arbitrarily there are functions of the form in (4) having exactly n zeros in \({\mathbb {R}}^+.\)

We separate the proof of Theorem 1 in two parts: the part concerning the upper bound and the part providing an example with one crossing limit cycle.

First note that in Theorem 1 we are assuming that the piecewise differential system must be continuous, and so systems (1) and (2) must coincide on \(\{x= 0, y\ge 0\},\) systems (2) and (3) must coincide on \(\{x\le 0, y=0\},\) and systems (3) and (1) must coincide on \(\{x\ge 0, y=0\}.\) Imposing these three conditions we obtain that

$$\begin{aligned}{} & {} a_0=a_1=b_0=c_0=c_1=c_3=c_5=d_0=d_3=d_5=0,\\{} & {} b_1=d_1=1,\ a_2=c_2,\ b_2=d_2, \end{aligned}$$

and the continuous piecewise differential system to study is the one formed by the following three differential systems

$$\begin{aligned}{} & {} \dot{x}=c_2 y + c_4 x y,\quad \dot{y}=x + d_2 y + d_4 x y, \quad \text{ in } \ R_1\ \text{ with }\ c_4^2+d_4^2 \ne 0.\nonumber \\{} & {} \dot{x}=c_2 y,\quad \dot{y}=x + d_2 y, \quad \text{ in } \ R_2\ \text{ with }\ c_2\ne 0,\nonumber \\{} & {} \dot{x}=-y,\quad \dot{y}=x, \quad \text{ in } \ R_3. \end{aligned}$$
(5)

Note that \(c_4^2+d_4^2 \ne 0,\) otherwise the first system in (5) will not be a quadratic system. Moreover, if \(c_2=0\) then in the second system in (5) we have \(\dot{x}=0,\) so its solutions live on the straight lines \(x=\) constant and then the piecewise differential system cannot have crossing periodic orbits. Hence we have that \(c_2 (c_4^2 +d_4^2) \ne 0.\)

2.1 The upper bound

We start imposing that the quadratic system in (1) has a center. The equilibrium points of such a quadratic system are

$$\begin{aligned} E_0=(0,0)\quad \text{ and }\quad E_1=\left( -\dfrac{c_2}{c_4},\ \dfrac{c_2}{c_4 d_2 - c_2 d_4}\right) . \end{aligned}$$

Since \(c_2 (c_4^2+d_4^2 ) \ne 0\) we have \(c_4^2 +(c_4 d_2 -c_2 d_4)^2 \ne 0.\) We consider different cases:

Case 1: \(c_4(c_4 d_2-c_2d_4)\ne 0.\) In this case we define

$$\begin{aligned} T=d_4 x + c_4 y +d_2,\quad D=-c_4x+(c_4d_2-c_2d_4)y-c_2, \end{aligned}$$

and

$$\begin{aligned} \Delta= & {} c_4^2 y^2+(2 c_4 d_2-4 (c_4 d_2-c_2 d_4))y+d_4^2 x^2+(4 c_4+2 d_2 d_4)x\\{} & {} +2 c_4 d_4 xy+d_2^2+4 c_2, \end{aligned}$$

where T,  D and \(\Delta \) are, respectively, the trace, the determinant and the discriminant associated to the linear part of the quadratic system in (5). Then at the equilibrium point \(E_0\) we obtain

$$\begin{aligned} T_0=d_2,\quad D_0=-c_2,\quad \Delta _0=4 c_2 + d_2^2, \end{aligned}$$

and at the equilibrium point \(E_1\) we have

$$\begin{aligned} T_1=\dfrac{c_2 c_4^2+c_4^2 d_2^2+c_2^2 d_4^2-2 c_2 c_4 d_2 d_4}{c_4 (c_4 d_2-c_2 d_4)},\quad D_1=c_2, \end{aligned}$$

and

$$\begin{aligned} \Delta _1=\left( \dfrac{-c_2 c_4^2+c_2^2 d_4^2+c_4^2 d_2^2 -2 c_2 c_4 d_2 d_4}{c_4 (c_4 d_2-c_2 d_4)}\right) ^2. \end{aligned}$$

Observe that \(E_1\) cannot be a center because \(\Delta _1 \ge 0.\) On the other hand \(E_0\) is either a weak focus or a center if and only if \(D_0>0,\) \(\Delta _0<0\) and \(T_0=0.\) Thus, \(c_2<0\) (that we can write as \(c_2=-c^2\) with \(c > 0\)), \(d_2=0\) and \(c_4 d_4\ne 0.\)

Hence the quadratic system in the region \(R_1\) is

$$\begin{aligned} \dot{x}=-c^2 y + c_4 x y,\quad \dot{y}= x + d_4 x y, \end{aligned}$$
(6)

and the arbitrary linear system in the region \(R_2\) is

$$\begin{aligned} \dot{x}=-c^2 y,\quad \dot{y}= x. \end{aligned}$$
(7)

Note that in system (6) we can assume without loss of generality that \(c_4<0\) and \(d_4>0.\) Indeed, if originally \(c_4>0\) then doing the change of variables \((x,y,t)\rightarrow (-x,y,-t),\) \(c_4\) becomes negative, and if originally \(d_4<0\) then doing the change of variables \((x,y,t)\rightarrow (x,-y,-t),\) \(d_4\) becomes positive.

The first integrals for systems (6), (7) and (3) are

$$\begin{aligned} H_1(x,y)= & {} {\textrm{e}}^{-d_4(d_4 x+c_4y)} (1+d_4 y)^{-c_4} \left( c^2-c_4 x\right) ^{-\frac{c^2 d_4^2}{c_4}}\quad \text{ in } \ R_1,\\ H_2(x,y)= & {} x^2 + c^2 y^2\quad \text{ in } \ R_2,\\ H_3(x,y)= & {} x^2+y^2 \quad \text{ in } \ R_3, \end{aligned}$$

as it is easy to check. The existence of the first integral \(H_1(x,y)\) defined in the point (0, 0) forces that the equilibrium (0, 0) of the quadratic system (6) is a center.

Now we study the limit cycles of these continuous piecewise differential systems which intersect the non-regular line of discontinuity \(\Sigma \) in the points \((x_1,0),\) \((0,y_1)\) and \((x_2,0)\) with \(x_1>0,\ y_1>0\) and \(x_2<0.\) These points must satisfy

$$\begin{aligned} e_1= & {} H_1(x_1, 0)-H_1(0, y_1)=0,\nonumber \\ e_2= & {} H_2(x_2, 0)-H_2(0, y_1)=0,\nonumber \\ e_3= & {} H_3(x_2, 0)-H_3(x_1, 0)=0, \end{aligned}$$
(8)

or equivalently

$$\begin{aligned} e_1= & {} {\textrm{e}}^{-d_4^2 x_1} \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{-\frac{c^2 d_4^2}{c_4}}- {\textrm{e}}^{c_4 d_4 y_1} (1+d_4 y_1)^{-c_4}=0,\\ e_2= & {} x_2^2 - c^2 y_1^2=0,\\ e_3= & {} x_2^2-x_1^2=0. \end{aligned}$$

Solving \(e_2=0\) and \(e_3=0\) we obtain

$$\begin{aligned} x_2=-x_1,\quad y_1=\dfrac{x_1}{c}. \end{aligned}$$

Substituting \(y_1\) into \(e_1=0\) we get

$$\begin{aligned} {\textrm{e}}^{-d_4^2 x_1} \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{-\frac{c^2 d_4^2}{c_4}}-{\textrm{e}}^{\frac{c_4 d_4 }{c}x_1} \left( \frac{d_4}{c} x_1+1\right) ^{-c_4}=0, \end{aligned}$$

which can be written as

$$\begin{aligned} {\textrm{e}}^{d_4 x_1 \left( \frac{d_4}{c_4}-\frac{1}{c}\right) } \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{\frac{c^2 d_4^2}{c_4^2}}-\frac{d_4 }{c} x_1-1=0. \end{aligned}$$
(9)

We note that this last equation in the particular case \(c=1\) and \(c_4=-d_4,\) assumes the form

$$\begin{aligned} (d_4 x_1+1)( {\textrm{e}}^{-2 d_4 x_1} -1)=0. \end{aligned}$$

Which does not vanish in \({\mathbb {R}}^+=(0,\infty )\) because \(x_1=-1/d_4<0\) with \(d_4>0\) and the other is \(x_1=0.\) So there is not limit cycle for the system (8) when \(c=1\) and \(c_4=-d_4.\)

We write the equation in (9) as

$$\begin{aligned} a_0 f_0(x_1) + a_1 f_1(x_1)+a_2 f_2(x_1)=0, \end{aligned}$$
(10)

where

$$\begin{aligned} f_0(x_1)=1,\quad f_1(x_1)=x_1,\quad f_2(x_1)={\textrm{e}}^{d_4 x_1 \left( \frac{d_4}{c_4}-\frac{1}{c}\right) } \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{\frac{c^2 d_4^2}{c_4^2}}, \end{aligned}$$

and

$$\begin{aligned} a_0=-1,\quad a_1=-d_4/c,\quad a_2=1. \end{aligned}$$

The functions \(f_0,\) \(f_1\) and \(f_2\) form an extended Chebyshev system on \({\mathbb {R}}^+\) because the Wronskians of these functions are

$$\begin{aligned} W(f_0)(x_1)=1, \quad W(f_0,f_1)(x_1)=1, \end{aligned}$$

and

$$\begin{aligned} W(f_0, f_1, f_2)(x_1)=\frac{d_4^2 (c d_4-c_4) x_1 \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{\frac{c^2 d_4^2}{c_4^2}} \left( 2 c^2+(c d_4 -c_4 )x_1\right) {\textrm{e}}^{d_4 x_1 \left( \frac{d_4}{c_4}-\frac{1}{c}\right) }}{c^6\left( 1-\frac{c_4}{c^2}\ x_1\right) ^2}, \end{aligned}$$

which does not vanish in \({\mathbb {R}}^+=(0,\infty )\) because from the three zeros of this last Wronskian two are negative (namely \(c^2/c_4\) and \(-\frac{2 c^2}{c d_4-c_4}\)) and the other is the 0. In view of Theorem 2 the function (10) has at most two zeros and so the piecewise differential system has at most two limit cycles in this case. The upper bound provided by the theorem is proved in this case.

Note that from Theorem 2 we cannot say that the Eq. (9) has values of the parameters c,  \(c_4\) and \(d_4\) for which it has exactly two zeros, because the coefficients \(a_0,\) \(a_1\) and \(a_2\) are not free parameters. Moreover we also do not know if the possible zeros of the Eq. (9) are positive.

Case 2: \(c_4\ne 0\) and \(c_4 d_2-c_2 d_4 = 0.\) We write this condition as \(c_4\ne 0\) and \(d_2=c_2 d_4/c_4.\) In this case, system (5) becomes

$$\begin{aligned}{} & {} \dot{x}=c_2 y + c_4 x y,\quad \dot{y}=\frac{c_2 d_4 }{c_4} y+d_4 x y+x, \quad \text{ in } \ R_1,\nonumber \\{} & {} \dot{x}=c_2 y,\quad \dot{y}=x + \frac{c_2 d_4 }{c_4} y, \quad \text{ in } \ R_2,\nonumber \\{} & {} \dot{x}=-y,\quad \dot{y}=x, \quad \text{ in } \ R_3. \end{aligned}$$
(11)

Taking into account that \(c_2 \ne 0,\) the quadratic system in (11) has a unique equilibrium \(E_0=(0,0).\) So, the trace and the determinant associated to the linear part of the quadratic system in (11) at \(E_0\) are \(c_2 d_4/c_4\) and \(-c_2,\) respectively. In order that \(E_0\) can be a weak focus or a center, we must have that \(d_4=0\) and \(c_2=-c^2 <0\) with \(c>0.\) Now system (11) is written as

$$\begin{aligned}{} & {} \dot{x}=-c^2 y +c_4 x y,\quad \dot{y}=x, \quad \text{ in } \ R_1,\\{} & {} \dot{x}=-c^2 y,\quad \dot{y}=x, \quad \text{ in } \ R_2,\\{} & {} \dot{x}=-y,\quad \dot{y}=x, \quad \text{ in } \ R_3, \end{aligned}$$

with first integrals

$$\begin{aligned} H_1(x,y)= & {} \left( c^2-c_4 x\right) ^{-\frac{c^2}{c_4^2}} {\textrm{e}}^{\frac{y^2}{2}-\frac{x}{c_4}}\quad \text{ in } \ R_1,\nonumber \\ H_2(x,y)= & {} x^2 + c^2 y^2\quad \text{ in } \ R_2,\nonumber \\ H_3(x,y)= & {} x^2+y^2 \quad \text{ in } \ R_3. \end{aligned}$$
(12)

The existence of the first integral \(H_1(x,y)\) defined in the point (0, 0) forces that the equilibrium (0, 0) of the quadratic system in (11) is a center.

Assume that this continuous piecewise differential system has some crossing limit cycle with the points intersecting \(\Sigma \) being \((x_1,0),\) \((0,y_1)\) and \((x_2,0)\) with \(x_1>0,\) \(y_1>0,\) \(x_2<0.\) Then the first integrals given in (12) must satisfy system (8), or equivalently,

$$\begin{aligned} e_1= & {} {\textrm{e}}^{-\frac{x_1}{c_4}} \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{-\frac{c^2}{c_4^2}}-{\textrm{e}}^{\frac{y_1^2}{2}} =0,\\ e_2= & {} x_2^2-c^2 y_1^2=0,\\ e_3= & {} x_2^2-x_1^2=0. \end{aligned}$$

From equations \(e_2=0\) and \(e_3=0,\) we get \(x_2=-x_1\) and \(y_1=\dfrac{x_1}{c}.\) Introducing \(x_2\) and \(y_1\) in \(e_1=0\) we obtain

$$\begin{aligned} {\textrm{e}}^{-\frac{x_1}{c_4}} \left( 1-\frac{c_4}{c^2}\ x_1\right) ^{-\frac{c^2}{c_4^2}}-{\textrm{e}}^{\frac{x_1^2}{2 c^2}}=0. \end{aligned}$$

which can be written as

$$\begin{aligned} {\textrm{e}}^{-\frac{c_4}{c^2}(c_4 x_1 +1)x_1}+\frac{c_4}{c^2}x_1-1=0. \end{aligned}$$
(13)

Note that Eq. (13) can be written as (10), where

$$\begin{aligned} f_0(x_1)=1, \quad f_1(x_1)=x_1,\quad f_2(x_1)={\textrm{e}}^{-\frac{c_4}{c^2}(c_4 x_1 +1)x_1}, \end{aligned}$$

and

$$\begin{aligned} a_0=-1,\quad a_1=c_4/c^2,\quad a_2=1. \end{aligned}$$

The functions \(f_0,\) \(f_1\) and \(f_2\) form an extended Chebyshev system on \({\mathbb {R}}^+\) because the Wronskians of these functions are

$$\begin{aligned} W(f_0)(x_1)=1, \quad W(f_0,f_1)(x_1)=1, \end{aligned}$$

and

$$\begin{aligned} W(f_0, f_1, f_2)(x_1)=\frac{c_4^3 x_1 \left( c_4 x_1+2 c^2\right) {\textrm{e}}^{-\frac{c_4}{c^2}(c_4 x_1 +1)x_1}}{c^8}, \end{aligned}$$

which does not vanish in \({\mathbb {R}}^+\) because its two zeros are one negative (namely \(-\frac{2 c^2}{c_4}\)) and the other is the 0. In view of Theorem 2 the function (13) has at most two zeros. So the piecewise differential system has at most two limit cycles in this case. Hence the upper bound provided by the theorem is proved in this case.

Case 3: \(c_4=0\) and \(-c_2 d_4\ne 0.\) System (5) becomes

$$\begin{aligned}{} & {} \dot{x}=c_2 y,\quad \dot{y}=x + d_2 y + d_4 x y, \quad \text{ in } \ R_1,\nonumber \\{} & {} \dot{x}=c_2 y,\quad \dot{y}=x + d_2 y, \quad \text{ in } \ R_2,\nonumber \\{} & {} \dot{x}=-y,\quad \dot{y}=x, \quad \text{ in } \ R_3. \end{aligned}$$
(14)

The quadratic system in (14) has a unique equilibrium point \(E_0=(0,0).\) The trace and the determinant associated to the linear part of the quadratic system in (14) are \(d_2\) and \(-c_2,\) respectively. The point \(E_0\) is either a weak focus or a center if and only if \(d_2=0\) and \(c_2=-c^2\) with \(c>0.\) So taking \(d_2=0\) and \(c_2=-c^2,\) system (14) is equivalently to

$$\begin{aligned}{} & {} \dot{x}=-c^2 y,\quad \dot{y}=x+ d_4 x y \quad \text{ in } \ R_1,\nonumber \\{} & {} \dot{x}=-c^2 y,\quad \dot{y}=x \quad \text{ in } \ R_2,\nonumber \\{} & {} \dot{x}=-y,\quad \dot{y}=x \quad \text{ in } \ R_3, \end{aligned}$$
(15)

with first integrals

$$\begin{aligned} H_1(x,y)= & {} (d_4 y+1)^{-\frac{1}{d_4^2}} {\textrm{e}}^{\frac{y}{d_4}+\frac{x^2}{2 c^2}}\quad \text{ in } \ R_1,\\ H_2(x,y)= & {} x^2 + c^2 y^2\quad \text{ in } \ R_2,\\ H_3(x,y)= & {} x^2+y^2\quad \text{ in } \ R_3. \end{aligned}$$

The existence of the first integral \(H_1(x,y)\) defined in the point (0, 0) forces that the equilibrium (0, 0) of the quadratic system in (14) is a center.

Now repeating the same steps as the ones in the proof of Case 2, we get

$$\begin{aligned} e_1={\textrm{e}}^{\frac{d_4}{c} x_1(1-\frac{d_4}{2 c}x_1)}-\frac{d_4}{c} x_1-1=0, \end{aligned}$$
(16)

where

$$\begin{aligned} f_0(x_1)=1, \quad f_2(x_1)=x_1,\quad f_3(x_1)={\textrm{e}}^{\frac{d_4}{c} x_1\left( 1-\frac{d_4}{2 c}x_1\right) }, \end{aligned}$$

and

$$\begin{aligned} a_0=-1,\ a_1=-d_4/c,\quad a_2=1. \end{aligned}$$

The Wronskians of these functions are

$$\begin{aligned} W(f_0)(x_1)=1,\quad W(f_0, f_1)(x_1)=1 \end{aligned}$$

and

$$\begin{aligned} W(f_0,f_1,f_2)(x_1)=\frac{d_4^3 x_1 (d_4 x_1-2 c){\textrm{e}}^{\frac{d_4}{c}(1-\frac{d_4 x_1}{2 c})x_1}}{c^4}. \end{aligned}$$

which does not vanish in \({\mathbb {R}}^+\) because has two solutions, namely \(\frac{2c}{d_4}\) and 0. So, by Theorem 2 the function (16) has at most two zeros and we conclude that (15) has at most two limit cycles which proves the upper bound in the theorem in this case.

2.2 The example

The planar continuous piecewise differential system separated by \(\Sigma \) and formed by the quadratic center and the two linear centers

$$\begin{aligned} \dot{x}= & {} -36 y + 2 x y,\quad \dot{y}= x + \frac{12}{100} x y,\quad \text{ in }\ R_1\nonumber \\ \dot{x}= & {} -36 y,\quad \dot{y}= x,\quad \text{ in }\ R_2\nonumber \\ \dot{x}= & {} -y,\quad \dot{y}= x,\quad \text{ in }\ R_3 \end{aligned}$$
(17)

with the first integrals

$$\begin{aligned} H_1= & {} \frac{{\textrm{e}}^{\frac{3}{25} \left( 2 y-\frac{3}{25}x \right) }}{(36-2 x)^{162/625} \left( \frac{3}{25}y+1\right) ^2}\quad \text{ in }\ R_1\\ H_2= & {} x^2 + 36 y^2\quad \text{ in }\ R_2\\ H_3= & {} x^2 + y^2\quad \text{ in }\ R_3 \end{aligned}$$

has one crossing limit cycle. Indeed, for this differential system equation (9) is

$$\begin{aligned} \dfrac{{\textrm{e}}^{-9 x_1/625}}{(36-2 x_1)^{162/625}}-\dfrac{\frac{6172}{15625}\ {\textrm{e}}^{x_1/25}}{\left( \frac{x_1}{50}+1\right) ^2}=0. \end{aligned}$$

This equation has the approximated solution \(x_1=0.0000583439..\) and then system (17) has a unique solution

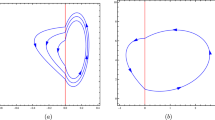
$$\begin{aligned} (x_1, y_1, x_2)=(0.0000583439..,\ 0.00000972399..,\ -0.0000583439..), \end{aligned}$$

which provides the limit cycle of Fig. 1. This limit cycle is a crossing limit cycle which is traveled in counterclockwise sense.

Fig. 1
figure 1

The unique crossing limit cycle of the continuous piecewise differential system (17)

Full size image