Limit Cycles for Discontinuous Piecewise Differential Systems in $\mathbb {R}^3$ Separated by a Paraboloid

Abstract

In planar piecewise differential systems it is known that when the discontinuity curve is a straight line and both differential systems are linear centers, these piecewise differential systems have no limit cycles but if they are separated by other types of discontinuity curves, such as parabolas, then they have limit cycles. All these results are in the plane and although the qualitative theory of planar piecewise differential systems has been the subject of many research, this is not the case for piecewise differential systems in higher dimensions. In this paper, we study the maximum number of limit cycles of discontinuous piecewise differential systems in $\mathbb {R}^3$ separated by a paraboloid (elliptic or hyperbolic), and formed by what we call two linear differential centers. We prove that these systems can have at most one limit cycle and that this upper bound is reached. We also provide systems of these types without periodic solutions and with a continuum of periodic solutions.

Introduction and Statement of the Main Result

The study of piecewise linear differential systems goes back to Andronov et al. [1] and still continues to receive attention from researchers. These last years a renewed interest has appeared in the mathematical community for understanding the dynamical richness of these piecewise linear differential systems because they are widely used to model processes appearing in electronics, mechanics, economy, etc., see for instance the books of di Bernardo et al. [5], Simpson [18], the survey of Makarenkov and Lamb [14] and the hundreds of references quoted in these works.

In the qualitative theory of dynamical systems the existence of periodic orbits and more precisely of limit cycles is very important because when they exist, they enable us to understand the dynamical behavior of differential systems. Moreover many real world phenomena are related to their existence, see for instance the Van der Pol oscillator [19, 20], among many others. In order to understand the dynamical behavior of the discontinuous piecewise differential systems it is also important to know if they have crossing periodic orbits and crossing limit cycles. In discontinuous piecewise differential systems a crossing periodic orbit is a periodic orbit that intersects the discontinuity manifold in a finite number of crossing points and a crossing limit cycle is a crossing periodic orbit that is isolated in the set of all periodic orbits of the system.

In the last years, the study of the existence and maximum number of limit cycles of planar piecewise differential systems has been a subject of intense research. Most of the studies developed in this direction were done considering piecewise linear differential systems with only two zones and separated by a straight line and only a few of them were done taking into account more zones or considering discontinuity curves with different shapes than a straight line.

In the case of planar piecewise differential systems separated by a straight line, the following interesting question emerged: discontinuous piecewise linear differential systems with only centers can create limit cycles? In 2018 Llibre and Teixeira answered this question by proving that these piecewise differential systems have no limit cycles, see [11].

In this regard, recently in [2, 4, 7, 8, 13] some authors studied the existence and the maximum number of limit cycles for discontinuous piecewise differential systems formed by differential centers that have either two or more zones, and they are separated either straight line or conics (reducible or irreducible) and they proved that these systems have limit cycles. In particular, in [13] the authors proved that discontinuous piecewise differential systems separated by a parabola and formed by two linear differential centers have at most 3 limit cycles and that this upper bound is reached. From these works, it is apparent that the shape of the discontinuity curve plays an important role in the number of limit cycles that a discontinuous piecewise differential system can have.

In this way, a natural question arises, namely, to consider discontinuous piecewise differential systems in $\mathbb {R}^3$, since although the qualitative theory of planar piecewise differential systems has been a subject of many research this is not the case for piecewise differential systems in higher dimensions. Most of the existing results are related to very specific families of systems (see for instance [12], where the authors characterized the families of periodic orbits of two discontinuous piecewise differential systems in $\mathbb {R}^3$ where the discontinuity surface is a plane).

Our objective is to study the existence and the maximum number of crossing limit cycles for discontinuous piecewise differential systems in $\mathbb {R}^3$ formed by two linear differential systems which we will call linear centers in $\mathbb {R}^3$ and separated by a paraboloid ( elliptic or hyperbolic). Without loss of generality, we can consider that an elliptic paraboloid is of the form

$$\begin{aligned} P_E=\left\{ (X,Y,Z)\in {\mathbb {R}^3}: Z=X^2+Y^2 \right\} . \end{aligned}$$

And a hyperbolic paraboloid is of the form

$$\begin{aligned} P_H=\left\{ (X,Y,Z)\in {\mathbb {R}^3}: Z=X^2-Y^2 \right\} . \end{aligned}$$

We observe that indeed $P_E$ and $P_H$ divide the space $\mathbb {R}^3$ in two regions, namely

$$\begin{aligned} \begin{aligned} \mathcal {R}_E^1 =&\left\{ (X,Y,Z) \in {\mathbb {R}^3}: Z-X^2-Y^2\ge 0 \right\} ; \\ \mathcal {R}_E^2 =&\left\{ (X,Y,Z)\in {\mathbb {R}^3}: Z-X^2-Y^2\le 0 \right\} , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mathcal {R}_H^1 =&\left\{ (X,Y,Z) \in {\mathbb {R}^3}: Z-X^2+Y^2\ge 0 \right\} ;\\ \mathcal {R}_H^2 =&\left\{ (X,Y,Z)\in {\mathbb {R}^3}: Z-X^2+Y^2\le 0 \right\} , \end{aligned} \end{aligned}$$

respectively.

We recall that a center of a differential system in the plane $\mathbb {R}^2$ is an equilibrium point p having a neighborhood U such that $U\setminus \{p\}$ is filled of periodic orbits. A global center is a center p such that $\mathbb {R}^2{\setminus } \{p\}$ is filled with periodic orbits. The notion of a center appeared already in the works of Poincaré [15,16,17] in 1881 and Dulac [6] in 1908.

In $\mathbb {R}^3$ there are no centers in the sense that there are no equilibrium points p having a neighborhood U such that $U\setminus \{p\}$ is filled of periodic orbits, see for instance [3]. In the following, we introduce the notion of the linear center in $\mathbb {R}^3$ that we shall use.

One of the differential systems in $\mathbb {R}^3$ with more periodic orbits is

$$\begin{aligned} \dot{x}=-y,\quad \dot{y}=x,\quad \dot{z}=0. \end{aligned}$$

(1)

This differential system has two linearly independent first integrals, namely

$$\begin{aligned} H_1(x,y,z)=x^2+y^2,\quad H_2(x,y,z)=z. \end{aligned}$$

Moreover system (1) has a global center at the equilibrium point $(0, 0, z_0)$ of each plane $z = z_0$. So all its orbits are periodic except the points of the z- axis which are equilibrium points. We denote this differential system as a linear center in $\mathbb {R}^3$.

The aim of this paper is to study the maximum number of crossing limit cycles that the discontinuous piecewise differential systems formed by two linear centers (after applying an affine change of variables) and separated by the paraboloid either $P_E$ or $P_H$ can have. Moreover, we also want to show that this maximum is reached.

Our main result is as follows.

Theorem 1

Consider discontinuous piecewise linear differential systems in $\mathbb {R}^3$ formed by two linear centers (after applying an affine change of variables) and separated by a paraboloid ( elliptic or hyperbolic). The following statements hold:

(i):

The maximum number of limit cycles in both cases is one.

(ii):

In both cases there are systems without crossing periodic orbits.

(iii):

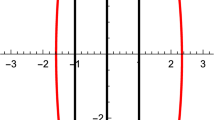
In both cases there are systems with a continuum of crossing periodic orbits. See Fig. 1 for the case of the elliptic paraboloid and Fig. 2 for the case of the hyperbolic paraboloid.

(iv):

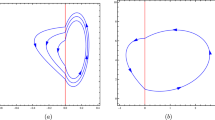
In both cases there are systems with one crossing limit cycle. See Fig. 3 for the case of the elliptic paraboloid and Fig. 4 for the case of the hyperbolic paraboloid.

Theorem 1 is proved in Sect. 3.

Fig. 1

The three crossing periodic orbits $S^i$, $i=1,2,3$ of the discontinuous piecewise differential system formed by the linear systems (26) and (27)

Fig. 2

The three crossing periodic orbits $S^i$, $i=1,2,3$ of the discontinuous piecewise differential system formed by the linear systems (29) and (30)

Fig. 3

One crossing limit cycle intersecting $P_E$

Fig. 4

One crossing limit cycle intersecting $P_H$

Preliminaries

The linear differential systems considered in each piece $\mathcal {R}_E^1, \mathcal {R}_E^2, \mathcal {R}_H^1$ and $\mathcal {R}_H^2$ are linear differential centers (1) after applying a general affine transformation. More precisely, we shall use the next result.

Lemma 1

Doing a rescaling of the independent variable after the affine change of variables given by

$$\begin{aligned} x=a_1X+a_2Y+a_3Z+a_4,\quad y=b_1X+b_2Y+b_3Z+b_4\ \ \text{ and } \quad z=c_1X+c_2Y+c_3Z+c_4, \end{aligned}$$

where $a_i, b_i, c_i \in {\mathbb {R}}$ for $i=1,2,3,4$ and

$$\begin{aligned} ( a_2 b_3-a_3 b_2 )c_1 +( a_3 b_1 - a_1 b_3 )c_2 +( a_1 b_2- a_2 b_1 ) c_3\ne 0, \end{aligned}$$

system (1) becomes

$$\begin{aligned} \begin{aligned} \dot{X}=&((a_1 a_3 + b_1 b_3 )c_2 -( a_1 a_2+ b_1 b_2) c_3) X + ((a_2 a_3 + b_2 b_3 )c_2 - (a_2^2 + b_2^2 )c_3) Y \\ {}&+ ((a_3^2 + b_3^2 )c_2 - (a_2 a_3 + b_2 b_3) c_3) Z+(a_3 a_4 + b_3 b_4 )c_2 - (a_2 a_4 + b_2 b_4 )c_3,\\ \dot{Y}=&(-(a_1 a_3 + b_1 b_3) c_1 + (a_1^2 + b_1^2 )c_3) X + (-(a_2 a_3 + b_2 b_3 )c_1 + (a_1 a_2 + b_1 b_2) c_3) Y\\ {}&+ (-(a_3^2 + b_3^2) c_1 + (a_1 a_3 + b_1 b_3) c_3) Z-(a_3 a_4 + b_3 b_4 )c_1 + (a_1 a_4 + b_1 b_4) c_3,\\ \dot{Z}=&((a_1 a_2 + b_1 b_2) c_1 - (a_1^2 + b_1^2) c_2) X + ((a_2^2 + b_2^2) c_1 -( a_1 a_2 + b_1 b_2 )c_2) Y \\ {}&+ ((a_2 a_3 + b_2 b_3) c_1 - (a_1 a_3 + b_1 b_3 )c_2) Z+(a_2 a_4 + b_2 b_4) c_1 -( a_1 a_4 + b_1 b_4) c_2. \end{aligned} \end{aligned}$$

(2)

Moreover, two linearly independent first integrals of the differential system (2) are

$$\begin{aligned} \begin{aligned} F_1(X,Y,Z)&=( a_1 X + a_2 Y + a_3 Z+a_4)^2 + ( b_1 X + b_2 Y + b_3 Z+b_4)^2,\\ F_2(X,Y,Z)&= c_1 X + c_2 Y + c_3 Z+c_4. \end{aligned} \end{aligned}$$

(3)

In general, studying crossing periodic orbits of discontinuous piecewise differential systems is a very difficult problem. And a useful tool that allows studying these periodic orbits is to verify if the differential systems that compose the piecewise differential system are completely integrable. We recall that a differential system in $\mathbb {R}^3$ is completely integrable if it has two first integrals linearly independent because then we can describe an orbit that passes through a given point p as the intersection of all level surfaces to which the point p belongs. It is known that linear differential systems are always completely integrable.

Therefore in order to study crossing periodic orbits of a piecewise differential system in $\mathbb {R}^3$ formed by two linear differential systems, which intersect the discontinuity surface in the points $p_0$ and $p_1$, these points must belong to the intersection of the same level surfaces to both differential systems, this is, they must satisfy the following closing equations

$$\begin{aligned} \begin{array}{rl} F_1(p_0)&{}=F_1(p_1),\\ F_{2}(p_0)&{}=F_{2}(p_1),\\ G_1(p_0)&{}=G_1(p_1),\\ G_{2}(p_0)&{}=G_{2}(p_1), \end{array} \end{aligned}$$

(4)

where $F_{i}(x_1, x_2, x_3)$ and $G_i(x_1, x_2, x_3)$ for $i=1,2$, are the linearly independent first integrals of the systems that compose the discontinuous piecewise differential system. This tool has been used in the papers [9, 10]. We use the same technique in the proof of Theorem 1.

Proof of Theorem 1

Proof of statement (i)

We have two cases, first when the discontinuity surface is an elliptic paraboloid $(P_E)$ and second when the discontinuity surface is a hyperbolic paraboloid $(P_H)$. Here we only provide all the details of the proof of statement (i) considering that the discontinuity surface is $P_E$, because the proof considering the paraboloid $P_H$ is completely analogous.

By Lemma 1, we consider the discontinuous piecewise differential systems such that in the region $\mathcal {R}_E^1$ is considered the linear differential center (2), which has the two linearly independent first integrals (3) and in the region $\mathcal {R}_E^2$ we consider the linear differential center

$$\begin{aligned} \begin{aligned} \dot{X}=&( (\alpha _1 \alpha _3 + \beta _1 \beta _3) \gamma _2 - (\alpha _1 \alpha _2 + \beta _1 \beta _2) \gamma _3) X + ((\alpha _2 \alpha _3 + \beta _2 \beta _3) \gamma _2 - (\alpha _2^2 + \beta _2^2) \gamma _3) Y \\ {}&+ ((\alpha _3^2 + \beta _3^2) \gamma _2 - (\alpha _2 \alpha _3 + \beta _2 \beta _3) \gamma _3) Z+(\alpha _3 \alpha _4 + \beta _3 \beta _4) \gamma _2 - (\alpha _2 \alpha _4 + \beta _2 \beta _4 )\gamma _3,\\ \dot{Y}=&(-(\alpha _1 \alpha _3 +\beta _1 \beta _3) \gamma _1 +( \alpha _1^2 + \beta _1^2 )\gamma _3) X + (-(\alpha _2 \alpha _3+ \beta _2 \beta _3) \gamma _1 + (\alpha _1 \alpha _2 + \beta _1 \beta _2 )\gamma _3) Y\\ {}&+ ((-\alpha _3^2 + \beta _3^2) \gamma _1 + (\alpha _1 \alpha _3 + \beta _1 \beta _3) \gamma _3) Z-(\alpha _3 \alpha _4 + \beta _3 \beta _4) \gamma _1 + (\alpha _1 \alpha _4 + \beta _1 \beta _4) \gamma _3,\\ \dot{Z}=&((\alpha _1 \alpha _2 + \beta _1 \beta _2) \gamma _1 - (\alpha _1^2 + \beta _1^2 )\gamma _2) X + ((\alpha _2^2 + \beta _2^2) \gamma _1 - (\alpha _1 \alpha _2 + \beta _1 \beta _2) \gamma _2) Y \\ {}&+ ((\alpha _2 \alpha _3 + \beta _2 \beta _3 )\gamma _1 - (\alpha _1 \alpha _3 + \beta _1 \beta _3 )\gamma _2) Z+(\alpha _2 \alpha _4 + \beta _2 \beta _4) \gamma _1 - (\alpha _1 \alpha _4 + \beta _1 \beta _4) \gamma _2. \end{aligned} \end{aligned}$$

(5)

Where $\alpha _i, \beta _i, \gamma _i \in {\mathbb {R}}$ for $i=1,2,3,4$ and

$$\begin{aligned} ( \alpha _2 \beta _3-\alpha _3 \beta _2 )\gamma _1 +( \alpha _3 \beta _1 - \alpha _1 \beta _3 )\gamma _2 +( \alpha _1 \beta _2- \alpha _2 \beta _1 ) \gamma _3\ne 0. \end{aligned}$$

This system has the two linearly independent first integrals

$$\begin{aligned} \begin{aligned} G_1(X,Y,Z)&=( \alpha _1 X + \alpha _2 Y + \alpha _3 Z+\alpha _4)^2 + ( \beta _1 X + \beta _2 Y + \beta _3 Z+\beta _4)^2,\\ G_2(X,Y,Z)&= \gamma _1 X + \gamma _2 Y + \gamma _3 Z+\gamma _4. \end{aligned} \end{aligned}$$

In order to have a crossing periodic orbit that intersects the discontinuity surface $P_E$ in two points $p_0=(X_0, Y_0, Z_0)$ and $p_1=(X_1, Y_1, Z_1)$, using (4) we obtain that these points must satisfy the following equivalent system

$$\begin{aligned} \begin{array}{cc} e_1:&{} (a_4 + a_1 X_0 + a_2 Y_0 + a_3 Z_0)^2 + (b_4 + b_1 X_0 + b_2 Y_0 + b_3 Z_0)^2 \\ {} &{}- (a_4 + a_1 X_1 + a_2 Y_1 + a_3 Z_1)^2 - (b_4 + b_1 X_1 + b_2 Y_1 + b_3 Z_1)^2=0,\\ e_2:&{} c_1 X_0 - c_1 X_1 + c_2 Y_0 - c_2 Y_1 + c_3 Z_0 - c_3 Z_1=0,\\ e_3:&{} (X_0 \alpha _1 + Y_0 \alpha _2 + Z_0 \alpha _3 + \alpha _4)^2+ (X_0 \beta _1 + Y_0 \beta _2 + Z_0 \beta _3 + \beta _4)^2 \\ {} &{} - (X_1 \alpha _1 + Y_1 \alpha _2 + Z_1 \alpha _3 + \alpha _4)^2 - (X_1 \beta _1 + Y_1 \beta _2 + Z_1 \beta _3 + \beta _4)^2=0,\\ e_4:&{} X_0 \gamma _1 - X_1 \gamma _1 + Y_0 \gamma _2 - Y_1 \gamma _2 + Z_0 \gamma _3 - Z_1 \gamma _3=0,\\ &{}Z_0 - X_0^2 - Y_0^2=0,\\ &{}Z_1 - X_1^2 - Y_1^2=0. \end{array} \end{aligned}$$

(6)

We study two cases: $c_3\gamma _3\ne 0$ and $c_3\gamma _3=0$.

Case 1: $c_3\gamma _3\ne 0$. Setting $E_1=\gamma _3e_2-c_3e_4$, we obtain

$$\begin{aligned} E_1=( c_3 \gamma _1-c_1\gamma _3)(X_1-X_0) - ( c_3 \gamma _2- c_2 \gamma _3 )(Y_1-Y_0). \end{aligned}$$

(7)

We have two subcases: $c_3 \gamma _1 - c_1 \gamma _3 =0$, or $c_3 \gamma _1 - c_1 \gamma _3 \ne 0$.

Subcase 1.1: $c_3 \gamma _1 - c_1 \gamma _3 =0$.

We have $E_1=(c_3\gamma _2-c_2\gamma _3)(Y_0-Y_1)=0$. We have two subcases: $c_3\gamma _2-c_2\gamma _3\ne 0$, or $c_3\gamma _2-c_2\gamma _3=0$.

Subcase 1.1.1: $c_3\gamma _2-c_2\gamma _3\ne 0$. From $E_1$ we obtain that

$$\begin{aligned} Y_1=Y_0. \end{aligned}$$

(8)

Then equations $e_1$, $e_3$ and $e_4$ in system (6) reduce to

$$\begin{aligned} e_1:&(X_0 - X_1) \big (2 a_1 a_4 + 2 b_1 b_4 + (a_1^2 + 2 a_3 a_4 + b_1^2 + 2 b_3 b_4) X_0 + 2( a_1 a_3 + b_1 b_3) X_0^2 \\ {}&+(a_3^2 + b_3^2 )X_0^3 + (a_1^2 + 2 a_3 a_4 + b_1^2 + 2 b_3 b_4) X_1 + 2 (a_1 a_3 + b_1 b_3) X_0 X_1\\&+ (a_3^2 + b_3^2) X_0^2 X_1 + 2 (a_1 a_3 + b_1 b_3 )X_1^2 + (a_3^2 + b_3^2) X_0 X_1^2 + (a_3^2 b_3^2 )X_1^3 \\ {}&+ 2( a_1 a_2 + b_1 b_2 )Y_0 + 2 (a_2 a_3 + b_2 b_3) X_0 Y_0 + 2 (a_2 a_3 + b_2 b_3) X_1 Y_0 + 2 (a_1 a_3 \\ {}&+ b_1 b_3) Y_0^2 + 2 (a_3^2 + b_3^2) X_0 Y_0^2 + 2 (a_3^2 + b_3^2) X_1 Y_0^2\big ),\\ e_3:&(X_0 - X_1) \big ((X_0 + X_1) \alpha _1^2 + 2 Y_0 \alpha _1 \alpha _2 + 2(X_0^2 + X_0 X_1 + X_1^2 + Y_0^2 )\alpha _1 \alpha _3 \\ {}&+ 2 (X_0+X_1) Y_0 \alpha _2 \alpha _3 + X_0^3 \alpha _3^2 + X_0^2 X_1 \alpha _3^2 + X_0 X_1^2 \alpha _3^2 + X_1^3 \alpha _3^2 + 2 X_0 Y_0^2 \alpha _3^2 \\ {}&+ 2 X_1 Y_0^2 \alpha _3^2 + 2 \alpha _1 \alpha _4 + 2 (X_0 + X_1 )\alpha _3 \alpha _4 + (X_0 + X_1) \beta _1^2 + 2 Y_0 \beta _1 \beta _2 + 2 X_0^2 \beta _1 \beta _3 \\ {}&+ 2 (X_0 X_1 + X_1^2 + Y_0^2 )\beta _1 \beta _3 + 2 X_0 Y_0 \beta _2 \beta _3 + 2 X_1 Y_0 \beta _2 \beta _3 + X_0^3 \beta _3^2 + X_0^2 X_1 \beta _3^2\\ {}&+ X_0 X_1^2 \beta _3^2 + X_1^3 \beta _3^2 + 2 X_0 Y_0^2 \beta _3^2 + 2 X_1 Y_0^2 \beta _3^2 + 2 \beta _1 \beta _4 + 2 X_0 \beta _3 \beta _4+ 2 X_1 \beta _3 \beta _4\big ),\\ e_4:&(X_0 - X_1) (\gamma _1 + X_0 \gamma _3 + X_1 \gamma _3). \end{aligned}$$

We observe that we can consider $X_0\ne X_1$, because if $X_0= X_1$ from (8), we would have that $p_0=p_1$, and consequently we would not have limit cycles. From equation $e_4$ we get

$$\begin{aligned} X_1=\dfrac{-\gamma _1-X_0\gamma _3}{\gamma _3}. \end{aligned}$$

(9)

Now we introduce $X_1$ into $e_1$ and $e_3$ and we obtain

$$\begin{aligned} \begin{array}{rl} e_1:&{}-((a_3^2 + b_3^2) \gamma _1^3) + 2 (a_1 a_3 + b_1 b_3) \gamma _1^2 \gamma _3 - (a_1^2 + 2 a_3 a_4 + b_1^2 + 2 b_3 b_4) \gamma _1 \gamma _3^2 + 2 (a_1 a_4 \\ {} &{}+ b_1 b_4) \gamma _3^3+ 2 \gamma _3 X_0 \gamma _1(- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3) + 2 Y_0 (- a_2 a_3 \gamma _1 \gamma _3^2 \\ {} &{}- b_2 b_3 \gamma _1 \gamma _3^2 + a_1 a_2 \gamma _3^3 + b_1 b_2 \gamma _3^3)+ 2\gamma _3^2 X_0^2 (- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3)\\ {} &{} + 2\gamma _3^2 Y_0^2 (- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3),\\ e_3:&{}-((\alpha _3^2 + \beta _3^2) \gamma _1^3) + 2 (\alpha _1 \alpha _3 + \beta _1 \beta _3) \gamma _1^2 \gamma _3 - (\alpha _1^2 + 2 \alpha _3 \alpha _4 + \beta _1^2 + 2 \beta _3 \beta _4) \gamma _1 \gamma _3^2 \\ {} &{}+ 2 (\alpha _1 \alpha _4 + \beta _1 \beta _4) \gamma _3^3+2\gamma _1 \gamma _3X_0 (-\alpha _3^2 \gamma _1 - \beta _3^2 \gamma _1 + \alpha _1 \alpha _3 \gamma _3 + \beta _1 \beta _3 \gamma _3) \\ {} &{}+ 2Y_0 (- \alpha _2 \alpha _3 \gamma _1 \gamma _3^2 - \beta _2 \beta _3 \gamma _1 \gamma _3^2 + \alpha _1 \alpha _2 \gamma _3^3 + \beta _1 \beta _2 \gamma _3^3) + 2\gamma _3^2 X_0^2 (- \alpha _3^2 \gamma _1 - \beta _3^2 \gamma _1 \\ {} &{}+ \alpha _1 \alpha _3 \gamma _3^2 + \beta _1 \beta _3 \gamma _3^2) + 2\gamma _3^2 Y_0^2 (- \alpha _3^2 \gamma _1 - \beta _3^2 \gamma _1 + \alpha _1 \alpha _3 \gamma _3^2 + \beta _1 \beta _3 \gamma _3^2). \end{array} \end{aligned}$$

(10)

Analyzing equation $e_1$ we have two subcases: $\gamma _1(- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3)\ne 0$, or $\gamma _1(- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3)= 0$.

Subcase 1.1.1.1: $\gamma _1(- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3)\ne 0.$ From equation $e_1$ we can isolate the variable $X_0$ and we get

$$\begin{aligned} X_0^{\pm }=&\dfrac{1}{4(- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3)}\bigg (2 (a_3^2+ b_3^2)\gamma _1^2 \gamma _3 - 2 (a_1 a_3+b_1 b_3) \gamma _1 \gamma _3^2 \\ {}&\pm \sqrt{}\big (-2( a_3^2 + b_3^2) \gamma _1^2 \gamma _3 + 2 a_1 a_3 \gamma _1 \gamma _3^2 + 2 b_1 b_3 \gamma _1 \gamma _3^2)^2 - 4 (-2 a_3^2 \gamma _1 \gamma _3^2 - 2 b_3^2 \gamma _1 \gamma _3^2 \\ {}&+ 2 (a_1 a_3 + b_1 b_3) \gamma _3^3) (-(a_3^2 + b_3^2) \gamma _1^3 + 2 (a_1 a_3+ b_1 b_3) \gamma _1^2 \gamma _3 - (a_1^2 + 2 a_3 a_4 )\gamma _1 \gamma _3^2 \\ {}&+(- b_1^2 - 2 b_3 b_4 - 2 a_2 a_3 Y_0 - 2 b_2 b_3 Y_0 - 2 a_3^2 Y_0^2 - 2 b_3^2 Y_0^2 )\gamma _1 \gamma _3^2 + 2 (a_1 a_4 \\ {}&+ 2 b_1 b_4 + 2 a_1 a_2 Y_0 + 2 b_1 b_2 Y_0 + 2 a_1 a_3 Y_0^2 + 2 b_1 b_3 Y_0^2) \gamma _3^3)\big )\bigg ). \end{aligned}$$

We observe that

$$\begin{aligned} X_0^++X_0^-=-\dfrac{\gamma _1}{\gamma _3}. \end{aligned}$$

(11)

Consider $X_0^{-}$. From (9) we have $X_1^-=(-\gamma _1-X_0^- \gamma _3)/\gamma _3$ and from equation $e_3$ in (10), we obtain

$$\begin{aligned} Y_0^-=&\big ((\gamma _3 ((a_1^2 + b_1^2) \gamma _1 - 2 (a_1 a_4 + b_1 b_4) \gamma _3) + 2 (a_3 a_4+ b_3 b_4) \gamma _1 \gamma _3) ((\alpha _3^2 + \beta _3^2) \gamma _1 \\ {}&- (\alpha _1 \alpha _3+ \beta _1 \beta _3) \gamma _3) + (a_3^2 \gamma _1 + b_3^2 \gamma _1) ((\alpha _1 \alpha _3 + \beta _1 \beta _3) \gamma _1^2 - (\alpha _1^2 + 2 \alpha _3 \alpha _4 + \beta _1^2\\ {}&+ 2 \beta _3 \beta _4) \gamma _1 \gamma _3 + 2 (\alpha _1 \alpha _4 + \beta _1 \beta _4) \gamma _3^2) + (a_1 a_3 + b_1 b_3 ) (-((\alpha _3^2 + \beta _3^2) \gamma _1^3) + (\alpha _1^2 \\ {}&+ 2 \alpha _3 \alpha _4 + \beta _1^2 + 2 \beta _3 \beta _4)\gamma _1 \gamma _3^2 - 2 (\alpha _1 \alpha _4 + \beta _1 \beta _4) \gamma _3^3) \big )/\big (2 \gamma _3 ((a_3^2 \gamma _1 + b_3^2 \gamma _1 - a_3 a_1 \gamma _3 \\ {}&- b_3 b_1 \gamma _3) (\alpha _2 \alpha _3 \gamma _1 + \beta _2 \beta _3 \gamma _1- \alpha _1 \alpha _2 \gamma _3 - \beta _1 \beta _2 \gamma _3) + ((a_1 a_2 + b_1 b_2) \gamma _3 - a_3 a_2 \gamma _1 \\ {}&- b_3 b_2 \gamma _1 ) ((\alpha _3^2 + \beta _3^2) \gamma _1 - ( \alpha _1 \alpha _3 + \beta _1 \beta _3) \gamma _3))\big ). \end{aligned}$$

Using this and also (8), we have that

$$\begin{aligned} (X_0^-,Y_0^-,Z_0^-,X_1^-,Y_0^-,Z_1^-) \end{aligned}$$

(12)

is a solution of system (6).

Now if we consider $X_0^+$, by (9) we have $X_1^+=(-\gamma _1-X_0^+\gamma _3)/\gamma _3$ and by equation $e_3$ we get $Y_0^+$, which satisfies that

$$\begin{aligned} Y_0^+=Y_0^-. \end{aligned}$$

Moreover by (9) and (11) we have that

$$\begin{aligned} X_1^+=-\dfrac{\gamma _1}{\gamma _3}-X_0^+=X_0^- \ \text{ and }\ \ X_1^-=-\dfrac{\gamma _1}{\gamma _3}-X_0^-=X_0^+. \end{aligned}$$

From the above conditions and by (8), the second solution is given by

$$\begin{aligned} (X_0^+,Y_0^+,Z_0^+,X_1^+,Y_0^+,Z_1^+)=(X_1^-,Y_0^-,Z_1^-,X_0^-,Y_0^-,Z_0^-). \end{aligned}$$

That is, the second solution provides the same periodic orbit than the solution (12). Therefore in this case we have proved that it is possible to have at most one limit cycle intersecting the paraboloid $P_E$ in two different points $p_0$ and $p_1$.

Subcase 1.1.1.2: $\gamma _1 (- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3)= 0.$ We have three subcases: $\gamma _1=0$ and $-2 a_3^2 \gamma _1 - 2 b_3^2 \gamma _1 + 2 a_1 a_3 \gamma _3 + 2 b_1 b_3 \gamma _3\ne 0$, or $\gamma _1\ne 0$ and $-2 a_3^2 \gamma _1 - 2 b_3^2 \gamma _1 + 2 a_1 a_3 \gamma _3 + 2 b_1 b_3 \gamma _3= 0$, or $\gamma _1=0$ and $-2 a_3^2 \gamma _1 - 2 b_3^2 \gamma _1 + 2 a_1 a_3 \gamma _3 + 2 b_1 b_3 \gamma _3= 0$.

Subcase 1.1.1.2.1: $\gamma _1=0$ and $- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3\ne 0$. When $\gamma _1=0$, from $e_1$ in (10) we obtain

$$\begin{aligned} X_0^{\pm }=\pm \dfrac{\sqrt{-a_1 a_4 - b_1 b_4 - a_1 a_2 Y_0 - b_1 b_2 Y_0 - a_1 a_3 Y_0^2 - b_1 b_3 Y_0^2}}{\sqrt{a_1 a_3 + b_1 b_3}}. \end{aligned}$$

If we consider $X_0^-$, from (9) and $e_3$ we obtain $X_1^-$ and $Y_0^-$, respectively. Similarly to Subcase 1.1.1.1, if we consider $X_0^+$ we get $X_1^+$ and $Y_0^+$. But then we have that

$$\begin{aligned} X_0^-=X_1^+, \ X_1^-=X_0^+, \ \text{ and }\ \ Y_0^-=Y_0^+. \end{aligned}$$

So we only have one solution of system (6) and therefore at most one limit cycle.

Subcase 1.1.1.2.2: $\gamma _1\ne 0$ and $- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3= 0$. If $a_3^2+b_3^2\ne 0$, from $- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3= 0$ we get

$$\begin{aligned} \gamma _1=\dfrac{(a_1 a_3+b_1 b_3)\gamma _3}{a_3^2+b_3^2}. \end{aligned}$$

Substituting into equation $e_1$, we get

$$\begin{aligned} e_1:&\dfrac{\gamma _3^3 (a_3 b_1 - a_1 b_3)}{(a_3^2 + b_3^2) }\Big ( \dfrac{(a_1a_3+b_1 b_3 )(a_1b_3 -a_3 b_1)}{(a_3^2 + b_3^2)} +2(a_3 b_4- a_4 b_3) + 2 (a_3 b_2 - a_2 b_3) Y_0\Big ). \end{aligned}$$

If $a_1 b_3 - a_3 b_1=0$ we have that $e_1\equiv 0$ and equation $e_3=0$ has two unknowns $X_0$ and $Y_0$. Then if there are solutions for this equation, we would have a continuum of solutions that would generate a continuum of crossing periodic solutions, and so we would not have limit cycles.

If $a_1 b_3 - a_3 b_1\ne 0$ and $a_3 b_2 - a_2 b_3=0$ then equation $e_1=0$ only provides conditions for the parameters $a_i, b_i$ for $i=1,3,4$, and moreover to solve system (6) it is equivalent to solve equation $e_3=0$ which has two unknowns $X_0$ and $Y_0$. As before, we cannot have limit cycles.

If $a_1 b_3 - a_3 b_1\ne 0$ and $a_3b_2-a_2b_3\ne 0$, then we have

$$\begin{aligned}Y_0=&\dfrac{(a_1a_3+b_1b_3)(a_3b_1-a_1b_3)+2(a_4 b_3-a_3b_4)(a_3^2+b_3^2)}{2(a_3b_2-a_2b_3)(a_3^3+b_3^2)}. \end{aligned}$$

Substituting $Y_0$ into equation $e_3$ we obtain $X_0^{\pm }$. Similarly to the above case, if we consider $X_0^-$, using (9) we obtain $X_1^-$ and then we have the solution $(X_0^-,Y_0,Z_0^-,X_1^-,Y_0,Z_1^-)$. Considering $X_0^+$ we get $X_1^+$, but we have that

$$\begin{aligned} X_0^-=X_1^+, \ X_1^-=X_0^+. \end{aligned}$$

Then the second solution provides the same periodic orbit as the first one. Therefore in this case we only have one solution for system (6), and hence at most one limit cycle intersecting the paraboloid $P_E$ in two points.

If $a_3^2+b_3^2= 0$, equation $e_1$ in (10) becomes

$$\begin{aligned} e_1: 2\gamma _3^3 (a_1 a_2 + b_1 b_2 ) Y_0+ \gamma _3^2 ( 2\gamma _3 (a_1 a_4 + b_1 b_4)-(a_1^2 + b_1^2) \gamma _1). \end{aligned}$$

If $a_1 a_2 + b_1 b_2=0$, equation $e_1=0$ provides conditions for the parameters $a_1, a_4, b_1, b_4$, $\gamma _1, \gamma _3$, and similarly to the above case, equation $e_3=0$ has two unknowns $X_0$ and $Y_0$ and as before, we cannot have limit cycles.

Considering that $a_1a_2+b_1b_2\ne 0$, from $e_1$ we get

$$\begin{aligned} Y_0=\dfrac{a_1^2 \gamma _1 + b_1^2 \gamma _1 - 2 a_1 a_4 \gamma _3 - 2 b_1 b_4 \gamma _3}{2 (a_1 a_2 + b_1 b_2) \gamma _3}. \end{aligned}$$

Substituting it in equation $e_3$ we obtain $X_0^{\pm }$, and similarly to the above cases, the two possible solutions generate the same periodic orbit, and so we have at most one limit cycle.

Subcase 1.1.1.2.3: $\gamma _1=0$ and $- a_3^2 \gamma _1 - b_3^2 \gamma _1 + a_1 a_3 \gamma _3 + b_1 b_3 \gamma _3= 0.$ This condition is equivalent to $\gamma _1=0$ and

$$\begin{aligned} a_1 a_3 +b_1 b_3=0. \end{aligned}$$

(13)

From (13) we obtain that when $a_3 \ne 0$ then $a_1=-b_1b_3/a_3$. In this case equation $e_1$ becomes

$$\begin{aligned} e_1:\dfrac{2 b_1 \gamma _3^3}{a_3}\Big ((a_3 b_4 - a_4 b_3 )+ (a_3 b_2 - a_2 b_3) Y_0\Big ). \end{aligned}$$

If $b_1=0$ then $e_1\equiv 0$ and as in the above case, equation $e_3=0$ has two unknowns $X_0$ and $Y_0$, and if there are solutions for this equation, we would have a continuum of crossing periodic orbits and so we do not have limit cycles.

If $b_1\ne 0$ and $a_3b_2-a_3b_3=0$, equation $e_1=0$ provides conditions for the parameters $a_3, a_4, b_3$ and $b_4$, and again $e_3=0$ has two unknowns $X_0$ and $Y_0$, and so we cannot have limit cycles.

If $b_1\ne 0$ and $a_3b_2-a_3b_3\ne 0$ then from equation $e_1$, we get $Y_0=(a_4b_3-a_3b_4)/(a_3b_2-a_2b_3)$. In this case, substituting it in equation $e_3$ we obtain $X_0^{\pm }$, and as in the above cases the two possible solutions generate only one periodic orbit and then we have at most one limit cycle.

When $a_3=0$, from the condition (13) we obtain three possibilities, namely either $b_1=0$ and $b_3\ne 0$, or $b_1\ne 0$ and $b_3=0$, or $b_1=0=b_3$. In all cases, we obtain the expression for $Y_0$ by equation $e_1$ in (10) and substituting it in equation $e_3$ we obtain $X_0^{\pm }$. These points satisfy $X_0^+=X_1^-$ and $X_0^-=X_1^+$, that is, the two possible solutions $(X_0^{\pm },Y_{0},Z_0^{\pm },X_1^{\pm },Y_0,Z_1^{\pm })$ generate the same periodic orbit. Therefore we can have at most one crossing limit cycle.

Subcase 1.1.2: $c_3 \gamma _2 - c_2 \gamma _3 = 0$. In this case, we have that equations $e_2$ and $e_4$ in (6) satisfy,

$$\begin{aligned} e_2=\dfrac{c_3}{\gamma _3}e_4, \end{aligned}$$

this is, system (6) reduces to system which has three polynomial equations and four unknowns $X_0, X_1, Y_0, Y_1$, if there are solutions for this system, then it would have a continuum of solutions that produce a continuum of crossing periodic solutions, then we cannot have crossing limit cycles.

Subcase 1.2: $c_3 \gamma _1 - c_1 \gamma _3 \ne 0$. From (7) we get

$$\begin{aligned} X_0=\dfrac{(c_3 \gamma _1 - c_1 \gamma _3)X_1 -(c_3 \gamma _2 - c_2 \gamma _3 )(Y_1-Y_0)}{ c_3 \gamma _1 - c_1 \gamma _3}. \end{aligned}$$

(14)

Substituting this expression of $X_0$ into system (6), we obtain that equations $e_1, e_3 \ \text{ and }\ e_4,$ have as common factor $Y_1-Y_0$, and we observed that this factor can be eliminated because if $Y_1 = Y_0$, by (14) we would have that $p_0=p_1$, and consequently we would not have limit cycles.

The expression for equation $e_4$ is

$$\begin{aligned} \begin{array}{rl}e_4:&{}-(c_2 \gamma _1 - c_1 \gamma _2) (c_3 \gamma _1 - c_1 \gamma _3)+2X_1 (c_3 \gamma _2 - c_2 \gamma _3) (c_3 \gamma _1 - c_1 \gamma _3) +Y_0(-c_3^2 (\gamma _1^2 + \gamma _2^2) \\ {} &{}+ 2 c_3 (c_1 \gamma _1 + c_2 \gamma _2) \gamma _3 - (c_1^2 + c_2^2) \gamma _3^2)-Y_1((c_3 (\gamma _1 - \gamma _2) + (c_2 - c_1) \gamma _3) (c_3 (\gamma _1 + \gamma _2)\\ {} &{} - (c_1 + c_2) \gamma _3)).\end{array}\end{aligned}$$

(15)

Then we have two subcases, either $c_3 \gamma _2 - c_2 \gamma _3=0$, or $c_3 \gamma _2 - c_2 \gamma _3\ne 0.$

Subcase 1.2.1: $c_3 \gamma _2 - c_2 \gamma _3 = 0$. We obtain that $c_2=c_3\gamma _2/\gamma _3.$ Moreover by (14), we get that

$$\begin{aligned} X_0=X_1. \end{aligned}$$

(16)

And from (15) we obtain

$$\begin{aligned} Y_0=-Y_1-\dfrac{\gamma _2}{\gamma _3}. \end{aligned}$$

(17)

Substituting these expressions into equations $e_1$ and $e_3$, we have

$$\begin{aligned} \begin{array}{rl} e_1=&{}(a_3^2 + b_3^2) \gamma _2^3 - 2 (a_2 a_3 + b_2 b_3) \gamma _2^2 \gamma _3 + (a_2^2 + 2 a_3 a_4 + b_2^2 + 2 b_3 b_4) \gamma _2 \gamma _3^2 - 2 (a_2 a_4 \\ {} &{}+ b_2 b_4) \gamma _3^3 + 2 \gamma _2 \gamma _3 Y_1 ((a_3^2 + b_3^2) \gamma _2 - (a_2 a_3 + b_2 b_3) \gamma _3)+ 2 \gamma _3^2 X_1 (a_1 a_3 \gamma _2 \\ {} &{}+ b_1 b_3 \gamma _2 - a_1 a_2 \gamma _3 - b_1 b_2 \gamma _3)+ 2 \gamma _3^2 X_1^2 ( (a_3^2 + b_3^2) \gamma _2 - (a_2 a_3+ b_2 b_3) \gamma _3) \\ {} &{}+ 2 \gamma _3^2 Y_1^2 ((a_3^2 + b_3^2) \gamma _2 - (a_2 a_3 + b_2 b_3) \gamma _3),\\ e_3=&{}(\alpha _3^2 + \beta _3^2) \gamma _2^3 - 2 (\alpha _2 \alpha _3 + \beta _2 \beta _3) \gamma _2^2 \gamma _3 + (\alpha _2^2 + 2 \alpha _3 \alpha _4 + \beta _2^2 + 2 \beta _3 \beta _4) \gamma _2 \gamma _3^2 \\ {} &{}- 2 (\alpha _2 \alpha _4 + \beta _2 \beta _4) \gamma _3^3 + 2 \gamma _2 \gamma _3 Y_1 ((\alpha _3^2 + \beta _3^2) \gamma _2 - ( \alpha _2 \alpha _3 + \beta _2 \beta _3) \gamma _3) + 2 \gamma _3^2 X_1 \\ {} &{} (\alpha _1 \alpha _3 \gamma _2 + \beta _1 \beta _3 \gamma _2- \alpha _1 \alpha _2 \gamma _3 - \beta _1 \beta _2 \gamma _3) + 2 \gamma _3^2 X_1^2 ((\alpha _3^2 + \beta _3^2) \gamma _2 - (\alpha _2 \alpha _3 \\ {} &{}+ \beta _2 \beta _3) \gamma _3)+ 2 \gamma _3^2Y_1^2 ((\alpha _3^2 + \beta _3^2) \gamma _2 - (\alpha _2 \alpha _3 + \beta _2 \beta _3) \gamma _3). \end{array} \end{aligned}$$

(18)

By equation $e_1$ we can have two subcases: $(a_3^2 + b_3^2) \gamma _2 - (a_2 a_3+ b_2 b_3) \gamma _3=0$, or $(a_3^2 + b_3^2) \gamma _2 - (a_2 a_3+ b_2 b_3) \gamma _3\ne 0$.

Subcase 1.2.1.1: $(a_3^2 + b_3^2) \gamma _2 - (a_2 a_3+ b_2 b_3) \gamma _3=0$. If we consider $a_3^2 + b_3^2\ne 0$, by $(a_3^2 + b_3^2) \gamma _2 - (a_2 a_3+ b_2 b_3) \gamma _3=0$, we obtain

$$\begin{aligned} \gamma _2=\dfrac{(a_2 a_3 + b_2 b_3) \gamma _3}{a_3^2 + b_3^2}. \end{aligned}$$

(19)

Hence from $e_1$ we get

$$\begin{aligned} X_1=-\dfrac{2(a_3b_1-a_1b_3)(a_3 b_2 - a_2 b_3) \gamma _3^2}{a_3^2 + b_3^2}. \end{aligned}$$

Now we introduce $X_1$ into $e_3$ and we obtain two options for $Y_1$, namely $Y_1^+$ and $Y_1^-$, which satisfy

$$\begin{aligned} Y_1^+ +Y_1^-=-\dfrac{a_2a_3+b_2b_3}{a_3^2+b_3^2}. \end{aligned}$$

(20)

Then we have two real solutions, namely $S^{\pm }=(X_0^{\pm },Y_0^{\pm },Z_0^{\pm },X_1^{\pm },Y_1^{\pm },Z_1^{\pm })$, but from (16), we have that $X_0^{\pm }=X_1^{\pm }$. Moreover from equation (17) we obtain two options for $Y_0$, this is,

$$\begin{aligned} Y_0^{\pm }=-Y_1^{\pm }-\dfrac{\gamma _2}{\gamma _3}. \end{aligned}$$

(21)

Then by equations (19), (20) and (21), we have that

$$\begin{aligned} Y_0^+&=-Y_1^+ -\dfrac{\gamma _2}{\gamma _3}=Y_1^- +\dfrac{a_2 a_3+b_2b_3}{a_3^2+b_3^2}-\dfrac{\gamma _2}{\gamma _3}=Y_1^-,\\ Y_0^-&=-Y_1^- -\dfrac{\gamma _2}{\gamma _3}=Y_1^+ +\dfrac{a_2 a_3+b_2b_3}{a_3^2+b_3^2}-\dfrac{\gamma _2}{\gamma _3}=Y_1^+. \end{aligned}$$

Then the solution

$$\begin{aligned} S^-=(X_0^-,Y_0^{-},Z_0^{-},X_1^-,Y_1^{-},Z_1^{-})=&(X_0,Y_0^{-},Z_0^{-},X_0,Y_1^{-},Z_1^{-})\\=&(X_0,Y_1^{+},Z_1^{+},X_0,Y_0^{+},Z_0^{+}), \end{aligned}$$

generates the same periodic orbit than the solution $S^+$. Therefore we have proved that it is possible to have at most one real solution of system (6) and so at most one limit cycle that intersects the paraboloid $P_E$ in two points.

If $a_3^2 + b_3^2=0$, we can find the expression for $X_1$ from equation $e_1$ and substituting in equation $e_3$ we get two options for $Y_1$, namely $Y_1^{\pm }$. Moreover these points satisfy that $Y_1^++Y_1^-=-\gamma _2/\gamma _3$ and similarly to the above case, we obtain that $Y_0^+=Y_1^-$ and $Y_0^-=Y_1^+$ and so the two possible solutions $S^{\pm }=(X_0^{\pm },Y_0^{\pm },Z_0^{\pm },X_1^{\pm },Y_1^{\pm },Z_1^{\pm })$ generate the same periodic orbit. In short, we can have at most one limit cycle.

Subcase 1.2.1.2: $(a_3^2 + b_3^2) \gamma _2 - (a_2 a_3+ b_2 b_3) \gamma _3\ne 0$. By equation $e_1$ in (18) we obtain

$$\begin{aligned} Y_1^{\pm }=&\dfrac{-1}{2 \gamma _3^2 ((a_3^2 + b_3^2) \gamma _2 - (a_2 a_3 + b_2 b_3) \gamma _3)}\Big (\gamma _2 \gamma _3 ((a_3^2 + b_3^2) \gamma _2 - (a_2 a_3 + b_2 b_3) \gamma _3) \\ {}&\pm \sqrt{}\big (-\gamma _3^2 ((a_3^2 + b_3^2) \gamma _2 - (a_2 a_3 + b_2 b_3) \gamma _3) ((a_3^2 + b_3^2) \gamma _2^3 - 3 (a_2 a_3 + b_2 b_3) \gamma _2^2 \gamma _3 \\ {}&+ 2 (a_2^2 + b_2^2 + 2 a_3^2 X_1^2 + 2 a_3 (a_4 + a_1 X_1) + 2 b_3 (b_4 + X_1 (b_1 + b_3 X_1))) \gamma _2 \gamma _3^2 \\ {}&- 4 (a_2 (a_4 + X_1 (a_1 + a_3 X_1)) + b_2 (b_4 + X_1 (b_1 + b_3 X_1))) \gamma _3^3)\big )\Big ). \end{aligned}$$

Moreover we observe that

$$\begin{aligned} Y_1^+ +Y_1^-=-\dfrac{\gamma _2}{\gamma _3}. \end{aligned}$$

(22)

Then we have two reals solution, namely $S^{\pm }=(X_0^{\pm },Y_0^{\pm },Z_0^{\pm },X_1^{\pm },Y_1^{\pm },Z_1^{\pm })$. Substituting $Y_1^{\pm }$ in equation $e_3$ in (18) we get expressions for $X_1^{\pm }$. From (17) we have $Y_0^{\pm }=-Y_1^{\pm }-\gamma _2/\gamma _3$. More precisely from (17) and (22) we have that

$$\begin{aligned} Y_0^+=&-Y_1^+-\dfrac{\gamma _2}{\gamma _3}=Y_1^-,\\ Y_0^-=&-Y_1^- -\dfrac{\gamma _2}{\gamma _3}=Y_1^+. \end{aligned}$$

Then for conditions above and by (16) the solution $S^{-}=(X_0,Y_0^{-},Z_0^{-},X_0,Y_1^{-},Z_1^{-})=(X_0,Y_1^{+},Z_1^{+},X_0,Y_0^{+},Z_0^{+})$, generates the same periodic orbit than the solution $S^+$. Therefore we only have one real solution of system (6), and so at most one limit cycle.

Subcase 1.2.2: $c_3 \gamma _2 - c_2 \gamma _3\ne 0.$ From equation $e_4$ in (15) we get

$$\begin{aligned} X_1=&\dfrac{1}{2 (c_3 \gamma _1 - c_1 \gamma _3) (c_3 \gamma _2 - c_2 \gamma _3)}\big ((c_2\gamma _1-c_1\gamma _2)(c_3\gamma _1-c_1\gamma _3)+Y_1(c_3 (\gamma _1 - \gamma _2) \\ {}&+ (c_2 - c_1) \gamma _3) (c_3 (\gamma _1 + \gamma _2) - (c_1 + c_2) \gamma _3) +Y_0(c_3^2 (\gamma _1^2 + \gamma _2^2) - 2 c_3 (c_1 \gamma _1 \\ {}&+ c_2 \gamma _2) \gamma _3 + (c_1^2 + c_2^2) \gamma _3^2)\big ). \end{aligned}$$

Then substituting this expression into equations $e_1$ and $e_3$, they become

$$\begin{aligned} e_1:&k_0+k_1(Y_0+Y_1)+k_2(Y_0^2+Y_1^2)+k_3 Y_0Y_1,\\ e_3:&\eta _0+\eta _1(Y_0+Y_1)+\eta _2(Y_0^2+Y_1^2)+\eta _3 Y_0Y_1. \end{aligned}$$

Where the expressions of the coefficients $k_i$ for $i=0,1,2,3$ are

$$\begin{aligned} k_0=&(c_3 \gamma _1 - c_1 \gamma _3)^2 (a_3^2 (c_2 \gamma _1 - c_1 \gamma _2)^3 + b_3^2 (c_2 \gamma _1 - c_1 \gamma _2)^3 + 2 (c_3 \gamma _2 - c_2 \gamma _3) (-a_1 a_2 (c_2 \gamma _1 \\ {}&- c_1 \gamma _2) (c_3 \gamma _1 - c_1 \gamma _3) - b_1 b_2 (c_2 \gamma _1 - c_1 \gamma _2) (c_3 \gamma _1 - c_1 \gamma _3) - 2 (a_2 a_4 + b_2 b_4) (c_3 \gamma _1 \\ {}&- c_1 \gamma _3)(c_3 \gamma _2 - c_2 \gamma _3) + 2 a_1 a_4 (c_3 \gamma _2 - c_2 \gamma _3)^2 + 2 b_1 b_4 (c_3 \gamma _2 - c_2 \gamma _3)^2 - a_1^2 (c_2 \gamma _1 \\ {}&- c_1 \gamma _2) (-c_3 \gamma _2 + c_2 \gamma _3) - b_1^2 (c_2 \gamma _1 - c_1 \gamma _2) (-c_3 \gamma _2 + c_2 \gamma _3)) - a_3 (c_2 \gamma _1 - c_1 \gamma _2) \\ {}&(a_2 (c_2 \gamma _1 - c_1 \gamma _2) (c_3 \gamma _1 - c_1 \gamma _3) + (-c_3 \gamma _2 + c_2 \gamma _3) (3 a_1 c_2 \gamma _1 - 3 a_1 c_1 \gamma _2 + 4 a_4 c_3 \gamma _2 \\ {}&- 4 a_4 c_2 \gamma _3)) - b_3 (c_2 \gamma _1 - c_1 \gamma _2) (b_2 (c_2 \gamma _1 - c_1 \gamma _2)(c_3 \gamma _1 - c_1 \gamma _3) + (-c_3 \gamma _2 + c_2 \gamma _3) \\ {}&(3 b_1 c_2 \gamma _1 - 3 b_1 c_1 \gamma _2 + 4 b_4 c_3 \gamma _2 - 4 b_4 c_2 \gamma _3))),\\ k_1=&-2 (c_3 \gamma _1 - c_1 \gamma _3)^2 (-a_3^2 (c_2 \gamma _1 - c_1 \gamma _2)^2 (c_3 \gamma _1 - c_1 \gamma _3) - b_3^2 (c_2 \gamma _1 - c_1 \gamma _2)^2 (c_3 \gamma _1 \\ {}&- c_1 \gamma _3) - a_3 (c_2 \gamma _1 - c_1 \gamma _2) (2 a_1 (c_3 \gamma _1 - c_1 \gamma _3) (c_3 \gamma _2 - c_2 \gamma _3) - a_2 (c_3 (\gamma _1 - \gamma _2) \\ {}&+ (-c_1 + c_2) \gamma _3)(c_3 (\gamma _1 + \gamma _2) - (c_1 + c_2) \gamma _3)) - (c_3 \gamma _2 - c_2 \gamma _3) (a_1^2 (c_3 \gamma _1 - c_1 \gamma _3) \\ {}&(c_3 \gamma _2 - c_2 \gamma _3) + b_1^2 (c_3 \gamma _1 - c_1 \gamma _3) (c_3 \gamma _2 - c_2 \gamma _3) - (a_2^2 + b_2^2) (c_3 \gamma _1 - c_1 \gamma _3) (c_3 \gamma _2 \\ {}&- c_2 \gamma _3) - b_1 b_2 (c_3 \gamma _1 - c_3 \gamma _2 - c_1 \gamma _3 + c_2 \gamma _3)(c_3 (\gamma _1 + \gamma _2) - (c_1 + c_2) \gamma _3) - a_1 a_2 (c_3\\ {}&(\gamma _1 - \gamma _2) + (-c_1 + c_2) \gamma _3) (c_3 (\gamma _1 + \gamma _2) - (c_1 + c_2) \gamma _3)) - b_3 (c_2 \gamma _1 - c_1 \gamma _2) (2 b_1 \\ {}&(c_3 \gamma _1 - c_1 \gamma _3) (c_3 \gamma _2 - c_2 \gamma _3) - b_2 (c_3 (\gamma _1 - \gamma _2) + (-c_1 + c_2) \gamma _3) (c_3 (\gamma _1 + \gamma _2) \\ {}&- (c_1 + c_2) \gamma _3))), \\ k_2=&(c_3^2 (\gamma _1^2 + \gamma _2^2) - 2 c_3 (c_1 \gamma _1 + c_2 \gamma _2) \gamma _3 + (c_1^2 + c_2^2) \gamma _3^2)^2 (a_3^2 (c_2 \gamma _1 - c_1 \gamma _2)+ a_3 (-a_2 c_3 \gamma _1 \\ {}&+ a_1c_3 \gamma _2 + a_2 c_1 \gamma _3 - a_1 c_2 \gamma _3) + b_3 (b_3 c_2 \gamma _1 - b_2 c_3 \gamma _1 - b_3 c_1 \gamma _2 + b_1 c_3 \gamma _2 + b_2 c_1 \gamma _3 \\ {}&- b_1 c_2 \gamma _3)), \\ k_3=&2 (c_3 (\gamma _1 - \gamma _2) + (-c_1 + c_2) \gamma _3) (c_3 (\gamma _1 + \gamma _2) - (c_1 + c_2) \gamma _3) (c_3^2 (\gamma _1^2 + \gamma _2^2) - 2 c_3 (c_1 \gamma _1 \\ {}&+ c_2 \gamma _2) \gamma _3 + (c_1^2 + c_2^2) \gamma _3^2) (a_3^2 (c_2 \gamma _1 - c_1 \gamma _2)+ a_3 (-a_2 c_3 \gamma _1 + a_1 c_3 \gamma _2 + a_2 c_1 \gamma _3 \\ {}&- a_1 c_2 \gamma _3) + b_3 (b_3 c_2 \gamma _1 - b_2 c_3 \gamma _1 - b_3 c_1 \gamma _2 + b_1 c_3 \gamma _2 + b_2 c_1 \gamma _3 - b_1 c_2 \gamma _3)). \end{aligned}$$

The expressions of $\eta _i$ for $i=0,1,2,3$ are equals, only interchanging $a_j$ by $\alpha _j$ and $b_j$ by $\beta _j$ for $j=1,2,3,4$.

We know that if $(Y_0, Y_1)$ is a solution of the system $e_1=0$, $e_3=0$, the point $Y_0$ must be a root of the resultant of $e_1$ and $e_3$ with respect to the variable $Y_1$. We denote such a resultant as $R(Y_0)$. Moreover the point $Y_1$ must be a root of the resultant of $e_1$ and $e_3$ with respect to the variable $Y_0$, which we denote it as $R(Y_1)$. In this case, it is possible to verify that by interchanging the variable $Y_0$ by $Y_1$, the expressions of the resultants $R(Y_0)$ and $R(Y_1)$ are the same. Moreover in this case the resultants are polynomials of degree 2. Then we would have at most two reals solutions $Y_0$, $Y_1$ for system $e_1=0=e_3$, and consequently two real solutions $S^{i}=(X_0^i,Y_0^i,Z_0^i,X_1^i,Y_1^i,Z_1^i)$ for system (6). But we can observe that if $(X_0, Y_0, Z_0, X_1, Y_1, Z_1)$ is a solution of system (6) then $(X_1, Y_1, Z_1, X_0, Y_0, Z_0)$ is also a solution, and this last solution generates the same periodic orbit than the first one. Therefore we can conclude that system (6) has at most one real solution and consequently the discontinuous piecewise differential system formed by the linear differential systems (2) and (5) has at most one limit cycle.

We do not give the explicit expressions of the polynomials $R(Y_0)$ and $R(Y_1)$ because their expressions are huge. These resultants can be computed immediately using an algebraic manipulator, such as Mathematica or Maple.

Case 2: $c_3\gamma _3=0$. We have three subcases: $c_3=\gamma _3=0$, or $c_3=0$ and $\gamma _3\ne 0$, or $c_3\ne 0$ and $\gamma _3=0$.

Subcase 2.1: $c_3=\gamma _3=0$. Equation $e_2$ in system (6) becomes

$$\begin{aligned} e_2:c_1(X_0-X_1)+c_2(Y_0-Y_1). \end{aligned}$$

(23)

then we have two subcases $c_2\ne 0$, or $c_2=0$.

Subcase 2.1.1: $c_2\ne 0$. From (23), we get

$$\begin{aligned} Y_1=\dfrac{c_1(X_0-X_1)+c_2Y_0}{c_2}. \end{aligned}$$

(24)

Then equation $e_4$ in system (6) reduces to

$$\begin{aligned} e_4:\dfrac{(X_0-X_1)(c_2\gamma _1-c_1\gamma _2)}{c_2}. \end{aligned}$$

First, we assume that $c_2\gamma _1-c_1\gamma _2\ne 0$. Then from $e_4$ we get $X_0=X_1$, and from (24) we get $Y_0=Y_1$. So we have that $p_0=p_1$ and we do not have limit cycles.

Second we consider that $c_2\gamma _1-c_1\gamma _2= 0$, that is, $\gamma _1=c_1\gamma _2/c_2$. Then $e_4\equiv 0$, and equation $e_1$ becomes

$$\begin{aligned} e_1:&(a_4 + a_1 X_0 + a_2 Y_0 + a_3 (X_0^2 + Y_0^2))^2 + (b_4 + b_1 X_0 + b_2 Y_0 + b_3 (X_0^2 + Y_0^2))^2 \\ {}&- \Big (a_4 + a_1 X_1 + a_2 \Big (\dfrac{c_1 (X_0 - X_1)}{c_2} + Y_0\Big ) + a_3 \Big (X_1^2 + \dfrac{(c_1 (X_0 - X_1) + c_2 Y_0)^2}{c_2^2}\Big )\Big )^2\\ {}&- \Big (b_4 + b_1 X_1 + b_2 \Big (\dfrac{c_1 (X_0 - X_1)}{c_2} + Y_0\Big ) + b_3 \Big (X_1^2 + \dfrac{(c_1 (X_0 - X_1) + c_2 Y_0)^2}{c_2^2}\Big )\Big )^2. \end{aligned}$$

Moreover, the expression for equation $e_3$ are the same, changing $(a_1, a_2, a_3,a_4,b_1,b_2,b_3,b_4)$ by $(\alpha _1,\alpha _2,\alpha _3,\alpha _4,\beta _1,\beta _2,\beta _3,\beta _4)$. This means that we must solve system $e_1=0=e_3$, which has two polynomial equations and three unknowns $X_0, X_1, Y_0$. Hence, if there are solutions for this system, then it would have a continuum of solutions that produce a continuum of crossing periodic solutions and therefore we cannot have crossing limit cycles.

Subcase 2.1.2: $c_2=0$. Equation (23) becomes

$$\begin{aligned} e_2:c_1(X_0-X_1). \end{aligned}$$

First, we consider that $c_1\ne 0$. Then we have that $X_0=X_1$ and equation $e_4$ in system (6) reduces to

$$\begin{aligned} e_4=\gamma _2(Y_0-Y_1). \end{aligned}$$

We observe that we can consider $Y_0\ne Y_1$, because if $Y_0=Y_1$ we have that $p_0=p_1$ and we do not have limit cycles. Hence $\gamma _2=0$ and equation

$$\begin{aligned} e_1:&(a_4 + a_1 X_0 + a_2 Y_0 + a_3 (X_0^2 + Y_0^2))^2 + (b_4 + b_1 X_0 + b_2 Y_0 + b_3 (X_0^2 + Y_0^2))^2 \\ {}&- (a_4 + a_1 X_0 x+ a_2 Y_1 + a_3 (X_0^2 + Y_1^2))^2 - (b_4 + b_1 X_0 + b_2 Y_1 + b_3 (X_0^2 + Y_1^2))^2. \end{aligned}$$

Moreover the expression for equation $e_3$ is the same changing $a_i$ by $\alpha _i$ and $b_i$ by $\beta _i$, respectively, for $i=1,2,3,4$. Then similar arguments used for Subcase 2.1.1 show that if system $e_1=0=e_3$ has real solutions then it has a continuum of solutions and therefore we do not have limit cycles.

Second, if we consider $c_1=0$, then we have $c_2=0=c_3$. In this case, we obtain that the linear differential system (2) considered in the region $\mathcal {R}_E^1$, becomes $\dot{X}=0,\quad \dot{Y}=0,\quad \dot{Z}=0$ and so we cannot have limit cycles.

Subcase 2.2: $c_3=0$ and $\gamma _3\ne 0.$ Equation $e_2$ in system (6) reduces to equation (23). Then we have two subcases $c_2\ne 0$, or $c_2=0$.

Subcase 2.2.1: $c_2\ne 0$. From equation $e_2$, we obtain the expression for $Y_1$ given in (24). Then equation $e_4$ in system (6) becomes

$$\begin{aligned} e_4:\dfrac{(X_0 - X_1) (c_1^2 (X_1 - X_0) \gamma _3 + c_2^2 (\gamma _1 + (X_0 + X_1) \gamma _3) - c_1 c_2 (\gamma _2 + 2 Y_0 \gamma _3))}{c_2^2}. \end{aligned}$$

(25)

We can consider $X_0\ne X_1$, because if $X_0=X_1$, from equation (24), we get $Y_0=Y_1$ and then $p_0=p_1$ implying that we cannot have limit cycles. So, considering $X_0\ne X_1$ in $e_4$ (25), we get

$$\begin{aligned} X_1=\dfrac{-c_2^2 \gamma _1 + c_1 c_2 \gamma _2 + c_1^2 X_0 \gamma _3 - c_2^2 X_0 \gamma _3 + 2 c_1 c_2 Y_0 \gamma _3}{(c_1^2 + c_2^2) \gamma _3}. \end{aligned}$$

Substituting $Y_1$ and $X_1$ in equations $e_1$ and $e_3$ of system (6), we have

$$\begin{aligned} e_1=&\dfrac{1}{(c_1^2 + c_2^2)^2 \gamma _3^2}\Big (\lambda _0 (c_1^2 + c_2^2)\gamma _3\Big (X_0^3-\dfrac{c_1}{c_2} Y_0^3+Y_0^2X_0-\dfrac{c_1}{c_2}Y_0X_0^2\Big )-2\lambda _1Y_0^2\\ {}&+2\lambda _2X_0^2+\lambda _3X_0Y_0-\dfrac{2}{ \gamma _3}\lambda _4X_0-\dfrac{2}{ \gamma _3}\lambda _5Y_0-\dfrac{ (c_2 \gamma _1 - c_1 \gamma _2)}{ \gamma _3}\lambda _6\Big ),\\ e_3=&\dfrac{1}{(c_1^2 + c_2^2)^2 \gamma _3^2}\Big (\delta _0 (c_1^2 + c_2^2)\gamma _3\Big (X_0^3-\dfrac{c_1}{c_2} Y_0^3+Y_0^2X_0-\dfrac{c_1}{c_2}Y_0X_0^2\Big )-2\delta _1Y_0^2\\ {}&+2\delta _2X_0^2+\delta _3X_0Y_0-\dfrac{2}{ \gamma _3}\delta _4X_0-\dfrac{2}{ \gamma _3}\delta _5Y_0-\dfrac{ (c_2 \gamma _1 - c_1 \gamma _2)}{ \gamma _3} \delta _6\Big ), \end{aligned}$$

and the expressions of the coefficients $\lambda _i$ for $i=0,1,2,3,4,5,6$ are

$$\begin{aligned} \lambda _0=&-4 (a_3^2 + b_3^2) c_2 (c_2 \gamma _1 - c_1 \gamma _2) + 4 c_2 (-a_2 a_3 c_1 - b_2 b_3 c_1 + a_1 a_3 c_2 + b_1 b_3 c_2) \gamma _3,\\ \lambda _1=&(a_3^2 + b_3^2) (3 c_1^2 + c_2^2) (c_2 \gamma _1 - c_1 \gamma _2)^2 - (a_2 a_3 c_1 (-3 c_1^2 + c_2^2) + b_2 b_3 c_1 ( c_2^2-3 c_1^2) \\ {}&+ (a_1 a_3 + b_1 b_3) c_2 (5 c_1^2 + c_2^2)) (c_2 \gamma _1 - c_1 \gamma _2) \gamma _3 + 2 c_1 c_2 (-((a_1 a_2 + b_1 b_2) c_1^2) \\ {}&+ (a_1^2 - a_2^2 + b_1^2 - b_2^2) c_1 c_2+ (a_1 a_2 + b_1 b_2) c_2^2)\gamma _3^2,\\ \lambda _2=&-((a_3^2 + b_3^2) (c_1^2 + 3 c_2^2) (c_2 \gamma _1 - c_1 \gamma _2)^2) + ((a_1 a_3 + b_1 b_3) c_2 (c_1^2 - 3 c_2^2) + a_2 a_3 c_1 (c_1^2 \\ {}&+ 5 c_2^2) + b_2 b_3 c_1 (c_1^2 + 5 c_2^2)) (-c_2 \gamma _1 + c_1 \gamma _2) \gamma _3 + 2 c_1 c_2 (-((a_1 a_2 + b_1 b_2) c_1^2) + (a_1^2 \\ {}&- a_2^2 + b_1^2 - b_2^2)c_1 c_2 + (a_1 a_2 + b_1 b_2) c_2^2) \gamma _3^2, \\ \lambda _3=&(8 (a_3^2 + b_3^2) c_1 c_2 (c_2 \gamma _1 - c_1 \gamma _2)^2 - 4 (a_1 a_3 c_1 (c_1^2 - 3 c_2^2) + b_1 b_3 c_1 (c_1^2 - 3 c_2^2) - (a_2 a_3 \\ {}&+ b_2 b_3) c_2 (-3 c_1^2 + c_2^2)) (-c_2 \gamma _1 + c_1 \gamma _2) \gamma _3 + 4 (c_1 - c_2) (c_1 + c_2) ((a_1 a_2 + b_1 b_2) c_1^2 \\ {}&+ (a_2^2 - a_1^2 - b_1^2 + b_2^2)c_1 c_2 - (a_1 a_2 + b_1 b_2) c_2^2) \gamma _3^2,\\ \lambda _4=&2 (a_3^2 + b_3^2) c_2 (c_2 \gamma _1 - c_1 \gamma _2)^3 + ((a_1 a_3 + b_1 b_3) c_1^2 + 4 (a_2 a_3 + b_2 b_3) c_1 c_2 - 3 (a_1 a_3 \\ {}&+ b_1 b_3) c_2^2)(c_2 \gamma _1 - c_1 \gamma _2)^2 \gamma _3 + ((a_1 a_2 + b_1 b_2) c_1^3 - (a_1^2 - 2 a_2^2 - 2 a_3 a_4 + b_1^2 - 2 (b_2^2 \\ {}&+ b_3 b_4)) c_1^2 c_2- 3 (a_1 a_2 + b_1 b_2) c_1 c_2^2 + (a_1^2 + 2 a_3 a_4 + b_1^2 + 2 b_3 b_4) c_2^3)(c_2 \gamma _1 - c_1 \gamma _2) \gamma _3^2\\ {}&- 2 c_2 (-a_2 a_4 c_1 - b_2 b_4 c_1 + a_1 a_4 c_2 + b_1 b_4 c_2) (c_1^2 + c_2^2) \gamma _3^3,\\ \lambda _5=&2 (a_3^2 + b_3^2) c_1 (-c_2 \gamma _1 + c_1 \gamma _2)^3 + \gamma _3 ( 4 (a_1 a_3 + b_1 b_3) c_1 c_2-3 (a_2 a_3 + b_2 b_3) c_1^2 + (a_2 a_3 \\ {}&+ b_2 b_3) c_2^2)(c_2 \gamma _1 - c_1 \gamma _2)^2 + ((a_2^2 + 2 a_3 a_4 + b_2^2 + 2 b_3 b_4) c_1^3 - 3 (a_1 a_2 + b_1 b_2) c_1^2 c_2 \\ {}&+ (2 a_1^2 - a_2^2 + 2 a_3 a_4 + 2 b_1^2 - b_2^2 + 2 b_3 b_4) c_1 c_2^2 + (a_1 a_2 + b_1 b_2) c_2^3) (c_1 \gamma _2 -c_2 \gamma _1) \gamma _3^2 \\ {}&- 2 c_1 (a_2 a_4 c_1 + b_2 b_4 c_1 - (a_1 a_4 + b_1 b_4) c_2) (c_1^2 + c_2^2) \gamma _3^3,\\ \lambda _6=&(a_3^2 + b_3^2) (c_2 \gamma _1 - c_1 \gamma _2)^3 + 2 (a_2 a_3 c_1 + b_2 b_3 c_1 - (a_1 a_3 + b_1 b_3) c_2)(c_2 \gamma _1 - c_1 \gamma _2)^2 \\ {}&\gamma _3+ ((a_2^2 + 2 a_3 a_4 + b_2^2 + 2 b_3 b_4) c_1^2 - 2 (a_1 a_2 + b_1 b_2) c_1 c_2 + (a_1^2 + 2 a_3 a_4 + b_1^2 \\ {}&+ 2 b_3 b_4) c_2^2)(c_2 \gamma _1 - c_1 \gamma _2) \gamma _3^2 + 2 (a_2 a_4 c_1 + b_2 b_4 c_1 - (a_1 a_4 + b_1 b_4) c_2) (c_1^2 + c_2^2) \gamma _3^3. \end{aligned}$$

Moreover the expressions of $\delta _i$ for $i=0,1,2,3,4,5,6$ are equal, only interchanging $a_j$ by $\alpha _j$ and $b_j$ by $\beta _j$, respectively, for $j=1,2,3,4$. We know that if $(X_0, Y_0)$ is a solution of the system $e_1=0$, $e_3=0$, the point $X_0$ must be a root of the resultant of $e_1$ and $e_3$ with respect to the variable $Y_0$, that we denote it by $R(X_0)$. Moreover the point $Y_0$ must be a root of the resultant of $e_1$ and $e_3$ with respect to the variable $X_0$, which we denote by $R(Y_0)$. In this case, it is possible to verify that $R(Y_0)=R(X_0)=0$. Therefore we cannot have limit cycles.

Subcase 2.2.2: $c_2=0$. Equation $e_2$ given in (23) reduces to

$$\begin{aligned} e_2=c_1(X_0-X_1). \end{aligned}$$

First if we consider that $c_1\ne 0$, then $X_0=X_1$ and equation $e_4$ in (6) becomes

$$\begin{aligned} e_4=(Y_0 - Y_1) (\gamma _2 + (Y_0 + Y_1) \gamma _3). \end{aligned}$$

We observe that we can consider $Y_0\ne Y_1$, because if $Y_0=Y_1$ we obtain that $p_0=p_1$ and we cannot have limit cycles. Then from $e_4$, we get $Y_0=-(\gamma _2-Y_1\gamma _3)/\gamma _3$, and substituting them in equations $e_1$ and $e_3$ we obtain two polynomials of degree 4 whose resultants are zero. Therefore we cannot have limit cycles.

Second, we consider that $c_1=0$. But then since $c_2=c_3=0$, we obtain that the linear differential system (2) considered in the region $\mathcal {R}_E^1$ becomes $\dot{X}=0,\quad \dot{Y}=0,\quad \dot{Z}=0,$ and so we cannot have limit cycles.

Subcase 2.3: $c_3\ne 0$ and $\gamma _3=0$. The proof in this case is analogous to the Subcase 2.2 $\square$

Proof of statement (ii)

If the discontinuity surface is $P_E$ it is sufficient to consider the discontinuous piecewise linear differential system formed by a linear differential center (1) in the region $\mathcal {R}_E^1$ and an arbitrary linear differential center (5) in the region $\mathcal {R}_E^2$. We have that this discontinuous piecewise differential system has no crossing periodic orbits. If the discontinuity surface is $P_H$ we consider the linear differential systems (2) and (5) in $\mathcal {R}_H^1$ and $\mathcal {R}_H^2$, respectively, considering $c_3=0=\gamma _3$, $c_2\ne 0$, and $c_2\gamma _1-c_1\gamma _2\ne 0$, as in the proof of Subcase 2.1.1 in a statement (i). In this case, we obtain that the unique real solution for system (4) is $(X_0, Y_0, Z_0, X_0, Y_0, Z_0)$ for $X_0, Y_0, Z_0\in {\mathbb {R}}$, which do not generates crossing periodic orbits.

Proof of statement (iii)

First, we provide a discontinuous piecewise differential system that has a continuum of crossing periodic orbits when the discontinuity surface is $P_E$. For this we consider in the region $\mathcal {R}_E^1$ the linear differential system

$$\begin{aligned} \dot{X}=-\dfrac{15}{8}(-1+2Y+4Z),\quad \dot{Y}=-\dfrac{X}{20},\quad \dot{Z}=\dfrac{X}{10}, \end{aligned}$$

(26)

and in the region $\mathcal {R}_E^2$ the linear differential system

$$\begin{aligned} \dot{X}=\dfrac{319(15Y+16(Z-15))}{19200},\quad \dot{Y}=\dfrac{29}{4}X,\quad \dot{Z}=-\dfrac{87}{4}X. \end{aligned}$$

(27)

Considering $Z_0=X_0^2+Y_0^2$ and $Z_1=X_1^2+Y_1^2$ we get that system (6) is equivalent to

$$\begin{aligned} \begin{array}{rl} e_1:&{} \dfrac{ 1}{20} (X_0^2 - X_1^2) (-49 + 100 X_0^2 + 100 X_1^2 + 100 Y_1 + 200 Y_1^2),\\ e_2:&{}-X_0^2 + X_1^2 - 2 Y_0 - Y_0^2 + 2 Y_1 + Y_1^2,\\ e_3:&{} \dfrac{29 (X_0^2 - X_1^2) (210 + 8 X_0^2 + 8 X_1^2 + 15 Y_1 + 16 Y_1^2)}{1800},\\ e_4:&{}(X_0^2 - X_1^2). \end{array} \end{aligned}$$

(28)

We observe that the points $p_{0,1}=(\pm X_0,Y_0,Z_0)$ for $X_0,Y_0,Z_0\in {\mathbb {R}}$ are solutions of system (28). Therefore, the discontinuous piecewise linear differential system formed by the differential systems (26) and (27) has a continuum of crossing periodic solutions, which intersect the paraboloid $P_E$ at the two points $p_0$ and $p_1$. See the three crossing periodic solutions $S^i=(p_0^i,p_1^i)$ for $i=1,2,3$, of this continuum of crossing periodic solutions in Fig. 1, where

$$\begin{aligned} S^1= \Big (-1,\dfrac{1}{2},\dfrac{5}{4},1,\dfrac{1}{2},\dfrac{5}{4} \Big ),\ \ \ \ S^2= \Big (-\dfrac{6}{5},\dfrac{7}{10},\dfrac{193}{100},\dfrac{6}{5},\dfrac{7}{10},\dfrac{193}{100} \Big ),\\ S^3=\Big (-\dfrac{4}{5},\dfrac{3}{10},\dfrac{73}{100},\dfrac{4}{5},\dfrac{3}{10},\dfrac{73}{100} \Big ).\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{aligned}$$

Now we consider that the discontinuity surface is $P_H$ and we provide a discontinuous piecewise differential system that has a continuum of crossing periodic orbits. In the region $\mathcal {R}_H^1$ we consider the linear differential system

$$\begin{aligned} \dot{X}=-\dfrac{15}{8}(-1+2Y+4Z),\quad \dot{Y}=-\dfrac{X}{20},\quad \dot{Z}=\dfrac{X}{10}, \end{aligned}$$

(29)

and in the region $\mathcal {R}_H^2$ the linear differential system

$$\begin{aligned} \dot{X}=\dfrac{1073(15Y+16(Z-15))}{38400},\quad \dot{Y}=-\dfrac{29}{8}X,\quad \dot{Z}=-\dfrac{87}{4}X. \end{aligned}$$

(30)

Considering $Z_0=X_0^2-Y_0^2$ and $Z_1=X_1^2-Y_1^2$ we get that system (4) is equivalent to

$$\begin{aligned} \begin{array}{rl} e_1:&{} \dfrac{1}{20} (X_0^2 - X_1^2) (-49 + 100 X_0^2 + 100 X_1^2 + 100 Y_1 - 200 Y_1^2),\\ e_2:&{}-X_0^2 + X_1^2 - 2 Y_0+ 2 Y_1 +Y_0^2 - Y_1^2,\\ e_3:&{} \dfrac{29 (X_0^2 - X_1^2) (210 + 8 X_0^2 + 8 X_1^2 + 15 Y_1 - 16 Y_1^2)}{1800},\\ e_4:&{}\dfrac{-(X_0^2 - X_1^2)}{2}. \end{array}\end{aligned}$$

(31)

We observe that the points $p_{0,1}=(\pm X_0,Y_0,Z_0)$ for $X_0,Y_0,Z_0\in {\mathbb {R}}$ are solutions of system (31). Then, the discontinuous piecewise linear differential system formed by the differential systems (29) and (30) has a continuum of crossing periodic solutions, which intersect the paraboloid $P_H$ at the two points $p_0$ and $p_1$. See the three crossing periodic solutions $S^i=(p_0^i,p_1^i)$ for $i=1,2,3$, of this continuum of crossing periodic solutions in Fig. 2, where

$$\begin{aligned} S^1= \Big (1,\dfrac{1}{2},\dfrac{3}{4},-1,\dfrac{1}{2},\dfrac{3}{4} \Big ),\ \ \ \ S^2= \Big (\dfrac{6}{5},\dfrac{7}{10},\dfrac{19}{20},-\dfrac{6}{5},\dfrac{7}{10},\dfrac{19}{20} \Big ),\\ S^3=\Big (\dfrac{7}{5},\dfrac{9}{10},\dfrac{23}{20},-\dfrac{7}{5},\dfrac{9}{10},\dfrac{23}{20} \Big ).\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{aligned}$$

Proof of statement (iv)

We provide two examples of discontinuous piecewise differential systems separated by either $P_E$ or $P_H$ and which have one crossing limit cycle. With these examples we can conclude that the upper bound found is reached.

First, we provide a discontinuous piecewise differential system whose discontinuity surface is $P_E$ and that has one crossing limit cycle. In the region $\mathcal {R}_E^1$ we consider the linear differential system

$$\begin{aligned} \dot{X}=&\dfrac{5 (-77131 + 7 \sqrt{146892247}) X - 16 (1040 + 5385 Y + 1818 Z)}{1200},\\ \dot{Y}=&\dfrac{1}{14400}\Big ((307751207 - 25325 \sqrt{146892247}) X - 16 (74045 - 5 \sqrt{146892247} \\ {}&+ 15 (-9748 + \sqrt{146892247}) Y + 9 (-62959 + 5 \sqrt{146892247}) Z)\Big ),\\ \dot{Z}=&\dfrac{1}{28800}\Big ((154454086 - 12715 \sqrt{146892247}) X - 40 (14185 - \sqrt{146892247} \\ {}&+ 3 (-10825 + \sqrt{146892247}) Y + 9 (-12713 + \sqrt{146892247}) Z)\Big ), \end{aligned}$$

and in the region $\mathcal {R}_E^2$ the linear differential system

$$\begin{aligned} \dot{X}=&\dfrac{(-984749 + 1676 \sqrt{291071}) X - 16 (-9790 + 17066 Y + 17485 Z)}{8000},\\ \dot{Y}=&\dfrac{1}{32000}\Big ((2953428 - 5327 \sqrt{291071}) X - 16 (5990 - 10 \sqrt{291071}+( - 7996 \\ {}&+ 14 \sqrt{291071}) Y +(- 8660 + 15 \sqrt{291071}) Z)\Big ),\\ \dot{Z}=&\dfrac{1}{128000}\Big ((319954973 - 576992 \sqrt{291071}) X - 16 (656710 - 1080 \sqrt{291071} \\ {}&+(- 880634 + 1512 \sqrt{291071} )Y +(- 952765 + 1620 \sqrt{291071} )Z)\Big ).\\ \end{aligned}$$

With these linear differential systems, system (6) has only one real solution which generates one limit cycle that intersects the paraboloid $P_E$ in two different points $p_0=(X_0, Y_0, Z_0)$ and $p_1=(X_1, Y_1, Z_1)$, namely

$$\begin{aligned} p_0=\Big (1,\dfrac{1}{4},\dfrac{17}{16} \Big ) \ \ \text{ and }\ \ \ p_1=\Big (-\dfrac{17}{16},\dfrac{1}{4},\dfrac{305}{256} \Big ). \end{aligned}$$

See this crossing limit cycle in Fig. 3.

Now we provide a discontinuous piecewise differential system whose discontinuity surface is $P_H$ and that has one crossing limit cycle. We consider in the region $\mathcal {R}_H^1$ the linear differential system

$$\begin{aligned} \dot{X}=&\dfrac{5 (-67051 + 7 \sqrt{112701463}) X - 16 (1040 + 5385 Y + 1818 Z)}{1200},\\ \dot{Y}=&\dfrac{1}{14400}\Big ((239166023- 22445 \sqrt{112701463}) X - 16 (66845- 5 \sqrt{112701463} \\ {}&+ 15 (-8308+ \sqrt{112701463}) Y + 9 (-55759 + 5 \sqrt{112701463}) Z)\Big ),\\ \dot{Z}=&\dfrac{1}{28800}\Big ((120085894 - 11275 \sqrt{112701463}) X - 40 (12745- \sqrt{112701463} \\ {}&+ 3 (-9385 + \sqrt{112701463}) Y + 9 (-11273 + \sqrt{112701463}) Z)\Big ), \end{aligned}$$

and in the region $\mathcal {R}_H^2$ the linear differential system

$$\begin{aligned} \dot{X}=&\dfrac{(-783629 + 1676 \sqrt{166911}) X - 16 (-9790 + 17066 Y + 17485 Z)}{8000},\\ \dot{Y}=&\dfrac{1}{32000}\Big (11(170468- 397 \sqrt{166911}) X+ 32(3158 - 7 \sqrt{166911})Y\\ {}&-80(958 -2 \sqrt{166911}+(-1372+3 \sqrt{166911}) Z)\Big ),\\ \dot{Z}=&\dfrac{1}{128000}\Big ((203299613 - 473312 \sqrt{166911}) X - 16 (527110- 1080 \sqrt{166911} \\ {}&+(- 699194 + 1512 \sqrt{166911} )Y +(- 758365 + 1620 \sqrt{166911} )Z)\Big ).\\ \end{aligned}$$

With these linear differential systems, system (4) has only one real solution which generates one crossing limit cycle that intersects the paraboloid $P_H$ in two different points $p_0= (X_0,Y_0, Z_0)$ and $p_1=(X_1, Y_1, Z_1)$, namely

$$\begin{aligned} p_0=\Big (1,\dfrac{1}{4},\dfrac{15}{16}\Big ) \ \ \text{ and }\ \ \ p_1=\Big (-\dfrac{17}{16},\dfrac{1}{4},\dfrac{273}{256} \Big ). \end{aligned}$$

See this crossing limit cycle in Fig. 4.

This completes the proof of Theorem 1.

Conclusions

In Theorem 1 we have solved the extension of the 16th Hilbert problem to the discontinuous piecewise linear differential systems formed by linear centers and separated by a paraboloid (elliptic or hyperbolic) restricted to the crossing limit cycles which intersect the quadric in two points. We recall that this problem was studied intensively in the plane but this is not the case for piecewise differential systems in higher dimensions.