1 Introduction and Main Results

Mutational behavior after slow change is ubiquitous in natural and artificial systems and is usually described by piecewise smooth mathematical models. For a long time, this research has attracted much attention in the field of nonlinear science. As a part of nonlinear dynamical systems, piecewise smooth dynamical systems are applied in many fields of applied science and engineering, such as collision vibration system in mechanical engineering, stick slip vibration system with dry friction, circuit system with controllable switch, see [1, 8, 17].

Similar to smooth differential systems, the number and distribution of limit cycles is one of the important problems of non-smooth differential systems. So far as we know, there are two basic methods to study the number of limit cycles. One is the Melnikov function method developed in [6, 14] and the other is the averaging method established in [12, 13]. By using the above two methods, many researchers have been extensively studied the upper or lower bound of the number of limit cycles for the following piecewise smooth near-Hamiltonian system

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} {\dot{x}} = H^+_y(x,y)+\varepsilon f^+(x,y),\\ {\dot{y}} = -H^+_x(x,y)+\varepsilon g^+(x,y),\\ \end{array}\right. }x\ge 0,\\&{\left\{ \begin{array}{ll} {\dot{x}} = H^-_y(x,y)+\varepsilon f^-(x,y),\\ {\dot{y}} = -H^-_x(x,y)+\varepsilon g^-(x,y),\\ \end{array}\right. }x<0, \end{aligned} \end{aligned}$$
(1.1)

where \(0<|\varepsilon |\ll 1\), \(H^\pm (x,y)\) are polynomials of x and y of degree \(m+1\) and

$$\begin{aligned} f^\pm (x,y)=\sum \limits _{i+j=0}^na_{i,j}^{\pm }x^iy^j,\ g^\pm (x,y)=\sum \limits _{i+j=0}^nb_{i,j}^{\pm }x^iy^j,\ a_{i,j}^{\pm },b_{i,j}^{\pm }\in \mathbb {R}, i,j\in \mathbb {N}. \end{aligned}$$

For the purpose of getting the upper bound, one usually analyzed the algebraic structure of the corresponding first order Melnikov function M(h) of system (1.1) with the help of Picard-Fuchs equations. Then, the upper bound is obtained by comprehensively applying the methods in the literatures [7, 9, 22, 26] or argument principle or Chebyshev criterion etc, see [2, 5, 10, 16, 20, 21, 23, 25] that have used these methods. Fortunately, the independence of the coefficients of the coefficient polynomials of the generators of M(h) does not need to be verified. Because this is very intricate. However, this is inevitable if you want to get the lower bound. In [11, 14, 24], the authors got the lower bound of the number of limit cycles bifurcating from the period annulus of system (1.1) with a homoclinic loop or heteroclinic loop or eye-figure loop. In order to get the independence of the coefficients, they took some special perturbed polynomials \(f^\pm (x,y)\) and \(g^\pm (x,y)\) for the sake of simplifying the calculation. In [4, 15, 18, 19], the authors obtained the lower bound for the general perturbed polynomials. But, the proof of the independence of the coefficients involves a lot of computations. With that in mind, in the present paper, we provide a way to verify the independence of coefficients which largely reduces calculation and illustrate this method with a concrete example.

Consider the following perturbed piecewise smooth Hamiltonian system

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} {\dot{x}} = y+\varepsilon f^+(x,y), \\ {\dot{y}} = x -1+\varepsilon g^+(x,y),\\ \end{array}\right. } x\ge 0,\\&{\left\{ \begin{array}{ll} {\dot{x}} = y+\varepsilon f^-(x,y), \\ {\dot{y}} = -x+\varepsilon g^-(x,y),\\ \end{array}\right. } \quad x<0. \end{aligned} \end{aligned}$$
(1.2)

The corresponding Hamiltonian functions for system (1.2)\(|_{\varepsilon =0}\) are

$$\begin{aligned} H^+(x,y)=\frac{1}{2}y^2-\frac{1}{2}x^2+x,\ \ x\ge 0, \end{aligned}$$
(1.3)

and

$$\begin{aligned} H^-(x,y)=\frac{1}{2}y^2+\frac{1}{2}x^2,\ \ x<0. \end{aligned}$$
(1.4)

When \(\varepsilon =0\), system (1.2) has a family of periodic orbits as follows

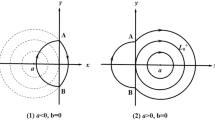
$$\begin{aligned} \begin{aligned}\Gamma _h=&\,\{(x,y)|H^+(x,y)=h,x\ge 0\}\cup \{(x,y)|H^-(x,y)=h,x<0\}\\ :=&\,\Gamma ^+_h\cup \Gamma ^-_h\end{aligned} \end{aligned}$$

with \(h\in (0,\frac{1}{2})\). As h tends to 0, \(\Gamma _h\) approaches to the origin, and as h tends to \(\frac{1}{2}\), \(\Gamma _h\) approaches to a homoclinic loop passing through the saddle point (1,0), see Fig. 1.

Fig. 1
figure 1

The phase portrait of system (1.2) with \(\varepsilon =0\)

Full size image

By [6, 14], corresponding to periodic orbits \(\{\Gamma _h|h\in (0,\frac{1}{2})\}\), system (1.2) has the first order Melnikov function described by

$$\begin{aligned} \begin{aligned} M(h)=\int _{\Gamma ^+_h}g^+(x,y)dx-f^+(x,y)dy+\int _{\Gamma ^-_h}g^-(x,y)dx-f^-(x,y)dy, \end{aligned}\nonumber \\ \end{aligned}$$
(1.5)

and the number of zeros of M(h) controls the number of limit cycles of system (1.2) if M(h) is not identically zero. In [10] the authors posed the following conjecture.

Conjecture

By using the first order Melnikov function, the maximal number of limit cycles of system (1.2) bifurcating from the period annulus around the origin is \(n+[\frac{n+1}{2}]\).

We confirm the conjecture with the following theorem.

Theorem 1.1

By using the first order Melnikov function, the number of limit cycles of system (1.2) bifurcating from the period annulus around the origin is not more than \(n+[\frac{n+1}{2}]\), and this bound can be reached.

This paper is organized as follows. In Sect. 2, we obtain the detailed expression of the first order Melnikov function M(h) and verify the independence of the coefficients of the coefficient polynomials of the generators of M(h) by using mathematical induction. Section 3 is devoted to the proof of Theorem 1.1. Finally, conclusion is drawn in Sect. 4.

2 The Algebraic Structure of the First Order Melnikov Function

In order to estimate the number of zeros of the first order Melnikov function M(h), one should study the algebraic structure of M(h). To this end, we denote

$$\begin{aligned} I_{i,j}(h)=\int _{\Gamma ^+_h}x^iy^jdy,\ J_{i,j}(h)=\int _{\Gamma ^-_h}x^iy^jdy,\ h\in \left( {0,\frac{1}{2}}\right) . \end{aligned}$$

Since the orbits \(\Gamma ^\pm _h\) are symmetric with respect to the x-axis, \(I_{i,2j+1}(h)=J_{i,2j+1}(h)\equiv 0\). So we only need to consider \(I_{i,2j}(h)\) and \(J_{i,2j}(h)\).

The next Lemma shows that M(h) can be expressed as a combination of some generator integrals with polynomial coefficients and the coefficients of these polynomials can be taken as free parameters.

Lemma 2.1

For \(h\in (0,\frac{1}{2})\) and any \(n\in \mathbb {N} \) it holds that

$$\begin{aligned} \begin{aligned} M(h)=&\sqrt{h}\sum \limits _{i=0}^{[\frac{n}{2}]}\alpha _ih^i+\left( {\sum \limits _{i=0}^{[\frac{n-1}{2}]}\beta _ih^i}\right) I_{1,0}(h) +h\sum \limits _{i=0}^{[\frac{n-1}{2}]}\gamma _ih^{i}, \end{aligned}\end{aligned}$$
(2.1)

where \(\alpha _i\), \(\beta _i\) and \(\gamma _i\) are constants and can be chosen arbitrarily.

Proof

Let D be the interior of \(\Gamma _{h}^+\cup \overrightarrow{BA}\), see Fig. 1. Using the Green’s Formula, one has

$$\begin{aligned} \begin{aligned} \int _{\Gamma ^+_{h}}x^iy^jdx =&\oint _{\Gamma ^+_{h}\cup \overrightarrow{BA}}x^iy^jdx-\int _{\overrightarrow{BA}}x^iy^jdx\\ =&\oint _{\Gamma ^+_{h}\cup \overrightarrow{BA}}x^iy^jdx =j\iint \limits _Dx^iy^{j-1}dxdy, \end{aligned} \\ \begin{aligned} \int _{\Gamma ^+_{h}}x^{i+1}y^{j-1}dy= \oint _{\Gamma ^+_{h}\cup \overrightarrow{BA}}x^{i+1}y^{j-1}dy =-(i+1)\iint \limits _Dx^iy^{j-1}dxdy. \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \int _{\Gamma ^+_{h}}x^iy^jdx =-\frac{j}{i+1}\int _{\Gamma ^+_{h}}x^{i+1}y^{j-1}dy.\end{aligned}$$
(2.2)

Similarly, one has

$$\begin{aligned} \int _{\Gamma ^-_{h}}x^iy^jdx =-\frac{j}{i+1}\int _{\Gamma ^-_{h}}x^{i+1}y^{j-1}dy.\end{aligned}$$
(2.3)

By (1.5), (2.2) and (2.3), one obtains

$$\begin{aligned} \begin{aligned} M(h)=&\int _{\Gamma _h^+}\sum \limits _{i+j=0}^nb^+_{i,j}x^iy^jdx-\int _{\Gamma _h^+}\sum \limits _{i+j=0}^na^+_{i,j}x^iy^jdy\\&+\int _{\Gamma _h^-}\sum \limits _{i+j=0}^nb^-_{i,j}x^iy^jdx-\int _{\Gamma _h^-}\sum \limits _{i+j=0}^na^-_{i,j}x^iy^jdy\\ =&-\sum \limits _{i+j=1,j\ge 1}^n\frac{j}{i+1}b^+_{i,j}\int _{\Gamma ^+_h}x^{i+1}y^{j-1}dy -\sum \limits _{i+j=0}^na^+_{i,j}\int _{\Gamma _h^+}x^iy^jdy\\&-\sum \limits _{i+j=1,j\ge 1}^n\frac{j}{i+1}b^-_{i,j}\int _{\Gamma ^-_h}x^{i+1}y^{j-1}dy -\sum \limits _{i+j=0}^na^-_{i,j}\int _{\Gamma _h^-}x^iy^jdy\\ =&\sum \limits _{i+j=0}^n\xi _{i,j}I_{i,j}(h)+\sum \limits _{i+j=0}^n\eta _{i,j}J_{i,j}(h), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\xi _{i,j}={\left\{ \begin{array}{ll}-a^+_{i,j}-\frac{j+1}{i}b^+_{i-1,j+1}, &{}1\le i\le n,1\le i+j\le n,\\ -a^+_{i,j}, &{}i=0,0\le j\le n,\\ \end{array}\right. }\\&\eta _{i,j}={\left\{ \begin{array}{ll}-a^-_{i,j}-\frac{j+1}{i}b^-_{i-1,j+1}, &{}1\le i\le n,1\le i+j\le n,\\ -a^-_{i,j}, &{} i=0,0\le j\le n.\\ \end{array}\right. } \end{aligned} \end{aligned}$$

It is easy to check that \(\xi _{i,j}\) and \(\eta _{i,j}\) can be taken as free parameters.

\(\square \)

Now we claim that

$$\begin{aligned} \sum \limits _{i+j=0}^n\xi _{i,j}I_{i,j}(h)=\left( {\sum \limits _{i=0}^{[\frac{n}{2}]}{\bar{\alpha }}_ih^i}\right) I_{0,0}(h) +\left( {\sum \limits _{j=0}^{[\frac{n-1}{2}]}{\bar{\beta }}_jh^j}\right) I_{1,0}(h),\end{aligned}$$
(2.4)

where \({\bar{\alpha }}_i\), \(i=0,1,2,\cdots ,[\frac{n}{2}]\) and \({\bar{\beta }}_j\), \(j=0,1,2,\cdots ,[\frac{n-1}{2}]\) can be taken as free parameters.

In fact, differentiating \(H^+(x,y)=h\) both sides with respect to y, one obtains

$$\begin{aligned} y-x\frac{\partial x}{\partial y}+\frac{\partial x}{\partial y}=0. \end{aligned}$$
(2.5)

Multiplying (2.5) by the one-form \(x^{i}y^{j-1}dy\) and integrating over \(\Gamma _h^+\), one obtains the relation

$$\begin{aligned} I_{i,j}=\frac{j-1}{i+1}I_{i+1,j-2}-\frac{j-1}{i+2}I_{i+2,j-2}, \ i\ge 0, j\ge 1. \end{aligned}$$
(2.6)

Similarly, multiplying \(H^+(x,y)=h\) both sides by \(x^{i-2}y^{j}dy\) and integrating over \(\Gamma _h^+\), one gets another relation

$$\begin{aligned} I_{i,j}=-2hI_{i-2,j}+2I_{i-1,j}+I_{i-2,j+2},\ i\ge 2, j\ge 0. \end{aligned}$$
(2.7)

Elementary manipulations reduce equations (2.6) and (2.7) to

$$\begin{aligned} I_{i,j}=-\frac{i}{i+j+1}\left[ {2hI_{i-2,j}-\frac{2i+j-1}{i-1}I_{i-1,j}}\right] ,\ i\ge 2, j\ge 0 \end{aligned}$$
(2.8)

and

$$\begin{aligned} I_{i,j}=\frac{j-1}{i+j+1}\left[ {2hI_{i,j-2}-\frac{i}{i+1}I_{i+1,j-2}}\right] ,\ i\ge 0, j\ge 1. \end{aligned}$$
(2.9)

Now we will prove the claim by induction on n. Without loss of generality, we only prove the claim if n is an even number (the claim can be proved similarly if n is an odd number). Indeed, a direct computation using the above two equalities (2.8) and (2.9) gives

$$\begin{aligned} {\left\{ \begin{array}{ll} I_{0,2}(h)=\frac{2}{3}hI_{0,0}(h),\\ I_{2,0}(h)=-\frac{4}{3}hI_{0,0}(h)+2I_{1,0}(h),\\ I_{1,2}(h)=\frac{1}{6}hI_{0,0}(h)+(\frac{1}{2}h-\frac{1}{4})I_{1,0}(h),\\ I_{3,0}(h)=-\frac{5}{2}hI_{0,0}(h)-(\frac{3}{2}h-\frac{15}{4})I_{1,0}(h).\\ \end{array}\right. } \end{aligned}$$
(2.10)

Hence, one has for \(n=2,3\)

$$\begin{aligned} \begin{aligned} \sum \limits _{i+j=0}^2\xi _{i,j}I_{i,j}(h)=&\left[ {\left( {\frac{2}{3}\xi _{0,2}-\frac{4}{3}\xi _{2,0}}\right) h+\xi _{0,0}}\right] I_{0,0}(h) +(\xi _{1,0}+2\xi _{2,0})I_{1,0}(h),\\ \sum \limits _{i+j=0}^3\xi _{i,j}I_{i,j}(h)=&\left[ {\left( {\frac{2}{3}\xi _{0,2}-\frac{4}{3}\xi _{2,0}+\frac{1}{6}\xi _{1,2}-\frac{5}{2}\xi _{3,0}}\right) h+\xi _{0,0}}\right] I_{0,0}(h)\\&+\left[ {\left( {\frac{1}{2}\xi _{1,2}-\frac{3}{2}\xi _{3,0}}\right) h-\frac{1}{4}\xi _{1,2}+\frac{15}{4}\xi _{3,0}+\xi _{1,0}+2\xi _{2,0}}\right] I_{1,0}(h).\end{aligned} \end{aligned}$$

That is, the claim holds for \(n=2,3\).

Now assume that the claim holds for all \(i+j\le n-1\). Then, taking \((i,j)=(0,n),(2,n-2),\cdots ,(n-2,2)\) in (2.9) and \((i,j)=(n,0)\) in (2.8), respectively, one has

$$\begin{aligned} \left( \begin{matrix} I_{0,n}(h)\\ I_{2,n-2}(h)\\ I_{4,n-4}(h)\\ \vdots \\ I_{n-2,2}(h)\\ I_{n,0}(h) \end{matrix}\right) \ \ =\frac{1}{n+1}\left( \begin{matrix} 2(n-1)hI_{0,n-2}(h)\\ 2(n-3)\big (hI_{2,n-4}(h)-\frac{1}{3}I_{3,n-4}(h)\big )\\ 2(n-5)\big (hI_{4,n-6}(h)-\frac{2}{5}I_{5,n-6}(h)\big )\\ \vdots \\ 2\big (hI_{n-2,0}(h)-\frac{n-2}{2(n-1)}I_{n-1,0}(h)\big )\\ -n\big (2hI_{n-2,0}(h)-\frac{2n-1}{n-1}I_{n-1,0}(h)\big ) \end{matrix}\right) . \end{aligned}$$
(2.11)

Therefore, by the induction hypothesis and (2.11), one obtains

$$\begin{aligned} \sum \limits _{i+j=0}^n\xi _{i,j}I_{i,j}(h)= & {} \sum \limits _{i+j=0}^{n-1}\xi _{i,j}I_{i,j}(h)+\sum \limits _{i+j=n}\xi _{i,j}I_{i,j}(h)\nonumber \\= & {} \left( {\sum \limits _{i=0}^{[\frac{n-1}{2}]}{\tilde{\alpha }}_ih^i}\right) I_{0,0}(h)+\left( {\sum \limits _{j=0}^{[\frac{n-2}{2}]}{\tilde{\beta }}_jh^j}\right) I_{1,0}(h)\nonumber \\&+\xi _{0,n}\frac{2(n-1)}{n+1}hI_{0,n-2}(h)+\xi _{2,n-2} \frac{2(n-3)}{n+1}\nonumber \\&\times \left( {hI_{2,n-4}(h)-\frac{1}{3}I_{3,n-4}(h)}\right) \nonumber \\&+\cdots - \xi _{n,0}\frac{n}{n+1}\big (2hI_{n-2,0}(h)-\frac{2n-1}{n-1}I_{n-1,0}(h)\big )\nonumber \\&\triangleq \left( {\sum \limits _{i=0}^{[\frac{n}{2}]}{\bar{\alpha }}_ih^i}\right) I_{0,0}(h)+\left( {\sum \limits _{j=0}^{[\frac{n-1}{2}]}{\bar{\beta }}_jh^j}\right) I_{1,0}(h),\end{aligned}$$
(2.12)

where \({\tilde{\alpha }}_i\), \({\tilde{\beta }}_i\), \({\bar{\alpha }}_i\) and \({\bar{\beta }}_i\) are constants.

Next, we prove that \({\bar{\alpha }}_i\), \(i=0,1,2,\cdots ,[\frac{n}{2}]\) and \({\bar{\beta }}_j\), \(j=0,1,2,\cdots ,[\frac{n-1}{2}]\) can be taken as free parameters. In fact, by the induction hypothesis, one has \({\tilde{\alpha }}_i\), \(i=0,1,2,\cdots ,[\frac{n-1}{2}]\) and \({\tilde{\beta }}_j\), \(j=0,1,2,\cdots ,[\frac{n-2}{2}]\) are independent of each other. That is, the determinant of the following Jacobian matrix

$$\begin{aligned} \begin{aligned} {\mathbf {A}}=\frac{\partial \Big ({\tilde{\alpha }}_{[\frac{n-1}{2}]},\cdots ,{\tilde{\alpha }}_0,{\tilde{\beta }}_{[\frac{n-2}{2}]},\cdots ,{\tilde{\beta }}_0\Big )}{\partial \Big (\xi _{i_0,j_{[\frac{n-1}{2}]}},\cdots ,\xi _{i_{[\frac{n-1}{2}]},j_0}, \xi _{k_0,l_{[\frac{n-2}{2}]}},\cdots ,\xi _{k_{[\frac{n-2}{2}]},l_0}\Big )}\\ \end{aligned} \end{aligned}$$

is different from zero, here the sum of subscripts of \(\xi _{i,j}\) in the above Jacobian matrix is less than or equal to \(n-1\). A directly calculation implies the following Jacobian matrix

$$\begin{aligned} \begin{aligned} {\mathbf {C}}=&\frac{\partial \Big ({\bar{\alpha }}_{[\frac{n-1}{2}]},\cdots ,{\bar{\alpha }}_0,{\bar{\beta }}_{[\frac{n-2}{2}]},\cdots ,{\bar{\beta }}_0,{\bar{\alpha }}_{[\frac{n}{2}]}\Big )}{\partial \Big (\xi _{i_0,j_{[\frac{n-1}{2}]}},\cdots ,\xi _{i_{[\frac{n-1}{2}]},j_0}, \xi _{k_0,l_{[\frac{n-2}{2}]}},\cdots ,\xi _{k_{[\frac{n-2}{2}]},l_0},\xi _{0,n}\Big )}\\ =&\left( \begin{matrix} {\mathbf {A}}&{}{\mathbf {B}}\\ {\mathbf {0}}&{}\frac{2^{[\frac{n}{2}]}}{n+1}\\ \end{matrix}\right) ,\ \ \end{aligned} \end{aligned}$$

where \({\mathbf {0}}\) is a row vector and \({\mathbf {B}}\) is a column vector. It is easy to get that

$$\begin{aligned} | {\mathbf {C}}|=\frac{2^{[\frac{n}{2}]}}{n+1}|{\mathbf {A}}|\ne 0, \end{aligned}$$

which yields \({\bar{\alpha }}_i\), \(i=0,1,2,\cdots ,[\frac{n}{2}]\) and \({\bar{\beta }}_j\), \(j=0,1,2,\cdots ,[\frac{n-1}{2}]\) can be taken as free parameters.

In a similar way, one can prove that

$$\begin{aligned} \sum \limits _{i+j=0}^n\eta _{i,j}J_{i,j}(h)=\left( {\sum \limits _{i=0}^{[\frac{n}{2}]}{\hat{\alpha }}_ih^i}\right) J_{0,0}(h) +\left( {\sum \limits _{j=0}^{[\frac{n-1}{2}]}{\hat{\beta }}_jh^j}\right) J_{1,0}(h), \end{aligned}$$
(2.13)

where \({\hat{\alpha }}_i\), \(i=0,1,2,\cdots ,[\frac{n}{2}]\) and \({\hat{\beta }}_j\), \(j=0,1,2,\cdots ,[\frac{n-1}{2}]\) can be taken as free parameters.

Observe that \({\bar{\alpha }}_i\) and \({\bar{\beta }}_j\) are expressed by \(\xi _{i,j}\) and \({\hat{\alpha }}_i\) and \({\hat{\beta }}_j\) are expressed by \(\eta _{i,j}\), one has that \({\bar{\alpha }}_i\), \({\bar{\beta }}_j\), \({\hat{\alpha }}_i\) and \({\hat{\beta }}_j\) are independent of each other. A straightforward calculation yields that

$$\begin{aligned} I_{0,0}(h)=-2\sqrt{2h},\ J_{0,0}(h)=2\sqrt{2h},\ J_{1,0}(h)=-\pi h. \end{aligned}$$
(2.14)

In view of (2.4), (2.13) and (2.14), one gets the equality (2.1), where

$$\begin{aligned} \alpha _i=2\sqrt{2}({\hat{\alpha }}_i-{\bar{\alpha }}_i),\ \beta _i={\bar{\beta }}_i,\ \gamma _i=-\pi {\hat{\beta }}_i, \end{aligned}$$

which means that \(\alpha _i\), \(\beta _i\) and \(\gamma _i\) can be chosen arbitrarily. This ends the proof.   \(\lozenge \)

Remark 2.1

In the proof of Lemma 2.1, we have verified that the coefficients of the coefficient polynomials of \(I_{0,0}(h)\), \(I_{1,0}(h)\), \(J_{0,0}(h)\) and \(J_{1,0}(h)\) are independent of each other under general polynomial perturbations by using mathematical induction. Compared with the verification processes in the previous literatures, the calculation in this paper is simpler.

3 Proof of Theorem 1.1

In order to obtain the lower bound of the number of zeros of M(h), we resort to a result of Coll, Gasull and Prohens published in [3]. We review this result here for the convenience of the reader.

Lemma 3.1

[3]. Consider \(p+1\) linearly independent analytical functions \(f_i:U\rightarrow {\mathbb {R}},\ i=0,1,2,\cdots , p\), where \(U\in {\mathbb {R}}\) is an interval. Suppose that there exists \(j\in \{0,1,\cdots ,p\}\) such that \(f_j\) has constant sign. Then there exists \(p+1\) constants \(\delta _i,\ i=0,1,\cdots ,p\), such that \(f(x)=\sum _{i=0}^p\delta _if_i(x)\) has at least p simple zeros in U.

To apply the above Lemma 3.1 one should show that the first order Melnikov function M(h) can be expressed as a combination of some linearly independent functions. To this end, let us start with some preliminary considerations.

Let \(u=\sqrt{h},\ h\in (0,\frac{1}{2})\). Then (2.1) can be written as

$$\begin{aligned} \begin{aligned} M(u)=&\sum \limits _{i=0}^{[\frac{n}{2}]}\alpha _iu^{2i+1}+\left( {\sum \limits _{i=0}^{[\frac{n-1}{2}]}\beta _iu^{2i}}\right) I_{1,0}(u^2) +\sum \limits _{i=0}^{[\frac{n-1}{2}]}\gamma _iu^{2i+2}\\ =&\sum \limits _{i=1}^{n+1}\delta _iu^i+\left( {\sum \limits _{i=0}^{[\frac{n-1}{2}]}\beta _iu^{2i}}\right) I_{1,0}(u^2), \end{aligned} \end{aligned}$$

where \(\delta _i\) are constants and can be chosen as free parameters. Therefore, one finds that

$$\begin{aligned} M(u)=\sum \limits _{i=1}^{n+1}\delta _iu^i+\left( {\sum \limits _{i=0}^{[\frac{n-1}{2}]}\beta _iu^{2i}}\right) \varphi (u), \end{aligned}$$
(3.1)

in view of

$$\begin{aligned} I_{1,0}(h)=-\sqrt{2h}+\frac{1}{2}(2h-1)\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}, \end{aligned}$$

where

$$\begin{aligned} \varphi (u)=-\sqrt{2}u+\frac{1}{2}(2u^2-1)\ln \frac{1-\sqrt{2}u}{1+\sqrt{2}u}. \end{aligned}$$

It is easy to check that \(\varphi (u)\) satisfies the following differential equation

$$\begin{aligned} (2u^2-1)\varphi '(u)=4u\varphi (u)+4\sqrt{2}u^2. \end{aligned}$$
(3.2)

In order to show the linear independence of generating functions of M(u) in (3.1), we extend M(u) to a complex domain. From now on, we suppose that u is complex. We know that \(\varphi (u)\) can be analytically extended to the complex domain \(\Omega = {\mathbb {C}}\backslash \{u\in {\mathbb {R}}|\, |u|\ge \frac{\sqrt{2}}{2}\}\). For \(|u|>\frac{\sqrt{2}}{2}\) and let \(\varphi ^\pm (u)\) donates the analytic continuation of \(\varphi (u)\) along an arc with \(\pm Im (u)>0\), respectively. Then by (3.2) the function \(\varphi ^\pm (u)\) satisfies

$$\begin{aligned} \varphi ^+(u)-\varphi ^-(u)=c (2u^2-1)\mathbf{i}, \ u\in \left( {-\infty ,-\frac{\sqrt{2}}{2}}\right) \cup \left( {\frac{\sqrt{2}}{2},+\infty }\right) , \end{aligned}$$
(3.3)

where \(\mathbf{i}^2=-1\) and c is a nonzero real number.

The following Proposition plays a key role in estimating the lower bound of the number of zeros of M(h).

Proposition 3.1

The Melnikov function M(u) in (3.1) can be represented as a linear combination of the following \(n+[\frac{n+1}{2}]+1\) linearly independent generating functions

$$\begin{aligned} u,\cdots ,u^{n+1},\varphi (u),u^2\varphi (u),\cdots ,u^{2[\frac{n-1}{2}]}\varphi (u). \end{aligned}$$

Proof

We assume that there exist constants \(\sigma _1,\cdots ,\sigma _{n+1},\mu _0,\mu _1,\cdots ,\mu _{[\frac{n-1}{2}]}\) such that

$$\begin{aligned} \begin{aligned} {\overline{M}}(u)\triangleq&\,\sigma _1u+\cdots +\sigma _{n+1}u^{n+1}+\mu _0\varphi (u)\\ {}&+\mu _1u^2\varphi (u)+\cdots +\mu _{[\frac{n-1}{2}]}u^{2[\frac{n-1}{2}]}\varphi (u)\equiv 0. \end{aligned}\end{aligned}$$
(3.4)

To show the linear independence of generating functions, we only need to prove that all the coefficients in (3.4) are zeros.

Since \(\varphi (u)\) can be analytically extended to domains \(\Omega \), M(h) can be analytically extended to the domain \(\Omega \). For \(u\in (-\infty ,-\frac{\sqrt{2}}{2})\cup (\frac{\sqrt{2}}{2},+\infty )\), by (3.3) and (3.4), one has that

$$\begin{aligned} {\overline{M}}^+(u)-{\overline{M}}^-(u)=c(2u^2-1)\mathbf{i}\sum \limits _{i=0}^{[\frac{n-1}{2}]}\mu _iu^{2i}\equiv 0, \end{aligned}$$

which implies \(\mu _i=0\), \(i=0,1,2,\cdots ,[\frac{n-1}{2}].\) Then \({\overline{M}}(u)\) in (3.4) is simplified into the form

$$\begin{aligned} {\overline{M}}(u)\triangleq \sigma _1u+\cdots +\sigma _{n+1}u^{n+1}\equiv 0. \end{aligned}$$

Taking for granted that the functions \(u,u^2,\cdots ,u^{n+1}\) are independent of each other, one obtains that \(\sigma _i=0\), \(i=1,2,\cdots ,n+1\). This ends the proof.

\(\square \)

The following Lemma proves to be extremely useful in estimating the upper bound of the number of zeros of M(h).

Lemma 3.2

Let \(f^{(n)}(h)\) represents the nth-order derivative of f(h). Then for \(n\ge m+1\) and any \(m,n\in \mathbb {N}\), it holds that

$$\begin{aligned} \left( {h^m\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) ^{(n)}=\frac{P_{n-1}(h)}{h^{n-m-\frac{1}{2}}(2h-1)^n}, \end{aligned}$$

where \(P_{n-1}\)(h) is a polynomial of degree \(n-1\).

Proof

It is easy to get that

$$\begin{aligned} \left( {\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) ^{(k)}=\frac{Q_{k-1}(h)}{h^{k-\frac{1}{2}}(2h-1)^k}, \end{aligned}$$

in view of induction on k, where \(Q_{k-1}\)(h) is a polynomial of degree \(k-1\). Hence, by Leibniz formula and the above equality, one finds that

$$\begin{aligned} \begin{aligned}\left( {h^m\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) ^{(n)}=&\sum \limits _{k=0}^nC_n^k(h^m)^{(n-k)} \left( {\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) ^{(k)}\\ =&\sum \limits _{k=0}^n\frac{C_n^km(m-1)\cdots (m-n+k+1)Q_{k-1}(h)}{h^{n-m-\frac{1}{2}}(2h-1)^k}\\ :=&\frac{P_{n-1}(h)}{h^{n-m-\frac{1}{2}}(2h-1)^n}. \end{aligned} \end{aligned}$$

The proof is completed. \(\square \)

Proof of Theorem 1.1

In accordance with Lemma 2.1, Lemma 3.1 and Proposition 3.1, one knows that M(u) in (3.1) can have \(n+[\frac{n+1}{2}]\) zeros on \((0,\frac{\sqrt{2}}{2})\), which means that M(h) in (2.1) can have \(n+[\frac{n+1}{2}]\) zeros on the interval \((0,\frac{1}{2})\). Therefore, system (1.2) can have \(n+[\frac{n+1}{2}]\) limit cycles for \(h\in (0,\frac{1}{2})\).

Next we want to obtain the upper bound of the number of limit cycles of system (1.2). (2.1) can be written as

$$\begin{aligned} \begin{aligned} M(h)=&\left( {\sum \limits _{i=0}^{\left[ {\frac{n-1}{2}}\right] }\beta _ih^i}\right) \left( {-\sqrt{2h}+(h-\frac{1}{2})\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) \\&+\sqrt{h}\sum \limits _{i=0}^{[\frac{n}{2}]}\alpha _ih^i+\sum \limits _{i=0}^{\left[ {\frac{n-1}{2}}\right] }\gamma _ih^{i+1}\\ :=&\left( {h-\frac{1}{2}}\right) \sum \limits _{i=0}^{\left[ {\frac{n-1}{2}}\right] }\beta _ih^i\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}} +\sqrt{h}\sum \limits _{i=0}^{[\frac{n}{2}]}\zeta _ih^i+\sum \limits _{i=0}^{\left[ {\frac{n-1}{2}}\right] }\gamma _ih^{i+1}, \end{aligned}\end{aligned}$$
(3.5)

where \(\zeta _i\) are constants. Differentiating (3.5) \([\frac{n-1}{2}]+2\) times using Lemma 3.2 gives that

$$\begin{aligned} \begin{aligned}M^{{\left( {\left[ {\frac{n-1}{2}}\right] +2}\right) }}(h)=&\left( {\sqrt{h}\sum \limits _{i=0}^{[\frac{n}{2}]}\zeta _ih^i+ \left( {h-\frac{1}{2}}\right) \sum \limits _{i=0}^{\left[ {\frac{n-1}{2}}\right] }\beta _ih^i\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) ^{\left( {\left[ {\frac{n-1}{2}}\right] +2}\right) }\\ =&\frac{P_{[\frac{n}{2}]}(h)}{h^{\left[ {\frac{n-1}{2}}\right] +\frac{3}{2}}}+\sum \limits _{k=0}^{\left[ {\frac{n-1}{2}}\right] +2}C_{\left[ {\frac{n-1}{2}}\right] +2}^k \left( {h-\frac{1}{2}}\right) ^{(k)}\\&\times \left( {\sum \limits _{i=0}^{\left[ {\frac{n-1}{2}}\right] }\beta _ih^i\ln \frac{1-\sqrt{2h}}{1+\sqrt{2h}}}\right) ^{\left( {\left[ {\frac{n-1}{2}}\right] +2-k}\right) }\\ =&\frac{P_{\left[ {\frac{n}{2}}\right] +\left[ {\frac{n-1}{2}}\right] +1}(h)}{h^{\left[ {\frac{n-1}{2}}\right] +\frac{3}{2}}(2h-1)^{\left[ {\frac{n-1}{2}}\right] +1}}. \end{aligned} \end{aligned}$$

Thus \(M^{\left( {\left[ {\frac{n-1}{2}}\right] +2}\right) }(h)\) has at most \([\frac{n}{2}]+\left[ {\frac{n-1}{2}}\right] +1\) zeros on \((0,\frac{1}{2})\). Therefor, by Rolle’s theorem, M(h) has at most \(n+\left[ {\frac{n+1}{2}}\right] +1\) zeros on \([0,\frac{1}{2})\). Notice that \(M(0)=0\) and hence M(h) has at most \(n+[\frac{n+1}{2}]\) zeros on \((0,\frac{1}{2})\). This completes the proof of Theorem 1.1. \(\square \)

4 Conclusion

The motivation of this work is to find a simple approach to verify the independence of the coefficients of the coefficient polynomials of the generators of the first order Melnikov function M(h) of system (1.1). Because this is an essential step in estimating the lower bound of the number of zeros of M(h) and the existing methods for verifying independence are cumbersome.

To achieve our goal, we illustrate this approach by estimating the number of limit cycles of a near-Hamiltonian system with a homoclinic loop. Using this method, we have proved that this near-Hamiltonian system (1.2) has at most \(n+[\frac{n+1}{2}]\) limit cycles and this number can be reached. This is a new result on the bound of the number of limit cycles for such system with a homoclinic loop and the method in this paper can be applied in the study of limit cycle bifurcations of integrable differential systems.