Keywords

81.1 Introduction

Queueing systems with customer impatience such as hospital emergency rooms handling critical patients, and inventory systems that store perishable goods, is very popular. Due to their potential application, many authors are interest in studying the queueing systems with impatient customers and treat the impatience phenomenon by various assumptions. The first to analyze queueing systems with impatient customers seems to be Palm’s pioneering work (1953) by considering the \( {M \mathord{\left/ {\vphantom {M {{M \mathord{\left/ {\vphantom {M c}} \right. \kern-0pt} c}}}} \right. \kern-0pt} {{M \mathord{\left/ {\vphantom {M c}} \right. \kern-0pt} c}}}\) queue, where the waiting times is assumed to be independent exponential distribution. Daley (1965) studied the GI/G/1 queue with impatient customers, in which customers may abandons the system before starting or completing their service when they have to wait too long. And these results are extended by several authors in many different directions. A customer abandons the queue when he has a long wait already experienced, or a long wait anticipated upon arrival, for example Takacs (1974), Baccelli et al. (1984), Boxma and de Waal (1994), Van Houdt et al. (2003), and Yue and Yue (2009). Recently, the queueing models with server vacation and impatient customers are analized by Altman and Yechiali (2006) .

This work is supported by the Fundamental Research Funds for the Central Universities, No. ZYGX2010J111, No. ZYGX2011J102, and Yunnan Provincial Natural Science Foundation of China under Grant No. 2011FZ025.

In 2002, A class of semi-vacation policies had been introduced by Servi and Finn (2002). In this system the server don’t completely stop service but works at a lower rate during a vacation. This system is called a working vacation (WV) system. The vacation time is assumed to be exponentially distributed. The service times during a regular service period and during a working vacation follow exponential distribution but with different rates. Zhao et al. (2008) ultilize the quasi birth and death process and the matrix-geometric solution method to study an M/M/1 queueing system with a single working vacation and obtain various performance measures. An M/G/1 queue with multiple working vacations has been studied by Wu and Takagi (2006). In addition, many authors extended these results such as Baba (2005), Li et al. (2009).

However, there are few literatures which take customers’ impatient during a working vacation into consideration. An M/M/1 queueing system with working vacations and impatient customers is considered by Yue and Yue (2011). We extend the research in Yue and Yue 2011 to an M/M/1 queueing system with a single working vacation and impatient customers. For practical application, the single working vacation policy has been widely used in managing science. When the system has relatively few the number of customers, it becomes important to economize operation cost and energy consumption, so the system needs to work at a lower rate operation state. The model (Yue and Yue 2011) is one case of our analysis. We analyze the queueing system where the server has a slow rate to serve during a working vacation and customers become impatient due to a slow service rate in this paper. The server waits dormant to the first arrival in case that the server comes back to an empty system from a vacation, thereafter, opens a busy period. Otherwise, the server starts a busy period directly if the queue system has customers. The customers’ impatient time follows independently exponential distribution. If the customer’s service has not been completed before the customer becomes impatient, the customer abandons the queue and doesn’t return.

We organize the rest of this paper as follows: the model description is given in Sect. 81.2. Then we derive the balance equations for the system. A differential equation for \( G_{0} \left( z \right) \) is obtained, where \( G_{0} \left( z \right) \) is the generating function of the queue size when the server is on vacation. It is easy to calculate the fractions of time the server being in working vacation or busy period. Various performance measures including the mean system size, the mean sojourn time of a customer served is obtained. Section 81.3 gives are some numerical results.

81.2 Analysis of the Model

81.2.1 Description of the Model

We study an M/M/1 queue with a single working vacation and impatient customers. We assume that arrival process follows Poisson proccess with parameter \( \lambda \), and the rule of serving is on a first-come first-served (FCFS) basis. If the server returns from a working vacation to find the system empty, he waits dormant to the first arrival thereafter and open a busy period. The working vacation follows exponential distribution with parameter \( \gamma \), and the service times during a service period and a working vacation follow exponential distribution with parameters \( \mu_{b} \) and \( \mu_{v} \), respectively, where \( \mu_{b} > \mu_{v} \). During the working vacation, customers become impatient and the impatient times follows exponential distribution with parameter \( \xi \). If the customer’s service has not been completed before the customer becomes impatient, the customer abandons the queue and doesn’t return.

Remark 1. If \( \mu_{v} = 0 \), the current model becomes the M/M/1 queueing model which has a single vacation and impatient customers, and was studied by Altman and Yechiali (2006). If \( \xi = 0 \), the current model has a single working vacation, it was studied by Zhao et al. (2008).

81.2.2 Balance Equations of the Model

The total number of customers in the system and the number of working servers are denoted by \( L \) and J, respectively. In other words, when \( J = 0 \). The server is in a working vacation, and when \( J = 1 \), the server is in a service period. Then, the pair \( \left\{ {J,L} \right\} \) constructs a continuous-time Markov process with transition-rate diagram shown in Fig. 81.1. Here, the steady-state transition probabilities are defined by \( P_{jn} = P\left\{ {J = j,L = n} \right\} \). \( j = 0,1;n = 0,1,2, \ldots \).

Fig. 81.1
figure 1

State transition rate diagram

Full size image

Then, we can get the set of balance equations as follows:

$$ j = 0\left\{ {\begin{array}{*{20}c} {n = 0} \hfill & \begin{gathered} (\gamma + \lambda )P_{00} = (\xi + \mu_{v} )P_{01} + \hfill \\ \mu_{b} P_{11} \hfill \\ \end{gathered} \hfill \\ {n \ge 1} \hfill & \begin{gathered} (\lambda + \gamma + \mu_{v} + n\xi )P_{0n} = \hfill \\ \lambda P_{0,n - 1} + [\mu_{v} + (n + 1)\xi ]P_{0,n + 1} , \hfill \\ \end{gathered} \hfill \\ \end{array} } \right. $$
(81.1)
$$ j = 1\left\{ {\begin{array}{*{20}c} {n = 0} \hfill & {\lambda P_{10} = \gamma P_{00} } \hfill \\ {n \ge 1} \hfill & \begin{gathered} (\lambda + \mu_{b} )P_{1n} = \lambda P_{1,n - 1} + \hfill \\ \gamma P_{0n} + \mu_{b} P_{1,n + 1} . \hfill \\ \end{gathered} \hfill \\ \end{array} } \right. $$
(81.2)

The probability generating functions (PGFs) is defined by

$$ G_{j} \left( z \right) = \sum\limits_{n = 0}^{\infty } P_{jn} z^{n} ,\;\;j = 0,1. $$

Then, multiplying (81.1) by \( z^{n} \), summing over \( n \), and rearranging terms, we get

$$ \left[ {\lambda z^{2} - \left( {\lambda + \gamma + \mu_{v} } \right)z + \mu_{v} } \right]G_{0} \left( z \right) + \xi z\left( {1 - z} \right)G_{0}^{'} (z) = \mu_{v} P_{00} \left( {1 - z} \right) - \mu_{b} P_{11} z\;\;, $$
(81.3)

where \( G_{0}^{'} \left( z \right) = \frac{{dG_{0} \left( z \right)}}{dz}. \) We also use the same way and obtain from (81.2)

$$ \left[ {\lambda z^{2} - \left( {\lambda + \mu_{b} } \right)z + \mu_{b} } \right]G_{1} \left( z \right) + \gamma zG_{0} \left( z \right) = \mu_{b} P_{10} (1 - z) + \mu_{b} P_{11} z. $$
(81.4)

Remark 2.

  1. (1)

    Letting \( \mu_{v} = 0 \) in (81.3), we get

$$ \left( {\lambda + \gamma } \right)G_{0} \left( z \right) + \xi zG_{0}^{'} \left( z \right) = \lambda zG_{0} \left( z \right) + \xi G_{0}^{'} \left( z \right) + \mu_{b} P_{11} . $$
(81.5)

This agrees with Altman and Yechiali (2006) (see (5.3), p. 274).

  1. (2)

    Letting \( \xi = 0 \) in (81.4), we get the \( {M \mathord{\left/ {\vphantom {M {{M \mathord{\left/ {\vphantom {M 1}} \right. \kern-0pt} 1}}}} \right. \kern-0pt} {{M \mathord{\left/ {\vphantom {M 1}} \right. \kern-0pt} 1}}} \) with a single working vacation. This agrees with Zhao et al. (2008).

81.2.3 Solution of the Differential Equation

For \( z \ne 0 \) and \( z \ne 1 \), (81.3) can be written as follows:

$$ G_{0}^{'} \left( z \right) + \left[ { - \frac{\lambda }{\xi } - \frac{\gamma }{\xi (1 - z)} + \frac{{\mu_{v} }}{\xi z}} \right]G_{0} \left( z \right) = \frac{{\mu_{v} P_{00} }}{\xi z} - \frac{{\mu_{b} P_{11} }}{\xi (1 - z)}. $$
(81.6)

Multiplying both sides of (81.6) by

$$ e^{{ - \frac{\lambda }{\xi }z}} \left( {1 - z} \right)^{{\frac{\gamma }{\xi }}} z^{{\frac{{\mu_{v} }}{\xi }}} , $$

we get

$$ \frac{d}{dz}\left[ {e^{{ - \frac{\lambda }{\xi }z}} \left( {1 - z} \right)^{{\frac{\gamma }{\xi }}} z^{{\frac{{\mu_{v} }}{\xi }}} G_{0} \left( z \right)} \right] = \frac{1}{\xi }\left(\frac{{\mu_{v} P_{00} }}{z} - \frac{{\mu_{b} P_{11} }}{1 - z}\right)e^{{ - \frac{\lambda }{\xi }z}} (1 - z)^{{\frac{\gamma }{\xi }}} z^{{\frac{{\mu_{v} }}{\xi }}} . $$
(81.7)

Integrating from 0 to z we have

$$ G_{0} \left( z \right) = \frac{{ - \mu_{b} P_{11} k_{1} \left( z \right) + \mu_{v} P_{00} k_{2} \left( z \right)}}{{\xi e^{{ - \frac{\lambda }{\xi }z}} \left( {1 - z} \right)^{{\frac{\gamma }{\xi }}} z^{{\frac{{\mu_{v} }}{\xi }}} }} $$
(81.8)

where

$$ k_{1} \left( z \right) = \int_{0}^{z} e^{{ - \frac{\lambda }{\xi }x}} \left( {1 - x} \right)^{{\frac{\gamma }{\xi } - 1}} x^{{\frac{{\mu_{v} }}{\xi }}} dx, $$
$$ k_{2} \left( z \right) = \int_{0}^{z} e^{{ - \frac{\lambda }{\xi }x}} \left( {1 - x} \right)^{{\frac{\gamma }{\xi }}} x^{{\frac{{\mu_{v} }}{\xi } - 1}} dx. $$

Equation (81.8) expresses \( G_{0} \left( z \right) \) in terms of \( P_{00} \) and \( P_{11} \). Also, from (81.4), \( G_{1} \left( z \right) \) is a function of \( G_{0} (z) \), \( P_{00} \), \( P_{11} \). Thus, once \( P_{00} \) and \( P_{11} \) are calculated, \( G_{0} \left( z \right) \) and \( G_{1} \left( z \right) \) are completely determined. We derive the probabilities \( P_{00} \), \( P_{11} \) and the mean system sizes in the next subsection.

81.2.4 Derivation of Various Performance Measures

Let \( P_{j.} = G_{j} \left( 1 \right) = \sum\nolimits_{n = 0}^{\infty } P_{jn} \) and \( E\left[ {L_{j} } \right] \). \( = G_{j}^{'} \left( 1 \right) = \sum\nolimits_{n = 0}^{\infty } nP_{jn} \) \( j = 0,1, \ldots \). Then from (81.3) we get

$$ \mu_{b} P_{11} = \gamma G_{0} \left( 1 \right) = \gamma P_{0.} . $$
(81.9)

From (81.8), we have

$$ G_{0} \left( 1 \right) = \frac{{e^{{\frac{\lambda }{\xi }}} }}{\xi }\left[ { - \mu_{b} P_{11} k_{1} \left( 1 \right) + \mu_{v} P_{00} k_{2} \left( 1 \right)} \right] \times \mathop {\lim }\nolimits_{z \to 1} \left( {1 - z} \right)^{{ - \frac{\gamma }{\xi }}}, $$
(81.10)

, since \( G_{0} \left( 1 \right) = P_{0.} = \sum\nolimits_{n = 0}^{\infty } P_{0n} > 0 \),

and \( \mathop {\lim }\nolimits_{z \to 1} \left( {1 - z} \right)^{{ - \frac{\gamma }{\xi }}} \,=\, \infty \), we must have

$$ - \mu_{b} P_{11} k_{1} \left( 1 \right) + \mu_{v} P_{00} k_{2} \left( 1 \right) = 0 $$

implying that

$$ P_{00} = \frac{{\mu_{b} P_{11} k_{1} \left( 1 \right)}}{{\mu_{v} k_{2} \left( 1 \right)}} = \frac{{\gamma G_{0} \left( 1 \right)k_{1} \left( 1 \right)}}{{\mu_{v} k_{2} \left( 1 \right)}}. $$
(81.11)

And (81.4) can be written as

$$ G_{1} \left( z \right) = \frac{{\gamma zG_{0} \left( z \right) + \mu_{b} P_{10} z - \mu_{b} P_{11} z - \mu_{b} P_{10} }}{{\left( {\lambda z - \mu_{b} } \right)\left( {1 - z} \right)}}. $$
(81.12)

By using L’Hopital rule, we derive

$$ G_{1} \left( 1 \right) = \frac{{\mu_{b} P_{10} + \gamma G_{0}^{'} \left( 1 \right)}}{{\mu_{b} - \lambda }}, $$
(81.13)

implying that

$$ E\left[ {L_{0} } \right] = G_{0}^{'} \left( 1 \right) = \frac{{\mu_{b} - \lambda }}{\gamma }P_{1} - \frac{{P_{00} }}{\lambda }\mu_{b} . $$
(81.14)

On the other hand, from (81.3),

$$ E\left[ {L_{0} } \right] = \mathop {\lim }\limits_{z \to 1} G_{0}^{'} \left( z \right) = \frac{{\left( {\mu_{v} - \lambda } \right)G_{0} \left( 1 \right) + \gamma G_{0}^{'} \left( 1 \right) - \mu_{v} P_{00} }}{ - \xi }, $$
(81.15)

implying that

$$ G_{0}^{'} \left( 1 \right) = \frac{{\left( {\lambda - \mu_{v} } \right)G_{0} \left( 1 \right) + \mu_{v} P_{00} }}{\gamma + \xi }. $$
(81.16)

Equating the two expressions (81.14) and (81.16) for \( E\left[ {L_{0} } \right] \), and using \( 1 = P_{0} + P_{1} \), we get

$$ G_{0} \left( 1 \right) = \frac{{\left( {\lambda \xi \mu_{b} + \lambda \gamma \mu_{b} - \xi \lambda^{2} - \gamma \lambda^{2} } \right)\mu_{v} k_{2} \left( 1 \right)}}{{\eta_{1} + \eta_{2} }}, $$
(81.17)
$$ P_{00} = \frac{{\gamma k_{1} \left( 1 \right)}}{{\mu_{v} k_{2} \left( 1 \right)}}G_{0} \left( 1 \right), $$
(81.18)

where

$$ \begin{aligned} & \eta_{1} = \left( {\lambda \xi \mu_{b} + \lambda \gamma \mu_{b} - \lambda \gamma \mu_{v} - \xi \lambda^{2} } \right)\mu_{v} k_{2} \left( 1 \right) \hfill \\& \eta_{2} = \left( {\mu_{b} \gamma^{2} + \gamma \xi \mu_{b} + \lambda \gamma \mu_{v} } \right)\gamma k_{1} \left( 1 \right) \hfill \\ \end{aligned} $$

From (81.12) we have

$$ E\left[ {L_{1} } \right] = \frac{{\eta_{3} }}{{2\left( {\mu_{b} - \lambda } \right)^{2} }}, $$
(81.19)

where

$$ \eta_{3} = \left( {\mu_{b} - \lambda } \right)\gamma G_{0}^{{'^{\prime}}} \left( 1 \right) + 2\gamma \mu_{b} G_{0}^{'} \left( 1 \right) + 2\gamma \mu_{b} P_{00} . $$

From (81.3) we get

$$ G_{0}^{{'^{\prime}}} \left( 1 \right) = \frac{{2\lambda G_{0} \left( 1 \right) + 2\left( {\lambda - \gamma - \xi - \mu_{v} } \right)G_{0}^{'} \left( 1 \right)}}{\gamma + 2\xi }. $$
(81.20)

Thus, the mean system size

$$ E\left[ L \right] = E\left[ {L_{0} } \right] + E\left[ {L_{1} } \right]. $$
(81.21)

From (81.14), the necessary and sufficient condition for stability \( \lambda < \mu_{b} \), for otherwise \( E\left[ {L_{0} } \right] = - P_{00} < 0 \).

81.2.5 Sojourn Times

Denote \( S \) the total sojourn time of a customer in the system, which is measured from the moment of arrival to departure, including completion of service and a result of abandonment. By using Little’s law,

$$ E\left[ S \right] = \frac{E\left[ L \right]}{\lambda } = \frac{{E\left[ {L_{0} } \right] + E\left[ {L_{1} } \right]}}{\lambda } $$
(81.22)

Denote \( S_{served} \) the total sojourn time of a customer who completes his service. We note that\( S_{served} \)is more important porfermance measure. Denote \( S_{jn} \) the conditional sojourn time of a customer who does not leave the system, and \( \left( {j,n} \right) \) is the state on his arrival. Evidently, \( E\left[ {S_{1n} } \right] = {{\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)} \mu }} \right. \kern-0pt} \mu } \), but this is for \( n = 0,1,2, \ldots \) rather than for \( n \ge 1 \) in (81.15).

Now, we derive \( E\left[ {S_{0n} } \right] \) by using the method used by Altman and Yechiali (2006), when \( J = 0 \), for \( n \ge 1 \),

$$ E\left[ {S_{0n} } \right] = \frac{\gamma }{{\theta_{n + 1} }}\left( {\frac{1}{{\theta_{n + 1} }} + E\left[ {S_{1n} } \right]} \right) + \frac{\lambda }{{\theta_{n + 1} }}\left( {\frac{1}{{\theta_{n + 1} }} + E\left[ {S_{0n} } \right]} \right) + \frac{{n\xi + \mu_{v} }}{{\theta_{n + 1} }}\left(\frac{1}{{\theta_{n + 1} }} + E[S_{0,n - 1} ]\right), $$
(81.23)

where

$$ \theta_{n} = \gamma + \lambda + \mu_{v} + n\xi $$

for \( n = 0,1,2, \)…. The second term above is derived from the fact that a new arriving customer does not influence the sojourn time of a customer present in the system. The probability \( {n \mathord{\left/ {\vphantom {n {\left( {n + 1} \right)}}} \right. \kern-0pt} {\left( {n + 1} \right)}} \)in the third term comes from the fact that when one of the \( n + 1 \) waiting customers abandons, our customer is not the one to leave.

Then,

$$ \begin{gathered} \left[ {\gamma + \left( {n + 1} \right)\xi + \mu_{v} } \right]E\left[ {S_{0n} } \right] = \frac{{\theta_{n} }}{{\theta_{n + 1} }} + \frac{\gamma (n + 1)}{{\mu_{b} }} + (n\xi + \mu_{v} )E[S_{0,n - 1} ]. \hfill \\ \quad \quad \quad \quad \hfill \\ \end{gathered} $$
(81.24)

We also have

$$ E\left[ {S_{00} } \right] = \frac{\lambda }{{\theta_{1} }}\left( {\frac{1}{{\theta_{1} }} + \frac{1}{{\mu_{b} }}} \right) + \frac{\lambda }{{\theta_{1} }}\left( {\frac{1}{{\theta_{1} }} + E\left[ {S_{00} } \right]} \right) + \frac{{\mu_{v} }}{{\theta_{1}^{2} }}, $$
(81.25)

implying that

$$ E\left[ {S_{00} } \right] = \frac{1}{{\gamma + \xi + \mu_{v} }}\left( {\frac{{\theta_{0} }}{{\theta_{1} }} + \frac{\gamma }{{\mu_{b} }}} \right). $$
(81.26)

Iterating (81.23) we obtain, for \( n \ge 1 \),

$$ E\left[ {S_{0n} } \right] = \frac{1}{{\gamma + \left( {n + 1} \right)\xi + \mu_{v} }}\left[ {\frac{{\theta_{n} }}{{\theta_{n + 1} }} + \frac{{\left( {n + 1} \right)\gamma }}{{\mu_{b} }}} \right] + \sum\limits_{i = 1}^{n} \left\{ {\frac{1}{{\gamma + \left( {i + 1} \right)\xi + \mu_{v} }} \times } \right.\left. {\left[ {\frac{{\theta_{i} }}{{\theta_{i + 1} }} + \frac{{\left( {i + 1} \right)\gamma }}{{\mu_{b} }}} \right] \times \prod\limits_{j = i}^{n} \frac{{j\xi + \mu_{v} }}{{\gamma + \left( {j + 1} \right)\xi + \mu_{v} }}} \right\}. $$
(81.27)

Finally, we use the expression for \( E\left[ {S_{1n} } \right] \) and drive

$$ E\left[ {S_{served} } \right] = \sum\limits_{n = 0}^{\infty } P_{1n} E\left[ {S_{1n} } \right] + \sum\limits_{n = 0}^{\infty } P_{0n} E\left[ {S_{0n} } \right]. $$
(81.28)

implying that

$$ E\left[ {S_{served} } \right] = \frac{{E\left[ {L_{1} } \right] + P_{1.} }}{{\mu_{b} }} + \sum\limits_{n = 0}^{\infty } P_{0n} E\left[ {S_{0n} } \right]. $$
(81.29)

But the first sum in (81.28) starts from \( n = 0 \), it’s different from [15].

81.3 Numerical Results

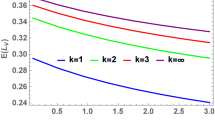
In this section, we show the numerical examples for the results obtained in Sect. 81.2.4. The effectes of \( \mu_{v} \) and \( \xi \) on \( E\left[ {L_{0} } \right] \) and \( E\left[ L \right] \) in (81.14) and (81.21) are shown in Fig. 81.2. Evidently, with \( \mu_{v} \) increaseing, namely, the server works faster and faster, the mean system size of working vacation \( E\left[ {L_{0} } \right] \) and the mean system size \( E\left[ L \right] \) decreases when \( \xi \) is fixed. We also find that if \( \xi \) is smaller, \( E\left[ {L_{0} } \right] \) and \( E\left[ L \right] \) are bigger. From the numerical analysis, the influence of parameters on the performance measures in the system is well demonstrated. The results are suitable to practical situations.

Fig. 81.2
figure 2

The relation of \( E\left[ {L_{0} } \right] \) and \( E\left[ L \right] \) with \( \xi \) and \( \mu_{v} \)

Full size image

81.4 Conclusions

In this paper, we have studied M/M/1 queueing systems with a single working vacation and impatient customers. In this system, the server has a slow rate to serve during a working vacation and customers become impatient due to a slow service rate. The server waits dormant to the first arrival in case that the server comes back to an empty system from a vacation, thereafter, opens a busy period. Otherwise, the server starts a busy period directly if the queue system has customers. The customers’ impatient time follows independently exponential distribution. If the customer’s service has not been completed before the customer becomes impatient, the customer abandons the queue and doesn’t return. The probability generating functions of the number of customers in the system is derived and the corresponding mean system sizes are obtained when the server was both in a service period and in a working vacation. Also, we have obtained closed-form expressions for other performance measures, such as the mean sojourn time when a customer is served.