Measuring Parametric and Volumetric Errors in a Four-Axis CMM Using a Hole Plate

Abstract

Recently, a four-axis coordinate measuring machine (four-axis CMM), which consists of three linear axes and a single rotary axis, has been more widely used than a traditional three-axis CMM. The volumetric error influences the accuracy of the four-axis CMM. There are 27 parametric errors that contribute to the volumetric error. This study utilized a touch probe to measure the hole plate. This methodology can evaluate errors more accurately and reflect the operational conditions of the machines. The main procedures are as follows: (1) The hole plate was sequentially set up in three different planes. The touch probe was used to measure the hole plate using five different styluses. (2) The 27 parametric errors were analyzed using the coordinate deviations. The volumetric error was constructed using homogeneous transformation matrices. The volumetric error ranged from 0.35 to 1.55 μm without the single rotary axis and from 0.35 to 2.83 μm with the single rotary axis. (3) Three metrology instruments, namely a laser interferometer, an autocollimator, and a polygon-autocollimator, were used to validate the proposed methodology and verify the measured parametric errors. The absolute maximum differences compared to the laser interferometer for three parametric positioning errors and the autocollimator for six parametric rotational errors for the three linear axes were 0.56 μm and 0.54″, respectively. Additionally, the absolute maximum difference of one parametric positioning error for the single rotary axis, compared with the polygon-autocollimator, was 0.75″. The En-values were 0.27, 0.54, and 0.27, respectively. These results demonstrate the effectiveness and reliability of the proposed methodology for the industry’s four-axis CMMs.

1 Introduction

CMMs are precise instruments used for precision inspections, encompassing parameters such as flatness, roughness, roundness, and freeform characteristics. A traditional CMM consists of three orthogonal linear axes. The accuracy of measurements is influenced by both parametric and volumetric errors. A single rotary axis conjunct with the three linear axes leads to a four-axis CMM. Accurate measurement necessitates the evaluation of parametric and volumetric errors conducted by the single rotary axes. Consequently, the challenge remains to accurately measure errors in the three linear and single rotary axes.

Numerous references have been proposed for traditional CMMs. The ISO 10360-2 standard [1] is widely adopted for acceptance and re-verification processes. This standard entails performing seven spatial line length measurements to ascertain combined parametric errors. Historically, several references have employed one-dimensional or two-dimensional objects to analyze 21 parametric errors and assess volumetric errors. For instance, several references proposed reference objects [2,3,4,5], Zhang et al. [6] utilized a 1-D ball array, Lin et al. [7] and Lee et al. [8] designed a hole plate, Lim et al. [9] investigated a hole bar, and Kruth et al. [10] developed a ball plate. These studies used holes or balls on the plate as references or standards. In contrast, some references focused only on specific parametric errors, such as an optical flat [11, 12], a horizontal plane [13], and a ring gauge [14]. Pahk et al. [15] measured a horizontal plane by observing the stylus locus to determine parametric roll and straightness errors. Sudatham et al. [16] employed an optical-comb pulsed interferometer to measure parametric positioning errors. Huang et al. [17] proposed a laser optical multi-degree-of-freedom measurement system to measure 12 specific parametric errors. Laser interferometers were also used for various parametric errors [18,19,20,21]. Umetsu et al. [22] developed a new laser-tracking system to measure 21 parametric errors. LaserTRACER [23,24,25], a commercial instrument, was employed to analyze 21 parametric errors. The laser tracking system and LaserTRACER had to be set up at four spatial positions during the measurement. Despite these contributions, these methods were limited in application to traditional CMMs.

In the context of the single rotary axis, six parametric errors are relevant. ISO 10360-3 was introduced to validate the performance of the single rotary axis in the four-axis configuration [26]. This method involves using two spheres to measure the maximum permissible error. Spheres A and B, both at an identical radius, are positioned approximately diametrically opposite and at varying heights. Previous studies have demonstrated that ball plate artifacts containing seven or twelve balls could be used to analyze these six parametric errors [27,28,29,30,31]. Similarly, commercial instruments like LaserTRACER [32, 33] or Laser Tracker [34] have been employed for this purpose. However, these methods necessitated the instrument's placement at multiple spatial positions and were limited to the three linear axes and single rotary axis of the CMM. Our approach explores an alternative methodology utilizing a touch probe and a hole plate to assess parametric and volumetric errors, explicitly targeting the four-axis CMM.

The configuration for this paper is depicted in Fig. 1. We introduce the use of a hole plate to measure the four-axis CMM. Precedents have also utilized hole or ball plates to analyze 21 parametric errors on traditional CMMs [2,3,4,5,6,7,8,9,10]. However, our focus is on the four-axis CMM, encompassing both parametric and volumetric errors. We conduct a comprehensive analysis of 27 parametric errors, covering the three linear axes and a single rotary axis, along with presenting the volumetric error. Three distinct stylus types are employed. The hole plate setup is performed three times to account for the three linear axes and single rotary axis. The subsequent sections discuss related research, the theoretical framework encompassing the 21 parametric errors in the linear axes and the 6 parametric errors in the single rotary axis, the construction of the volumetric error using homogeneous transformation matrices, and the experimental setup utilizing the four-axis CMM. Metrology instruments like a laser interferometer, an autocollimator, and a polygon-autocollimator were employed to validate the parametric errors. The discrepancies between the metrology instruments and the proposed method are analyzed, employing uncertainties and En-values to demonstrate the feasibility of our approach. Finally, the paper concludes and discusses by summarizing the findings.

Fig. 1

a The hole plate with 20 holes and 4 points. b Schematic of the stylus. c The moving table-type four-axis CMM. d 21 parametric errors associated with the three linear axes. e 6 parametric errors associated with the single rotary axis

2 Hole Plate

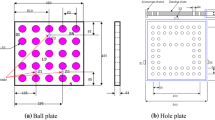
The hole plate (manufactured by Krosaki, Inc.) is designed with 20 holes arranged in a 250 mm × 250 mm square, as depicted in Fig. 1a. The diagonal length measures approximately 353.553 mm. The hole plate numbers range from 1 to 21, with holes 1 and 21 being the same. Each hole is designed to have a diameter of 20 mm with minimal roundness deviation, remaining below 0.1 μm. The upper flat surface of the hole plate also exhibits flatness below 0.1 μm. Hence, the influence of roundness and flatness on the measurement of parametric and volumetric errors is disregarded. The nominal distance between two holes is set at 50 mm, and the height is standardized at 20 mm. The material used is NEXCERA, an ultra-low thermal expansion ceramic with a cordierite base (2MgO–2Al₂O₃–5SiO₂), boasting a thermal expansion coefficient of approximately 1.3 × 10^–8 K⁻¹. Hole coordinates are calibrated using the hole plate calibration system at the National Metrology Institute of Japan (NMIJ). The calibrated positions are situated at the mid-height of the hole plate, denoted by calibrated coordinates in the 1-axis, 2-axis, and 3-axis directions. The original reference coordinate is positioned at the center and upper flat of the hole plate. These calibrated coordinates are outlined in Table 1.

Table 1 The hole plate calibrated coordinates

The hole plate is oriented in three configurations aligned with the X–Y, X–Z, and Y–Z planes to measure parametric errors along the three linear axes. In the X–Y plane, the 1-axis of the calibrated coordinates corresponds to the X-axis, and the 2-axis corresponds to the Y-axis. For the X–Z plane, the 1-axis of the calibrated coordinates corresponds to the X-axis, while the 2-axis corresponds to the Z-axis. Similarly, for the Y–Z plane, the 1-axis of the calibrated coordinates is aligned with the Y-axis, and the 2-axis is aligned with the Z-axis. The horizontal fixture comprises three elements to support the hole plate and is designed for the X–Y plane. A vertical fixture is utilized to mount the hole plate for measurements in the X–Z and Y–Z planes. In the case of the single rotary axis, the hole plate is positioned at the center of the single rotary axis. The setup mirrors that of the X–Y plane for the three linear axes. Specifically, the four corner holes and four corner points of the hole plate, namely numbers 1, 6, 11, 16, P1, P6, P11, and P16, are measured. Consequently, the hole plate needs to be configured in three orientations for measurement. Notably, an additional setup is not required for assessing the single rotary axis.

3 A Moving-Table-Type Four-Axis CMM

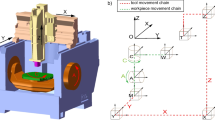
The measurement process employs a touch probe to measure the hole plate. To cater to various measurement planes, three distinct stylus types are employed, as illustrated in Fig. 1b. Here, S_D,j denotes the probe diameter for stylus number j, while S_L,j represents the stylus length from the reference point to the probe center for the same stylus. Moreover, S_A,j signifies the azimuth angle, measuring the rotation from the X-axis towards the Y-axis for stylus number j. In this context, a counterclockwise rotation is positive, and a clockwise rotation is negative. Furthermore, S_E,j indicates the elevation angle towards the X–Y plane for the number j stylus, where downward is considered negative, and upward is deemed positive. As depicted in Fig. 1c, a moving-table-type four-axis CMM comprises three linear axes and a single rotary axis.

Stylus number 1, with an azimuth angle of 0° and an elevation angle of − 90°, is employed for measurements in both the X–Y plane and the single rotary axis. Styluses number 2 and number 4, featuring distinct lengths and possessing an azimuth angle of 90° and elevation angle of 0°, are utilized for measurements in the X–Z plane of the hole plate. Similarly, styluses number 3 and number 5, with differing lengths and azimuth angles of 180°, are chosen for measurements in the Y–Z plane of the hole plate. To sum up, this study employs a total of five distinct styluses to facilitate measurements.

4 Theory

This study employs the hole plate as calibrated coordinates to measure the parametric and volumetric errors inherent in the four-axis CMM. To accomplish this, it is essential to measure and calculate parametric errors. In the context of the three linear axes, a total of 21 parametric errors are present, while the single rotary axis comprises 6 parametric errors. Hence, a total of 27 parametric errors necessitate measurement and calculation.

4.1 Parametric Errors of The Three Linear Axes

The notation for parametric errors adheres to the ISO 230-1 standard [35]. Each parametric error is denoted by the symbol E followed by two subscripts, signifying translational and angular errors. The first subscript indicates the direction of the error, while the second indicates the direction of movement. For instance, E_XX signifies the parametric positioning error, indicating the translational deviation along the X-axis’s linear direction.

The parametric squareness error (denoted as E_COY) quantifies the angle between the X-axis and Y-axis. The value is positive when the angle exceeds 90°, and negative when it’s less than 90°. There are a total of 21 parametric errors under rigid body kinematics, as depicted by the symbols in Fig. 1d.

In the case of the X–Y plane, the measurement process entails determining the measured coordinates of the hole plate (X_M,i,j,XY, Y_M,i,j,XY). Here, i represents the hole number, while j signifies the stylus number. The deviations (DX_i,j,XY(L), DY_i,j,XY(L)) are measured directly and subsequently compared to the calibrated coordinates (X_C,i, Y_C,i), as illustrated in Fig. 2.

Fig. 2

Schematic of the deviations in the X–Y plane

Similarly, for the X–Z plane, the hole plate’s measured coordinates become (X_M,i,j,XZ, Z_M,i,j,XZ), with the deviations (DX_i,j,XZ(L), DZ_i,j,XZ(L)) obtained from direct measurements and compared to the calibrated coordinates (X_C,i, Z_C,i). Analogously, the Y–Z plane involves measured coordinates (Y_M,i,j,YZ, Z_M,i,j,YZ), deviations (DY_i,j,YZ(L), DZ_i,j,YZ(L)), and calibrated coordinates (Y_C,i, Z_C,i). In this process, the measurement position L is calculated as 50 × (i-1)-125, where i ranges from 1 to 6 in increments of 1.

The three parametric positioning errors (E_XX(L), E_YY(L) and E_ZZ(L)) can be expressed as follows:

$$\begin{gathered} E_{{{\text{XX}}}} \left( L \right) \, = \left( {DX_{{{\text{i}},{\text{j}},{\text{XY}}}} \left( L \right) \, + DX_{{{17} - {\text{i}},{\text{j}},{\text{XY}}}} \left( L \right) \, + DX_{{{\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right) \, + DX_{{{17} - {\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right)} \right)/{4} \hfill \\ E_{{{\text{YY}}}} \left( L \right) \, = (DY_{{5 + {\text{i}},{\text{j}},{\text{XY}}}} \left( L \right) \, + DY_{{{22} - {\text{i}},{\text{j}},{\text{XY}}}} \left( L \right) \, + DY_{{{\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right) \, + DY_{{{17} - {\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right))/{4} \hfill \\ E_{{{\text{ZZ}}}} \left( L \right) = (DZ_{{{5} + {\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right) \, + DZ_{{{22} - {\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right) \, + DZ_{{{5} + {\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right) \, + DZ_{{{22} - {\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right))/{4} \hfill \\ \end{gathered}$$

(1)

The six parametric straightness errors (E_YX(L), E_ZX(L), E_XY(L), E_ZY(L), E_XZ(L) and E_YZ(L)) are treated as parametric rotational errors for the X–Y plane. Similar schematics apply to the X–Z and Y–Z planes.

$$\begin{gathered} E_{{{\text{YX}}}} \left( L \right) \, = \left( {DY_{{{\text{i}},{\text{j}},{\text{XY}}}} \left( L \right) + DY_{{{17} - {\text{i}},{\text{j}},{\text{XY}}}} \left( L \right)} \right)/{2} \hfill \\ E_{{{\text{ZX}}}} \left( L \right) = \left( {DZ_{{{\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right)_{{}} + DZ_{{{17} - {\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right)} \right)/{2} \hfill \\ E_{{{\text{XY}}}} \left( L \right) = (DX_{{5 + {\text{i}},{\text{j}},{\text{XY}}}} \left( L \right) + DX_{{{22} - {\text{i}},{\text{j}},{\text{XY}}}} \left( L \right))/{2} \hfill \\ E_{{{\text{ZY}}}} \left( L \right) = \left( {DZ_{{{\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right)_{{}} + DZ_{{{17} - {\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right)} \right)/{2} \hfill \\ E_{{{\text{XZ}}}} \left( L \right) = (DX_{{5 + {\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right)_{{}} + DX_{{{22} - {\text{i}},{\text{j}},{\text{XZ}}}} \left( L \right))/{2} \hfill \\ E_{{{\text{YZ}}}} \left( L \right) = (DY_{{{5} + {\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right)_{{}} + DY_{{{22} - {\text{i}},{\text{j}},{\text{YZ}}}} \left( L \right))/{2} \hfill \\ \end{gathered}$$

(2)

In the X–Y plane, the measured vectors $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XY}}} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,XY}}} }}$ represent the measured positions from (X_M,i,j,XY, Y_M,i,j,XY) to (X_M,17-i,j,XY, Y_M,17-i,j,XY), and from (X_M,5+i,j,XY, Y_M,5+i,j,XY) to (X_M,22-i,j,XY, Y_M,22-i,j,XY). Correspondingly, in the X–Z plane and Y–Z plane, the measured vectors $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XZ}}} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,XZ}}} }}$ denote the measured positions from (X_M,i,j,XZ, Z_M,i,j,XZ) to (X_M,17-i,j,XZ, Z_M,17-i,j,XZ), and from (X_M,5+i,j,XZ, Z_M,5+i,j,XZ) to (X_M,22-i,j,XZ, Z_M,22-i,j,XZ). Similarly, for the Y–Z plane, the measured vectors $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,YZ}}} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,YZ}}} }}$ indicate the measured positions from (Y_M,i,j,YZ, Z_M,i,j,YZ) to (Y_M,17-i,j,YZ, Z_M,17-i,j,YZ) and from (Y_M,5+i,j,YZ, Z_M,5+i,j,YZ) to (Y_{M, 22-i,j,YZ}, Z_M,22-i,j,YZ).

The corresponding calibrated vectors $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XY}}} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,XY}}} }}$ represent the calibrated positions from (X_C,i, Y_C,i) to (X_C,17-i, Y_C,17-i) and from (X_C,5+i, Y_C,5+i) to (X_C,22-i, Y_C,22-i) for the X–Y plane. Similarly, for the X–Z and Y–Z planes, the calibrated vectors $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XZ}}} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,XZ}}} }}$ denote the calibrated positions from (X_C,i, Z_C,i) to (X_C,17-i, Z_C,17-i) and from (X_C,5+i, Z_C,5+i) to (X_C,22-i, Z_C,22-i), and for the Y–Z plane, the calibrated vectors $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,YZ}}} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,YZ}}} }}$ indicate the calibrated positions from (Y_C,i, Z_C,i) to (Y_C,17-i, Z_C,17-i) and from (Y_C,5+i, Z_C,5+i) to (Y_C,22-i, Z_C,22-i).

The six measured vectors are then:

$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XY}}} }} = (X_{{\text{M,i,j,XY}}} - X_{{\text{M,17 - i,j,XY}}} )\hat{i} + \, (Y_{{\text{M,i,j,XY}}} - Y_{{\text{M,17 - i,j,XY}}} )\hat{j} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,XY}}} }} = (X_{{\text{M,5 + i,j,XY}}} - X_{{\text{M,22 - i,j,XY}}} )\hat{i} + \, (Y_{{\text{M,5 + i,j,XY}}} - Y_{{\text{M,22 - i,j,XY}}} )\hat{j} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XZ}}} }} = (X_{{\text{M,i,j,XZ}}} - X_{{\text{M,17 - i,j,XZ}}} ) \hat{i} + \, (Z_{{\text{M,i,j,XZ}}} - Z_{{\text{M,17 - i,j,XZ}}} )\hat{k} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,XZ}}} }} = (X_{{\text{M,5 + i,j,XZ}}} - X_{{\text{M,22 - i,j,XZ}}} )\hat{i} + \, (Z_{{\text{M,5 + i,j,XZ}}} - Z_{{\text{M,22 - i,j,XZ}}} )\hat{k} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,YZ}}} }} = (Y_{{\text{M,i,j,YZ}}} - Y_{{\text{M,17 - i,j,YZ}}} )\hat{j} + \, (Z_{{\text{M,i,j,YZ}}} - Z_{{\text{M,17 - i,j,YZ}}} )\hat{k} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,YZ}}} }} = (Y_{{\text{M,5 + i,j,YZ}}} - Y_{{\text{M,22 - i,j,YZ}}} ) \hat{j} + \, (Z_{{\text{M,5 + i,j,YZ}}} - Z_{{\text{M,22 - i,j,YZ}}} )\hat{k} \hfill \\ \end{gathered}$$

(3)

The six calibrated vectors can be calculated as follows:

$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XY}}} }} = (X_{{\text{C,i}}} {-}X_{{\text{C,17 - i}}} )\hat{i} + \, (Y_{{\text{C,i}}} - Y_{{\text{C,17 - i}}} )\hat{j} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,XY}}} }} = (X_{{\text{C,5 + i}}} - X_{{\text{C,22 - i}}} ) \hat{i} + \, (Y_{{\text{C,5 + i}}} - Y_{{\text{C,22 - i}}} )\hat{j} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XZ}}} }} = (X_{{\text{C,i}}} {-}X_{{\text{C,17 - i}}} ) \hat{i} + \, (Z_{{\text{C,i}}} - Z_{{\text{C,17 - i}}} ) \hat{k} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,XZ}}} }} = (X_{{\text{C,5 + i}}} - X_{{\text{C,22 - i}}} ) \hat{i} + \, (Z_{{\text{C,5 + i}}} - Z_{{\text{C,22 - i}}} )\hat{k} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,YZ}}} }} = (Y_{{\text{C,i}}} {-}Y_{{\text{C,17 - i}}} )\hat{j} + \, (Z_{{\text{C,i}}} - Z_{{\text{C,17 - i}}} )\hat{k} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,YZ}}} }} = (Y_{{\text{C,5 + i}}} - Y_{{\text{C,22 - i}}} ) \hat{j} + \, (Z_{{\text{C,5 + i}}} - Z_{{\text{C,22 - i}}} )\hat{k} \hfill \\ \end{gathered}$$

(4)

The six parametric rotational errors (E_BX(L), E_CX(L), E_AY(L), E_CY(L), E_AZ(L) and E_CZ(L)), which are illustrated in Fig. 3, can be calculated as follows:

$$\begin{gathered} E_{{{\text{BX}}}} \left( L \right) = \cos^{ - 1} \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XZ}}} }} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XZ}}} }} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XZ}}} }} } \right| \times \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XZ}}} }} } \right|}}} \right) \hfill \\ E_{{{\text{CX}}}} \left( L \right) = \cos^{ - 1} \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XY}}} }} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XY}}} }} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{X,i,j,XY}}} }} } \right| \times \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{X,i,XY}}} }} } \right|}}} \right) \hfill \\ E_{{{\text{AY}}}} \left( L \right) = \cos^{ - 1} \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,YZ}}} }} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,YZ}}} }} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,YZ}}} }} } \right| \times \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,YZ}}} }} } \right|}}} \right) \hfill \\ E_{{{\text{CY}}}} \left( L \right) \, = \cos^{ - 1} \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,XY}}} }} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,XY}}} }} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Y,i,j,XY}}} }} } \right| \times \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Y,i,XY}}} }} } \right|}}} \right) \hfill \\ E_{{{\text{AZ}}}} \left( L \right) = \cos^{ - 1} \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,YZ}}} }} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,YZ}}} }} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,YZ}}} }} } \right| \times \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,YZ}}} }} } \right|}}} \right) \hfill \\ E_{{{\text{BZ}}}} \left( L \right) = \cos^{ - 1} \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,XZ}}} }} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,XZ}}} }} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{M_{{\text{Z,i,j,XZ}}} }} } \right| \times \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{C_{{\text{Z,i,XZ}}} }} } \right|}}} \right) \hfill \\ \end{gathered}$$

(5)

Fig. 3

Schematic of the calibrated vectors, the measured vectors, and the two parametric rotational errors (E_CX and E_CY) in the X–Y plane

Figure 4 illustrates the calculation process for the three parametric rotational errors. Specifically, when dealing with the X–Z and Y–Z planes, where the hole plate is measured using two distinct-length styluses S_L,j and S_L,j’, the three parametric rotational errors (E_AX(L), E_BY(L), and E_CZ(L)) can be calculated using the following procedure:

$$\begin{gathered} E_{{{\text{AX}}}} \left( L \right) = \left( {\tan^{ - 1} \left( {\frac{{DZ_{{\text{i,j,XZ}}} - DZ_{{{\text{i,j}}^{\prime } {\text{,XZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right) + \tan^{ - 1} \left( {\frac{{DZ_{{\text{17 - i,j,XZ}}} - DZ_{{{\text{17 - i,j}}^{\prime } {\text{,XZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right)} \right)/2 \hfill \\ E_{{{\text{BY}}}} \left( L \right) = \left( {\tan^{ - 1} \left( {\frac{{DZ_{{\text{i,j,YZ}}} - DZ_{{{\text{i,j}}^{\prime } {\text{,YZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right) + \tan^{ - 1} \left( {\frac{{DZ_{{\text{17 - i,j,YZ}}} - DZ_{{{\text{17 - i,j}}^{\prime } {\text{,YZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right)} \right)/2 \hfill \\ E_{{{\text{CZ}}}} \left( L \right) = \left( {\tan^{ - 1} \left( {\frac{{DY_{{\text{5 + i,j,YZ}}} - DY_{{{\text{5 + i,j}}^{\prime } {\text{,YZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right) + \tan^{ - 1} \left( {\frac{{DY_{{\text{22 - i,j,YZ}}} - DY_{{{\text{22 - i,j}}^{\prime } {\text{,YZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right) + \tan^{ - 1} \left( {\frac{{DX_{{\text{5 + i,j,XZ}}} - DX_{{{\text{5 + i,j}}^{\prime } {\text{,XZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right) + \tan^{ - 1} \left( {\frac{{DX_{{\text{22 - i,j,XZ}}} - DX_{{{\text{22 - i,j}}^{\prime } {\text{,XZ}}}} }}{{S_{{\text{L,j}}} - S_{{{\text{L,j}}^{\prime } }} }}} \right)} \right)/4 \hfill \\ \end{gathered}$$

(6)

Fig. 4

Schematic of the parametric rotational error (E_AX) in the X–Z plane

Figure 5 provides an illustration of the parametric squareness error calculation for the X–Y plane, and similar concepts apply to the X–Z and Y–Z planes. The least-squares method is employed to fit the measured coordinates and the calibrated coordinates.

Fig. 5

Schematic of the parametric squareness error (E_C0Y) in the X–Y plane

For the hole plate situated in the X–Y plane, the fitting function for the measured X-axis and Y-axis coordinates can be expressed as Y_M,i,j,XY = L_M,X,j,XY × X_M,i,j,XY and Y_M,22-i,j,XY = L_M,Y,j,XY × X_M,22-i,j,XY. In parallel, the fitting function for the calibrated X-axis and Y-axis coordinates is Y_C,i = L_C,X × X_C,i and Y_C,22-i = L_C,Y × X_C,22-i. Consequently, the parametric squareness error E_C0Y can be calculated as per Eq. (7). This same approach is extended to the X–Z plane, with the fitting functions for the measured X-axis and Z-axis coordinates being Z_M,i,j,XZ = L_M,X,j,XZ × X_M,i,j,XZ and Z_M,22-i,j,XZ = L_M,Z,j,XZ × X_M,22-i,j,XZ. The corresponding fitting functions for the calibrated X-axis and Z-axis coordinates are Z_C,i = L_C,X × X_C,i and Z_C,22-i = L_C,Y × X_C,22-i, with the parametric squareness error E_B0Z calculated using Eq. (7).

Similarly, for the hole plate in the Y–Z plane, the measured Y-axis and Z-axis coordinates are fit using the function Z_M,i,j,YZ = L_M,Y,j,YZ × Y_M,i,j,YZ and Z_M,17-i,j,YZ = L_M,Z,j,YZ × Y_M,22-i,j,YZ. The fitting functions for the calibrated Y-axis and Z-axis coordinates are Z_C,i = L_C,Y × Y_C,i and Z_C,17-i = L_C,Z × Y_C,22-i. The parametric squareness error E_A0Z can then be calculated using Eq. (7). Ultimately, the three parametric squareness errors can be treated as follows:

$$\begin{gathered} E_{{{\text{C0Y}}}} = \tan^{ - 1} \left( {\frac{{L_{{\text{M,X,j,XY}}} - L_{{\text{M,Y,j,XY}}} }}{{1 - L_{{\text{M,X,j,XY}}} \times L_{{\text{M,Y,j,XY}}} }}} \right) - \tan^{ - 1} \left( {\frac{{L_{{\text{C,X}}} - L_{{\text{C,Y}}} }}{{1 - L_{{\text{C,X}}} \times L_{{\text{C,Y}}} }}} \right) \hfill \\ E_{{{\text{B0Z}}}} = \tan^{ - 1} \left( {\frac{{L_{{\text{M,X,j,XZ}}} - L_{{\text{M,Z,j,XZ}}} }}{{1 - L_{{\text{M,X,j,XZ}}} \times L_{{\text{M,Z,j,XZ}}} }}} \right) - \tan^{ - 1} \left( {\frac{{L_{{\text{C,X}}} - L_{{\text{C,Z}}} }}{{1 - L_{{\text{C,X}}} \times L_{{\text{C,Z}}} }}} \right) \hfill \\ E_{{{\text{A0Z}}}} = \tan^{ - 1} \left( {\frac{{L_{{\text{M,Y,j,YZ}}} - L_{{\text{M,Z,j,YZ}}} }}{{1 - L_{{\text{M,Y,j,YZ}}} \times L_{{\text{M,Z,j,YZ}}} }}} \right) - \tan^{ - 1} \left( {\frac{{L_{{\text{C,Y}}} - L_{{\text{C,Z}}} }}{{1 - L_{{\text{C,Y}}} \times L_{{\text{C,Z}}} }}} \right) \hfill \\ \end{gathered}$$

(7)

4.2 Parametric Errors of The Single Rotary Axis

Figure 1e illustrates the symbols associated with the six parametric errors [36]. In the context of the single rotary axis, the measurement process involves determining the coordinate deviations (DX(θ)_i,S, DY(θ)_i,S, DZ(θ)_Pi,S). where i takes on values 1, 6, 11, and 16. The measured coordinates of the hole plate (X(θ)_M,i,S, Y(θ)_M,i,S, Z(θ)_M,Pi,S) are directly measured, and they are compared to the calibrated coordinates (X(θ)_C,i, Y(θ)_C,i, Z(θ)_C,Pi) at different rotated angles θ, with the initial coordinates (X_C,i, Y_C,i, Z_C,Pi). The calibrated coordinates can be represented as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {X(\theta )_{{\text{C,i}}} } \\ {Y(\theta )_{{\text{C,i}}} } \\ {Z(\theta )_{{\text{C,Pi}}} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} {\cos \theta } & {\sin \theta } & 0 \\ { - \sin \theta } & {\cos \theta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {X_{{\text{C,i}}} } \\ {Y_{{\text{C,i}}} } \\ {Z_{{\text{C,Pi}}} } \\ \end{array} } \right] \\ = & R(\theta ) \times \left[ {\begin{array}{*{20}c} {X_{{\text{C,i}}} } \\ {Y_{{\text{C,i}}} } \\ {Z_{{\text{C,Pi}}} } \\ \end{array} } \right] \\ \end{aligned}$$

(8)

where R (θ) is the coordinate rotation matrix. The six parametric errors of the single rotary axis can be expressed as a parametric error matrix, E (θ), as shown below:

$$E\left( \theta \right) = \left[ {\begin{array}{*{20}c} 1 & { - E_{{{\text{CC}}}} (\theta )} & {E_{{{\text{BC}}}} (\theta )} & {E_{{{\text{XC}}}} (\theta )} \\ {E_{{{\text{CC}}}} (\theta )} & 1 & { - E_{{{\text{AC}}}} (\theta )} & {E_{{{\text{YC}}}} (\theta )} \\ { - E_{{{\text{BC}}}} (\theta )} & {E_{{{\text{AC}}}} (\theta )} & 1 & {E_{{{\text{ZC}}}} (\theta )} \\ \end{array} } \right]$$

(9)

The measured coordinate deviations (DX(θ)_i,S, DY(θ)_i,S, DZ(θ)_Pi,S) can be determined from the following equation:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {DX(\theta )_{{\text{i,S}}} } \\ {DY(\theta )_{{\text{i,S}}} } \\ {DZ(\theta )_{{\text{Pi,S}}} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} { X_{{\text{M,i,S}}} } \\ {Y_{{\text{M,i,S}}} } \\ {Z_{{\text{M,Pi,S}}} } \\ \end{array} } \right] - R\left( \theta \right) \times \left[ {\begin{array}{*{20}c} {X_{{\text{C,i}}} } \\ {Y_{{\text{C,i}}} } \\ {Z_{{\text{C,i}}} } \\ \end{array} } \right] \\ = & R\left( \theta \right) \times E\left( \theta \right) \times \left[ {\begin{array}{*{20}c} {X_{{\text{C,i}}} } \\ {Y_{{\text{C,i}}} } \\ {Z_{{\text{C,i}}} } \\ \end{array} } \right] - R\left( \theta \right) \times \left[ {\begin{array}{*{20}c} {X_{{\text{C,i}}} } \\ {Y_{{\text{C,i}}} } \\ {Z_{{\text{C,i}}} } \\ \end{array} } \right] \\ \end{aligned}$$

(10)

Subsequently, Eq. (10) be expanded as:

$$\left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & 0 & {Z_{{\text{C,Pi}}} \sin \theta } & {Z_{{\text{C,Pi}}} \cos \theta } & { - X_{{\text{C,i}}} \sin \theta - Y_{{\text{C,i}}} \cos \theta } \\ { - \sin \theta } & {\cos \theta } & 0 & { - Z_{{\text{C,Pi}}} \cos \theta } & {Z_{{\text{C,Pi}}} \sin \theta } & { - Y_{{\text{C,i}}} \sin \theta + X_{{\text{C,i}}} \cos \theta } \\ 0 & 0 & 1 & {Y_{{\text{C,i}}} } & { - X_{{\text{C,i}}} } & 0 \\ {\begin{array}{*{20}c} \vdots \\ {\cos \theta } \\ {\sin \theta } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ { - \sin \theta } \\ {\cos \theta } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {Z_{{\text{C,Pi}}} \sin \theta } \\ { - Z_{{\text{C,Pi}}} \cos \theta } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {Z_{{\text{C,Pi}}} \cos \theta } \\ {Z_{{\text{C,Pi}}} \sin \theta } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ { - X_{{\text{C,i}}} \sin \theta - Y_{{\text{C,i}}} \cos \theta } \\ { - Y_{{\text{C,i}}} \sin \theta + X_{{\text{C,i}}} \cos \theta } \\ \end{array} } \\ 0 & 0 & 1 & {Y_{{\text{C,i}}} } & { - X_{{\text{C,i}}} } & 0 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {E_{{{\text{XC}}}} (\theta )} \\ {E_{{{\text{YC}}}} (\theta )} \\ {E_{{{\text{ZC}}}} (\theta )} \\ {E_{{{\text{AC}}}} (\theta )} \\ {E_{{{\text{BC}}}} (\theta )} \\ {E_{{{\text{CC}}}} (\theta )} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {DX(\theta )_{{\text{i,S}}} } \\ {DY(\theta )_{{\text{i,S}}} } \\ {DZ(\theta )_{{\text{Pi,S}}} } \\ {\begin{array}{*{20}c} \vdots \\ {DX(\theta )_{{\text{i,S}}} } \\ {DY(\theta )_{{\text{i,S}}} } \\ {DZ(\theta )_{{\text{Pi,S}}} } \\ \end{array} } \\ \end{array} } \right]$$

(11)

By utilizing the pseudo-inverse method, Eq. (11) can be solved, thereby enabling the calculation of the six parametric errors.

4.3 Volumetric Error of The Four-Axis CMM

Homogeneous transformation matrices are employed to assemble the volumetric error, which encompasses the previously described 27 parametric errors. The volumetric error (DX_V(L, θ), DY_V(L, θ), DZ_V(L, θ)) can be regarded as the resulting discrepancy at specified spatial positions (X(L, θ), Y(L, θ), Z(L, θ)) within the measurement volume, as indicated by the equation:

$$\left[ {\begin{array}{*{20}l} {DX_{V} (L, \theta )} \hfill \\ {DY_{V} (L, \theta )} \hfill \\ {DZ_{V} (L, \theta )} \hfill \\ 1 \hfill \\ \end{array} } \right] = H_{C} (\theta ) \times H_{X} \left( L \right) \times H_{Y} \left( L \right) \times H_{Z} \left( L \right) \times H_{S} \left( L \right) \times \left[ {\begin{array}{*{20}l} {X(L, \theta )} \hfill \\ {Y(L, \theta )} \hfill \\ {Z(L, \theta )} \hfill \\ 1 \hfill \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {X(L, \theta )} \hfill \\ {Y(L, \theta )} \hfill \\ {Z(L, \theta )} \hfill \\ 1 \hfill \\ \end{array} } \right]$$

(12)

Here, five distinct homogeneous transformation matrices are involved:

• (1) H_C(θ): This matrix represents the six parametric errors of the single rotary axis.

• (2) H_X(L): Corresponds to the six parametric errors for the X-axis.

• (3) H_Y(L): Corresponds to the six parametric errors for the Y-axis.

• (4) H_Z(L): Corresponds to the six parametric errors for the Z-axis.

• (5) H_S(L): Represents the three parametric squareness errors.

  $$\begin{aligned} \left[ {\begin{array}{*{20}l} {DX_{{\text{V}}} (L, \theta )} \hfill \\ {DY_{{\text{V}}} (L, \theta )} \hfill \\ {DZ_{{\text{V}}} (L, \theta )} \hfill \\ 1 \hfill \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} 1 & { - E_{{{\text{CC}}}} (\theta )} & {E_{{{\text{BC}}}} (\theta )} & {E_{{{\text{XC}}}} (\theta )} \\ {E_{{{\text{CC}}}} (\theta )} & 1 & { - E_{{{\text{AC}}}} (\theta )} & {E_{{{\text{YC}}}} (\theta )} \\ { - E_{{{\text{BC}}}} (\theta )} & {E_{{{\text{AC}}}} (\theta )} & 1 & {E_{{{\text{ZC}}}} (\theta )} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & { - E_{{{\text{CX}}}} (L)} & {E_{{{\text{BX}}}} (L)} & {E_{{{\text{XX}}}} (L)} \\ {E_{{{\text{CX}}}} (L)} & 1 & { - E_{{{\text{AX}}}} (L)} & {E_{{{\text{YX}}}} (L)} \\ { - E_{{{\text{BX}}}} (L)} & {E_{{{\text{AX}}}} (L)} & 1 & {E_{{{\text{ZX}}}} (L)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ & \times \left[ {\begin{array}{*{20}c} 1 & { - E_{{{\text{CY}}}} (L)} & {E_{{{\text{BY}}}} (L)} & {E_{{{\text{XY}}}} (L)} \\ {E_{{{\text{CY}}}} (L)} & 1 & { - E_{{{\text{AY}}}} (L)} & {E_{{{\text{YY}}}} (L)} \\ { - E_{{{\text{BY}}}} (L)} & {E_{{{\text{AY}}}} (L)} & 1 & {E_{{{\text{ZY}}}} (L)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & { - E_{{{\text{CZ}}}} (L)} & {E_{{{\text{BZ}}}} (L)} & {E_{{{\text{XZ}}}} (L)} \\ {E_{{{\text{CZ}}}} (L)} & 1 & { - E_{{{\text{AZ}}}} (L)} & {E_{{{\text{YZ}}}} (L)} \\ { - E_{{{\text{BZ}}}} (L)} & {E_{{{\text{AZ}}}} (L)} & 1 & {E_{{{\text{ZZ}}}} (L)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ & \times \left[ {\begin{array}{*{20}c} 1 & { - E_{{{\text{C0Y}}}} } & {E_{{{\text{B0Z}}}} } & 0 \\ {E_{{{\text{C0Y}}}} } & 1 & { - E_{{{\text{A0Z}}}} } & 0 \\ { - E_{{{\text{B0Z}}}} } & {E_{{{\text{A0Z}}}} } & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}l} {X(L, \theta )} \hfill \\ {Y(L, \theta )} \hfill \\ {Z(L, \theta )} \hfill \\ 1 \hfill \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {X(L, \theta )} \hfill \\ {Y(L, \theta )} \hfill \\ {Z(L, \theta )} \hfill \\ 1 \hfill \\ \end{array} } \right] \\ \end{aligned}$$

  (13)

This calculation permits the determination of the volumetric error at any spatial point within the entire measurement volume of the four axes. The total volumetric error is represented as the root square of the sum of the squared values across the three directions:

$$E_{{\text{v}}} = \sqrt {(DX_{{\text{V}}} (L, \theta ))^{2} + (DX_{{\text{V}}} (L, \theta ))^{2} + (DX_{{\text{V}}} (L, \theta ))^{2} }$$

(14)

5 Experiment

The four-axis CMM used in this study was a moving-table-type machine (Leitz, Ultra PMMC) with a C-X-Y-Z configuration. Its dimensional measurement range covered 1200 mm × 1000 mm × 800 mm. Additionally, a single rotary axis (Leitz, LRT4) with a diameter of 415 mm was integrated. Both the linear and single rotary axes were active for the compensation mode. The single rotary axis could rotate along the Z-axis, covering an angle θ range from 0° to 360°. Importantly, the four-axis CMM did not establish a local coordinate system; the original coordinate was set at the center of the single rotary axis for all measurements. The hole plate, for the purpose of measurement, had a cubic shape with a diameter of 353.553 mm and a height of 250 mm. This encompassed the measuring area for the single rotary axis. Figure 6 presents the flowchart of the measurement and calculation of the parametric and volumetric errors.

Fig. 6

Flowchart of the measurement and calculation of the parametric and volumetric errors

Measurement of the hole plate was conducted using a touch probe. Five styluses were employed to measure the hole plate in three different planes, as shown in Fig. 7a and b. Two stylus lengths were utilized without any specific limitations. Calibration of these styluses was accomplished using a high-precision sphere, ensuring that both lengths and diameters were calibrated and the values were corrected and traceable. The specifics of the styluses are as follows:

• No. 1 Stylus: Used for measurements in the X–Y plane and the single rotary axis, it had a probe diameter S_D,1 of 5.0008 mm and a stylus length S_L,1 of 149.8866 mm.

• No. 2 and No. 4 Styluses: Employed for measurements in the X–Z plane, stylus no. 2 had a probe diameter S_D,2 of 5.0010 mm and a stylus length S_L,2 of 152.1612 mm, while stylus no. 4 had a probe diameter S_D,4 of 5.0011 mm and a stylus length S_L,4 of 198.9714 mm.

• No. 3 and No. 5 Styluses: Used for measurements in the Y–Z plane, stylus no. 3 had a probe diameter S_D,3 of 5.0007 mm and a stylus length S_L,3 of 152.4826 mm, while stylus no. 5 had a probe diameter S_D,5 of 5.0010 mm and a stylus length S_L,5 of 199.4904 mm.

Fig. 7

Photograph of the touch probe. a The three styluses are from No.1 to No. 3. b The two styluses are from No. 4 to No. 5

For measuring the hole plate, British Standards recommended the use of at least five different points to determine a circle [37]. These five touchpoints were evenly distributed around the circle. The probing was carried out in the mid-plane of the hole plate, specifically 10 mm below the upper flat surface of the hole plate.

5.1 Three Linear Axes Measurement

The measurement process of the hole plate involved sequential setups in three different planes: the X–Y, X–Z, and Y–Z planes. The alignment criterion was set within a range of ± 5 μm at both the initial and maximum measured positions, as defined based on the maximum permissible error of the CMM. The entire measurement procedure was carried out in triplicate to ensure accuracy, with the calculation of parametric errors for each iteration. The experimental procedure for the three linear axes unfolded as follows:

(1) X–Y Plane Setup:

The hole plate was positioned on the single rotary axis, forming the X-Y plane, as illustrated in Fig. 8a. The horizontal fixture consisted of three supporting elements for the hole plate. The 1-axis and 2-axis of the hole plate were aligned with the X-axis and Y-axis of the four-axis CMM, respectively. The hole plate was centered on the single rotary axis.

Fig. 8

Photograph of the hole plate setup a the X–Y plane, b the X–Z plane, and c the Y–Z plane

(2) Measurement Using No. 1 Stylus (X–Y Plane):

The hole plate was measured using the no. 1 stylus, resulting in measured coordinates (X_M,i,1,XY, Y_M,i,1,XY). Deviations (DX_i,1,XY(L), DY_i,1,XY(L)) were calculated, where i was an integer ranging from 1 to 21.

(3) X–Z Plane Setup:

The hole plate was repositioned to form the X-Z plane setup, as depicted in Fig. 8b. The vertical fixture included two supporting and one mounting elements, used for the X–Z plane setup. The 1-axis and 2-axis of the hole plate were aligned with the X-axis and Z-axis of the four-axis CMM, respectively. The hole plate was positioned at the midpoint of the Y-axis.

(4) Measurement Using No. 2 and No. 4 Styluses Sequentially (X–Z Plane):

The no. 2 and no. 4 styluses were employed sequentially to measure the hole plate. The measured coordinates, (X_M,i,2,XZ, Z_M,i,2,XZ) and (X_M,i,4,XZ, Z_M,i,4,XZ), were obtained. Deviations (DX_i,2,XZ(L), DZ_i,4,XZ(L)) and (DX_i,4,XZ(L), DZ_i,2,XZ(L)) were calculated, where i ranged from 1 to 21.

(5) Y–Z Plane Setup:

The hole plate was sequentially adjusted to form the Y-Z plane setup, as shown in Fig. 8c. The vertical fixture included two supporting and one mounting elements, used for the Y–Z plane setup. The 1-axis and 2-axis of the hole plate were aligned with the Y-axis and Z-axis of the four-axis CMM, respectively. The hole plate was positioned at the midpoint of the X-axis.

(6) Measurement Using No. 3 and No. 5 Styluses Sequentially (Y–Z Plane):

The no. 3 and no. 5 styluses were utilized sequentially to measure the hole plate. The measured coordinates, (Y_M,i,3,YZ, Z_M,i,3,YZ) and (Y_M,i,5,YZ, Z_M,i,5,YZ), were acquired. Deviations (DY_i,3,YZ(L), DZ_i,3,YZ(L)) and (DY_i,5,YZ(L), DZ_i,5,YZ(L)) were calculated, where i ranged from 1 to 21.

The computation of the 21 parametric and volumetric errors using the three linear axes was carried out through the following steps:

(1) Parametric Positioning Errors and Parametric Straightness Errors:

The three parametric positioning errors (E_XX, E_YY, and E_ZZ) were determined using equation (1). The six parametric straightness errors (E_YX, E_ZX, E_XY, E_ZY, E_XZ, and E_YZ) were calculated according to equation (2).

(2) Parametric Rotational Errors:

By applying equations (3) and (4), six measured vectors and calibrated vectors were derived. The six parametric rotational errors (E_BX, E_CX, E_AY, E_CY, E_AZ, and E_CZ) were computed using equation (5).

(3) Parametric Rotational Errors for Different Styluses:

Using the stylus lengths no. 2, no. 3, no. 4, and no. 5 (S_L,2, S_L,3, S_L,4, and S_L,5), the three parametric rotational errors (E_AX, E_BY, and E_CZ) were calculated using equation (6). Fig. 9a, b, and c, depicted the six parametric errors for each axis.

Fig. 9

Measurement results of six parametric errors for different axes, a the X-axis, b the Y-axis, and c the Z-axis

(4) Parametric Squareness Errors:

Employing equation (7), the three parametric squareness errors (E_C0Y, E_B0Z, and E_A0Z) were determined as − 1.40″, − 2.46″, and − 1.94″, respectively.

(5) Volumetric Error Calculation Without Rotation Angle:

The volumetric error without considering the rotation angle was calculated using equation (14), as illustrated in Fig. 10. The volumetric error encompassed all parametric errors from the three linear axes within the measuring volume of 250 mm × 250 mm × 250 mm. The volumetric error was found to range from 0.35 to 1.55 μm.

Fig. 10

The measurement result of the volumetric error for the three linear axes

These steps encompass the systematic calculation of the parametric and volumetric errors associated with the three linear axes.

5.2 Single Rotary Axis Measurement

The measurement and calculation procedure for the single rotary axis was conducted as follows:

(1) Initial Setup:

The hole plate was positioned on the single rotary axis, aligning with the X-Y plane of the three linear axes, as depicted in Fig. 11.

Fig. 11

Photograph of the hole plate setup for the single rotary axis

(2) Rotation to 0°:

The single rotary axis was initially rotated to a rotation angle of θ = 0°.

(3) Measurement at 0° Rotation:

The four corner holes and four corner points were measured at the rotation angle θ = 0°, yielding coordinates (X(0°)_M,i,S, Y(0°)_M,i,S, Z(0°)_M,Pi,S). The measured coordinate deviations (DX(0°)_i,S, DY(0°)_i,S, DZ(0°)_Pi,S) were calculated for each corner point, where i indicated numbers 1, 6, 11, and 16.

(4) Rotation to 15°:

The single rotary axis was rotated to the next rotation angle, θ = 15°.

(5) Measurement at 15° Rotation:

Similar to procedure 3, the four corner holes and four corner points were measured at the rotation angle θ = 15°, producing coordinates (X(15°)_M,i,S, Y(15°)_M,i,S, Z(15°)_M,Pi,S). The measured coordinate deviations (DX(15°)_i,S, DY(15°)_i,S, DZ(15°)_Pi,S) were calculated for each corner point.

(6) Repeat for Other Rotation Angles:

The above process was repeated for subsequent rotation angles. At each rotation angle, coordinates and measured deviations were obtained for the four corner holes and four corner points.

(7) Calculation of Parametric Errors:

Utilizing equation (11), the six parametric errors of the single rotary axis were computed, as illustrated in Fig. 12.

Fig. 12

Measurement results of six parametric errors for the C-axis

(8) Volumetric Error Calculation with Rotation:

The volumetric error with consideration of the rotation angle was constructed using equations (13) and (14). Fig. 13 displayed the volumetric error at various rotated angles ranging from 15° to 345° in steps of 15°. The volumetric error encompassed all parametric errors from the three linear axes and single rotary axis within a cube with a diameter of 353.553 mm and a height of 250 mm. The volumetric error ranged from 0.35 to 2.83 μm.

Fig. 13

The measurement result of the volumetric error for the four axes

These steps encompassed the comprehensive measurement and calculation process for the single rotary axis, involving the acquisition of parametric errors and volumetric errors at different rotation angles.

5.3 Verification

To validate the effectiveness of the proposed method, several verification experiments were conducted using different metrology instruments on the same four-axis CMM:

(1) Verification of Parametric Positioning Errors:

Laser interferometer (SIOS, SP 15000) was employed to verify the three parametric positioning errors (E_XX, E_YY, and E_ZZ) as per ISO 10360-2 standards, as shown in Fig. 14a, b, anc c. For each axis, the laser interferometer and autocollimator were positioned at the X-axis, Y-axis, and Z-axis setups. Measurement positions were aligned with the middle positions of the hole plate. Experimental results obtained using the hole plate were compared with those obtained using the laser interferometer.

Fig. 14

Photograph of the laser interferometer setup, a the X-axis, b the Y-axis, and c the Z-axis

(2) Verification of Parametric Rotational Errors:

Autocollimator (MOLLER-WEDEL OPTICAL GmbH, ELCOMAT 3000) was used to verify the six parametric rotational errors (E_BX, E_CX, E_AY, E_CY, E_AZ, and E_BZ), as shown in Fig. 15a, b, and c. Similar to the positioning errors, the autocollimator was positioned at the X-axis, Y-axis, and Z-axis setups. Measurement positions were aligned with the middle positions of the hole plate. Experimental results obtained using the hole plate were compared with those obtained using the autocollimator.

Fig. 15

Photograph of the autocollimator setup, a the X-axis, b the Y-axis, and c the Z-axis

(3) Verification of Single Rotary Axis Parametric Error:

A 24-sided polygon and autocollimator were employed to verify the parametric rotational error of the single rotary axis, as shown in Fig. 16. The measurement procedure followed a reference source [38]. The measured angles coincided with those of the hole plate. Experimental results obtained using the hole plate were compared with those obtained using the polygon-autocollimator.

Fig. 16

Photograph of the polygon-autocollimator setup

(4) Results:

Figure 17, 18, and 19 display the comparisons between the experimental results obtained using the hole plate and the respective metrology instruments for parametric positioning errors, parametric rotational errors, and single rotary axis parametric positioning error. In the case of parametric positioning and rotational errors, the maximum absolute differences were recorded as 0.56 μm for parametric positioning error E_YY at – 125 mm using the laser interferometer (Fig. 17a), 1.55″ for parametric rotational error E_BZ at 200 mm with the autocollimator (Fig. 18c), and 0.75″ for parametric rotational error E_CC at 225° with the polygon-autocollimator (Fig. 19).

Fig. 17

Measurement results for the parametric positioning errors were obtained using the hole plate and the laser interferometer, a. the X-axis and Y-axis, and b the Z-axis

Fig. 18

Measurement results for the parametric rotational errors were obtained using the hole plate and the autocollimator for different axes, a the X-axis, b the Y-axis, and c the Z-axis

Fig. 19

Measurement results for the parametric positioning error obtained using the hole plate and the polygon-autocollimator

Subsequent uncertainty evaluation can further investigate whether these maximum absolute differences meet the required criteria. The validation process aimed to verify the accuracy of the proposed method by comparing its results with established metrology instruments.

5.4 Uncertainty Evaluation

In the process of evaluating uncertainty and verifying the reliability of the proposed method, the following steps were taken:

(1) Accuracy Uncertainty:

The accuracy uncertainty for each measurement instrument and the hole plate was determined based on their specifications and calibration certificates. For the hole plate, the accuracy uncertainties were obtained from calibration certificate No. 193139 from the National Metrology Institute of Japan, expressed as $\sqrt{{0.24}^{2}+{{0.44}{\text{L}}}^{2}}$, where L represents the measurement position in millimeters. Given a hole plate size of 250 mm, the linear measurement uncertainty was 0.26 μm, and for angular measurement, it was 0.21″. The accuracy uncertainty for the laser interferometer was ± 0.10 μm [39], for the autocollimator, it was ± 0.25″ [40], and for the polygon-autocollimator, it was 0.03″ [38].

(2) Repeatability Uncertainty:

This uncertainty arises from the four-axis CMM measurement and the hole plate setup. The maximum repeatability from the measurements was chosen and divided by the square root of three to calculate the repeatability uncertainty. The hole plate was 0.98 μm for parametric positioning error (E_ZZ) at 250 mm and 1.35″ for parametric rotational error (E_CX) at 250 mm. For the single rotary axis at 60°, the maximum repeatability was 0.13″. The laser interferometer, autocollimator, and polygon-autocollimator were 0.08 μm for parametric positioning error E_ZZ at 100 mm, 0.36″ for parametric rotational error E_AZ at 100 mm, and 1.35″ at 30°, respectively.

(3) Combined Standard Uncertainty:

The combined standard uncertainty was calculated by taking the root sum square of the accuracy and repeatability uncertainties.

(4) Expanded Uncertainty:

The combined standard uncertainty was multiplied by a coverage factor of 2 to obtain the expanded uncertainty. The hole plate was 2.03 μm (2 × $\sqrt{{0.26}^{2}+{0.98}^{2}}$) and 2.73″ (2 × $\sqrt{{0.21}^{2}+{1.35}^{2}}$) for the three linear axis. For the single rotary axis, it was 0.49″(2 × $\sqrt{{0.21}^{2}+{0.13}^{2}}$). The laser interferometer was 0.26 μm (2 × $\sqrt{{0.10}^{2}+{0.08}^{2}}$), the autocollimator was 0.88″ (2 × $\sqrt{{0.25}^{2}+{0.36}^{2}}$), and the polygon-autocollimator 2.70″ (2 × $\sqrt{{0.03}^{2}+{1.35}^{2}}$).

(5) Reliability Evaluation:

The reliability of the measurements was assessed using the En-value, which is the ratio of the absolute maximum difference between the proposed method and the reference metrology instrument (e.g., laser interferometer, autocollimator, polygon-autocollimator) to the square root of the sum of the squared expanded uncertainties of both the proposed method and the reference metrology instrument [41]. For parametric positioning errors, the En-value was calculated to be 0.27 (0.56 /$\sqrt{{0.26}^{2}+{2.03}^{2}}$), indicating high reliability, as it is less than unity. For parametric rotational errors, the En-value was calculated to be 0.54 (1.55/$\sqrt{{0.88}^{2}+{2.73}^{2}}$), again indicating a high level of reliability. For the single rotary axis, the En-value for the parametric rotational error was 0.27 (0.75 /$\sqrt{{2.70}^{2}+{0.49}^{2}}$), demonstrating the method's reliability in this context as well.

Overall, all calculated En-values were less than unity, signifying that the proposed hole plate method for parametric error measurement is reliable. This reliability extends to the calculated volumetric errors derived from the parametric errors.

6 Discussion and Conclusion

The presented study introduces a novel approach for measuring the parametric and volumetric errors of four-axis CMMs using a hole plate. This method offers several advancements over existing techniques. By directly placing the hole plate on the machine during the experiment, a more accurate representation of the actual measurement conditions is achieved. Through this approach, a total of 27 parametric errors were accurately measured, encompassing the effects of the three linear axes and the single rotary axis.

The method further involved the calculation of volumetric errors, incorporating the 27 parametric errors both with and without consideration of the single rotary axis. The verification utilized three distinct metrology instruments. A laser interferometer and an autocollimator were engaged to compare three parametric positioning errors and six parametric rotational errors in relation to the three linear axes. A polygon-autocollimator was employed to assess the parametric rotational error specific to the single rotary axis.

The assessment of uncertainty provided valuable insight into the method's reliability. The En-values obtained from the comparison with the metrology instruments consistently remained below unity, signifying a high level of reliability for the proposed parametric and volumetric errors measurement technique.

In conclusion, this study primarily focuses on evaluating and identifying the machine's performance, including parametric and volumetric errors. This innovative approach has the potential to significantly enhance the accuracy of four-axis CMMs for future research. Parametric and volumetric errors represent position-dependent compensation values on each axis. These errors can be fed back to the CMM controllers to eliminate these errors. Its practical application could not only contribute to improved measurement accuracy but also integrate into various industries and fields that rely on precise dimensional measurements. The integration of the hole plate method into the measurement process holds promise for advancing the overall quality and precision of coordinate metrology.