1 Introduction

Coordinate measuring machines (CMMs) are important instruments in manufacturing. Geometrical features of the products (e.g., size, form and position) are inspected using CMMs. To guarantee the inspection, the measurement result using the CMM must be validated under a rigorous traceability system [1].

The measurement performance of the CMM is ensured through the calibration and the verification on it with proper manners. In the traceability system, it is necessary that traceably calibrated dimensional standards are used in the both processes. Typically, one dimensional standards (e.g. gauge blocks and line scales) are used for the purpose [2]. Here, the recent major application of the measurement using CMM is the validation of the geometrical features of the products against the designed tolerances. The geometrical feature to be tested is extracted from the coordinates of the points on the product surface with the least squares method, therefore, the significant performance of the CMM is not the ability of the size measurement, but that of the point coordinates measurement. To visualize the coordinates measurement performance of the CMM, the test using the one dimensional standard is not sufficient for the purpose.

Since the 1990s, the use of two dimensional standards (e.g. ball plates, hole plates and grid plates) are increased in the performance test of CMMs. That is because the kinematic parameters compensations [3] or the measurement error assessments of the CMMs can be done efficiently by using two dimensional standards. And more, the three dimensional coordinate measurement performance using the CMM can be estimated from the observed measurement errors on the two dimensional standards [4].

In several countries, the national metrology institutes or accredit laboratories provide the calibration service of the two dimensional standards such as ball plates, hole plates and grid plates. In the calibration of the standards, the two dimensional coordinates of the feature points on the standards are calibrated because they are the essential measurands on the artefacts. The metrological equivalence of the measurement standards is validated through the key comparison program. In the previous key comparison for a ball plate and a hole plate [5], the equivalences among the participants’ calibration results were verified on the distances between the No. 1 ball/hole (i.e., the origins of the workpiece coordinates) and other balls/holes on the plates respectively. Therefore, the measurement equivalence on two dimensional coordinates has not been verified.

In this study, the authors propose the coordinates-based evaluation of the reference values and their uncertainty in two dimensional standard calibration comparisons. Applying the proposed protocol, the verification of coordinate measurement equivalence on the two dimensional standard becomes possible among the participants. First, the computation of the reference value and its uncertainty of two dimensional standard calibration comparisons are formulated. Second, the evaluation process is demonstrated with an actual calibration comparison data of the two dimensional standard.

2 Evaluation Manner

2.1 General Approach

The general approach of the reference value and its uncertainty evaluation is common to those in the previous key comparisons. A calibration comparison of a two dimensional standard (e.g. a ball plate) is assumed. In the comparison, the measurement procedure (e.g. the definition of the workpiece coordinate system and the measurement sequence on it) is stated in the protocol of the comparison. The participants report the coordinates of the feature points (e.g. the centres of balls) and their expanded uncertainty. The proposed evaluation of the comparison data is done through the following manner:

  1. 1.

    Preparation of the data for the reference value and its expanded uncertainty calculation;

  2. 2.

    Calculation of the temporary reference value and its expanded uncertainty;

  3. 3.

    Evaluation of \( E_{n} \) number between the temporary reference value and each participant’s reported value;

  4. 4.

    Elimination of the outlier participants’ data from the computation;

  5. 5.

    Re-execution of the process (2)–(4) until no outlier detection;

  6. 6.

    Calculation of the reference value of the comparison and its expanded uncertainty; and

  7. 7.

    Evaluation of \( E_{n} \) number between the reference value of the comparison and each participant’s reported value.

The details of the above process in this research are described in the following subsections.

2.2 Data Preparation

Label the participants of the comparison \( 1,2, \ldots ,n \). Let \( {\mathbf{x}}_{ij} \) denote the position of the jth feature point on the two dimensional artefact (e.g. a ball, a hole and a mark) reported by the ith participant. Let \( {\mathbf{U}}_{{{\mathbf{x}}_{ij} }} \) denote the expanded uncertainty of \( {\mathbf{x}}_{ij} \).

\( {\mathbf{U}}_{{{\mathbf{x}}_{ij} }} \) is reported in specific figure (e.g. 0.5 μm) or formula (e.g. \( U = k\sqrt {a^{2} + b^{2} L^{2} } \) μm). In both cases, the numerical value of each \( {\mathbf{U}}_{{{\mathbf{x}}_{ij} }} \) is calculated and stored for the reference value computation in the next step.

Note that it is postulated that the coordinates of all featured points of the two dimensional standard have non-zero uncertainty in this research. That is because no feature point can be measured without the measurement uncertainty. Some participants may report a particular \( {\mathbf{U}}_{{{\mathbf{x}}_{ij} }} \) is \( o \) (e.g. the expanded uncertainty of the origin of the workpiece coordinate system). In that case, the approximation uncertainty formula is estimated with the values on the other feature points. Then, the non-zero uncertainty value of the particular point is estimated anew.

2.3 Computation of the Temporary Reference Value and Uncertainty

All measurement results except those by outliers are used to compute the two dimensional reference values by the best fit algorithm. When the reference value takes into account the uncertainty of each participant’s measurement, the computation is done with the weighted best fit algorithm. Otherwise, it is done with the simple one.

To evaluate the reference values, the respective participants’ measurement results shall be registrated into one coordinate system. The coordinate system of the ith participant result is rotated and then shifted. The amount and direction of the rotation and shift are calculated using the least square method. The observation equation of the least square method is defined as follows:

$$ O = {\hat{\mathbf{x}}}_{ij} - {\mathbf{x}}_{0j} = \left[ {{\mathbf{R}}_{i} {\mathbf{x}}_{ij} + {\mathbf{t}}_{i} - {\mathbf{x}}_{0j} } \right], $$
(1)

where \( {\hat{\mathbf{x}}}_{ij} \) is the coordinate of the \( {\mathbf{x}}_{ij} \) after transformation and \( {\mathbf{x}}_{0j} \) is the temporary reference value at the calculation step. The rotation matrix \( {\mathbf{R}}_{i} \) and the translation vector \( {\mathbf{t}}_{i} \) are as follows:

$$ {\mathbf{R}}_{i} = \left[ {\begin{array}{*{20}c} {\cos \theta_{i} } & { - \sin \theta_{i} } \\ { - \sin \theta_{i} } & {\cos \theta_{i} } \\ \end{array} } \right],\quad {\mathbf{t}}_{i} = \left[ {\begin{array}{*{20}c} {t_{{x_{i} }} } \\ {t_{{y_{i} }} } \\ \end{array} } \right]. $$
(2)

Here it can be assumed that \( \theta_{i} \), \( t_{{x_{i} }} \) and \( t_{{y_{i} }} \) are small, however, not zero. In the previous reported comparison [5], the registration is done without any coordinate system transformation. It means that the measurement errors of the featured points used for the origin and the axes of the workpiece coordinate system are ignored.

Since the definition of the workpiece coordinate system and the measurement sequence to fix it are stated in the comparison protocol, the gap between the coordinate systems determined by each participant is small. However, the measurement results for the determination by each participant must have measurement error. Therefore, the fixed coordinate systems are not matched strictly. In this research, the effects of those measurement errors are considered in the reference value evaluation.

The temporary reference value \( {\mathbf{x}}_{0j} \) is calculated as follows:

$$ {\mathbf{x}}_{0j} = \frac{1}{{\sum\nolimits_{i = 1}^{n} {\frac{1}{{{\mathbf{U}}_{{{\hat{\mathbf{x}}}_{ij} }} }}} }}\sum\limits_{i = 1}^{n} {\frac{{{\hat{\mathbf{x}}}_{ij} }}{{{\mathbf{U}}_{{{\hat{\mathbf{x}}}_{ij} }} }}} \quad ( {\text{with}}\;{\text{the}}\;{\text{weighted}}\;{\text{best}}\;{\text{fit}}\;{\text{algorithm),}}\;{\text{or}} $$
(3)
$$ {\mathbf{x}}_{0j} = \frac{{\sum\nolimits_{i = 1}^{n} {{\hat{\mathbf{x}}}_{ij} } }}{n}\quad ( {\text{with}}\;{\text{the}}\;{\text{simple}}\;{\text{best}}\;{\text{fit}}\;{\text{algorithm),}} $$
(4)

where \( {\mathbf{U}}_{{{\hat{\mathbf{x}}}_{ij} }} \) is the expanded uncertainty of \( {\hat{\mathbf{x}}}_{ij} \). Since the rotation \( \theta_{i} \) is assumed to be small, it is allowed to approximate \( {\mathbf{U}}_{{{\hat{\mathbf{x}}}_{ij} }} \) by \( {\mathbf{U}}_{{{\mathbf{x}}_{ij} }} \).

After the iterative calculation, \( {\mathbf{x}}_{0j} \) and its expanded uncertainty \( {\mathbf{U}}_{{{\mathbf{x}}_{0j} }} \) are derived. \( {\mathbf{U}}_{{{\mathbf{x}}_{0j} }} \) is calculated as follows:

$$ {\mathbf{U}}_{{{\mathbf{x}}_{0j} }} = \sqrt {\frac{1}{{\sum\nolimits_{i = 1}^{n} {\frac{1}{{{\mathbf{U}}_{{{\mathbf{x}}_{ij} }}^{2} }}} }}} \quad ( {\text{with}}\;{\text{the}}\;{\text{weighted}}\;{\text{best}}\;{\text{fit}}\;{\text{algorithm),}}\;{\text{or}} $$
(5)
$$ {\mathbf{U}}_{{{\mathbf{x}}_{0j} }} = \frac{1}{n}\sqrt {\sum\limits_{i = 1}^{n} {{\mathbf{U}}_{{{\mathbf{x}}_{ij} }}^{2} } } \quad ( {\text{with}}\;{\text{the}}\;{\text{simple}}\;{\text{best}}\;{\text{fit}}\;{\text{algorithm)}} . $$
(6)

2.4 Outlier Elimination

When the temporary reference values and their expanded uncertainties are determined, \( E_{n} \) number of each feature point coordinates is calculated for each participant’s result. In one dimensional case, \( E_{n} \) number can be defined as follows:

$$ E_{n} = \frac{{x_{i} - x_{0} }}{{u\left( {x_{i} - x_{0} } \right)}}, $$
(7)
$$ u\left( {x_{i} - x_{0} } \right) = \sqrt {u\left( {x_{i} } \right)^{2} + u\left( {x_{0} } \right)^{2} - 2\text{cov} \left( {x_{i} ,x_{0} } \right)} . $$
(8)

Since the measurand of the comparison is two dimensional coordinate, the definition of \( E_{n} \) should be extended to a two dimensional case as follows:

$$ E_{n} = \frac{{\left| {{\mathbf{x}}_{i} - {\mathbf{x}}_{0} } \right|}}{{u\left( {\left| {{\mathbf{x}}_{i} - {\mathbf{x}}_{0} } \right|} \right)}}, $$
(9)
$$ u\left( {\left| {{\mathbf{x}}_{i} - {\mathbf{x}}_{0} } \right|} \right) = \sqrt {{\mathbf{n}}^{\text{T}} {\varvec{\uppsi}}_{1} {\mathbf{n}} + {\mathbf{n}}^{\text{T}} {\varvec{\uppsi}}_{0} {\mathbf{n}} - 2{\mathbf{n}}^{\text{T}} {\varvec{\uppsi}}_{i,0} {\mathbf{n}},} $$
(10)
$$ {\mathbf{n}} = \frac{{{\mathbf{x}}_{i} - {\mathbf{x}}_{0} }}{{\left| {{\mathbf{x}}_{i} - {\mathbf{x}}_{0} } \right|}}. $$
(11)

Here the rotation \( \theta_{i} \) is assumed to be small, the correlation between the coordinate on the first axis and that on the second axis is negligible, i.e.,

$$ {\varvec{\uppsi}}_{i} = \left[ {\begin{array}{*{20}c} {U_{{x_{ij} }}^{2} } & 0 \\ 0 & {U_{{y_{ij} }}^{2} } \\ \end{array} } \right], $$
(12)
$$ {\varvec{\uppsi}}_{0} = \left[ {\begin{array}{*{20}c} {U_{{x_{0j} }}^{2} } & 0 \\ 0 & {U_{{y_{0j} }}^{2} } \\ \end{array} } \right]. $$
(13)

The correlation between the participant’s result and the temporary reference value is given as follows [6]:

$$ {\varvec{\uppsi}}_{i,0} = \left[ {\begin{array}{*{20}c} {U_{{x_{0j} }}^{2} } & 0 \\ 0 & {U_{{y_{0j} }}^{2} } \\ \end{array} } \right],\quad ( {\text{with}}\;{\text{the}}\;{\text{weighted}}\;{\text{best}}\;{\text{fit}}\;{\text{algorithm),}}\;{\text{or}} $$
(14)
$$ {\varvec{\uppsi}}_{i,0} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right]\quad ( {\text{with}}\;{\text{the}}\;{\text{simple}}\;{\text{best}}\;{\text{fit}}\;{\text{algorithm)}} . $$
(15)

The participant which has the most numbers of \( E_{n} \) being larger than unity will be eliminated from the group of participants as an outlier; whose results are not used for the calculation of the reference value. Then a new reference value is calculated again. This process is repeated until all \( E_{n} \) numbers of all participants, which are taken into account to the temporary reference value, are smaller than unity.

2.5 Equivalence Checking

After the reference value computation terminated, the equivalence between the reference value and each participant’s reported value is checked. The \( E_{n} \) number of the ith participant result is evaluated by (9)–(13).

When the reference value is computed with the weighted best fit algorithm, the correlation between the participant’s reported value and the reference value depends on whether the participant’s is the outlier or not. When the participant’s results is taken into account the reference value calculation, the correlation is given by (14), otherwise, i.e., when the participant is the outlier, it is given by (15) [6]. When the reference value is computed with the simple best fit algorithm, the correlation between the participant’s reported value and the reference value is given by (15) [6].

2.6 Previous Manner: Length Based Analysis

Now, the evaluation procedure applied in the previous key comparison [5] is reviewed briefly. The purpose of reviewing is to clarify the difference between the proposed manner in this research and previously reported one.

In the previous international comparison, the procedure summarized in Sect. 2.1 is executed based on the length measurement error. Therefore, the measurand for the equivalency validation is the distance between the centres of No. 1 ball/hole and each one as follows;

$$ E_{{ij,{\text{Previous}}}} = \left| {{\mathbf{x}}_{ij} - {\mathbf{x}}_{i1} } \right| - \left| {{\mathbf{x}}_{0j} - {\mathbf{x}}_{01} } \right| = \left| {{\mathbf{x}}_{ij} } \right| - \left| {{\mathbf{x}}_{0j} } \right|, $$
(16)

where the coordinates for any \( {\mathbf{x}}_{i1} \) are fixed to \( {\mathbf{0}} \). The error evaluation based on the Eq. (16) includes two problems.

Firstly, the coordinate measurement error may not affect the length measurement error in the Eq. (16). When the coordinate measurement error vector \( {\mathbf{x}}_{ij} - {\mathbf{x}}_{0j} \) is perpendicular to \( {\mathbf{x}}_{0j} \), the length measurement error is insensitive to the coordinate measurement error. Note that the no coordinate system transformation is applied in the previous inter comparison. When the ith participant performs the measurement with the certain direction errors on:

  • The jth ball/hole, or

  • The ball/hole to be the element for the \( X \) axis direction definition,

it is possible that the length measurement error on \( {\mathbf{x}}_{ij} \) is judged as non-outlier.

Secondly, the evaluation by (16) ignores the measurement error of the coordinates on the No. 1 ball/hole. To be precise, (16) shall be;

$$ E_{{ij,{\text{Previous}}}} = \left| {{\mathbf{x}}_{ij} - \delta {\mathbf{x}}_{i0} } \right| - \left| {{\mathbf{x}}_{0j} } \right|, $$
(17)

where \( \delta {\mathbf{x}}_{0j} \) is the coordinate measurement error on the No. 1 ball/hole by the ith participants. The error \( \delta {\mathbf{x}}_{0j} \) cannot be acquired from the participant’s reported value because the participant reports the coordinates of the balls/holes in the transformed coordinate systems whose origin is shifted onto the observed centres of No. 1 ball/hole. It means that the reported coordinates of the other balls/holes have the respective measurement errors and superposed measurement error \( \delta {\mathbf{x}}_{0j} \). Therefore, the participant which performs the measurement on No. 1 ball/hole with large error takes a significant penalty in the outlier elimination procedure.

3 Evaluation Example

The application of the proposed manner is demonstrated through the evaluation executions of the reported international comparison for ball plate and hole plate calibration [5]. The key comparison reference values (KCRV) in this article are evaluated with the weighted best fit algorithm. Equivalence between the KCRV and each participant’s result is also checked.

3.1 Overview of the Comparison

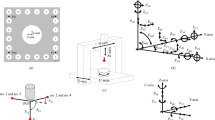
Figure 1 shows the schematic drawings of the ball plate and the hole plate measured in the comparison [5]. The measurands are the centre coordinates of the balls/holes installed on the artefact. 12 laboratories (national metrology institutes: NMIs) participated in the comparison. According to the agreed protocol, each participant measured the centre coordinates of the balls/holes using CMM with reversal technique, and compensated the length measurement error of the CMM with the participant’s manner. Each participant reported the measurement results and the uncertainty formula evaluated with the participant’s manner to the pilot laboratory [5].

Fig. 1
figure 1

Ball plate and hole plate for the comparison [5]

Full size image

3.2 Data Preparation

Participants reported the centre coordinates on the workpiece coordinate system. Therefore, the coordinates of the centre of ball No. 1 and the \( Y \) coordinate of the centre of ball No. 5 were reported as zero. In the case of the hole plate, the coordinates of the centre of hole No. 1 and the \( Y \) coordinate of the centre of hole No. 9 were reported as zero. Table 1 shows uncertainty formulas reported by all participants [5]. The uncertainty formulas for the Lab-8 were adjusted by the pilot of the comparison because the participant reported only the numerical data of their measurement uncertainty. The sets of numerical data for KCRV calculation are prepared with the reported values and the formulas. The illustration of the prepared data for the ball plate and the hole plate are skipped due to limitations of space.

Table 1 Uncertainty formulas of participants’ results
Full size table

Note that the origin and the direction of the axis of the coordinate system on the two dimensional artefact are floated through the KCRV computation procedure. That is because the ball/hole labelled as the origin of the coordinate system on the artefact shall be measured with non-zero uncertainty (see Sect. 2.2). In contrast to above, the origin and the axis direction of the coordinate system on the artefact is fixed in the reported international comparison [5].

In the KCRV computation, arbitrary point on the artefact can be set as the origin of the coordinate system on the artefact. In another international comparison [7], the centre of gravity of all balls/holes are set as the origin of the coordinate system; that is for the purpose of minimize the overall errors in the best fit calculation in the intercomparison [7]. On the other hand, the evaluated temporary KCRV of the centre of No. 1 ball/hole is set as the origin of the coordinate system in this research. It is same as that in the reported international comparison for the demonstration. That is because to demonstrate the difference between the KCRVs evaluated with the reported manner and the proposed manner.

3.3 Reference Value/Uncertainty Calculation Process

3.3.1 Ball Plate Calibration

As the first step, temporary KCRVs and their expanded uncertainties are computed by (1)–(3) and (5) with all 12 participants’ data. \( E_{n} \) numbers between the temporary KCRVs and respective participant’s results are calculated by (7)–(14). Figure 2a shows the results of \( E_{n} \) computation at the first step. Figure 2a indicates that the result by the 9th participant is outlier. In the previous inter comparison, the 9th participant was the outlier at the first step, too [5].

Fig. 2
figure 2

\( E_{n} \) numbers calculated participants’ results

Full size image

As the second step, the temporary KCRVs and their expanded uncertainties are re-computed with the data except for the 9th participant’s. Figure 2b shows the results of \( E_{n} \) computation at the second step. Figure 2b indicates that the result by the 1st participant is outlier. In the previous inter comparison, the 1st participant was the outlier at the second step, too [5].

As the third step, the temporary KCRVs and their expanded uncertainties are re-computed with the data except for the 9th and the 1st participants’. Figure 2c shows the results of \( E_{n} \) computation at the third step.

In the previous inter comparison, there was no outlier at the third step [5]. However, Fig. 2c indicates that the result by the 3rd participant is outlier. Therefore as the fourth step, the temporary KCRVs and their expanded uncertainties are re-computed with the data except for the 9th, the 1st and 3rd participants’. Figure 2d shows the results of \( E_{n} \) computation at the fourth step.

Figure 2d shows that no outlier exists in the data used for temporary KCRV calculation at the fourth step. Therefore the temporary KCRV and its expanded uncertainty computed with the 9 participants’ data, all participants excepting the 1st, the 3rd and the 9th laboratories, are adopted as the KCRV and its expected uncertainty of the international comparison. Table 2 shows the actual values of them. Table 3 shows the outliers in the intercomparison extracted by the reported manner and being proposed manner respectively. Table 4 shows the evaluated rotation and translation parameters in (2). The coordinate transformation parameters are the order of 0.1 μrad and 0.1 μm respectively; which validate the assumption on the KCRV evaluation in Sect. 2.3.

Table 2 Evaluated KCRVs and their expanded uncertainty (ball plate)
Full size table
Table 3 Outliers in the international comparison (ball plate)
Full size table
Table 4 Rotation and translation parameters in (2) (ball plate)
Full size table

3.3.2 Hole Plate Calibration

As well as the case of the ball plate calibration, the KCRVs evaluation for the hole plate calibration is executed. Figure 3 shows the \( E_{n} \) numbers calculated from the participants’ result except for the outliers. The actual KCRVs and the expanded uncertainty of them are skipped due to limitations of space. Table 5 shows the outliers in the intercomparison extracted by the reported manner and being proposed manner respectively. Table 6 shows the evaluated rotation and translation parameters in (2). The coordinate transformation parameters are less than the order of 1.0 μrad and 1.0 μm respectively; which also validate the assumption on the KCRV evaluation in Sect. 2.3.

Fig. 3
figure 3

\( E_{n} \) numbers calculated from participants’ results except Lab-9, Lab-11, Lab-7, Lab-3 and Lab-10

Full size image
Table 5 Outliers in the international comparison (hole plate)
Full size table
Table 6 Rotation and translation parameters in (2) (hole plate)
Full size table

3.4 Equivalence Checking

After the KCRV computation is terminated, the equivalence between the KCRV and each participant’s reported value is checked with (9)–(13). For the outlier participants, the correlations between the KCRV and the result by each of them are calculated with (15). For the other participants, those are done with (14). Table 6 shows the evaluated \( E_{n} \) numbers on all participants’ results for ball plate calibration. That for hole plate calibration is skipped due to limitations of space. In the tables, the \( E_{n} \) values and participants labels of the outliers are in parentheses.

4 Discussion

In the previous reported intercomparison, the 3rd participant was not the outlier in the ball plate calibration [5]. In contrast, the same participant is judged as the outlier under the proposing manner. That is because only the measurement error of distance between the respective balls centre and the No. 1 ball centre was considered in the previous reported intercomparison. Table 7 shows that the 3rd participant marked large \( E_{n} \) value on No. 6 and No. 21 balls. Those balls are located along \( Y \) axis of the coordinate system on the ball plate. It implies that the 3rd participant measured the coordinates of the centres of No. 6 and No. 21 balls with significant large errors in \( X \) direction.

Table 7 \( E_{n} \) numbers between each KCRV and each participant’s result (ball plate)
Full size table

According to the outlier verification manner applied in the previous reported intercomparison, the distance between the centres of No. 6 or No. 21 and No. 1 balls is insensitive to the \( X \) coordinate error on No. 6 or No. 21 balls. Table 8 shows the length and coordinates measurement error by the 3rd participant on the ball plate. As shown in the table, the observed length measurement errors are smaller than the one-third of the coordinates measurement error.

Table 8 Lab-3’s measurement error against the KCRV (ball plate)
Full size table

As well as the case of ball plate calibration, more participants in the hole plate calibration are judges as outliers by the proposed analysis. It means that the judgment procedure ruled by the length measurement error can lead the misestimation of the ability of coordinate measurement. Also the fact means that the manner proposed in this study gives more precise validation on the coordinate measurement ability than that in the previous reported intercomparison.

Table 5 shows that the 5th participant in the hole plate calibration is not the outlier in contrast to the previous reported intercomparison. According to the result of the equivalence checking, the 5th participant marks the largest \( E_{n} \) value on No. 1 hole. It means that the 5th participant measure the coordinates of the centre of No. 1 hole with significant large error, however, it’s smaller than acceptable limit.

In the previous reported intercomparison, the outlier elimination is done in consideration of the length measurement error between the respective holes and No. 1 hole, the hole for the origin of the coordinate system on the artefact. The participants which measures the coordinates of the hole No. 1 with large error can be easily judged as an outlier under the rule in the previous reported intercomparison. Even though the other holes are measured with small errors, the length measurement error between the holes and No. 1 hole is dominantly affected by the measurement error on No. 1 hole.

The probability of coordinate measurement error is equal on the respective elements on the artefact. However, the judgment is strongly affected only one element measurement using the outlier elimination manner based on length measurement error from the origin. In contrast, the manner proposed in this research deals the coordinate measurement errors on respective elements evenly in the outlier elimination procedure. As the result, it is avoided to make misjudgement that the participant which can perform the coordinates measurement with small error as a whole is an outlier.

5 Summary

In this study, the reference value and its uncertainty evaluation for two dimensional standard calibration is developed. The verification method to check the equivalence between the KCRV and participant’s measurement result is also described. The features of this method include:

  • The coordinates-based reference value evaluation,

  • Applying the best fit algorithm for KCRV computation, and

  • The coordinates-based equivalence verification.

The proposed manner gives more precise validation on the coordinate measurement ability than the manner based on length measurement error. Using the length error based manner, there are two problems. One is that the length measurement error analysis cannot detect the coordinate measurement error in certain cases. The other is that the outlier elimination procedure is executed with a heavy penalty on the participant which makes large measurement error on the particular elements. The problems cause an erroneous decision on the outlier elimination. This paper demonstrated that the both problems are solved using the coordinate error base manner.

Using the proposed evaluation method, the verification of coordinate measurement equivalence on the two dimensional standard becomes possible among the participants without misestimating.