On Accurate and Efficient Judgment Method of Milling Stability Based on Predictor–Corrector Scheme

Abstract

The accurate and efficient identification of milling stability region is key to suppressing chatter and improving production efficiency. Therefore, the theory of “predictor–corrector” is dependent on proposing a new method for milling stability prediction. Firstly, the delay differential equation on regenerative chatter is turned into the state space expression. Then, the Milne formula is used to predict the displacement whereas the Simpson formula corrects this predicted value. Furthermore, a discrete prediction-correction expansion with higher precision is constructed to obtain the state transition express. Based on the Floquet theory, the milling stability can be judged. Finally, the comparison of local discretization errors obtained by the proposed method with other methods shows that the proposed method has a faster convergence speed than the contrast methods. Obviously, under the same discretization conditions, the proposed method can not only achieve higher computational accuracy than the contrast methods but also obtain faster computational efficiency. Both 29 groups of the simulation results and 9 groups of experimental measurements can further validate the presented method in actual prediction effect.

1 Introduction

Milling technology plays an important role in aerospace and mechanical engineering. In comparison to traditional material removal methods, it can maintain relatively lower cutting forces and faster material removal rates so that it can achieve better part surface quality. However, milling chatter is an important problem that seriously affects the workpiece surface quality and production efficiency. One of the most important factors that cause milling chatter is the regeneration effect [1]. The regenerative chatter results mainly from the phase difference caused by the inconsistent cutting thickness of two adjacent tooth passing periods.

In the field of mechanical manufacturing, the prediction of milling chatter has always attracted lots of attention [1, 2, 5]. In recent decades, extensive and profound theoretical research and experimental verification have been carried out on regenerative chatter in academic and industrial circles [3,4,5,6,7,8]. Altintas et al. [9] used the Fourier expansion to propose a zero-order approximation (ZOA) method by preserving the zero-order term in the frequency domain. But ZOA is not suitable for the small radial depth of cut conditions. Merdol and Altintas [10] took into account the higher-order terms of the Fourier series to construct a multi-frequency (MF) solution for milling stable regions. Since MF must repeatedly search the chatter frequency, it is not computationally efficient. Bayly et al. [11] proposed a time finite element analysis (TFEA) method by using the weighted residual method to deduce the state transition matrix for the discretized cutting time nodes. Certainly, this method is not computationally efficient not to fully apply to all working conditions. Insperger et al. [12, 13] explored the semi-discretization method (SDM). The tooth passing period was discretized uniformly into small time intervals. The delay- and periodic-term of DDE took the averaged values of two endpoints in every time interval so that the DDE could be transformed into an ordinary differential equation (ODE). Afterward, they again proposed a high-order SDM with higher algebraic accuracy [14]. Ding et al. [15] introduced the full-discretization method (FDM) based on the direct integration scheme. Also, Ding et al. [16] improved the FDM to obtain the second-order FDM by increasing the interpolation order on the state term. Though the 2nd FDM could improve the computational accuracy, the computational efficiency was decreased with the improvement of the interpolation order. Likewise, the state term of DDE can be interpolated by a third-order method [17, 18] and other FDM-based enhanced methods [19,20,21,22,23]. Niu et al. [24] proposed the generalized Runge–Kutta method (GRKM). Li et al. [25] proposed a complete discretization scheme (CDS). Zhang et al. [26] used Simpson numerical integration formula to propose a concise SLD method. By replacing the fourth-order Runge Kutta formula with the Euler formula in the CDS, Li et al. [27] obtained an improved Runge–Kutta method.

Accurate calibration of cutting force coefficients and accurate identification of tool system dynamic parameters are crucial for predicting milling stability correctly. Mostaghimi et al. [28] combined the artificial neural network and receptance coupling method to propose a method for predicting the dynamic parameters of the tool system. Kang et al. [29] used an optimization method to obtain coefficients from individual cutting conditions to identify cutting force coefficients. By modifying the design parameters to reduce the difference between the measured and simulated cutting forces, and to determine the optimal cutting force coefficient. Compared with traditional methods, the proposed method can predict the cutting force more accurately. In terms of SLD predictions, recently, Qin et al. [30] adopted the second-order Lagrange interpolation polynomial for the approximation of the displacement at every time node to propose a holistic-discretization method (HIM). Dai et al. [31] presented a precise integration method (PIM). Lou et al. [32] suggested a new numerical integration method by combining Lagrange interpolation with Cotes integral formula. Wu et al. [33] employed Milne and Simpson formula to obtain a correction method based on local truncation error being estimated in the state term. Moreover, they also proposed an implicit exponential fitting method based on the Fibonacci search [34]. Liu et al. [35] proposed an improved SDM based on predictor–corrector scheme. Qin et al. [36] used the Adams formula as a predictor item and proposed a series of predictor–corrector methods, which achieved good prediction results. Wei et al. [37] systematically analyzed the influence mechanism of parameters such as spindle speed and radial depth of cut on milling stability and established a three-dimensional stability prediction model under multiple milling parameters. Chen et al. [38] proposed a generalized numerical differentiation method for predicting the stability of nonautonomous DDEs with periodic coefficients and discrete delays, and the theory was applied to predict the milling stability under multiple time delays.

As above stated, the general analyzing process of milling stability can be summarized as follows: By discretizing the tooth passing period of DDE, the numerical calculation method is adopted to deduce the state transition matrix. And then, the Floquet theory is depended on to carry out the chatter analysis. In fact, the aim of chatter analysis method is the realization of two seemingly contradictory aspects. One is to obtain a better calculation accuracy of the SLD under the small periodic discrete number. Another is to improve the computational efficiency as high as possible under the increase of periodic discrete numbers. However, today’s prediction methods for SLD do not perfectly solve these two computation performance problems. Usually, the ODE can numerically be solved by a linear multi-step method. In the predictor–corrector linear multi-step method, the predictor value is calculated by using the explicit formula whereas the corrector value is calculated by using the implicit formula. It can always obtain better numerical stability for both low-order and high-order methods [39]. In this paper, Taylor expansion is used to obtain the higher-order Milne explicit formula and Simpson implicit formula so that a new Milne Simpson predictor–corrector method (MS-PCM) is applied to predict the milling stability region. It is worth mentioning that MS-PCM only needs to calculate three discrete point values for the next discrete point value whereas the same-order Adams [36] needs four discrete point values. Therefore, MS-PCM is of more simple calculation. Moreover, the Milne formula has the main truncation error coefficient of 14/45 while the Adams formula is 251/720. Obviously, the MS-PCM is slightly smaller mathematical calculation error than the Adams method [36].

The remainder of this paper is arranged as follows: Sect. 2 is to establish the dynamic model of two degrees of freedom (DOF) milling system. Section 3 is to give the detailed mathematical derivation of the MS-PCM. Section 4 illustrates the advantages of the MS-PCM over other methods. Section 5 demonstrates the accuracy and effectiveness of MS-PCM through numerical simulations and experiments. Finally, Sect. 6 is to summarize the characteristic conclusions of the MS-PCM.

2 Dynamics Model of Milling System

Without losing generality, suppose the workpiece is rigid but milling tool is flexible. Figure 1 is the two-DOF milling dynamic model along the feed direction X and the workpiece wall thickness direction Y. The dynamic milling process with the regeneration effect [3, 4, 40] is written as

$${\mathbf{M\ddot{q}}}(t) + {\mathbf{C\dot{q}}}(t) + {\mathbf{Kq}}(t)\; = {\mathbf{Q}}(t)[{\mathbf{q}}(t) - {\mathbf{q}}(t - \tau )]$$

(1)

where M, C and K are the modal parameter matrices. q(t) is the vibration displacement vector of milling tool. τ = 60/N/Ω is the time delay. N is the tooth number. Ω is the spindle speed. Q(t) = Q(t + τ) is the dynamic milling force coefficient matrix whose expression is

$${\mathbf{Q}}(t) = \left[ {\begin{array}{*{20}c} { - a_{p} h_{xx} (t)} & { - a_{p} h_{xy} (t)} \\ { - a_{p} h_{yx} (t)} & { - a_{p} h_{yy} (t)} \\ \end{array} } \right]$$

(2)

where

$$\left\{ {\begin{array}{*{20}l} {h_{xx} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t))\sin (\phi_{j} (t))\left[ {K_{t} \cos (\phi_{j} (t)) + K_{r} \sin (\phi_{j} (t))} \right]} \hfill \\ {h_{xy} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t)){\text{cos}}(\phi_{j} (t))\left[ {K_{t} \cos (\phi_{j} (t)) + K_{r} \sin (\phi_{j} (t))} \right]} \hfill \\ {h_{yx} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t))\sin (\phi_{j} (t))\left[ {K_{r} \cos (\phi_{j} (t)) - K_{t} \sin (\phi_{j} (t))} \right]} \hfill \\ {h_{yy} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t))\cos (\phi_{j} (t))\left[ {K_{r} \cos (\phi_{j} (t)) - K_{t} \sin (\phi_{j} (t))} \right]} \hfill \\ \end{array} } \right.$$

(3)

where h_xx(t), h_xy(t), h_yx(t), h_yy(t) is milling force coefficient matrix. K_t and K_r are respectively milling force coefficients in the tangential and the normal direction. $\phi_{j} (t)$ is the current angular of the tooth j which is expressed as

$$\phi_{j} (t) = \frac{2\pi \Omega }{{60}}t + \frac{2\pi (j - 1)}{N}$$

(4)

$g(\phi_{j} (t))$ is a window function to judge whether the tooth j is cutting and

$$g(\phi_{j} (t)) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\phi_{{{\text{st}}}} < \phi_{j} (t) < \phi_{{{\text{ex}}}} } \hfill \\ {0,} \hfill & {{\text{other}}} \hfill \\ \end{array} } \right.$$

(5)

with the start angle $\phi_{{{\text{st}}}}$ of the jth tooth and exit angle $\phi_{{{\text{ex}}}}$. It is worth noting that there are $\phi_{{{\text{st}}}} { = }\arccos \left( {{{2a} \mathord{\left/ {\vphantom {{2a} D}} \right. \kern-0pt} D} - 1} \right)$, $\phi_{{{\text{ex}}}} { = }\pi$ and $\phi_{{{\text{st}}}} { = }0$, $\phi_{{{\text{ex}}}} { = }\arccos \left( {1 - 2a/D} \right)$ in the down milling and the up milling, respectively. a is the radial depth of cut, D is the diameter of the tool and a/D is defined as the radial immersion ratio.

Fig. 1

Two-DOF milling dynamics model

Let ${\mathbf{p}}(t) = {\mathbf{M\dot{q}}}(t) + {\mathbf{Cq}}(t)/2$ and ${\mathbf{V}}(t) = [{\mathbf{q}}(t) \, {\mathbf{p}}(t)]^{{\text{T}}}$, Eq. (1) can be further expressed as

$${\dot{\mathbf{V}}}(t) = {\mathbf{LV}}(t) + {{\varvec{\Theta}}}(t)\left[ {{\mathbf{V}}(t) - {\mathbf{V}}(t - \tau )} \right]$$

(6)

with ${\mathbf{L}} = \left[ {\begin{array}{*{20}l} { - {\mathbf{M}}^{ - 1} {\mathbf{C}}/2} \hfill & {{\mathbf{M}}^{ - 1} } \hfill \\ {{\mathbf{CM}}^{ - 1} {\mathbf{C}}/4 - {\mathbf{K}}} \hfill & { - {\mathbf{CM}}^{ - 1} /2} \hfill \\ \end{array} } \right]$, ${{\varvec{\Theta}}}(t) = \left[ {\begin{array}{*{20}l} {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {{\mathbf{Q}}(t)} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]$.

Clearly, L is a constant coefficient matrix with only respect to the modal parameters. Θ(t) is the periodic coefficient matrix which is related to the milling force coefficient. Just like the milling force coefficient matrix Q(t), Θ(t) is also a periodic function of τ, i.e., Θ(t) = Θ(t + τ).

3 MS-PCM Based Stability Analysis

Evidently, it is difficult in obtaining a strict analytical solution of Eq. (6). Therefore, a numerical method must be sophisticatedly adopted to solve Eq. (6).

Here, t₀ and t₁ are used to denote the initial time of a cutting period and the cut-in time of the cutter tooth, respectively. Moreover, the time τ + t₀ is called the cut-out time of the cutter tooth. Thus, the time between t₀ and t₁ is named the free vibration period t_f = t₁ − t₀. Likewise, the time from t₁ to τ + t₀ is defined as the forced vibration period. If τ − t_f is uniformly discretized into m small intervals, the length of each interval is equal to h = (τ − t_f)/m, as shown in Fig. 2. Thus, an arbitrary discrete time note point can be expressed as

$$t_{i} = t_{0} + t_{f} + (i - 1)h,\quad i = 1,2, \ldots ,m,m + 1$$

(7)

Fig. 2

Schematic diagram of discrete tooth passing period

Similar to Volterra integral equations of the second kind [Refer to appendix 1], Eq. (6) can be expressed as the following form by considering ${{\varvec{\Theta}}}(t)[{\mathbf{V}}(t) - {\mathbf{V}}(t - \tau )]$ as the inhomogeneous term of the homogeneous equation ${\dot{\mathbf{V}}}(t) = {\mathbf{LV}}(t)$, i.e.,

$${\mathbf{V}}(t) = e^{{(t - t_{0} ){\mathbf{L}}}} {\mathbf{V}}(t_{0} ) + \int_{{t_{0} }}^{t} {\left\{ {e^{{(t - \sigma ){\mathbf{L}}}} {{\varvec{\Theta}}}(\sigma )\left[ {{\mathbf{U}}(\sigma ) - {\mathbf{U}}(\sigma - \tau )} \right]} \right\}} d\sigma$$

(8)

According to Eq. (7), if t is within the t_i and t_i+1, the following expression can be achieved as

$${\mathbf{V}}(t) = {\mathbf{s}}(t,t_{i} ) + \int_{{t_{i} }}^{t} {{\mathbf{R}}\left[ {t,\sigma ,{\mathbf{V}}(\sigma )} \right]} d\sigma$$

(9)

where ${\mathbf{s}}(t,t_{i} ) = e^{{(t - t_{i} ){\mathbf{L}}}} {\mathbf{V}}(t_{i} )$, ${\mathbf{R}}\left[ {t,\sigma ,{\mathbf{V}}(\sigma )} \right] = e^{{(t - \sigma ){\mathbf{L}}}} {{\varvec{\Theta}}}(\sigma )\left[ {{\mathbf{V}}(\sigma ) - {\mathbf{V}}(\sigma - \tau )} \right]$.

If the tooth is in the free vibration period t_f, the milling force coefficient matrix Q(t) is a zero matrix. Therefore, there is Θ(σ) = 0 in Eq. (8) so it is easy to obtain

$${\mathbf{V}}(t) = {\mathbf{s}}(t,t_{0} ) = e^{{(t - t_{0} ){\mathbf{L}}}} {\mathbf{V}}(t_{0} )$$

(10)

In the forced vibration period τ − t_f, Eq. (8) is numerically integrated to achieve V(t) obviously. Consequently, the fourth-order Milne–Simpson predictor–corrector formula [Refer to appendix 2] is adopted to solve the V(t) at each discrete time note point when t is not less than t₄. Thus, the linear multi-step formula of Eq. (8) can be described as

$${\mathbf{V}}_{i + 4}^{P} = {\mathbf{s}}\left( {t_{i + 4} ,t_{i} } \right) + \frac{4h}{3}\left[ \begin{gathered} 2{\mathbf{R}}\left( {t_{i + 4} ,t_{i + 3} ,{\mathbf{V}}_{i + 3} } \right) - {\mathbf{R}}\left( {t_{i + 4} ,t_{i + 2} ,{\mathbf{V}}_{i + 2} } \right) \hfill \\ + 2{\mathbf{R}}\left( {t_{i + 4} ,t_{i + 1} ,{\mathbf{V}}_{i + 1} } \right) \hfill \\ \end{gathered} \right]$$

(11)

$${\mathbf{V}}_{{_{i + 4} }}^{C} = {\mathbf{s}}\left( {t_{i + 4} ,t_{i + 2} } \right){ + }\frac{h}{3}\left[ \begin{gathered} {\mathbf{R}}\left( {t_{i + 4} ,t_{i + 4} ,{\mathbf{V}}_{i + 4}^{P} } \right) + 4{\mathbf{R}}\left( {t_{i + 4} ,t_{i + 3} ,{\mathbf{V}}_{i + 3} } \right) \hfill \\ + {\mathbf{R}}\left( {t_{i + 4} ,t_{i + 2} ,{\mathbf{V}}_{i + 2} } \right) \hfill \\ \end{gathered} \right]$$

(12)

Equations (11, 12) are both fourth-order algebraic precision formulas, called the Milne formula and Simpson formula, respectively. Their local truncation errors are $LTE_{M} = {{14} \mathord{\left/ {\vphantom {{14} {45}}} \right. \kern-0pt} {45}}h^{5} {\mathbf{V}}^{(5)} (t) + O(h^{6} )$ and $LTE_{S} = - {1 \mathord{\left/ {\vphantom {1 {90}}} \right. \kern-0pt} {90}}h^{5} {\mathbf{V}}^{(5)} (t) + O(h^{6} )$, respectively. Obviously, Eq. (9) can be iteratively solved by taking Eq. (11) as the predictor item whereas Eq. (12) is the corrector item.

In the closed interval [t_i+4, t_m+1], Eq. (9) can be further expressed as

$${\mathbf{V}}_{i + 4}^{P} = e^{{4h{\mathbf{L}}}} {\mathbf{V}}_{i} + \frac{4h}{3}\left[ {\begin{array}{*{20}l} {2e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 3} \left( {{\mathbf{V}}_{i + 3} - {\mathbf{V}}_{i + 3 - \tau } } \right) - e^{{2h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 2} \left( {{\mathbf{V}}_{i + 2} - {\mathbf{V}}_{i + 2 - \tau } } \right)} \hfill \\ { + \;2e^{{3h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 1} \left( {{\mathbf{V}}_{i + 1} - {\mathbf{V}}_{i + 1 - \tau } } \right)} \hfill \\ \end{array} } \right]$$

(13)

$${\mathbf{V}}_{i + 4}^{C} = e^{{2h{\mathbf{L}}}} {\mathbf{V}}_{i + 2} + \frac{h}{3}\left[ {\begin{array}{*{20}l} {{{\varvec{\Theta}}}_{i + 4} \left( {{\mathbf{V}}_{i + 4}^{P} - {\mathbf{V}}_{i + 4 - \tau } } \right) + 4e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 3} \left( {{\mathbf{V}}_{i + 3} - {\mathbf{V}}_{i + 3 - \tau } } \right)} \hfill \\ {{ + }\;e^{{2h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 2} \left( {{\mathbf{V}}_{i + 2} - {\mathbf{V}}_{i + 2 - \tau } } \right)} \hfill \\ \end{array} } \right]$$

(14)

For the sake of simplicity, V_i, V_i−τ and Θ_i−τ are used to denote V(t_i), V(t_i − τ) and Θ(t_i − τ), respectively. Thus, the predictor–corrector linear multi-step formula of Eq. (9) can be obtained as

$${\mathbf{V}}_{i + 4} = e^{{2h{\mathbf{L}}}} {\mathbf{V}}_{i + 2} + \left[ {\begin{array}{*{20}l} {\frac{1}{3}he^{{4h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 4} {\mathbf{V}}_{i} - \frac{1}{3}h{{\varvec{\Theta}}}_{i + 4} {\mathbf{V}}_{i + 4 - \tau } + {\mathbf{G}}_{i + 1}^{{}} \left( {{\mathbf{V}}_{i + 1} - {\mathbf{V}}_{i + 1 - \tau } } \right)} \hfill \\ { + \;{\mathbf{G}}_{i + 2}^{{}} \left( {{\mathbf{V}}_{i + 2} - {\mathbf{V}}_{i + 2 - \tau } } \right) + {\mathbf{G}}_{i + 3}^{{}} \left( {{\mathbf{V}}_{i + 3} - {\mathbf{V}}_{i + 3 - \tau } } \right)} \hfill \\ \end{array} } \right]$$

(15)

with the expressions of ${\mathbf{G}}_{i + 1}^{{}}$, ${\mathbf{G}}_{i + 2}^{{}}$, ${\mathbf{G}}_{i + 3}^{{}}$ can be found in Appendix 3, similarly hereinafter.

By separating the time-delay term from the state term, Eq. (15) can be rewritten as

$$\begin{aligned} & {\mathbf{F}}_{i + 4 - \tau } {\mathbf{V}}_{i + 4 - \tau } + {\mathbf{F}}_{i + 3 - \tau } {\mathbf{V}}_{i + 3 - \tau } + {\mathbf{F}}_{i + 2 - \tau } {\mathbf{V}}_{i + 2 - \tau } + {\mathbf{F}}_{i + 1 - \tau } {\mathbf{V}}_{i + 1 - \tau } \\ & \quad = {\mathbf{F}}_{i + 4} {\mathbf{V}}_{i + 4} + {\mathbf{F}}_{i + 3} {\mathbf{V}}_{i + 3} + {\mathbf{F}}_{i + 2} {\mathbf{V}}_{i + 2} + {\mathbf{F}}_{i + 1} {\mathbf{V}}_{i + 1} + {\mathbf{F}}_{i} {\mathbf{V}}_{i} \\ \end{aligned}$$

(16)

In fact, only when multiple initial values V(t_i), V(t_i+1), V(t_i+2) and V(t_i+3) are determined in advance can Eq. (16) be taken effect for V(t_i+4). In other words, if the MS-PCM is used to solve V(t_i+4), the periodic discrete number m must be satisfied the condition of m ≥ 4. If m < 4, other methods such as the Newton–Cotes numerical integration can be used to solve V(t_i). At t₁ = t₀ + t_f, the relationship between the first value V₁ of the state item and the last value V_m+1−τ of the time-delay item can be easily obtained as

$${\mathbf{V}}_{{1}} = {\mathbf{V}}(t + t_{f} ) = e^{{t_{f} {\mathbf{L}}}} {\mathbf{V}}_{{0}} = e^{{t_{f} {\mathbf{L}}}} {\mathbf{V}}_{m + 1 - \tau }$$

(17)

In the case of m = 1, V₂ can be implicitly expressed by the Trapezoidal formula as

$${\mathbf{V}}_{{2}} = e^{{h{\mathbf{L}}}} {\mathbf{V}}_{{1}} + \frac{h}{2}\left[ {e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{1}} \left( {{\mathbf{V}}_{{1}} - {\mathbf{V}}_{{{1} - \tau }} } \right) + {{\varvec{\Theta}}}_{{2}} \left( {{\mathbf{V}}_{{2}} - {\mathbf{V}}_{{{2} - \tau }} } \right)} \right]$$

(18)

By analogy, the time-delay term of Eq. (18) is separated from the state term to be achieved as

$${\mathbf{P}}_{2,2 - \tau }^{{}} {\mathbf{U}}_{{{2} - \tau }} \; + {\mathbf{P}}_{2,1 - \tau }^{{}} {\mathbf{U}}_{{{1} - \tau }} \; = {\mathbf{P}}_{2,2}^{{}} {\mathbf{U}}_{{2}} + {\mathbf{P}}_{2,1}^{{}} {\mathbf{U}}_{{1}}$$

(19)

When m = 2, the Simpson method can be adopted to implicitly express V₃ as

$${\mathbf{V}}_{{3}} = e^{{{2}h{\mathbf{L}}}} {\mathbf{V}}_{{1}} + \frac{h}{{3}}\left[ {e^{{{2}h{\mathbf{L}}}} {{\varvec{\Theta}}}_{1} \left( {{\mathbf{V}}_{1} - {\mathbf{V}}_{1 - \tau } } \right)} \right.\left. { + {4}e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{2} \left( {{\mathbf{V}}_{2} - {\mathbf{V}}_{2 - \tau } } \right) + {{\varvec{\Theta}}}_{3} \left( {{\mathbf{V}}_{3} - {\mathbf{V}}_{3 - \tau } } \right)} \right]$$

(20)

Thus, the separation of the time-delay term with the state term can re-express Eq. (20) as

$${\mathbf{P}}_{3,3 - \tau }^{{}} {\mathbf{V}}_{3 - \tau } + {\mathbf{P}}_{3,2 - \tau }^{{}} {\mathbf{V}}_{2 - \tau } + {\mathbf{P}}_{3,1 - \tau }^{{}} {\mathbf{V}}_{1 - \tau } = {\mathbf{P}}_{3,3}^{{}} {\mathbf{V}}_{3} + {\mathbf{P}}_{3,2}^{{}} {\mathbf{V}}_{2} + {\mathbf{P}}_{3,1}^{{}} {\mathbf{V}}_{1}$$

(21)

But if m = 3, the Newton integral formula is selected to obtain V₄ as

$${\mathbf{P}}_{4,4 - \tau }^{{}} {\mathbf{V}}_{{{4} - \tau }} + {\mathbf{P}}_{4,3 - \tau }^{{}} {\mathbf{V}}_{{{3} - \tau }} + {\mathbf{P}}_{4,2 - \tau }^{{}} {\mathbf{V}}_{{{2} - \tau }} + {\mathbf{P}}_{4,1 - \tau }^{{}} {\mathbf{V}}_{{{1} - \tau }} = {\mathbf{P}}_{4,4}^{{}} {\mathbf{V}}_{{4}} + {\mathbf{P}}_{4,3}^{{}} {\mathbf{V}}_{{3}} + {\mathbf{P}}_{4,2}^{{}} {\mathbf{V}}_{{2}} + {\mathbf{P}}_{4,1}^{{}} {\mathbf{V}}_{{1}}$$

(22)

By uniting Eqs. (16, 17, 19, 21) with Eq. (22), the discrete mapping relationship from the time-delay term to the state term can be constructed as

$${{\varvec{\Gamma}}}\left[ {\begin{array}{*{20}c} {{\mathbf{V}}_{1} } \\ {{\mathbf{V}}_{2} } \\ \vdots \\ {{\mathbf{V}}_{m} } \\ {{\mathbf{V}}_{m + 1} } \\ \end{array} } \right] = {{\varvec{\Lambda}}}\left[ {\begin{array}{*{20}c} {{\mathbf{V}}_{1 - \tau } } \\ {{\mathbf{V}}_{2 - \tau } } \\ \vdots \\ {{\mathbf{V}}_{m - \tau } } \\ {{\mathbf{V}}_{m + 1 - \tau } } \\ \end{array} } \right]$$

(23)

where

$${{\varvec{\Gamma}}}{ = }\left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{P}}_{2,1}^{{}} } & {{\mathbf{P}}_{2,2}^{{}} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{P}}_{3,1}^{{}} } & {{\mathbf{P}}_{3,2}^{{}} } & {{\mathbf{P}}_{3,3}^{{}} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{P}}_{4,1}^{{}} } & {{\mathbf{P}}_{4,2}^{{}} } & {{\mathbf{P}}_{4,3}^{{}} } & {{\mathbf{P}}_{4,4}^{{}} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1} } & {{\mathbf{F}}_{2} } & {{\mathbf{F}}_{3} } & {{\mathbf{F}}_{4} } & {{\mathbf{F}}_{5} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4} } & {{\mathbf{F}}_{m - 3} } & {{\mathbf{F}}_{m - 2} } & {{\mathbf{F}}_{m - 1} } & {{\mathbf{F}}_{m} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3} } & {{\mathbf{F}}_{m - 2} } & {{\mathbf{F}}_{m - 1} } & {{\mathbf{F}}_{m} } & {{\mathbf{F}}_{m + 1} } \\ \end{array} } \right]$$

(24)

$${{\varvec{\Lambda}}}{ = }\left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {e^{{{\mathbf{A}}t_{f} }} } \\ {{\mathbf{P}}_{2,1 - \tau }^{{}} } & {{\mathbf{P}}_{2,2 - \tau }^{{}} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{P}}_{3,1 - \tau }^{{}} } & {{\mathbf{P}}_{3,2 - \tau }^{{}} } & {{\mathbf{P}}_{3,3 - \tau }^{{}} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{P}}_{4,1 - \tau }^{{}} } & {{\mathbf{P}}_{4,2 - \tau }^{{}} } & {{\mathbf{P}}_{4,3 - \tau }^{{}} } & {{\mathbf{P}}_{4,4 - \tau }^{{}} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{F}}_{2 - \tau } } & {{\mathbf{F}}_{3 - \tau } } & {{\mathbf{F}}_{4 - \tau } } & {{\mathbf{F}}_{5 - \tau } } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3 - \tau } } & {{\mathbf{F}}_{m - 2 - \tau } } & {{\mathbf{F}}_{m - 1 - \tau } } & {{\mathbf{F}}_{m - \tau } } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{F}}_{m - 2 - \tau } } & {{\mathbf{F}}_{m - 1 - \tau } } & {{\mathbf{F}}_{m - \tau } } & {{\mathbf{F}}_{m + 1 - \tau } } \\ \end{array} } \right]$$

(25)

Thus, the state transition matrix in one tooth passing period can be obtained as

$${{\varvec{\Psi}}} = {{\varvec{\Gamma}}}^{ - 1} {{\varvec{\Lambda}}}$$

(26)

Based on Floquet theory, the judgment criterion of system stability can be proposed according to the spectral radius of the Ψ. If the spectral radius ρ(Ψ) is less than 1, i.e., $\rho ({{\varvec{\Psi}}}) < 1$, the system is in a stable state. If $\rho ({{\varvec{\Psi}}}) > 1$, the system is in an unstable state. But if $\rho ({{\varvec{\Psi}}}) = 1$, the system is in a critically stable state.

In order to clearly understand the obtainment of the SLD, Fig. 3 illustrates the flow of the calculation process.

Fig. 3

Flow chart of obtaining SLD for milling process using MS-PCM

4 Numerical Tests

Here, several typical examples are demonstrated to validate the computational performance of MS-PCM.

4.1 Milling System with One-DOF

A one-DOF milling dynamic model is used to verify the effectiveness of the proposed method. Here, the milling tool in the down milling has 2 teeth. The one-DOF model along the feed direction X [12,13,14,15,16] can be expressed as follows

$$m_{t} \ddot{x}(t) + 2m_{t} \zeta \omega_{n} \dot{x}(t) + m_{t} \omega_{n}^{2} x(t) = - a_{p} h_{xx} (t)\left[ {x(t) - x(t - \tau )} \right]$$

(27)

where ζ, ω_n, m_t are the damping ratio, natural angular frequency, and modal mass of the tool system, respectively. a_p is the axial depth of cut.

By substituting M = m_t, C = 2m_tζω_n and q(t) = x(t) into Eq. (1), Eq. (27) can be further expressed as

$${\dot{\mathbf{V}}}(t) = {\mathbf{LV}}(t) + {{\varvec{\Theta}}}(t)\left[ {{\mathbf{V}}(t) - {\mathbf{V}}(t - \tau )} \right]$$

(28)

where

$${\mathbf{L}} = \left[ {\begin{array}{*{20}l} { - \zeta \omega_{n} } \hfill & {{1 \mathord{\left/ {\vphantom {1 {m_{t} }}} \right. \kern-0pt} {m_{t} }}} \hfill \\ {m_{t} (\zeta \omega_{n} )^{2} - m_{t} \omega_{n}^{2} } \hfill & { - \zeta \omega_{n} } \hfill \\ \end{array} } \right]$$

(29)

$${{\varvec{\Theta}}}(t) = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill \\ { - a_{p} h_{xx} (t)} \hfill & 0 \hfill \\ \end{array} } \right]$$

(30)

Next is to calculate the SLD by using the proposed MS-PCM, 1st SDM and the 2nd FDM. The modal parameters and cutting force coefficients are taken from Ref. [14], as shown in Table 1.

Table 1 Modal parameters

For 1st SDM and 2nd FDM, the Refs. [14, 16] respectively prove that the local truncation error of 1st SDM and 2nd FDM is Ο(τ₃). They have 2nd algebraic precision in the mathematical approximation method. However, the local truncation error of MS-PCM is Ο(τ₅), that is, it has 4th order algebraic precision. It is known that the MS-PCM has better calculation accuracy over the 1st SDM and 2nd FDM.

In order to intuitively understand the computational performance, a comparison of the convergence rate is carried out for three methods. Firstly, nine groups of milling parameters are given in Table 2.

Table 2 Simulation parameters for obtaining convergence rate

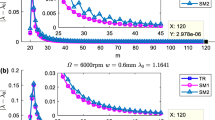
If |μ| is the modulus of the maximum eigenvalue of the transition matrix Ψ, |μ| which is obtained for each group of milling parameters by 1st SDM at m = 1000 can be taken as its theoretical value |μ₀|. Because |μ| is different with different discrete numbers m, the absolute value of the difference ||μ| − |μ₀|| between |μ| and |μ₀| is defined to measure the calculation accuracy. Here, ||μ| − |μ₀|| is called the local discrete error. Thus, the variation of the local discrete error with m can be clearly seen according to Fig. 4.

Fig. 4

Comparisons of convergence rate: a a_p = 0.7 mm, Ω = 3000 rpm, a/D = 0.2; b a_p = 1.3 mm, Ω = 3000 rpm, a/D = 0.2; c a_p = 1.9 mm, Ω = 3000 rpm, a/D = 0.2; d a_p = 0.6 mm, Ω = 9000 rpm, a/D = 0.5; e a_p = 1.2 mm, Ω = 9000 rpm, a/D = 0.5; f a_p = 1.8 mm, Ω = 9000 rpm, a/D = 0.5; g a_p = 0.9 mm, Ω = 7000 rpm, a/D = 1.0; h a_p = 1.7 mm, Ω = 7000 rpm, a/D = 1.0; i a_p = 2.5 mm, Ω = 7000 rpm, a/D = 1.0

As the discrete number m increases, the local discrete errors ||μ| − |μ₀|| obtained by the three methods gradually approach zero. But at an arbitrary value of m (m ≥ 30), the MS-PCM has a smaller value of ||μ| − |μ₀|| than the other two methods. In other words, the MS-PCM has a faster convergence rate no matter which m is valued. Therefore, under the same milling parameters, the cave obtained by the MS-PCM is approach to the actual value than the SLD obtained by the other two methods.

A set of SLD curves are compared with each other to further demonstrate the computational performance of the MS-PCM. Here, the radial immersion ratio is selected as 0.05, 0.5 and 1, respectively. Thus, the corresponding SLD curves can be obtained by the 1st SDM, 2nd FDM and MS-PCM for the discrete value m = 30 or m = 60, as shown in Fig. 5. All calculation procedures are carried out on MATLAB 9.11 installed on a personal computer [Intel(R) Core™ i7-10,700 CPU @ 2.90 GHz 16 GB]. Evidently, the three SLDs are almost identical to each other under the same discrete number and radial immersion ratio, except for slight differences at the peaks of SLDs which will be further analyzed in Sect. 5. However, their computation efficiencies are significantly different as illustrated in Fig. 6. When the computational accuracy is almost equal, the time consumption of MS-PCM is greatly less than 1st SDM and 2nd FDM. If m = 30, the time consumption of MS-PCM is about 75% and 50% less than that of the other two methods, respectively. But if m = 60, the computational efficiency of MS-PCM is further improved so that its time consumption will be further reduced by 77% and 70%.

Fig. 5

Comparisons of SLDs predicted by three methods of one-DOF with different discretization numbers m. a and b a/D = 0.05; c and d a/D = 0.5; e and f a/D = 1

Fig. 6

Comparison of computing time. a m = 30; b m = 60

In order to reasonably measure the prediction accuracy of the SLD computation method, two statistical formulas are introduced. One is the sum of squared errors (SSE) and another is the arithmetic mean of relative error (AMRE). Their expressions are written as

$$\left\{ {\begin{array}{*{20}l} {{\text{SSE}} = \sum\limits_{i = 1}^{r} {\left( {a_{pi} - a_{pi0} } \right)^{2} } } \hfill \\ {{\text{AMRE}} = \frac{1}{r}\sum\limits_{i = 1}^{r} {\frac{{\left| {a_{pi} - a_{pi0} } \right|}}{{a_{pi0} }}} } \hfill \\ \end{array} } \right.$$

(31)

where a_pi, a_p0 are the predicted and expected critical axial depth of cut corresponding to the ith spindle speed, respectively. r is the discrete number of the spindle speed.

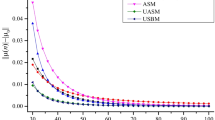
Now, the SLD corresponding to a/D = 1 in Fig. 5 is selected to calculate the SSE and AMRE. According to three SLDs obtained by three methods at m = 200, three critical axial depths of cut at the ith spindle speed are averaged as the expected critical axial depth of cut a_pi0. Thus, the prediction accuracy under arbitrary period discrete value can be evaluated for the MS-PCM, 1st SDM and 2nd FDM, as shown in Fig. 7. Obviously, the larger the m value, the smaller their SSE and AMRE. But the SSE and AMRE of the MS-PCM are significantly smaller than the 1st SDM and 2nd FDM at arbitrary m value. It can be concluded from Fig. 7b that their AMRE is less than 1% when m > 60. In the actual stability analysis, the AMRE is taken as a criterion to reasonably select the period discrete number m.

Fig. 7

Comparisons of SSE and AMRE. a SSE; b AMRE

Figure 8 illustrates the calculation times with the different discrete numbers m for 1st SDM, 2nd FDM and MS-PCM. Obviously, with the increase of discrete number m, the computational times of 1st SDM and 2nd FDM are exponential increase approximately whereas the computational time of MS-PCM is linear increase nearly. The main reasons for the different computational efficiency include the following two aspects:

Fig. 8

Comparisons of simulation time

On the one hand, every element in the state transition matrix of 1st SDM relies on the spindle speed and the depth of cut whereas that of the 2nd FDM and the MS-PCM only depend on the spindle speed. If r_a and r_s are respectively the discrete numbers of the spindle speed and the depth of cut, the 1st SDM will calculate r_a × r_s × m elements whereas the 2nd FDM and the MS-PCM only need to calculate r_s elements.

On the other hand, the number of state transition matrices of 2nd FDM is related to the discrete number m whereas that of the MS-PCM has nothing to do with the discrete number m. Therefore, the 1st SDM and 2nd FDM will calculate r_a × r_s × m matrix whereas the MS-PCM only needs to calculate r_a × r_s state transition matrices.

4.2 Milling System with Two-DOF

As shown in Fig. 1, if milling dynamic mode is considered to be two-DOFs, the corresponding DDE [12,13,14,15,16] can be expressed as

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {m_{t} } & 0 \\ 0 & {m_{t} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x}(t)} \\ {\ddot{y}(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {2m_{t} \zeta \omega_{n} } & 0 \\ 0 & {2m_{t} \zeta \omega_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}(t)} \\ {\dot{y}(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {m_{t} \omega_{n}^{2} } & 0 \\ 0 & {m_{t} \omega_{n}^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right] \\ & \quad = a_{p} \left[ {\begin{array}{*{20}c} { - h_{xx} (t)} & { - h_{xy} (t)} \\ { - h_{yx} (t)} & { - h_{yy} (t)} \\ \end{array} } \right]\left\{ {\left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {x(t - \tau )} \\ {y(t - \tau )} \\ \end{array} } \right]} \right\} \\ \end{aligned}$$

(32)

Let ${\mathbf{M}} = \left[ {\begin{array}{*{20}l} {m_{t} } \hfill & 0 \hfill \\ 0 \hfill & {m_{t} } \hfill \\ \end{array} } \right]$, ${\mathbf{C}} = \left[ {\begin{array}{*{20}l} {2m_{t} \zeta \omega_{n} } \hfill & 0 \hfill \\ 0 \hfill & {2m_{t} \zeta \omega_{n} } \hfill \\ \end{array} } \right]$, ${\mathbf{q}}(t) = \left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right]$, ${\mathbf{p}}(t) = {\mathbf{M\dot{q}}}(t) + {\mathbf{Cq}}(t)/2$, and ${\mathbf{V}}(t) = [{\mathbf{q}}(t) \, {\mathbf{p}}(t)]^{{\text{T}}}$, Eq. (32) can be further described as

$${\dot{\mathbf{V}}}(t) = {\mathbf{LV}}(t) + {{\varvec{\Theta}}}(t)[{\mathbf{V}}(t) - {\mathbf{V}}(t - \tau )]$$

(33)

where

$${\mathbf{L}} = \left[ {\begin{array}{*{20}l} { - \zeta \omega_{n} } \hfill & 0 \hfill & {{1 \mathord{\left/ {\vphantom {1 {m_{t} }}} \right. \kern-0pt} {m_{t} }}} \hfill & 0 \hfill \\ 0 \hfill & { - \zeta \omega_{n} } \hfill & 0 \hfill & {{1 \mathord{\left/ {\vphantom {1 {m_{t} }}} \right. \kern-0pt} {m_{t} }}} \hfill \\ {\left( {\zeta^{2} - 1} \right)\omega_{n}^{2} m_{t} } \hfill & 0 \hfill & { - \zeta \omega_{n} } \hfill & 0 \hfill \\ 0 \hfill & {\left( {\zeta^{2} - 1} \right)\omega_{n}^{2} m_{t} } \hfill & 0 \hfill & { - \zeta \omega_{n} } \hfill \\ \end{array} } \right]$$

(34)

$${{\varvec{\Theta}}}(t) = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - a_{p} h_{xx} (t)} \hfill & { - a_{p} h_{xy} (t)} \hfill & 0 \hfill & 0 \hfill \\ { - a_{p} h_{yx} (t)} \hfill & { - a_{p} h_{yy} (t)} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

(35)

in which the meaning of each parameter is the same as Sect. 4.1.

Because the MS-PCM has faster computing efficiency and higher computing precision, the SLD curve calculated by the MS-PCM at m = 200 can be completely thought to be a theoretical SLD. Here, three special cutting conditions are selected to analyze the stability of down milling. They are the minimal radial immersion ratio of a/D = 0.05, the maximum radial immersion ratio of a/D = 1 and the half-tooth radial immersion ratio of a/D = 0.5, respectively.

When the m is 40, the SLDs of the two-DOFs milling system can be obtained under the condition of 200 intervals of spindle speed Ω and 100 intervals of axial depth of cut a, as shown in Table 3. When a/D = 0.05 and a/D = 0.5, the SLDs obtained by the MS-PCM almost completely coincided with the theoretical SLD. However, there are still subtle differences among these two SLDs obtained by the 1st SDM and 2nd FDM and the theoretical SLD. But when a/D = 1, three SLD curves are coincident with the theoretical curve. Therefore, the MS-PCM has an advantage in computational accuracy over the 1st SDM and 2nd FDM.

Table 3 SLDs of two-DOF milling system

5 Simulation and Experimental Verification

It is known from Sect. 4.1 that the SLD curves obtained by the three methods are basically the same at m = 30. However, there are still significant differences at the peaks of SLD curves. The actual prediction effect of MS-PCM at the peaks can be validated according to the cutting force and vibration displacement. The specific details of the simulation on cutting force and vibration displacement can be found in Ref. [5]. Here, one peak in Fig. 5e is taken as an example in which the spindle speed ranges from 22,000 to 24,000 rpm whereas the axial depth of cut is 3.3–4.1 mm. Thus, near the specified peak, 29 groups of parameter combinations of the spindle speed with the axial depth of cut can be selected to analyze their stability, as shown in Fig. 9.

Fig. 9

Prediction accuracy verification of local SLD boundaries, a/D = 1 and m = 30

The simulation method can be used to obtain the corresponding cutting force and vibration displacement of these 29 groups of parameter combinations. According to the time-domain waveform, it can be judged whether the cutting process is stable under the specific parameter combination. “*” means the simulation result is unstable, and “◊” is stable. From the simulation results of 29 groups of parameter combinations, it can be seen that MS-PCM can more accurately predict the stability boundary than 1st SDM and 2nd FDM. Figure 10 shows the simulation results of the four groups of typical parameters corresponding from A to D in Fig. 9. It is worth noting that the red symbol “○” is the sampling of vibration displacement when the milling tool rotates one circle. Obviously in stable cutting conditions, whether the waveform and peak value of cutting force or those of vibration displacement cannot almost change. Moreover, the periodic sampling value of vibration displacement is basically on the same horizontal line. Under the condition of unstable cutting, the waveform and peak value of cutting force have very obvious irregular changes as well as those of vibration displacement. In addition, the periodic sampling value of vibration displacement is not in one horizontal line, but in one irregular curve.

Fig. 10

Signal simulation of vibration and force. a and b point A; c and d point B; e and f point C; g and h point D

A set of milling experiments are adopted to validate the actual prediction results of the proposed method. All of the experiments are done on a three-axis CNC machine tool XKA715, as shown in Fig. 11. The workpiece material is aluminum alloy 7075-T7451. The milling tool is a three-tooth flat end mill with a diameter of D = 12 mm. The radial depth of cut is 0.24 mm so the radial immersion ratio is a/D = 0.2. The cutting force coefficients are K_t = 13.85 × 108 N/m² and K_r = 11.65 × 108 N/m², respectively. The modal parameters of the tool are listed in Table 4.

Fig. 11

Experimental setup

Table 4 Modal parameters of tool

The SLD calculated by MS-PCM (m = 100) is shown in Fig. 12a. 9 groups of parameter combinations are selected near the SLD curve for milling experiments. The cutting force signal and the surface morphology of the workpiece machined surface can be used to comprehensively judge the stability of the milling process. The stability results of 9 groups of parameter combinations are shown in Table 5 and Fig. 12a. “*” represents being unstable whereas “◊” stable. Figure 12b gives the time-domain diagram and frequency spectrum diagram of the measured milling forces corresponding to A and B, as well as the surface morphology of the machined workpiece. It can show the milling process is stable at B with the spindle speed of 5750 rpm and the axial depth of cut of 0.75 mm. In this case, the frequency domain signal of milling force only contains the integral multiple of tooth passing frequency whose expression is TF = ΩN/60. But if the parameter combination of A (5700 rpm, 1.0 mm) is selected to machine a workpiece, the frequency domain signal of milling force contains other so-called non-tooth passing frequencies in addition to the integral multiple of tooth passing frequency. In fact, these non-tooth passing frequencies belong to the chatter frequencies. Therefore, the milling process of A is unstable. As has further been analyzed above, the proposed MS-PCM is accurate and effective to predict milling stability.

Fig. 12

Experimental verification of the stability prediction boundary obtained by applying the proposed method. a Stability lobe diagram and selection of cutting parameters; b Cutting force in time and frequency domains and workpiece surface topography after processing

Table 5 Cutting parameters and stability

6 Conclusion

A linear multi-step predictor–corrector method is adopted for milling stability prediction in this paper. Based on the DDE of the dynamic milling process, the Milne formula and the Simpson formula as the predictor- and the corrector-term are used to constructing the state transition matrix. According to the Floquet theory, the stability lobe can be obtained.

The analysis of the error convergence rate and computational efficiency is done to validate the MS-PCM by using a one-DOF milling model. The results show that whether the computational accuracy or the computational time, the MS-PCM has advantages. The bigger the discrete number m is, the more obvious the advantage of MS-PCM is in computational efficiency.

The simulation results on the cutting force and vibration displacement of 29 groups of parameter combinations show that the proposed method has higher prediction accuracy. Again, 9 groups of parameter combinations are further determined to carry out the milling experiments. Whether the frequency domain signal of milling force or the surface morphology of the machined workpiece can demonstrate the proposed method is effective and accurate in the actual prediction of the milling stability.

Appendices

Appendix 1: Integral Equation

Integral equations are equations involving integral operations on unknown functions, as opposed to differential equations. Many mathematical physics problems need to be solved by integral equations or differential equations.

The most basic form of an integral equation is Fredholm integral equation of the first kind:

$$f(x) = \int_{a}^{b} {K(x,t)} \phi (t)dt,$$

where, f and K are known, K is also called the kernel function, and $\phi$ is the unknown function to be sought. The upper and lower limits of integration a, b are constants.

If the unknown function appears both inside and outside the integral sign, the equation is called a Fredholm integral equation of the second kind:

$$\phi (x) = f(x) + \lambda \int_{a}^{b} {K(x,t)} \phi (t)dt,$$

as an unknown factor, λ plays a role similar to the eigenvalue in linear algebra.

If the upper or lower bound of the integration is a variable, the equation is called the Volterra integral equation. The Volterra integral equations of the first and second kind have the following forms:

$$f(x) = \int_{a}^{x} {K(x,t)} \phi (t)dt,$$

$$\phi (x) = f(x) + \lambda \int_{a}^{x} {K(x,t)} \phi (t)dt,$$

All the above equations are called homogeneous if f is always 0, otherwise, they are called inhomogeneous.

Appendix 2: Linear Multi-step Methods

• 1. Fourth-order Milne formula:

  $$y_{n + 4} = \frac{4}{3}h\left[ {2f_{n + 3} - f_{n + 2} + 2f_{n + 1} } \right],$$

  where $y^{\prime} = f(x,y)$, its local truncation error is:

  $$R_{n + 4} = \frac{14}{{45}}h^{5} y^{(5)} (x_{n} ) + O(h^{6} ).$$

• 2. Fourth-order Simpson formula:

  $$y_{n + 2} = \frac{h}{3}\left[ {f_{n + 2} + 4f_{n + 1} + f_{n} } \right],$$

  where $y^{\prime} = f(x,y)$, its local truncation error is:

  $$R_{n + 4} = \frac{1}{90}h^{5} y^{(5)} (x_{n} ) + O(h^{6} ).$$

Appendix 3: Partial Formula Expression

$$\begin{aligned} & {\mathbf{G}}_{i + 1} = {8 \mathord{\left/ {\vphantom {8 9}} \right. \kern-0pt} 9}h^{2} e^{{3h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 1} {{\varvec{\Theta}}}_{i + 4} ;\;{\mathbf{G}}_{i + 2}^{{}} = \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}{\mathbf{I}} - {4 \mathord{\left/ {\vphantom {4 9}} \right. \kern-0pt} 9}h{{\varvec{\Theta}}}_{i + 4} } \right)he^{{2h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 2} ; \\ & {\mathbf{G}}_{i + 3} = \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}{\mathbf{I}} + {8 \mathord{\left/ {\vphantom {8 9}} \right. \kern-0pt} 9}h{{\varvec{\Theta}}}_{i + 4} } \right)he^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{i + 3} . \\ \end{aligned}$$

$$\begin{aligned} & {\mathbf{F}}_{i + 1 - \tau } = {\mathbf{G}}_{i + 1}^{{}} ;\;{\mathbf{F}}_{i + 2 - \tau } = {\mathbf{G}}_{i + 2}^{{}} ;\;{\mathbf{F}}_{i + 3 - \tau } = {\mathbf{G}}_{i + 3}^{{}} ;\;{\mathbf{F}}_{i + 4 - \tau }^{{}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}h{{\varvec{\Theta}}}_{i + 4} ;\;{\mathbf{F}}_{i} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}h{{\varvec{\Theta}}}_{i + 4} e^{{4h{\mathbf{L}}}} ; \\ & {\mathbf{F}}_{i + 1}^{{}} = {\mathbf{G}}_{i + 1}^{{}} ;\;{\mathbf{F}}_{i + 2}^{{}} = e^{{2h{\mathbf{L}}}} { + }{\mathbf{G}}_{i + 2}^{{}} ;\;{\mathbf{F}}_{i + 3}^{{}} = {\mathbf{G}}_{i + 3}^{{}} ;\;{\mathbf{F}}_{i + 4}^{{}} = - {\mathbf{I}}. \\ \end{aligned}$$

$$\begin{aligned} & {\mathbf{P}}_{2,1} = - \left( {e^{{h{\mathbf{L}}}} + {1 \mathord{\left/ {\vphantom {1 {2h}}} \right. \kern-0pt} {2h}}e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{1}} } \right);\;{\mathbf{P}}_{2,2} = \left( {{\mathbf{I}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}h{{\varvec{\Theta}}}_{{2}} } \right);\;{\mathbf{P}}_{2,1 - \tau } = - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{1}} ;\;{\mathbf{P}}_{2,2 - \tau } = - {1 \mathord{\left/ {\vphantom {1 {2h}}} \right. \kern-0pt} {2h}}{{\varvec{\Theta}}}_{{2}} ; \\ & {\mathbf{P}}_{3,1}^{{}} = - \left( {e^{{2h{\mathbf{L}}}} + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}he^{{{2}h{\mathbf{L}}}} {{\varvec{\Theta}}}_{1} } \right);\;{\mathbf{P}}_{3,2}^{{}} = - {{4} \mathord{\left/ {\vphantom {{4} 3}} \right. \kern-0pt} 3}he^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{2} ;\;{\mathbf{P}}_{3,3}^{{}} = \left( {{\mathbf{I}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}{{\varvec{\Theta}}}_{3} } \right);\;{\mathbf{P}}_{3,1 - \tau }^{{}} = - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}he^{{{2}h{\mathbf{L}}}} {{\varvec{\Theta}}}_{1} ; \\ & {\mathbf{P}}_{3,2 - \tau }^{{}} = - {{4} \mathord{\left/ {\vphantom {{4} {3h}}} \right. \kern-0pt} {3h}}e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{2} ;\;{\mathbf{P}}_{3,3 - \tau }^{{}} = - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}h{{\varvec{\Theta}}}_{3} . \\ \end{aligned}$$

$$\begin{aligned} & {\mathbf{P}}_{4,1}^{{}} = - \left( {e^{{{3}h{\mathbf{L}}}} + {{3} \mathord{\left/ {\vphantom {{3} 8}} \right. \kern-0pt} 8}he^{{3h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{1}} } \right);\;{\mathbf{P}}_{4,2}^{{}} = - {{9} \mathord{\left/ {\vphantom {{9} 8}} \right. \kern-0pt} 8}he^{{{2}h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{2}} ;\;{\mathbf{P}}_{4,3}^{{}} = - {{9} \mathord{\left/ {\vphantom {{9} {8h}}} \right. \kern-0pt} {8h}}e^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{3}} ; \\ & {\mathbf{P}}_{4,4}^{{}} = - \left( {{\mathbf{I}} + {{3} \mathord{\left/ {\vphantom {{3} 8}} \right. \kern-0pt} 8}h{{\varvec{\Theta}}}_{{4}} } \right);\;{\mathbf{P}}_{4,1 - \tau }^{{}} = - {3 \mathord{\left/ {\vphantom {3 8}} \right. \kern-0pt} 8}he^{{3h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{1}} ;\;{\mathbf{P}}_{4,2 - \tau }^{{}} = - {{9} \mathord{\left/ {\vphantom {{9} 8}} \right. \kern-0pt} 8}he^{{{2}h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{2}} ; \\ & {\mathbf{P}}_{4,3 - \tau }^{{}} = - {{9} \mathord{\left/ {\vphantom {{9} 8}} \right. \kern-0pt} 8}he^{{h{\mathbf{L}}}} {{\varvec{\Theta}}}_{{3}} ;\;{\mathbf{P}}_{4,4 - \tau }^{{}} = - {{3} \mathord{\left/ {\vphantom {{3} 8}} \right. \kern-0pt} 8}h{{\varvec{\Theta}}}_{{4}} . \\ \end{aligned}$$