1 Introduction

In milling process, chatter is a bad cutting condition that seriously reduces the surface quality of the workpiece and restricts the production efficiency. Although there is regenerative effect, vibration mode coupling effect, hysteresis effect, and negative friction effect, the dynamic change of cutting thickness caused by regenerative effect is considered to be one of the most important factors causing chatter [1]. In recent decades, extensive and profound theoretical research and experimental verification have been carried out on the problem of regenerative chatter [1,2,3,4]. In light of the research works of Tobias and Tlusty on the mechanism of milling chatter, Altintas and Weck established the corresponding mathematical model [1]. In fact, to achieve the problem on the regenerative effect cutting chatter is to establish the dynamic model which is a time-delay differential equation (DDE) with periodic coefficients firstly and, secondly, its solution method which can solve the DDE to obtain the stability lobe diagram (SLD) [1, 5, 6]. Up to now, the research methods on SLD can mainly be categorized into direct time-domain solution method, semi-analytical frequency-domain solution method, and semi-analytical time-domain solution method.

For the direct time-domain solution method, Wiercigroch and Budak [6] found that the amplitude of the milling force would increase rapidly when the machining parameters were selected at the boundary of the milling stability region. The difference between the maximum and the minimum force amplitude was used as the stability criterion to obtain the peak-to-peak (PTP) contour map of milling force. Li and Shin [7] proposed a comprehensive time-domain simulation model of the milling process, and the PTP criterion is used for the milling stability of thin-walled parts with a large axial depth of cut. Minis and Yanushevsky [8] used a set of differential-difference equations with time-varying periodic coefficients to describe the dynamic behavior of the milling process. And the stability of the system could be checked by Fourier analysis and linear periodic system parameter transfer functions. Campomanes and Altintas [9] proposed an improved milling time-domain model, in which the ratio of dynamic cutting thickness to nominal static cutting thickness was used as a stability criterion. It can not only be used to predict cutting force, surface finish, and chatter stability but also accurately explain difficult modeled nonlinear effects. Davies et al. [10, 11] established a new theoretical framework for predicting the stability of highly interrupted cutting. It modeled the interrupted cutting as a kicked harmonic oscillator with time-delay to validly predict the additional unstable regions at the depth of cut. Obviously, the judgment of the system stability is actually based on the cutting thickness or cutting force changes in the time domain during the cutting process in the direct time-domain solution method. It mainly takes the milling force model as the research object. When the milling force model considers the nonlinear effect factors in the milling process, such as tool runout, eccentricity, and so on, the direct time-domain solution method can achieve high precision. However, because these judgment criteria do not define the stability limit value, it is difficult to give an accurate conclusion of the stability under arbitrary milling parameters. Moreover, either a large calculation amount or a low calculation efficiency restricts the wide use of the direct time-domain solution method.

For semi-analytical methods, based on the work of Minis and Yanushevsky [8], Altintas and Budak [12] expanded the periodically changing milling force coefficient matrix onto the frequency domain to only retain the zeroth-order term by using the Fourier transform method. And the critical stable region could be obtained by solving the eigenvalue of the differential equation. He was the first to establish a zero-order approximation method (ZOA) for solving the milling stability region in the frequency domain. ZOA is widely used due to its fast calculation speed and high accuracy. Nevertheless, ZOA ignores the high-order terms of the Fourier series so that it cannot predict the additional stable region that appears under the small radial depth of cut. In order to solve this shortcoming of ZOA, Merdol and Altintas [13] established again a multi-frequency method (MF) to solve the milling stability domain in the frequency domain. However, since the MF method needs to iteratively search the chatter frequency in the calculation process, it is of low calculation efficiency. Subsequently, Altintas and his research team extended the frequency-domain solution method to stability judgment of various complex machining conditions, such as the ball nose milling [14], variable pitch milling [15], 3D milling with axial vibration [16], variable helix angle milling [17], and plunge milling operation [18]. Based on the works of Davies et al. [10, 11], Bayly et al. [19] proposed a temporal finite element analysis (TFEA). The TFEA utilizes the weighted residual method to obtain the state transition matrix between two adjacent cutting periods of the milling system by discretizing the cut-in time. And then, the Floquet theory is relied on to judge the milling stability according to the state transition matrix. One weakness of this method is low computational efficiency, and another is not fully applicable to the working conditions of large radial depth of cut.

Insperger and Stepan [20, 21] created a rigorous semi-analytical method for computing the stability domain of milling process which was the semi-discretization method (SDM). In the SDM, the tooth passing period is uniformly discretized into finite time intervals. The time-delay term and periodic term of the DDE are averaged in each time interval, and the DDE in the discrete time interval is transformed into an ordinary differential equation (ODE). Thus, the state transfer matrix of the milling system in a single cutting period is further constructed to determine the stability of the system based on the Floquet theory. This SDM can well calculate the stability region under different cutting conditions. But its calculation accuracy and calculation efficiency depend heavily on the periodic discrete number. The larger the discrete number is, the higher the calculation accuracy is whereas the lower the calculation efficiency is. Moreover, the computational efficiency of the SDM is also subject to the mesh density of the “spindle speed-depth of cut” plane. Subsequently, Insperger et al. [22] proposed again a higher-order semi-discrete method with higher algebraic precision. It is worth noting that the higher-order approximation for each discrete time interval can improve the calculation accuracy, but also reduce the computational efficiency simultaneously. Ding et al. [23] used the direct integration formula to establish a semi-analytical method called the full-discretization method (FDM). Likewise, the tooth passing period is firstly discretized into a finite number of uniform time intervals. Then the time-delay term, state term, and periodic term of the DDE were linearly interpolated according to two end-point values of each time interval. Similar to the SDM, the FDM also converted the DDE in the discrete time interval into an ODE. Thus, the state transfer matrix of the milling system could be constructed in a tooth passing period such that the Floquet theory is used to determine the stability. The FDM can greatly improve the calculation efficiency compared with the SDM without losing calculation accuracy. This is because the exponential matrix, which has a great influence on the calculation efficiency, does not depend on the depth of cut in the “spindle speed-depth of cut” plane but the spindle speed. Again, Ding et al. [24] also improved the FDM as the second-order FDM by applying the second-order Lagrange interpolation to the state term. The 2nd-FDM can reduce the truncation error of the algorithm to improve the calculation accuracy. But its calculation efficiency will also decrease with the increase of the interpolation order number. Wan et al. [25] considered the effects of the runout and the pitch angles on the milling stability. And a unified method was suggested for predicting the stability lobes of milling process with multiple delays. Based on the FDM of Ding et al. [23, 24], the third-order FDM [26, 27] and the other enhanced FDM [28,29,30,31] have been successively proposed by performing higher-order interpolation on the state term. Tang et al. [32] proposed and verified an effective stability prediction model with consideration of multiple modes and the cross-frequency response functions in the time domain. Zhou et al. [33] took into account the impact of helix angle and multi-mode on the milling stability. The fourth-order FDM was adopted to establish the stability analysis model. Zhang et al. [34] proposed a stability analysis method for the high speed milling system with two degrees of freedom (DOF) based on the finite difference method. Li et al. [35] proposed a complete discrete scheme (CDS) based on Euler formula by adopting the same homogenization treatment as the SDM on the periodic coefficient term and linear interpolation approximation as the FDM on the delay and state terms. Compared with SDM and FDM, CDS has higher computational efficiency. But the larger accumulation truncation error can also cause a relatively large computational error. Ding et al. [36] operated numerically integration on the integral term in discrete time intervals. And the Floquet transition matrix of the system was constructed in a tooth passing period to explore a numerical integration method (NIM). Niu et al. [37] calculated further the state term with the fourth-order Runge-Kutta formula to propose the CRKM and GRKM (i.e., Classical Runge-Kutta Method, and Generalized Runge-Kutta Method) which have high convergence speed and computational efficiency. Olvera et al. [38] proposed an enhanced multistage homotopy perturbation method (EMHPM). In combination with the simulated annealing algorithm, the EMHPM was used to deduce a three-dimensional SLD calculation method considering the material removal rate. Zhang et al. [39] adopted the Simpson numerical integration formula to propose a concise SLD prediction method by turning the solution process of the milling process into the initial value problem of ordinary differential equations. Recently, Qin et al. [40] used a second-order Lagrange interpolation polynomial for the approximation of the state term, delay term, and time period parameter matrix to be the holistic-discretization method (HDM). Dai et al. [41] used the Taylor formula to expand the inhomogeneous terms to be the exponential matrix which can be solved by the 2nd-order algorithm. Thus, the complete discretization of the iterative formula was successfully realized to establish a precise integration method (PIM). Dong and Qiu [42] proposed a numerical integration method based on the Hermite method. Lou et al. [43] proposed and verified a new numerical integration method combining Lagrange interpolation and Cotes integration. In addition, Wu et al. [44] proposed a cubic Hermite-Newton approximation method to predict the milling stability boundary.

As above stated, because the semi-analytical time-domain method is of wide adaptability and better calculation accuracy, it has now become the focus of current research. Figure 1 shows a flow chart on the construction of SLD by using the semi-analytical time-domain method. By discretizing the tooth passing period, an equivalent discrete system is constructed with various numerical calculation methods to obtain the state transition matrix of the DDE. The next is to judge the stability according to the relationship between the spectral radius of the state transition matrix and one. The focus of these methods is on the following two contradictory concerns. One is how to obtain a faster discrete error convergence speed under less period discretization number when the numerical calculation method is utilized to solve the state transition matrix ​​(that is, how to obtain better calculation accuracy). Another is how to improve the calculation efficiency as high as possible when the period discretization number is increased. Up to now, the judgment methods on the milling stability have not better dealt with the two problems on the computational performance. In numerical analysis theory, the numerical solutions of ODE are mainly categorized into the single-step method, the multi-step method, and the explicit method, the implicit method. Generally speaking, the calculation of the explicit formula on the predicted value in combination with that of the implicit formula on the correction value can always achieve better numerical stability for both low-order and high-order methods [45]. The main methods for the ODE are the direct replacement of differential quotient by the differential quotient, numerical integration method, and Taylor expansion method. Among them, the Taylor expansion method is more flexible and general. It can also realize the estimation of the truncation error as well as the construction of the calculation formula. Therefore, a series of new linear multi-step predictor-corrector methods (PCM) are proposed to quickly calculate accurately the milling stability region. The Taylor expansion method is adopted to obtain the linear multi-step methods including the fourth-order Adams-Bashforth-Moulton explicit-implicit, Simpson implicit, and Hamming implicit formula. And then, the positions corresponding to the two endpoints of every discretization interval of the tooth passing period are approximated in sequence by employing the fourth-order Adams-Bashforth explicit formula and the fourth-order Adams-Moulton (or Simpson, Hamming) implicit formula. The state transition expression is finally concluded for the DDE so that its state transition matrix can be relied on to judge the stability of the milling system.

Fig. 1
figure 1

The flow chart of obtaining SLD with semi-analytical time-domain method

Full size image

2 Dynamics model

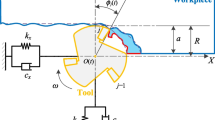
If the vibration of the tool system is taken along the feed direction x into account as well as that along the thickness direction y, the dynamic milling process can be represented by the two-DOF milling dynamics model shown in Fig. 2. The dynamic milling process considering the regeneration effect can be described by the following second-order DDE [2, 3, 46]:

$${\mathbf{M\ddot{q}}}(t) + {\mathbf{C\dot{q}}}(t) + {\mathbf{Kq}}(t)\; = a_{p} {\mathbf{K}}(t)[{\mathbf{q}}(t) - {\mathbf{q}}(t - T)]$$
(1)

where M, C, and K are the modal mass matrix, modal damping matrix, and modal stiffness matrix of the tool system, respectively. q(t) is the tool vibration displacement vector. T is the time-delay of the DDE. Usually, in milling process, T = 60/N/Ω represents the tooth passing period in which N is the number of teeth and Ω is the spindle speed. K(t) is the dynamic milling force coefficient matrix. It is the periodic function of T, so K(t) = K(t + T). K(t) can be expressed as

$${\mathbf{K}}(t) = \left[ {\begin{array}{*{20}c} { - h_{xx} (t)} & { - h_{xy} (t)} \\ { - h_{yx} (t)} & { - h_{yy} (t)} \\ \end{array} } \right]$$
(2)

with

$$\left\{ \begin{gathered} h_{xx} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t))\sin (\phi_{j} (t))\left[ {K_{t} \cos (\phi_{j} (t)) + K_{r} \sin (\phi_{j} (t))} \right] \hfill \\ h_{xy} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t)){\text{cos}}(\phi_{j} (t))\left[ {K_{t} \cos (\phi_{j} (t)) + K_{r} \sin (\phi_{j} (t))} \right] \hfill \\ h_{yx} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t))\sin (\phi_{j} (t))\left[ {K_{r} \cos (\phi_{j} (t)) - K_{t} \sin (\phi_{j} (t))} \right] \hfill \\ h_{yy} (t) = \sum\limits_{j = 1}^{N} g (\phi_{j} (t))\cos (\phi_{j} (t))\left[ {K_{r} \cos (\phi_{j} (t)) - K_{t} \sin (\phi_{j} (t))} \right] \hfill \\ \end{gathered} \right.$$
(3)

where Kt and Kr are, respectively, the linearized cutting force coefficient in the tangential direction and the normal direction which can be obtained from the calibration experiment of the milling force coefficient. \(\phi_{j} (t)\) is the current angular of the tooth j whose expression is as follows:

$$\phi_{j} (t) = \frac{2\pi \Omega }{{60}}t + \frac{2\pi (j - 1)}{N}$$
(4)
Fig. 2
figure 2

Two-DOF milling dynamics model

Full size image

\(g(\phi_{j} (t))\) is a window function to judge whether the tooth j is cutting. It is defined as

$$g(\phi_{j} (t)) = \left\{ \begin{array}{ll} 1, & \phi_{{{\text{st}}}} < \phi_{j} (t) < \phi_{{{\text{ex}}}} \\ 0,&{\mathrm{ others}} \end{array} \right.$$
(5)

where \(\phi_{{{\text{st}}}}\) and \(\phi_{{{\text{ex}}}}\) denote the start and exit angle of the jth tooth, respectively. It is worth noting that there are \(\phi_{{{\text{st}}}} = \arccos ({{2a} \mathord{\left/ {\vphantom {{2a} D}} \right. \kern-\nulldelimiterspace} D} - 1)\), \(\phi_{{{\text{ex}}}} = \pi\) and \(\phi_{{{\text{st}}}} = 0\), \(\phi_{{{\text{ex}}}} = \arccos (1 - 2{a \mathord{\left/ {\vphantom {a D}} \right. \kern-\nulldelimiterspace} D})\) in the down milling and the up milling, respectively. a is the radial depth of cut, and D is the diameter of the milling tool.

Two new matrices \({\mathbf{p}}(t) = {\mathbf{M\dot{q}}}(t) + {\mathbf{Cq}}(t)/2\) and \({\mathbf{U}}(t) = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}(t)} \\ {{\mathbf{p}}(t)} \\ \end{array} } \right]\) are introduced to rewritten Eq. (1). By substituting U(t) and p(t) into Eq. (1), the DDE can be transformed into the state space form, i.e.,

$${\dot{\mathbf{U}}}(t) = {\mathbf{AU}}(t) + a_{p} {\mathbf{B}}(t)[{\mathbf{U}}(t) - {\mathbf{U}}(t - T)]$$
(6)

where \({\mathbf{A}} = \left[ {\begin{array}{*{20}c} { - {\mathbf{M}}^{ - 1} {\mathbf{C}}/2} & {{\mathbf{M}}^{ - 1} } \\ {{\mathbf{CM}}^{ - 1} {\mathbf{C}}/4 - {\mathbf{K}}} & { - {\mathbf{CM}}^{ - 1} /2} \\ \end{array} } \right]\), \({\mathbf{B}}(t) = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{K}}(t)} & {\mathbf{0}} \\ \end{array} } \right]\).

It can be clearly seen from Eq. (6) that matrix A is a constant coefficient matrix only related to the modal parameters. It characterizes the time-invariant property of the milling system. B(t) is the periodic coefficient matrix related to the dynamic milling force. It meets the condition of B(t) = B(t + T).

3 Solution method

In order to successfully obtain q(t) in Eq. (1), it is crucial to effectively convert the continuous state equation of Eq. (6) into a discrete form. The end time of the previous tooth passing period is defined as the start time of the current tooth passing period, and it is denoted as t0. The time interval from t0 to the start time t1 of the cutter tooth is denoted as tf in which the cutter tooth is of free vibration. Again, a second time interval from t1 to the exit time tm+1 of the cutter tooth is implied as T − tf in which the cutter tooth is in the forced vibration state. Therefore, the tooth passing period T consists of the non-cutting time interval tf and the cutting time interval T − tf.

Now the forced vibration time interval T − tf is uniformly divided into m small time intervals. Obviously, the range of each interval is τ = (T − tf)/m, as shown in Fig. 3. Thus, the continuous time t in the tooth passing period T can be expressed as the following discrete time nodes:

$$t_{i} = t_{0} + t_{f} + (i - 1)\tau \; i = 1,2, \cdots ,m,m + 1$$
(7)
Fig. 3
figure 3

Schematic diagram of periodic dispersion

Full size image

Similar to the second kind of the Volterra integral equation, if the term of \(a_{p} {\mathbf{B}}(t)[{\mathbf{U}}(t) - {\mathbf{U}}(t - T)]\) in state equation Eq. (6) is considered as the inhomogeneous term of the homogeneous equation \({\dot{\mathbf{U}}}(t) = {\mathbf{AU}}(t)\), then Eq. (6) can be written as

$${\mathbf{U}}(t) = e^{{{\mathbf{A}}(t - t_{0} )}} {\mathbf{U}}(t_{0} ) + a_{p} \int_{{t_{0} }}^{t} {\left\{ {e^{{{\mathbf{A}}(t - s)}} {\mathbf{B}}(s)[{\mathbf{U}}(s) - {\mathbf{U}}(s - T)]} \right\}} ds$$
(8)

It is known from the Eq. (7) that, when t is on the closed interval from ti to ti+1, the following expression can be further obtained as

$${\mathbf{U}}(t) = e^{{{\mathbf{A}}(t - t_{i} )}} {\mathbf{U}}(t_{i} ) + a_{p} \int_{{t_{i} }}^{t} {{\mathbf{K}}[s,{\mathbf{U}}(s)]} ds$$
(9)

with \({\mathbf{K}}[s,{\mathbf{U}}(s)] = e^{{{\mathbf{A}}(t - s)}} {\mathbf{B}}(s)[{\mathbf{U}}(s) - {\mathbf{U}}(s - T)]\).

When the tool is not cutting, that is, t is within the time range tf, there is B(s) = 0. Thus, Eq. (8) degenerates into

$${\mathbf{U}}(t) = e^{{{\mathbf{A}}(t - t_{0} )}} {\mathbf{U}}(t_{0} )$$
(10)

However, when the tooth is in cutting, i.e., t belongs in the time range T − tf, Eq. (8) obviously needs to be solved by the more sophisticated methods. Accordingly, a series of semi-analytical solution methods are created by using a linear multi-step “predictor–corrector” formula.

3.1 ABM-PCM linear multi-step method

According to the linear multi-step method, a fourth-order Adams-Bashforth-Moulton “predictor-corrector” formula (i.e., ABM-PCM) is proposed as the following expression:

$$\begin{aligned} {\mathbf{U}}^{P} (t_{i + 4} ) & = e^{{{\mathbf{A}}\tau }} {\mathbf{U}}(t_{i + 3} ) + \frac{{a_{p} \tau }}{24}(55{\mathbf{K}}[t_{i + 3} ,{\mathbf{U}}(t_{i + 3} )] - 59{\mathbf{K}}[t_{i + 2} ,{\mathbf{U}}(t_{i + 2} )] \\ & + 37{\mathbf{K}}[t_{i + 1} ,{\mathbf{U}}(t_{i + 1} )] - 9{\mathbf{K}}[t_{i} ,{\mathbf{U}}(t_{i} )]) \\ \end{aligned}$$
(11)
$$\begin{aligned} {\mathbf{U}}(t_{i + 4} ) & = e^{{{\mathbf{A}}\tau }} {\mathbf{U}}(t_{i + 3} ){ + }\frac{{a_{p} \tau }}{24}(9{\mathbf{K}}[t_{i + 4} ,{\mathbf{U}}^{P} (t_{i + 4} )] + 19{\mathbf{K}}[t_{i + 3} ,{\mathbf{U}}(t_{i + 3} )] \\ & - 5{\mathbf{K}}[t_{i + 2} ,{\mathbf{U}}(t_{i + 2} )] + {\mathbf{K}}[t_{i} ,{\mathbf{U}}(t_{i} )]) \\ \end{aligned}$$
(12)

Equation (11) is the Adams-Bashforth formula which is a four-step fourth-order explicit formula. If the error produced by replacing the differential equation with the difference equation is defined as the local truncation error, the local truncation error of Eq. (11) is \(R_{AB} = {{251} \mathord{\left/ {\vphantom {{251} {720}}} \right. \kern-\nulldelimiterspace} {720}}\tau^{5} {\mathbf{U}}^{(5)} (t) + O(\tau^{6} )\). Therefore, Eq. (11) has the fourth-order algebraic precision. Equation (12) is a three-step fourth-order implicit Adams-Moulton formula. Because the local truncation error of Eq. (12) is \(R_{AM} = - {{19} \mathord{\left/ {\vphantom {{19} {720}}} \right. \kern-\nulldelimiterspace} {720}}\tau^{5} {\mathbf{U}}^{(5)} (t) + O(\tau^{6} )\), its algebraic precision is also fourth-order.

The next step is to iteratively solve Eq. (9) by, respectively, using Eq. (11) as a predictor and Eq. (12) as a corrector. In principle, Eq. (9) can be further expressed on the closed interval \([t_{i + 4} {,} t_{m + 1} ]\) as

$$\begin{aligned} {\mathbf{U}}_{i + 4}^{P} & = e^{{{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 3} + \frac{{a_{p} \tau }}{24}(55e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 3} ({\mathbf{U}}_{i + 3} - {\mathbf{U}}_{i + 3 - T} ) - 59e^{{2{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 2} ({\mathbf{U}}_{i + 2} - {\mathbf{U}}_{i + 2 - T} ) \\ & + 37e^{{3{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 1} ({\mathbf{U}}_{i + 1} - {\mathbf{U}}_{i + 1 - T} ) - 9e^{{4{\mathbf{A}}\tau }} {\mathbf{B}}_{i} ({\mathbf{U}}_{i} - {\mathbf{U}}_{i - T} )) \\ \end{aligned}$$
(13)
$$\begin{gathered} {\mathbf{U}}_{i + 4}^{{}} = e^{{{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 3} + \frac{{a_{p} \tau }}{24}(9{\mathbf{B}}_{i + 4} ({\mathbf{U}}_{i + 4}^{P} - {\mathbf{U}}_{i + 4 - T} ) + 19e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 3} ({\mathbf{U}}_{i + 3} - {\mathbf{U}}_{i + 3 - T} ) \\ - 5e^{{2{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 2} ({\mathbf{U}}_{i + 2} - {\mathbf{U}}_{i + 2 - T} ) + e^{{3{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 1} ({\mathbf{U}}_{i + 1} - {\mathbf{U}}_{i + 1 - T} )) \\ \end{gathered}$$
(14)

In order to simplify the representation of Eqs. (13) and (14), denote Ui, Ui−T, Bi, Bi−T to be U(ti), U(ti − T), B(ti), B(ti − T). Thus, the combination of Eq. (13) with Eq. (14) can be depended on to obtain the following “predictor-corrector” formula as

$$\begin{aligned} {\mathbf{U}}_{i + 4} & = e^{{{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 3} + \frac{\tau }{24}(9a_{p} e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} {\mathbf{U}}_{i + 3} - 9a_{p} {\mathbf{B}}_{i + 4} {\mathbf{U}}_{i + 4 - T} \\ & + {\mathbf{G}}_{i + 3} {\mathbf{B}}_{i + 3} ({\mathbf{U}}_{i + 3} - {\mathbf{U}}_{i + 3 - T} ) + {\mathbf{G}}_{i + 2} {\mathbf{B}}_{i + 2} ({\mathbf{U}}_{i + 2} - {\mathbf{U}}_{i + 2 - T} ) \\ & + {\mathbf{G}}_{i + 1} {\mathbf{B}}_{i + 1} ({\mathbf{U}}_{i + 1} - {\mathbf{U}}_{i + 1 - T} ) + {\mathbf{G}}_{i} {\mathbf{B}}_{i} ({\mathbf{U}}_{i} - {\mathbf{U}}_{i - T} )) \\ \end{aligned}$$
(15)

where \({\mathbf{G}}_{i} = - \frac{{27a_{p} \tau {\mathbf{B}}_{i + 4} }}{8}a_{p} e^{{4{\mathbf{A}}\tau }}\), \({\mathbf{G}}_{i + 1} = ({\mathbf{I}} + \frac{{111a_{p} \tau {\mathbf{B}}_{i + 4} }}{8})a_{p} e^{{3{\mathbf{A}}\tau }}\), \({\mathbf{G}}_{i + 2} = ( - 5{\mathbf{I}} - \frac{{177a_{p} \tau {\mathbf{B}}_{i + 4} }}{8})a_{p} e^{{2{\mathbf{A}}\tau }}\), \({\mathbf{G}}_{i + 3} = (19{\mathbf{I}}{ + }\frac{{165a_{p} \tau {\mathbf{B}}_{i + 4} }}{8})a_{p} e^{{{\mathbf{A}}\tau }}\), I is the unit matrix.

By separating into the delay term and the state term, Eq. (15) can further be rewritten as

$$\begin{aligned} {\mathbf{F}}_{i + 4 - T} {\mathbf{U}}_{i + 4 - T} & + {\mathbf{F}}_{i + 3 - T} {\mathbf{U}}_{i + 3 - T} + {\mathbf{F}}_{i + 2 - T} {\mathbf{U}}_{i + 2 - T} + {\mathbf{F}}_{i + 1 - T} {\mathbf{U}}_{i + 1 - T} + {\mathbf{F}}_{i - T} {\mathbf{U}}_{i - T} \\ & = {\mathbf{F}}_{i + 4} {\mathbf{U}}_{i + 4} + {\mathbf{F}}_{i + 3} {\mathbf{U}}_{i + 3} + {\mathbf{F}}_{i + 2} {\mathbf{U}}_{i + 2} + {\mathbf{F}}_{i + 1} {\mathbf{U}}_{i + 1} + {\mathbf{F}}_{i} {\mathbf{U}}_{i} \hfill \\ \end{aligned}$$
(16)

where \({\mathbf{F}}_{i} = \frac{\tau }{24}{\mathbf{G}}_{i} {\mathbf{B}}_{i}\), \({\mathbf{F}}_{i + 1} = \frac{\tau }{24}{\mathbf{G}}_{i + 1} {\mathbf{B}}_{i + 1}\), \({\mathbf{F}}_{i + 2} = \frac{\tau }{24}{\mathbf{G}}_{i + 2} {\mathbf{B}}_{i + 2}\), \({\mathbf{F}}_{i + 3} = e^{{{\mathbf{A}}\tau }} + \frac{{9a_{p} \tau }}{24}{\mathbf{B}}_{i + 4} e^{{{\mathbf{A}}\tau }} + \frac{\tau }{24}{\mathbf{G}}_{i + 3} {\mathbf{B}}_{i + 3}\), \({\mathbf{F}}_{i + 4} = - {\mathbf{I}}\), \({\mathbf{F}}_{i - T} = \frac{\tau }{24}{\mathbf{G}}_{i} {\mathbf{B}}_{i}\) , \({\mathbf{F}}_{i + 1 - T} = \frac{\tau }{24}{\mathbf{G}}_{i + 1} {\mathbf{B}}_{i + 1}\), \({\mathbf{F}}_{i + 2 - T} = \frac{\tau }{24}{\mathbf{G}}_{i + 2} {\mathbf{B}}_{i + 2}\) , \({\mathbf{F}}_{i + 3 - T} = \frac{\tau }{24}{\mathbf{G}}_{i + 3} {\mathbf{B}}_{i + 3}\), \({\mathbf{F}}_{i + 4 - T} = \frac{{9a_{p} \tau }}{24}{\mathbf{B}}_{i + 4}\).

It is worth noting that the ABM-PCM is a linear four-step method. Only there are not less than five discrete time notes, can it be applied. Therefore, the condition of m ≥ 4 can use the ABM-PCM, whereas the condition of m < 4 should apply other methods including Runge-Kutta method, trapezoidal formula, Simpson linear two-step method, Adams linear two-step method, Newton-Cotes numerical integration, and so forth. The detail discussion is carried out as follows.

First of all, at the time of t1 = t0 + tf, the relationship between the initial value U1 of the state item and Um+1−T can be easily obtained

$${\mathbf{U}}_{{1}} = {\mathbf{U}}(t + t_{f} ) = e^{{{\mathbf{A}}t_{f} }} {\mathbf{U}}_{{0}} = e^{{{\mathbf{A}}t_{f} }} {\mathbf{U}}_{m + 1 - T}$$
(17)

When m = 1, the value of U2 can be implicitly expressed by a Trapezoidal formula, that is

$${\mathbf{U}}_{{2}} = e^{{{\mathbf{A}}\tau }} {\mathbf{U}}_{{1}} + \frac{{a_{p} \tau }}{2}\left[ {e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{{1}} \left( {{\mathbf{U}}_{{1}} - {\mathbf{U}}_{{{1} - T}} } \right) + {\mathbf{B}}_{{2}} \left( {{\mathbf{U}}_{{2}} - {\mathbf{U}}_{{{2} - T}} } \right)} \right]$$
(18)

Similar to Eq. (16), Eq. (18) can be clarified as follows according to the delay term and state term:

$${\mathbf{L}}_{2 - T}^{2} {\mathbf{U}}_{{{2} - T}} \; + {\mathbf{L}}_{1 - T}^{2} {\mathbf{U}}_{{{1} - T}} \; = {\mathbf{L}}_{2}^{2} {\mathbf{U}}_{{2}} + {\mathbf{L}}_{1}^{2} {\mathbf{U}}_{{1}}$$
(19)

where \({\mathbf{L}}_{1}^{2} = - (e^{{{\mathbf{A}}\tau }} + \frac{{a_{p} \tau }}{2}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{{1}} )\), \({\mathbf{L}}_{2}^{2} = ({\mathbf{I}} - \frac{{a_{p} \tau }}{2}{\mathbf{B}}_{{2}} )\), \({\mathbf{L}}_{1 - T}^{2} = - \frac{{a_{p} \tau }}{2}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{{1}}\), \(\;{\mathbf{L}}_{2 - T}^{2} = - \frac{{a_{p} \tau }}{2}{\mathbf{B}}_{{2}}\).

When m = 2, since the Simpson method, which is a two-step fourth-order method, has the highest algebraic accuracy in the linear two-step method, the value of U3 is implicitly expressed using the Simpson method:

$${\mathbf{U}}_{{3}} = e^{{{2}{\mathbf{A}}\tau }} {\mathbf{U}}_{{1}} + \frac{{a_{p} \tau }}{{3}}\left[ {e^{{{2}{\mathbf{A}}\tau }} {\mathbf{B}}_{1} ({\mathbf{U}}_{1} - {\mathbf{U}}_{1 - T} )} \right.\left. { + {4}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{2} ({\mathbf{U}}_{2} - {\mathbf{U}}_{2 - T} ) + {\mathbf{B}}_{3} ({\mathbf{U}}_{3} - {\mathbf{U}}_{3 - T} )} \right]$$
(20)

Likewise, by separating the time-delay term from the state term, Eq. (20) can further be simplified as

$${\mathbf{L}}_{3 - T}^{3} {\mathbf{U}}_{3 - T} + {\mathbf{L}}_{2 - T}^{3} {\mathbf{U}}_{2 - T} + {\mathbf{L}}_{1 - T}^{3} {\mathbf{U}}_{1 - T} = {\mathbf{L}}_{3}^{3} {\mathbf{U}}_{3} + {\mathbf{L}}_{2}^{3} {\mathbf{U}}_{2} + {\mathbf{L}}_{1}^{3} {\mathbf{U}}_{1}$$
(21)

where \({\mathbf{L}}_{1}^{3} = - (e^{{{\mathbf{A}}2\tau }} + \frac{{a_{p} \tau }}{{3}}e^{{{2}{\mathbf{A}}\tau }} {\mathbf{B}}_{1} )\), \({\mathbf{L}}_{2}^{3} = - \frac{{{4}a_{p} \tau }}{{3}}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{2}\), \({\mathbf{L}}_{3}^{3} = ({\mathbf{I}} - \frac{{a_{p} \tau }}{{3}}{\mathbf{B}}_{3} )\) , \({\mathbf{L}}_{1 - T}^{3} = - \frac{{a_{p} \tau }}{{3}}e^{{{2}{\mathbf{A}}\tau }} {\mathbf{B}}_{1}\), \({\mathbf{L}}_{2 - T}^{3} = - \frac{{{4}a_{p} \tau }}{{3}}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{2}\), \({\mathbf{L}}_{3 - T}^{3} = - \frac{{a_{p} \tau }}{{3}}{\mathbf{B}}_{3}\).

When m = 3, a similar operation is carried out to obtain the following formula according to the Newton integral formula

$${\mathbf{L}}_{4 - T}^{4} {\mathbf{U}}_{{{4} - T}} + {\mathbf{L}}_{3 - T}^{4} {\mathbf{U}}_{{{3} - T}} + {\mathbf{L}}_{2 - T}^{4} {\mathbf{U}}_{{{2} - T}} + {\mathbf{L}}_{1 - T}^{4} {\mathbf{U}}_{{{1} - T}} = {\mathbf{L}}_{4}^{4} {\mathbf{U}}_{{4}} + {\mathbf{L}}_{3}^{4} {\mathbf{U}}_{{3}} + {\mathbf{L}}_{2}^{4} {\mathbf{U}}_{{2}} + {\mathbf{L}}_{1}^{4} {\mathbf{U}}_{{1}}$$
(22)

where \({\mathbf{L}}_{1}^{4} = - (e^{{{3}{\mathbf{A}}\tau }} + \frac{{{3}a_{p} \tau }}{{8}}e^{{3{\mathbf{A}}\tau }} {\mathbf{B}}_{{1}} )\), \({\mathbf{L}}_{2}^{4} = - \frac{{{9}a_{p} \tau }}{{8}}e^{{{2}{\mathbf{A}}\tau }} {\mathbf{B}}_{{2}}\), \({\mathbf{L}}_{3}^{4} = - \frac{{{9}a_{p} \tau }}{{8}}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{{3}}\),\({\mathbf{L}}_{4}^{4} = - ({\mathbf{I}} + \frac{{{3}a_{p} \tau }}{{8}}{\mathbf{B}}_{{4}} )\), \({\mathbf{L}}_{1 - T}^{4} = - \frac{{{3}a_{p} \tau }}{{8}}e^{{3{\mathbf{A}}\tau }} {\mathbf{B}}_{{1}}\), \({\mathbf{L}}_{2 - T}^{4} = - \frac{{{9}a_{p} \tau }}{{8}}e^{{{2}{\mathbf{A}}\tau }} {\mathbf{B}}_{{2}}\), \({\mathbf{L}}_{3 - T}^{4} = - \frac{{{9}a_{p} \tau }}{{8}}e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{{3}}\), \({\mathbf{L}}_{4 - T}^{4} = - \frac{{{3}a_{p} \tau }}{{8}}{\mathbf{B}}_{{4}}\).

By combining Eq. (22) with Eqs. (16), (17), (19) and (21), the discrete map of the delay term to the state term can be deduced as

$${{\varvec{\Gamma}}}\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1} } \\ {{\mathbf{U}}_{2} } \\ \vdots \\ {{\mathbf{U}}_{m} } \\ {{\mathbf{U}}_{m + 1} } \\ \end{array} } \right] = {{\varvec{\Lambda}}}\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1 - T} } \\ {{\mathbf{U}}_{2 - T} } \\ \vdots \\ {{\mathbf{U}}_{m - T} } \\ {{\mathbf{U}}_{m + 1 - T} } \\ \end{array} } \right]$$
(23)

with

$${{\varvec{\Gamma}}}{ = }\left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{2} } & {{\mathbf{L}}_{2}^{3} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{3} } & {{\mathbf{L}}_{2}^{3} } & {{\mathbf{L}}_{3}^{3} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{4} } & {{\mathbf{L}}_{2}^{4} } & {{\mathbf{L}}_{3}^{4} } & {{\mathbf{L}}_{4}^{4} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1} } & {{\mathbf{F}}_{2} } & {{\mathbf{F}}_{3} } & {{\mathbf{F}}_{4} } & {{\mathbf{F}}_{5} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4} } & {{\mathbf{F}}_{m - 3} } & {{\mathbf{F}}_{m - 2} } & {{\mathbf{F}}_{m - 1} } & {{\mathbf{F}}_{m} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3} } & {{\mathbf{F}}_{m - 2} } & {{\mathbf{F}}_{m - 1} } & {{\mathbf{F}}_{m} } & {{\mathbf{F}}_{m + 1} } \\ \end{array} } \right]$$
(24)
$${{\varvec{\Lambda}}}{ = }\left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {e^{{{\mathbf{A}}t_{f} }} } \\ {{\mathbf{L}}_{1 - T}^{2} } & {{\mathbf{L}}_{2 - T}^{3} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1 - T}^{3} } & {{\mathbf{L}}_{2 - T}^{3} } & {{\mathbf{L}}_{3 - T}^{3} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1 - T}^{4} } & {{\mathbf{L}}_{2 - T}^{4} } & {{\mathbf{L}}_{3 - T}^{4} } & {{\mathbf{L}}_{4 - T}^{4} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1 - T} } & {{\mathbf{F}}_{2 - T} } & {{\mathbf{F}}_{3 - T} } & {{\mathbf{F}}_{4 - T} } & {{\mathbf{F}}_{5 - T} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4 - T} } & {{\mathbf{F}}_{m - 3 - T} } & {{\mathbf{F}}_{m - 2 - T} } & {{\mathbf{F}}_{m - 1 - T} } & {{\mathbf{F}}_{m - T} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3 - T} } & {{\mathbf{F}}_{m - 2 - T} } & {{\mathbf{F}}_{m - 1 - T} } & {{\mathbf{F}}_{m - T} } & {{\mathbf{F}}_{m + 1 - T} } \\ \end{array} } \right]$$
(25)

Therefore, the state transition matrix in one milling period can be expressed as

$${{\varvec{\Psi}}} = {{\varvec{\Gamma}}}^{ - 1} {{\varvec{\Lambda}}}$$
(26)

It is known from the Floquet theory, the system stability can be judged according to the spectral radius \(\rho ({{\varvec{\Psi}}})\) of the state transition matrix Ψ. If \(\rho ({{\varvec{\Psi}}}) < 1\), the system is of stability. If \(\rho ({{\varvec{\Psi}}}) > 1\), the system is in an unstable state. But if \(\rho ({{\varvec{\Psi}}}) = 1\), the system is in the limit stability.

Consequently, if the spectral radio of the state transition matrix corresponding to every point on the “spindle speed-depth of cut” plane is calculated, obtain the limit stability boundary of the milling system can be obtained.

3.2 AS-PCM/AH-PCM linear multi-step method

If the Adams-Moulton formula expressed by Eq. (12) is replaced by the Simpson formula or Hamming formula in the linear multi-step methods, this solution method is called the Adams-Simpson predictor-corrector method (AS-PCM) or the Adams-Hamming predictor-corrector method (AH-PCM). The local truncation errors of the two-step Simpson formula is \(R_{S} = - {1 \mathord{\left/ {\vphantom {1 {90}}} \right. \kern-\nulldelimiterspace} {90}}\tau^{5} {\mathbf{U}}^{(5)} (t) + O(\tau^{6} )\), whereas that of the three-step Hamming formula is \(R_{H} = - {1 \mathord{\left/ {\vphantom {1 {40}}} \right. \kern-\nulldelimiterspace} {40}}\tau^{5} {\mathbf{U}}^{(5)} (t) + O(\tau^{6} )\). Both of them have fourth-order algebraic precision.

Thus, Eq. (12) can be rewritten as follows according to the two-step fourth-order Simpson formula:

$$\begin{aligned} {\mathbf{U}}(t_{i + 4} ) & = e^{{2{\mathbf{A}}\tau }} {\mathbf{U}}(t_{i + 2} ){ + }\frac{{a_{p} \tau }}{3}({\mathbf{K}}[t_{i + 4} ,{\mathbf{U}}^{P} (t_{i + 4} )] \\ & + 4{\mathbf{K}}[t_{i + 3} ,{\mathbf{U}}(t_{i + 3} )] + {\mathbf{K}}[t_{i + 2} ,{\mathbf{U}}(t_{i + 2} )]) \\ \end{aligned}$$
(27)

By analogy, if Eq. (11) is taken as the predictor whereas Eq. (27) is taken as the corrector, the following “predictor-corrector” formula can be obtained as

$$\begin{aligned} {\mathbf{U}}_{i + 4} & = e^{{2{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 2} { + (}\frac{1}{3}a_{p} \tau {\mathbf{B}}_{i + 4} e^{{{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 3} - \frac{1}{3}a_{p} \tau {\mathbf{B}}_{i + 4} {\mathbf{U}}_{i + 4 - T} \\ & + {\mathbf{G}}_{i,AS} ({\mathbf{U}}_{i} - {\mathbf{U}}_{i - T} ) + {\mathbf{G}}_{i + 1,AS} ({\mathbf{U}}_{i + 1} - {\mathbf{U}}_{i + 1 - T} ) \\ & + {\mathbf{G}}_{i + 2,AS} ({\mathbf{U}}_{i + 2} - {\mathbf{U}}_{i + 2 - T} ) + {\mathbf{G}}_{i + 3,AS} ({\mathbf{U}}_{i + 3} - {\mathbf{U}}_{i + 3 - T} ){)} \\ \end{aligned}$$
(28)

where \({\mathbf{G}}_{i,AS} = - \frac{1}{8}(a_{p} \tau )^{2} {\mathbf{B}}_{i + 4} e^{{4{\mathbf{A}}\tau }} {\mathbf{B}}_{i}\), \({\mathbf{G}}_{i + 1,AS} = \frac{37}{{72}}(a_{p} \tau )^{2} {\mathbf{B}}_{i + 4} e^{{3{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 1}\),\({\mathbf{G}}_{i + 2,AS} = \frac{1}{3}a_{p} \tau (e^{{2{\mathbf{A}}\tau }} - \frac{59}{{24}}a_{p} \tau {\mathbf{B}}_{i + 4} e^{{2{\mathbf{A}}\tau }} ){\mathbf{B}}_{i + 2}\), \({\mathbf{G}}_{i + 3,AS} = \frac{1}{3}a_{p} \tau (\frac{55}{{24}}a_{p} \tau {\mathbf{B}}_{i + 4} e^{{{\mathbf{A}}\tau }} + 4e^{{{\mathbf{A}}\tau }} ){\mathbf{B}}_{i + 3}\).

By separating the time-delay term from the state term, Eq. (28) can be clearly reorganized as

$$\begin{aligned} {\mathbf{F}}_{i + 4 - T,AS} {\mathbf{U}}_{i + 4 - T} & + {\mathbf{F}}_{i + 3 - T,AS} {\mathbf{U}}_{i + 3 - T} + {\mathbf{F}}_{i + 2 - T,AS} {\mathbf{U}}_{i + 2 - T} + {\mathbf{F}}_{i + 1 - T,AS} {\mathbf{U}}_{i + 1 - T} + {\mathbf{F}}_{i - T,AS} {\mathbf{U}}_{i - T} \\ & = {\mathbf{F}}_{i + 4,AS} {\mathbf{U}}_{i + 4} + {\mathbf{F}}_{i + 3,AS} {\mathbf{U}}_{i + 3} + {\mathbf{F}}_{i + 2,AS} {\mathbf{U}}_{i + 2} + {\mathbf{F}}_{i + 1,AS} {\mathbf{U}}_{i + 1} + {\mathbf{F}}_{i,AS} {\mathbf{U}}_{i} \end{aligned}$$
(29)

where \({\mathbf{F}}_{i - T,AS} = {\mathbf{G}}_{i,AS}\), \({\mathbf{F}}_{i + 1 - T,AS} = {\mathbf{G}}_{i + 1,AS}\), \({\mathbf{F}}_{i + 2 - T,AS} = {\mathbf{G}}_{i + 2,AS}\), \({\mathbf{F}}_{i + 3 - T,AS} = {\mathbf{G}}_{i + 3,AS}\), \({\mathbf{F}}_{i + 4 - T,AS} = \frac{1}{3}a_{p} \tau {\mathbf{B}}_{i + 4}\), \({\mathbf{F}}_{i,AS} = {\mathbf{G}}_{i,AS}\), \({\mathbf{F}}_{i + 1,AS} = {\mathbf{G}}_{i + 1,AS}\), \({\mathbf{F}}_{i + 2,AS} = e^{{2{\mathbf{A}}\tau }} { + }{\mathbf{G}}_{i + 2,AS}\), \({\mathbf{F}}_{i + 3,AS} = \frac{1}{3}a_{p} \tau {\mathbf{B}}_{i + 4} e^{{{\mathbf{A}}\tau }} + {\mathbf{G}}_{i + 3,AS}\), \({\mathbf{F}}_{i + 4,AS} = - {\mathbf{I}}\).

By unifying Eq. (29) with Eqs. (16), (17), (19) and (21), the matrix ΓAS and ΛAS can be constructed to judge the system stability.

$${{\varvec{\Gamma}}}_{AS} { = }\left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{2} } & {{\mathbf{L}}_{2}^{3} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{3} } & {{\mathbf{L}}_{2}^{3} } & {{\mathbf{L}}_{3}^{3} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{4} } & {{\mathbf{L}}_{2}^{4} } & {{\mathbf{L}}_{3}^{4} } & {{\mathbf{L}}_{4}^{4} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1,AS} } & {{\mathbf{F}}_{2,AS} } & {{\mathbf{F}}_{3,AS} } & {{\mathbf{F}}_{4,AS} } & {{\mathbf{F}}_{5,AS} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4,AS} } & {{\mathbf{F}}_{m - 3,AS} } & {{\mathbf{F}}_{m - 2,AS} } & {{\mathbf{F}}_{m - 1,AS} } & {{\mathbf{F}}_{m,AS} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3,AS} } & {{\mathbf{F}}_{m - 2,AS} } & {{\mathbf{F}}_{m - 1,AS} } & {{\mathbf{F}}_{m,AS} } & {{\mathbf{F}}_{m + 1,AS} } \\ \end{array} } \right]$$
(30)
$${{\varvec{\Lambda}}}_{AS} { = }\left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {e^{{{\mathbf{A}}t_{f} }} } \\ {{\mathbf{L}}_{1 - T}^{2} } & {{\mathbf{L}}_{2 - T}^{3} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1 - T}^{3} } & {{\mathbf{L}}_{2 - T}^{3} } & {{\mathbf{L}}_{3 - T}^{3} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1 - T}^{4} } & {{\mathbf{L}}_{2 - T}^{4} } & {{\mathbf{L}}_{3 - T}^{4} } & {{\mathbf{L}}_{4 - T}^{4} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1 - T,AS} } & {{\mathbf{F}}_{2 - T,AS} } & {{\mathbf{F}}_{3 - T,AS} } & {{\mathbf{F}}_{4 - T,AS} } & {{\mathbf{F}}_{5 - T,AS} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4 - T,AS} } & {{\mathbf{F}}_{m - 3 - T,AS} } & {{\mathbf{F}}_{m - 2 - T,AS} } & {{\mathbf{F}}_{m - 1 - T,AS} } & {{\mathbf{F}}_{m - T,AS} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3 - T,AS} } & {{\mathbf{F}}_{m - 2 - T,AS} } & {{\mathbf{F}}_{m - 1 - T,AS} } & {{\mathbf{F}}_{m - T,AS} } & {{\mathbf{F}}_{m + 1 - T,AS} } \\ \end{array} } \right]$$
(31)

Also, Eq. (12) can be rewritten into the following equation in light of the three-step fourth-order Hamming formula

$$\begin{aligned} {\mathbf{U}}(t_{i + 4} ) & = \frac{1}{8}(9e^{{{\mathbf{A}}\tau }} {\mathbf{U}}(t_{i + 3} ) - e^{{3{\mathbf{A}}\tau }} {\mathbf{U}}(t_{i + 1} )){ + }\frac{{3a_{p} \tau }}{8}({\mathbf{K}}[t_{i + 4} ,{\mathbf{U}}^{P} (t_{i + 4} )] \\ & + 2{\mathbf{K}}[t_{i + 3} ,{\mathbf{U}}(t_{i + 3} )] - {\mathbf{K}}[t_{i + 2} ,{\mathbf{U}}(t_{i + 2} )]) \\ \end{aligned}$$
(32)

If Eq. (11) is still used as the predictor but Eq. (32) is chosen as the corrector, the “predictor-corrector” formula of Adams-Hamming can be obtained as

$$\begin{aligned} {\mathbf{U}}_{i + 4} & = \frac{1}{8}(9e^{{{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 3} - e^{{3{\mathbf{A}}\tau }} {\mathbf{U}}_{i + 1} ){ + (}\frac{3}{8}a_{p} \tau e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} {\mathbf{U}}_{i + 3} - \frac{3}{8}a_{p} \tau {\mathbf{B}}_{i + 4} {\mathbf{U}}_{i + 4 - T} \\ & + {\mathbf{G}}_{i + 3,AH} ({\mathbf{U}}_{i + 3} - {\mathbf{U}}_{i + 3 - T} ) + {\mathbf{G}}_{i + 2,AH} ({\mathbf{U}}_{i + 2} - {\mathbf{U}}_{i + 2 - T} ) \\ & + {\mathbf{G}}_{i + 1,AH} ({\mathbf{U}}_{i + 1} - {\mathbf{U}}_{i + 1 - T} ) + {\mathbf{G}}_{i,AH} ({\mathbf{U}}_{i} - {\mathbf{U}}_{i - T} ){)} \end{aligned}$$
(33)

where \({\mathbf{G}}_{i,AH} = - \frac{27}{{192}}(a_{p} \tau )^{2} e^{{4{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} {\mathbf{B}}_{i}\), \({\mathbf{G}}_{i + 1,AH} = \frac{111}{{192}}(a_{p} \tau )^{2} e^{{3{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} {\mathbf{B}}_{i + 1}\),\({\mathbf{G}}_{i + 2,AH} = - \frac{177}{{192}}(a_{p} \tau )^{2} e^{{2{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} {\mathbf{B}}_{i + 2} - \frac{3}{8}a_{p} \tau e^{{2{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 2}\), \({\mathbf{G}}_{i + 3,AH} = \frac{3}{4}a_{p} \tau e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 3} + \frac{165}{{192}}(a_{p} \tau )^{2} e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} {\mathbf{B}}_{i + 3}\).

By putting Eq. (33) in order according to the delay term and the state term, its clearer form can be achieved as

$$\begin{aligned} {\mathbf{F}}_{i + 4 - T,AH} {\mathbf{U}}_{i + 4 - T} & + {\mathbf{F}}_{i + 3 - T,AH} {\mathbf{U}}_{i + 3 - T} + {\mathbf{F}}_{i + 2 - T,AH} {\mathbf{U}}_{i + 2 - T} + {\mathbf{F}}_{i + 1 - T,AH} {\mathbf{U}}_{i + 1 - T} + {\mathbf{F}}_{i - T,AH} {\mathbf{U}}_{i - T} \\ & = {\mathbf{F}}_{i + 4,AH} {\mathbf{U}}_{i + 4} + {\mathbf{F}}_{i + 3,AH} {\mathbf{U}}_{i + 3} + {\mathbf{F}}_{i + 2,AH} {\mathbf{U}}_{i + 2} + {\mathbf{F}}_{i + 1,AH} {\mathbf{U}}_{i + 1} + {\mathbf{F}}_{i,AH} {\mathbf{U}}_{i} \end{aligned}$$
(34)

where \({\mathbf{F}}_{i - T,AH} = {\mathbf{G}}_{i,AH}\), \({\mathbf{F}}_{i + 1 - T,AH} = {\mathbf{G}}_{i + 1,AH}\), \({\mathbf{F}}_{i + 2 - T,AH} = {\mathbf{G}}_{i + 2,AH}\), \({\mathbf{F}}_{i + 3 - T,AH} = {\mathbf{G}}_{i + 3,AH}\),\({\mathbf{F}}_{i + 4 - T,AH} = \frac{3}{8}a_{p} \tau {\mathbf{B}}_{i + 4}\), \({\mathbf{F}}_{i,AS} = {\mathbf{G}}_{i,AH}\), \({\mathbf{F}}_{i + 1,AS} = {\mathbf{G}}_{i + 1,AH} - \frac{1}{8}e^{{3{\mathbf{A}}\tau }}\), \({\mathbf{F}}_{i + 2,AH} = {\mathbf{G}}_{i + 2,AH}\), \({\mathbf{F}}_{i + 3,AH} = \frac{9}{8}e^{{{\mathbf{A}}\tau }} + \frac{3}{8}a_{p} \tau e^{{{\mathbf{A}}\tau }} {\mathbf{B}}_{i + 4} + {\mathbf{G}}_{i + 3,AH}\), \({\mathbf{F}}_{i + 4,AH} = - {\mathbf{I}}\).

As a result, the combination of Eq. (34) with Eqs. (16), (17), (19), and (21) can construct the matrix ΓAH and ΛAH in order that the system stability is analyzed.

$${{\varvec{\Gamma}}}_{AH} { = }\left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{2} } & {{\mathbf{L}}_{2}^{3} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{3} } & {{\mathbf{L}}_{2}^{3} } & {{\mathbf{L}}_{3}^{3} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1}^{4} } & {{\mathbf{L}}_{2}^{4} } & {{\mathbf{L}}_{3}^{4} } & {{\mathbf{L}}_{4}^{4} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1,AH} } & {{\mathbf{F}}_{2,AH} } & {{\mathbf{F}}_{3,AH} } & {{\mathbf{F}}_{4,AH} } & {{\mathbf{F}}_{5,AH} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4,AH} } & {{\mathbf{F}}_{m - 3,AH} } & {{\mathbf{F}}_{m - 2,AH} } & {{\mathbf{F}}_{m - 1,AH} } & {{\mathbf{F}}_{m,AH} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3,AH} } & {{\mathbf{F}}_{m - 2,AH} } & {{\mathbf{F}}_{m - 1,AH} } & {{\mathbf{F}}_{m,AH} } & {{\mathbf{F}}_{m + 1,AH} } \\ \end{array} } \right]$$
(35)
$${{\varvec{\Lambda}}}_{AH} { = }\left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {e^{{{\mathbf{A}}t_{f} }} } \\ {{\mathbf{L}}_{1 - T}^{2} } & {{\mathbf{L}}_{2 - T}^{3} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1 - T}^{3} } & {{\mathbf{L}}_{2 - T}^{3} } & {{\mathbf{L}}_{3 - T}^{3} } & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{L}}_{1 - T}^{4} } & {{\mathbf{L}}_{2 - T}^{4} } & {{\mathbf{L}}_{3 - T}^{4} } & {{\mathbf{L}}_{4 - T}^{4} } & {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{F}}_{1 - T,AH} } & {{\mathbf{F}}_{2 - T,AH} } & {{\mathbf{F}}_{3 - T,AH} } & {{\mathbf{F}}_{4 - T,AH} } & {{\mathbf{F}}_{5 - T,AH} } & \cdots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{m - 4 - T,AH} } & {{\mathbf{F}}_{m - 3 - T,AH} } & {{\mathbf{F}}_{m - 2 - T,AH} } & {{\mathbf{F}}_{m - 1 - T,AH} } & {{\mathbf{F}}_{m - T,AH} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{F}}_{m - 3 - T,AH} } & {{\mathbf{F}}_{m - 2 - T,AH} } & {{\mathbf{F}}_{m - 1 - T,AH} } & {{\mathbf{F}}_{m - T,AH} } & {{\mathbf{F}}_{m + 1 - T,AH} } \\ \end{array} } \right]$$
(36)

4 Numerical verification and analysis

Here, two typical examples are chosen to demonstrate the calculation accuracy and efficiency of the proposed PCM.

4.1 One-DOF model

Suppose the milling system shown in Fig. 2 has a unique one-DOF along the feed direction. The modal parameters and cutting force coefficients are taken from the Insperger et al. [22, 24], as shown in Table 1. Furthermore, the milling system applies a milling tool with two teeth to down milling the workpiece. Obviously, the milling system belongs one-DOF milling model along the feed direction with the expression [20,21,22,23, 47] of

$$m_{t} \ddot{x}(t) + 2m_{t} \zeta \omega_{n} \dot{x}(t) + m_{t} \omega_{n}^{2} x(t) = - a_{p} h_{xx} (t)\left[ {x(t) - x(t - T)} \right]$$
(37)

where ζ is the damping ratio of the tool, ωn is the natural angular frequency of the tool, ap is the axial depth of cut, and mt is the modal mass of the tool.

Table 1 Calculation parameters
Full size table

Let \({\mathbf{p}}(t) = {\mathbf{M\dot{q}}}(t) + \frac{{\mathbf{C}}}{2}{\mathbf{q}}(t)\) and \({\mathbf{U}}(t) = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}(t)} \\ {{\mathbf{p}}(t)} \\ \end{array} } \right]\) with M = [mt], C = [2mtζωn] and q(t) = [x(t)]. When the state space transformation is performed on Eq. (37), it can ultimately be expressed as the same as Eq. (6), that is

$${\dot{\mathbf{U}}}(t) = {\mathbf{AU}}(t) + {\mathbf{B}}(t)[{\mathbf{U}}(t) - {\mathbf{U}}(t - T)]$$
(38)

where

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} { - \zeta \omega_{n} } & {{1 \mathord{\left/ {\vphantom {1 {m_{t} }}} \right. \kern-\nulldelimiterspace} {m_{t} }}} \\ {m_{t} (\zeta \omega_{n} )^{2} - m_{t} \omega_{n}^{2} } & { - \zeta \omega_{n} } \\ \end{array} } \right]$$
(39)
$${\mathbf{B}}(t) = \left[ {\begin{array}{*{20}c} 0 & 0 \\ { - a_{p} h_{xx} (t)} & 0 \\ \end{array} } \right]$$
(40)

4.1.1 Calculation accuracy

It is known from the Refs. [22, 24] that the local truncation errors of the 1st-SDM and the 2nd-FDM are Ο(τ3). From the point of view of mathematical approximation, they have second-order algebraic precision. Likewise, the local truncation error of the PCM can easily be obtained as Ο(τ5). In other words, the PCM has fourth-order algebraic precision. In order to illustrate the computational performance of these methods, a further comparison can be on their convergence rate curve.

Firstly, in order to avoid interrupted cutting, the radial immersion ratio a/D is determined to be 1. Four sets of milling parameters are considered as listed in Table 2. Secondly, when the discrete number is selected as m = 800, the 1st-SDM is used to calculate the state transition matrix Ψ for every group of milling parameters listed in Table 2. Finally, the modulus \(\left| {\mu {}_{0}} \right|\) of the critical eigenvalue corresponding to the state transition matrix can be taken as the theoretical value of every group of milling parameters. The convergence rate coordinate system is established by, respectively, taking the discrete number m and the difference \(\left| \mu \right| - \left| {\mu {}_{0}} \right|\) between the modulus of the critical eigenvalue and the exact value as the horizontal and vertical coordinate axis. Here \(\left| \mu \right| - \left| {\mu {}_{0}} \right|\) is defined as the local discrete error which is caused by the discrete number m.

Table 2 Milling parameters
Full size table

Thus, the convergence rate curve can be obtained by the 1st-SDM, 2nd-FDM, AS-PCM, ABM-PCM, and AH-PCM under four groups of milling parameters, as shown in Fig. 4. It is worth mentioning that the “spindle speed-depth of cut” plane constructed by every group of milling parameters is uniformly divided into 200 × 200 meshes. All calculations were programmed in MATLAB 9.11, and they are run on the same personal computer [Intel(R) Core™ i7-10,700 CPU @ 2.90 GHz 8 GB].

Fig. 4
figure 4

Convergence rate comparisons of the 1st-SDM, the 2nd-FDM and the PCMs. a ap = 0.5 mm and |μ0|= 0.8892 (stable). b ap = 0.8 mm and |μ0|= 0.9564 (stable). c ap = 1.1 mm and |μ0|= 0.9948 (stable). d ap = 1.4 mm and |μ0|= 1.0198 (unstable)

Full size image

It can be obviously seen that with the increase of m, the local discrete errors gradually approach 0, but the convergence speeds of the proposed PCMs including AS-PCM, ABM-PCM, and AH-PCM are greatly faster than 1st-SDM and 2nd-FDM. Under the arbitrary discrete number m, the solution accuracies of the proposed PCMs are higher than 1st-SDM and 2nd-FDM. That is to say, under the same conditions, the SLDs obtained by the proposed PCMs are closer to the theoretical value than the SLD obtained by the 1st-SDM and 2nd-FDM. In addition, it can be seen from this example, the PCMs have basically tended to be numerically stable when m equals 50, which is significantly better than 1st-SDM and 2nd-FDM.

4.1.2 Calculation efficiency

Here, the radial immersion ratio a/D is respectively considered as 0.05, 0.5, and 1. Other milling conditions remain unchanged. In the computing process, the periodic discrete number is selected as m = 40. Moreover, the “spindle speed-depth of cut” plane still meshed 200 × 200 grids. Thus, the calculation results with various methods are shown in Table 3. Figure 5 illustrates the corresponding calculation times. The results show that in order to obtain higher calculation accuracy, the computational times of the PCMs are greatly less than 1st-SDM and 2nd-FDM. The PCMs are about 76% and 48% less than 1st-SDM and 2nd-FDM, respectively.

Table 3 One-DOF SLDs obtained by the discrete number m = 40
Full size table
Fig. 5
figure 5

Computing time comparisons of the 1st-SDM, the 2nd-FDM, and the PCMs

Full size image

The reasons for the significant improvement in the computational efficiency of the PCMs mainly include the following two aspects.  On the one hand, the exponential state transition matrix of the SDM depends not only on the spindle speed but also on the depth of cut. Thus, the calculation is done at every value of m and every grid of the “spindle speed-depth of cut” plane. That is to say, the SDM need to calculate 200 × 200 × 40 matrix indices and 200 × 200 × 40 state transition matrices. A large amount of computation would be very time-consuming. However, FDM and PCMs only depend on the spindle speed, so they merely need to calculate 200 matrix indices. On the other hand, the construction number of the state transition matrix of FDM in the computing process is related to the discrete number m, whereas that of the PCMs have nothing to do with the discrete number m. Obviously, the FDM need to calculate 200 matrix indices and 200 × 200 × 40 state transition matrices, whereas the PCMs need calculate 200 matrix indices and 200 × 200 state transition matrices. As above stated, the PCMs improve greatly faster calculation speed than the SDM and FDM.

Again, when the discrete number m is creased to improve the calculation accuracy, the calculation time of the PCMs will increase approximately linearly, while those of SDM and FDM will increase approximately exponentially. In other words, the larger the periodic discrete number m is, the more the calculation efficiency of the PCMs will be improved than the 1st-SDM and the 2nd-FDM.

4.2 Two-DOF model

The workpiece is still supposed to be in down milling process, as shown in Fig. 2. Here, the milling system is not only considered to have one degree of freedom along the feed direction, but also another degree of freedom along the workpiece thickness direction. This is the so-called two-DOF milling dynamics model whose DDE [20,21,22,23] can be expressed as

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {m_{t} } & 0 \\ 0 & {m_{t} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x}(t)} \\ {\ddot{y}(t)} \\ \end{array} } \right] & + \left[ {\begin{array}{*{20}c} {2m_{t} \zeta \omega_{n} } & 0 \\ 0 & {2m_{t} \zeta \omega_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{x}(t)} \\ {\dot{y}(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {m_{t} \omega_{n}^{2} } & 0 \\ 0 & {m_{t} \omega_{n}^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right] \hfill \\ & = a_{p} \left[ {\begin{array}{*{20}c} { - h_{xx} (t)} & { - h_{xy} (t)} \\ { - h_{yx} (t)} & { - h_{yy} (t)} \\ \end{array} } \right]\left\{ {\left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {x(t - T)} \\ {y(t - T)} \\ \end{array} } \right]} \right\} \hfill \\ \end{aligned}$$
(41)

Let \({\mathbf{q}}(t) = \left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right]\), \({\mathbf{p}}(t) = {\mathbf{M\dot{q}}}(t) + \frac{{\mathbf{C}}}{2}{\mathbf{q}}(t)\) and \({\mathbf{U}}(t) = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}(t)} \\ {{\mathbf{p}}(t)} \\ \end{array} } \right]\) in which M and C are defined as \({\mathbf{M}} = \left[ {\begin{array}{*{20}c} {m_{t} } & 0 \\ 0 & {m_{t} } \\ \end{array} } \right]\) and \({\mathbf{C}} = \left[ {\begin{array}{*{20}c} {2m_{t} \zeta \omega_{n} } & 0 \\ 0 & {2m_{t} \zeta \omega_{n} } \\ \end{array} } \right]\). Thus, Eq. (41) can be further redescribed as

$${\dot{\mathbf{U}}}(t) = {\mathbf{AU}}(t) + {\mathbf{B}}(t)[{\mathbf{U}}(t) - {\mathbf{U}}(t - T)]$$
(42)

where

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} { - \zeta \omega_{n} } & 0 & {{1 \mathord{\left/ {\vphantom {1 {m_{t} }}} \right. \kern-\nulldelimiterspace} {m_{t} }}} & 0 \\ 0 & { - \zeta \omega_{n} } & 0 & {{1 \mathord{\left/ {\vphantom {1 {m_{t} }}} \right. \kern-\nulldelimiterspace} {m_{t} }}} \\ {(\zeta^{2} - 1)\omega_{n}^{2} m_{t} } & 0 & { - \zeta \omega_{n} } & 0 \\ 0 & {(\zeta^{2} - 1)\omega_{n}^{2} m_{t} } & 0 & { - \zeta \omega_{n} } \\ \end{array} } \right]$$
(43)
$${\mathbf{B}}(t) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ { - a_{p} h_{xx} (t)} & { - a_{p} h_{xy} (t)} & 0 & 0 \\ { - a_{p} h_{yx} (t)} & { - a_{p} h_{yy} (t)} & 0 & 0 \\ \end{array} } \right]$$
(44)

It is worth mentioning that the milling parameters in Eqs. (41), (42) (43) and (44) are exactly the same definitions and magnitudes as the above section. Likewise, the calculation parameters still use the data listed in Table 1.

According to the conclusion of the convergence analysis of Sec. 4.1, it can be seen that when the value of m is large enough, the convergence of the PCMs is better than that of other methods. This implies that the simulated curve obtained by the PCMs is better closer to the theoretical curve. Therefore, the SLD calculated by the PCMs under m = 200 can be thought as the reference. Based on the obtained SLD reference, the calculation performance of the PCMs can be comparably analyzed with that of 1st-SDM and 2nd-FDM under a small radial depth of cut (a/D = 0.05) and large radial depth of cut (a/D = 1), respectively. It is worth noting that, when the value of m is large enough, three curves obtained, respectively, by the AS-PCM, ABM-PCM, and AH-PCM have completely coincident with each other, as shown in Fig. 6.

Fig. 6
figure 6

References obtained by the PCMs under m = 200. a a/D = 0.05. b a/D = 1

Full size image
Fig. 7
figure 7

Calculation result under m = 8 and a/D = 0.05. a 1st-SDM. b 2nd-FDM. c AS-PCM. d AH-PCM. e ABM-PCM

Full size image
Fig. 8
figure 8

Calculation result under m = 25 and a/D = 0.05. a 1st-SDM. b 2nd-FDM. c AS-PCM. d AH-PCM. e ABM-PCM

Full size image
Fig. 9
figure 9

Calculation result under m = 60 and a/D = 0.05. a 1st-SDM. b 2nd-FDM. c AS-PCM. d AH-PCM. e ABM-PCM

Full size image
Fig. 10
figure 10

Calculation result under m = 8 and a/D = 1. a 1st-SDM. b 2nd-FDM. c AS-PCM. d AH-PCM. e ABM-PCM

Full size image
Fig. 11
figure 11

Calculation result under m = 25 and a/D = 1. a 1st-SDM. b 2nd-FDM. c AS-PCM. d AH-PCM. e ABM-PCM

Full size image
Fig. 12
figure 12

Calculation result under m = 60 and a/D = 1. a 1st-SDM. b 2nd-FDM. c AS-PCM. d AH-PCM. e ABM-PCM

Full size image

The “spindle speed-depth of cut” plane still meshed as 200 × 200 note points. Figures 7 and 10 are the calculation result when m = 8. Figures 8 and 11 are corresponding to the calculation result under m = 25. The condition of m = 60 can obtain the result in Figs. 9 and 12. Accordingly, under the small radial depth of cut (a/D = 0.05), when the periodic discrete number is selected as the smaller value, for example, m = 8, although five SLDs have already begun to converge to the reference, the convergence of the AS-PCM, AH-PCM, and ABM-PCM is slightly better than 1st-SDM and 2nd-FDM. With the increase of m value, five SLDs trend gradually to the reference. When m is 25, the five curves are basically close to the reference, but the PCMs are closer to the reference than 1st-SDM and 2nd-FDM. When m is 60, the curves obtained by 1st-SDM and 2nd-FDM are still slightly different from the reference, whereas the curves obtained by the AS-PCM and ABM-PCM almost agree with the reference completely.

Under the large radial depth of cut (a/D = 1), however, the convergence rates of the five methods are basically the same as each other when m = 8. When m increases to 25, especially to 60, the curves obtained by five methods have almost coincided with the reference.

The above analysis shows that the presented PCMs can well predict the milling stability no matter under the small radial depth of cut or the large radial depth of cut. By comparing with 1st-SDM and 2nd-FDM, the PCMs achieve not only higher calculation efficiency, but also better calculation accuracy under the same calculation conditions.

5 Stability analysis with effects of helix angle and multiple modes

In the actual milling process, it is often necessary to consider a more complex machining environment. The consideration of the tool with a helical cutting edge and effect of multiple modes can reflect the actual machining state more accurately. The milling dynamics model shown in Fig. 2 will be changed to the typical dynamic milling system of multiple DOFs shown in Fig. 13 if the multi-order modes along the feed and wall thickness directions are considered. The vibration differential equations of multiple DOFs system [32, 33] is written as.

$${\mathbf{M\ddot{q}}}(t) + {\mathbf{C\dot{q}}}(t) + {\mathbf{Kq}}(t)\; = {\mathbf{F}}$$
(45)

where,

$$\left\{ \begin{array}{l} {\mathbf{M}} = diag(m_{x,1} ,m_{x,2} , \cdots ,m_{{x,{\text{n}}}} ,m_{y,1} ,m_{y,2} , \cdots ,m_{{y,{\text{n}}}} ) \hfill \\ {\mathbf{C}} = diag(2m_{x,1} \zeta_{x,1} \omega_{x,1} ,2m_{x,2} \zeta_{x,2} \omega_{x,2} , \cdots ,2m_{{x,{\text{n}}}} \zeta_{{x,{\text{n}}}} \omega_{{x,{\text{n}}}} \hfill \\ \quad \quad 2m_{y,1} \zeta_{y,1} \omega_{y,1} ,2m_{y,2} \zeta_{y,2} \omega_{y,2} , \cdots ,2m_{{y,{\text{n}}}} \zeta_{{y,{\text{n}}}} \omega_{{y,{\text{n}}}} ) \hfill \\ {\mathbf{K}} = diag(m_{x,1} \omega_{x,1}^{2} ,m_{x,2} \omega_{x,2}^{2} , \cdots ,m_{{x,{\text{n}}}} \omega_{{x,{\text{n}}}}^{2} ,m_{y,1} \omega_{y,1}^{2} ,m_{y,2} \omega_{y,2}^{2} , \cdots ,m_{{y,{\text{n}}}} \omega_{{x,{\text{n}}}}^{2} ) \hfill \\ {\mathbf{q}}(t) = [x_{1} (t),x_{2} (t), \cdots ,x_{{\text{n}}} (t),y_{1} (t),y_{2} (t), \cdots ,y_{{\text{n}}} (t)]^{{\text{T}}} \hfill \\ {\mathbf{F}} = [\underbrace {{F_{x} ,F_{x} , \cdots ,F_{x} }}_{n},\underbrace {{F_{y} ,F_{y} , \cdots ,F_{y} }}_{n}]^{{\text{T}}} \hfill \\ \end{array} \right.$$
(46)
$$\left[ \begin{gathered} F_{x} \hfill \\ F_{y} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} { - h_{xx} } & { - h_{xy} } \\ { - h_{yx} } & { - h_{yy} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} { - h_{xx} } & { - h_{xy} } \\ { - h_{yx} } & { - h_{yy} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(t - T)} \\ {y(t - T)} \\ \end{array} } \right]$$
(47)
Fig. 13
figure 13

Typical dynamic milling system of multiple DOFs

Full size image

If the effect of helix angle is considered, the cutting force direction coefficients hxx, hxy, hyx, hyy in Eq. (47) are detailedly expressed as Eq. (48) whose derivation process can be found in Ref. [33].

$$\left\{ \begin{gathered} h_{xx} (t) = \sum\limits_{l = 1}^{H} {\sum\limits_{j = 1}^{N} g (\phi_{j} (t))\sin (\phi_{j} (t))\left[ {K_{t} \cos (\phi_{j} (t)) + K_{r} \sin (\phi_{j} (t))} \right]dz} \hfill \\ h_{xy} (t) = \sum\limits_{l = 1}^{H} {\sum\limits_{j = 1}^{N} g (\phi_{j} (t)){\text{cos}}(\phi_{j} (t))\left[ {K_{t} \cos (\phi_{j} (t)) + K_{r} \sin (\phi_{j} (t))} \right]dz} \hfill \\ h_{yx} (t) = \sum\limits_{l = 1}^{H} {\sum\limits_{j = 1}^{N} g (\phi_{j} (t))\sin (\phi_{j} (t))\left[ {K_{r} \cos (\phi_{j} (t)) - K_{t} \sin (\phi_{j} (t))} \right]dz} \hfill \\ h_{yy} (t) = \sum\limits_{l = 1}^{H} {\sum\limits_{j = 1}^{N} g (\phi_{j} (t))\cos (\phi_{j} (t))\left[ {K_{r} \cos (\phi_{j} (t)) - K_{t} \sin (\phi_{j} (t))} \right]dz} \hfill \\ \end{gathered} \right.$$
(48)

where H is the number of layers divided by the tool along the axial direction and dz is the thickness of each layer of microelements.

Similarly, let \({\mathbf{p}}(t) = {\mathbf{M\dot{q}}}(t) + \frac{{\mathbf{C}}}{2}{\mathbf{q}}(t)\) and \({\mathbf{U}}(t) = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}(t)} \\ {{\mathbf{p}}(t)} \\ \end{array} } \right]\), Eq. (45) can be further redescribed as

$${\dot{\mathbf{U}}}(t) = {\mathbf{AU}}(t) + {\mathbf{B}}(t)[{\mathbf{U}}(t) - {\mathbf{U}}(t - T)]$$
(49)

where

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} { - {\mathbf{M}}^{ - 1} {\mathbf{C}}/2} & {{\mathbf{M}}^{ - 1} } \\ {{\mathbf{CM}}^{ - 1} {\mathbf{C}}/4 - {\mathbf{K}}} & { - {\mathbf{CM}}^{ - 1} /2} \\ \end{array} } \right]$$
(50)
$${\mathbf{B}}(t) = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ { - {\mathbf{W}}} & {\mathbf{0}} \\ \end{array} } \right]$$
(51)

where

$${\mathbf{W}} = \left[ {\begin{array}{*{20}c} {h_{xx} } & {h_{xx} } & \cdots & {h_{xx} } & {h_{xy} } & {h_{xy} } & \cdots & {h_{xy} } \\ {h_{xx} } & {h_{xx} } & \cdots & {h_{xx} } & {h_{xy} } & {h_{xy} } & \cdots & {h_{xy} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ {h_{xx} } & {h_{xx} } & \cdots & {h_{xx} } & {h_{xy} } & {h_{xy} } & \cdots & {h_{xy} } \\ {h_{yx} } & {h_{yx} } & \cdots & {h_{yx} } & {h_{yy} } & {h_{yy} } & \cdots & {h_{yy} } \\ {h_{yx} } & {h_{yx} } & \cdots & {h_{yx} } & {h_{yy} } & {h_{yy} } & \cdots & {h_{yy} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ {h_{yx} } & {h_{yx} } & \cdots & {h_{yx} } & {h_{yy} } & {h_{yy} } & \cdots & {h_{yy} } \\ \end{array} } \right]$$
(52)

In addition to the derivation of the stability prediction method in Sec. 3, the numerical comparison analysis in Sec. 4 shows that the computational performance of AS-PCM is the basic same as ABM-PCM and AH-PCM. Therefore, only the AS-PCM is applied to analyze the influence of the helix angle and multiple modes on milling stability.

5.1 Effect of helix angle

It is generally believed that the non-zero helix angle of the tool will cause the SLD to appear the phenomenon of period-doubling bifurcation instability island under the small radial depth of cut [48]. Here, the influence of the helix angle effect on SLD under different radial depths of cut will be further revealed by using AS-PCM.

In the up milling process, the used milling tool with the teeth number N = 1 has a diameter of D = 12.75 mm. The cutting force coefficients are Kt = 536 N/mm2 and Kr = 187 N/mm2. Other parameters [49] are listed in Table 4. Here, six kinds of the radial immersion ratio a/D are considered, i.e., 0.05, 0.1, 0.2, 0.5, 0.7, and 1. Moreover, four kinds of helix angle β are considered, i.e., 0°, 20°, 30°, and 45°.

Table 4 Modal parameters
Full size table

If only the first mode in Table 4 is considered, the SLDs are obtained for different radial immersion ratios by AS-PCM under the periodic discrete number m = 40, as shown in Fig. 14. For small radial depth of cut, unstable islands gradually appeared on the right of the first lobe with the increase of helix angle. With the increase of helix angle, the unstable island decreases gradually, while the stable region increases. A proper helix angle can weaken the influence of milling interruption on milling vibration to separate the stability lobe and improves the stability of milling process evidently. But with the increases of the radial immersion ratio, the effect of helix angle on the lobe diagrams decreases until the stability curves gradually coincide with each other at a/D = 0.2. If the first two modes in Table 4 are considered, 3D SLD under the condition of β = 30° can be obtained in the coordinate system of spindle speed-axial depth of cut-radial immersion ratio, as shown in Fig. 15. It is evident that whether only the first mode or the first two modes are considered, the stability region decreases gradually with the increase of radial immersion ratio.

Fig. 14
figure 14

The effect of helix angle on the stability region: a a/D = 0.05; b a/D = 0.1; c a/D = 0.2; d a/D = 0.5; e a/D = 0.7; f a/D = 1

Full size image
Fig. 15
figure 15

3D stability lobe diagram considering the two modes with β = 30°

Full size image

5.2 Stability verification

An experiment is carried out to mill the 7075-T6 aluminum alloy block on a precise vertical machining center [33]. The down milling with half radial immersion ratio is adopted with the cutting parameters of Kt = 796.1 MPa and Kr = 168.8 MPa. The milling tool is the diameter of 8 mm, the teeth number of 3, and the helix angle of 45°, respectively. The dominant mode is the first two orders, and the corresponding modal parameters are listed in Table 5.

Table 5 Modal parameters at the tool point
Full size table

Thus, the stability lobe can be plotted in consideration with the first two modes, as shown in Fig. 16. The red solid line is obtained by applying AS-PCM, whereas the blue dotted line is calculated by 4th-FDM taking from Ref. [33]. It can be seen that two stability lobes are basically consistent with each other. Moreover, 30 sets of milling experiments were done to verify the prediction accuracy of SLD. It is observed that the predicted stability boundaries are in good agreement with the experiment results except for very few parameter points. The misjudgment of milling states at these points could be caused by the measurement error or other random factors in the actual milling process. Accordingly, the proposed method can predict the stability boundary with excellent accuracy in the case of multiple mode milling operation.

Fig. 16
figure 16

Comparison and verification for stability lobe with two order modes

Full size image

6 Conclusions

After a mathematical skill is adopted to convert the second-order DDE describing the dynamic milling process into the form of state space, the linear multi-step “predictor–corrector” method is for the first time suggested to conclude the state transition matrix. Subsequently, the Floquet theory is relied on to establish the judgment criterion of the milling stability. The proposed PCMs can greatly improve the calculation accuracy as well as the calculation efficiency.

In the calculating process of the state transition matrix for a one-DOF milling system, the results of the local truncation error and computational efficiency show that the proposed PCMs have a faster convergence speed than 1st-SDM and 2nd-FDM at arbitrary discrete number. This means that the calculation result of the PCMs is closer to the theoretical value under the same periodic discrete number. In addition, the PCMs can reduce more calculation time than 1st-SDM and 2nd-FDM. When m is 40, it is decreased by about 76% and 48% over 1st-SDM and 2nd-FDM, respectively. Moreover, with the increase of discrete number m, the calculation efficiency will be further improved.

By calculating the SLD of a two-DOF milling model, the conclusions can be achieved that the PCMs can better predict the milling stability whether it is under a small or a large radial depth of cut. In the whole calculating process, the calculation efficiency of the PCMs is far higher than that of 1st-SDM and 2nd-FDM. Therefore, under the conditions of multiple DOFs and larger discrete number, the calculation efficiency of the PCMs will have more advantages in practical applications.

By considering the practical multiple mode milling environment, the influence of the helix angle on the stable region is investigated for different radial immersion ratios by using the AS-PCM. The results show that the effect of the helix angle on the stability lobe is obvious under the condition of a small radial depth of cut. With the gradual increase of the radial immersion ratio, the helix angle effect is also weaker and weaker. The milling experiment on multiple modes verifies the proposed PCM is of excellent stability prediction accuracy.