Improved semi-discretization method based on predictor-corrector scheme for milling stability analysis

Abstract

Chatter has a detrimental effect on the milling process, which makes the chatter stability prediction very critical in milling. This paper presents a new semi-discretization method (SDM) based on predictor-corrector scheme to predict the stability of milling process. Firstly, the dynamic of the milling system is modelled by delay-differential equation (DDE), and the forced vibration duration is divided into many parts. Secondly, the DDE is integrated on the small time interval. The time-delay term and the periodic coefficient matrix are taken as an operator and approximated by second-order interpolation polynomial. And then, the state transition matrix is constructed based on predictor-corrector scheme. The proposed method is validated by comparing it with the benchmark. In general, the proposed method is superior compared with the benchmark in terms of the rate of convergence. Besides, the proposed method is also a robust method. The computational efficiency of the proposed method is proved to be good. For a one degree of freedom (1-DOF) milling system under full immersion condition, the stability lobe diagrams obtained by the proposed method are much closer to the reference than those obtained by the PCHDM and UNIM, especially in the peak of the lobes. The proposed method also can be used to predict the stability for a 2-DOF milling system accurately. It is also indicated from this study that the prediction accuracy of the SDM can be improved by combining the predictor-corrector scheme.

1 Introduction

Chatter has a detrimental effect on the milling process. It may cause undesirable precision and inefficient processing. Therefore, for nearly a century, it has been a hot research topic in the manufacturing field. A great deal of researchers has been devoted to the study of chatter. Chatter avoidance can be achieved by predicting the stability of milling in advance and selecting chatter-free processing parameters. Stability lobe diagram can be used to determine the chatter-free parameters. The model of the milling dynamics can be established by the delay-differential equation (DDE). Then, the stability lobe diagram can be acquired by solving DDE using different methods.

So far, the extensive literature on chatter stability prediction in milling has been reported. In general, the stability prediction methods mainly fall into two kinds, namely, frequency-domain methods and time-domain methods. The most well-known frequency-domain method is the zeroth-order approximation (ZOA) method. The ZOA method is proposed by Altintas et al. [1]; it can predict milling stability efficiently. However, the shortcoming of this method is that it cannot be used for low immersion conditions. Then, Budak and Altintas [2, 3] developed a general formulation for the milling system with multi-degree of freedom based on the ZOA method. The shortcoming of the ZOA method is overcome in the multi-frequency method, which is reported by Merdol et al. [4]. The multi-frequency method can predict milling stability under low immersion conditions accurately.

Compared with the frequency-domain-based methods, more methods are proposed in the time domain. Bayly et al. [5] reported a temporal finite element analysis method, which can only predict the stability of milling with one degree of freedom. Butcher et al. [6] developed a Chebyshev collocation method which takes advantage of the derivative property of Chebyshev polynomial. Insperger et al. [7] proposed a semi-discretization method (SDM) to analyze the stability in milling. In this method, the time-delay term is approximated by piecewise constant function. To improve accuracy, Insperger et al. [8] suggested the first-order semi-discretization method (1st SDM). Recently, Jiang et al. [9] proposed an accurate second-order semi-discretization method (2nd SDM). In this method, only the time-delay term is approximate by the second-order polynomial. Ding et al. [10] presented a famous full-discretization method (FDM). And then, Ding et al. [11] proposed the second-order FDM (2nd FDM) followed by the third-order FDM (3rd FDM) suggested by Guo et al. [12]. Based on least squares approximation scheme, Ozoegwu et al. [13, 14] presented a series of least squares approximation methods. Tang et al. [15] proposed a second-order updated full-discretization method (2nd UFDM). In this method, the Floquet transition matrix is obtained directly. After that, Yan et al. [16] suggested a third-order updated full-discretization method (3rd UFDM). Zhou et al. [17] proposed the high-order FDMs to predict milling stability. In their work, the time-delay term is interpolated by different high-order polynomials. Qin et al. [18] proposed a novel method for milling stability analysis based on the holistic-interpolation scheme (HIM). And then, to update the HIM, Qin et al. [19] represented a predictor-corrector-based holistic-discretization method (PCHDM) to predict the milling stability accurately and efficiently. Dai et al. [20] proposed an improved full-discretization method and a precise integration method (PIM) [21] to predict the stability in milling. After that, Li et al. [22] presented an improved PIM for milling stability analysis. Yang et al. [23] recommended the precise integration-based third-order full-discretization method for stability analysis in milling. Besides, some methods based on the numerical solution of the differential equation are also presented, such as the differential quadrature method [24], numerical differentiation method [25], Runge-Kutta-based methods [26], Simpson-based method [27], and the Adams-Moulton-based method [28]. Some numerical integration-based methods are also developed to analyze the milling stability, such as the numerical integration method (NIM) [29], the updated NIM (UNIM) [30], and the Newton-Cotes-based method [31].

Generally, most prediction methods are in the framework of FDM. The corresponding methods based on SDM are relatively scarce. The SDM-based methods are also worthy of some attention. In the literature [19], it is proved that the predictor-corrector scheme can be used to improve the accuracy of the algorithm. Therefore, this work proposed a new semi-discretization method based on predictor-corrector scheme to predict the milling stability by combining the ideal of semi-discretization and the predictor-corrector scheme.

The rest of this paper is organized as follows: Section 2 presents the dynamic milling model firstly and then gives the derivation process of the proposed method. Section 3 validates the proposed method from the aspect of accuracy and efficiency. Section 4 sums up the main conclusions.

2 Milling dynamic model and the proposed method

Without loss of generality, the basic dynamic model of milling is considered here, where the tool is assumed to be flexible compared with the rigid workpiece. The milling system can be simplified into a 2-DOF system in two orthogonal directions (X and Y) with a single mode in each direction, and the feed direction of the workpiece is along the X-axis [17, 21]. The schematic of the basic dynamic milling system is as shown in Fig. 1.

Fig. 1

Schematic of the basic dynamic milling system

By taking the regenerative chatter into account, the dynamic milling system can be described as follows:

$$ \left(\begin{array}{cc}{m}_x& 0\\ {}0& {m}_x\end{array}\right)\left(\begin{array}{c}\dot{x}(t)\\ {}\dot{y}(t)\end{array}\right)+\left(\begin{array}{cc}{c}_x& 0\\ {}0& {c}_x\end{array}\right)\left(\begin{array}{c}\dot{x}(t)\\ {}\dot{y}(t)\end{array}\right)+\left(\begin{array}{cc}{k}_x& 0\\ {}0& {k}_x\end{array}\right)\left(\begin{array}{c}x(t)\\ {}y(t)\end{array}\right)=-{a}_p\left(\begin{array}{cc}{h}_{xx}(t)& {h}_{xy}(t)\\ {}{h}_{yx}(t)& {h}_{yy}(t)\end{array}\right)\left(\begin{array}{c}x(t)-x\left(t-T\right)\\ {}y(t)-y\left(t-T\right)\end{array}\right) $$

(1)

where a_p is the axial depth of cut; T is the time delay which is equal to the tooth-passing period; m_x, c_x, and k_x are the modal mass, damping, and stiffness in the X direction, respectively; and m_y, c_y, and k_y are the modal mass, damping, and stiffness in the Y direction, respectively. Specifically, the modal parameters c_x, c_y, k_x, and k_y can be further expressed as follows: c_x = 2m_xζ_xω_nx, c_y = 2m_yζ_yω_ny, ${k}_x={m}_x{\omega}_{nx}^2$, and ${k}_y={m}_y{\omega}_{ny}^2$, where ζ_x, ζ_y, ω_nx, and ω_ny are the modal damping ratios and angular natural frequencies in the X and Y directions, respectively.

The directional cutting force coefficients h_xx(t), h_xy(t), h_yx(t), and h_yy(t) are given as follows:

$$ {h}_{xx}(t)=\sum \limits_{j=1}^Ng\left[{\varphi}_j(t)\right]\sin \Big(\left({\varphi}_j(t)\right)\left[{K}_t\cos \left({\varphi}_j(t)\right)+{K}_n\sin \left({\varphi}_j(t)\right)\right] $$

(2)

$$ {h}_{xy}(t)=\sum \limits_{j=1}^Ng\left[{\varphi}_j(t)\right]\cos \Big(\left({\varphi}_j(t)\right)\left[{K}_t\cos \left({\varphi}_j(t)\right)+{K}_n\sin \left({\varphi}_j(t)\right)\right] $$

(3)

$$ {h}_{yx}(t)=\sum \limits_{j=1}^Ng\left[{\varphi}_j(t)\right]\sin \Big(\left({\varphi}_j(t)\right)\left[-{K}_t\sin \left({\varphi}_j(t)\right)+{K}_n\cos \left({\varphi}_j(t)\right)\right] $$

(4)

$$ {h}_{yy}(t)=\sum \limits_{j=1}^Ng\left[{\varphi}_j(t)\right]\cos \Big(\left({\varphi}_j(t)\right)\left[-{K}_t\sin \left({\varphi}_j(t)\right)+{K}_n\cos \left({\varphi}_j(t)\right)\right] $$

(5)

where K_t and K_n are the tangential and the normal cutting force coefficients, N is the cutter teeth number, g[φ_j(t)] is a window function which is used to determine whether the tooth is in cut [7], and φ_j(t) is the angular position of the tooth j and it is given as follows:

$$ {\varphi}_j(t)=\left(2\pi \Omega /60\right)t+\left(j-1\right)2\pi /N $$

(6)

where Ω is the spindle speed in rpm.

Equation (1) can be represented by the matrix equation as follows:

$$ \mathbf{M}\ddot{\mathbf{q}}(t)+\mathbf{C}\dot{\mathbf{q}}(t)+\mathbf{Kq}(t)={a}_p\mathbf{K}\mathrm{c}(t)\left[\mathbf{q}(t)-\mathbf{q}\left(t-T\right)\right] $$

(7)

where the modal mass, damping, stiffness, and the dynamic response matrices M, C, K, and q(t) are given as follows:

$$ {\displaystyle \begin{array}{c}\mathbf{M}=\left[\begin{array}{cc}{m}_x& 0\\ {}0& {m}_y\end{array}\right],\mathbf{C}=\left[\begin{array}{cc}2{m}_x{\zeta}_x{\omega}_{nx}& 0\\ {}0& 2{m}_y{\zeta}_y{\omega}_{ny}\end{array}\right]\\ {}\mathbf{K}=\left[\begin{array}{cc}{m}_x{\omega}_{nx}^2& 0\\ {}0& {m}_y{\omega}_{ny}^2\end{array}\right],\mathbf{q}(t)=\left[\begin{array}{c}x(t)\\ {}y(t)\end{array}\right]\end{array}} $$

(8)

The directional cutting force coefficient matrix Kc(t) is written as follows:

$$ \mathbf{K}\mathrm{c}(t)=\left[\begin{array}{cc}{h}_{xx}(t)& {h}_{xy}(t)\\ {}{h}_{yx}(t)& {h}_{yy}(t)\end{array}\right] $$

(9)

Using the transformations $\mathbf{x}(t)=\left[\begin{array}{c}\mathbf{q}(t)\\ {}\dot{\mathbf{q}}(t)\end{array}\right]=\left[\begin{array}{c}x(t)\\ {}y(t)\\ {}\dot{x}(t)\\ {}\dot{y}(t)\end{array}\right]$, Eq. (7) can be rewritten as follows:

$$ \dot{\mathbf{x}}(t)=\mathbf{A}(t)\mathbf{x}(t)+\mathbf{B}(t)\mathbf{x}\left(t-T\right) $$

(10)

where A(t) and B(t) are periodic coefficient matrixes that reflect the dynamic characteristics of the milling system; they can be given as follows:

$$ \mathrm{A}(t)={\mathrm{A}}_0-\mathbf{B}(t) $$

(11)

$$ {\mathbf{A}}_0=\left[\begin{array}{cccc}0& 0& 1& 0\\ {}0& 0& 0& 1\\ {}-{\omega}_{nx}^2& 0& -2{\zeta}_x{\omega}_{nx}& 0\\ {}0& -{\omega}_{ny}^2& 0& -2{\zeta}_y{\omega}_{ny}\end{array}\right] $$

(12)

$$ \mathbf{B}(t)=\left[\begin{array}{cccc}0& 0& 0& 0\\ {}0& 0& 0& 0\\ {}\frac{a_p{h}_{xx}(t)}{m_x}& \frac{a_p{h}_{xy}(t)}{m_x}& 0& 0\\ {}\frac{a_p{h}_{yx}(t)}{m_y}& \frac{a_p{h}_{yy}(t)}{m_y}& 0& 0\end{array}\right] $$

(13)

where A₀ represents the time-invariant nature of the system.

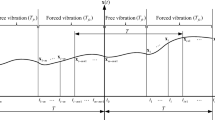
The Eq. (10) should be solved by numerical methods since it has no analytical solution. To solve Eq. (10) numerically, the relevant time period should be divided into many parts. In this study, the forced vibration period (T_fc) rather than tooth passing period (T) is divided into m equal parts, and any part is expressed as [t_i, t_i + 1] with the length of h, namely, T_fc = mh. Then, discrete time points are expressed as follows:

$$ {t}_i={t}_0+{T}_{fr}+\left(i-1\right)h,\kern1em i=1,2,\cdots, m+1 $$

(14)

where T_fr is the free vibration duration, and t₀ is the intimal time instant.

The discretization mechanism and the variation of the dynamic system with time are shown in Fig. 2. Specifically, Fig. 2a illustrates the variation of the directional cutting force coefficient matrix with discrete time, and Fig. 2b illustrates the variation of the of motion of the dynamic system with discrete time. In Fig. 2a and b, t₀ is the intimal time instant of the current tooth passing period, and t_0 − T is the intimal time instant of the previous tooth passing period.

Fig. 2

The discretization mechanism and the variation of the dynamic system with time. a The variation of the specific cutting force coefficient matrix with discrete time. b The variation of the of motion of the dynamic system with discrete time

From Fig. 2a, it is found that the directional cutting force coefficient matrix becomes zero when the tool is out of cut, and the dynamic system experiences free vibration process. Therefore, the free vibration duration T_fr can be determined by using the directional cutting force coefficient matrix. Then the forced vibration period T_fc can also be obtained, that is, T_fc = T − T_fr. In Ding’s work [29], it is pointed out that the T_fr can be found by sampling the directional cutting force coefficient matrix Eq. (9) during one tooth passing period with a high sampling frequency. In this study, the method recommended by Ding et.al [29] is also adopted to determine the free vibration duration T_fr. When there are multiple modes in multiple degrees of freedom, the free vibration period also can be determined by sampling the updated directional cutting force coefficient matrix during one tooth passing period with a high sampling frequency.

As shown in Fig. 2b, the dynamic milling system experiences free vibration process from time point t_{m + 1 − T} to time point t₁. When the cutting tool leaves the workpiece, it experiences free vibration process. Accordingly, the directional cutting force coefficients h_xx(t), h_xy(t), h_yx(t), and h_yy(t) become zero. The matrix A(t) becomes a constant matrix A₀. Therefore, the relation between x(t₁) and x(t_{m + 1 − T}) can be obtained as follows:

$$ \mathbf{x}\left({t}_1\right)={e}^{{\mathbf{A}}_0{T}_{fr}}\mathbf{x}\left({t}_{m+1-T}\right) $$

(15)

As described in Eq. (15), the free vibration period (T-T_fc) and the matrix A₀ co-determine the milling system’s free vibration state. The modal parameters are included in the matrix A₀.

Equation (10) is integrated over the interval [t_i, t_i + 1]; we can get

$$ {\mathbf{x}}_{i+1}={e}^{{\mathbf{A}}_ih}{\mathbf{x}}_i+{\int}_{t_i}^{t_{i+1}}{e}^{{\mathbf{A}}_i\left({t}_{i+1}-s\right)}\mathbf{B}(s)\mathbf{x}\left(s-T\right) ds $$

(16)

In Eq. (16), A_i is the abbreviation of A(t_i), and s is given by s = t − t_i. It should be noted that the matrix exponential in the ref. [19] is ${e}^{{\mathbf{A}}_0}$ which is a constant matrix, while the matrix exponential in this study is ${e}^{{\mathbf{A}}_i}$ which is a variable matrix. The matrices A_i (A(t_i)) and A₀ are given by Eqs. (11) and (12), respectively.

Let the operator r(s) = B(s)x(s − T), and it is interpolated over the interval [t_i, t_i + 1]. In the interpolation process, the time nodes t_i − 1, t_i, and t_i + 1 and their node values r_i − 1, r_i, and r_i + 1 are employed for calculation. By using the second-order Newton interpolation, r(s) can be obtained as follows:

$$ \mathbf{r}(s)=\left(\frac{s^2}{2{h}^2}-\frac{s}{2h}\right){\mathbf{r}}_{i-1}+\left(1-\frac{s^2}{h^2}\right){\mathbf{r}}_i+\left(\frac{s^2}{2{h}^2}+\frac{s}{2h}\right){\mathbf{r}}_{i+1} $$

(17)

For a better understanding, the interpolation process of Eq. (17) is presented, as shown in Fig. 3.

Fig. 3

The interpolation process of Eq. (17)

It is seen from Fig. 3 that the interpolation interval is [t_i, t_i + 1]. The combination (t_i − 1, r_i − 1), which is located out of the interpolation interval, is also used in the calculation.

Substituting Eq. (17) into Eq. (16), we can get

$$ {\mathbf{x}}_{i+1}-{\boldsymbol{\Phi}}_{i,0}{\mathbf{x}}_i={\mathbf{F}}_{i-1}{\mathbf{x}}_{i-1-T}+{\mathbf{F}}_i{\mathbf{x}}_{i-T}+{\mathbf{F}}_{i+1}{\mathbf{x}}_{i+1-T} $$

(18)

where

$$ {\mathbf{F}}_{i-1}=\left(-\frac{{\boldsymbol{\Phi}}_{i,2}}{2h}+\frac{{\boldsymbol{\Phi}}_{i,3}}{2{h}^2}\right){\mathbf{B}}_{i-1} $$

(19)

$$ {\mathbf{F}}_i=\left({\boldsymbol{\Phi}}_{i,1}-\frac{{\boldsymbol{\Phi}}_{i,3}}{h^2}\right){\mathbf{B}}_i $$

(20)

$$ {\mathbf{F}}_{i+1}=\left(\frac{{\boldsymbol{\Phi}}_{i,2}}{2h}+\frac{{\boldsymbol{\Phi}}_{i,3}}{2{h}^2}\right){\mathbf{B}}_{i+1} $$

(21)

and

$$ {\boldsymbol{\Phi}}_{i,0}={e}^{{\mathbf{A}}_ih} $$

(22)

$$ {\boldsymbol{\Phi}}_{i,1}={\mathbf{A}}_i^{-1}\left({\boldsymbol{\Phi}}_{i,0}-\mathbf{I}\right) $$

(23)

$$ {\boldsymbol{\Phi}}_{i,2}={\mathbf{A}}_i^{-1}\left({\boldsymbol{\Phi}}_{i,1}-h\mathbf{I}\right) $$

(24)

$$ {\boldsymbol{\Phi}}_{i,3}={\mathbf{A}}_i^{-1}\left({\boldsymbol{\Phi}}_{i,2}-{h}^2\mathbf{I}\right) $$

(25)

Then, Eq. (10) is integrated over the interval [t_i − 1, t_i + 1]; the result is as follows

$$ {\mathbf{x}}_{i+1}={e}^{{\mathbf{A}}_{i-1}h}{\mathbf{x}}_{i-1}+{\int}_{t_{i-1}}^{t_{i+1}}{e}^{{\mathbf{A}}_{i-1}\left({t}_{i+1}-s\right)}\mathbf{B}(s)\mathbf{x}\left(s-T\right) ds $$

(26)

In Eq. (26), A_i − 1 is the abbreviation of A(t_i − 1). Since the lower limit of integral in Eq. (26) is t_i − 1, s here is given by s = t − t_i − 1. Then, the operator r(s) = B(s)x(s − T) in Eq. (26) is approximated over the interval [t_i ‐ 1, t_i + 1]. The time nodes t_i − 1, t_i, and t_i + 1 and their node values r_i − 1, r_i, and r_i + 1 are also employed for calculation. By using the second-order Newton interpolation, the approximation of r(s) is as follows:

$$ \mathbf{r}(s)=\left(1-\frac{3\mathrm{s}}{2h}+\frac{s^2}{2{h}^2}\right){\mathbf{r}}_{i-1}+\left(\frac{2\mathrm{s}}{h}-\frac{s^2}{h^2}\right){\mathbf{r}}_i+\left(\frac{s^2}{2{h}^2}-\frac{s}{2h}\right){\mathbf{r}}_{i+1} $$

(27)

The interpolation process of Eq. (27) is depicted in Fig. 4.

Fig. 4

The interpolation process of Eq. (27)

As shown in Fig. 4, the interpolation interval is [t_i − 1, t_i + 1]. The combinations (t_i − 1,r_i − 1), (t_i, r_i), and (t_i + 1, r_i + 1), which are all located in the interpolation interval, are used for calculation.

For the proposed method, Eq. (17) plays the role of a predictor, and Eq. (27) plays the role of corrector. Generally, these two equations are both obtained by using the second-order Newton interpolation, and all the combinations (t_i − 1,r_i − 1), (t_i, r_i), and (t_i + 1, r_i + 1) are employed in the calculation process. However, the interpolation intervals for obtaining Eq. (17) and Eq. (27) are different.

Equation (27) is inserted into Eq. (26); the following result can be acquired

$$ {\mathbf{x}}_{i+1}-{\mathbf{D}}_{i,0}^2{\mathbf{x}}_{i-1}={\mathbf{E}}_{i-1}{\mathbf{x}}_{i-1-T}+{\mathbf{E}}_i{\mathbf{x}}_{i-T}+{\mathbf{E}}_{i+1}{\mathbf{x}}_{i+1-T} $$

(28)

where

$$ {\mathbf{E}}_{i-1}=\left[{\mathbf{D}}_{i,0}\left(\frac{{\mathbf{D}}_{i,3}}{2{h}^2}-\frac{3{\mathbf{D}}_{i,2}}{2h}+{\mathbf{D}}_{i1}\right)+\frac{{\mathbf{D}}_{i,3}}{2{h}^2}-\frac{{\mathbf{D}}_{i,2}}{2h}\right]{\mathbf{B}}_{i-1} $$

(29)

$$ {\mathbf{E}}_i=\left[{\mathbf{D}}_{i,0}\left(-\frac{{\mathbf{D}}_{i,3}}{h^2}+\frac{2{\mathbf{D}}_{i,2}}{h}\right)-\frac{{\mathbf{D}}_{i,3}}{h^2}-{\mathbf{D}}_{i,1}\right]{\mathbf{B}}_i $$

(30)

$$ {\mathbf{E}}_{i+1}=\left[{\mathbf{D}}_{i,0}\left(\frac{{\mathbf{D}}_{i,3}}{2{h}^2}-\frac{3{\mathbf{D}}_{i,2}}{2h}\right)+\frac{{\mathbf{D}}_{i,3}}{2{h}^2}+\frac{{\mathbf{D}}_{i,2}}{2h}\right]{\mathbf{B}}_{i+1} $$

(31)

and

$$ {\mathbf{D}}_{i,0}={e}^{{\mathbf{A}}_{i-1}h} $$

(32)

$$ {\mathbf{D}}_{i,1}={\mathbf{A}}_{i-1}^{-1}\left({\mathbf{D}}_{i,0}-\mathbf{I}\right) $$

(33)

$$ {\mathbf{D}}_{i,2}={\mathbf{A}}_{i-1}^{-1}\left({\mathbf{D}}_{i,1}-h\mathbf{I}\right) $$

(34)

$$ {\mathbf{D}}_{i,3}={\mathbf{A}}_{i-1}^{-1}\left({\mathbf{D}}_{i,2}-{h}^2\mathbf{I}\right) $$

(35)

For a 2-DOF milling system with a single mode, the dimension of the matrices E_i − 1, E_i, E_i + 1, D_{i, 0}, D_{i, 1}, D_{i, 2}, and D_{i, 3} depend on the dimension of the matrix A_i − 1, where A_i − 1 is the abbreviation of A(t_i − 1). From Eq. (11) and Eq. (12), it can be found that the matrix A_i − 1 is with the dimension of 4 rows and 4 columns.

Combining Eqs. (15), (18), and (28), the following discrete map can be obtained

$$ {\mathbf{G}}_1\left[\begin{array}{c}{\mathbf{x}}_1\\ {}{\mathbf{x}}_2\\ {}\vdots \\ {}{\mathbf{x}}_m\\ {}{\mathbf{x}}_{m+1}\end{array}\right]={\mathbf{G}}_2\left[\begin{array}{c}{\mathbf{x}}_{1-T}\\ {}{\mathbf{x}}_{2-T}\\ {}\vdots \\ {}{\mathbf{x}}_{m-T}\\ {}{\mathbf{x}}_{m+1-T}\end{array}\right] $$

(36)

where

$$ {\mathbf{G}}_1=\left[\begin{array}{c}\mathbf{I}\\ {}\begin{array}{c}0\\ {}\begin{array}{c}-{\mathbf{D}}_{2,1}^2\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{c}0\\ {}\begin{array}{c}-{\boldsymbol{\Phi}}_{2,2}\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{cc}\begin{array}{c}0\\ {}\begin{array}{c}\mathbf{I}\\ {}\begin{array}{c}\mathbf{I}\\ {}\begin{array}{c}0\\ {}\begin{array}{c}-{\mathbf{D}}_{4,1}^2\\ {}\begin{array}{c}\mathbf{\vdots}\\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}-{\boldsymbol{\Phi}}_{4,2}\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\mathbf{I}\\ {}\begin{array}{c}\mathbf{I}\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\mathbf{\cdots}\\ {}\begin{array}{c}\mathbf{\cdots}\\ {}\begin{array}{c}\mathbf{\cdots}\\ {}\begin{array}{c}\mathbf{\cdots}\\ {}\begin{array}{c}\mathbf{\cdots}\\ {}\begin{array}{c}\mathbf{\ddots}\\ {}\begin{array}{c}\mathbf{\cdots}\\ {}\mathbf{\cdots}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}0\\ {}-{\mathbf{D}}_{m-1,1}^2\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}-{\boldsymbol{\Phi}}_{m-1,2}\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{l}0\\ {}\begin{array}{cc}\begin{array}{l}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}0\\ {}\begin{array}{c}\vdots \\ {}\begin{array}{c}\mathbf{I}\\ {}\mathbf{I}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& 0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right] $$

(37)

$$ {\mathbf{G}}_2=\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& \cdots & 0& 0& {e}^{{\mathrm{A}}_0 tf}\\ {}{\mathbf{F}}_1& {\mathbf{F}}_2& {\mathbf{F}}_3& 0& 0& \cdots & 0& 0& 0\\ {}{\mathbf{E}}_1& {\mathbf{E}}_2& {\mathbf{E}}_3& 0& 0& \cdots & 0& 0& 0\\ {}0& 0& {\mathbf{F}}_3& {\mathbf{F}}_4& {\mathbf{F}}_5& \cdots & 0& 0& 0\\ {}0& 0& {\mathbf{E}}_3& {\mathbf{E}}_4& {\mathbf{E}}_5& \cdots & 0& 0& 0\\ {}\vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {}0& 0& 0& 0& 0& \cdots & {\mathbf{F}}_{m-1}& {\mathbf{F}}_m& {\mathbf{F}}_{m+1}\\ {}0& 0& 0& 0& 0& \cdots & {\mathbf{E}}_{m-1}& {\mathbf{E}}_m& {\mathbf{E}}_{m+1}\end{array}0\right] $$

(38)

By using the matrixes G₁ and G₂, the Floquet transition matrix Ψ can be calculated as follows:

$$ \boldsymbol{\Psi} ={\left({\mathbf{G}}_1\right)}^{-1}{\mathbf{G}}_2 $$

(39)

The stability of the milling system can be predicted by using the module of the state transition matrix.

Remarkably, in the PCHDM [19], the periodic coefficient matrix, state term, and the time-delay term are taken as a unit, and the second-order Newton polynomial is used to approximate this unit. However, in this study, only the periodic coefficient matrix and the time-delay term are taken as an operator, and this operator is approximated by second-order Newton interpolation polynomial. Besides, the PCHDM is in the framework of FDM, while the proposed method is in the framework of SDM.

3 Comparison and discussion

3.1 Rate of convergence

The one degree of freedom (1-DOF) milling system is usually used for the analysis of rate of convergence [11,12,13,14,15,16,17,18,19,20,21]. For the 1-DOF milling system, the matrixes B(t) and A(t) in Eq. (10) are given as follows:

$$ {\mathbf{A}}_0=\left[\begin{array}{cc}0& 1\\ {}-{\omega}_n^2& -2{\xi \omega}_n\end{array}\right] $$

(40)

$$ \mathbf{B}(t)=\left[\begin{array}{cc}0& 0\\ {}\frac{a_ph(t)}{m_t}& 0\end{array}\right] $$

(41)

$$ \mathbf{A}(t)={\mathbf{A}}_0-\mathbf{B}(t) $$

(42)

where the modal mass, damping ratio, and angular natural frequency are denoted as m_t, ξ, and ω_n, respectively, a_p is the axial depth of cut, and h(t) is a function of time and it is defined as

$$ h(t)=\sum \limits_{j=1}^Ng\left({\varphi}_j(t)\right)\sin \left({\varphi}_j(t)\right)\left({K}_t\cos \left({\varphi}_j(t)\right)+{K}_n\sin \left({\varphi}_j(t)\right)\right) $$

(43)

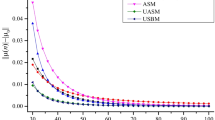
The rate of convergence is often used to estimate the accuracy of the stability prediction methods. It reflects how the local discretization error varies with the increase of the parameter m, where the local discretization error is the difference between the approximated module of the state transition matrix |μ(m)| and exact one |μ₀|. In this work, the classical 1st SDM [8] and recently proposed methods PCHDM [19], 2nd SDM [9], and UNIM [30] are taken as the benchmark. The value calculated by the 1st SDM with m = 1000 is taken as the value of |μ₀|. The spindle speed (Ω = 5000 rpm) and axial depths of cut (w = 0.2, 0.5, 1.0 mm), which are the commonly used values in many works of literature, are also employed in this study. In the calculation process, the cutter teeth number is N = 2, and the radial immersion ratio is a/D=1, down milling. The cutting force coefficients and modal parameters are adopted from ref. [7], and they are as follows: the angle natural frequency is ω_n = 5793 rad/s, the relative damping ratio is ζ = 0.011, the modal mass of the tool is m_t = 0.03993 kg, and the tangential and normal cutting force coefficients are K_t = 6 × 10⁸ N/m², and K_n = 2 × 10⁸ N/m², respectively. The rate of convergence of the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method is described in Fig. 5.

Fig. 5

The rates of convergence of the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method. a a_p = 0.2 mm, |μ₀| = 0.819723. b a_p = 0.5 mm, |μ₀| = 1.073920. c a_p = 1.0 mm, |μ₀| = 1.406373

As shown in Fig. 5, the UNIM converges faster than the other methods when the axial depth of cut is a_p = 0.2 mm. However, it converges slower than the 2nd SDM and the proposed method when a_p is chosen as 1.0 mm. Similarly, the rate of convergence of the 2nd SDM is higher than the other methods when a_p is set as 1.0 mm. However, it converges slower than the PCHDM, UNIM, and the proposed method when a_p equals to 0.2 mm. That is, the robustness of the rate of convergence of the UNIM and 2nd SDM requires further improvement. Besides, although the PCHDM and the proposed method are both predictor-corrector scheme-based methods, the proposed method converges faster than the PCHDM under different parameter combinations. Overall, the proposed method is superior compared with the benchmark methods in terms of the rate of convergence. Besides, the robustness of the rate of convergence of the proposed method is also good.

3.2 Stability lobe diagram for 1-DOF milling system

To further evaluate the accuracy and efficiency of the stability prediction methods, the stability lobe diagrams calculated by the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method are obtained. The stability lobe diagrams are computed on a parameter plane of spindle speed and axial depth of cut, where the spindle speed belongs to the interval [5000, 10000] rpm, the axial depth of cut belongs to the interval [0, 0.01] m. The parameter plane includes an equidistance grid with the size of 200 × 200. The stability lobe diagrams calculated by the PCHDM with m = 300 is taken as the reference. The stability lobes calculated by different methods with m = 30 and 40 are presented. Figure 6 shows the stability lobe diagrams as well as the computational time for different methods under full immersion condition (a/D = 1), down milling.

Fig 6

The stability lobe diagrams calculated by the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method under full immersion condition (a/D = 1) for 1-DOF milling system

As shown in Fig. 6, the proposed method takes less time than the 1st SDM and 2nd SDM to obtain stability lobe diagrams. Therefore, the efficiency of the proposed method is proved to be good. For a 1-DOF milling system under full immersion condition, although the proposed method takes more time than the PCHDM and UNIM to obtain the stability charts, the stability lobe diagrams obtained by the proposed method are much closer to the reference than those obtained by the PCHDM and UNIM, especially in the peak of the lobes. That is, the 1st SDM, PCHDM, 2nd SDM, and UNIM may fall short of the stability prediction when the parameters are around the peak of the lobes. In the 2nd SDM, the precise integration scheme is adopted to improve the computational efficiency. It should be noted that the precise integration scheme is not used in the calculating process by using the 2nd SDM and the proposed method in this study. Therefore, the computational efficiencies of the 2nd SDM and the proposed method can be further improved if the precise integration scheme is adopted in the calculation process.

To further evaluate the effectiveness of the proposed method, the stability lobe diagrams obtained by different methods with a/D = 0.05 are also presented, as shown in Fig. 7.

Fig 7

The stability lobe diagrams calculated by the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method with a/D = 0.05 for 1-DOF milling system

From Fig. 7, it can be found that the stability lobe diagrams obtained by the PCHDM, UNIM, and the proposed method are more accurate than those obtained by the 1st SDM and 2nd SDM. The comparison result indicates that the prediction accuracy of the SDM can be improved by combining the predictor-corrector scheme.

3.3 Stability lobe diagram for 2-DOF milling system

In this section, the stability lobe diagrams calculated by the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method are obtained for the 2-DOF milling system. In the calculation process, the dynamics of the milling system in the X and Y directions are considered. The modal parameters are also derived from ref. [7], and they are assumed to be equal in X and Y directions. The detailed modal parameters are as follows: the angle natural frequencies are ω_nx = ω_ny = 5793 rad/s, the relative damping ratios are ζ_x = ζ_y = 0.011, and the modal masses of the tool are m_x = m_y = 0.03993 kg. The tangential and normal cutting force coefficients are still chosen as K_t = 6 × 10⁸ N/m² and K_n = 2 × 10⁸ N/m², respectively.

In the parameter plane, the spindle speed belongs to the interval [5000, 25000] rpm, and the axial depth of cut belongs to the interval [0, 0.01] m. The reference is also the stability lobe diagram calculated by the PCHDM with m = 300. The stability lobes calculated by different methods under the full immersion condition (a/D = 1) for a 2-DOF milling system are shown in Fig. 8.

Fig 8

The stability lobe diagrams calculated by the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method with a/D = 1 for a 2-DOF milling system

The stability lobe diagrams calculated by different methods under low immersion condition (a/D = 0.05) for a 2-DOF milling system are also obtained, as shown in Fig. 9.

Fig 9

The stability lobe diagrams calculated by the 1st SDM, PCHDM, 2nd SDM, UNIM, and the proposed method with a/D = 0.05 for a 2-DOF milling system

From Fig. 8, it shows that all the methods can predict the stability of milling for a 2-DOF system under full immersion condition accurately. However, as shown in Fig. 9, the PCHDM, UNIM, and the proposed method are more accurate than the 1st SDM and 2nd SDM under the low immersion condition (a/D = 0.05). The results about the 2-DOF milling system further demonstrate that the prediction accuracy of the SDM can be improved through combining the predictor-corrector scheme.

4 Conclusion

This study presents a new semi-discretization method based on predictor-corrector scheme for milling stability analysis. In this study, the time-delay term and the periodic coefficient matrix are taken as an operator and approximated by second-order interpolation polynomial. The main conclusions sum up as follows:

• (1) Generally, the proposed method is superior compared with the benchmark in terms of the rate of convergence. In addition, the proposed method is also a robust method.

• (2) Although the PCHDM and the proposed method are both predictor-corrector scheme-based methods, the proposed method converges faster than the PCHDM under different parameter combinations.

• (3) The proposed method takes less time than the 1st SDM and 2nd SDM to obtain stability lobe diagrams. For a 1-DOF milling system under full immersion condition (a/D = 1), although the proposed method takes more time than the PCHDM and UNIM to obtain the stability charts, the stability lobe diagrams obtained by the proposed method is much closer to the reference than those obtained by the PCHDM and UNIM, especially in the peak of the lobes.

• (4) The prediction accuracy of the SDM can be improved by combining the predictor-corrector scheme.