1 Introduction

In the process of sheet metal forming, the existence of elastic deformation leads to the inevitable springback, and the research on springback in sheet metal forming has never stopped. In order to realize the effective control of springback, two methods of process control and die surface compensation control are generally adopted in engineering. The process control method is to control the springback by adjusting the blank holder force, punch stroke and other parameters [1, 2], changing the loading method [3, 4], increasing the forming steps [5, 6], and increasing the forming temperature [7, 8], etc.

After years of research, engineers have gained a relatively clear theoretical understanding of bending springback. The unloading process of the workpiece during forming is equivalent to the reverse loading process of the workpiece [9]. According to this theory, the springback amount of various processes can be characterized, so that the springback law of metal parts can be preliminarily predicted and the next process parameters can be corrected and compensated. Lansheng Xie et al. [10] discussed two factors affecting springback amount for asymmetric stretch-bending forming process of T-section aluminum profile. They are pre-tension and supplementary tension. The results show that the springback decreases with the increase of pretension and decreases with the increase of supplementary tension. When the two influencing factors increase to a certain extent, the impact on the resilience is not obvious. Zhiping Qian [11] et al. used a special stretch-bending process to conduct stretch-bending rebound experiment on automotive guide profiles, filling the cavity of profiles with supporting materials and applying lateral pressure during stretch-bending, which effectively reduced the section distortion of profiles. Through theoretical analysis, they obtained the springback formula of stretch-bending profiles. Dianqi Li et al. [12, 13] analyzed the stress–strain relationship of metal pipe under bending conditions. They studied the relationship between springback angle and material elastic modulus E, material hardening coefficient n, plasticity coefficient K and pipe wall thickness t, as well as the relationship between springback angle and bending angle and curvature radius during bending. Jinwu Liu et al. [14] derived the calculation formula of springback bending moment of rectangular cross section bar by analyzing the process of bending springback stress and strain. They proposed a method to improve the calculation accuracy of springback angle by analyzing the source of calculation error of the calculation formula of classical springback bending moment.

With the development of numerical simulation technology, the shortcomings of experimental methods have been effectively overcome, and a series of springback compensation strategies have been gradually proposed [15,16,17]. The commonly used methods are Powerful Descriptor method (FDM) [18, 19] and displacement adjustment method (DA) [20]. Xiaohui Cui et al. [21] proposed an electromagnetic zonal forming method which is convenient for precise machining and accurate springback control of single curvature parts. The deformation and stress–strain distribution of sheet metal were analyzed by numerical simulation. Xiaohui Cui et al. [22] used electromagnetic assisted stamping (EMAS) with magnetic force reverse loading to control springback.

The iterative compensation mechanism for plane bending proposed in this paper is designed to reduce the work of mold repair, so that the forming parts can reach the expected value after finite compensation of the iterative parameters, which is of great significance for practical engineering applications. After proving the theory of the iterative compensation mechanism for plane bending theoretically, the feasibility of the iterative compensation mechanism for plane bending is also verified from the perspective of experimental analysis.

2 Theoretical and Experimental Study on Iterative Compensation of Uniform Curvature

2.1 Bending Springback Iterative Method

When discussing the factors affecting springback, Yunxi Wang [23] clearly pointed out that "the larger the bending angle is \(\alpha\), the longer the deformation zone will be, and the larger the springback accumulation will be, so the springback angle \(\Delta \phi\) will be." Jingrong Xiao et al. [24] also emphasized that "the larger the bending angle is, the larger the proportion of elastic deformation in the total deformation will be, and the larger the rebound value will be. Therefore, for ordinary metal materials, when the deformation condition is not changed, the greater the deformation is, the greater the springback is. It is also the theoretical basis of this paper.

Suppose \(f(x)\) is the function relation of the control parameter before and after springback, then the springback quantity can be expressed as

$$\Delta \left( x \right) = x - f(x)$$
(1)

According to the above theoretical basis, if \(\Delta \left( x \right)\) is a monotone increasing function, mean \(\Delta^{\prime } \left( x \right) > 0\). Then

$$f^{\prime } (x) < 1$$
(2)

The purpose of springback control is to determine a springback pre-value \(a\), so that its springback post-value \(a_{p}\) satisfies the following relationship:

$$f(x) - a_{p} = 0$$
(3)

For this reason, a simple iterative method [25] was introduced, and an iterative equation was constructed according to its idea of finding the root.

$$x = x + a_{p} - f(x) = \varphi \left( x \right)$$
(4)

It can be seen from Eq. (2)

$$\left| {\varphi^{^{\prime}} (x)} \right| < 1$$
(5)

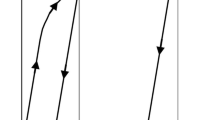
According to the local convergence theorem of the simple iterative method, the iterative Eq. (4) is convergent, that is, \(x^{*}\) satisfies \(x^{*} = \varphi \left( {x^{*} } \right)\). Therefore, as shown in Fig. 1, the initial value is \(a_{p}\), and the iterative sequence is obtained according to the iterative equation.

$$\begin{array}{*{20}c} {x_{0} = a_{p} } \\ {x_{1} = x_{0} + a_{p} - f\left( {x_{0} } \right)} \\ {x_{2} = x_{1} + a_{p} - f\left( {x_{1} } \right)} \\ \cdots \\ {x_{i} = x_{i - 1} + a_{p} - f\left( {x_{i} } \right)} \\ \cdots \\ {x_{k} = x_{k - 1} + a_{p} - f\left( {x_{k} } \right)} \\ \end{array}$$
(6)
Fig. 1
figure 1

Parameters relation curve before and after springback based on simple iterative method

Full size image

For the advance set the value error \(\varepsilon\), when \(\left| {x_{k} - x_{k - 1} } \right| \le \varepsilon\), it is considered that \(x^{*} \approx x_{k}\) and \(f(x^{*} ) - a_{p} = 0\). It is the desired.

For the springback control problem, the parameter function before and after springback \(y = f(x)\) can be constructed. And \(f^{^{\prime}} (x) < 1\) is a necessary condition for iterative convergence. The springback calculation problem can be transformed into the root solution of the implicit equation. Although the test method can give the error with the target quantity, there is no theoretical guidance to determine the next compensation quantity. The iterative compensation in this paper is based on theoretical analysis \(f^{^{\prime}} (x) < 1\) to determine the iteration convergence, and then based on the springback amount of each test to determine the next compensation amount.

2.2 Theory and Experiment of Springback Compensation for Uniform Curvature Free Bending

2.2.1 Theory and Experiment of Curvature Compensation for Free Bending Neutral Layer

According to the classical unloading theory, the springback of curvature is as follows:

$$\Delta K = K - K^{\prime } = \frac{1}{\rho } - \frac{1}{{\rho^{\prime } }} = \frac{M}{EI}$$
(7)

where \(K\) is the curvature of the neutral layer before unloading, \(K^{^{\prime}}\) is the sheet material the curvature of the neutral layer after unloading, \(\rho\) is radius of neutral layer before unloading, \(\rho^{^{\prime}}\) is radius of neutral layer after unloading, \(M\) is load bending moment before unloading of sheet metal. The post-springback curvature is obtained from the loading moment and the springback value of the elastic plastic bending deformation:

$$K^{\prime} = \left( {1 - \frac{D}{E}} \right) \cdot \left[ {K + \frac{4}{{K^{2} t^{3} }} \cdot \left( {\frac{{\sigma_{s} }}{E}} \right)^{3} } \right] - \frac{{3\sigma_{s} }}{Et}\left( {1 - \frac{D}{E}} \right)\;\;\left( {K > \frac{{2\sigma_{s} }}{tE}} \right)$$
(8)

where \(D\) is the plastic line cutting modulus, \(E\) is elastic modulus, \(\sigma_{s}\) is yield stress, \(t\) is thickness of sheet. Therefore, the curvature elastic complex expression of neutral layer in free bending of sheet metal is:

$$K^{\prime} = f_{k} \left( K \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left( {0 \le K \le \frac{{2\sigma_{s} }}{tE}} \right)} \hfill \\ {\left( {1 - \frac{D}{E}} \right)\left[ {K + \frac{4}{{K^{2} t^{3} }} \cdot \left( {\frac{{\sigma_{s} }}{E}} \right)^{3} - \frac{{3\sigma_{s} }}{tE}} \right]} \hfill & {\left( {K > \frac{{2\sigma_{s} }}{tE}} \right)} \hfill \\ \end{array} } \right.$$
(9)

When \(K > \frac{{2\sigma_{s} }}{tE}\),

$$0 < \frac{{{\text{d}}K^{\prime } }}{{{\text{d}}K}} = \left( {1 - \frac{D}{E}} \right)\left( {1 - \left( {\frac{{2\sigma_{S} }}{tE}} \right)^{3} /K^{3} } \right) < 1 - \frac{D}{E} < 1$$
(10)

As can be seen from the above equation, the curvature of the neutral layer can be used as the iterative parameter to carry out compensation operation, which can make it reach the predetermined engineering value.

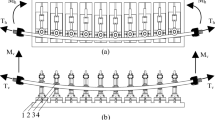
According to the iterative compensation strategy proposed above, experimental verification is carried out, and the experimental scheme is shown in Fig. 2. In this experiment, "bending die and gasket" is used to form the slab, which can be equivalent to another radius of bending die forming the slab. Now the "bending die and gasket" is called the equivalent upper die, to achieve the bending radius of the micro-segment change.

Fig. 2
figure 2

Curvature iteration compensation experimental die

Full size image

Forming force will increase sharply during the final forming of the slab. In order to prevent overloading of the testing machine, the maximum load of the testing machine is limited to 100kN. In addition, the computer interface is used to set the maximum pressure of bending die.

$$H_{{\lim }} = (r_{1} + \rho _{{in}} + t) \cdot \left( {1 - \cos \left( {\arcsin \left( {\frac{L}{{r_{1} + \rho _{{in}} + t}}} \right)} \right)} \right)$$
(11)

where \(r_{1}\) is the chamfering radius of lower die circle,\(\rho_{{{\text{in}}}}\) is inner diameter of billet in the coating area at the end of loading, L is distance from center of chamfer of lower die. The actual expression of each quantity in the above equation is shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of the experiment

Full size image

In order to facilitate the measurement of experimental data, the bending radius \(\rho\) is controlled and measured during the test process, and converted to curvature \(K\) for analysis and calculation. The following takes the target bending radius \(\rho^{d}\) of 70 mm as an example to detail its compensation process.

Taking the target value as the initial iteration value, the radius \(\rho_{1}\) of the upper die of the first bending is \(70.021\,{\text{mm}}\). After the slab is covered with the upper die, it is unloaded and the bending radius after springback \(\rho_{1}^{^{\prime}}\) is measured. It is \(73.072\,{\text{mm}}\). The compensation error \(\left| {K_{1}^{^{\prime}} - K^{\prime } } \right|\) is \(59.940 \times 10^{ - 5} {\text{mm}}^{ - 1}\). If the accuracy requirement is not met, the second compensation is made. The second bending curvature \(K_{{{\text{next}}}}^{1} = K_{i} + \left| {K_{i - 1}^{^{\prime}} - K^{^{\prime}} } \right|\) is \(1488.08 \times 10^{ - 5} {\text{mm}}^{ - 1}\). The radius of the upper die \(\rho_{{{\text{next}}}}^{1} = 1/K_{{{\text{next}}}}^{1}\) of the secondary bending can be adjusted by the gasket, and repeat the above operation, and adjust to the third time to meet the accuracy requirements, and the compensation is over.

Through three compensations, the error can be controlled within 0.1%. As can be seen from Table 1, with the increase of compensation times, the compensation error decreases rapidly. The iterative parameters approach the target value rapidly. It is shown that for the free bending process, the bending curvature can be used as the iterative parameter, and the size of the upper die can be determined by finite iteration compensation, so that the forming parts meeting the precision requirements can be obtained.

Table 1 Curvature iteration compensation calculation
Full size table

2.2.2 Theory and Experiment of Sheet Metal Bending Angle Compensation

According to the invariant length theory of the neutral layer, it can be known that:\(\rho \alpha = \rho^{\prime}\alpha^{\prime}\), then the elastic complex angle is:

$$\Delta \alpha = \alpha - \alpha^{\prime } = \frac{M}{EI}\rho \alpha-\frac{M}{EI}\rho^{\prime } \alpha^{\prime }$$
(12)

The relationship between \(\alpha\) and \(\alpha^{\prime }\) is shown in Fig. 4. The elastic complex expression of the bending angle of free bending of sheet metal can be obtained by the loading bending moment and elastic recovery angle of elastic–plastic bending deformation:

$$\alpha^{\prime} = f_{\alpha } (\alpha ) = \begin{array}{*{20}c} {\left\{ {1 - \frac{D}{E} + \left( {1 - \frac{D}{E}} \right) \cdot \frac{{\sigma_{S} }}{E} \cdot \frac{\rho }{t} \cdot \left[ {4 \cdot \left( {\frac{{\sigma_{s} }}{E}} \right)^{2} \cdot \left( {\frac{\rho }{t}} \right)^{2} - 3} \right]} \right\} \cdot (\alpha + \alpha_{0} )} & {\left( {0 < \frac{\rho }{t} \le \frac{E}{{2\sigma_{S} }}} \right)} \\ \end{array}$$
(13)

where \(\alpha_{0}\) is the corrected constant of the bending angle of the sheet material before unloading. In fact, it is known that the radius of the neutral layer \(\rho\) is independent of the bending angle of the sheet material \(\alpha\), so to verify the convergence of the bending Angle, the derivative of the bending Angle after unloading is taken with respect to the bending Angle before unloading. And since this is less than 1, this is less than 1−D/E, and it is less than 1.

$$0 < \frac{{{\text{d}}\alpha^{\prime } }}{{{\text{d}}\alpha }} = \begin{array}{*{20}c} {\left( {1 - \frac{D}{E}} \right)\left\{ {1 + \frac{{\sigma_{s} }}{E} \cdot \frac{\rho }{t} \cdot \left[ {4\left( {\frac{{\sigma_{s} }}{E} \cdot \frac{\rho }{t}} \right)^{2} - 3} \right]} \right\} < 1 - \frac{D}{E} < 1} & {\left( {0 < \frac{\rho }{t} \le \frac{E}{{2\sigma_{s} }}} \right)} \\ \end{array}$$
(14)
Fig. 4
figure 4

Schematic diagram of free bending Angle of sheet metal

Full size image

It can be known \(0 < \frac{{{\text{d}}\alpha^{^{\prime}} }}{{{\text{d}}\alpha }} < 1 - \frac{D}{E} < 1\) from the above formula. Then the free bending angle of sheet metal can be used as the iterative parameter to make compensation operation, so that it can reach the predetermined engineering value.

According to the iterative compensation strategy proposed above, experimental verification is carried out. The experimental scheme is shown in Fig. 5.

Fig. 5
figure 5

Bending angle iterative compensation experiment die

Full size image

In view of the above analysis, the compensation process is set as follows: taking the target value of the slab bending angle \(\alpha^{d}\) is 120°as an example, and the initial value of the coating angle is set as:\(\varphi_{1} = 180^{o} - \alpha^{d}\). Then, according to Eq. (11), the reduction amount \(H_{\lim }\) of the upper module is limited at the test control interface. After the upper die stops descending, the bending angle of the slab \(\alpha_{1}\) before springback is measured. After the upper die is moved up and unloaded, the bending angle of the slab \(\alpha^{\prime}_{1}\) after springback is measured. The next bend is \(\alpha_{{{\text{next}}}} = \alpha_{i - 1} + \alpha_{i}^{^{\prime}} - \alpha_{i}\). The second step compensates by setting the second coating angle as:\(\varphi_{2} = 180^{o} - \alpha_{{{\text{next}}}}\). The others are similar to the first one. After the third compensation, the post-rebound bend angle value \(\alpha_{3}^{^{\prime}}\) is 120.591°. The compensation error is 0.591°, which is already within the fluctuation error range of \(\pm {1}^\circ\). The compensation results are shown in Table 2. It is shown that the bending angle can be used as the iterative parameter for the free bending process, and the forming parts meeting the precision requirements can be obtained through finite iteration compensation.

Table 2 Compensation test results of slabs with a target Angle of 120°
Full size table

2.3 Theory and Experiment of Central Layer Radius Compensation in Stretch-bending

Section stress at the end of plate stretching:

$$\sigma_{T} = \frac{T}{A}$$
(15)

where \(T\) is the loading load at the end of stretching, A is rectangular cross-sectional area.

Section strain at the end of plate stretching:

$$\varepsilon_{T} = \frac{{\sigma_{T} - \sigma_{s} }}{D} + \frac{{\sigma_{s} }}{E}$$
(16)

Strain neutral layer radius:

$$\rho_{\varepsilon } = \frac{{k^{ * } t + \rho }}{{1 + \varepsilon_{T} }}$$
(17)

\(k^{ * }\) is obviously the material constant, and its expression is \(k^{*} = \frac{1}{2} \cdot \frac{{\sqrt {D/E} - 1}}{{\sqrt {D/E} + 1}}\).

The elastic combination process of the first bending and then drawing process is

$$\rho^{\prime } = - \frac{1}{{4k^{ * } (1 + k^{ * } )}}\left[ {\rho - \frac{{\sigma_{T} }}{{E(1 + \frac{{\sigma_{T} - \sigma_{s} }}{D} + \frac{{\sigma_{s} }}{E})}}\left( {\rho + k^{ * } t} \right)} \right]$$
(18)

Characteristics of stretch-bending process is

$$\frac{{{\text{d}}\rho^{\prime } }}{{{\text{d}}\rho }}^{{}} = - \frac{1}{{4k^{ * } (1 + k^{ * } )}} \cdot \left[ {1 - \frac{{\varepsilon_{T} \cdot D/E + \sigma_{s} /E \cdot (1 - D/E)}}{{1 + \varepsilon_{T} }}} \right]$$
(19)

For general materials, it is known that \(0 < \frac{D}{E} < 0.2\) and \(k^{*} = \frac{1}{2} \cdot \frac{{\sqrt {D/E} - 1}}{{\sqrt {D/E} + 1}}\).

So

$$1 < \frac{2}{{(1 + k^{ * } )(2k^{ * } - 1)^{2} }} = - \frac{{1 - \frac{D}{E}}}{{4k^{ * } (1 + k^{ * } )}} < \frac{{{\text{d}}\rho^{^{\prime}} }}{{{\text{d}}\rho }} < - \frac{1}{{4k^{ * } (1 + k^{ * } )}} < \frac{\sqrt 5 + 1}{2} < 2$$
(20)
$${\text{Provided that}}:,{\text{ there is obviously}}\,0 < 0.5 < 0.5 \cdot \frac{{{\text{d}}\rho^{^{\prime}} }}{{{\text{d}}\rho }} < 1$$
(21)

From the above equation, it can be seen that the radius of the center layer of sheet metal stretch-bending can be used as the iterative parameter to carry out compensation operation, which can make it reach the predetermined engineering value.

According to the iterative compensation strategy proposed above, experimental verification is carried out, as shown in Fig. 6. The stretch-bending experimental system consists of a stretch-bending testing machine (Fig. 6a), signal monitoring equipment (Fig. 6b) and measuring equipment (Fig. 6c). The stretching process before bending is carried out according to the following steps. First, the stretching cylinders on both sides are fixed at appropriate equidistant positions. Adjust the stretching length L through the limit device of the stretching barrel. Then, the specimen is installed, and the tensile cylinder provides a certain tension to the specimen. After that, the bending cylinder comes into play and drives the bending die forward to complete the bending process. Finally, the loading is stopped and the specimen is removed. The radius of the neutral layer after springback \(\rho^{\prime }\) is measured by CMM, as shown in Fig. 6d.

Fig.6
figure 6

a Stretch–bending testing machine; b Signal monitoring equipment; c and d Measuring equipment; e Concrete structure of the actuator: 1-tension sensor, 2-jigs, 3-specimen, 4-bending cylinder, 5-bending mould, 6-stretch cylinder

Full size image

The compensation test with the target radius \(\rho^{d}\) of central layer of 231 mm is taken as an example, the compensation operation process of ST12 sheet material under ordinary stretch-bending process: First of all, the "bending die and gasket" (that is, "equivalent bending die") is used to calculate the value of the radius of the next neutral layer to form the slab, so that the center layer radius of the slab before the first springback is the target value \(\rho^{d}\). The outer diameter of the slab after the springback \(\rho_{{{\text{out}}}}\) is measured, and the center layer radius after the springback \(\rho^{\prime }\) is obtained. The compensation error is calculated to determine whether it can meet the requirements of engineering application. From \(\rho_{{{\text{next}}}} = \rho_{i}^{^{\prime}} + 0.5\left( {\rho^{d} - \rho_{{_{i - 1} }}^{^{\prime}} } \right)\) can calculate the radius of the next time, the second step compensates and sets the coating angle of the second time as \(\rho_{{{\text{next}}}}\), and the rest is similar to the first time.

As can be seen from the data in Table 3, the compensation error gradually decreases with the increase of compensation times. For the compensation test of \(\rho^{d}\) is 231 mm, the compensation error is 0.47 mm, which is within the error range of 0.5 mm. It is shown that the neutral layer radius can be used as the iterative parameter to obtain the forming parts that meet the requirements of precision through finite iteration compensation.

Table 3 Compensation test results for target radius of sheet material center layer of 231 mm
Full size table

3 Theory and Experiment of Free Bending Compensation with Variable Curvature

3.1 Theory of Iterative Compensation Mechanism

Since the length of the neutral layer of the work piece remains unchanged in bending, the curvature change of the neutral layer can accurately represent the bending degree change. Elastic–plastic bending occurs in sheet metal. The bending radius is always larger. The curvature and bending angle are always smaller after the unloading of external force. The theory is mathematically verifiable.

When \(K > \frac{{2\sigma_{s} }}{E}\), The derivative of \(K^{\prime }\) will be:

$$\frac{{{\text{d}}K^{^{\prime}} }}{{{\text{d}}K}} = (1 - \frac{D}{E}) \cdot \left[ {1 - \left( {\frac{{\sigma_{s} }}{E}} \right)^{3} /K^{3} } \right]$$
(22)

After sorting, the following can be obtained:

$$0 < \frac{{{\text{d}}K^{^{\prime}} }}{{{\text{d}}K}} < 1 - \frac{D}{E} < 1$$
(23)

The convergence of iterative compensation parameter in numerical analysis is satisfied, which indicates that the curvature can be used as the iterative compensation parameter in the free bending process of sheet metal. Similarly, in order to verify the convergence of the bending angle, the derivative of the bending angle after unloading with respect to the bending angle before unloading is:

$$\begin{array}{*{20}c} {\frac{{{\text{d}}\alpha^{\prime } }}{{{\text{d}}\alpha }} = \left( {1 - \frac{D}{E}} \right) \cdot \left\{ {1 + \frac{{\sigma_{S} }}{E} \cdot \frac{\rho }{{\text{t}}} \cdot \left[ {4 \cdot (\frac{{\sigma_{S} }}{E} \cdot \frac{\rho }{{\text{t}}})^{2} - 3} \right]} \right\}} & {0 < \frac{\rho }{{\text{t}}} \le \frac{E}{{2\sigma_{S} }}} \\ \end{array}$$
(24)

After sorting, the following can be obtained:

$$0 < \frac{{{\text{d}}\alpha^{^{\prime}} }}{{{\text{d}}\alpha }} < 1 - \frac{D}{E} < 1$$
(25)

It also meets the convergence requirement of iterative compensation parameter in numerical analysis. But the bending angle correction is introduced into the elastic compound equation of bending angle. However, the modified values of bending angle of different models are different, so the curvature is often used as the iterative compensation parameter in bending process.

3.2 Mathematical Basis of Iterative Compensation Mechanism

The length of the neutral layer remains constant when elastoplastic deformation occurs. Therefore, in the study of the springback process with variable curvature, the coordinates of the springback and compensated data points can be obtained by the arc length restriction condition. The corresponding curvature can be obtained by the elastic compound equation and the compensation method. The coordinates and curvature values of each data point are determined by the restriction conditions of arc length and curvature. The function equations of springback and correction compensation can be solved.

3.2.1 Arc length and its Limitation Conditions

When the object of study is a curve, arc length is often introduced as a parameter. For the same data point \({\text{Node}} - i,i = 0,1,...,n\), when the fixed point \(x = \eta\) is set for analysis. The corresponding coordinate before springback is written as \(x_{0 - i}\), and the corresponding coordinate after springback is written as \(x_{0s - i}\). After the curvature is iteratively compensated, the coordinate corresponding to the data point is \(x_{1 - i}\). At this point, on the curves before and after springback and after compensation, the arc length to the fixed point \(x = \eta\) to \({\text{Node}} - i\) can be respectively expressed as:

$$\left\{ \begin{gathered} L_{0} = \int\limits_{\eta }^{{x_{0 - i} }} {\sqrt {1 + \left( {y_{0} } \right)^{^{\prime}2} (x)} {\text{d}}x} \hfill \\ L_{0s} = \int\limits_{\eta }^{{x_{0s - i} }} {\sqrt {1 + \left( {y_{0s} } \right)^{^{\prime}2} (x)} {\text{d}}x} \hfill \\ L_{1} = \int\limits_{\eta }^{{x_{1 - i} }} {\sqrt {1 + \left( {y_{1} } \right)^{^{\prime}2} (x)} {\text{d}}x} \hfill \\ \end{gathered} \right.$$
(26)

It is known that \(L_{0} = L_{0s} = L_{1}\), in order to reduce the error, the equivalence relation in the calculation is springback calculation \(L_{0} = L_{0s}\) and iterative compensation calculation \(L_{0} = L_{1}\).

3.2.2 Curvature Constraint Condition

For the same data points \({\text{Node}} - i\), the corresponding X coordinate on the type surface is \(x_{0 - i}\); after springback, the corresponding X coordinate is \(x_{0s - i}\); after iterative compensation for curvature, the corresponding X coordinate of the data point is:\(x_{1 - i}\). Therefore, the curvature of data points \({\text{Node}} - i\) is expressed as:

$$K_{{{\text{Node}} - i}} = K_{x0 - i} = \frac{{y_{0 - i}^{^{\prime\prime}} }}{{[1 + (y_{x0 - i}^{^{\prime}} )^{2} ]^{3/2} }}$$
(27)
$$K_{{{\text{Node}} - i}}^{'} = K_{{x0s - i}} = \frac{{y_{{0s - i}}^{{''}} }}{{[1 + (y_{{x0s - i}}^{'} )^{2} ]^{{3/2}} }}$$
(28)

For the elastic model of continuous curvature sheet material in free bending, it is considered that the curvature relation of each data point of continuous curvature equation satisfies the curvature elastic complex equation of neutral layer in uniform curvature plane bending. So the relation is as follows:

$$K_{{{\text{Node}} - i}}^{^{\prime}} = \left\{ {\begin{array}{*{20}c} 0 & {\left( {K_{{{\text{Node}} - i}} \le \frac{{2\sigma_{S} }}{tE}} \right)} \\ {\left( {1 - \frac{D}{E}} \right) \cdot \left[ {K_{{{\text{Node}} - i}} + \frac{4}{{K_{{{\text{Node}} - i}}^{2} t^{3} }} \cdot \left( {\frac{{\sigma_{S} }}{E}} \right)^{3} - \frac{{3\sigma_{S} }}{Et}\left( {1 - \frac{D}{E}} \right)} \right]} & {\left( {K_{{{\text{Node}} - i}} > \frac{{2\sigma_{S} }}{E}} \right)} \\ \end{array} } \right.$$
(29)

In fact, in many engineering problems, it is often necessary to determine the relationship between two variables, and determine the function expression between two variables according to their pairs of data values. Thus, the approximate expression obtained is called an empirical formula. After the empirical formula is obtained, the data or empirical values obtained in the production or experiment can be analyzed theoretically.

3.3 Experimental Verification and Results

The curve equation of the bending die is determined by the target shape of the sheet material. The actual shape of the sheet material after unloading and springback is measured. The least square method is used to fit the measured data, and the curve equation of the formed parts is obtained. The curvature iterative compensation theory is used to compensate the curvature of the bending die during the initial loading, and the curve of the forming die is modified. The curvature of each point approximates the target value within the allowable error range until the shape of the springback meets the target shape. At the end of each load-unloading process, the forming condition of sheet metal is observed to determine whether iteration compensation is needed.

In the bending experiment, the four models of sheet metal have elastoplastic deformation. The target shape is taken as the shape of the die surface. After the first loading and unloading process, the four forming parts are observed. After deformation, the thickness of the sheet material is uniform, and no extrusion thinning or fracture occurred, indicating that the experimental scheme is feasible. After checking the overall condition of the sheet material is intact, data analysis is carried out on the experimental results.

Each forming part is measured separately, and the measured result is the data point in the three-dimensional space. Each data point is projected onto the datum plane initially set to obtain the plane coordinate value of each measurement point.

Curve fitting is carried out for the sheet metal coordinate information after the springback of the four measured models. The fitting results are shown in Table 4.

Table 4 Sheet metal curve fitting results of the four models after the first bending test
Full size table

After the curve equation of the first forming part is obtained, the curvature is modified. According to the curvature restriction condition and arc length restriction condition, the compensated profile curve is obtained. Seeing Table 5 for the curve equations of the profile after curvature compensation by the four models.

Table 5 Profile curve equation
Full size table

After determining the profile curve of the compensation die, the experimental operation is repeated. After the compensation experiment, the sheet metal forming part is obtained, as shown in Fig. 7.

Fig. 7
figure 7

the formed part after the second bending and springback

Full size image

Coordinate measurement is carried out on the specimen obtained from the compensation experiment. Fitting the function curve of the related type to the measured data. Whether the iteration process is over is judged from the coefficient value of the functional equation expression. The curve results of data fitting function are shown in Table 6. As can be seen from Table 6, after the compensation experiment, the curve fitting results of the springback of the sheet metal reached the expected value on the parameter values. It is judged that the iterative compensation process of the four models is over, and the target specimen can be obtained by the bending loading of the compensating die.

Table 6 Sheet metal curve fitting results of the four models after the compensation experiment
Full size table

4 Theory and Experiment of Stretch-bending Compensation with Variable Curvature

4.1 Iterative Compensation Theory of Variable Curvature Stretch-bending Process

For the sheet material whose central layer is a parabola, the schematic diagram is as follows Fig. 8:

On the geometrical central layer of curved sheet metal, where the thickness is \(\frac{t}{2}\),\(\frac{t}{2}\) is the distance along the normal direction, and the set of these points is the equation of the inner and outer curves.

Based on these conditions, setting up a system of equations.

$$\left\{ \begin{gathered} \left( \frac{t}{2} \right)^{2} = (y_{1} - y_{0} )^{2} + (x_{1} - x_{0} )^{2} \hfill \\ y_{0} = ax_{0}^{2} \hfill \\ y_{1} - y_{0} = - \frac{1}{{2ax_{0} }}(x_{1} - x_{0} ) \hfill \\ \end{gathered} \right.$$
(30)

The curve characteristics of inner and outer diameters are analyzed from the aspect of precision of engineering application by using the method of assigning tracing points. It is found that the error is very small.It can be considered that the inner and outer layers of the sheet are parabola in the effective measurement range studied after bending, and the characteristic parameters \(a\) are consistent with the characteristic parameters \(a\) of the quadratic function equation of the geometric center layer.

In order to simplify the calculation and proof process, the equation of the curve is discussed in the first and second quadrants of the same coordinate system. As shown is in the figure below Fig. 9:

Let's say that some node P, is on the curve \(y = ax^{2}\) before it bounces back, coordinate is \((x_{0} ,y_{0} )\). Then the pre-elastic curvature K of the node is

$$K = \frac{2a}{{[1 + (2ax_{0} )^{2} ]^{\frac{3}{2}} }}$$
(31)

One node P, is on the curve \(y = a^{^{\prime}} x^{2}\) after it bounces back,coordinate is \((x_{1} ,y_{1} )\). The post-springback curvature \(K^{^{\prime}}\) of the node is

$$K^{^{\prime}} = \frac{{2a^{^{\prime}} }}{{\left[ {1 + (2a^{^{\prime}} x_{1} )^{2} } \right]^{\frac{3}{2}} }}$$
(32)

At the same point there is the following relationship, \(\frac{{{\text{d}}K^{^{\prime}} }}{{{\text{dK}}}} < 1\), \(x_{0} < x_{1}\), \(y_{0} > y_{1}\), \(K > K^{\prime}\), \(ax_{0}^{2} > a^{^{\prime}} x_{1}^{2}\).

So you can figure out the following.

$$0 < \frac{{{\text{d}}a^{^{\prime}} }}{{{\text{d}}a}} < 1$$
(33)

It is proved that the variable curvature stretch-bending technology of the conic shape surface can \(p\) be used as the iteration parameter and has local convergence. The proof process of cubic curve or higher height polynomial curve and quadratic function are similar, which \(0 < \frac{{{\text{d}}a^{^{\prime}} }}{{{\text{d}}a}} < 1\) can be judged. It is shown that the shape parameters \(a\) of the curve equation can also be regarded as iterative parameters and have local convergence.

Fig. 8
figure 8

Diagram of parabolic bending of sheet metal

Full size image
Fig. 9
figure 9

Curve equations before and after springback

Full size image

4.2 Experiment and Results of Stretch-bending Compensation with Variable Curvature

For the bending die of second and third order functional shape, the iterative compensation is embodied in the difference of the shape parameters before and after springback. The compensation of each die surface depends on the difference between the last die shape parameters and the springback sheet shape parameters. After finite compensation operations, the final modified die shape parameters can be obtained and the high-precision forming parts can be obtained.

When the actuator is loading the quadratic function die, the blank is loaded on the stretch-bending test machine, as shown in Fig. 10.

Fig. 10
figure 10

Variable curvature stretch-bending loading of slablet under quadratic function surface bending die

Full size image

As shown is in Fig. 10, in order to prepare for the subsequent processing of experimental data, marks must be made several time. The central axis is marked on the bending die in advance. At the end of stretch-bending loading, the marking point on the sheet material is consistent with the central axis of the bending die. A symmetric line is drawn on both sides of the sheet material according to the edges of both sides of the fixed plate, and a line is marked on the fitting area between the sheet material and the die.

For the variable curvature stretch-bending process of ST12 steel plate, the compensation of quadratic function shape parameters are shown in Fig. 11. The figure (a)shows the mold profile after the initial stretch-bending and the profile after the first compensation. The figure (b) shows two stretch-bending forming conditions of sheet metal before and after compensation. The test results and parameters are shown in Table 7.

Fig. 11
figure 11

Experimental reality of stretch-bending compensation of ST12 slab with quadratic function shape variable curvature

Full size image
Table 7 Experimental results of iterative compensation of parameter a of quadratic function shape variable curvature stretch-bending process
Full size table

The compensation of cubic function shape parameter a is shown in Fig. 12a) is the mold profile of the initial stretch-bending and the profile after two compensations. Figure 12b) is the forming reality of the sheet metal in the third stretch-bending before and after the compensation. The test results and parameters are shown in Table 8.

Fig. 12
figure 12

Experimental reality of stretch-bending compensation for ST12 slab with cubic function shape variable curvature

Full size image
Table 8 Iterative compensation test results of parameter A of cubic function shape variable curvature stretch-bending process
Full size table

Taking the stretching and bending compensation experiment of quadratic function profile when \(a = 0.0035\) as an example, the compensation operation process is detailed as follows.

The first step is to load the clamping quadratic function surface when \(a = 0.0035\) on the stretch-bending experimental machine. The stretch-bending loading method of first stretch-bending is carried out and then bending on the ST12 steel plate slab. The forming parts and various marks can be obtained. The CMM is used to measure the forming parts. After data processing, the shape parameters \(a^{^{\prime}} = 0.003443\) of the springback forming parts are obtained. The compensation error of the shape parameter before and after the springback is calculated. The value is \(0.000057\). Then compensate to the value before the next springback \(a_{{{\text{next}}}} = a + \left| {a - a^{^{\prime}} } \right| = 0.003557\).

The second step is to install the modified quadratic function profile \(a = 0.003557\) on the stretch-bending test machine. The forming parts and various marks are obtained after the stretch-bending unloading and springback of the slab. The CMM is used to measure the forming parts.After data processing, the shape parameters \(a^{^{\prime}} = 0.003500\) of the springback forming parts are obtained. The compensation error of the shape parameters before and after springback are calculated. The theoretical calculation results show that the error is zero within the accuracy range of 10–6, then the compensation operation is over.

According to the data in and Table 7, as the number of compensation increases, the compensation error gradually decreases. The iteration parameter gradually approaches the target value. It is shown that under the iterative compensation mechanism, for the variable curvature stretch-bending compensation process of the second and third function shape die, the shape parameters of the die surface equation can be compensated for a finite number of times, so that the size of the forming part can reach the target precision.

5 Conclusion

  1. (1).

    A new method of parametric iterative compensation mechanism is proposed to solve the bending springback problem. The convergence criterion of iterative compensation is established.That is, the derivative of parameter relation equation before and after springback is less than 1. On this basis, the springback compensation problem is transformed into iterative solution of implicit equation.

  2. (2).

    The proposed iterative compensation strategy is applied to free bending and stretch-bending compensation of different models respectively. Experimental results show that after 2–3 iterations, the target value with small error can be obtained, which avoids the repeated operation of mold processing. It improves experimental efficiency, and saves manpower and material resources.

  3. (3).

    Compared with the difference iteration method, the slope compensation iteration method has faster convergence speed and higher accuracy. In addition, the iterative compensation method is independent of material properties and mechanical model, and has good applicability to springback compensation in forming process.