1 Introduction

Springback is one of the common defects in metal plastic forming. Springback is a phenomenon that the shape and size of workpieces change after unloading due to residual stress and elastic recovery, which seriously affects the dimensional accuracy and forming quality of workpieces and brings great difficulties to the subsequent assembly process. In order to improve the forming accuracy of workpieces, the springback of workpieces is usually restrained by adjusting the process parameters, die parameters, and material parameters or adding additional processes to reduce the shape error [1,2,3].

In recent years, the springback compensation method based on modified die surface has been widely used in sheet and profile forming. The die compensation method is an iterative process, that is, under the premise of known springback, the blank is over-bent by modifying the die surface. By using the law of springback, the shape after unloading is similar to the desired shape, so as to reduce the springback error. The traditional method of die compensation is generally trial and error method [4]. Only by changing the die surface repeatedly can the forming requirements be achieved. Die design mainly depends on the actual experience and skills of operators, which leads to the long cycle of die development [5].

With the development of finite element theory and computer technology, numerical simulation has gradually replaced the trial and error method [6,7,8]. By establishing the finite element model, the springback of the workpiece can be predicted. According to the value of springback, the optimal die surface can be obtained by modifying the die surface continuously. The use of numerical simulation not only shortens the die development cycle, but also reduces the production cost [9, 10]. Karafillis et al. used the finite element method to propose a method (K&B method) to design sheet metal forming die by using the calculated springback. The compensation effect could be achieved after several iterations by applying the traction force opposite to the forming direction [11,12,13]. Gan et al. put forward a displacement adjustment method (DA method) for the reverse compensation of the nodes of the formed workpiece. By applying a displacement opposite to the springback direction, the die surface was constructed to compensate the springback [14, 15]. Lingbeek et al. established a stretch bending model and found that the value of compensation was closely related to material, process, and geometric parameters, and a compensation factor was needed to realize one-step iteration of DA method. Weiher et al. modified the DA method and proposed a smooth displacement adjustment method (SDA method) for springback compensation, which had greatly improved the compensation accuracy. Lingbeek et al. also proposed a surface controlled overbending method (SCO method), and the results showed that both SDA and SCO methods were effective in springback compensation of industrial products [16,17,18,19]. Yang et al. put the emphasis on the die design and put forward a comprehensive compensation method considering the adjustment of compensation direction displacement [20]. Jia et al. proposed a new process of multi-point forming with individually controlled force-displacement (MPF-ICFD) to reduce springback in traditional multi-point forming [21]. Cai et al. proposed a springback compensation and correction algorithm for hyperbolic panel, which was verified by theoretical analysis, numerical simulation and forming experiment [22]. Liang et al. proposed an iterative correction method to compensate springback by using the overbending envelope surface [23, 24].

Springback is one of the main defects in the process of stretch bending, which seriously affects the forming accuracy of the workpiece. The methods mentioned in the above literature have no obvious effect on springback compensation in 3D FSB-MPRD process, so it cannot be used directly. In this paper, the variable curvature T-profile with complex section is studied. Firstly, the forming principle of 3D flexible stretch bending of multi-point roller die (3D FSB-MPRD) process is introduced. Then, a new springback compensation method based on the variable compensation factor is proposed for the workpiece with 3D deformation. This method can accelerate the convergence speed of springback compensation. Finally, the finite element model of 3D FSB-MPRD process is established. The numerical simulation is used to optimize the die surface for several iterations, and the shape obtained after compensation is compared with the desired shape. By comparing the simulation results with the test results, the effectiveness of the springback compensation method based on the variable compensation factor is verified.

2 The 3D FSB-MPRD process and springback compensation method

2.1 The 3D FSB-MPRD process

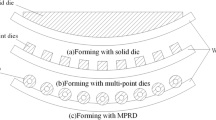
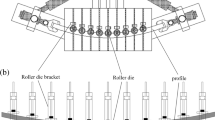
In this paper, a 3D FSB-MPRD process is proposed, which can be used to form three-dimensional profile and meet the requirements of multi-directional deformation of profile in space. In this process, the traditional integral die is divided into several multi-point roller dies (MPRD), so that the profile can be deformed in three-dimensional space. The forming principle of the 3D FSB-MPRD process is shown in Fig. 1. The profile is deformed in horizontal direction and vertical direction respectively. The roller die is installed on the flexible fundamental unit, and the flexible fundamental unit is arranged regularly and its position is adjustable. Through the precise control of the position of each flexible fundamental unit and the independent adjustment of the MPRD, the forming surface of the three-dimensional stretch bending process can be constructed.

Fig. 1
figure 1

Forming principle of the 3D FSB-MPRD process 1 worktable, 2 flexible fundamental unit, 3 profile, 4 roller die. a Stretch bending in the horizontal direction. b Stretch bending in the vertical direction

Full size image

The 3D FSB-MPRD equipment is shown in Fig. 2. The bending deformation of the blank in the horizontal direction can be increased or reduced by changing the position of the flexible fundamental unit (as shown in Fig. 2a). By changing the displacement of the roller die, the bending deformation of the blank in the vertical direction can be increased or decreased (as shown in Fig. 2b). By changing the shape of the roller die, various profiles with complex cross-section can be formed. Therefore, the 3D FSB-MPRD process has the advantages of high efficiency, flexible operation, and short research and development cycle.

Fig. 2
figure 2

The 3D FSB-MPRD equipment

Full size image

2.2 Principle of the springback compensation method based on the variable compensation factor

The commonly used springback compensation methods mainly include DA method and SCO method. In this paper, the DA method is studied deeply [14, 15]. In the three-dimensional deformation process of profile, the springback process is complex and the springback law is not easy to grasp. A new springback compensation method based on variable compensation factor is proposed for the three-dimensional deformation process of variable curvature profile.

In this study, the centerline of the profile is discretized into n geometric nodes. In three-dimensional space, \( \overset{\rightharpoonup }{\mathrm{D}} \) is assumed to be the desired shape, and \( \overset{\rightharpoonup }{\mathrm{S}} \) is the shape of profile after springback [19].

$$ \overset{\rightharpoonup }{D}=\left[{\overset{\rightharpoonup }{d}}_1,{\overset{\rightharpoonup }{d}}_2,{\overset{\rightharpoonup }{d}}_3,\dots, {\overset{\rightharpoonup }{d}}_n\right] $$
(1)
$$ \overset{\rightharpoonup }{S}=\left[{\overset{\rightharpoonup }{s}}_1,{\overset{\rightharpoonup }{s}}_2,{\overset{\rightharpoonup }{s}}_3,\dots, {\overset{\rightharpoonup }{s}}_n\right] $$
(2)

After compensation, the die surface is \( \overset{\rightharpoonup }{\mathrm{C}} \), which can be defined by Eq. (3):

$$ \overset{\rightharpoonup }{C}=\left[{\overset{\rightharpoonup }{c}}_1,{\overset{\rightharpoonup }{c}}_2,{\overset{\rightharpoonup }{c}}_3,\dots, {\overset{\rightharpoonup }{c}}_n\right] $$
(3)

Therefore, the springback compensation process can be expressed as follows:

$$ \overset{\rightharpoonup }{C}=\overset{\rightharpoonup }{D}-\alpha \left(\overset{\rightharpoonup }{S}-\overset{\rightharpoonup }{D}\right)\iff {\overset{\rightharpoonup }{c}}_i={\overset{\rightharpoonup }{d}}_i+\alpha \left({\overset{\rightharpoonup }{s}}_i-{\overset{\rightharpoonup }{d}}_i\right)\forall i\in n $$
(4)

where α is the compensation factor, and \( {\overset{\rightharpoonup }{c}}_i \), \( {\overset{\rightharpoonup }{s}}_i \), and \( {\overset{\rightharpoonup }{d}}_i \) are the coordinates of the corresponding shape at the ith node .

$$ \left\{\begin{array}{c}{\overset{\rightharpoonup }{d}}_i=\left({x}_{di},{y}_{di},{z}_{di}\right)\\ {}{\overset{\rightharpoonup }{s}}_i=\left({x}_{si},{y}_{si},{z}_{si}\right)\\ {}{\overset{\rightharpoonup }{c}}_i=\left({x}_{ci},{y}_{ci},{z}_{ci}\right)\end{array}\right. $$
(5)

In the actual compensation process, multiple iterations are needed to reduce the shape error and approach the desired shape (as shown in Eq. (6)).

$$ {\displaystyle \begin{array}{l}{\overset{\rightharpoonup }{C}}^{j+1}={\overset{\rightharpoonup }{C}}^j-\alpha \left({\overset{\rightharpoonup }{S}}^j-\overset{\rightharpoonup }{D}\right)\iff {\overset{\rightharpoonup }{c}}_i^{j+1}={\overset{\rightharpoonup }{c}}_i^j+\alpha \left({\overset{\rightharpoonup }{s}}_i^j-{\overset{\rightharpoonup }{d}}_i\right)\\ {}\iff \left({x}_{ci}^{j+1},{y}_{ci}^{j+1},{z}_{ci}^{j+1}\right)=\left({x}_{ci}^j,{y}_{ci}^j,{z}_{ci}^j\right)+\alpha \left[\left({x}_{si}^j,{y}_{si}^j,{z}_{si}^j\right)-\left({x}_{di},{y}_{di},{z}_{di}\right)\right]\\ {}\forall i\in n,j\ge 1\end{array}} $$
(6)

where \( {\overset{\rightharpoonup }{\mathrm{C}}}^j \) is the die surface after the jth iteration, \( {\overset{\rightharpoonup }{\mathrm{C}}}^{j+1} \) is the die surface after the j + 1 iteration, and \( {\overset{\rightharpoonup }{S}}^j \) is the springback shape of profile after the jth iteration.

When the shape error is reached to Eq. (7) or Eq. (8), the iteration stops:

$$ {\left\Vert {\overset{\rightharpoonup }{S}}^j-\overset{\rightharpoonup }{D}\right\Vert}_{\mathrm{max}}=\left\Vert \left({x_{si}}^j,{y_{si}}^j,{z_{si}}^j\right)\hbox{-} \left({x}_{di},{y}_{di},{z}_{di}\right)\right\Vert <\xi \hbox{'} $$
(7)
$$ {\left\Vert {\overset{\rightharpoonup }{\mathrm{C}}}^{j+1}-{\overset{\rightharpoonup }{C}}^j\right\Vert}_{\mathrm{max}}={\left\Vert \left({x_{ci}}^{j+1},{y_{ci}}^{j+1},{z_{ci}}^{j+1}\right)-\left({x_{ci}}^j,{y_{ci}}^j,{z_{ci}}^j\right)\right\Vert}_{\mathrm{max}}<\xi $$
(8)

where ξ' and ξ are allowable forming errors.

The iterative process of springback compensation in 3D stretch bending of profile is shown in Fig. 3. Generally speaking, after several iterations to modify the die surface, the profile will converge to the desired shape. In order to speed up the convergence, the compensation factor is improved in this study (as shown in Eq. (9)).

Fig. 3
figure 3

Springback compensation iterative process of 3D stretch bending profile

Full size image
$$ {\alpha}_k={\alpha}_k\left(\delta \right)=\left\{\begin{array}{lll}{\alpha}_1&, & 0<\delta \le {\delta}_1\\ {}{\alpha}_2&, & {\delta}_1<\delta \le {\delta}_2\\ {}\cdots & & \cdots \\ {}{\alpha}_k&, & {\delta}_{k-1}<\delta \le {\delta}_k\end{array}\right.k\in {N}^{\ast } $$
(9)

In this study, the n nodes of the profile centerline are divided into k parts, αk represents the value of compensation factor of the kth part of the profile, N∗ is a positive integer, and δk is the springback error at the kth part. And the value of αk is closely related to δ. Therefore, Eq. (4) can be rewritten as:

$$ {\displaystyle \begin{array}{l}{\overset{\rightharpoonup }{C}}_k={\overset{\rightharpoonup }{D}}_k-{\alpha}_k\left({\overset{\rightharpoonup }{S}}_k-{\overset{\rightharpoonup }{D}}_k\right)=\left\{\begin{array}{cc}{\overset{\rightharpoonup }{D}}_1-{\alpha}_1\left({\overset{\rightharpoonup }{S}}_1-{\overset{\rightharpoonup }{D}}_1\right),& 0<\delta \le {\delta}_1\\ {}{\overset{\rightharpoonup }{D}}_2-{\alpha}_2\left({\overset{\rightharpoonup }{S}}_2-{\overset{\rightharpoonup }{D}}_2\right),& {\delta}_1<\delta \le {\delta}_2\\ {}\begin{array}{l}\cdots \\ {}{\overset{\rightharpoonup }{D}}_k-{\alpha}_k\left({\overset{\rightharpoonup }{S}}_k-{\overset{\rightharpoonup }{D}}_k\right),\end{array}& \begin{array}{l}\cdots \\ {}{\delta}_{k-1}<\delta \le {\delta}_k\end{array}\end{array}\right.\iff \\ {}{\overset{\rightharpoonup }{c}}_{ki}={\overset{\rightharpoonup }{d}}_{ki}-{\alpha}_k\left({\overset{\rightharpoonup }{s}}_{ki}-{\overset{\rightharpoonup }{d}}_{ki}\right)=\left\{\begin{array}{cc}{\overset{\rightharpoonup }{d}}_{1i}+{\alpha}_1\left({\overset{\rightharpoonup }{s}}_{1i}-{\overset{\rightharpoonup }{d}}_{1i}\right),& 0<\delta \le {\delta}_1\\ {}{\overset{\rightharpoonup }{d}}_{2i}+{\alpha}_2\left({\overset{\rightharpoonup }{s}}_{2i}-{\overset{\rightharpoonup }{d}}_{2i}\right),& {\delta}_1<\delta \le {\delta}_2\\ {}\begin{array}{l}\cdots \\ {}{\overset{\rightharpoonup }{D}}_{ki}-{\alpha}_k\left({\overset{\rightharpoonup }{S}}_{ki}-{\overset{\rightharpoonup }{D}}_{ki}\right),\end{array}& \begin{array}{l}\cdots \\ {}{\delta}_{k-1}<\delta \le {\delta}_k\end{array}\end{array}\right.\forall k\in {N}^{\ast },i\in n\end{array}} $$
(10)

In the iterative process, in order to accelerate the convergence and make the compensation shape approach the desired shape quickly, the value of compensation factor αk which is closest to the accurate solution must be obtained. Thus, Eq. (11) is obtained:

$$ {\displaystyle \begin{array}{l}{\overset{\rightharpoonup }{C}}_k^{j+1}={\overset{\rightharpoonup }{C}}_k^j-{\alpha}_k^j\left({\overset{\rightharpoonup }{S}}_k^j-{\overset{\rightharpoonup }{D}}_k\right)=\left\{\begin{array}{cc}{\overset{\rightharpoonup }{C}}_1^j={\alpha}_1^j\left({\overset{\rightharpoonup }{S}}_1^j-{\overset{\rightharpoonup }{D}}_1\right),& 0<\delta \le {\delta}_1\\ {}{\overset{\rightharpoonup }{C}}_2^j-{\alpha}_2^j\left({\overset{\rightharpoonup }{S}}_2^j-{\overset{\rightharpoonup }{D}}_2\right),& {\delta}_1<\delta \le {\delta}_2\\ {}\begin{array}{l}\cdots \\ {}{\overset{\rightharpoonup }{C}}_k^j-{\alpha}_k^j\left({\overset{\rightharpoonup }{S}}_k^j-{\overset{\rightharpoonup }{D}}_k\right),\end{array}& \begin{array}{l}\cdots \\ {}{\delta}_{k-1}<\delta \le {\delta}_k\end{array}\end{array}\right.\iff \\ {}{\overset{\rightharpoonup }{C}}_{ki}^{j+1}={\overset{\rightharpoonup }{C}}_{ki}^j-{\alpha}_k^j\left({\overset{\rightharpoonup }{S}}_{ki}^j-{\overset{\rightharpoonup }{D}}_{ki}\right)=\left\{\begin{array}{cc}\begin{array}{c}{\overset{\rightharpoonup }{d}}_{1i}^j+{\alpha}_1^j\left({\overset{\rightharpoonup }{s}}_{1i}^j-{\overset{\rightharpoonup }{d}}_{1i}\right),\\ {}{\overset{\rightharpoonup }{d}}_{2i}^j+{\alpha}_2^j\left({\overset{\rightharpoonup }{s}}_{2i}^j-{\overset{\rightharpoonup }{d}}_{2i}\right),\\ {}\cdots \\ {}{\overset{\rightharpoonup }{d}}_{ki}^j-{\alpha}_k^j\left({\overset{\rightharpoonup }{s}}_{ki}^j-{\overset{\rightharpoonup }{d}}_{ki}\right),\end{array}& \begin{array}{c}0<\delta \le {\delta}_1\\ {}{\delta}_1<\delta \le {\delta}_2\\ {}\cdots \\ {}{\delta}_{k-1}<\delta \le {\delta}_k\end{array}\end{array}\right.\forall k\in {N}^{\ast },i\in n\end{array}} $$
(11)

where αkj is the value of compensation factor of the kth part of the profile in the jth iteration.

When the springback error is reached to Eq. (12), the iteration is stopped:

$$ \left\{\begin{array}{c}{\left\Vert {{\overset{\rightharpoonup }{C}}_1}^{j+1}-{{\overset{\rightharpoonup }{C}}_1}^j\right\Vert}_{\mathrm{max}}<{\xi}_1\\ {}{\left\Vert {{\overset{\rightharpoonup }{C}}_2}^{j+1}-{{\overset{\rightharpoonup }{C}}_2}^j\right\Vert}_{\mathrm{max}}<{\xi}_2\\ {}\cdots \\ {}{\left\Vert {{\overset{\rightharpoonup }{C}}_k}^{j+1}-{{\overset{\rightharpoonup }{C}}_k}^j\right\Vert}_{\mathrm{max}}<{\xi}_k\end{array}\right.\kern0.5em \forall k\in {N}^{\ast } $$
(12)

ξk is the maximum springback tolerance.

In this study, the basic idea of dichotomy in mathematics is used to narrow the solution range, quickly find the approximate solution of αk, and gradually approach the accurate solution. Taking α1 as an example, it is assumed that the solution interval of compensation factor is [a, b] and \( {\alpha}_1=\frac{\mathrm{a}+\mathrm{b}}{2} \). After the first compensation, Eq. (12) is used to judge whether to stop iteration. If further iteration is required, the value of compensation factor α12 required for the second iteration is in accordance with the following relationship: if ξ < 0, then \( {\alpha_1}^2=\frac{\frac{a+b}{2}+\mathrm{b}}{2} \); if ξ > 0, then \( {\alpha_1}^2=\frac{\frac{a+b}{2}+\mathrm{a}}{2} \).

At the end of the second iteration, Eq. (12) is used to determine whether the springback error meets the forming accuracy requirements. And so on until Eq. (12) is reached, and the iteration stops. In the same way, α2, α3, …, αk can also be obtained by using the above laws.

2.3 Use of the springback compensation method based on the variable compensation factor

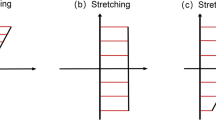
In the 3D FSB-MPRD process, the forming process of the profile is very complex. If the workpiece springback compensation is directly carried out in the three-dimensional space, the process of springback compensation is very complicated and difficult to achieve the forming accuracy due to the multi directionality of the three-dimensional deformation of the profile. According to the principle of 3D FSB-MPRD process, the total springback process is divided into horizontal bending springback compensation and vertical bending springback compensation (as shown in Fig. 4).

Fig. 4
figure 4

Springback compensation method of the FSBRD process. a Springback compensation in horizontal bending process. b Springback compensation in vertical bending process

Full size image

The deformation of profile is large in the horizontal bending process and small in the vertical bending process. According to the forming experience of the 3D FSB-MPRD process, the value of αk1 in the first iteration is within the range of [0, 1] in horizontal bending springback compensation and αk'1 in the first iteration is within the range of [0, 2] in vertical bending springback compensation. The maximum springback tolerance is defined by Eq. (13):

$$ {\xi}_1={\xi}_2=\cdots ={\xi}_{\mathrm{k}}=0.01\cdot {\mathrm{L}}_{\mathrm{k}} $$
(13)

where Lk is the length of the profile at the kth part of profile.

3 Material model

In this paper, aluminum alloy profile is used, its model is 6005A. Figure 5 shows the stress-strain curve of the specimen measured in uniaxial tensile test.

Fig. 5
figure 5

Stress-strain curve

Full size image

Some material parameters of aluminum alloy profile are shown in Table 1. Since the value of true stress and strain is needed in setting material parameters in numerical simulation, Eq. (14) is used to calculate the required value.

$$ \varepsilon =\mathrm{In}\left(1+{\varepsilon}_{\mathrm{nom}}\right)\kern0.5em \sigma ={\sigma}_{\mathrm{nom}}\left(1+{\varepsilon}_{\mathrm{nom}}\right) $$
(14)
Table 1 The material parameters of aluminum alloy 6005A
Full size table

4 Numerical simulation

4.1 Finite element model

At present, ABAQUS finite element software is widely used in numerical simulation. It is a dynamic process that large deformation is produced in the 3D FSB-MPRD process. Therefore, the explicit analysis module of the software is used for numerical simulation analysis. First of all, determine the profile section shape and plan the number of dies according to the profile length. The two-dimensional drawing module of Auto CAD software is used to design the trajectory of the horizontal bending and vertical bending process of 3D stretch bending. Then, the profile is established in the part module of the ABAQUS software, the shape of the die is designed, and the steps of assembly, defining interactions, setting material properties, and boundary conditions, and meshing are performed in order. Owing to the large length of the profile in the forming process of FSB-MPRD, the simulation results are distorted when using single-precision calculation. Thus, in order to improve the calculation accuracy, double precision is used to calculate when the job is submitted in this paper.

The profile used in this paper is a variable curvature T-profile with complex cross-section shape. The simplified assembly diagram of 3D FSB-MPRD process is shown in Fig. 6a. The model is mainly composed of profile, clamps, several MPRD, and threaded rods.

Fig. 6
figure 6

a The simplified assembly diagram of 3D FSB-MPRD process. b Meshing of each part

Full size image

When meshing the finite element model, the T-profile is a deformable body, C3D8R solid element is used. The clamp, MPRD, and threaded rods are rigid bodies, and R3D4 rigid body element is used. The mesh size of T-profile needs to be defined separately. The mesh size of clamps, MPRD, and threaded rods can adopt the default size. The meshing of the model is shown in Fig. 6b.

4.2 Trajectory design of clamps and roller dies

The 3D FSB-MPRD process mainly consists of four processes: pre-stretching, horizontal bending, vertical bending, and post-stretching. The whole stretch bending process mainly relies on the clamp to drive the profile to deform. Figure 7 shows the forming trajectory of the clamp and the roller die during the process.

Fig. 7
figure 7

Forming trajectory of the clamp and the roller die

Full size image

In the pre-stretching stage, the profile is elongated δpr along the x-axis direction to reach the plastic state. In the horizontal bending stage, the profile is bent in the X-Y plane, and the trajectory of the clamp is shown in Eq. (15). In the vertical bending stage, the profile is bent in the X-Z plane, the path of the clamp is shown in Eq. (16), and the path of the die is shown in Eq. (17). In the stage of post-stretching, the profile is elongated δpo along the deformation direction to reduce the springback, and the clamp trajectory is shown in Eq. (21).

$$ \left\{\begin{array}{l}X=\left(L+{\delta}_{pr}\right)-\cos \left(\sum \limits_{i=1}^n{\alpha}_i\right)\left(L+{\delta}_{pr}-\sum \limits_{i=1}^n{\rho}_i{\alpha}_i\right)-\sum \limits_{i=1}^n{\rho}_i\left[\sin \left(\sum \limits_{i=1}^n{\alpha}_i\right)-\sin \left(\sum \limits_{i=1}^n{\alpha}_{i-1}\right)\right]+{d}_1\sin \left(\sum \limits_{i=1}^n{\alpha}_i\right)\\ {}\mathrm{Y}=\left[\left(L+{\delta}_{pr}\right)-\sum \limits_{i=1}^n{\rho}_i{\alpha}_i\right]\sin \left(\sum \limits_{i=1}^n{\alpha}_i\right)+{\rho}_1\left(1-\cos\ {\alpha}_1\right)+\sum \limits_{i=2}^n{\rho}_i\left[\cos \left(\sum \limits_{i=2}^n{\alpha}_{i-1}\right)-\cos \left(\sum \limits_{i=2}^n{\alpha}_i\right)\right]+{d}_1\left[1-\cos \left(\sum \limits_{i=1}^n{\alpha}_i\right)\right]\end{array}\right. $$
(15)

where X is the distance that the clamp moves along the X-axis, and Y is the distance that the clamp moves along the Y-axis. L is the initial length of the profile, δpr is the pre-stretching length of profile, n is the number of arc segments of the profile, αi is the bending angle of the ith arc, d1 is the distance from the clamp reference point to the geometric center of the profile.

$$ \mathrm{Z}=\rho \hbox{'}\left(1-\cos \beta \hbox{'}\right) $$
(16)
$$ {z}_j=\rho \hbox{'}\left(1-\cos {\beta}_j\right) $$
(17)
$$ \beta \hbox{'}=\arcsin \left(\frac{L\hbox{'}}{\rho \hbox{'}}\right) $$
(18)
$$ {\beta}_j=\arcsin \left(\frac{D_j}{\rho \hbox{'}}\right) $$
(19)
$$ \mathrm{L}\hbox{'}=\sum \limits_{i=1}^n{\rho}_i\left[\sin \left(\sum \limits_{i=1}^n{\alpha}_i\right)-\sin \left(\sum \limits_{i=1}^n{\alpha}_{i-1}\right)\right]+\left[\left(L+{\delta}_{pr}\right)-\sum \limits_{i=1}^n{\rho}_i{\alpha}_i\right]\cos \left(\sum \limits_{i=1}^n{\alpha}_i\right)+{d}_1\sin \left(\sum \limits_{i=1}^n{\alpha}_i\right) $$
(20)

where Z is the distance that the clamp moves along the Z-axis during the vertical bending, ρ’ is the vertical bending radius, and zj is the distance that the jth die moves along the Z-axis. β′ is the bending angle of the clamp at the end of the vertical bending of the profile, βj is the bending angle of the profile at the jth die, L’ is the projected length of the profile at the end of the horizontal bending, and Dj is the horizontal distance between the jth die and the first die.

$$ \left\{\begin{array}{l}{x}_{po}={\delta}_{po}\sin \beta \hbox{'}\\ {}{y}_{po}={\delta}_{po}\cos \beta \hbox{'}\sin \left(\sum \limits_{i=1}^n{\alpha}_i\right)\\ {}{z}_{po}={\delta}_{po}\cos \beta \hbox{'}\cos \left(\sum \limits_{i=1}^n{\alpha}_i\right)\end{array}\right. $$
(21)

where δpo is the post-stretching length of the clamp along the axial direction of the profile after the vertical bending, xpo, ypo, and zpo are the components of the post-stretching length respectively in the direction of the xyz axis, and β′ is the vertical bending angle.

5 Results and discussion

5.1 Numerical simulation results and experimental results

The length of the T-profile is 6 m, and its processing parameters are shown in Table 2. Figure 8 is the simulation result of 3D FSB-MPRD process. It can be seen from Fig. 8a that the profile has undergone three-dimensional deformation, and the portion of the profile that is held by the clamp has stress concentration. The stress distribution of the middle part of the profile and the contact part of the roller die is relatively uniform.

Table 2 Processing parameters
Full size table
Fig. 8
figure 8

Simulation result of 3D FSB-MPRD process

Full size image

In this study, ABAQUS/implicit algorithm is used to calculate the springback of three-dimensional deformed workpiece. In order to observe the springback of the workpiece after unloading, the load and boundary conditions are deleted in the springback simulation. Figure 8b is the result of the springback simulation of the profile. Due to the springback effect, the maximum shape deviation is 69.6 mm. The formed part cannot meet the requirements of forming accuracy.

Figure 9a is a picture of a workpiece formed by the 3D FSB-MPRD process. It can be seen from the test results that the forming effect of the profile is good and there are no obvious defects such as crease, fold, and necking. The test results are in good agreement with the finite element simulation results shown in Fig. 8a. Therefore, using the finite element simulation to analyze the 3D FSB-MPRD process can provide sufficient guidance for the actual production. Figure 9b is a springback detection device of the workpiece. The formed workpiece is placed on the springback detection device to measure the shape deviation. The springback detection device is arranged regularly according to the adjustment parameters of each roller die.

Fig. 9
figure 9

a Workpiece formed by 3D FSB-MPRD process. b Springback detection device

Full size image

5.2 Springback compensation analysis

In the first springback compensation process of horizontal bending, the profile centerline is divided into 20 nodes. And these 20 points is divided into three parts. \( {\alpha}_3^1 \) is defined by Eq. (22).

$$ {\alpha}_3^1\left(\varDelta \mathrm{y}\right)=\left\{\begin{array}{l}{\alpha}_1^1=0\kern0.5em ,\varDelta {\mathrm{y}}_i\le 0.01\cdot {\mathrm{L}}_{\mathrm{i}}\\ {}\begin{array}{cc}{\alpha}_2^1=1&, 0<\varDelta {\mathrm{y}}_i<\overline{y}\end{array}\\ {}\begin{array}{cc}{\alpha}_3^1=0.5&, \varDelta {\mathrm{y}}_i\ge {\overline{y}}_i\end{array}\end{array}\right. $$
(22)

where \( \overline{y}=\frac{\sum \limits_{i=1}^{20}\varDelta {y}_i}{20} \), Li is the length of the profile at the ith node, Δyi is the springback error at the ith node, and \( \overline{y} \) is the average springback error. After the end of the first iteration, Eq. (12) is used to check whether the springback error is required. After checking that the shape error does not meet the accuracy requirements, the dichotomy principle is used to solve \( {\alpha}_3^2 \):

$$ {\alpha}_3^2\left(\varDelta \mathrm{y}\right)=\left\{\begin{array}{l}{\alpha}_1^2=0\\ {}{\alpha}_2^2=0.5\\ {}{\alpha}_3^2=0.5\end{array}\right. $$
(23)

Again, Eq. (12) is used to check. And so on, until the shape error meets the requirements, the iteration stops. Therefore, the optimal springback compensation factor α3(Δy) can be obtained:

$$ {\alpha}_3\left(\varDelta \mathrm{y}\right)=\left\{\begin{array}{l}{\alpha}_1=0\kern0.5em ,\varDelta \mathrm{y}\le 0.01\cdot {\mathrm{L}}_{\mathrm{i}}\\ {}\begin{array}{cc}{\alpha}_2=0.5&, 0<\varDelta \mathrm{y}<\overline{y}\end{array}\\ {}\begin{array}{cc}{\alpha}_3=0.25&, \varDelta \mathrm{y}\ge {\overline{y}}_i\end{array}\end{array}\right. $$
(24)

In the whole process of horizontal bending springback compensation, Eq. (25) is used to reflect the effectiveness of springback compensation.

$$ \varDelta {\varepsilon}_y=\sqrt{\sum \limits_{i=1}^{20}\frac{1}{20}{\left(\varDelta {y}_i-\overline{y}\right)}^2} $$
(25)

Figure 10a is the result of multiple iterations of springback compensation of the profile in the x-y plane. Figure 10b is a histogram of the variation of the standard deviation of springback error Δεy with the times of iteration. It can be seen from Fig. 10a that the profile formed after three times of modification of die envelope is almost the same as the desired shape. As can be seen from Fig. 10b, uncompensated workpiece’s Δεy is the largest, which is 16.57 mm. After the first springback compensation, Δεy continues to increase, indicating that the shape error increases due to the excessive compensation factor. However, after two iterations of springback compensation, Δεy decreases sharply, and the iterative compensation should be continued at this time. When the third iteration of springback compensation is carried out, the workpiece has met the requirements of forming accuracy, Δεy reduced to 1.62 mm. This fully shows that the method has a fast convergence speed.

Fig. 10
figure 10

Springback compensation results of horizontal bending

Full size image

In the same way, in the process of vertical bending springback iterative compensation, the optimal springback compensation factor α3 ' (Δz) can be obtained by using the principle of dichotomy.

$$ {\alpha}_3\hbox{'}\left(\varDelta \mathrm{z}\right)=\left\{\begin{array}{l}{\alpha}_1\hbox{'}=0\kern0.5em ,\varDelta z\le 0.01\cdot {\mathrm{L}}_{\mathrm{i}}\\ {}\begin{array}{cc}{\alpha}_2\hbox{'}=0.5&, 0<\varDelta z<\overline{z}\end{array}\\ {}\begin{array}{cc}{\alpha}_3\hbox{'}=1&, \varDelta z\ge {\overline{z}}_i\end{array}\end{array}\right. $$
(26)

where \( \overline{z}=\frac{\sum \limits_{i=1}^{20}\varDelta {z}_i}{20} \), Δzi is the springback error at the ith node, and \( \overline{\mathrm{z}} \) is the average springback error.

Figure 11a is the result of multiple iterations of springback compensation of the profile in the x-z plane. After two times modification of the die envelope, the profile and the desired shape almost coincide. Figure 11b is a histogram of the variation of the standard deviation of springback error Δεz with the times of iteration. After two times of springback compensation, Δεz decreases from 5.24 to 1.15 mm.

Fig. 11
figure 11

Springback compensation results of vertical bending

Full size image

Therefore, after several times of horizontal and vertical bending springback compensation, the springback error of profile is almost eliminated by using the springback compensation method based on the variable compensation factor. Figure 12 is the outline before and after the springback compensation of the profile centerline. Figure 12 shows that the shape error of the uncompensated profile varies greatly. After springback compensation, the die surface deviates greatly from the initial surface. And the outline of the compensated profile almost coincides with the shape of the desired. It can be seen that springback compensation is an effective method to reduce the shape error.

Fig. 12
figure 12

Changes of profile before and after springback compensation

Full size image

5.3 Application of the springback compensation method based on the variable compensation factor

Based on the effectiveness of the springback compensation method based on the variable compensation factor in numerical simulation, this study attempts to apply the optimal compensation factor to profiles with different lengths for testing. Processing parameters are shown in Table 3.

Table 3 Processing parameters
Full size table

Figure 13 shows the comparison results before and after springback compensation of different profile lengths. It can be seen from Fig. 13a, b that the effect before and after springback compensation is very obvious. Especially from the projection of profile in x-y plane and x-z plane, it is clear that the profile before springback compensation is quite different from the desired shape, and the profile after springback compensation almost coincides with the desired shape. This also fully shows the effectiveness of the springback compensation method based on the variable compensation factor.

Fig. 13
figure 13

Comparison results before and after springback compensation of different profiles. a 7m. b 8m

Full size image

Figure 14 is the change of the springback error along the X-axis direction for different profile lengths. Before and after horizontal bending springback compensation, the maximum springback error of the profile with the length of 7 m is reduced from 88.83 to 7.74 mm, and the maximum springback error is reduced by 91.29% The maximum springback error of the profile with the length of 8 m is reduced from 109.09 to 14.93 mm, and the maximum springback error is reduced by 86.31%.

Fig. 14
figure 14

Change of the springback error along the X-axis direction for different profile lengths. a Springback error in horizontal plane. b Springback error in vertical plane

Full size image

Before and after vertical bending springback compensation, the maximum springback error of the profile with the length of 7 m is reduced from 17.636 to 2.4 mm, and the maximum springback error is reduced by 86.39%. The maximum springback error of the profile with the length of 8 m is reduced from 20.838 to 4.06 mm, and the maximum springback error is reduced by 80.52%.

6 Conclusion

Springback compensation is one of the effective ways to reduce the springback error of profile. The springback compensation factor determines the convergence speed of springback compensation. In this paper, the 3D FSB-MPRD process is studied. The finite element model of the 3D FSB-MPRD process is established. The numerical simulation and test results of the formed profile are compared, and the accuracy of the finite element model is verified by the test. The die surface was optimized repeatedly by numerical simulation, and the shape after springback compensation is compared with the desired shape. By comparing the simulation results with the test results, the validity of the springback compensation method based on the variable compensation factor is verified. The main conclusions are as follows:

  1. 1)

    Based on the principle of DA method, a new springback compensation method based on variable compensation factor is proposed for 3D deformed workpiece in this paper. In order to improve the accuracy of springback compensation, the three-dimensional springback compensation of workpiece is divided into horizontal bending springback compensation and vertical bengding springback compensation. By using the principle of dichotomy, the optimal springback compensation factor is solved.

  2. 2)

    The springback compensation of 3D workpiece is analyzed by numerical simulation. In the process of horizontal bending springback compensation, the standard deviation of springback error Δεy is reduced from 16.57 to 1.62 mm after three iterations of compensation. In the process of springback compensation of vertical bending, the standard deviation of springback error Δεz is reduced from 5.24 to 1.15 mm after two iterations of compensation. This fully shows the effectiveness of the method, and the springback is significantly reduced.

  3. 3)

    Based on the optimal springback compensation factor obtained by numerical simulation, the method is verified by the tests of different length profiles. Before and after horizontal bending springback compensation, the maximum springback error of the profile with the length of 7 m reduced by 91.29%, and that of the profile with the length of 8 m reduced by 86.31%. Before and after vertical bending springback compensation, the maximum springback error of the profile with the length of 7 m is reduced by 86.39%, and that of the profile with the length of 8 m is reduced by 80.52%.