1 Introduction

The power transmission system is an important part of the helicopter power system. Spiral bevel gears are widely used in helicopter power transmission systems because of their advantages. In recent years, helicopter engine performance has improved with improvements in science and technology, and helicopter's power has also increased. Unfortunately, the running vibration of the spiral bevel gear also increases with the increasing helicopter power. Spiral bevel gears have high strength and dynamic performance requirements. The contact path of the traditional spiral bevel gear is approximately perpendicular to the root cone [1], and its design contact ratio (DCR) and strength are both low. How to increase the DCR and improve the strength performance of spiral bevel gears has attracted extensive attention from experts [2]. Based on the local synthesis method (LSM), Deng improved the DCR of the spiral bevel gear, and he also analyzed the strength performance of the HCR spiral bevel gear [3,4,5,6,7].

In view of the defects of Gleason Technology based on Literatures [8, 9], Litvin [10, 11] proposed the LSM. However, the LSM cannot control the meshing characteristics of the tooth surface far away from the reference point. Therefore, Oricon developed ease-off technology, which has been subject to much research by experts. Shih [12,13,14] provided a detailed definition of ease-off technology, proposed the tooth surface design method for the spiral bevel gear based on ease-off technology, and finally verified it through computer simulation. Based on the ease-off technology, Stadtfeld [15] modified the pinion tooth surface of the spiral bevel gear, Kolivand [16, 17] studied the loaded meshing performance of the spiral bevel gear, and proposed the best ease-off tooth surface to reduce the LTE and contact stress of the hypoid gears. Artoni [18, 19] established a least square model of the hypoid gear based on the ease-off technology to optimize the loaded transmission error (LTE) and obtained the corresponding machining parameters. Fan [20] analyzed the ease-off theory and its application in the contact analysis of the spiral bevel gears and hypoid gears in detail. To improve the meshing performance of the spiral bevel gear, Wang [21] proposed a tooth surface modification method based on ease-off technology. Ding [22,23,24,25] proposed the machine parameter identification algorithm for the hypoid gear based on nonlinear analysis and the multi-objective optimization method for the meshing performance of the spiral bevel gear based on nonlinear interval optimization algorithm to evaluate the tooth contact performance. Mu [26,27,28,29] presented a new method to design a high-order transmission error for the HCR spiral bevel gear by the modified curvature motion method to reduce or eliminate gear vibration based on ease-off.

Due to scientific advancement, the spiral bevel gears are developing towards obtaining high-speeds and heavy-loads, and the problem of spiral bevel gear running vibration is becoming increasingly prominent. The running vibration of the spiral bevel gear not only leads to the unstable operation of the transmission system; but also causes the failure of the transmission system. The running vibration of the spiral bevel gear has increasingly become a bottleneck problem affecting product quality. The dynamic performance analysis and control of spiral bevel gears have become a problem that must be solved in modern industry.

To improve the meshing performance of spiral bevel gears and improve the design level of helicopter power transmission system, a HCR design method for the spiral bevel gear is proposed based on ease-off technology, and its dynamic performance is analyzed. Through comparative analysis, it is verified that ease-off technology can overcome the contrast of HCR spiral bevel gears designed by the LSM. Combined with ease-off technology, the HCR spiral bevel gear is designed by improving the angle between the contact path and pitch cone of pinion tooth surface. Through comparative analysis, the advantages of HCR design in reducing the load transmission error and meshing impact of spiral bevel gear and improving the dynamic performance of spiral bevel gear are verified. The HCR design method based on ease-off technology can be used for the design and analysis of other gear pairs.

2 Design of DCR Spiral Bevel Gear Based on Ease-off

2.1 Geometric Transmission Error

The concave transmission error (TE) curve is shown in Fig. 1, where φ1 is the pinion rotation angle, and δ is the TE amplitude. A detailed introduction to the TE curve is given in Literature 27.

Fig. 1
figure 1

Geometrical transmission error

Full size image

The concave TE curve is defined as follows:

$$\left\{ {\begin{array}{*{20}c} {\varphi_{2} = \varphi_{2}^{\left( 0 \right)} + {\raise0.7ex\hbox{${\left( {\varphi_{1} - \varphi_{1}^{\left( 0 \right)} } \right)Z_{1} }$} \!\mathord{\left/ {\vphantom {{\left( {\varphi_{1} - \varphi_{1}^{\left( 0 \right)} } \right)Z_{1} } {Z_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${Z_{2} }$}}\delta \varphi_{2} } \\ {\delta \varphi_{2} = - {\raise0.7ex\hbox{${\delta_{TE} \left( {\varphi_{1} - \varphi_{1}^{\left( 0 \right)} } \right)^{2} Z_{1}^{2} }$} \!\mathord{\left/ {\vphantom {{\delta_{TE} \left( {\varphi_{1} - \varphi_{1}^{\left( 0 \right)} } \right)^{2} Z_{1}^{2} } {\pi^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\pi^{2} }$}}} \\ \end{array} } \right.$$
(1)

where φ(0) 2and φ(0) 1denote the original rotation angles, while Z2 and Z1 denote the tooth numbers.

2.2 Contact Path

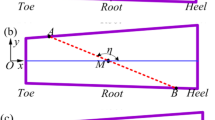
The contact path of the spiral bevel gear runs through the whole working surface. The DCR of the spiral bevel gear is closely related to the contact path. When the contact path is perpendicular to the pitch cone, the DCR is smallest. Increasing the angle between the contact path and the pitch cone can increase the DCR. Based on the requirements of the DCR, the straight-line contact path on the pinion tooth surface shown in Fig. 2 is designed, and its equation is as follows:

$$y = (x - x_{M} )\tan \eta + y_{M}$$
(2)

where (xM, yM) are the coordinates of the reference point M.

Fig. 2
figure 2

The contact path

Full size image

2.3 Pinion Auxiliary Tooth Surface

The gear tooth surface is treated as a virtual cutter to create pinion auxiliary surface based on the predesigned TE, as shown in Fig. 3. The coordinate systems S1 and S2 are rigidly attached to the pinion and the gear cutter, respectively.

Fig. 3
figure 3

The virtual gear cutter and pinion auxiliary surface

Full size image

The gear tooth surface is given by:

$$\left\{ {\begin{array}{*{20}c} {r_{2} = r_{2} \left( {s_{g} ,\theta_{g} ,\varphi_{g} } \right)} \\ {n_{2} = n_{2} \left( {s_{g} ,\theta_{g} ,\varphi_{g} } \right)} \\ {f_{2} \left( {s_{g} ,\theta_{g} ,\varphi_{g} } \right) = 0} \\ \end{array} } \right.$$
(3)

where sg and θg are the surface parameters, φg is the gear cradle angle, rs2 is the position vector of the gear tooth surface, n2 is the unit normal vector of the gear tooth surface. f2 denotes the meshing equation between the cutter and gear.

The parameters of the pinion auxiliary surface are calculated as follows:

$$\left\{ {\begin{array}{*{20}l} {r_{1}^{^{\prime}} = M_{1h} \left( {\varphi_{1} } \right)M_{h2} \left( {\varphi_{2} } \right)r_{2} } \hfill \\ {n_{1}^{^{\prime}} = L_{1h} \left( {\varphi_{1} } \right)L_{h2} \left( {\varphi_{2} } \right)n_{2} } \hfill \\ {f_{12} \left( {s_{g} ,\theta_{g} ,\phi_{g} ,\varphi_{1} } \right) = 0} \hfill \\ \end{array} } \right.$$
(4)

where φ1 is the pinion rotation angle, φ2 is the gear cutter rotation angle, and f12 indicates the meshing equation between gear cutter and pinion. Matrices Mh2 and M1h are the homogenous coordinate transform matrices from S2 to Sh and Sh to S1, respectively. L1h and Lh2 are the upper-left 3 × 3 sub-matrix of M1h and Mh2, respectively.

$${\varvec{M}}_{{h{2}}} = \left[ {\begin{array}{*{20}c} {\cos \Sigma } & {\sin \Sigma \sin \phi_{2} } & { - \sin \Sigma \cos \phi_{2} } & 0 \\ 0 & { - \cos \phi_{2} } & { - \sin \phi_{2} } & 0 \\ { - \sin \Sigma } & {\cos \Sigma \sin \phi_{2} } & { - \cos \Sigma \cos \phi_{2} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
$${\varvec{M}}_{{{1}h}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {\cos \varphi_{1} } & {\sin \varphi _{1} } & 0 \\ 0 & { - \sin \varphi_{1} } & {\cos \varphi_{1} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

2.4 Pinion Target Tooth Surface

To obtain the ease-off target surface, the pinion auxiliary surface needs to be modified along the instantaneous meshing line. The pinion auxiliary surface and the target surface are divided into q meshing points, and the position vector and unit normal vector of discrete point i (i = 1, 2, …, q) on the pinion auxiliary surface are presented as follows:

$$\left\{ \begin{gathered} \varvec{p^{\prime}}_{i} = \varvec{p^{\prime}}\left( {s_{g} ,\theta_{g} ,\varphi_{g} ,\phi_{1} } \right) \hfill \\ \varvec{n^{\prime}}_{i} = \varvec{n^{\prime}}_{i} \left( {s_{g} ,\theta_{g} ,\varphi_{g} ,\phi_{1} } \right) \hfill \\ \end{gathered} \right.$$
(5)

where p' is the position vector of the discrete points, and n' is the unit normal vector of the discrete points.

The position vector of the discrete points on the target surface (shown in Fig. 4) can be obtained based on the following equation:

$${\varvec{p}}_{i}^{ * } = \varvec{p^{\prime}}_{i} + \varvec{n^{\prime}}_{i} \delta_{yi}$$
(6)

where δsy represent the flank modification value.

Fig. 4
figure 4

Ease-off target tooth surface

Full size image

2.5 Calculation of Pinion Machining Parameters

The position vector rp and the normal vector np of the pinion cutting cone are as follows:

$$r_{p} \left( {s_{p} ,\theta_{p} } \right) = \left[ {\begin{array}{*{20}c} {\left( {R_{p} + s_{p} \sin \alpha_{1} } \right)\cos \theta_{p} } \\ {\left( {R_{p} + s_{p} \sin \alpha_{1} } \right)\sin \theta_{p} } \\ { - s_{p} \cos \alpha_{1} } \\ 1 \\ \end{array} } \right]$$
(7)
$${\varvec{n}}_{p} (\theta_{p} ) = \left[ {\begin{array}{*{20}c} {\cos \alpha_{1} \cos \theta_{p} } \\ {\cos \alpha_{1} \sin \theta_{p} } \\ { - \sin \alpha_{1} } \\ \end{array} } \right]$$
(8)

where sp and θp are the cutter-head parameters, Rp is the cutter radius, and α1 represents the profile angle.

The position vector r1 of the pinion tooth surface is as follows:

$$r_{1} = M_{1p} r_{p}$$
(9)

where

$$M_{1p} = \left[ {\begin{array}{*{20}l} {a_{11} } \hfill & {a_{12} } \hfill & {a_{12} } \hfill & {a_{14} } \hfill \\ {a_{21} } \hfill & {a_{22} } \hfill & {a_{23} } \hfill & {a_{24} } \hfill \\ {a_{31} } \hfill & {a_{32} } \hfill & {a_{33} } \hfill & {a_{34} } \hfill \\ {a_{41} } \hfill & {a_{42} } \hfill & {a_{43} } \hfill & {a_{44} } \hfill \\ \end{array} } \right]$$
$$\begin{gathered} a_{11} = \cos \gamma_{1} \cos \phi_{p} \hfill \\ a_{12} = - \cos \gamma_{1} \sin \phi_{p} \hfill \\ a_{13} = \sin \gamma_{1} \hfill \\ a_{14} = S_{r1} \cos \gamma_{1} \cos \phi_{p} \cos q_{1} - X_{b1} \sin \gamma_{1} - X_{G1} - S_{r1} \cos \gamma_{1} \sin \phi_{p} \sin q_{1} \hfill \\ a_{21} = \cos \phi_{1} \sin \phi_{p} - \cos \phi_{p} \sin \gamma_{1} \sin \phi_{1} \hfill \\ a_{22} = \cos \phi_{1} \cos \phi_{p} + \sin \phi_{p} \sin \gamma_{1} \sin \phi_{1} \hfill \\ a_{23} = \cos \gamma_{1} \sin \phi_{1} \hfill \\ a_{24} = E_{m1} \cos \phi_{1} - X_{b1} \cos \gamma_{1} \sin \phi_{1} + S_{r1} \sin q_{1} \left( {\cos \phi_{1} \sin \phi_{p} - \cos \phi_{p} \sin \gamma_{1} \sin \phi_{1} } \right) \hfill \\ + S_{r1} \sin q_{1} \left( {\cos \phi_{1} \cos \phi_{p} + \sin \gamma_{1} \sin \phi_{1} \sin \phi_{p} } \right) \hfill \\ a_{31} = - \sin \phi_{1} \sin \phi_{p} - \cos \phi_{p} \sin \gamma_{1} \cos \phi_{1} \hfill \\ a_{32} = - \cos \phi_{1} \sin \gamma_{1} \sin \phi_{p} - \cos \phi_{p} \sin \phi_{1} \hfill \\ a_{33} = \cos \gamma_{1} \cos \phi_{1} \hfill \\ a_{34} = - E_{m1} \sin \phi_{1} - X_{b1} \cos \gamma_{1} \cos \phi_{1} - S_{r1} \cos q_{1} \left( {\sin \phi_{1} \sin \phi_{p} + \cos \phi_{p} \sin \gamma_{1} \cos \phi_{1} } \right) - S_{r1} \sin q_{1} \left( {\sin \phi_{1} \cos \phi_{p} - \sin \gamma_{1} \cos \phi_{1} \sin \phi_{p} } \right) \hfill \\ a_{41} = a_{42} = a_{43} = 0 \cdot a_{44} = 1 \hfill \\ \end{gathered}$$

Then the position vectors and the unit normal vectors of the discrete points on the pinion modification surface are as follows:

$$\left\{ \begin{gathered} {\varvec{p}}_{{\text{i}}} = {\varvec{r}}_{{1}} (s_{pi} ,\theta_{pi} ,\varphi_{pi} ) \hfill \\ {\varvec{n}}_{i} = {\varvec{n}}_{1} (\theta_{pi} ,\varphi_{pi} ) \hfill \\ \end{gathered} \right.$$
(10)

The deviation between the pinion modification surface and the target surface at the discrete points can be expressed by the following equations:

$${\varvec{h}}_{{\varvec{i}}} = ({\varvec{p}}_{{\varvec{i}}}^{ * } - {\varvec{p}}_{{\varvec{i}}}^{{}} ){\varvec{n}}_{{\varvec{i}}}^{{}}$$
(11)
$${\varvec{h}} = [{\varvec{h}}_{1} ,{\varvec{h}}_{2} ,{\varvec{h}}_{3} ,...,{\varvec{h}}_{k} ]^{{\varvec{T}}}$$
(12)

Finally, the optimization model is established as shown in Eq. (13), in which the pinion machining parameters L are variables and the minimum sum of squares of the normal deviation between the pinion modification surface and the target surface is the object. In this paper, the NSGA-II algorithm is used, and the corresponding Matlab program is written to solve the optimization model:

$$\min f({\varvec{L}}^{(i)} ) = \frac{1}{2}{\varvec{h}}^{T} {\varvec{h}}$$
(13)

3 Calculation of Vibration Excitation

3.1 LTE

LTE is the main vibration excitation of the spiral bevel gear transmission in the low speed range, and it can be obtained by the LTCA method [30]. Figure 5 shows the LTCA model of the spiral bevel gear, and the LTE can be obtained by transforming the normal displacement Z into angular displacement.

Fig. 5
figure 5

Model for LTCA of spiral bevel gear

Full size image

Before load is applied to the gear, the initial clearance between two meshing teeth is as follows:

$$w_{k} = \delta_{k}^{^{\prime\prime}} + b_{k} \;k = I,II$$
(14)

where

$${\varvec{w}}_{k} = [w_{1} ,w_{2} ,....,w_{i} ,w_{j} ,...,w_{n} ]^{T}$$
$$\varvec{\delta^{\prime\prime}}_{k} = \delta^{\prime\prime}[1,1,...,1,...,1]^{T}$$
$${\varvec{b}}_{k} = [b_{1} ,b_{2} ,....,b_{i} ,b_{j} ,...,b_{n} ]^{T}$$

The parameter δ" is the gap between two teeth of a meshing gear, and b represents the normal clearance.

If the pinion is fixed and the normal displacement of gear under the load is Z, then the displacement compatibility equation after deformation is as follows:

$${\varvec{F}}_{k} {\varvec{p}}_{k} + {\varvec{w}}_{k} = {\varvec{Z}} + {\varvec{d}}_{k} \;k = I,II$$
(15)

where

$${\varvec{p}}_{k} = [p_{1} ,p_{2} ,....,p_{i} ,p_{j} ,...,p_{n} ]^{T}$$
$${\varvec{d}}_{k} = [d_{1} ,d_{2} ,....,d_{i} ,d_{j} ,...,d_{n} ]^{T}$$
$${\varvec{Z}} = Z[1,1,...,1,...,1]^{T}$$

The parameter pj (j = 1, 2,…, n) is the normal load at discrete point j on the major axis of the ellipse, the parameter dj (j = 1, 2,…, n) represents the tooth surface clearance at discrete point j on the major axis of the ellipse, and Fk is the comprehensive normal flexibility matrix.

The discrete load pjk satisfies the force equilibrium conditions as follows:

$$\sum\limits_{j = 1}^{n} {p_{jI} } + \sum\nolimits_{j = 1}^{n} {p_{jII} } = P$$
(16)

The discrete load pjk and the deformed gap djk satisfy non embedding conditions as follows:

$$\begin{array}{*{20}c} {p_{jk} > 0 \Rightarrow d_{jk} = 0} \\ {p_{jk} = 0 \Rightarrow d_{jk} > 0} \\ \end{array} \left( {k = {\text{I}},{\text{ II}}} \right)$$
(17)

Based on above conditions, a mathematical programming model for the loaded contact problem of spiral bevel gear transmission is established as follows:

$$\begin{gathered} f = \min \sum\limits_{j = 1}^{2n + 1} {X_{j} } \hfill \\ {\varvec{w}} = {\varvec{wFp}} + {\varvec{Z}} + {\varvec{d}} + {\varvec{X}} \hfill \\ {\varvec{P}} = {\varvec{e}}^{{\varvec{T}}} {\varvec{p}} + {\varvec{X}}_{2n + 1} \hfill \\ \end{gathered}$$
(18)

\(\begin{gathered} \begin{array}{*{20}c} {s.t.} & {p_{j} \ge 0,} \\ \end{array} d_{j} \ge 0,Z_{j} \ge 0,X_{j} \ge 0 \hfill \\ \begin{array}{*{20}c} {} & {p_{j} = 0} & {d_{j} = 0} \\ \end{array} \hfill \\ \end{gathered}\).where Xj (j = 1,2,3,…,2n + 1) represents an artificial variable. The parameter e is n-dimensional unit column vector.

By solving the equations shown above, the normal displacement of the gear under load can be obtained. By converting the normal displacement into angular displacement, the LTE of the gear under a given load can be obtained.

3.2 Meshing Impact

As shown in Fig. 6, during gear transmission, the base pitch difference generated from the loaded deformation results in the speed difference of the gear and pinion at the initial meshing point. The speed difference is the impact velocity. Because of the impact velocity, the impact force will be produced at the initial meshing point. Meshing impact is the main vibration excitation of spiral bevel gear transmission in the high-speed range, and the detailed calculation method of the meshing impact of spiral bevel gear is given in Literature [31].

Fig. 6
figure 6

Meshing impact principle

Full size image

As shown in Fig. 7, the impact velocity vs is as follows:

$$v_{s} = (v_{1} - v_{2} )n_{h}$$
(19)

where v2 and v1 is the velocity of the gear and pinion, respectively.

Fig. 7
figure 7

The impact model

Full size image

The meshing impact force is as follows:

$$F_{s} = \left( {\frac{n + 1}{2}\frac{{J_{1} J_{2} }}{{J_{1} r_{b2}^{2} + J_{2} r_{b1}^{2} }}{\varvec{v}}_{s}^{2} K_{s}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}} } \right)^{{{n \mathord{\left/ {\vphantom {n {(n + 1)}}} \right. \kern-\nulldelimiterspace} {(n + 1)}}}}$$
(20)

where J1 and J2 represent the rotary inertia. Ks represents the meshing stiffness. n represents the meshing force exponent coefficient. rb1 and rb2 represent the instantaneous base circle radius.

3.3 Dynamic analysis

There is vibration excitation in the process of spiral bevel gear transmission, which induces the running vibration of spiral bevel gear transmission. With the development of science, people have put forward higher requirements for the dynamic performance of spiral bevel gear transmission. The traditional dynamic analysis of spiral bevel gears adds the static analysis results into the dynamic equations established by the lumped mass method, and the influence of meshing impact on the dynamic characteristics is not considered, so the calculation results cannot fully conform to the actual situation. Based on TCA and LTCA, the meshing impact of the spiral bevel gear is obtained. According to the dynamic model of the 8-DOF spiral bevel gear shown in Fig. 8, the vibration equation of the spiral bevel gear dynamic model is established as follows. The dynamic response of spiral bevel gear is analyzed by applying LTE excitation and meshing impact excitation in the vibration equation.

$$\left\{ {\begin{array}{*{20}l} {m_{1} \ddot{X}_{1} + c_{1x} \ddot{X}_{1} + k_{1x} X_{1} = - F_{x} } \hfill \\ {m_{1} \ddot{Y}_{1} + c_{1y} \ddot{Y}_{1} + k_{1y} Y_{1} = - F_{y} } \hfill \\ {m_{1} \ddot{Z}_{1} + c_{1z} \dot{Z}_{1} + k_{1z} Z_{1} = - F_{z} } \hfill \\ {J_{1} \ddot{\theta }_{1} = T_{1} - F_{n} r_{1} + F_{s} r_{1} } \hfill \\ {m_{2} \ddot{X}_{2} + c_{2x} \dot{X}_{2} + k_{2x} X_{2} = F_{x} } \hfill \\ {m_{2} \ddot{Y}_{2} + c_{2y} \dot{Y}_{2} + k_{2y} Y = F_{y} } \hfill \\ {m_{2} \ddot{Z}_{2} + c_{2z} \dot{Z}_{2} + k_{2z} Z_{2} = F_{z} } \hfill \\ {J_{2} \ddot{\theta }_{2} = - T_{2} + F_{n} r_{2} - F_{s} r_{2} } \hfill \\ \end{array} } \right.$$
(21)

where Fs represents the impact force, and it is obtained based on impact theory shown in Sect. 4.2

Fig. 8
figure 8

Dynamic model of 8-DOF spiral bevel gear

Full size image

Fn represents the normal load, \(F_{n} = k_{n} \left( t \right)f\left( {\lambda_{n} } \right) + c_{n} \dot{\lambda }_{n}\)

kn represents the meshing stiffness. LTE (or meshing stiffness) is one of the main vibration excitation of gear transmission.

λn represents the normal relative displacement of gear meshing point.

Fx, Fy, Fz represent the components of normal load Fn along x, y, and z axes, respectively.

di (i = 1,2,3) represents the component of normal vector at meshing point along x, y, and z axes.

k1x, k1y and k1z represent the supporting stiffness of driving gear along x, y, and z axes respectively.

k2x, k2y and k2z represent the supporting stiffness of driven gear along x, y, and z axes respectively.

k1x = 4.35 × 107 N/mm. k1y = 9.4 × 109 N/mm. k1z = 9.4 × 109 N/mm.

k2x = 7.3 × 109 N/mm. k2y = 1.2 × 108 N/mm. k2z = 7.3 × 109 N/mm.

m1 and m2 represent the mass of driving gear and driven gear respectively.

Ip, Ig represent moment of inertia. Ip = 0.0024 kg·m2. Ig = 0.1527 kg·m2.

me represents gear equivalent mass.

$$m_{e} = \frac{{m_{1} m_{2} }}{{m_{1} + m_{2} }}$$
(22)

cn represents meshing damping.

$$c_{n} = 2\xi \sqrt {k_{m} m_{e} }$$
(23)

ζ represents the meshing damping ratio, which is 0.08.

c1x, c1y and c1z represent the damping of driving gear along x, y, and z axes respectively.

c2x, c2y and c2z represent the damping of driven gear along x, y, and z axes respectively.

$$c_{ij} = 2\xi \sqrt {k_{ij} m_{i} } (i = 1,2,3.j = x,y,z)$$
(24)

T1 and T2 represent the torque of driving gear and driven gear respectively.

$$T_{1} = T_{1m} + T_{1v}$$
(25)
$$T_{2} = T_{2m}$$
(26)

T1m represents average moment, T1v represents variable partial moment, T2m represents constant moment.

4 Numerical example

The geometric parameters of the spiral bevel gear are given in Table 1. The machine settings of the spiral bevel gear based on the LSM are given in Table 2. The machine settings of the spiral bevel gear based on ease-off technology are given in Table 3.

Table 1 Geometric parameters
Full size table
Table 2 Machine settings based on LSM
Full size table
Table 3 Machine settings based on ease-off technology
Full size table

The meshing performance of the HCR spiral bevel gear designed by the LSM and ease-off technology is analyzed with the TCA method. The contact path of the gear tooth surface is shown in Fig. 9. By comparison, it is found that the contact path of the HCR spiral bevel gear designed by the LSM is curved, while the contact path of the HCR spiral bevel gear designed based on the ease-off technology is a straight line. Therefore, ease-off technology can overcome the phenomenon that the contact path of the HCR spiral bevel gears designed by the LSM may be seriously bent in the whole meshing process, and then improve the meshing performance and the design level of the HCR spiral bevel gears.

Fig. 9
figure 9

The contact path of the gear tooth surface

Full size image

Based on the pre-set geometric TE curve and contact path, the ease-off target surfaces of pinions 1 and 2 are built, respectively. According to the optimization model shown in Eq. 13, the pinion modified tooth surface and the corresponding machining parameters are calculated and listed in Table 4. The meshing performance of the gear pair 1 (composed of pinion 1 and gear) and the gear pair 2 (composed of pinion 2 and gear) is analyzed with the TCA method. The contact path of the pinion (a) and gear (b) and the transmission error curve (c) are shown in Fig. 10. The blue one is gear pair 1, and the red one is gear pair 2. It is obvious that the angles between the pinion contact path and the pitch cone on the pinion 1 and pinion 2 are 135° and 169°, respectively, and the DCR of gear pair 1 is 1.8, and the DCR of gear pair 2 is 2.8, respectively. Therefore, the DCR of the spiral bevel gear can be improved by increasing the angle between the contact path and the pitch cone on pinion based on ease-off technology.

Table 4 Machine settings of pinions based on ease-off technology
Full size table
Fig. 10
figure 10

The TCA results

Full size image

When the load is 1600 Nm, the LTE of the spiral bevel gear is calculated with the LTCA method, and the calculation results are shown in Fig. 11. By comparison, it is found that the LTE amplitude of gear pair 1 is 4.5270" with low-contact-ratio, and the LTE amplitude of gear pair 2 with high-contact-ratio is only 1.6800″, 62.89% less than gear pair 1 with high-contact-ratio. Therefore, increasing the DCR can reduce the LTE amplitude of the spiral bevel gear. The LTE is one of the main excitations of running vibration and noise of the spiral bevel gear. Therefore, increasing the DCR can improve the dynamic performance of the spiral bevel gear.

Fig. 11
figure 11

Comparison of LTE, a LTCA results and b FEA results

Full size image

To further verify the advantages of the gear pair 2 with high-contact-ratio in reducing LTE, the LTE of the spiral bevel gear obtained by the LTCA method is compared with that obtained by the FEA method. To ensure the accuracy of the FEA results, first, the accuracy of the FEA model should be guaranteed. The accuracy of the FEA model can be divided into the following two parts: tooth surface accuracy and gear assembly accuracy. To ensure the tooth surface accuracy, based on the tooth surface equation, the finite element mesh model of the tooth surface is built by rotating and arraying the position coordinates of discrete points of the tooth surface, and the tooth surface obtained by this method can meet the requirements of high accuracy. The solid model of the gear and the pinion is constructed with discrete points, and the gear and the pinion are placed in the same meshing coordinate system based on the principle of coordinate transformation to complete the assembly of the spiral bevel gear. The seven-tooth FEA model of the spiral bevel gear shown in Fig. 12 is obtained, and the assembly accuracy meets the requirements.

Fig. 12
figure 12

Finite element analysis model of spiral bevel gear

Full size image

When the load is 1600 Nm, the LTE of the spiral bevel gear is carried out based on the seven-tooth FEA model. In addition, Fig. 11 shows the FEA results. A comparison shows that although the LTE amplitudes obtained by the two methods are slightly different, the variation of the LTE curve is basically the same; gear pair 2 with high-contact-ratio has lower LTE amplitude than gear pair 1 with low-contact-ratio. Therefore, increasing DCR can effectively reduce the LTE of the spiral bevel gear, and improve the meshing performance of the spiral bevel gear.

When the load is 1600 Nm, the pinion rotational speed is 7000 r/min, the meshing impact of the spiral bevel gear is calculated based on the meshing impact theory, and the calculation results are shown in Fig. 13. By comparison, it is found that the impact velocity and impact force of gear pair 1 with low-contact-ratio are 0.3300 m/s and 3610 N, while the impact velocity and impact force of gear pair 2 with high-contact-ratio are 0.1551 m/s and 1466 N, respectively, 53.00% and 59.39% lower than those of gear pair 1 with low-contact-ratio. Therefore, increasing the DCR can reduce the meshing impact of the spiral bevel gear. The meshing impact is one of the main excitations of running vibration and noise of the spiral bevel gear. Therefore, increasing the DCR can improve the dynamic performance of the spiral bevel gear.

Fig. 13
figure 13

Comparison of meshing impact

Full size image

When the load is 1600 Nm, the pinion rotating speed is 7000 r/min. According to the 8-DOF dynamic model established by the lumped mass method as shown in Fig. 8, the dynamic response of the spiral bevel gear is analyzed, and the calculation results are shown in Fig. 14. The dynamic load factor can effectively reflect the vibration characteristics of the spiral bevel gear. The larger the dynamic load factor is, the more severe the vibration is. By comparison, it is found that under the same working conditions, the dynamic load factor of gear pair 1 with low-contact-ratio is 1.0904, while the dynamic load factor of gear pair 2 with high-contact-ratio is only 1.0379. Therefore, increasing the DCR can reduce the dynamic load factor of the spiral bevel gear, and improve the dynamic performance of the spiral bevel gear.

Fig. 14
figure 14

Comparison of dynamic load factor

Full size image

To show the advantage of the HCR spiral bevel gear, the LTEs of gear pair 1 and gear pair 2 under multiple working conditions is analyzed with the LTCA method. The calculation results are shown in Fig. 15. By comparison, it is found that the LTE amplitude of gear pair 1 with low-contact-ratio is larger than gear pair 2 with high-contact-ratio, and they all decrease as the load increases. Therefore, increasing the DCR can effectively reduce the LTE amplitude of the spiral bevel gear, and improve the meshing performance of spiral bevel gear transmission.

Fig. 15
figure 15

Comparison of LTE

Full size image

Then, the meshing impact (the pinion rotational speed is 7000 r/min) of the spiral bevel gear transmission under the multiple working conditions is calculated based on meshing impact theory, and the calculation results are shown in Fig. 16. By comparison, it is found that the impact velocity and impact force of gear 2 with high-contact-ratio are both smaller than those of gear pair 1 with low-contact-ratio. Furthermore, the impact velocity and impact force both increase with increasing loads. Therefore, increasing the DCR can effectively reduce the meshing impact of the spiral bevel gear and improve the meshing performance of the spiral bevel gear.

Fig. 16
figure 16

Comparison of meshing impact

Full size image

When the rotating speed is 7000 r/min, the dynamic response of the spiral bevel gear is analyzed based on the 8-DOF dynamic model shown in Fig. 8, and the calculation results are shown in Fig. 17. By comparison, it is found that under the same working conditions, the dynamic load factors of gear pair 2 with high-contact-ratio are smaller than those of gear pair 1 with low-contact-ratio. Therefore, increasing the DCR can effectively reduce the dynamic load factor, and improve the dynamic performance of the spiral bevel gear.

Fig. 17
figure 17

Comparison of the dynamic load factor

Full size image

5 Conclusions

The LTE (the main vibration excitation of gear transmission in the low-speed range) and meshing impact (the main vibration excitation of gear transmission in the high-speed range) are the main vibration excitations of aviation spiral bevel gear. To improve the dynamic performance of the spiral bevel gear, an ease-off flank modification method for the HCR spiral bevel gear is proposed by increasing the angle between the contact path and the pitch cone on the pinion tooth surface. According to the simulation analysis of the HCR spiral bevel gear designed based on ease-off technology, the following results are obtained:

  1. (1)

    The contact path of the HCR spiral bevel gear designed by the LSM is curved, while the contact path of the HCR spiral bevel gear designed based on ease-off technology is a straight line. Therefore, ease-off technology can effectively improve the meshing performance of the HCR spiral bevel gear.

  2. (2)

    Under the same working conditions, the LTE, meshing impact, and dynamic load factor of the HCR spiral bevel gear are all smaller than those of the low-contact-ratio spiral bevel gear. Therefore increasing the DCR can effectively reduce the dynamic load factor of the spiral bevel gear, and improve the dynamic performance of the spiral bevel gear.

  3. (3)

    Aimed at the variable working conditions of the spiral bevel gear, the LTE, meshing impact and dynamic load factor of the HCR spiral bevel gear under multiple loads are analyzed. It is found that increasing the DCR can effectively improve the dynamic performance of the spiral bevel gear.

The HCR design method based on ease-off technology can be used for the design and analysis of other gear pairs.