Nonlinear vibration of the spiral bevel gear with a novel tooth surface modification method

Abstract

The issue of gear noise is fairly common in power transmission systems. This noise largely stems from the gear pairs vibration triggered by transmission error excitation. This is mainly caused by tooth profile errors, misalignment and tooth deflections. This research endeavors to examine nonlinear spiral bevel gears vibration with the innovative method of tooth surface modification. To design spiral bevel gears with the higher-order transmission error (HTE), the nonlinear vibration of a novel method is investigated. The meshing quality of the HTE spiral bevel gears, as the results demonstrate, sounds more suitable than of the meshing quality gears. Their design was made by means of the parabolic transmission error (PTE). The maximum time response root mean square of the HTE method decreases by 44% concerning the PTE method. The peak-to-peak of the transmission error is decreased by 35% via HTE overall frequency range. However, HTE method is not able to decrease the vibration level on all frequency ratios.

1 Introduction

As a pivotal machine element, bevel gear is extensively employed to transmit the rotation between non-parallels shafts. The spiral bevel gear—as one of the most frequent bevel gears— is capable of transmitting heavy loads between non-parallels shafts at high speeds. Durability and vibration have come to the forefront of researchers’ attention. Stresses, and consequently, bending and contact fatigue life of a gear set are affected by vibratory behavior. Due to backlash, time-varying mesh stiffness, and many other nonlinear factors, gear transmission system generates complex dynamic behaviors. One of the main sources of the noise and vibration in gears is Transmission Error (TE) [1]. The industry and researchers have employed many methods to work on gear pairs [2,3,4].

Increasing the contact-ratio of spiral bevel gears which results in the improvement of dynamic performance has been a great concern for the researchers [5]. Engineers have attempted to find the minimal vibration for spiral bevel gears, especially for high speeds. For example, Fang and Deng demonstrated the high-contact-ratio spiral bevel gears applications; they proposed the adjustment of the contact pattern direction and the contact path enlargement [6, 7]. TE greatly affects noise and gear vibration. Parabolic design of TE employed to decrease the vibration level [8]. For decreasing the loaded transmission error of hypoid gears, drawing on ease-off an optimization method is put forward by Artoni [9]. With the goal of decreasing vibration, Stadtfeld [4] and Su [10] presented the seventh-order TE for spiral bevel gears. Whenever the actual contact-ratio is bigger than two, the amplitude of load transmission error (ALTE) of spiral bevel gears with seventh-order TE is much larger than that of the parabolic transmission error (PTE) [8]. Therefore, the seventh-order TE is not capable of decreasing the ALTE of high contact ration (HCR) in terms of spiral bevel gears, and a novel transmission error curve has to be designed. Litvin [11,12,13] proposed the local synthesis method so as to measure the machine settings for gears [14]. A mathematical model was offered which employed a higher-order tooth surface correction motion [15]. Stadtfeld presented a method which is worked based on higher-order tooth surface correction [16].

The present inquiry aims at examining the nonlinear dynamics of a spiral bevel gear pair by comparing HTE and PTE methods. The governing equations of motion are nonlinear and time-dependent because of backlash function and mesh stiffness. A nonlinear dynamic model is, therefore, employed to study the vibration behavior. The procedure detects the dynamic behavior of HTE and PTE methods with a careful comparison of the two based on dynamic vibration. The effect of time-varying mesh stiffness is taken into account for the sake of analysis. Two different control equations of the spiral bevel gear model were adopted and the static transmission error was expressed in two patterns: predesigned parabolic function and higher-order function of transmission errors. In addition, the comparisons suggest that the HTE failed to effectively modify the dynamic behavior.

For the modification of the noise and vibration of a spiral bevel gear pair, two methods are employed. The statically optimization of the transmission error is the first method which is commonly used. This method enhances the tooth profile to reduce the peak-to-peak of transmission error or equivalently mesh stiffness. The second method is the dynamical optimization modifying the vibration behavior of a gear pair according to one of dynamic factors including a fluctuation root mean square (RMS). This is likely to happen that static optimization has no significant effect on dynamic behavior and may aggravate the situation.

Drawing on the function-oriented design, an original method with the purpose of designing high-contact-ratio spiral bevel gears with the higher-order transmission is offered. It establishes a mathematical model for the computerized numerically controlled cradle-style pinion generator by considering these design parameters: tool parameters, initial machine settings and polynomial coefficients of the auxiliary tooth surface correction motion. To solve the polynomial coefficients, an optimal model was suggested. The tooth surface correction method has served as a basis for the modification of high-contact-ratio (HCR) spiral bevel gears, i.e., the higher-order transmission error (HTE), which is drawn on the function-oriented design.

2 Physical model

Figure 1 shows a portrait of spiral bevel gear pair. It is assumed that the translational degrees of freedom (DOF) for the considered bevel gears are restricted in all directions by means of bearings. Both gears are free to rotate about their axes.

Fig. 1

Spiral bevel gear pair

By applying Lagrange formulation [17,18,19,20,21,22], the equation of motion of the system is achieved:

$$\begin{aligned} & I_{1} \ddot{\theta }_{1} + C_{m} r_{b1} (r_{b1} \dot{\theta }_{1} - r_{b2} \dot{\theta }_{2} - \dot{e}) + k_{m} r_{b1} f(r_{b1} \theta_{1} - r_{b2} \theta_{2} - e) = T_{1} \\ & I_{2} \ddot{\theta }_{2} - C_{m} r_{b2} (r_{b1} \dot{\theta }_{1} - r_{b2} \dot{\theta }_{2} - \dot{e}) - k_{m} r_{b2} f(r_{b1} \theta_{1} - r_{b2} \theta_{2} - e) = - T_{2} \\ \end{aligned}$$

(1)

where $I_{1}$, $I_{2}$ rotary inertia of pinion and gear, $r_{b1}$, $r_{b2}$ base radii of pinion and gear, $\theta_{1}$ angular displacement for the for driver, $\theta_{2}$ angular displacement for the driven, $T_{1}$ constant driver torque and $T_{2}$ constant breaking torque, $k$ time-varying meshing stiffness, $c_{ }$ damping coefficient between the meshing gear teeth of the pairs.

Also, as a result of manufacturing error or some intentional modification on the teeth profile, a free space is produced between mating teeth, named no-load transmission error (NLTE) or $e\left( t \right)$.

Furthermore, Eq. (1) is changed into a new rotational equation of motion:

$$I_{eq} \ddot{\lambda }_{\theta } + C_{eq} (\dot{\lambda }_{\theta } - \dot{e}_{\theta } ) + K_{eq} (t)f(\lambda_{\theta } - e_{\theta } ) = T_{1}$$

(2a)

$$f(\lambda_{\theta } - e_{\theta } ) = \left\{ {\begin{array}{*{20}l} {\lambda_{\theta } - e_{\theta } - \theta_{b} ,} \hfill & {\lambda_{\theta } - e_{\theta } > \theta_{b} } \hfill \\ {0,} \hfill & { - \theta_{b} \le \lambda_{\theta } - e_{\theta } \le \theta_{b} } \hfill \\ {\lambda_{\theta } - e_{\theta } + \theta_{b} ,} \hfill & {\lambda_{\theta } - e_{\theta } < - \theta_{b} } \hfill \\ \end{array} } \right.$$

(2b)

where $C_{eq} = cr_{b1}^{2}$ damping coefficient Equivalent, $K_{eq} = kr_{b1}^{2}$ meshing stiffness Equivalent, $I_{eq} = (\frac{1}{{I_{1} }} + \frac{{n^{2} }}{{I_{2} }})^{ - 1}$ rotary inertia Equivalent, $\lambda = r_{1} \theta_{1} - r_{2} \theta_{2}$ linear DTE along the line of action, $n = r_{2} /r_{1}$ gear ratio of the gear pair, $\lambda_{\theta } = \theta_{1} - n\theta_{2}$ angular dynamic transmission error, $e_{\theta } \left( t \right)$ time-varying circumferential NLTE, $\theta_{b}$ angular backlash.

Moreover, this is obvious that involute profile holds zero value for $e_{\theta } \left( t \right)$ [19]. Equation (2a) expresses the dimensional nonlinear displacement function of the gear pairs. It should be mentioned that the torsional mesh stiffness of the gear pair is simultaneously time-varying and periodic by fundamental meshing frequency, (see Fig. 2). The Fourier series is presented as Eq. (3).

$$K_{m} (t) = k_{0} + \sum\limits_{j = 1}^{S} {a_{j} \cos (j\omega_{m} t)} + \sum\limits_{j = 1}^{S} {b_{j} \sin (j\omega_{m} t)}$$

(3)

where $K_{m}$ equivalents of the torsional mesh stiffness of the gear pair, $k_{0}$ average value of torsional mesh stiffness, $N_{1}$ teeth number of pinion, $\gamma_{s}$ (rpm) input shaft speed, $a_{j} ,b_{j}$ Fourier coefficients, $N_{p}$ number of samples, $N_{1}$ teeth number of pinion, $\gamma_{s}$ (rpm) input shaft speed, $\omega_{m} = \frac{2\pi }{60}N_{1} \gamma_{s}$ fundamental meshing frequency, $S = \left( {N_{p} - 1} \right)/2$ number of harmonics.

Fig. 2

Static transmission error, Red line HTE [8], Red dot Fourier Spot (HTE), Black line PTE [8], Black dot Fourier Spot (PTE). (Color figure online)

Mu et al. [8] obtained mesh stiffness with novel method which is used in this study to investigate the dynamic behavior. Moreover, for validation, mesh stiffness and rigid static transmission error are calculated by “HelicalPair” software [22] developed in the Center Intermech MO.RE. (Aster, High Technology Network of the Emilia Romagna Region). The number of harmonics is determined the number of samples. Figure 3 shows the mesh stiffness variation for the pinion.

Fig. 3

Mesh stiffness of pinion for a HTE and b PTE Blue line PTE [8], Red dot Fourier Spot, Black line HTE. (Color figure online)

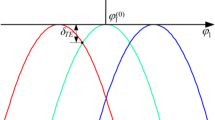
As evident in this model, the gear meshes hold single angular clearance $2\theta_{b}$ despite different normal backlash $2b_{n}$ along face width for other types of the gears.$f\left( {\lambda_{\theta } - e_{\theta } } \right)$ is the rotational displacement function which is multiplied by stiffness and produces the restoring force function in the equation of motion as shown in Fig. 4.

Fig. 4

Nonlinear displacement function with angular backlash

Whenever $\lambda_{\theta } - e_{\theta }$ allocate between $- \theta_{b }$ and $+ \theta_{b }$, the displacement function returns zero, therefore, the mating teeth is separated from each other and the contact loss easily happens because of the clearance between the gear teeth [21]. For $\lambda_{\theta } - e_{\theta } > \theta_{b}$, the mesh is expected to be in the forward contact, while in the state $\lambda_{\theta } - e_{\theta } < - \theta_{b}$ undesired backside contact happens resulting in several problems in gear systems; see Ref. [19]. Equation (2a) can be normalized by substituting new parameters:

$$\tau = \omega_{n} t,\quad \omega_{n} = \sqrt {\frac{{k_{0} }}{{I_{eq} }}} ,\quad \overline{e}_{\theta } = \frac{{e_{\theta } }}{{\theta_{b} }},\quad \lambda^{{\prime }} = \frac{d\lambda }{d\tau },\quad \overline{T}_{g} = \frac{{T_{1} }}{{\theta_{b} I_{eq} \omega_{n}^{2} }},\quad \zeta = \frac{{C_{m} }}{{2I_{eq} \omega_{n} }}$$

(4a)

$$\overline{K}_{m} (t) = 1 + \sum\limits_{j = 1}^{S} {\frac{{a_{j} }}{{I_{eq} \omega_{n}^{2} }}\cos (j\omega_{m} t)} + \sum\limits_{j = 1}^{S} {\frac{{b_{j} }}{{I_{eq} \omega_{n}^{2} }}\sin (j\omega_{m} t)}$$

(4b)

$$f(\overline{\lambda }_{\theta } - \overline{e}_{\theta } ) = \left\{ {\begin{array}{*{20}l} {\overline{\lambda }_{\theta } - \overline{e}_{\theta } - 1} \hfill & {\overline{\lambda }_{\theta } - \overline{e}_{\theta } > 1} \hfill \\ 0 \hfill & { - 1 \le \overline{\lambda }_{\theta } - \overline{e}_{\theta } \le 1} \hfill \\ {\overline{\lambda }_{\theta } - \overline{e}_{\theta } + 1} \hfill & {\overline{\lambda }_{\theta } - \overline{e}_{\theta } < - 1} \hfill \\ \end{array} } \right.$$

(4c)

$$\overline{{\lambda^{{\prime \prime }} }}_{\theta } + 2\zeta (\overline{{\lambda^{{\prime }} }}_{\theta } - \overline{{e_{\theta }^{{\prime }} }} ) + \overline{K}_{m} (\tau )f(\overline{\lambda }_{\theta } - \overline{{e_{\theta } }} ) = \overline{T}_{g}$$

(4d)

Equation (4d) presents a description of a nonlinear differential equation with time-varying coefficient which causes chaos in the system. Based on the fourth order Runge–Kutta, the dynamic behavior of the system is computed by a numerical integration.

3 Validation

To make sure about the output, a validation is done. What is compared with the numerical results of the dynamic solver is the experimental data of Kahraman and Blankenship [23]. The test is conducted on a spur gear utilizing data from Table 1.

Table 1 Common design parameters of the spur gear pairs of benchmark model, Refs. [23, 24]

Details of the mesh on gear pair model is shown in Fig. 5. In order to evaluate the mesh stiffness of gear pair (Fig. 6), the “Helicalpair” software and MSC Marc commercial finite element code are used. “Helicalpair” software has been developed by Vibration and Powertrain laboratory in the University of Modena and Reggio Emilia.

Fig. 5

Gear pair model with detail of the mesh

Fig. 6

Mesh stiffness of pinion which is used as validation. Red line Mesh Stiffness, Black dot Fourier Spot. (Color figure online)

The finite element model with all boundary conditions and other details are prepared by “Helicalpair” software. The model, which possesses nonlinearity due to contact, send to MSC Marc finite element solver to obtain the solution. The obtained results return to “Helicalpair” software in order to compute the mesh stiffness (k). After evaluating mesh stiffness by means of “Helicalpair” (Fig. 6), the dynamical model is simulated mathematically in “adams” code [22, 24]. Furthermore, “adams” is a program prepared in Fortran language by Vibration and Powertrain laboratory in the University of Modena and Reggio Emilia. “Helicalpair” and “Adams” have been widely used in the recent studies and the correctness of the results has been proved in Refs. [22, 24,25,26].

Along the last ten steady state periods, the root-mean-square (RMS) of DTEs is calculated in 100 increments. All parameters for both pinion and gear are the same. The numerical solutions quite match with the experimental data (Fig. 7). Nonlinear softening behavior and jump phenomena almost coincide with the experimental data.

Fig. 7

Comparison between numerical simulation and experimental data from Ref. [23]

4 Numerical results

In order to analysis the behavior of spiral bevel gear pairs, a standard spiral bevel has been chosen. Table 2 includes the geometrical specification of the considered spiral bevel gear.

Table 2 geometric parameters of the spiral bevel gear pairs, Ref. [8]

Dynamic behaviors of structures were analyzed using different useful tools. The system characteristics experience a qualitative change—the number and type of solutions—by using the Bifurcation analysis base on the variation of one or more parameters [27]. Bifurcation map, therefore, displays some specific information of nonlinear dynamic responses.

Dimensionless frequency ($\omega_{m} /\omega_{n}$) is the bifurcation control parameter varying from 0.1 to 2.5 during the analysis, continuously. More applicable control parameters could be found in the geared system, see Ref. [28]. The variable control parameter domain was discritisized to three hundred steps. The state variables at the end of one integration step are considered the initial values for the next step. Dynamic behavior of involute tooth profile gear for speed-up and speed-down can be seen in Figs. 8 and 9, respectively. Figure 8 illustrates the root mean square of oscillation based on the forward and backward motion for the spiral bevel gear with the HTE and PTE.

Fig. 8

RMS diagram based on backward and forward motion of involute tooth profile: a HTE, b PTE, Blue dot Backward, Red dot Forward. (Color figure online)

Fig. 9

RMS diagram of forward and backward motion of involute tooth profile: a Backward, b Forward, Blue dot HTE, Red dot PTE. (Color figure online)

In the backward and forward motion—frequency ratio from 2.5 to 0.1—symmetric periodic solutions are obtained with the excitation frequency for both $\omega_{n}$ and $0.5\omega_{n}$ for the backward motion. Also, Fig. 8 showcases the backward and forward motion covering each other to a high degree with the exception of $\omega_{m} /\omega_{n} \approx 1$. By comparing the dynamic behavior of pinion with HTE and PTE, Jump phenomena happened twice at $\omega_{m} /\omega_{n} \approx 1$ and $\omega_{m} /\omega_{n} \approx 1/2$ for the HTE method when a comparison is made for the dynamic behavior of pinion with HTE and PTE while it can be seen at $\omega_{m} /\omega_{n} \approx 1$ for PTE. Moreover, the PTE experiences a nonlinear softening behavior obviously when compared with HTE. However, from Ref. [8], the ALTE of a spiral bevel gear with the HTE is only $3.326^{{\prime \prime }}$, which is a decrease greater than 35% from that of the PTE ($5.1520^{{\prime \prime }}$). As a result, the HTE can effectively reduce the ALTE of HCR spiral bevel gears. Moreover, it is improved load distribution factor, bending stress, tensile stress and contact stresses, Ref. [8]; also, it decreases the RMS amplitude. However, HTE does not suggest that the dynamic vibration behavior was modified or developed. Figure 9 shows difference between PTE and HTE which is explained in the following. Frequency ratio axis could be divided into three parts: super-harmonic, primary harmonic and sub-harmonic. In the backward motion, despite the primary resonance zone (harmonic stretch, $\omega_{m} /\omega_{n} \approx 1$), the main drawback of the spiral bevel gear which is designed with the HTE is the downside of its effect on dynamic behavior as opposed to PTE. For the forward motion, both PTE and HTE roughly follow the same trend with the exception of two frequency ratios which are located close to $\frac{{\omega_{m} }}{{\omega_{n} }} \approx 1\;{\text{and}}\;0.5$. Different from $\frac{{\omega_{m} }}{{\omega_{n} }} \approx 1$, when the ratio approach subharmonic oscillations ($\omega_{m} /\omega_{n} \approx 0.5$), the RMS amplitude in terms of PTE jumps dramatically.

As can be seen in Fig. 10, two main non-identical bifurcation trends occurred near to primary resonance and second natural frequency.

Fig. 10

Bifurcation diagram for a Backward, b Forward, Blue dot HTE, Red dot PTE. (Color figure online)

The time response curve and phase portrait of the presented spiral bevel gear system are illustrated for frequency ratios which are equal to 0.5 (Fig. 11) in the forward and backward simulation. The red circles on the time history curves depict the starting points of the corresponding excitation period.

Fig. 11

Vibration attractors in 0.5 by backward simulation

5 Discussion and conclusion

This paper attempted to compare the nonlinear vibration of the spiral bevel gear pair with HTE and PTE according to the time varying mesh stiffness and variable backlash. Using the Lagrange formulation, the equation of motion is acquired and is solved following the fourth order Runge–Kutta method. Building on the results of experimental data by Kahraman [23], the mathematical models have been validated. The nonlinear behavior of system has been studied according to the backward and forward simulation. The results of dynamical analysis are of significance in controlling and improving the behavior of the nonlinear gear system. Nonlinear softening behavior and jump phenomena occurred.

Although the HTE can improve the load sharing, and can decrease the tensile stress at the tooth root and, consequently, reduces the contact stresses, it failed to develop the dynamic vibration particularly on the super-harmonic resonances. The HTE method caused declining the average value of STE to 35% as far as the pure involute teeth case is concerned; though, it does not mean that minimizing the RMS of the DTE occurred. Both models, HTE and PTE are compared. There exist some regions in involute tooth profile model that RMS of responses jump up or down—based on the forward or backward motion. There is a noticeable reduction in the maximum amplitude of jumps for HTE, near 44%. In addition to the primary resonance at ω_m/ω_n≈ 1, two resonances at approximately ω_m/ω_n≈ 1/2 and ω_m/ω_n≈ 1/3 could be observed as super harmonics.