1 Introduction

The deformation behavior of metals and alloys at high temperatures is very complex [1]. However, because microstructure control is an important factor for improving the mechanical properties of the final products, studies to understand and predict microstructural changes are of major interest in the field of high-temperature forming processes. In general, metals and alloys with low stacking-fault energies (SFEs) undergo dynamic recrystallization (DRX) [2]. As the strain increases, work hardening, dynamic recovery (DRV), and DRX occur in a complex manner. Work hardening refers to the phenomenon in which the stress increases owing to an increase in the dislocation density. DRV, in contrast, refers to the dissipation of dislocations, which is accompanied by a decrease in the dislocation density and internal energy.

Liu et al. [3]. and Adam et al. [4]. reported the DRX mechanism of A230 alloys depends on the deformation temperature and strain rate. A230 alloys generally have a face-centered cubic (FCC) crystal structure combined with a low SFE, and DRX is promoted during hot deformation owing to the limited dislocation mobility. After reaching the peak in the flow stress, the stress softening stage, in which the dislocation density is reduced by the DRX mechanism, is reached. Softening occurs as a result of dislocation annihilation and rearrangement at high-angle grain boundaries (HAGBs), which results in the formation of fine recrystallized grains [5]. Therefore, a microstructure with fine grains can be obtained via DRX during hot deformation processes [6].

Figure 1 shows the microstructure development during DRX. When the accumulated strain reaches a critical value, nuclei are rapidly generated in the deformed microstructure and at grain boundaries. Thereafter, as the accumulated strain increases, DRX grains are continuously generated at the grain boundaries of both the DRX grains and initially formed grains; thus, the DRX fraction increases. The microstructural changes arising from DRX cause a decrease in the flow stress, which is maintained until it reaches a steady state.

Fig. 1
figure 1

Schematic of microstructure development during DRX

Full size image

DRV and DRX are the main causes of the stress softening mechanism in the high-temperature deformation process. In addition, DRX is known to be an important mechanism for refining the microstructure and reducing stress [7]. Therefore, over the past half century, many studies have been conducted to simulate the high-temperature deformation properties of various materials [8,9,10,11,12,13,14,15].

For example, Chen et al. [16]. and Quan et al. [17]. studied the DRX behavior of 42CrMo steel during hot deformation to establish a DRX kinetic model, and Yin et al. [18]. investigated the microstructural evolution of GCr15 steel using physical experiments and the finite element method. The growth of austenite grains and the DRX of GCr15 steel were modeled using linear regression and genetic algorithms. In addition, Lin et al. [19]. established a constitutive equation for 42CrMo steel based on the classical stress-dislocation relationship and kinematics of DRX. Later, Zeng et al. [20]. studied the hot deformation and DRX behavior of Nb-containing TiAl alloys and established an Avrami-type equation to predict the volume fractions of DRX grains. However, in the constitutive equation for high-temperature deformation, the effect of the activation energy with respect to the strain rate has not been sufficiently reported, and the empirical evaluation of the microstructure prediction via the related DRX kinetic models has been insufficient.

In this study, the high-temperature deformation characteristics of A230 alloy, which is widely used in various industries, were analyzed. The deformation behavior of the A230 alloy was measured using the Gleeble test at various temperatures and strain rates. Based on the measured data, stress–strain curves were modeled using the Arrhenius hyperbolic sine equation proposed by Garofalo et al. [21, 22]. To compare the effects of the differences in activation energy with respect to strain rate on the modeling accuracy, strain-rate-independent and strain-rate-dependent models were established, and the results reveal that the strain-rate-dependent models is more accurate than the strain-rate-independent model at high stress levels.

In addition, models that can predict the volume fraction and size of DRX grains were derived based on the Zener–Hollomon parameters. To confirm the accuracy of the established DRX kinetic model, finite element (FE) simulations with a built-in kinetic model were performed under the same deformation conditions. The results confirm that the DRX behavior of the material can be predicted via FE simulation.

2 Materials and Experimental Procedures

2.1 Material and Uniaxial Compression Tests

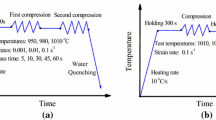
Table 1 shows the chemical composition of the A230 alloy used in this study. Nickel-based A230 alloys are known to have excellent high-temperature strength, oxidation resistance, and thermal stability [3]. The initial material was fabricated into cylindrical specimens with a diameter of 8 mm and a height of 12 mm for uniaxial compression tests. A Gleeble 3800 system was used for the compression tests at a constant strain rate and temperature. In the Gleeble tests, the heating rate was set to 10 °C/s. After reaching the target temperature, compression was performed after 5 min. The other Gleeble test conditions are listed in Table 2.

Table 1 Chemical composition of the A230 alloy
Full size table
Table 2 Experimental conditions for the Gleeble test
Full size table

2.2 Microstructural Characterization

The compressed specimens were cut parallel to the compression direction and mounted using carbon powder. Thereafter, mechanical polishing was performed first with diamond abrasives (3 and 1 µm sequentially) and then with colloidal suspensions. The polished surfaces were analyzed using electron backscattered diffraction (EBSD). In the EBSD measurements, the surface of each specimen was scanned in step sizes of 0.8, 0.4, and 0.2 µm at magnifications of 500, 1000, and 2000, respectively. The grain orientation spread (GOS) values were used to discriminate between the DRX grains and non-DRX grains. The GOS parameter refers to how much the orientation of pixels within a grain differs from the average orientation of the grain, and is derived using Eq. (1) [23,24,25,26,27].

$$GOS\left(i\right)=\frac{1}{J\left(i\right)}\sum_{j}{\omega }_{ij}$$
(1)

Here, J(i) is the number of pixels in grain i, and ωij is the misorientation angle between the orientation of pixel j and the mean orientation of grain i. The deformed grains have high GOS values because of the internal lattice distortions, whereas the DRX grains have low GOS values. The critical GOS value to distinguish between DRX and non-DRX grains generally ranges from 1° to 5° depending on the material and deformation conditions. In this study, DRX grains and non-DRX grains were distinguished using a GOS of 3° [28, 29].

3 Results and Discussion

3.1 Stress–Strain Behavior

Figure 2 shows the true stress–strain curves for the A230 alloy. Overall, the flow stress decreases with increase in temperature, which is characteristic high-temperature deformation behavior. This is because the mobility of the grain boundaries increases as the temperature increases [25, 26]. Therefore, both DRX and DRV occur. In addition, the low strain rate leads to a reduction in the flow stress because it provides sufficient time for the nucleation and growth of DRX grains [4, 27]. For all temperature conditions, the stress increases up to the peak stress as a result of the high work-hardening rate resulting from the increasing dislocation density at the beginning of deformation. After reaching the peak stress, the flow stress gradually decreases as the strain increases, and a steady state in which work hardening and dynamic softening are balanced can be clearly observed. However, the steady-state period does not occur under some conditions at low temperatures and high strain rates. In contrast, at 1200 °C at all strain rates and 1100 °C at strain rates of 0.001 and 0.01 s−1, work hardening after the steady state had been reached can be clearly seen. This is because the DRX goes to completion at a low strain level owing to the high temperature and low strain rate, so the newly generated dislocations begin to accumulate again in the DRX grains [28]. In general, the stress that was increased by the secondary work hardening is reduced again as secondary DRX occurs [29].

Fig. 2
figure 2

True stress–strain curves of the A230 alloy measured at a 900, b 1000, c 1100, and d 1200 °C

Full size image

3.2 Stress–Strain Modeling Using the Zener–Hollomon Parameters

The Arrhenius hyperbolic sine equation (Eq. (2)) has been widely used for modeling the relationship between the deformation conditions (temperature and strain rate) and flow stress at high temperatures [29, 30].

$$\mathrm{Z}=\acute{\varepsilon}exp\left(\frac{Q}{RT}\right)=C\mathrm{sinh}{\left(\alpha \sigma \right)}^{n}$$
(2)

Here, έ is the strain rate, Q is the activation energy (kJ/mol), R is the gas constant (8.314 J/mol K), T is the absolute temperature, σ is the flow stress, and C, α, and n are material constants. When the stress level is high or low, the relationship between the strain rate and stress can be defined by Eqs. (3) and (4) [31].

$$\mathrm{Z}=\acute{\varepsilon}exp\left(\frac{Q}{RT}\right)=A{\sigma }^{{n}^{^{\prime}}} \left(\mathrm{\alpha \sigma }<0.8\right)$$
(3)
$$\mathrm{Z}=\acute{\varepsilon}exp\left(\frac{Q}{RT}\right)=Bexp\left(\beta \sigma \right) \left(\mathrm{\alpha \sigma }>1.2\right)$$
(4)

Here, A, B, n', and β are material constants. Unlike Eqs. (3) and (4), Eq. (2) can be used for constitutive modeling over all stress ranges. Therefore, in this study, stress–strain modeling was performed using Eq. (2).

3.2.1 Calculation of n' and β

The material constant α in Eq. (2) can be obtained by dividing β by n'. Therefore, to calculate n' and β, the natural logarithms of Eqs. (3) and (4) are taken, yielding Eqs. (5) and (6), respectively [32].

$$\mathrm{ln}(\acute{\varepsilon})+\frac{Q}{RT}=\mathrm{ln}(A)+{n}^{^{\prime}}\mathrm{ln}(\sigma )$$
(5)
$$\mathrm{ln}(\acute{\varepsilon})+\frac{Q}{RT}=\mathrm{ln}(B)+\beta \sigma$$
(6)

Thus, n' and β can be obtained by linear fitting to plots of ln(σ) vs. ln(έ) and σ vs. ln(έ) and taking the gradient as shown in Fig. 3. The temperature-dependent n' and β values were obtained by averaging with respect to temperature so that one value was obtained for each strain value. The strain-dependent value of α was obtained by calculating α = β/n'.

Fig. 3
figure 3

Calculation of a n' by plotting ln(σ) vs. ln(έ) and b β by plotting σ vs. ln(έ). For simplicity, only the contents corresponding to a strain of 0.5 are presented

Full size image

3.2.2 Calculation of n and Tp

By taking the natural logarithm of Eq. (2), we obtain Eq. (7).

$$\mathrm{ln}(\acute{\varepsilon})=\mathrm{ln}(C)+n\left[\mathrm{ln}\{\mathit{sinh}\left(\alpha \sigma \right)\}\right]-\frac{Q}{RT}$$
(7)

Further, if the strain rate is constant, Eq. (7) can be expressed as Eq. (8).

$$Q=R\bullet {\left.\frac{\partial \mathrm{ln}(\acute{\varepsilon})}{\partial \mathrm{ln}\left[\mathit{sinh}\left(\alpha \sigma \right)\right]}\right|}_{T}\bullet {\left.\frac{\partial \mathrm{ln}\left[\mathit{sinh}\left(\alpha \sigma \right)\right]}{\partial \left(1/T\right)}\right|}_{\acute{\varepsilon}}$$
(8)

Figure 4 shows the linear relationship between ln[sinh(ασ)] vs. ln(έ), and ln[sinh(ασ)] vs. 1000/T at a strain of 0.5. By averaging the slopes of the linear fits shown in Fig. 4a and b, n and temperature sensitivity parameter (Tp) can be obtained. In the subsequent derivation, if the Tp values are averaged over the strain rate, the strain-rate-independent material constants can be calculated. Otherwise, if the Tp values obtained at each strain rate are applied (not averaged), the strain-rate-dependent material constants can be calculated. Therefore, we analyzed the effect of both the strain-rate-dependent and strain-independent constants on the model accuracy.

Fig. 4
figure 4

Calculation of a n by plotting ln[sinh(ασ)] vs. ln(έ) and b Tp by plotting ln[sinh(ασ)] vs. 1000/T. For simplicity, only the contents corresponding to a strain of 0.5 are presented

Full size image

3.2.3 Calculation of Q, C, and Z

Using the previously derived values of n and Tp, the activation energy (Q) with respect to the strain can be calculated using Eq. (9) [33, 34].

$$Q={\left.Rn{T}_{p}\right|}_{\acute{\varepsilon}}$$
(9)

In addition, by substituting the Q value into the equation below, the material constant C in Eq. (2) can be obtained.

$$\mathrm{ln}\left[\mathit{sinh}\left(\alpha \sigma \right)\right]=\frac{\mathrm{ln}(\acute{\varepsilon})}{n}+\frac{Q}{nRT}-\frac{\mathrm{ln}(C)}{n}$$
(10)

Figure 5 shows the strain-rate-independent and strain-rate-dependent values of Q and ln(C). For the strain-rate-independent results (Fig. 5a and b), one Q and ln(C) value averaged over the strain rate exist for each strain value [35]. In contrast, the strain-rate-dependent results have strain-rate-dependent Q and ln(C) values for each strain value (Fig. 5c and d). As shown in the figure, the Q and ln(C) values are significantly affected by the strain rate. At low strain, the two material constants are similar. However, as the strain increases, the values at strain rates of 0.001 and 0.01 s−1 decrease sharply, whereas those at strain rates of 0.1 and 1 s−1 are maintained or increase.

Fig. 5
figure 5

Calculated strain-rate-independent a deformation activation energy (Q) and b ln(C) and strain-rate-dependent c Q and d ln(C)

Full size image

The activation energy is a crucial material constant for determining the flow stress. Therefore, when there is such a large difference with respect to strain rate, the strain-rate-dependent Q and ln(C) values will yield more accurate results than the strain-rate-independent values. Table 3 lists the calculated Q and ln(C) values.

Table 3 Activation energies (Q) and ln(C) at different strain rates and strain values
Full size table

3.2.4 Modeling the Stress–Strain Curve Using the Zener–Hollomon Parameters

By substituting the previously calculated material constants into Eq. (2), the Zener–Hollomon parameters for each temperature, strain rate, and strain were calculated. Subsequently, the flow stresses were calculated by substituting the calculated Z and C values into Eq. (11), and the results for a temperature of 1200 °C are shown in Fig. 6a and b [36].

Fig. 6
figure 6

Experimental and predicted stress–strain curves calculated using the a strain-rate-independent and b strain-rate-dependent constants. Correlation between the experimental and predicted stresses calculated using the c strain-rate-independent and d strain-rate-dependent constants. For simplicity, only the stress–strain curves for 1200 °C are presented in a and b

Full size image
$$\sigma =\frac{1}{\alpha }\mathrm{ln}\left\{{\left(\frac{\mathrm{Z}}{C}\right)}^\frac{1}{n}+{\left[{\left(\frac{\mathrm{Z}}{C}\right)}^\frac{2}{n}+1\right]}^\frac{1}{2}\right\}$$
(11)

In the case of the strain-rate-independent results (Fig. 6a), the predicted stresses are similar to the experimental values at low strain rates. However, there are many differences between the predicted and experimental values at high strain rates (0.1 and 1 s−1).

In addition, the strain-rate-dependent results yielded more accurate predictions than the strain-rate-independent results (Fig. 6b). For example, at strain rates of 0.001 s−1 and 0.01 s−1, the trend in the flow stress caused by dynamic softening was accurately predicted, and the differences were negligible. In the case of high strain rates (0.1 s−1 and 1 s−1), although there is a slight difference between the predicted and experimental values, the trends in the flow stress are similar. The difference between the two values is also improved compared with the strain-rate-independent result.

Figure 6c and d show the differences between the predicted and experimental stresses for all deformation conditions. In the case of the strain-rate-independent results, the error is relatively low in the low-stress range. However, as the stress level increases, the error also increases. This is because the dependency of the activation energy on the strain rate increases as the strain (or stress) increases, as shown in Fig. 5c. In contrast, the strain-rate-dependent result shows relatively high accuracy over the entire stress range.

To compare the accuracies of the strain-rate-independent and strain-rate-dependent models more closely, the correlation coefficient (R) and the average absolute relative error (AARE) were calculated using Eqs. (12) and (13) [37].

$$\mathrm{R}=\frac{\sum_{i=1}^{n}({E}_{i}-\overline{E })({P}_{i}-\overline{P })}{\sqrt{\sum_{i=1}^{n}{\left({E}_{i}-\overline{E }\right)}^{2}\sum_{i=1}^{n}{\left({P}_{i}-\overline{P }\right)}^{2}}}$$
(12)
$$\mathrm{AARE}=\frac{1}{n}\sum_{i=1}^{n}\left|\frac{{E}_{i}-{P}_{i}}{{E}_{i}}\right|\times 100$$
(13)

Here, Ei, Pi, and n are the experimental flow stresses, predicted flow stresses, and total number of data points, respectively. For the strain-rate-independent results (Fig. 6c), R and AARE are 0.989 and 10.55, respectively, whereas, for the strain rate-dependent results (Fig. 6d), they are 0.997 and 6.37, respectively.

3.3 DRX Kinetic Model

In high-temperature deformation, the kinetics of DRX are predominantly affected by the density and distribution of dislocations [38]. The key variables for modeling the volume fraction of DRX grains include the critical strain (εc), peak strain (εp), strain when the volume fraction of DRX grains reaches 50% (ε0.5), and steady-state strain (εss). As shown in Fig. 7a, εc is the strain at which the DRX begins to occur, and the corresponding stress value is denoted as σc. εp is the strain corresponding to the maximum stress, and εss is the strain at which work hardening and dynamic softening are balanced such that the flow stress does not increase or decrease. The values corresponding to εc, εp, and εss (or σc, σp, and σss) can be obtained by plotting θ, which is the derivative of the stress with respect to strain, as shown in Fig. 7b. To calculate σc, which is the inflection point in the θ vs. σ graph, more accurately, -(dθ⁄dσ) vs. σ graphs are generally used [39].

Fig. 7
figure 7

a Relationship between the stress–strain curve and DRX volume fraction (\({X}_{DRX}\)) and b θ vs. σ showing representative strain values

Full size image

Figure 8 shows plots of θ vs. σ and -(dθ⁄dσ) vs. σ for 1100 °C. As shown, there are no σss values at strain rates of 0.1 and 1 s−1. This is because, when the deformation temperature is low or (and) the strain rate is high, DRX does not go to completion within the limited strain range, as shown in Fig. 2. Therefore, the εss values at all strain rates at 900 °C, 0.01, 0.1, and 1 s−1 at 1000 °C, and 0.1 and 1 s−1 at 1100 °C could not be determined. Table 4 summarizes the εc, εp, and εss values under all conditions.

Fig. 8
figure 8

Plots of a θ vs. σ and b –(dθ/dσ) vs. σ. For simplicity, only data corresponding to 1100 °C are presented

Full size image
Table 4 Summary of the representative strain values for the DRX kinetic model with respect to deformation conditions
Full size table

In general, the DRX kinetics can be modeled using the following exponent-type equation [40]:

$${X}_{DRX}=1-exp\left[-k{\left(\frac{\varepsilon -{\varepsilon }_{c}}{{\varepsilon }_{0.5}}\right)}^{{n}_{d}}\right],$$
(14)

where XDRX and nd are the volume fraction of the DRX grains and material constant, respectively. The value of ε0.5 can be obtained experimentally by plotting XDRX vs. ε using Eq. (15) [41].

$${X}_{DRX}=\frac{\sigma -{\sigma }_{p}}{{\sigma }_{ss}-{\sigma }_{p}}$$
(15)

Figure 9 shows the graph of XDRX for deformation at 1000 °C at 0.001 s−1. The graph shows that a strain of 0.419 resulted in a 50% volume fraction of DRX grains.

Fig. 9
figure 9

Relationship between the DRX grain volume fraction and true strain on deformation at 1000 °C at 0.001 s−1

Full size image

By taking the natural logarithm of Eq. (14), we obtain Eq. (16).

$$\mathrm{ln}\left[-\mathrm{ln}\left(1-{X}_{DRX}\right)\right]=\mathrm{ln}\left(-k\right)+{n}_{d}\mathrm{ln}\left(\frac{\varepsilon -{\varepsilon }_{c}}{{\varepsilon }_{0.5}}\right)$$
(16)

Figure 10 shows the plot of ln[-ln(1-XDRX)] vs. ln(ε-εc/ε0.5). The mean slope and y-intercept of the linear fitted line give nd and k, respectively, and nd and k were calculated to be 3.154 and 0.834, respectively.

Fig. 10
figure 10

Calculation of nd by plotting ln[-ln(1- XDRX)] vs. ln(ε-εc/ε0.5)

Full size image

3.3.1 DRX Kinetic Models for FE Simulation

To verify the validity of the DRX kinetic model, process analysis of high-temperature compression was performed using a commercial FE simulation package (Forge, Transvalor Co.). To apply the DRX kinetic model to the FE simulation, Eqs. (17)–(20), as well as Eqs. (2) and (14), are required [42].

$${\varepsilon }_{p}=\alpha {\mathrm{Z}}^{{n}_{1}}$$
(17)
$${\varepsilon }_{0.5}=\delta {\mathrm{Z}}^{{n}_{2}}$$
(18)
$${\varepsilon }_{c}=\gamma {\varepsilon }_{p}$$
(19)
$${D}_{DRX}=B{\mathrm{Z}}^{{n}_{3}}$$
(20)

Here, α, δ, γ, B, n1, n2, and n3 represent the material constants. DDRX is the average equivalent diameter of grains that have undergone complete DRX, as obtained from EBSD data of compression test specimens. To calculate each material constant, the above four equations were plotted, as shown in Fig. 11. Subsequently, the material constants were obtained by determining the slope and y-intercept of the fit to the data.

Fig. 11
figure 11

Calculation of α, δ, B, n1, n2, and n3 by plotting a ln(εp) vs. ln(Z), b ln(ε0.5) vs. ln(Z), c εc vs. εp, and d ln(DDRX) vs. ln(Z)

Full size image

The corresponding equations and material constants related to the DRX kinetic model for the FE simulation are summarized in Table 5. Figure 12 shows the XDRX graph obtained based on the values and equations listed in Table 5. The XDRX at 900 °C cannot be plotted because there is no steady state in the flow stresses. Furthermore, under deformation at 0.01 s−1 at 1000 °C and 0.1 s−1 at 1100 °C, there is no steady state in the flow stress. However, it can be seen that XDRX reaches 100% when the strain reaches approximately 1.0, as shown in the XDRX graph. This is because the normalized data from Eqs. (17) to (19) were used.

Table 5 Summary of the equations and material constants for FE simulation
Full size table
Fig. 12
figure 12

Volume fractions of DRX grains at a 1000, b 1100, and c 1200 °C

Full size image

3.4 Verification of the DRX Kinetics Model

Additional compression tests were performed for comparison with the FE simulations. Specimens with a diameter of 8 mm and a height of 12 mm were heated to 1100 and 1200 °C and pressed at speeds of 5.1 and 5.14 mm s−1, respectively, to a final stroke of 8 mm. The roughly estimated strain rates for these two conditions are 0.425 to 1.275 s−1 for 5.1 mm/s and 0.428 to 1.285 s−1 for 5.14 mm/s.

The FE simulations were performed under the same compression conditions, and the results are shown in Fig. 13. To compare the results of the EBSD measurements and FE simulation, three regions, the center, middle, and edge, were selected. As shown, the strain and strain rates tend to decrease from the center to the edge. A high volume fraction of the DRX grains was predicted at the center. On the other hand, a low value was estimated at the edge, similar to the trend in strain. Small and large DRX grain sizes were predicted at the center with a high strain rate and at the edge region with a low strain rate, respectively. This is because the Zener–Hollomon parameters that determine the DRX grain size are functions of the temperature and strain rate. However, the difference in DRX grain sizes was as small as 0.5 μm. With respect to the average grain size, a low value was estimated at the center with a high volume fraction of DRX grains because the coarse initial grains almost disappeared. Otherwise, a large value was predicted at the edge where the initial grains remained. Table 6 presents the effective strain according to the selected regions in Fig. 13 for all deformation conditions. Each effective strain was calculated by averaging the three node values around each point.

Fig. 13
figure 13

Results of FE simulation performed at 1100 °C

Full size image
Table 6 Effective strain in selected regions with respect to deformation conditions
Full size table

Figure 14 shows the EBSD results for the three selected regions. In the case of the center and middle under all deformation conditions, homogeneous fine grains were evenly distributed, and these fine grains were newly formed by DRX. In contrast, partially heterogeneous coarse grains appeared in the edge regions. The coarse grains seem to be non-DRX grains (original grains), so a low volume fraction of DRX grains is expected.

Fig. 14
figure 14

Inverse pole figure (IPF) maps of measured regions at a 1100 °C and a compression speed of 5.14 mm s−1 and b 1200 °C at a compression speed of 5.1 mm s−1

Full size image

The GOS maps used to distinguish between the DRX and non-DRX grains are presented in Fig. 15. For the 1100 °C case, in the middle and center regions, most of the grains had a low GOS value of 3° or less. However, there were still some non-DRX grains. On the other hand, for the microstructure deformed at 1200 °C, the edge region shows the same trend as that 1100 °C. However, unlike the 1100 °C case, the middle and center regions contain no non-DRX grains. Notably, for the 1100 °C case, although the strain of the center region was 1.7, non-DRX grains were still present in the center. This is not consistent with our results considering that a steady state exists in the flow stresses at 1100 °C for all strain rates and volume fractions of the DRX grains in Fig. 12b.

Fig. 15
figure 15

GOS maps of different measured regions at a 1100 °C and a compression speed of 5.14 mm s−1 and b 1200 °C at a compression speed of 5.1 mm s−1

Full size image

Figure 16 shows the GOS values and grain size distributions for each region to analyze the causes of the above results. In the case of the edge regions for the 1200 °C case (Fig. 16c), many coarse grains with a high GOS are present. For the middle and center regions, the grain size decreased, and the GOS values tended to converge to 3° or less. On the other hand, for the middle and center of the 1100 °C case, some grains are small but have high GOS values. This suggests that abnormal DRX did not occur despite the increase in the GOS value induced by the continued deformation of the fine grains.

Fig. 16
figure 16

Grain size distribution according to GOS values at a center, b middle, and c edge

Full size image

Figure 17 shows graphs comparing the results of EBSD measurement and FE simulation for the volume fraction of DRX grains, DRX grain size, and average grain size. With respect to the volume fraction of the DRX grains for the 1100 °C case, there is a slight difference between the results of EBSD measurements and FE simulation in the center and middle regions because of the abnormal DRX behavior at 1100 °C. However, the overall trend was accurately predicted in both deformation conditions. In the case of the DRX grain size and average grain size, although there is a slight absolute numerical difference, the variation with respect to strain level for each region is also effectively predicted. Therefore, it was concluded that DRX behavior can be effectively predicted by combining the DRX kinetic model and FE simulation.

Fig. 17
figure 17

Comparison between EBSD and FE simulation results for the a volume fraction of DRX grains, b DRX grain size, and c average grain size

Full size image

4 Conclusion

To analyze the high-temperature deformation behavior of nickel-based A230 alloy, high-temperature compression tests were conducted at strain rates of 0.001–1 s−1 and temperatures of 900–1200 °C. Based on the experimental results, the constitutive equations for the stress–strain curves and DRX kinetic model were established based on the Zener–Hollomon parameters. The analysis results obtained through various experiments and mathematical derivations conducted in this study are summarized below.

The Zener–Hollomon parameters were obtained to derive a constitutive equation for the stress–strain curves. Two types of Zener–Hollomon parameters, one derived using the strain-rate-independent activation energy and the other using strain-rate-dependent activation energy, were calculated. As a result, it was confirmed that the strain-rate-dependent result can more accurately predict the flow stresses (AARE = 6.37). In the strain-rate-independent case, the AARE was 10.55.

A DRX kinetic model was established based on the obtained parameters. The DRX kinetic model was applied to the FE simulation to predict the microstructural changes according to the deformation history. EBSD analysis was performed using the material deformed at high temperatures. From the EBSD results, the volume fraction of DRX grains, DRX grain size, and average grain size were measured and compared with the FE simulation results. The results show that the DRX behavior can be effectively predicted by combining the DRX kinetic model and FE simulation.