Introduction

Generally, Nickel-based corrosion-resistant alloy has to be processed through various hot deformation treatments before it is fabricated into final component (Ref 1-4). Therefore, determination of the load to carry out these operations is of paramount importance. Load depends on flow stress of the materials which can be controlled by the hot working parameters such as deformation temperature, strain rate, and strain. So far, many investigations have carried out for flow behaviors of AISI304 stainless steel (Ref 5), Ti-IF steel (Ref 6), 42CrMo steel (Ref 7-9), medium carbon micro-alloy steel (Ref 10), Austenitic Fe-Mn alloys (Ref 11), 410 martensitic stainless steel (Ref 12-14), etc., but the research on Nickel-based corrosion-resistant alloys is mainly focused on the improvement of its corrosion resistance (Ref 15, 16), and the knowledge about the flow behavior of alloy has been rarely reported. So it is very important and timely to understand the hot deformation behavior of the Nickel-based corrosion-resistant alloy.

Constitutive models are generally used to describe the plastic flow properties of metals and alloys, which are correlated with the flow stress, the strain, the strain rate, and the deformation temperature. For the past few years, the intrinsic relationships between the hot deformation behavior and processing conditions (strain, strain rate, and deformation temperature) have been constructed by a phenomenological approach from the experimentally measured data (Ref 17-26). This approach was first proposed by Sellars et al. (Ref 17), where the flow stress is expressed by the hyperbolic laws in an Arrhenius type of equation. Afterward, various modifications to this approach have been developed to improve its predictability. Slooff et al. (Ref 18) modified the hyperbolic sine constitutive model by considering that parameters in the constitutive equation are the function of strain, which can predict precisely the flow stress in a wrought magnesium alloy. Similarly, considering the deformation activation energy (Q) and material constants as function of strain, a strain-dependent hyperbolic sine constitutive equation was proposed to predict the flow stress at elevated temperature in magnesium alloy (Ref 19, 20), steels (Ref 21, 22), and Ni-based superalloys (Ref 23, 24). In order to further improve the predictive accuracy of the strain-dependent hyperbolic sine constitutive model, Lin et al. (Ref 25) and Mandal et al. (Ref 26) revised the strain-dependent hyperbolic sine constitutive equation through compensation of strain rate in Zener-Holloman parameter (Z) during constitutive analysis on 42CrMo steel and D9 steel. Similarly, through considering the compensation of strain rate, a modified constitutive equation was proposed by Peng et al. (Ref 27) and applied successfully to TC4-DT alloy under the high strain rate (10 s−1). Thus, the revised model can predict accurately the flow stress throughout the entire range of the deformation temperature and the strain rate.

Additionally, some physically based models have been developed. For example, Cram et al. (Ref 28) established a complex dynamic recrystallization (DRX) nucleation model by considering the dynamic evolving substructure size, and the proposed model has been able to successfully predict the flow stress over a wide range of deformation temperature, initial grain size, and strain rate. Recently, Bernard et al. (Ref 29) developed a new model of DRX using a two-site mean field approach, in which the elementary physical phenomena such as strain hardening, recovery, grain boundary migration, and nucleation were considered. Their model can predict accurately the flow stress curves and the microstructure evolution during hot forging in both dynamic and post-dynamic regimes. Based on the dislocation density theory and kinetics of DRX, Wang et al. (Ref 3) developed a two-stage model to determine the flow stress curves of Nickel-based corrosion-resistant alloy at hot deformation condition. Besides, Zerilli and Armstrong (Ref 30) established a physical model (ZA model) based on dislocation mechanisms and considered the effects of strain hardening, strain rate hardening, and thermal softening on the flow stress of the metals and alloys. On the other hand, recently, a new approach of artificial neural network (ANN), which does not need to postulate a mathematical model or identify its parameters, has been introduced to predict the hot deformation behavior of many materials (Ref 31-35). ANN is a robust and intelligent data information treatment system available for adaptive data mining and modeling ambiguous and complicated problems. Thus, the ANN model only needs to learn from sufficient experimental data and to recognize patterns in a series of inputs and outputs without any prior knowledge of their functional relationships or tedious regression analysis (Ref 32).

However, for physical-based models, some assumptions were given before some plastic flow stress models are proposed (Ref 3, 28-30), and many physical parameters in models are difficult to be precise determination (Ref 36). For the ANN model, it is merely a mathematical treatment and do not involve the physical nature of the hot deformation process, and the successful application of ANN model is inseparable from the availability of extensive, the high-quality data, and characteristic variables (Ref 36). Compared to the above two type models, the advantage of hyperbolic sine constitutive equation is that it has only a small number of physical meaning parameters, and it has been proven to be most applicable over a wide range of stresses (Ref 17). More importantly, the deformation activation energy (Q) of a material derived from this relation not only is usually used as indicator of the degree of difficulty of the hot deformation process, but also can also determine the deformation mechanism of materials and alloys. For example, for pure metals and dilute alloys, deformation activation energy (Q) satisfactorily agrees with activation energy for creep and diffusion (Ref 37). Furthermore, it can provide a guide line for optimizing the hot working process and furnish additional information about the microstructure and the flow stress evolution in hot deformation processes.

In majority of the research on the hot deformation behaviors of metals and alloys (Ref 1-3, 12-14), the deformation activation energy was usually calculated and considered as a constant value under different hot deformation conditions. As a matter of fact, the deformation activation energy of metals and alloys represents mainly the free energy barrier to dislocation movement (Ref 38, 39). Usually, the energy required for dislocation movement is affected by the deformation temperature and strain rate during hot working processes (Ref 40-42), so the activation energy for hot deformation should not be considered as constant, but instead be a function of the deformation parameters, including the deformation temperature, the strain rate, and the strain. Thus, the objective of this study is to establish a relationship between deformation activation energy (Q) and deformation conditions, especially the effect of strain rate, and further, through above relationship, predict accurately the high temperature flow stress of Nickel-based corrosion resistance alloy under different deformation conditions. For this purpose, typical solid solution strengthened Nickel-based corrosion-resistant alloy, N08028 (028) alloy was selected as the research material. Furthermore, the experimental data obtained from isothermal hot compression tests have been utilized and the function relation between the “material constants” in the hyperbolic sine constitutive equation and different deformation conditions has been established. Finally, validity of the new proposed hyperbolic sine constitutive equation was examined for the entire experimental range.

Experimental

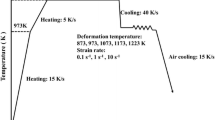
Nickel-based corrosion-resistant (028) alloy with chemical composition (wt.%) of Ni-27 wt.%Cr-29 wt.%Fe-0.03 wt.%C-3.5 wt.%Mo-2.5 wt.%Mn-1.0 wt.%Cu was used in this study. Cylindrical specimens of 8 mm in diameter and 12 mm in height were machined from the as-received forging product in accordance with ASTM: E209-00(2010) standard (Ref 3, 43). The specimens were then solution-treated for 150 min at 1200 °C before hot compression tests. The optical microstructure of the annealed Nickel-based corrosion-resistant alloy is composed of equiaxed grains with an average grain size of about 62 ± 3 µm. A computer-controlled, servo-hydraulic Gleeble 3500 thermal-mechanics simulator with a maximum load capacity of 100 kN was used for the compression experiments. This machine can be programmed to simulate both the thermal and the mechanical industrial process variables for a wide of hot deformation conditions. Concentric grooves of 0.5 mm depth were performed on the top and bottom faces of these cylindrical specimens to facilitate the retention of lubricant during testing. Graphite foils and MoS2 paste were used between specimens and the platens to minimize the friction during deformation. The specimens were resistance heated to 1200 °C with a heating rate of 30 °C/s and held at a certain temperature for 300 s by thermos-coupled feedback-controlled AC current, which decreased the anisotropy in flow deformation behavior effectively. Following, each sample was cooled down with a cooling rate of 10 °C/s and held for 30 s at the deformation temperatures, 1050, 1100, 1150, and 1200 °C, respectively. All compression tests corresponding to a height reduction of 50% were carried out at the temperature range of 1050-1200 °C (in steps of 50 °C) and in the strain rate range of 0.001-1 s−1. During the compressing process, the variations of stress and strain were monitored continuously by a personal computer equipped with an automatic data acquisition system. The true stress and true strain were derived from the measurement of the nominal stress-strain relationship according to the following formula (Ref 44, 45): σt = σ n (1 + ε n ), εt = ln (1 + ε n ), where σt is the true stress, σ n is the normal strain, ε t is the true strain, and ε n is the nominal strain. After deformation, the hot specimens were water quenched to freeze the hot deformed microstructure. To ensure the accuracy of the data, 2-3 tests have been repeated at each test conditions.

The deformed specimens were sectioned parallel to the compression axis and prepared for microstructure analysis by conventional mechanical grounding and polishing. The polished samples were etched with a solution-saturated acid (H2O2:HCl:H2O = 1:2:2) for about ten seconds. Micro-structural observation of deformed specimens was performed via light optical microscopy (OP, Olympus GX71). Grain sizes were measured by the mean linear intercept method. Furthermore, to observe the morphology of dislocation in the alloy, the foils for transmission electron microscopy (TEM) were prepared by standard procedures of mechanical grinding to 40-60 µm and ion milling. TEM examination was made on a Philips TENCAL-20 microscope operated at 200 kV.

Results and Discussion

Flow Stress Behaviors and Microstructures

Generally, in the initial stage of deformation, the strain-hardening rate is higher than the softening rate and thus the flow stress increases abruptly, and then the increasing rate decreases due to the occurrence of softening process, such as, dynamic recovery (DRV) and DRX. Once the hardening rate is equal to the softening rate, a peak stress is reached. After the peak stress appears, the softening rate caused by DRX exceeds the hardening rate and the flow stress drops slowly. As the strain increases continuously, the flow stress tends to a steady state, in which a new balance between hardening and softening is established (Ref 3).

The flow stress-strain curves of the 028 alloy resulting from hot compression tests are plotted in Fig. 1. When strain rate is below 1 s−1, all flow stress-strain curves reveal a obvious single peak followed by a gradual drop toward a steady state stress, which has typical characteristic of DRX (Ref 1-5). As shown in Fig. 1, the flow stress is sensitive to the deformation conditions. For example, when strain rate is 0.1 s−1 (Fig. 1c), the steady state stress is 117 MPa at 1100 °C and the steady state stress is just 63 MPa at 1200 °C. Under other strain rates, the similar pattern can be also found. It shows that the flow stress decreases with increasing deformation temperature at constant strain rate. It is mainly because that with increasing deformation temperature, the thermal activation process of material strengthens, the average energy of atoms increases and it results to higher mobility of grain boundary which can effectively reduce the dislocation density during deformation (Ref 7, 21). On the other hand, when the deformation temperature is 1050 °C, the steady state stress is 57 MPa (Fig. 1a) under the condition of strain rate of 0.001 s−1 and the steady state stress can be up to 156 MPa (Fig. 1c) at the strain rate of 0.1 s−1. The similar pattern can be found under other deformation temperatures, which shows that the flow stress increases with increasing strain rate under the constant deformation temperature. It is mainly because that dislocation appears tangle at the high strain rate and tangled dislocation structures can hinder badly the dislocation movement and thereby increase the flow stress. Besides, when strain rate is low, DRV and DRX have enough time to proceed fully, whose softening effect can offset the effect of work hardening to some extent, resulting in lower flow stress (Ref 20, 27). However, with increasing strain rate, DRV and DRX have not enough time fully proceeding and can not offset effectively the effect of strain hardening, so the flow stress is much higher under high strain rate.

Fig. 1
figure 1

Comparison between the experimental and predicted flow stress from constitutive equation at strain rate (a) 0.001 s−1, (b) 0.01 s−1, (c) 0.1 s−1, and (d) 1 s−1

Full size image

In order to verify the above analysis, deformed microstructure of the 028 alloy was observed. Figure 2 shows that microstructures of the specimens deformed at the strain rate of 0.1 s−1 under the temperatures of 1100-1200 °C, and at the deformation temperature of 1050 °C under the strain rates of 0.001-0.1 s−1. From Fig. 2, it can be seen that DRX grain size increases with increasing deformation temperature at the constant strain rate, which illustrated that mobility of grain boundary is enhanced at the high temperature. Besides, when deformation temperature is fixed (1050 °C), DRX has not been completed at strain of 0.7 under the strain rate of 0.1 s−1, where some untransformed austenite grains are elongated, as shown in Fig. 2(d). These are consistent with above result of analysis.

Fig. 2
figure 2

Microstructures of the 028 specimens obtain by water quenching under strain rate 0.1 s−1/1100 °C (a), 1200 °C (b) and under deformation temperature of 1050 °C/0.001 s−1 (c), 0.1 s−1 (d)

Full size image

At higher strain rate (1 s−1), the flow stress-strain curves show complex change (Fig. 1d). When deformation temperature is larger than 1100 °C, the flow stresses appear weaker peak. It shows that DRX occurs at the temperature range of 1150-1200 °C. When deformation temperature is below 1100 °C, the flow stress has not obvious peak even appearing upward at the large strain. In order to determine whether or not the occurrence of DRX, microstructures of alloy were observed. Figure 3 shows microstructures of the 028 alloy after deformation at strain rate of 1 s−1 under the temperatures of 1050, 1100, 1150, and 1200 °C, respectively.

Fig. 3
figure 3

Microstructures of the 028 specimens obtain by water quenching under strain rate 1 s−1 and deformation temperatures of (a) 1050 °C, (b) 1100 °C, (c) 1150 °C, and (d) 1200 °C

Full size image

It is obvious that DRX also occurs at the strain rate of 1 s−1 under the temperatures of 1050 °C and 1100 °C from Fig. 3(a) and (b). In order to further analyze the effect of temperature on DRX under this condition, the average DRX grain sizes are measured as 9.5 ± 2, 13.4 ± 3, 28.2 ± 4, and 34.1 ± 2 µm for the deformation temperatures of 1050, 1100, 1150, 1200 °C, respectively. It can be found that DRX grain size significantly decreased compared with the temperature of 1150-1200 °C. It is mainly because that with decreasing deformation temperature and increasing strain rate, more deformation energies are stored in the deformed microstructure, which will make the dislocation generation rate and the dislocation density increase in the deformed grains. Meanwhile, more substructures can be generated in the deformed grains when the deformation temperature is lower and strain rate is higher, which will produce more nuclei per unit volume of the grain. In other words, this phenomenon can be attributed to that the nucleation rate is stronger than the growth rate under lower deformation temperature and higher strain rate. Recently, Mandal et al. (Ref 46) also founded that DRX at higher strain rates (i.e., ≥1 s−1) is mainly controlled by higher nucleation resulting in higher DRX fraction with a finer grain size through studying a Nitrogen-Enhanced 316(N). Meanwhile, Cram et al. (Ref 28) also illustrated nucleation rate of DRX is enhanced at the low temperature through establishing complex nucleation model. Thus, disappearance of peak at the low temperature and high strain rate is closely related with higher nucleation rate and lower growth rate.

Constitutive Analysis

The Constitutive Equation

The correlation between the flow stress, the deformation temperature and the strain rate could be expressed by a hyperbolic sine constitutive equation and an Arrhenius-type equation. Furthermore, the effects of the temperature and the strain rate on the flow stress could be represented by Zener-Holloman parameter (Z) in an exponent-type equation (Ref 47),

$$A[\sinh (\upalpha \upsigma )]^{n} = \dot{\upvarepsilon }\exp \left( {\frac{Q}{RT}} \right) = Z,$$
(1)

where R is the universal gas constant (8.314 J/(mol K)); T is the absolute temperature in K; Q is the deformation activation energy (kJ/mol); and A, α, and n are the material constants.

To evaluate the material constants, the flow stress data from the hot compression tests at various deformation conditions were used. The following is the evaluation procedure of material constants at a true strain of 0.175.

For both low and high stress levels, the relationship between the flow stress and the strain rate can be described by the following models (Ref 17),

$$\dot{\upvarepsilon } = B\upsigma^{{n^{\prime}}} \quad (\upalpha \upsigma \, < \,0.8),$$
(2)
$$\dot{\upvarepsilon } = C\exp (\upbeta \upsigma )\quad (\upalpha \upsigma \, > \,1.2),$$
(3)

where B, C, and β are the material constants.

Natural logarithm of both sides of Eq 2 and 3 yields

$$\ln \,\dot{\upvarepsilon } = \ln \,B + n^{\prime}\ln \,\upsigma,$$
(4)
$$\ln \,\dot{\upvarepsilon } = \ln \,C + \upbeta \upsigma.$$
(5)

The value of n′ and β can be obtained from the slope of the lines in the \(\ln \,(\upsigma ) - \ln \,(\dot{\upvarepsilon })\) plot (Fig. 4a) and \(\upsigma - \ln (\dot{\upvarepsilon })\) plot (Fig. 4b), which are calculated, respectively, as 5.508 and 0.058. Then, this gives the value of α = β/n′ = 0.0105 MPa−1.

Fig. 4
figure 4

Evaluating the value of (a) n′ by plotting ln vs. ln σ and (b) S by plotting ln vs. σ

Full size image

The next step is taking the natural logarithm of Eq 1 as follows:

$$\ln \,A + n\ln \,[\sinh (\upalpha \upsigma )] = \ln \,\dot{\upvarepsilon } + \frac{Q}{RT}.$$
(6)

By partial differentiation of Eq 6, the following expression could be derived as Ref 40:

$$n = \left[ {\frac{{\partial \ln \,\dot{\upvarepsilon }}}{\partial \ln \,(\sinh (\upalpha \upsigma ))}} \right]_{T}$$
(7)

for constant temperature, and

$$Q = R\left[ {\frac{{\partial \ln \,\dot{\upvarepsilon }}}{\partial \ln \,(\sinh (\upalpha \upsigma ))}} \right]_{T} \left[ {\frac{{\partial \ln (\sinh (\upalpha \upsigma_{\text{p}} ))}}{\partial (1/T)}} \right]_{{\dot{\upvarepsilon }}} = RnS$$
(8)

for constant strain rate.

The mean value of n can be derived from the slopes in plotting \(\ln \,\dot{\upvarepsilon }\) against ln [sinh(ασ)] at different temperatures, which was calculated as 4.014 (Fig. 5a), and the mean value of S can be derived from the slopes in plotting ln [sinh(ασ)] against 1/T at different strain rates, which was obtained as 13279Sk (Fig. 5b). Then, the mean deformation activation energy (Q) can be determined directly from Eq 8 as 443.149 kJ/mol. Eventually, ln A was obtained from intercept of \((\ln \dot{\upvarepsilon } - Q/RT) - \ln \,[\sinh (\upalpha \upsigma )]\) plot and the mean value of lnA is obtained as 33.529 s−1.

Fig. 5
figure 5

Evaluating the value of (a) n by plotting ln vs. ln [sinh(ασ)] and (b) S by plotting ln[sinh(ασ)] vs. 1000/T

Full size image

The deformation activation energies at every temperature and strain rate are also calculated by Eq 8 and listed in Table 1. From Table 1, we can found that deformation temperature and strain rate have a great effect on the deformation activation energy, which increases with the deformation temperature increasing (<1150 °C) and the strain rate increasing. Generally, deformation activation energy determined from Fig. 8 is called as “apparent activation energy” (Ref 4, 48), which is significantly affected by the value of n and S. For the 028 alloy, the values of n, namely the slops of the \(\ln \,\dot{\upvarepsilon } - \ln \,[\sinh (\upalpha \upsigma )]\) curves at each temperature, slightly increase with temperature increasing from Fig. 5(a). In contrast, the values of S, namely the slopes of the ln [sinh(ασ)] − 1/T curves at each strain rate, are remarkably different in our experimental data (Fig. 5b), obviously showing that the slope increases with strain rate increasing. Thus, increase of n and S results in Q increasing, and, moreover, it can be found that influence of strain rate on the deformation activation energy is greater than that of temperature. Recently, Mirzadeh et al. (Ref 49) found that the decrease in value of n from the theoretical value of 5 (critical stress) to 4.8 (peak stress) during hot deformation of 17-4PH stainless steel, and pointed out that the value of n is related with DRX softening. On the other hand, under the fixed temperature, the stress significantly increases with increasing strain rate, which can lead to larger value of S at high strain rate. Therefore, it can be considered that the “apparent activation energy” varies with the change of dislocation density and microstructure, which is induced by the complex interaction among these kinetic processes of generation and annihilation of dislocations, DRV and DRX (Ref 50, 51).

Table 1 The value of deformation activation energy (kJ/mol) under different temperatures and strain rates at the true strain of 0.69
Full size table

Compensation of strain

In the hot deformation processing of metals and alloys, the flow stress is affected not only by the deformation temperature and the strain rate, but also by the strain, as shown in Fig. 1. Therefore, compensation of the strain should be taken into account in order to derive the constitutive model to predict accurately the flow stress, whose influence is incorporated by assuming that the material constant is polynomial function of the strain. In this paper, the value of every material constant was evaluated in a strain range of 0.035-0.69 at an interval of 0.035. The relationship of the strain and every material constant can be represented by a fourth-order polynomial. The fourth fitting curves are shown in Fig. 6 and all of them can be described as

$$\left\{ {\begin{array}{l} {\upalpha = 0.6999\upvarepsilon^{4} - 0.1393\upvarepsilon^{3} + 0.09678\upvarepsilon^{2} - 0.02556\upvarepsilon + 0.01267} \\ {n = - 9.8615\upvarepsilon^{4} + 12.5852\upvarepsilon^{3} - 1.0273\upvarepsilon^{2} - 3.8388\upvarepsilon + 4.6832} \\ {Q/R = - 265266\upvarepsilon^{4} + 388863\upvarepsilon^{3} - 145816\upvarepsilon^{2} - 608\upvarepsilon + 55519} \\ {\ln A = - 218.67\upvarepsilon^{4} + 301.4\upvarepsilon^{3} - 106.22\upvarepsilon^{2} - 0.52\upvarepsilon + 35.27} \\ \end{array} } \right.$$
(9)
Fig. 6
figure 6

The fitting curves between the material constants and the strain (a) the relation curve of α-ε; (b) the relation curve of n-ε; (c) the relation curve of Q-ε; and (d) the relation curve of ln A-ε

Full size image

Once the material constants in the constitutive model are evaluated, the flow stress at a given strain can be predicted, and the constitutive equation that relates flow stress and Z parameter can be written as follows: (considering Eq 1).

$$\upsigma = \frac{1}{\upalpha }\ln \left\{ {\left[ {\frac{Z}{A}} \right]^{1/n} + \left[ {\left( {\frac{Z}{A}} \right)^{2/n} + 1} \right]^{1/2}} \right\}$$
(10)

Verification of Constitutive Modeling

The predictive power of the strain-dependent hyperbolic sine constitutive equation is verified by comparing the experimental and the predicted data (Fig. 1), where obvious deviation in between occurs. As shown in Fig. 1, the predicted flow stresses are larger than the experimental results for the strain rate of 0.01 and 0.1 s−1 when the strain exceeds 0.35, while the contrary results are obtained for the strain rate of 1 and 0.001 s−1 except 1050 °C. From section 3.2.1, n and S are two key parameters in calculating the flow stress of metal and alloy, and their mean value are taken in the constitutive equation. Therefore, the deformation activation energy (Q) derived from Eq 8 became a constant value independent of deformation conditions. However, as shown in Table 1, deformation activation energy (Q) is affected by deformation temperature and strain rate, especially the strain rate. Liu et al. (Ref 30) have studied recently the deformation activation energy for FGH4096-GH4133B dual alloy under the hot compression tests and concluded that the deformation activation energy (Q) increases with increasing deformation temperature and strain rate. Similarly, Shastry et al. (Ref 38) have also confirmed that the deformation conditions have great effect on the deformation activation energy in the 2.5Cr-1Mo. Thus, the main reason for deviation between the predicted and the experimental data is due to that the mean values of n, Q, and lnA were used in Eq 10.

Modification of Constitutive Modeling

Evolution of Deformation Activation Energy (Q)

Based on the experimental data, values of n under different temperatures at a given strain are shown in Fig. 7(a), where they decrease with strain increasing and have the same variation tendency under different temperatures. The mean value of n is indicated by a full line in Fig. 7(a), and the deviation between the mean value and the values at the different deformation temperatures is small enough. Therefore, for the 028 alloy, the value of n can be considered approximately as a constant independent of the deformation temperature at a given strain. The values of S at each strain rate were calculated as shown in Fig. 7(b). Compared to n, the values of S under the different strain rates are remarkably different from the mean value (full line) and increase with strain rate increasing, especially at large strain conditions (ε > 0.2). According to Eq 8, values of Q at different strain rates can be calculated and shown in Fig. 7(c), where the values of Q increase with increasing strain rate at a given strain, and significantly deviate from the mean value of Q when the strain exceeds 0.2. It is worth noting that the deviation between the predicted and experimental flow stress (as shown in Fig. 1) appears when the strain is larger than 0.2 under strain rates of 0.001, 0.1, and 1 s−1. Especially, deviation appears under the strain of 0.35 at 0.01 s−1 (Fig. 1b), which is equal to the corresponding strain after which the mean value of Q is larger than the value of Q at 0.01 s−1, as shown in Fig. 7(c). Thus, it is concluded that the flow stress is closely related with relative magnitudes of Q at different strain rates.

Fig. 7
figure 7

Relationship between (a) n and T under different strain, (b) S, (c) Q/R, and (d) ln A and under different strain

Full size image

Transmission electron microscopy (TEM) is employed to demonstrate the evolution of the dislocation substructural, which is responsible for different activation energy (Q) value at different strain rates. Figure 8 shows the TEM micrographs of the 028 alloy deformed to the strain of 0.69 under the deformation temperature of 1050 °C and the strain rate of 0.001, 0.01, 0.1, and 1 s−1, respectively. It is found that the dislocation density and substructure are significantly dependent on the strain rate under a given deformation temperature. A comparison of two figures (Fig. 8a and b) shows that with strain rate increasing, the dislocation density increases significantly. Meanwhile, high dislocation density increases the possibility of dislocation tangling and thus reduces the mobility of dislocation, leading to enhancement of the flow stress (Fig. 1a and b). As shown in Fig. 8(c), the formation of a band-like structure with a relatively higher dislocation density is clearly observed within the grains in the regions of local deformation (indicated by arrows in Fig. 8c). With the dislocation density increasing and band-like structure appearing, the difficulty of dislocation motion is increased further, leading to more higher deformation activation energy (Q). Moreover, under the strain rate of 1 s−1, the dislocation density and the mount of tangled dislocations are the highest as shown in Fig. 8(d), indicating that dislocation movement is hindered to the utmost extent, and deformation activation energy (Q) is largest among the four strain rates. This is consistent with the results of Fig. 7(c). Similar dislocation structures were also identified by Lee et al. (Ref 52). Here, it is worth noting that some cell substructures form in the alloy (indicated by circles in Fig. 8d), which can illustrate that DRV occurred inside DRX grain. Nevertheless, overall, multiplication of dislocations is stronger than annihilation and recombination of dislocations, which can explain why the flow stress appears upward at the strain of 0.69 as shown in Fig. 1(d).

Fig. 8
figure 8

TEM photos of the 028 alloy under different deformation conditions (a) 1050 °C, true strain = 0.69, 0.001 s−1; (b) 1050 °C, true strain = 0.69, 0.01 s−1 (c) 1050 °C, true strain = 0.69, 0.1 s−1; and (d) 1050 °C, true strain = 0.69, 1 s−1

Full size image

Revised Constitutive Modeling

From section 3.2.3, the “material constants” in constitutive equation, n, Q, and lnA, should be treated as material variables. Thus, to overcome the shortcoming of the original constitutive equation, the following equation is proposed as,

$$\dot{\upvarepsilon } = A(T,\dot{\upvarepsilon },\upvarepsilon )\left[ {\sinh (\upalpha \upsigma_{\upvarepsilon } )^{n(T,\upvarepsilon )} } \right]\exp \left( { - \frac{{Q(T,\dot{\upvarepsilon },\upvarepsilon )}}{RT}} \right),$$
(11)

where σε is the stress corresponding to the strain (ε). The material variables, n, Q, and A are functions of the deformation temperature, the strain rate, and the strain.

Taking natural logarithm of both sides of Eq 11 leads to,

$$\ln \dot{\upvarepsilon } = \ln A(T,\dot{\upvarepsilon },\upvarepsilon ) + n(T,\upvarepsilon )[\sinh (\upalpha \upsigma_{\upvarepsilon } )] - \frac{{Q(T,\dot{\upvarepsilon },\upvarepsilon )}}{RT},$$
(12)
$$n(T,\upvarepsilon ) = \left. {\frac{{\partial \ln \dot{\upvarepsilon }}}{{\partial \ln [\sinh (\upalpha \upsigma_{\upvarepsilon } )]}}} \right|_{T,\upvarepsilon } + \left[ {\frac{{\partial Q(T,\dot{\upvarepsilon })}}{{RT\partial \ln [\sinh (\upalpha \upsigma_{\upvarepsilon } )]}}_{T,\upvarepsilon } - \frac{{\partial \ln \,A(T,\dot{\upvarepsilon })}}{{\partial \ln [\sinh (\upalpha \upsigma_{\upvarepsilon } )]}}_{{T,\dot{\upvarepsilon }}} } \right],$$
(13)

for constant temperature and strain, and

$$Q(T,\dot{\upvarepsilon },\upvarepsilon ) = Rn(T)\left[ {\frac{{\partial \ln (\sinh (\upalpha \upsigma_{\upvarepsilon } ))}}{\partial (1/T)}} \right]_{{\dot{\upvarepsilon },\upvarepsilon }} + \left\{ \begin{aligned} R\ln \left[ {\sinh (\upalpha \upsigma_{\upvarepsilon } )} \right]\left[ {\frac{\partial n(T)}{\upalpha (1/T)}} \right]_{{\dot{\upvarepsilon },\upvarepsilon }} \hfill \\ + R\left[ {\frac{{\partial \ln A(T,\dot{\upvarepsilon },\upvarepsilon )}}{\partial (1/T)}} \right]_{{\dot{\upvarepsilon },\upvarepsilon }} \hfill \\ - \frac{1}{T}\left. {\frac{{\partial Q(T,\dot{\upvarepsilon },\upvarepsilon )}}{\partial (1/T)}} \right|_{{\dot{\upvarepsilon },\upvarepsilon }} \hfill \\ \end{aligned} \right\},$$
(14)

for constant strain rate and strain.

It has been already known that the values of n at different temperatures are in consistent substantially with the mean value, as shown in Fig. 7(a). Thus, we can assume that n is independent of the deformation temperature at a given strain. So, Eq 14 can be rewritten as

$$Q(\dot{\upvarepsilon },\upvarepsilon ) = R\left[ {\frac{{\partial n\ln \,(\sinh (\upalpha \upsigma_{\upvarepsilon } ))}}{\partial (1/T)}} \right]_{{\dot{\upvarepsilon }}} + \left\{ {R\left[ {\frac{{\partial \ln A(\dot{\upvarepsilon },\upvarepsilon )}}{\partial (1/T)}} \right]_{{\dot{\upvarepsilon }}} - \left. {\frac{1}{T}\frac{{\partial Q(\dot{\upvarepsilon },\upvarepsilon )}}{\partial (1/T)}} \right|_{{\dot{\upvarepsilon }}} } \right\}.$$
(15)

Furthermore, the right brace of Eq 15 can be neglected for convenient calculation of the value of Q (Ref 1-5). Hence, Eq 14 can be simplified as

$$Q(\dot{\upvarepsilon },\upvarepsilon ) = R\left[ {\frac{{\partial n\ln \,(\sinh (\upalpha \upsigma_{\upvarepsilon } ))}}{\partial (1/T)}} \right]_{{\dot{\upvarepsilon }}} = Rn(\upvarepsilon )S(\dot{\upvarepsilon },\upvarepsilon ).$$
(16)

Using the 1stOpt software, an excellent polynomial relationship between Q, ε, and \(\dot{\upvarepsilon }\) is found, as shown in Fig. 9(a) (red grid), which is expressed in Eq 17. Similarly, a good polynomial relationship between lnA, ε, and \(\dot{\upvarepsilon }\) is calculated from Eq 18, and shown in Fig. 9(b) (red grid)

$$\frac{Q}{R} = \frac{{60447 - 1175\ln \,\dot{\upvarepsilon } - 139675\upvarepsilon + 92282\,\upvarepsilon^{2} }}{{1 - 0.0202\ln \dot{\upvarepsilon } + 0.00371(\ln \,\dot{\upvarepsilon })^{2} - 1.8495\upvarepsilon + 0.008649\upvarepsilon^{2} + 1.0269\upvarepsilon^{3} }},$$
(17)
$$\ln \,A = \frac{{38.17 - 0.4724\ln \dot{\upvarepsilon } - 101.98\upvarepsilon + 104.54\upvarepsilon^{2} - 37.37\upvarepsilon^{3} }}{{1 - 0.0123\ln \dot{\upvarepsilon } + 0.003734(\ln \dot{\upvarepsilon })^{2} - 2.27\upvarepsilon + 1.4235\upvarepsilon^{2} }}.$$
(18)
Fig. 9
figure 9

Comparison between the experimental and predicted flow stress from the revised constitutive equation at strain rate (a) 0.001 s−1, (b) 0.01 s−1, (c) 0.1 s−1, and (d) 1 s−1

Full size image

Through the above analysis, it is apparent that there are relatively polynomial relationships among the material variables (α, n, Q, and ln A), strain and strain rate. Therefore, a revised strain-dependent hyperbolic sine constitutive equation to evaluate the high temperature flow stress of the 028 alloy can be expressed as

$$\left\{ {\begin{array}{l} {\upalpha = 0.6999\upvarepsilon^{4} - 0.1393\upvarepsilon^{3} + 0.09678\upvarepsilon^{2} - 0.02556\upvarepsilon + 0.01267} \\ {n = - 9.8615\upvarepsilon^{4} + 12.5852\upvarepsilon^{3} - 1.0273\upvarepsilon^{2} - 3.8388\upvarepsilon + 4.6832} \\ {Q/R = \frac{{60447 - 1175\ln \dot{\upvarepsilon } - 139675\upvarepsilon + 92282\upvarepsilon^{1} }}{{1 - 0.0202\ln \dot{\upvarepsilon } + 0.00371(\ln \,\dot{\upvarepsilon })^{2} - 1.8495\upvarepsilon + 0.08639\upvarepsilon^{2} + 1.0269\upvarepsilon^{4} }}} \\ {\ln A = \frac{{38.17 - 0.4724\ln \dot{\upvarepsilon } - 101.98\upvarepsilon + 104.54\upvarepsilon^{2} - 37.37\upvarepsilon^{3} }}{{1 - 0.0123\ln \dot{\upvarepsilon } + 0.003734(\ln \,\dot{\upvarepsilon })^{2} - 2.27\upvarepsilon + 1.4235\upvarepsilon^{2} }}} \\ \end{array} } \right.$$
(19)

Verification of the Revised Constitutive Modeling

The predictability of the revised strain-dependent hyperbolic sine constitutive equation was assessed by comparing the experimental and the predicted data as shown in Fig. 10. It could be observed that the predicted flow stress from the revised hyperbolic sine constitutive equation can track perfectly the experimental data throughout the entire experimental range.

Fig. 10
figure 10

Fit of variation of (a) Q/R and (b) ln A with true strain and strain rate

Full size image

In order to quantify the accuracy of the revised constitutive equations, the standard statistical parameters, such as correlation coefficient (R) and average absolute relative error (AARE), have been employed. R provides information on the strength of linear relationship between the experimental and the predicted values, and AARE is applied to measure the predictability of a model (Ref 48). They are expressed as

$$R = \frac{{\sum\nolimits_{i = 1}^{N} {(E_{i} - \bar{E})(P_{i} - \bar{P})} }}{{\sqrt {\sum\nolimits_{i = 1}^{N} {(E_{i} - \bar{E})^{2} \sum\nolimits_{i = 1}^{N} {(P_{i} - \bar{P})^{2} } } } }},$$
(20)
$${\text{AARE}}\,(\% ) = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left| {\frac{{E_{i} - P_{i} }}{{E_{i} }}} \right|} \times 100\,\% ,$$
(21)

where E i is the experimental data and P i represents the predicted value. \(\bar{E}\) and \(\bar{P}\) are the mean values of E i and P i , respectively. N is the total number of data employed in the investigation. Generally, the value of R near 1 indicates that a regression line fits the date well, while the value of R close to 0 indicates a regression line does not fit the data very well (Ref 53, 54). AARE means the deviation between single value and mean value (Ref 53, 54), and the value of AARE near 0 indicates that every single value is close to the mean value. Mandal et al. (Ref 26) studied the high temperature flow stress of Ti-modified austenitic steel using the revised Arrhenius constitutive equation, and the values of correlation coefficient (R) and AARE are 0.992 and 6.74%, respectively. Recently, Peng et al. (Ref 27) proposed that revised Arrhenius constitutive equation based on the method of Mandal, and the correlation coefficient (R) and AARE can be promoted to 0.993 and 5.08%, respectively.

In the present work, the predicted results of strain-dependent hyperbolic sine constitutive model as shown in Fig. 11(a), in which the correlation coefficient (R) and AARE are 0.991 and 5.56%, respectively (similar to the previous works). In contract, a better correlation between the experimental and the predicted data using the new revised model is obtained. Obviously, most of the data points lie exactly close to the ideal 45° line in Fig. 11(b). The value of R for revised strain-dependent hyperbolic sine constitutive equation is 0.999, which is larger than value of strain-dependent hyperbolic sine constitutive equation (0.991). On the other hand, the value of AARE for revised strain-dependent hyperbolic sine constitutive equations is 1.95%, which is smaller than value of strain-dependent hyperbolic sine constitutive equation (5.56%). These results indicate that the new revised constitutive modeling can predict accurately the hot deformation behavior of the 028 alloy.

Fig. 11
figure 11

Correlation between the experimental and predicted flow stress: (a) the origin constitutive equation and (b) the revised constitutive equation

Full size image

Conclusions

The deformation characteristics of the 028 alloy have been investigated by means of the hot compression test over a practical range of temperatures and strain rates. Based on the experimental stress-strain data, it is found that the flow stress increases with strain rate increasing and deformation temperature decreasing. Furthermore, deformation activation energy increases with strain rate increasing at a given strain. This is mainly due to that dislocation movement is hindered badly at high strain rate. Finally, the revised strain-dependent hyperbolic sine constitutive equation was proposed, which considered the effects of the strain and strain rate on the “material constant.” The correlation coefficient (R) and average absolute relative error (AARE) were 0.999 and 1.95%, respectively, which reflect that the revised strain-dependent hyperbolic sine constitutive equation can predict accurately the high temperature flow stress of the 028 alloy under the entire experimental deformation conditions. Meanwhile, a problem that needs to be urgently solved is to extend the present model to other alloys, which will be of great significance to the actual industrial production.