Abstract
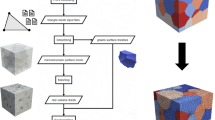
We present a new comprehensive scheme for generating grain boundary conformed, volumetric mesh elements from a three-dimensional voxellated polycrystalline microstructure. From the voxellated image of a polycrystalline microstructure obtained from the Monte Carlo Potts model in the context of isotropic normal grain growth simulation, its grain boundary network is approximated as a curvature-maintained conformal triangular surface mesh using a set of in-house codes. In order to improve the surface mesh quality and to adjust mesh resolution, various re-meshing techniques in a commercial software are applied to the approximated grain boundary mesh. It is found that the aspect ratio, the minimum angle and the Jacobian value of the re-meshed surface triangular mesh are successfully improved. Using such an enhanced surface mesh, conformal volumetric tetrahedral elements of the polycrystalline microstructure are created using a commercial software, again. The resultant mesh seamlessly retains the short- and long-range curvature of grain boundaries and junctions as well as the realistic morphology of the grains inside the polycrystal. It is noted that the proposed scheme is the first to successfully generate three-dimensional mesh elements for polycrystals with high enough quality to be used for the microstructure-based finite element analysis, while the realistic characteristics of grain boundaries and grains are maintained from the corresponding voxellated microstructure image.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For many years, the finite element method (FEM) simulations have been extensively utilized to predict the responses and properties of polycrystalline materials such as plasticity, elasticity, diffusion, etc. [1,2,3,4,5,6,7]. In order to map microstructure-property relationships correctly using the FEMs on polycrystalline microstructures, it is required that the microstructural mesh elements be as truthful as possible to the topology of microstructural entities and have a quality suitable for the FEM simulations. Even in ideal static cases, the morphology of the polycrystalline microstructures needs to satisfy the following aspects at least: (1) an ideal polycrystal is populated by more or less isotropically shaped grains that form a complex network of conformal grain boundaries and junctions without any voids; (2) the curvature of the grain boundary changes smoothly, having a short- and long-range curvature; and (3) at the intersections or junctions of grains, grain boundaries maintain the local energy/force equilibrium so that the Herring relations can be applied [8]. Obviously, it is not always an easy and tractable task to generate a set of realistic and FEM-suitable three-dimensional mesh elements on polycrystals that meet the above conditions.
There have been many attempts to approximate realistic topology of polycrystalline microstructures, by producing mesh elements using either numerical methods or the digital voxellated images from experimental measurements or simulations [9,10,11,12,13,14,15,16,17,18]. One of the widely accepted numerical algorithms in generating conformal mesh of polycrystalline materials is Voronoi tessellation [4, 5, 9, 10, 19,20,21,22]. Voronoi tessellation has been a popular choice over other tessellation methods due to its well-defined, simple analytical formulation. However, when a polycrystalline microstructure is generated by Voronoi tessellation, the following features are not properly represented: (1) The grain boundaries are flat faces, and the grain junctions are straight lines. In realistic polycrystals, both have smoothly changing short- and long-range curvatures; (2) it occasionally occurs that grains have unrealistic characteristics such as very thin plate-like regions or very sharp wedge-like corners, depending on the positions of the nearest neighboring grain centers, i.e. Voronoi cells. These narrow or sharp regions may generate tetrahedral elements with a poor quality. In such cases, Voronoi tessellation is not suitable for the FEM analysis unless those poor elements are fixed; and (3) the size distribution of Voronoi cells constructed from randomly positioned centers is known to follow Gamma distributions [20,21,22]. However, in many cases, the real grain size distributions in polycrystals usually have wider and less taller shapes with longer tails than that of Voronoi cells or the log-normal distributions [23,24,25,26,27,28].
Other methods have been proposed in order to approximate the realistic grain boundary shapes and curvatures during the surface or volumetric mesh generation for the FEM analysis. Some studies used polynomial functions to describe realistic grain boundaries, followed by the generation of the volumetric mesh inside grains [12, 13]. Other studies have adopted a surface energy minimization [16, 29], or a local volume conservation scheme in order to define grain boundaries during the mesh generation [17, 18]. However, they created either flat [16, 29], or unrealistic, corrugated features [17, 18] near grain boundary regions, giving rise to unrealistic, distorted grain boundary networks and grain morphologies when compared to those from real polycrystalline microstructure.
Conversely, numerical methods with experimental materials characterization often facilitate more accurate measurement of grain morphology. For example, Ullah et al. [23, 24] demonstrated three-dimensional reconstruction and visualization of the grains in α-iron polycrystals. In the studies, small sample portions were serial sectioned manually, and corresponding optical images were taken and stacked as a set of voxellated images. Then, a simple smoothing algorithm is applied to mitigate the stair-stepped morphology of the grain boundary voxels by averaging the locations of individual voxel corners with their closest neighbors. However, their smoothing algorithm produces a huge number of triangles on the surface of the microstructure. Even though a mesh decimation algorithm [30, 31] is implemented to decrease the number of triangles, the resultant mesh fidelity is limited by the position changes of the vertices. Moreover, repeating such smoothing iterations will make grain boundaries move towards the center of the curvature, leading to changes in grain volumes, which potentially distort the size distribution of the grains and grain boundaries in the polycrystals. A similar issue has been mentioned for other works [28, 29].
Recently, a set of grain boundary approximation algorithms that generate a conformal surface mesh of the grain boundary network were developed by one of the current authors [32]. At first, the grain boundary network of a digital polycrystalline microstructure was segmented using the multi-material marching cubes algorithm [33]. Unfortunately, the resultant conformal triangular mesh has aliased, stair-stepped grain boundaries and junctions. Therefore, in order to smooth those features and approximate the realistic grain boundary network, a constrained line smoothing (CLS) and a constrained Laplacian smoothing (CLpS) algorithms were proposed to approximate grain junctions and boundaries, respectively. It was noted that a conformal surface mesh of the grain boundary network in the digital, voxellated three-dimensional microstructure was generated while maintaining the realistic local curvature of the grain boundaries and the volumes of the grains at the same time. However, as it was pointed out in the paper, additional steps (such as mesh quality enhancement, mesh resolution control, tetrahedral element meshing from a quality enhanced grain boundary mesh, and etc.) are required to generate a volumetric mesh, appropriate for FEM analyses, using this well-approximated grain boundary surface mesh.
To overcome the challenges mentioned above, we propose here a new scheme to generate a volumetric mesh proper to the FEM analysis, which is true to the three-dimensional voxellated microstructures either from simulations or experimental reconstructions. Specifically, a hypothetical digital polycrystalline microstructure is prepared from Monte Carlo grain growth model, and its grain boundary network is extracted using the previously reported algorithms [32]. From now on, it is referred as “original (smoothed) surface mesh”. Because the resultant original smoothed surface mesh is reported to have sporadically poor quality elements, the mesh quality is then enhanced by using a couple of re-meshing techniques offered by a commercial software (HyperMesh) in this work before generating a volumetric mesh (from now on, the quality enhanced, re-meshed surface mesh is called “(quality-)enhanced surface mesh”). Again, the primary interest of this work is a realistic representation of a polycrystalline microstructure with tetrahedral elements suitable for FEM simulations. Before that, the improvement of the quality of the triangles on the enhanced surface mesh is quantitatively verified. Also, the grain boundary normal distributions with respect to the sample reference frame (GBNDs) are compared before and after the re-meshing steps to make it sure that each re-meshing technique from the commercial software does not distort the characteristics of the grain boundaries from the original smoothed surface mesh. Once the enhanced grain boundary network is prepared, the tetrahedral volumetric mesh elements are generated inside each grain using the commercial software (HyperMesh), while the previous enhanced grain boundary mesh remains intact. Again, the qualities of tetrahedral mesh elements are evaluated to assess their applicability to the FEM simulations. The remainder of this paper is organized as follows. In Sect. 2, the preparation of the three-dimensional polycrystalline microstructure is discussed. In Sect. 3, the grain boundary surface mesh approximation and its quality enhancement are reported. In Sect. 4, the generation of tetrahedral elements using the enhanced surface mesh and the relevant quality evaluation are presented. In Sect. 5, two exemplary three-dimensional FEM simulations, using the resultant tetrahedral mesh, are performed in order to validate the usability of the proposed mesh generation algorithm. Section 6 includes the discussion and summary.
2 Preparation of a Three-Dimensional Digital Polycrystalline Microstructure
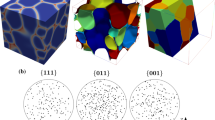
As an input microstructure for a series of mesh generation steps, a voxellated, three-dimensional polycrystalline microstructure is prepared using the Monte Carlo Potts model in the context of isotropic normal grain growth. The microstructure is discretized on a regular cubic voxel grid with size 100 × 100 × 100. The grain growth simulation begins with a random population of spin numbers from 1 to 500. As time elapses, scattered spin numbers nucleate at random positions and grow as well-coarsened, isotropic grains. Periodic boundary conditions are applied during grain growth process. Figure 1 illustrates the voxellated images of such generated microstructure where (a) shows the surface of the microstructure and (b) shows partial grains in this microstructure, selected to effectively visualize the shape-isotropy of the grains obtained from the simulation. In the figure, different color scales represent the different orientations (spin numbers) assigned to each grain in the microstructure. The total number of grains is 223.
Voxellated polycrystalline microstructures from the Monte Carlo, isotropic grain growth simulation: a surface and b some selected grains. In b, a portion of grains are selected to effectively visualize the fact that fairly isotropic shapes are generated for grains obtained from the applied Monte Carlo grain growth simulation. The total number of grains is 223 and different color scales denote the different orientations assigned to each grain. (Color figure online)
3 Surface Mesh Generation from the Voxellated Polycrystalline Microstructure Image
3.1 Approximation of Grain Boundary Network
In order to approximate the three-dimensional polycrystalline microstructure with a conformal triangular surface mesh, previously reported surface mesh approximation algorithms [32] are applied to the microstructural image prepared in Sect. 2. Since the details on the surface mesh approximation algorithms are reported in the paper, we highlight the process here.
The first step of the surface mesh approximation is called “segmentation process”, where conformal triangular surface mesh elements are created on the surface of the microstructure and at the grain boundary network. For this process, the in-house multi-material marching cubes algorithm is used, where the original algorithm [33] is modified in order to retrieve information on the microstructural features. Individual grain boundaries, triple junctions, quadruple points, and, hence, grains are identified as a collection of nodes, edges, and faces in the segmented surface mesh. The resultant microstructure images from the segmentation process on the microstructure shown in Fig. 1 are given in Fig. 2a and b. The total numbers of nodes, edges and triangles in the segmented mesh are 227,547, 854,543 and 579,215, respectively. In contrary to Fig. 1, the microstructure images in Fig. 2 are visualized using the surface mesh information obtained from the segmentation process. Figure 2a shows the surface of the microstructure, i.e., intersections of grains (colored faces) and traces of grain boundaries (solid black lines). Each grain boundary is colored with a unique color in Fig. 2b, showing that the proposed segmenting algorithm generates full description of the microstructural features in terms of nodes, edges and faces of the conformal triangular patches. Note, however, that the segmented grain boundaries and junctions are stair-stepped due to inherent nature of the marching cubes algorithm.
Approximated surface mesh of the polycrystal in Fig. 1: a and b are visualization of segmented surface mesh on Fig. 1a and b, respectively, and c and d are corresponding approximated mesh images of a and b. Note that, using this boundary approximation process, the voxellated, three-dimensional hypothetical polycrystalline microstructure is completely represented with corresponding mesh information, where boundaries and junctions explicitly maintain smoothly changing short- and long-range curvatures, representing more realistic polycrystalline structure. The total numbers of nodes, edges and triangles in the segmented mesh are 227,547, 854,543 and 579,215, respectively. (Color figure online)
The second step is called “smoothing process”, where the segmented grain junctions and boundaries are smoothed using in-house algorithms. Because the stair-stepped, aliased features are the characteristics of the segmentation algorithm, not of the physical, realistic grain boundaries and junctions, a set of smoothing algorithms [32] are applied to approximate more realistic grain network structures as well as to mitigate the aliased morphology. The constrained line smoothing (CLS) method is utilized to smooth the grain junctions, and, then, the grain boundaries are smoothed using the constrained Laplacian smoothing (CLpS) method. In Fig. 2c and d, the resultant mesh images after the smoothing process are presented. It is evident that the aliased grain boundaries, traces, and junctions in Fig. 2a and b are successfully smoothed. As reported in the previous work [32], all the nodes of the smoothed mesh are positioned well within the voxel length from the originally segmented positions, since a volume preserving criteria is enforced during the smoothing process. Also, the approximated boundaries and junctions explicitly feature smoothly changing short- and long-range curvatures, implicitly represented in the voxellated microstructure in Fig. 1. Note that, using this boundary approximation process, the voxellated, three-dimensional hypothetical polycrystalline microstructure is transformed into the corresponding surface mesh information, representing more realistic polycrystalline microstructure. As previously mentioned, such approximated boundary is referred to “original (smoothed) surface mesh”.
3.2 Enhancement of Original Smoothed Surface Mesh
Unfortunately, the surface mesh obtained from the grain boundary approximation procedures includes a handful of triangular elements with poor quality, especially at the regions of grain boundary junctions and grain corners. In Fig. 3a, the original smoothed surface mesh is visualized. In the figure, a portion of the mesh is omitted in order to visualize the smoothed mesh both inside and on the outer surface of the microstructure. On the outer surface of the microstructure, grain boundary traces are apparently identified by naked eyes, signifying that the triangles near the traces are more irregular and smaller than those in the interior of grain intersections. In addition, as will be shown later, the qualities of such triangles are often found to be poor. Since the quality and uniformity of the mesh play an important role in guaranteeing the solution accuracy and computation efficiency in the FEM simulations, it is necessary to take mesh enhancement procedures in order to improve the quality and uniformity of surface mesh elements before creating the volumetric mesh elements, representative of the polycrystalline microstructure in Fig. 1. Therefore, the original smoothed surface mesh shown in Fig. 3a cannot be used as an input for the FEM-suitable volumetric mesh generation process unless the qualities of the triangles in the mesh are improved.
Images of surface mesh for a three-dimensional hypothetical microstructure: a the original smoothed surface mesh before enhancement, b the quality-enhanced surface mesh using size and bias option and c the quality-enhanced surface mesh using QI option. It is clear from the figure that the both re-meshing techniques successfully improved the quality, especially in the grain boundary/junction regions
For that regard, two different re-meshing options are applied to the original smoothed surface mesh, provided by a commercial software (HyperMesh). One is “size and bias” and the other is “quality index (QI) optimize”. Figure 3b and c show the quality-enhanced, re-meshed surface meshes obtained from “size and bias” option and “quality index (QI) optimize” option, respectively. The “size and bias option” re-meshes the original smoothed surface mesh such that the regenerated triangles have fairly constant size. In the option, 1.0 is assigned to the target size and the triangle type is set to be “equilateral triangle element”. The “QI option” optimizes the quality of element topology under a set of conditions on element criteria. In other words, the option enables to refine the mesh until reaching the user-specified value of quality index. We set the quality optimize value in accordance with the quality criteria for FEM simulations with respect to two-dimensional element; aspect ratio < 5, Jacobian value range from 0 to 1, and warpage < 15 [34]. Note that darker regions, created due to the inhomogeneity of triangles in the original smoothed surface mesh in Fig. 3a, are mostly eliminated after re-meshing procedures as evidently shown in Fig. 3b and c. Therefore, it is reasonable to say that both re-meshing techniques substantially improve the quality of original smoothed surface mesh, at least in terms of the homogeneity of the size and shape of triangles.
Now, it is of interest to quantify the improvement of the qualities of re-meshed triangles. For two-dimensional triangular mesh elements, well-known measures of the element quality to be checked for the optimal performance in FEM simulations are the aspect ratio, the minimum angle and the Jacobian of the triangles [34]. These values are calculated and visualized using an open-source software (Paraview). In Fig. 4, compared are the aspect ratios of the triangles among (a) the original smoothed surface mesh, (b) the quality enhanced, re-meshed surface mesh from “size and bias” option, and (c) the re-meshed surface mesh from “QI optimize” option. For triangles, aspect ratio is defined as the ratio of the length of the longest edge to that of the shortest one. The optimal and the minimum value is 1.0. Aspect ratio between 1.0 and 4.0 is known to be good enough for stable FEM simulations [34,35,36,37,38,39]. Note that, after re-meshing, the maximum peak of the distribution becomes much higher and skewed to the left towards the optimal value of 1.0, signifying that triangles from both re-meshing options have much better quality than those from the original smoothed surface mesh. In Fig. 5, Jacobian values for the same cases are compared. The Jacobian of a triangle shows the degree of deviation of its area, shape and orientation from those of the ideally shaped triangle by mapping the vertices of the triangles back and forth. The Jacobian value ranges from 0 to 1.0, where 1.0 indicates a perfect shaped element and the proper value for the FEM simulations is recommended to be larger than 0.6 [34,35,36,37,38,39]. Note, after re-meshing, the maximum peak of the distribution becomes much taller and skewed to the right towards the optimal value of 1.0, signifying that triangles from both re-meshing options have much better quality than those from the original smoothed surface mesh. Finally, changes in the minimum angles of the triangles after re-meshing are shown for the same cases. The interior minimum angle is encouraged to be larger than 20° for the FEM simulations [34,35,36,37,38,39]. From the figure, it is obvious that the minimum values from both re-meshing techniques exceed 20°, and the distributions are well skewed to the right towards the ideal value of 60°. Again, both re-meshing options create triangles with much better quality than those from the original smoothed surface mesh.
Aspect ratio values of the triangles, colored on microstructure (left) and number distribution (right): a the original smoothed surface mesh, b the quality-enhanced surface mesh using size and bias option and c the quality-enhanced surface mesh using QI option. After both re-meshing steps, the maximum peaks of the distributions become much taller and skewed to the left towards the optimal value of 1.0, signifying that triangles have better quality. (Color figure online)
Jacobian values of the triangles, colored on microstructure (left) and number distribution (right): a the original smoothed surface mesh, b the quality-enhanced surface mesh using size and bias option and c the quality-enhanced surface mesh using QI option. After both re-meshing steps, the maximum peaks of the distributions become much taller and skewed to the right towards the optimal value of 1.0, signifying that triangles have better quality. (Color figure online)
Even though it can be concluded from Figs. 4, 5, and 6 that the qualities of triangles in re-meshed grain boundaries are vastly improved, it does not guarantee that the grain boundaries remain intact during the re-meshing process. If the total area and the normal distributions with respect to sample reference frame of the grain boundaries (GBNDs) remain constant during the re-meshing process, it is reasonable to say that the grain boundaries remain intact during the re-meshing process. In order to examine the changes of grain boundaries during the processes, the total area of grain boundaries and the grain boundary normal distributions are measured for each type of grain boundary mesh. It is found that the changes in grain boundary area from both surface re-meshing techniques, “size and bias” and “QI optimize” options, are less than 0.1%, respectively, signifying that both quality-enhanced grain boundary meshes experience virtually no changes in terms of area. In addition, the grain boundary normal distributions with respect to the sample reference frame are visualized as a value of area on the three-dimensional projection globe in Fig. 7 for (a) original smoothed surface mesh, (b) the quality-enhanced surface mesh using size and bias option and (c) the quality-enhanced surface mesh using QI option. It is apparent from the figure that the grain boundary normal distributions remain constant during the processes, signifying that morphologies and curvatures of individual grain boundaries remain intact during the processes. To confirm this, the error difference in area for each grain boundary normal types (a) between the original smoothed grain boundaries and the quality-enhanced grain boundaries from size and bias option, and (b) between the original smoothed grain boundaries and the quality-enhanced grain boundaries from QI option, are calculated and visualized respectively in Fig. 8. Most of the boundary types are found to experience very small or virtually zero area changes during the processes. The big, alternating errors around the + z poles are, however, observed. The errors are thought to be the artifacts of equi-angle grid visualization technique.
Triangle minimum angles, colored on microstructure (left) and number distribution (right): a the originally smoothed mesh b quality-enhanced surface mesh using the size and bias option and c re-meshed using the QI option. Again, the maximum peaks of the distributions become much taller and skewed to the right towards the optimal value of 60°, signifying that triangles have better quality. (Color figure online)
Grain boundary normal distributions as a function of area with respect to the sample reference frame are visualized on the three-dimensional projection globe: a original smoothed surface mesh, b the quality-enhanced surface mesh using size and bias option, and c the quality-enhanced surface mesh using QI option. It is apparent that the grain boundary normal distributions remain constant during the processes
Error in area difference calculated from grain boundary normal distributions a between the original smoothed grain boundaries and the quality-enhanced grain boundaries from size and bias option, and b between the original smoothed grain boundaries and the quality-enhanced grain boundaries from QI option
In conclusion, it is demonstrated that the mesh-enhancement processes successfully improve the quality of triangles of the surface mesh of the microstructure, while maintaining the grain boundary morphologies and areas approximated from the reported algorithm [32]. The results are highly desired instantiations for generating tetrahedral volumetric mesh elements from the surface mesh for the stable FEM simulations.
4 Volumetric Mesh Generation from Surface Mesh
In the present study, tetrahedral mesh elements are extracted from an enclosed volume of triangular surface mesh generated from Sect. 3 using a commercial software (HyperMesh), again. In the program, several options regarding the tradeoff between the number, the resolution and the quality of tetrahedral elements are provided, such as “standard”, “aggressive”, “interpolate”, and so on. The “standard” and “aggressive” options are selected here because they are typically used for the FEM simulations. Therefore, the two options are applied to generate the volumetric mesh of the polycrystal from the surface meshes from Sect. 3. Through the “standard” option, the tetrahedral elements are generated such that the size and quality of the elements are targeted to be uniform. The “aggressive” option also generate tetrahedral elements with uniform quality. However, the elements are finer near the grain boundaries and junctions while they become gradually and aggressively coarser as they get away from the grain boundary regions. Naturally, the “aggressive” option produces fewer elements than the “standard” option and its growth rate of interior volume elements is much higher than those in “standard” mesh elements. In addition, the distribution of the quality parameter of the resultant volumetric mesh elements will vary depending on the types of the input surface mesh. It is found that, by using the “standard” volumetric meshing technique, 4,380,491 tetrahedral elements are generated on the “original” smoothed surface mesh of the polycrystal, 3,186,342 elements on the “size and bias” enhanced surface mesh and 3,150,345 elements on “QI optimize” enhanced surface mesh, respectively. Through the “aggressive” option, corresponding numbers become much smaller: 2,779,175 for the “original” smoothed surface mesh, 1,938,377 for the “size and bias” enhanced surface mesh and 1,921,103 for “QI optimize” enhanced surface mesh. Therefore, if the mesh qualities are guaranteed, the tetrahedral mesh representation from the “aggressive” option may be much more efficient in terms of computation time for the FEM simulation on the polycrystal.
As a final step in generating a FEM suitable volumetric mesh on a polycrystal, the qualities of tetrahedral elements, obtained from both “standard” and “aggressive” options, are examined. While various parameters on the quality of tetrahedral elements for three-dimensional FEM simulations can be found in elsewhere [36,37,38,39], the aspect ratio and the tetra collapse ratio of the tetrahedral elements are measured here in order to guarantee the reliability of generated volumetric mesh elements. It is known that good aspect ratio with good collapse ratio makes the other quality parameters good enough for the FEM applications. The aspect ratio smaller than 5.0 and the tetra collapse ratio bigger than 0.5 are favored for the FEM simulation using three-dimensional tetrahedral elements [36,37,38,39].
In Figs. 9 and 10, the aspect ratios of the volumetric mesh elements are colored on the polycrystalline mesh images from “standard” and “aggressive” options respectively. In each figure, the results are visualized for the volumetric mesh elements obtained from (a) “original” smoothed surface mesh, (b) the quality-enhanced surface mesh using “size and bias” option, and (c) the quality-enhanced surface mesh using “QI optimize” option. In both options, the aspect ratio becomes smaller when quality enhanced surface meshes are used as inputs, compared to original smoothed surface mesh. Note that more blue-colored regions are observed in both (b) and (c) than (a), while more red regions are found in (a). In addition, for “aggressive” option, the mesh shows better aspect ratio values near the grain boundary regions than those from the “standard” options, as desired. The quantitative analysis on the distribution of aspect ratio is shown in Fig. 11. Obviously, the input surface mesh with better quality (“size and bias” and “QI optimize”) results in better aspect ratio distribution of the resultant volumetric mesh than poor input surface mesh (“original”).
Aspect ratios of three-dimensional mesh elements obtained from the “standard” volumetric mesh technique. The volumetric mesh elements are generated from a “original” smoothed surface, b quality-enhanced surface mesh using “size and bias” option and c quality-enhanced surface mesh using “QI optimize” option. Note that quality enhanced surface meshes result in volumetric mesh of better aspect ratio than the original smoothed mesh. (Color figure online)
Aspect ratio of three-dimensional mesh elements obtained from the “aggressive” volumetric mesh technique. The volumetric mesh elements are generated from a “original” smoothed surface, b quality-enhanced surface mesh using “size and bias” option and c quality-enhanced surface mesh using “QI optimize” option. Note that quality enhanced surface meshes result in volumetric mesh of better aspect ratio than the original smoothed mesh. (Color figure online)
Comparison of distributions of aspect ratio values: a “standard” meshing techniques and b “aggressive” meshing technique. It is found that, for both techniques, input surface meshes with better quality (“size and bias” and “QI optimize”) result in better aspect ratio distribution of the resultant volumetric mesh than poor input surface mesh (“original”)
Figures 12 and 13 show the collapse ratio values, colored on the polycrystalline mesh images from “standard” and “aggressive” options, respectively. Again, the results are visualized for the mesh elements obtained from (a) “original” smoothed surface mesh, (b) the quality-enhanced surface mesh using “size and bias” option, and (c) the quality-enhanced surface mesh using “QI optimize” option. Note that regions with red color in (a) turn into green and blue, which signifies the mesh elements generated from the quality enhanced surfaces have better collapse ratio than those from the original smoothed surface. In Fig. 14, distributions of collapse ratio for (a) “standard” option and (b) “aggressive” option are compared. It is found that the minimum value of tetra collapse ratio increases for both options when enhanced surface meshes are used as inputs. Note that the “aggressive” option results in tetra collapse ratio less than 0.5. However, the portion is small and the minimum value of 0.4 is known to be acceptable for stable FEM simulations [36,37,38,39].
Tetra collapse ratio of three-dimensional mesh elements obtained from the “standard” volumetric mesh technique. The volumetric mesh elements are generated from a “original” smoothed surface, b quality-enhanced surface mesh using “size and bias” option and c quality-enhanced surface mesh using “QI optimize” option. Note that quality enhanced surface meshes result in volumetric mesh of better tetra collapse ratio than the original smoothed mesh. (Color figure online)
Tetra collapse ratio of three-dimensional mesh elements obtained from the “aggressive” volumetric mesh technique. The volumetric mesh elements are generated from a “original” smoothed surface, b quality-enhanced surface mesh using “size and bias” option and c quality-enhanced surface mesh using “QI optimize” option. Note that quality enhanced surface meshes result in volumetric mesh of better tetra collapse ratio than the original smoothed mesh. (Color figure online)
Comparison of distributions of tetra collapse ratio values: a “standard” meshing techniques and b “aggressive” meshing technique. It is found that, for both techniques, input surface meshes with better quality (“size and bias” and “QI optimize”) result in better tetra collapse ratio distribution of the resultant volumetric mesh than poor input surface mesh (“original”)
5 Application to FEM Simulations: Examples
It is well known that irregular, badly shaped finite elements may give rise to numerical errors during the property simulation using the FEM [40, 41]. This section is dedicated to validate the usability of the resultant finite elements on the digital voxellated polycrystals, obtained from the proposed three-dimensional meshing algorithm. In order to do that, two successful examples of FEM simulations on the polycrystalline mesh generated using the proposed algorithm are presented. Specifically, both thermo-elastic and elasto-viscoplastic simulations were performed on tetrahedral elements on polycrystals. For thermo-elastic simulations, two different polycrystals were prepared: one meshed from the voxellated digital microstructure of the size 50 × 50 × 50, and with 63 grains, and the other of size 100 × 100 × 100, and containing 223 grains. The total numbers of tetrahedral elements in the polycrystals are 464,350 and 3,188,941, respectively. The elasto-viscoplastic simulation was only performed on the smaller polycrystalline mesh.
5.1 Thermo-Elastic Case
The details of the thermo-elastic simulation are highlighted as follows. Elastic behavior of the polycrystalline structure is governed by Hooke’s law.
where σ ij is the stress tensor, C ijkl is the stiffness tensor and ɛ elastic kl is the elastic strain tensor. In the thermo-elastic case, the total strain inside the polycrystal, ɛ total kl , is contributed by the elastic strain, ɛ elastic kl , and the thermal strain, \(\alpha_{kl} \Delta T\), and therefore,
Here, α kl is the thermal expansion coefficient tensor and \(\Delta T\) is the temperature change. The properties of copper, having FCC structure, were used for the isotropic thermal expansion simulation on the smaller hypothetical microstructure while those of HCP zinc were chosen for the anisotropic thermal expansion simulation (Table 1). The property information was provided as inputs to the thermo-elasticity model in the ABAQUS/implicit [42,43,44] in accordance with the randomly chosen orientations for individual grains inside the polycrystals. In order to see the effect of the thermal loading on the elastic field distributions in the polycrystal, fixed boundary conditions were applied on all six faces of the simulation domain, as the temperature of the system was increased from 60 K through 150 to 300 K.
As a result from the thermo-elastic FEM simulation, elastic energy densities (EEDs) of both cases after thermal loading are visualized on the microstructure scale in Fig. 15. In the figure, (a) and (b) represent the EED distributions of the Cu and Zn polycrystals, respectively. In the figure, two-dimensional cross-sectional images are also presented, overlapped with the corresponding grain boundary map, to effectively present the elastic field variation along the grain morphology. Note that the elastic fields inside both microstructures are predicted such that they change smoothly along the curvature-maintained grain boundary network, leaving no erratic, peculiar local hotspots.
Distributions of elastic energy densities (EEDs) of hypothetical polycrystalline microstructures when subjected to elastic thermal loading: a EED distribution in the smaller polycrystalline microstructure with the properties of Copper, and b EED distribution in the bigger polycrystalline microstructure with the properties of Zinc. Note that the elastic fields along the grain boundaries are distributed smoothly without any erratic hotspots as shown in the cross-sectional images for both cases
5.2 Elasto-Viscoplasticity Case
A typical crystal plasticity constitutive equation for the FEM modeling relates the shear strain rate (\(\dot{\gamma }^{\alpha }\)) to the critical shear stress (gα) of the slip systems of the polycrystal. For a given resolved shear stress state, the shear strain rate on each slip system is given by
where τα is the resolved shear stress on slip system α, and n is the rate sensitivity factor for viscoplasticity. gα represents slip hardness on slip system α, and \(\dot{\gamma }_{0}\) is the reference shear strain rate. For the exemplary simulation, FCC aluminum properties were used (\(C_{11} = 108.2\;{\text{GPa}}, C_{12} = 61.3\;{\text{GPa}}, C_{44} = 28.5\;{\text{GPa}}\)) [45] and twelve {111} < 110 > slip systems were incorporated in the model to predict the elasto-viscoplastic behavior of the polycrystalline Al. The reference shear strain rate, \(\dot{\gamma }_{0}\), and the rate of sensitivity exponent, n were chosen to be 0.001 s−1 and 10, respectively. The smaller polycrystalline mesh elements, previously used for thermo-elastic simulation, were used as the representative volume element (RVE). The boundary conditions were defined such that U1 = U2 = 0 for the all nodes on the faces perpendicular to Z-axis during the loading. All of the information were input to the rate-dependent elasto-viscoplasticity model [46,47,48] in a user-defined material subroutine (UMAT). Both uniaxial tension and compression along Z-direction were applied separately, and the mechanical field distribution inside the polycrystal for each case was examined. The amount of the elongation and contraction was 10% for each case. It took about 50 h when 32 nodes of a workstation were used in parallel for each simulation.
In Fig. 16, both simulation results are presented. Figure 16 (a) and (b) show the distribution of von Mises stress, σ VM , after tension and compression, respectively. Again, the resultant cross-sectional images are presented along with the grain boundary network in order to highlight the effect of the smoothly segmented grain boundaries on the mechanical field distribution. Note that the stress field along the grain boundaries are distributed smoothly, showing no erratic hotspots, as shown in the thermo-elastic simulations. The overall mechanical responses of the polycrystal during the tension and compression simulations are summarized using the stress and strain curve in Fig. 16c. The predicted yield strengths are comparable to the reference data [49], and, therefore, it is clear that the proposed meshing algorithm has successfully generated three-dimensional elements of polycrystal, suitable for the mechanical property simulation using the FEM.
Distributions of von Mises stress, σ VM , in a hypothetical polycrystalline microstructure with property of aluminum when subjected to uniaxial tensile loading and compressive loading: a after 10% tensile loading in z-direction, and b after 10% compression in z-direction. Note that the mechanical fields along the grain boundaries are distributed smoothly without any erratic hotspots as shown in the cross-sectional images for both cases. Also, the corresponding stress and strain curve of the simulations are presented in c. Note that the resultant yield strength is found to be comparable to the reference data [49]
6 Conclusions
In this work, we present a new comprehensive scheme for generating grain boundary conformed, volumetric mesh elements from a three-dimensional voxellated polycrystalline microstructure. In order to accomplish that, a series of in-house codes and a commercial software (HyperMesh) are sequentially used. First, the three-dimensional, voxellated image of a polycrystalline microstructure are prepared from an isotropic grain growth simulation using the Monte Carlo Potts model. Then, its grain boundary network is segmented and smoothed as a collection of conformal triangles. During this step, the short- and long-range curvatures of the grain boundaries are truthfully approximated. In order to improve the surface mesh quality, the “size and bias” option and the “QI optimize” option offered by the commercial software are used. The resultant mesh qualities are found to be well improved while maintaining the characteristics of the approximated grain boundaries and junctions from the original smoothed surface mesh. Using such an enhanced surface mesh, conformal volumetric tetrahedral mesh of the polycrystalline microstructure is successfully generated using the commercial software, again (“standard” and “aggressive” option). The resultant meshes are found to be good enough for the FEM applications. Furthermore, two more polycrystalline structures are prepared in voxellated images using the Monte Carlo grain growth simulation, meshed conformally with tetrahedrons using the proposed algorithm, and used successfully as inputs for both thermo-elastic and elasto-visoplastic simulations. In conclusion, the combined approach suggested here is the first to successfully generate three-dimensional mesh elements for polycrystals with high enough quality to be used for the finite element analysis, while the realistic characteristics of grain boundaries and grains are maintained from the corresponding voxellated microstructure image.
References
B. Sun, Z. Suo, W. Yang, Acta Mater. 45, 1907–1915 (1997)
B. Sun, Z. Suo, Acta Mater. 45, 4953–4962 (1997)
A.F. Bower, E. Wininger, J. Mech. Phys. Solids 52, 1289–1317 (2004)
M. Nygards, P. Gudmundson, Comput. Mater. Sci. 24, 513–519 (2002)
A. Musienko, A. Tatschl, K. Schmidegg, O. Kolednik, R. Pippan, G. Cailletaud, Acta Mater. 55, 4121–4136 (2007)
H.J. Chang, H.N. Han, S.J. Park, J.H. Cho, K.H. Oh, Met. Mater. Int. 16, 553–558 (2010)
S. Manchiraju, D. Gaydosh, O. Benafan, R. Noebe, R. Vaidyanathan, P.M. Anderson, Acta Mater. 59, 5238–5249 (2011)
C. Herring, in The Physics of Powder Metallurgy, ed. by W. Kingston (McGraw-Hill, New York, 1951), p. 143
R. Quey, P.R. Dawson, F. Barbe, Comput. Methods Appl. Mech. Eng. 200, 1729–1745 (2011)
F. Barbe, R. Quey, 18 ème Congrès Français de Mécanique (2007)
C. Konke, S. Eckardt, S. Hafner, T. Luther, J. Unger, Int. J. Multiscale Comput. Eng. 8, 17–36 (2010)
Y. Bhandari, S. Sarkar, M. Groeber, M.D. Uchic, D.M. Dimiduk, S. Ghosh, Comput. Mater. Sci. 41, 222–235 (2007)
S. Ghosh, Y. BlIandari, M. Groeber, Comput.-Aided Des. 40, 293–310 (2008)
A.C.O. Miranda, L.F. Martha, P.A. Wawrzynek, A.R. Ingraffea, Eng. Comput. 25, 207–219 (2009)
S.E. Dillard, J.F. Bingert, D. Thoma, B. Hamann, I.E.E.E. Trans, Vis. Comput. Graph. 13, 1528–1535 (2007)
K. Brakke, Exp. Math. 1, 141–165 (1992)
A. Kuprat, A. Khamayseh, D. George, L. Larkey, J. Comput. Phys. 172, 99–118 (2001)
R.H. Moore, G.S. Rohrer, S. Saigal, Eng. Comput. 25, 221–235 (2009)
F. Barbe, L. Decker, D. Jeulin, G. Cailletaud, Int. J. Plast 17, 513–536 (2001)
M. Tanemura, Forma 18, 221–247 (2003)
T.-C. Chen, T. Li, X. Zhang, S.B. Desu, J. Mater. Res. 12, 1569–1575 (1997)
S. Kumar, S.K. Kurtz, J.R. Banavar, M. Sharma, J. Stat. Phys. 67, 523–551 (1992)
A. Ullah, G.Q. Liu, J.H. Luan, W.W. Li, M.U. Rahman, M. Ali, Mater. Charact. 91, 65–75 (2014)
A. Ullah, G.Q. Liu, H. Wang, M. Khan, D.F. Khan, J.H. Luan, Mater. Express 3, 109–118 (2013)
J.C. Tucker, L.H. Chan, G.S. Rohrer, M.A. Groeber, A.D. Rollett, Scripta Mater. 66, 554–557 (2012)
S. Donegan, J. Tucker, A. Rollett, K. Barmak, M. Groeber, Acta Mater. 61, 5595–5604 (2013)
M. Groeber, B. Haley, M. Uchic, D. Dimiduk, S. Ghosh, Mater. Charact. 57, 259–273 (2006)
D. Rowenhorst, A. Lewis, G. Spanos, Acta Mater. 58, 5511–5519 (2010)
F. Wakai, N. Enomoto, H. Ogawa, Acta Mater. 48, 1297–1311 (2000)
W.J. Schroeder, J.A. Zarge, W.E. Lorensen, in SIGGRAPH ‘Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques’ (ACM, New York, 1992), pp. 65–70
D.P. Luebke, I.E.E.E. Comput, Graph. Appl. 21, 24–35 (2001)
S.B. Lee, G.S. Rohrer, A.D. Rollett, Model. Simul. Mater. Sci. Eng. 22, 21 (2014)
Z. Wu, J.M. Sullivan, Int. J. Numer. Methods Eng. 58, 189–207 (2003)
P.M. Knupp, 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, SAND2007-8128C, AIAA (2007)
M. Bern, D. Eppstein, J. Gilbert, J. Comput. Syst. Sci. 48, 384–409 (1994)
M. Goelke, Element quality and check (2014), http://www.altairuniversity.com. Accessed 25 July 2017
A. Hannukainen, S. Korotov, M. Křížek, Numer. Math. 120, 79–88 (2012)
T.A. Burkhart, D.M. Andrews, C.E. Dunning, J. Biomech. 46, 1477–1488 (2013)
J. Shewchuk, What is a good linear finite element? Interpolation, conditioning, anisotropy, and quality measures, University of California at Berkeley, p. 73 (2002)
R. Abgrall, J. Comput. Phys. 114, 45–58 (1994)
Wanai Li, Efficient Implementation of High-Order Accurate Numerical Methods on Unstructured Grids (Springer, Berlin, 2014), pp. 1–10
H. Ledbetter, E. Naimon, J. Phys. Chem. Ref. Data 3, 897–935 (1974)
C. Wert, E. Tyndall, J. Appl. Phys. 20, 587–589 (1949)
C. Hull, International Critical Tables of Numerical Data, Physics, Chemistry and technoLogy (National Academies, Washington, DC, 1929)
A. Alankar, I.N. Mastorakos, D.P. Field, Acta Mater. 57, 5936–5946 (2009)
D. Peirce, R.J. Asaro, A. Needleman, Acta Metall. 31, 1951–1976 (1983)
Y. Choi, T. Parthasarathy, D. Dimiduk, M. Uchic, Metall. Mater. Trans. A 37, 545–550 (2006)
Y. Choi, M. Uchic, T. Parthasarathy, D. Dimiduk, Scripta Mater. 57, 849–852 (2007)
ASM International Handbook Committee, Properties and Selection: Nonferrous Alloys and Special-Purpose Materials (ASM International, USA, 2001)
Acknowledgements
This work was supported by the Agency for Defense Development (ADD) and by the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science, ICT & Future Planning (MSIP) (No. NRF-2015R1A5A1037627).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lee, MJ., Jeon, YJ., Son, GE. et al. Grain Boundary Conformed Volumetric Mesh Generation from a Three-Dimensional Voxellated Polycrystalline Microstructure. Met. Mater. Int. 24, 845–859 (2018). https://doi.org/10.1007/s12540-018-0083-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12540-018-0083-x