1 Introduction

The ultimate goal of human beings is to build machines with the ability to think, learn, and behave like humans. Therefore, understanding the structure and function of the human brain is necessary for brain-like processing (Zurada 1992; Haykin 2007). The biological nervous system was first mathematically modeled by McCulloch and Pitts in 1943 (McCulloch and Pitts 1943; Ojha et al. 2017). It is the groundwork for simulating the behavior of the neural system, which causes the emergence of Artificial Neural Networks (ANNs) and associated learning algorithms. With regard to adaptability, generalization, real-time procedure, and self-organizing capability, ANNs can be supposed as the most successful approach among other machine learning schemes in classification, clustering, pattern recognition, and regression problems (Karaboga et al. 2007; Schmidhuber 2015; Chatterjee et al. 2017; Braik et al. 2008; Linggard et al. 2012). A simple schema of McCulloch and Pitts' model is illustrated in Fig. 1.

Fig. 1
figure 1

McCulloch-Pitts neural model

Full size image

The success of machine learning algorithms mostly depends on the learning procedure. Generally learning algorithms are divided into two main categories: supervised and unsupervised approaches. The mathematical model of neural neurons, introduced by McCulloch and Pitts, suffers from the lack of a learning strategy that tunes the neuron weights for solving a particular problem. In order to fill this gap, Hebb proposed an unsupervised rule-based learning strategy for tuning the connection weights of the network, in 1949 (Hebb 1949). Later in 1958, Rosenblatt proposed a supervised learning mechanism called perceptron with the capability of linear classification. In this mechanism, the weights of the network are updated according to the input data when errors occur. This network is the simplest case which is so-called single-layer feed-forward neural network (FFNN); however, this model is not able to solve non-linear classification problems. Consequently, developing the network and associated learning method to deal with this challenge is thus needed.

Researchers believe that increasing the number of hidden layers overcome this problem; however, it requires a training algorithm to train the multi-layer perceptron neural network (MLP). In 1984, Werbos, as the first researcher, proposed a back-propagation (BP) algorithm for training this network (Werbos 1989). Nonetheless, this was not popular until Rumelhart (McClelland et al. 1986) brought it up again. BP tunes the weights of the network layer by layer if the output of the network is not desired. As learning algorithms directly impact the performance of neural networks, a wide variety of studies have been conducted to effectively train the procedure. Supervised training methods are divided into two main categories: gradient-based and stochastic methods. As mentioned already, BP adjusts the weights with respect to distance from the minimum point of the lost function; however, because of the low convergence rate, it may get stuck in local minima. This problem arises from the fact that movement follows the gradient descent. On the other hand, stochastic algorithms are proven to be effective in dealing with such problems.

A wide variety of stochastic optimization techniques, including heuristic and metaheuristic algorithms, have been applied to tackle this problem. Genetic Algorithm (GA) (Holland 1992; Bhattacharjee and Pant 2019), Particle Swarm Optimization (PSO) (Eberhart and Kennedy 1995; R. K. 2020), Evolutionary Strategies (ES) (Schwefel 1984), Differential Evolution (DE) (Storn and Price 1997), Ant Colony Optimization (ACO) (Dorigo and Caro 1999), Artificial Bee Colony (ABC)(Karaboga and Basturk 2007), Grey Wolf Optimization (GWO) (Mirjalili et al. 2014a), whale optimization algorithm (Mirjalili and Lewis 2016), Biogeography-Based Optimization (BBO) (Simon 2008), Firefly Optimization Algorithm (FFA) (Yang 2009), Bat Algorithm (BA) (Failed 2010), Cuckoo Search (CS) (Yang and Deb 2009), Bird Mating Optimizer (BMO) (Askarzadeh 2014), etc. have been used for this purpose. A fair balance between exploitation and exploration lets such algorithms not only find an accurate solution but also escape from poor local optima.

Montana and Davis (1989) proposed a modified version of genetic algorithm to train FFNNs, where Zhang et al. (2007) applied a hybrid PSO to tuning the weights of FFNN;. Moreover, ES was utilized for optimizing the system error of FFNN in Wienholt (1993); DE was applied to optimize the learning mechanism of classifiers (Ilonen et al. 2003; Failed 2008); and finally ACO was extended to the continuous form for training the neural networks weights (Blum and Socha 2005). In 2007, Karaboga et al. (2007) used ABC to train the neural networks; later, the authors improved their work by hybridized ABC with Levenberq-Marquardt (Ozturk and Karaboga 2011). Mirjalili et al. proposed a GWO-based algorithm for training MLPs to reduce the system errors in FFNNs (Mirjalili 2015); the authors also suggested BBO and WOA algorithms to overcome the associated problem (Mirjalili et al. 2014b; Aljarah et al. 2018). Furthermore, FFA was utilized for FFNN in order to facilitate swift learning and decrease computational complexity (Nayak et al. 2016). Additionally, BA was utilized to optimize the connection weights and structure of the FFNNs for constructing a classifier. (Jaddi et al. 2015). An alternative optimization algorithm, namely CS, which has been applied to optimize the FFNNs training for classification problems (Nawi et al. 2013). Finally, for solving the classification problems, BMO was utilized to train the FFNNs (Askarzadeh and Rezazadeh 2013).

The no-free-lunch (NFL) theorem (Wolpert and Macready 1997) emphasizes that an optimization algorithm may not outperform other algorithms in solving all kinds of optimization problems. Therefore, new approaches are required to cope with new challenges. This issue motivated us to utilize a new optimization method (BRO) that is proved to perform as good as or sometimes superior to the existing approaches for training FFNNs. In this paper, for training the feed-forward ANNs, we used a recently proposed Battle Royale Optimization (BRO) algorithm, which is proven to be successful in solving continuous optimization problems (Rahkar Farshi 2020). This paper is organized as follows: Sect. 2 describes the concepts of MLP. Section 3 provides a brief summary of BRO. BRO-based training algorithm for MLP is described in Sect. 4. Section 5 includes experimental results and discussion. Finally, Sect. 6 presents the conclusions.

2 Multi-layer perceptron neural network

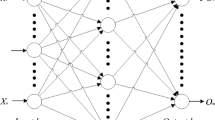
MLP is a specific model of FFNN which is able to solve the non-linear classification and regression problems. Neurons are considered as the processing elements in MLP. The neurons are distributed in parallel form over each layer, where the layers are stacked on each other. Moreover, the neurons of each layer are fully connected to all other neurons in the next layer (Fig. 2). The first and last layers are respectively named input and output. The layers between the input and output, are hidden layers. The first layer feeds input variables to the network (Zurada 1992; Haykin 2007). MLP arranges neurons in one-directional mode. The neurons of the first layer receive input from the outside while other layers' neurons receive the inputs from the output of previous layers’ neurons.

Fig. 2
figure 2

Multilayer perceptron neural network

Full size image

The connections between the layers are associated with weights to control the effect of related input on neurons. Each neuron in MLP uses summation and activation functions consecutively to produce the output, as illustrated in Fig. 1. The summation function computes the weighted sum of the inputs, see Eq. 1. Subsequently, the activation function applies a threshold on the obtained weighted sum to generate the output of the neuron.

$${net}_{j}= \sum_{i=1}^{n}{w}_{ji}.{x}_{i}+{b}_{j },$$
(1)

where, \(n\) indicates the total number of inputs, \({x}_{i}\) denotes the input variable \(i\), \({b}_{j}\) is a bias value of jth neuron, and \({w}_{ji}\) implies the weight of the connection from the ith input to jth neuron. The S-shaped sigmoid function is the most popular one among several non-linear activation functions which is broadly used in the MLP. This function is mathematically calculated per:

$$f\left(z\right)=\frac{1}{\left(1+{e}^{-z}\right)}$$
(2)

By using this activation function over the weighted sum, the output of a neuron is calculated by:

$${o}_{j}= f\left({net}_{j}\right)$$
(3)

Each classification or regression problem requires a specific network structure to be constructed. Consequently, for tuning the network connection weights, the training algorithm is triggered. Updating the weighting vectors is carried out by minimizing the total error of the network (Karaboga et al. 2007). The total error is estimated as follows:

$$E\left(W\left(t\right)\right)=\frac{1}{l}\sum_{j=1}^{l}\sum_{k=1}^{k}{\left({d}_{k}-{O}_{k}\right)}^{2},$$
(4)

where, \(E\left(W\left(t\right)\right)\) indicates the total error value at the tth iteration where \(W\left(t\right)\) is the weights of the network connections at the tth iteration; The desired and obtained output of kth node are represented by \({d}_{k}\) and \({O}_{k}\), respectively; \(k\) and \(l\) respectively indicate the number of output nodes and train instances.

Training the MLP is accomplished according to minimizing the total network error, which can be considered as an optimization problem. BP is a variation on the gradient search approach that is commonly used for training a network; however, it suffers from the scaling problem, which may cause in rapid diminishing of the of BP performance in high-dimensional problems (Montana and Davis 1989). As complex spaces are multimodal, and they consists of several local minima around the global minimum, gradient-based search approaches may get stuck in local minima; therefore, performance degradation might be observed. Metaheuristic optimization techniques would be effective in dealing with such problems. The exploitation and exploration mechanism of optimization algorithms not only prevent them from getting stuck in local optima but also provide a deep insight into the global optimum.

3 Battle royale optimizer

This section briefly overviews the BRO algorithm proposed by Rahkar-Farshi in 2020 (Rahkar Farshi 2020). The basic concept of this algorithm was inspired by the battle royale game, which is a multiplayer video game genre that blends survival. Player unknown battlegrounds (PUBG) is the well-known and most popular game among these kinds of games. Deathmatch is one of the well-played game modes of PUBG. In this mode, a player aims to kill as many other players as possible until a kill limit or a time limit is met. Generally, battles are fought on a specific battlefield map chosen by the players. Such an optimization problem space is considered as a game map in BRO. The game gets started by jumping the players from a plane onto the map. In this regard, the search agents of BRO are randomly initialized by uniform random initialization within the search space similar to many other population-based optimization algorithms. Throughout the game, a player may be killed by other rivals which causes him to be respawned at a random zoon of the battlefield. All players attempt to hurt other players by shooting. Players who take a more appropriate position, can damage their rivals. In this context, one may question who and how can shoot its opponent in the game? Actually, each search agent will be compared with the nearest agent according to the Euclidean distance. Players with a better cost function, therefore, cause damage to another one. The damage level of the player who gets damaged, will be increased by one and mathematically calculated per \({x}_{i}.damage= {x}_{i}.damage+1\), here \({x}_{i}.damage\) is the damage level of the ith soldier among the population. Then, the player randomly move to be protected from further injury. This movement is performed by moving the player toward the best position found so far. This operation causes the exploitation which is mathematically modeled as follows:

$${x}_{dam,d}={r}_{1}{x}_{dam,d}+{r}_{2}\left({x}_{best,d}-{x}_{dam,d}\right),$$
(5)

where \({r}_{1},{r}_{2}\) are two random variables, uniformly distributed over the interval [0,1]. However, r1 is set to 1.  \({x}_{dam,d}\) indicates the position of the damaged player in dimension d. Also, the level of damage for a damaged player will be reset to zero if it hurts another player. Furthermore, if a player gets damaged for a predetermined number of times (threshold value) in a row and the damaged level reaches the predefined threshold value, the player gets killed and would be respawned at a random space of the problem. In this case, the level of damage will reset to zero. Through trial and error, it is determined that the value of threshold = 3 was applicable for optimization benchmarks. This action prevents early convergence and provides good quality of exploration. Operations are mathematically calculated as:

$$x_{dam,d} = r\left( {ub_{d} - lb_{d} } \right) + lb_{d}$$
(6)

where \({lb}_{d}\) and \({ub}_{d}\) stand for the lower and upper bounds, respectively. Furthermore, in every \(\Delta\) step of the iteration, the algorithm adaptively narrows the problem scale towards the best solution. The initial value for \(\Delta\) is assumed as \(\Delta =\frac{MaxCicle}{{round(\mathrm{log}}_{10}\left(MaxCicle\right))}\). Then, after each \(\Delta\) step, \(\Delta\) will be updated as \(\Delta =\Delta +round(\Delta /2))\), if i  ≥∆. This operation provides both exploration and exploitation. Consequently, the \({lb}_{d}\) and \({ub}_{d}\) will be updated as follows:

$$\begin{gathered} lb_{d} = x_{{best,d}} - SD\left( {\overline{{x_{d} }} } \right) \hfill \\ ub_{d} = x_{{best,d}} + SD\left( {\overline{{x_{d} }} } \right) \hfill \\ \end{gathered}$$
(7)

where \(SD\left(\overline{{x }_{d}}\right)\) indicates the standard deviation of all search agents’ positions in dimension \(d\) and \({x}_{best,d}\) represents the position of the best-known solution. All these interactions will be repeated until the termination conditions are met.

4 BRO for training MLP

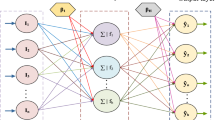
All kinds of non-linear optimization algorithms can be employed for tuning FFNN weights. BRO is a population-based approach that can be applied to single-objective optimization over continuous problem spaces. This section discusses how to apply BRO to train FFNN whit a single hidden layer. The intuition behind using a single hidden layer architecture is ease of understanding. BRO maximizes or minimizes a real objective function by systematically choosing values from a possible set for each input variable and calculating the value of the function. Integration of BRO whit MLP for generating a classifier is hinged on two important factors: encoding the search agents and constructing the objective function. In this work, each search agent (player) is encoded into a one-dimensional vector, which corresponds to network connection weights and neuron bias (see Fig. 3).

Fig. 3
figure 3

Encoding MLP with a single hidden layer to a search agent vector

Full size image

In order to evaluate the classification quality of each search agent, an objective function is required over the training set. To achieve this goal, a commonly used error function, Mean Square Error (MSE), has been used herein. The general form of MSE is mathematically calculated as follows:

$$MSE = \frac{1}{U}\sum\limits_{{u = 1}}^{U} {\left( {y_{u} - y^{\prime}_{u} } \right)^{2} },$$
(8)

where \(y\) indicates the actual value and \({y}^{^{\prime}}\) is the estimated value. \(U\) indicates the total number of instances in the training set. The number of the input variable (length of search agents’ vector) is computed by Eq. (9):

$$\left(Ni+1\right)\times \left|{h}_{i}\right|+\sum_{i=2}^{Nhl}\left(\left|{h}_{i}\right|\times \left(\left|{h}_{i-1}\right|+1\right)\right)+\left(\left|{h}_{Nhl}\right|+1\right)\times No$$
(9)

where \(Ni\) is the number of input variables; \(Nhl\) indicates the number of hidden layers in the network; \(\left|{h}_{i}\right|\) represents the number of neurons in the \({i}^{th}\) hidden layer and \(No\) is the number of the output layer’s neurons. For a network with one hidden layer Eq. 9 can be replaced by:

$$\left(Ni+1\right)\times \left|{h}_{1}\right|+\left(\left|{h}_{1}\right|+1\right)\times No$$
(10)

For instance, using Eq. (10) for the given sample in Fig. 3, the number of parameters to be tuned is calculated per \(\left(2+1\right)\times 3+\left(3+1\right)\times 2=17\). It can be observed that we can readily estimate the vector size when \(Nhl\) = 1.

It should be noted that the parameter vector is commonly initialized by a uniform distribution between [− 1, 1]. However, this range can be extended to a wider range. On the other hand, in order to prevent the gradients to be vanished or exploded too quickly, the weights should be set neither much greater than 1 nor much smaller than − 1. (Ng et al. 2020).

5 Experimental results and performance evaluation

To assess the performance of the proposed approach, an extensive experimental evaluation and comparison have been carried out with backpropagation (Generalized learning delta rule) and six well-accepted population-based metaheuristic algorithms: Genetic Algorithm (GA) (Holland 1992), Particle Swarm Optimization (PSO) (Eberhart and Kennedy 1995), Artificial Bee Colony (ABC)(Karaboga and Basturk 2007), Gravitational Search Algorithm (GSA)(Rashedi et al. 2009), and Whale Optimization Algorithm (WOA) (Mirjalili and Lewis 2016) Differential Evolution (DE) (Price 1996). The control parameter of optimization algorithms may significantly affect their performance. The best control parameters for all algorithms were set based on trial and error or directly taken from Aljarah et al. (2018). These parameters are reported in Table 1. Both the number of iterations and population size for all algorithms are set to 200. Also, the method has been compared with backpropagation (Generalized learning delta rule), such that the training seek was taken as 200, \(\eta\) and \(\lambda\) were 0.1 and 1, respectively. As the heuristic algorithms are stochastic optimization techniques, they can lead to different results. Therefore, all the empirical results are achieved by taking the average of 20 independent runs for each dataset. All algorithms were implemented in MATLAB and performed on a Core i7-7700 HQ 2.81 processor with 32 GB of RAM. In this study, ten real-world benchmark classification datasets, namely, Iris, Breast Cancer, Heart, Vertebral, Parkinson’s, Australian, Tic_Tac_Toe, Ionosphere, and Wine datasets were used to validate the methods. Table 2 shows the number of classes, attributes, training samples, and test samples for each dataset. Table 3 reports the associated network architecture and the total number of the parameters for each dataset.

Table 1 The initial values of the parameters of optimization algorithms
Full size table
Table 2 Characteristics of used benchmark datasets
Full size table
Table 3 MLP architect for datasets
Full size table

Additionally, in the case of scale invariance, the datasets which consist of floating point feature values, are normalized by min–max normalization method to the range [− 1, 1].

It should be noted that two different architectures of MLP classifier were used for the \({10}^{th}\) (Wine) dataset. In the first one (10.1), one-hot encoding was used for labeling. Hence, the number of output layer’s neurons equals the number of class.

Accuracy is a well-known performance criterion in order to evaluate the ability of a classifier. To assess the effect of training algorithm on MLP classifier, an accuracy performance measure was used in this paper. Accuracy is the number of correctly classified instances over the total number of instances. The numerical comparisons are conducted by taking the average of MSE and classification accuracy over 20 independent runs. Besides, in order to evaluate the stability of algorithms, standard deviation for both MSE and classification accuracy is calculated and reported in Tables 4 and 5. In these tables, “Best” indicates the best feasible solution among all runs of each algorithm.

Table 4 MLP classifier accuracy for each dataset
Full size table
Table 5 Training results of MLP for each dataset (MSE)
Full size table

After taking the average over the ranks of each algorithm, the highest averaged ranks are bolded in the last three rows of Table 4 and Table 5. As can be seen in Table 4, the BRO-based classifier ranked first in terms of classifier accuracy according to the mean and best values. In this table, ABC, DE, WOA, PSO, GA, BP, and GSA ranked second to eighth, respectively, according to the mean value. Also, ABC, WOA, DE, PSO, GA, GSA, and BP, correspondingly, with respect to best value. Moreover, DE performed the best in terms of the STD, whereas ABC, BRO, and BP ranked second to forth. PSO ranked fifth alongside GA. Consequently, WOA, and GSA ranked seventh to last, correspondingly. This table indicates that none of the metaheuristic algorithms could yield reasonable performance in the Heart dataset. This may arise because the number of training data is not sufficient, but too small compared to the number of test data. However, BP outperformed others in this dataset according to all performance criteria. As it is clear from this table BP perform best only in two cases out of eleven. In most cases, the classifier accuracy of BP is much lower than the classifier accuracy of metaheuristic-based methods. Also, in some cases, BP provides very different mean and best classifier accuracy values. For example, in Diabetes, the mean value is 0.69160, while the best value is 0.77862, and in Vertebral, although the mean value of classifier accuracy is 0.676415, the best try is 0.849056. Consequently, BP ranked worst in terms of STD due to unsatisfying results such as 0.076602 and 0.128556. All these observations prove that BP may stuck in local optima.

Apart from classifier accuracy, for each dataset, algorithms are also ranked according to the objective function. As Table 5 shows, the proposed method achieves the best results in six cases out of eleven by means of means fitness values and DE follows it with four superiority out of eleven cases. According to Mean and best values, the BRO-based MLP classifier ranks first overall, where, DE, ABC, WOA, PSO, GA, and GSA ranked second to eighth, respectively, according to the mean values. Also, ABC, DE, WOA, PSO, GA, and GSA, correspondingly, with respect to the best value. Moreover, DE performed the best in terms of the STD, whereas BRO, ABC, PS, GA, GSA and WOA ranked second to last, respectively. Furthermore, the fitness values obtained by PSO and WOA are competitive. Also, the last row proves that the DE and BRO provide more stable results than other compared algorithms. In contrast, the WOA ranks worst according to STD. Moreover, Fig. 4 illustrates how many times the algorithms have been ranked first in terms of accuracy and MSE over all data sets. As it is clear from Fig. 4, although DE offers better STD than BRO in terms of all performance metrics (accuracy and MSE), BRO outperforms DE in terms of the mean and best values. It indicates that DE may get stuck in local optima frequently.

Fig. 4
figure 4

Winner chart of algorithm respect to a accuracy and b MSE

Full size image

In order to do a deep investigation, the convergence rate analysis was performed for BRO and its competitors. Figure 5 portrays convergence curves of the best fitness values among all solutions for each dataset. Almost in all cases, the convergence curve of BRO plunges rapidly, and Fig. 5 proves that the BRO and DE have a faster overall convergence rate compared to others in all datasets. On the other hand, in most cases, WOA ranked second and outperformed other compared algorithms. Also, the convergence rate of GA, PSO, and WOA are competitive., and they may have similar convergence curves. Finally, Fig. 5 also demonstrates that the GSA has the worst convergence rate, and never outperforms other algorithms.

Fig. 5
figure 5figure 5

MSE convergence curves

Full size image

6 Conclusion

In this paper a BRO-based MLP training algorithm has been proposed. The performance of BRO for training the MLP is compared with five well-known optimization algorithms. Also, ten most-used classification benchmark datasets are used to evaluate the performance of BRO and its competitors. The numerical comparisons were conducted by taking the average of MSE and classification accuracy over 20 independent runs. BRO-based classifier ranked first in terms of classifier accuracy and error according to the means and best values. Moreover, BRO respectively ranked third and second in STD according to accuracy and error rate. Furthermore, most cases, the convergence curve of BRO and DE plunge rapidly; they have a faster overall convergence rate compared to others in all datasets. A good balance between exploitation and exploration lets BRO not only find an accurate solution but also escape from poor local optima. Moreover, in some cases, BP provides very different mean and best classifier accuracy values due to getting stuck in local optima. Overall, experiments confirm that, according to error rate, accuracy, and convergence, the proposed approach yields promising results and outperforms its competitors Metaheuristic-based learning algorithms may perform successfully for the MLP which includes a low number of hidden layers. The number of parameters to be optimized will increase exponentially by increasing the number of hidden layers. The BRO algorithm is no exception to this handicap. In the future work, it is planned to use hybrid BP and BRO to overcome the aforementioned handicap and extend the proposed algorithm for training the convolutional neural network.