1 Introduction

Neural Networks (NN) are one of the greatest inventions in the field of Computational Intelligence. They mimic the neurons of human brain to mostly solve classification problems. The rudimentary concepts of NNs were first proposed in 1943 [1]. There are different types of NNs proposed in the literature: Feedforward network [2], Kohonen self-organizing network [3], Radial basis function (RBF) network [4], Recurrent neural network [5], and Spiking neural networks [6]. In Feedforward NNs (FNN) the information is cascaded in one direction throughout the networks. As its name implies, however, recurrent NNs share the information between the neurons in two directions. Finally, spiking NNs activates neurons with spikes.

Despite the differences of NNs, they are common in learning. Learning refers to the ability of a NN in learning from experience. Similarly to biological neurons, the Artificial NNs (ANN) have been equipped with mechanisms to adapt themselves to a set of given inputs. There are two common types of learning here: supervised .[7, 8] and unsupervised [9, 10]. In the former case, the NN is provided with feedbacks from an external source (supervisor). In unsupervised learning, however, a NN adapts itself to inputs (learn) without any extra external feedbacks.

Generally speaking, the method that provides learning for a NN is called trainer. A trainer is responsible for training NNs to achieve the highest performance for new sets of given inputs. In the supervised learning, a training method first provides NNs with a set of samples called training samples. The trainer then modifies the structural parameters of the NN in each training step in order to improve the performance. Once the training phase is completed, the trainer is omitted and NN is ready to use. The trainer can be considered as the most important component of any NNs.

There are two types of learning methods in the literature: deterministic versus stochastic. Back-Propagation (BP) [11] and gradient-based methods are considered as deterministic methods. In such techniques, the training phase results in the same performance if the training samples remain consistent. The trainers in this group are mostly mathematical optimization techniques that aim to find the maximum performance (minimum error). In contrast, stochastic trainers utilize stochastic optimization techniques in order to maximize performance of a NN.

The advantages of the deterministic trainers are: simplicity and speed. Deterministic training algorithm usually starts with a solution and guides it toward an optimum. The convergence is very fast, but the quality of the obtained solution highly depends on the initial solution. In addition, there is a high probability of local optima entrapment. Local optima refer to the sub-optimal solutions in a search space that might mistakenly be assumed as the global optimum. The challenge here is the unknown number of runs that a trainer needs to be restarted with different initial solutions to find the global optimum.

In contrast, stochastic trainers start the training process with random solution(s) and evolve it (them). Randomness is the essential component of the stochastic trainers that apply to both initial solutions and method of solution’s improvement during the training process. The advantage of such methods is high local optima avoidance, but they are mostly much slower than deterministic approaches [12], [13]. The literature shows that stochastic training methods have gained much attention recently, which is due to the high local optima avoidance.

Stochastic training algorithms can be divided into two groups: single-solution and multi-solution based algorithms [14]. In the former class, a trainer starts the training with a single randomly constructed NN and evolves it iteratively until the satisfaction of an end criterion. Examples of single-solution based trainers are Simulated Annealing (SA) [15, 16] and hill climbing [17, 18]. In contrast to single-solution based methods, a multiple-solution based algorithm initiates the training process by a set of randomly created NNs and evolves them with respect to each other until the satisfaction of an end criterion. The literature shows that stochastic algorithms with multiple solutions provide higher ability of resolving local optima stagnation [19].

Some of the most popular multi-solution trainers in the literature are: Genetic Algorithm (GA) [19, 20], Particle Swarm Optimization (PSO) [21, 22], Ant Colony Optimization (ACO) [23, 24], Artificial Bee Colony (ABC) [25, 26], and Differential Evolution (DE) [27, 28]. The recent evolutionary training algorithms are: hybrid Central Force Optimization and Particle Swarm Optimization (CFO-PSO) [29], Social Spider Optimization algorithm (SSO) [30], Chemical Reaction Optimization (CRO) [31] Charged System Search (CSS) [32], Invasive Weed Optimization (IWO) [33] and Teaching-Learning Based Optimization (TLBO) trainer [34]. The reason as to why such optimization techniques have been employed as training algorithms is their high performance in terms of approximating the global optimum. This also motivates my attempts to investigate the efficiencies of my recently proposed algorithm called Grey Wolf Optimizer (GWO) [14] in training FNNs. In fact the main motivations of this work are twofold:

  • Current multi-solution stochastic trainers still prone to local optima stagnation

  • GWO shows high exploration and exploitation that may assist it to outperform other trainers in this field

The rest of the paper is organized as follows.

Section 2 presents the preliminary and essential definition of an MLP. The GWO algorithm is then presented in Section 3. The proposed GWO-based trainer is discussed in Section 4. Results and conclusion are provided in Sections 5 and 6 respectively.

2 Feed-forward neural network and multi-layer perceptron

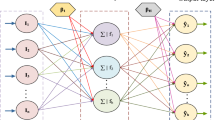
As discussed in the preceding section, FNNs are those NNs with only one-way and one-directional connections between their neurons. In this type of NNs, neurons are arranged in different parallel layers [2]. The first layer is always called the input layer, whereas the last layer is called the output layers. Other layers between the input and output layers are called hidden layer. A FNN with one hidden layer is called MLP as illustrated in Fig. 1.

Fig. 1
figure 1

MLP with one hidden layer

Full size image

After providing the inputs, weights, and biases, the output of MLPs are calculated throughout the following steps**[35]:

  1. 1.

    The weighted sums of inputs are first calculated by (2.1).

$$ s_{j}= \sum\nolimits_{i=1}^{n} {(W_{ij}} . X_{i})- \theta_{j},\quad j=1,2,\mathellipsis h $$
(2.1)

where n is the number of the input nodes, W i j shows the connection weight from the ith node to the jth node θ j is the bias (threshold) of the jth hidden node, and X i indicates the ith input.

  1. 2.

    The output of each hidden node is calculated as follows:

$$ S_{j}= sigmoid\left( s_{j} \right)=\frac{1}{\left( 1+\exp \left( -s_{j} \right) \right)}, j=1,2,\mathellipsis h $$
(2.2)
  1. 3.

    The final outputs are defined based on the calculated outputs of the hidden nodes as follows:

$$ o_{k}= \sum\nolimits_{j=1}^{h} {(w_{jk}} .{ S}_{j})- \theta_{k}^{\prime}, k=1,2,\mathellipsis ,m $$
(2.3)
$$ O_{k}= sigmoid\left( o_{k} \right)=\frac{1}{\left( 1+\exp \left( -o_{k} \right) \right)}, k=1,2,\mathellipsis ,m $$
(2.4)

where w j k is the connection weight from the jth hidden node to the kth output node, and \(\theta _{k}^{\prime }\) is the bias (threshold) of the kth output node.

As may be seen in the (2.1) to (2.4), the weights and biases are responsible for defining the final output of MLPs from given inputs. Finding proper values for weights and biases in order to achieve a desirable relation between the inputs and outputs is the exact definition of training MLPs. In the next sections, the GWO algorithm is employed as a trainer for MLPs

3 Grey Wolf Optimizer

The GWO is a recently proposed swarm-based meta-heuristic [14]. This algorithm mimics the social leadership and hunting behaviour of grey wolves in nature. In this algorithm the population is divided into four groups: alpha (α), beta (β), delta (δ), and omega (ω). The first three fittest wolves are considered as α, β, and δ who guide other wolves (ω) toward promising areas of the search space. During optimization, the wolves update their positions around α, β, or δ as follows:

$$ \overset{\rightarrow}{D} =\mid\vec{C}\cdot\overset{\longrightarrow}{X_{p}}(t)-\vec{X}(t)\mid $$
(3.1)
$$ \vec{X}(t+{1})=\overset{\longrightarrow}{X_{p}}(t)-\vec{A}\cdot\overset{\rightarrow}{D} $$
(3.2)

where t indicates the current iteration, \(\vec {A} =\) 2\(a\cdot \vec {r_{1}} a\), \(\vec {C}=2\cdot \vec {r_{2}}\) , \(\vec {X_{p}}\) is the position vector of the prey, \(\vec {X}\) indicates the position vector of a grey wolf, a is linearly decreased from 2 to 0, and \(\vec {r_{1}}\), \(\vec {r_{2}}\) are random vectors in [0,1].

The concepts of position updating using (3.1) and (3.2) are illustrated in Fig. 2. It may be seen in this figure that a wolf in the position of (X, Y) is able to relocate itself around the prey with the proposed equations. Although seven of the possible locations have been shown in Fig. 2, the random parameters A and C allow the wolves to relocate to any position in the continuous space around the prey.

Fig. 2
figure 2

Position updating mechanism of search agents and effects of A on it

Full size image

In the GWO algorithm, it is always assumed that α, β, and δ are likely to be the position of the prey (optimum). During optimization, the first three best solutions obtained so far are assumed as α, β, and δ respectively. Then, other wolves are considered as ω and able to re-position with respect to α, β, and δ. The mathematical model proposed to re-adjust the position of ω wolves are as follows [14]:

$$\begin{array}{@{}rcl@{}} \overset{\longrightarrow}{D_{\alpha}}=\mid\vec{C}_1\cdot\overset{\longrightarrow}{X_{\alpha}}-\vec{X}\mid \end{array} $$
(3.3)
$$\begin{array}{@{}rcl@{}} \overset{\longrightarrow}{D_{\beta}}=\mid\vec{C}_2\cdot\overset{\longrightarrow}{X_{\beta}}-\vec{X}\mid \end{array} $$
(3.4)
$$\begin{array}{@{}rcl@{}} \overset{\longrightarrow}{D_{\delta}}=\mid\vec{C}_3\cdot\overset{\longrightarrow}{X_{\delta}}-\vec{X}\mid \end{array} $$
(3.5)

where \(\vec {X_{\alpha }} \) shows the position of the alpha, \(\vec {X_{\beta }} \) shows the position of the beta, \(\vec {X_{\delta }} \) is the position of delta, \(\vec {C}_{1}\), \(\vec {C}_{2}\), \(\vec {C_{3}}\) are random vectors and \(\vec {X}\) indicates the position of the current solution.

Equations (3.3), (3.4), and (3.5) calculated the approximate distance between the current solution and alpha, beta, and delta respectively. After defining the distances, the final position of the current solution is calculated as follows:

$$\begin{array}{@{}rcl@{}} \overset{\longrightarrow}{X_1}=\overset{\longrightarrow}{X_{\alpha}}-\vec{A_1}\cdot\left(\overset{\longrightarrow}{D_{\alpha}}\right) \end{array} $$
(3.6)
$$\begin{array}{@{}rcl@{}} \overset{\longrightarrow}{X_2}=\overset{\longrightarrow}{X_{\beta}}-\overset{\longrightarrow}{A_2}\cdot\left(\overset{\longrightarrow}{D_{\beta}}\right) \end{array} $$
(3.7)
$$\begin{array}{@{}rcl@{}} \overset{\longrightarrow}{X_3}=\overset{\longrightarrow}{X_{\delta}}-\overset{\longrightarrow}{A_3}\cdot\left(\overset{\longrightarrow}{D_{\delta}}\right) \end{array} $$
(3.8)
$$\begin{array}{@{}rcl@{}} \vec{X}(t + 1)= \frac {\overset{\longrightarrow}{X_1}+\overset{\longrightarrow}{X_2}+\overset{\longrightarrow}{X_3}}{3} \end{array} $$
(3.9)

where \(\vec {X_{\alpha }} \) shows the position of the alpha, \(\vec {X_{\beta }} \) shows the position of the beta, \(\vec {X_{\delta }} \) is the position of delta, \(\vec {A}_{1}\), \(\vec {A_{2}}\), \(\vec {A_{3}}\) are random vectors, and t indicates the number of iterations.

As may be seen in these equations, the equations (3.3), (3.4) and (3.5) define the step size of the ω wolf toward α, β, and δ respectively. The equations (3.6), (3.7), (3.8), and (3.9) then define the final position of the ω wolves. It may also be observed that there are two vectors: \( \vec {A}\) and \(\vec {C}\) . These two vectors are random and adaptive vectors that provide exploration and exploitation for the GWO algorithm. As shown in Fig. 2, the exploration occurs when \(\vec {A}\) is greater than 1 or less than -1. The vector C also promotes exploration when it is greater than 1. In contrary, the exploitation is emphasized when |A| < 1 and C < 1 (see Fig. 2). It should be noted here that A is decreased linearly during optimization in order to emphasize exploitation as the iteration counter increases. However, C is generated randomly throughout optimization to emphasize exploration/exploitation at any stage, a very helpful mechanism for resolving local optima entrapment.

After all, the general steps of the GWO algorithm are as follows:

  1. a)

    Initialize a population of wolves randomly based on the upper and lower bounds of the variables

  2. b)

    Calculate the corresponding objective value for each wolf

  3. c)

    Choose the first three best wolves and save them as α, β, and δ

  4. d)

    Update the position of the rest of the population (ω wolves) using equations (3.3) to (3.9)

  5. e)

    Update parameters a, A, and C

  6. f)

    Go to step b if the end criterion is not satisfied

  7. g)

    Return the position of α as the best approximated optimum

Mirjalili et al. showed that the GWO algorithm is able to provide very competitive results compared to other well-known meta-heuristics [14]. For one, the exploration of this algorithm is very high and requires it to avoid local optima. Moreover, the balance of exploration and exploitation is very simple and effective in solving challenging problems as per the results of the real problems in [14]. The problem of training MLPs is considered as a challenging problem with an unknown search space, which is due to varying datasets and inputs that may be provided for the MLP. High exploration of the GWO algorithm, therefore, requires it to be efficient theoretically as an MLP learner. The following sections propose a GWO-based MLP trainer and investigate its effectiveness experimentally.

4 GWO-based MLP trainer

The first and most important step in training an MLP using meta-heuristics is the problem representation [36]. In other words, the problem of training MLPs should be formulated in a way that is suitable for meta-heuristics. As mentioned in the introduction, the most important variables in training an MLP are weights and biases. A trainer should find a set of values for weights and biases that provides the highest classification/approximation/prediction accuracy.

Therefore, the variables here are the weights and biases. Since the GWO algorithm accepts the variables in the form of a vector, the variables of an MLP are presented for this algorithm as follows:

$$ \overset{\rightarrow}{V}=\{\overset{\longrightarrow}{W},\vec{\theta}\}=\{W_{1,1},W_{1,2},\cdots,W_n,_n,h,\theta_1,\theta_2,\cdots,\theta_h\} $$
(4.1)

where n is the number of the input nodes, W i j shows the connection weight from the ith node in the input layer to the jth node in the hidden layer, θ j is the bias (threshold) of the jth hidden node.

After defining the variables, we need to define the objective function for the GWO algorithm. As mentioned above, the objective in training an MLP is to reach the highest classification, approximation, or predication accuracy for both training and testing samples. A common metric for the evaluation of an MLP is the Mean Square Error (MSE). In this metric, a given set of training samples is applied to the MLP and the following equation calculates the difference between the desirable output and the value that is obtained from the MLP:

$$ MSE=\sum\limits_{i=1}^{m}\left(o_{i}^{k}-d_{i}^{k}\right)^2 $$
(4.2)

where m is the number of outputs, \({d_{i}^{k}}\) is the desired output of the ith input unit when the kth training sample is used, and \({o_{i}^{k}}\) is the actual output of the ith input unit when the kth training sample appears in the input.

Obviously, an MLP should adapt itself to the whole set of training samples in order to be effective. Therefore, the performance of an MLP is evaluated based on the average of MSE over all the training samples as follows:

$$ \overline{MSE}=\sum\limits_{k=1}^{s}\frac{\sum\nolimits_{i=1}^{m} \left(o_{i}^{k}-d_{i}^{k}\right)^2}{s} $$
(4.3)

where s is the number of training samples, m is the number of outputs, \({d_{i}^{k}}\) is the desired output of the ith input unit when the kth training sample is used, and \({o_{i}^{k}}\) is the actual output of the ith input unit when the kth training sample appears in the input.

After all, the problem of training an MLP can be formulated with the variable and average MSE for the GWO algorithm as follows:

$$ Minimize: F(\vec{V})=\overline{MSE} $$
(4.4)

Figure 3 shows the overall process of training an MLP using GWO. It may be seen that the GWO algorithm provides MLP with weights/biases and receives average MSE for all training samples. The GWO algorithm iteratively changes the weights and biases to minimize average MSE of all training samples.

Fig. 3
figure 3

GWO provides MLP with weights/biases and receives average MSE for all traning samples

Full size image

The conceptual model of the way that search agents of the GWO algorithm train MLP is illustrated in Fig. 4.

Fig. 4
figure 4

Conceptual model of trainign MLP by search agents of GWO

Full size image

As may be seen in this figure, the variables of ω wolves have higher tendency to move toward α, β and δ respectively. This is the reasons that the next position of the ω wolf is closer to α and β. In other words, the contribution of the α wolf in re-defining the weights and biases of ω wolves is the highest. Fig. 4 shows that the number of weights and biases that turn to purple when the ω wolf moves is higher than β and δ. Less contribution of β and δ on the next position of the ω can are also clearly highlighted by blue and green colours in Fig. 4. It should be noted that although similar colours are used in Fig. 4, the weights and biases are not completely replaced by α, β and δ. In fact, a value between the values of the current weight/biases of ω are calculated using equation (3.9) and replaced with the current values.

Since the weights and biases tend to move toward the bests MLPs obtained so far, there would be a high probability of having an improved MLP in each iteration. With this method, there is no absolute guarantee for finding the most optimal MLP for a dataset using GWO due to the stochastic nature of this algorithm. Since we evolve MLPs using the best MLPs obtained so far in each iteration, however, the overall average MSE of the population is decreased over the course of iterations. In other words, GWO eventually converges to a solution that is better than the random initial solutions if this algorithm is iterated with an enough number of iterations.

The next section investigates the merits of the GWO algorithm in training an MLP in practice.

5 Results and discussion

In this section the proposed GWO-based MLP trainer is benchmarked using five standard classification datasets obtained from the University of California at Irvine (UCI) Machine Learning Repository [37]: XOR, balloon, iris, breast cancer, and heart. In addition there are three function-approximation datasets obtained from [38]: sigmoid, cosine, and sine.

5.1 Experimental setup:

The results are also compared with PSO, GA, ACO, ES [39–41], and Population-based Incremental Learning (PBIL) [42] for verification. It is assumed that the optimization process starts with generating random weights and biases in the range of [ −10,10] for all datasets. Other assumptions for the GWO and other algorithms are presented in Table 1.

Table 1 The initial parameters of algorithms
Full size table

Tables 2 and 3 show the specifications of the datasets. It may be observed in Table 2 that the easiest dataset is XOR with 8 training/test samples, 3 attributes, and two classes. The balloon dataset is more difficult that the XOR and has 4 attributes, 16 training samples, 16 test samples, and 2 classes. The Iris dataset has 4 attributes, 150 training/test samples, and three classes. In addition, the breast cancer dataset has 9 attributes, 599 training samples, 100 test samples, and 2 classes. Eventually, the heart dataset includes 22 attributes, 80 training samples, 187 test samples, and 2 classes. These classification datasets were deliberately chosen with different training/test samples and levels of difficulty to test the performance of the proposed GWO-based MLP trainer effectively. The difficulty of function-approximations datasets also are increased, in which the sigmoid is the easiest dataset and the sine is the hardest dataset.

Table 2 Classification datasets
Full size table
Table 3 Function-approximation datasets
Full size table

A similar problem representation and objective function is utilized to train MLPs with the algorithms in Table 1. The datasets are then solved 10 times using each algorithm to generate the results. The statistical results that are presented are average (AVE) and standard deviation (STD) of the obtained best MSEs in the last iteration by the algorithms. Obviously, lower average and standard deviation of MSE in the last iteration indicates the better performance. The statistical results are presented in the form of (AVE ±STD) in Tables 4, 6, 7, 8, 9, 10, 11 and 12. Please note that the best classification rates or test errors obtained by each of the algorithms during 10 runs are reported as another metrics of comparison.

Normalization is an essential step for MLP when solving datasets with attributes in different ranges. The normalization used in this work is called min-max normalization which is formulated as follows:

$$ X'= \frac{(x-a)\times(d-c)}{(b-a)}\,\, \,+\, \,\,{c} $$
(5.1)

This formula maps x in the interval of [ a, b] to [ c, d]

Another key factor in the experimental setup is the structure of MLPs. This work does not concentrate on finding the optimal number of hidden nodes and consider them equal to 2 × N + 1 where N is the number of features (inputs) of the datasets. The structure of each MLP that employed for each dataset is presented in Table 4.

Table 4 MLP structure for each dataset
Full size table

As the size of the neural network becomes larger, obviously, the more weights and biases would be involved in the system. Consequently, the training process also becomes more challenging.

5.2 XOR dataset:

As may be seen in Table 2, this dataset has 3 inputs, 8 training/test samples, and 1 output. The MLP for this dataset has to return the XOR of the input as the output. The statistical results of GWO, PSO, GA, ACO, ES, and PBIL on this dataset are presented in Table 5. Note that the training algorithms are named in the form of Alglorithm-MLP in the following tables.

Table 5 Experimental results for the XOR dataset
Full size table

The results show that the best average MSE belongs to GA-MLP and GWO-MLP. This shows that these two algorithms have the highest ability to avoid local optima, significantly better than other algorithms. GWO-MLP and GA-MLP also classifies this dataset with 100 percent accuracy. The GA-MLP algorithm is an evolutionary algorithm which has a very high level of exploration. These results show that the GWO-based trainer is able to show very competitive results compare to the GA-MLP algorithm

Another fact worth noticing here is the poor performance of ACO-MLP on this dataset. This might be due to the fact that this algorithm is more suitable for combinatorial problems.

5.3 Balloon dataset:

This dataset has 4 attributes, 18 training/test samples, and 2 classes. The trainers for this dataset have dimensions of 55. The results are provided in Table 6.

Table 6 Experimental results for the balloon dataset
Full size table

The first thing that can be observed in the results is the similar classification rate for all algorithms. This behaviour is due to simplicity of this dataset. However, the average and standard deviation of the MSE over 10 runs are different for algorithms. Similarly to the previous dataset, GWO-MLP and GA-MLP show the best local optima avoidance as per the statistical results of MSEs. This again justifies high performance of the GWO algorithm in training MLPs.

5.4 Iris dataset:

The Iris dataset is indeed one of the most popular datasets in the literature. It consists of 4 attributes, 150 training/test samples, and 3 classes. Therefore, the MLP structure for solving this dataset is of 4-9-3 and the problem has 75 variables. The results of training algorithms are presented in Table 7.

Table 7 Experimental results for the iris dataset
Full size table

This Table shows that the GWO-MLP outperforms other algorithms in terms of not only the minimum MSE but also the maximum classification accuracy. The results of GWO-MLP follow by those of GA-MLP and PBIL-MLP. Since the difficulty of this dataset and MLP structure is high for this dataset, these results are strong evidences for the efficiencies of GWO in training MLPs. The results testify that this algorithm has superior local optima avoidance and accuracy simultaneously.

5.5 Breast cancer dataset:

This dataset is another challenging well-known dataset in the literature. There are 9 attributes, 599 training samples, 100 test samples, and 2 classes in this dataset. As may be seen in Table 3, an MLP of 4-9-1 is chosen to be trained and solve this dataset. Therefore, every search agent of the trainers in this work have 209 variables to be optimized. This dataset is solved by the trainers 10 times, and the statistical results are provideed in Table 8.

Table 8 Experimental results for the breast cancer dataset
Full size table

The results of this table are consistent with those of Table 7, in which the GWO-MLP algorithm again shows the best results. The average and standard deviation provided by GWO-MLP proves that this algorithm has a high ability to avoid local minima and approximates the best optimal values for weights and biases. The second best results belong to GA-MLP and PBIL-MLP algorithms. In addition to MSEs, the best classification accuracy of the proposed GWO-MLP algorithm is higher than others. The breast cancer dataset has the highest difficulty compared to the previously discussed datasets in terms of the number of weights, biases, and training samples. Therefore, these results strongly evidence the suitability of the proposed GWO-MLP algorithm in training MLPs. For one, this algorithm shows high local optima avoidance. For another, the local search around to global optimum and exploitation are high.

It should be noted here that the classification rates of some of the algorithms are very small for this dataset because the end criterion for all algorithms is the maximum number of iteration. Moreover, the number of search agents is fixed throughout the experiments. Of course, increasing the number of iterations and population size would improve the absolute classification rate but it was the comparative performance between algorithms that was of interest. It was the ability of algorithms in terms of avoiding local minima in the classification that was the main objective of this work, so the focus was not on finding the best maximum number of iterations and population size.

5.6 Heart dataset:

The last classification dataset solved by the algorithms is the heart dataset, which has 22 features, 80 training samples, 187 test samples, and 2 classes. MLPs with the structure of 22-45-1 are trained by the algorithms. The results are reported in Table 9

Table 9 Experimental results for the heart dataset
Full size table

The results of this table reveal that GWO-MLP and GA-MLP have the best performances in this dataset in terms of improved MSE. The average and standard deviation of MSEs show that the performances of these two algorithms are very close. However, the classification accuracy of the GWO-MLP algorithm is much higher. Once more, these results evidence the merits of the proposed GWO-based algorithm in training MLPs.

5.7 Sigmoid dataset:

The sigmoid function is the simplest function employed in this work for approximation. It may be seen in Table 3 that there are 61 and 121 training and testing samples. The results of the algorithms are reported in Table 10.

Table 10 Experimental results for the sigmoid dataset
Full size table

This table shows that the best results are provided by the GWO-MLP algorithm. This shows that the proposed trainer can be also very effective in function-approximation datasets. The low AVE ±STD shows the superior local optima avoidance of this algorithm. The results also show that the best test error belongs the the GWO-MLP algorithm. This justifies the accuracy of this algorithm as well.

5.8 Cosine dataset:

The cosine dataset is more difficult than the sigmoid dataset, but the results of GWO-MLP follow a similar pattern in both datasets. Table 11 shows that once more the GWO-based trainer shows the best statistical results on not only the MSE but also the test error. The results of the GWO-MLP are closely followed by the GA-MLP algorithm.

Table 11 Experimental results for the cosine dataset
Full size table

5.9 Sine dataset:

The most difficult function-approximation dataset is the sine dataset. This function has four peaks that make it very challenging to be approximated. The results of algorithms on this dataset are consistent with those of other two function-approximation datasets. It is worth mentioning that the GWO-MLP algorithm provides very accurate results on this dataset as can be inferred from test errors in Table 12.

Table 12 Experimental results for the sine dataset
Full size table

5.10 Discussion and analysis of the results

Statistically speaking, the GWO-MLP algorithm provides superior local optima avoidance in six of the datasets (75%) and the best classification accuracy in all of the datasets (100%). The reason for improved MSE is the high local optima avoidance of this algorithm. According to the mathematical formulation of the GWO algorithm, half of the iterations are devoted to exploration of the search space (when |A| > 1). This promotes exploration of the search space that leads to finding diverse MLP structures during optimization. In addition, the C parameter always randomly obliges the search agents to take random steps towards/outwards the prey. This mechanism is very helpful for resolving local optima stagnation even when the GWO algorithm is in the exploitation phase. The results of this work show that although evolutionary algorithms have high exploration, the problem of training an MLP needs high local optima avoidance during the whole optimization process. This is because the search space is changed for every dataset in training MLPs. The results prove that the GWO is very effective in this regard.

Another finding in the results is the poor performance of PSO-MLP and ACO-MLP. These two algorithms belong to the class of swarm-based algorithms. In contrary to evolutionary algorithms, there is no mechanism for significant abrupt movements in the search space and this is likely to be the reason for the poor performance of PSO-MLP and ACO-MLP. Although GWO is also a swarm-based algorithm, its mechanisms described in the preceding paragraph are the reasons why it is advantageous in training MLPs.

It is also worth discussing the poor performance of the ES algorithm in this subsection. Generally speaking, the ES algorithm has been designed based on various mutation mechanisms. Mutation in evolutionary algorithms maintains the diversity of population and promotes exploitation, which is one of the main reasons for the poor performance of ES. In addition, selection of individuals in this algorithm is done by a deterministic approach. Consequently, the randomness in selecting an individual is less and therefore local optima avoidance is less as well. This is another reason why EA failed to provide good results in the datasets.

The reason for the high classification rate provided by the GWO-MLP algorithm is that this algorithm is equipped with adaptive parameters to smoothly balance exploration and exploitation. Half of the iteration is devoted to exploration and the rest to exploitation. In addition, the GWO algorithm always saves the three best obtained solutions at any stage of optimization. Consequently, there are always guiding search agents for exploitation of the most promising regions of the search space. In other words, GWO-MLP benefits from intrinsic exploitation guides, which also assist this algorithm to provide remarkable results.

According to this comprehensive study, the GWO algorithm is highly recommended to be used in hybrid intelligent optimization schemes such as training MLPs. Firstly, this recommendation is made because of its high exploratory behaviour, which results in high local optima avoidance when training MLPs. The high exploitative behaviour is another reason why a GWO-based trainer is able to converge rapidly towards the global optimum for different datasets. However, it should be noted here that GWO is highly recommended only when the dataset and the number of features are very large. Obviously, small datasets with very few features can be solved by gradient-based training algorithms much faster and without extra computational cost. In contrast, the GWO algorithm is useful for large datasets due to the extreme number of local optima that makes the conventional training algorithm almost ineffective.

6 Conclusion

In this paper, the recently proposed GWO algorithm was employed for the first time as an MLP trainer. The high level of exploration and exploitation of this algorithm were the motivations for this study. The problem of training an MLP was first formulated for the GWO algorithm. This algorithm was then employed to define the optimal values for weights and biases. The proposed GWO-based trainer was applied to five standard classification datasets (XOR, balloon, Iris, breast cancer, and heart) as well as three function-approximation datasets (sigmoid, cosine, and sine). For verification, the results of the GWO-MLP algorithm were compared to five other stochastic optimization trainers: PSO, GA, ACO, ES, and PBIL. The results showed that the proposed method is able to be very effective in training MLPs. For one, the GWO-MLP has very a high level of local optima avoidance, which enhances the probability of finding proper approximations of the optimal weights and biases for MLPs. Moreover, the accuracy of the obtained optimal values for weights and biases is very high, which is due to the high exploitation of the GWO-MLP trainer. This paper also identified and discussed the reasons for strong and poor performances of other algorithms. It was observed that the swarm-based algorithms suffer from low exploration, whereas the GWO does not.

For future work, it is recommended that the GWO algorithm be applied to find the optimal number of hidden nodes, layers, and other structural parameters of MLPs. Fine tuning of this algorithm is worth further research.