1 Introduction

Electric load forecasts play a crucial role in the electric power systems in all over the world (Hong and Fan 2016; Ravadanegh et al. 2016). Load forecasting leads the way about power system planning, energy trading, power system operation, etc. Since the early 1990s, the monopolistic way to conduct and govern the controlled power sectors has been reshaped by adding a deregulation structure and by the introduction of competitive markets (Weron 2014). Electricity trading is a hot topic, using market rules including spot and derivative contracts. However, electricity reveals a very special structure which is not stored and provides a balance between production and consumption (Soliman and Al-Kandari 2010; Khuntia et al. 2016). At the same time, electricity demand depends on weather (temperature, wind speed, humidity, etc.), the distribution of population (houses, industry, etc.) and the people’s life styles in intensity of business and everyday activities (on-peak vs. off-peak hours, weekdays vs. weekends, holidays and near-holidays, seasons, religious holidays, etc.) (Black and Henson 2014). These unique and specific characteristics lead to a change of the electricity demand needs to an adaptation of electricity supply. On the other side, they have led to a new research area for the development of more accurate and stable forecasting through characteristic techniques. At the same time, good forecasting on results allows for progress in the following matters: climate variability (global warming), joining electric vehicles to the power systems, wind, and solar power generation, the efficiency of energy and the response of electric demand.

Load forecasting methodologies consist of two main groups: statistical techniques and artificial intelligence techniques (Weron 2014; Khuntia et al. 2016; Liu et al. 2017). The boundary between these groups is quite ambiguous. In the literature commonly used, there are four statistical techniques, namely, multiple linear regression (MLR) models, semi-parametric additive models, autoregressive and moving average (ARMA) models, and exponential smoothing models; and four artificial intelligence (AI) techniques, namely, ANN, fuzzy regression models, support vector machines (SVMs) and, furthermore, there are gradient boosting machines (Hong and Fan 2016; Bezerra et al. 2017; Xie and Hong 2017). Multivariate adaptive regression splines (MARS) is a nonparametric and nonlinear technique from statistical learning which is used in modeling, regression, identification, prediction, forecasting, etc. (Friedman 1991). Artificial neural network (ANN) methodology is also a nonparametric learning and nonlinear technique which is used in those areas (Rumelhart et al. 1986; Rosenblatt 1962). Linear Regression (LR) is the earliest form of least-squares estimation in classification which has similar properties with ANN and MARS (Seber and Lee 2012; Montgomery et al. 2015). ANN, MARS, and LR provide powerful and very successful methods on forecasting constructions in related groups (Hastie et al. 2008; Vapnik 1998; Goude et al. 2014). Until now these three powerful methods have not been compared in load forecasting applications within power systems area of electrical engineering. It is expected that our project may inspire many researchers in this respect.

Load forecasting can be classified according to the time period addressed. An accurate standard is not determined yet for classifying the range of load forecasts. The forecasting processes may be classified into four categories: very short-term load forecasting (VSTLF), short-term load forecasting (STLF) (Saez-Gallego and Morales 2017), medium-term load forecasting (MTLF), and long-term load forecasting (LTLF) (Hong and Fan 2016). In this classification, VSTLF addresses a period up to 1 day, STLF is a period including 1 day–2 weeks, MTLF addresses a period from 2 weeks to 1 year, and LTLF refers to a period longer than 1 year. According to a rough classification, there are STLF periods till 2 weeks, and LTLF period succeeding 2 weeks (Wang et al. 2017).

LTLF is an important issue in effective and efficient power-system planning (Khuntia et al. 2016; Kandil et al. 2002; Xie et al. 2015). Sensitive estimation can greatly affect the road map of power system investments. Overestimation of the future load may lead to waste money in building new power generation units to supply this forecasting load. Underestimation of the future load may cause problems in supplying loads (Hong et al. 2014). Therefore, an accurate method is needed to forecast loads, as it leads to an accurate model that takes into account the factors which affect the growth of the load over a number of years.

LTLF is dependent on various factors like human habits and environmental influences. These factors can be classified to be time periods: hours of the day (day/night), day of the week (week day/weekend), time of the year (season), and holidays: furthermore they can be weather conditions (temperature, humidity and wind), class of customers and distribution of population, economic indicators, and electricity price (Xiao et al. 2016; De Giorgi et al. 2014; Black and Henson 2014; Hong et al. 2014). Measured weather parameters and load data are the most effective parameters in terms of accuracy of forecasting methods based on historical data (Khuntia et al. 2016).

The aim of our study is to present and underline the influence of powerful methodologies. It turns out that MARS is the best way, superior to the other two methods in load forecasting applications like energy purchasing and generation, load switching, contract evaluation, and infrastructure development (Chow et al. 2005). The input vectors used in the models are based on 5-year data consisting of hourly data, and as a result, 24 × 365 data for each year is composed of features such as humidity, temperature, load demand and wind speed. A matrix of \( \left[\left({(24 \times 365\,\left({{\text{hourly data}})} \right) \times \,5\,\left({\text{years}} \right)} \right),\,20\,({\text{other parameters}})\right] \) is obtained as input data, and all three models use the same input vectors. Other parameters can be expressed as date, year, month, day, including variations like weekend, hour, temperature, humidity, wind and electric demand variations, like previous electric demand, electricity demand on same day of previous week, etc. MARS, ANN and LR methods evaluate these input vectors in two main parts: as test and train. In the first part of our study, MARS, ANN and LR methods are introduced and explained clearly for understanding applications of the methods. In the second part, comparisons are presented between results obtained by MARS, ANN, and LR. A detailed error analysis and a comparison based on performance criteria are provided, too. For comparison purposes, the same data are used in all three models; their forms and structures are given below.

1.1 Multivariate adaptive regression splines (MARS)

In literature, regression, widely being used for prediction and forecasting, is mainly based on the methods of least-squares estimation, and maximum-likelihood estimation. There are many basic regression approaches: linear regression models, nonlinear regression models, generalized linear models, nonparametric regression models, additive models, and generalized additive models (Hastie et al. 2008; Vapnik 1998). MARS, an adaptive and nonparametric regression procedure proposed by Jerome Friedman, is particularly employed to estimate general functions of high-dimensional arguments (Friedman 1991). At the same time, MARS can be defined as a generalization of stepwise linear regression or a modification of classification and regression tree (CART) algorithm (Weber et al. 2012). There is no specific assumption about the underlying functional relationship between the dependent and independent variables in this procedure. MARS has the ability to estimate the contributions of the basis functions so that both the additive and the interactive effects of the predictors are allowed to determine the response variable (Kuter et al. 2014; Özmen and Weber 2014; Kuter et al. 2018; Cevik et al. 2017). MARS builds and includes expansions in terms of truncated piecewise linear basis functions (BFs) of the form (Seber and Lee 2012):

$$ c^{+} (x,\tau) = [x - \tau]_{+},\quad c^{-} (x,\tau) = [- x + \tau]_{+}, $$
(1)

where x, τ∊ ℝ. These two functions as shown in Fig. 1 can be named as a reflected pair. In the pair, the + symbol specifies only the positive parts used, and otherwise it is zero. Centering and scaling are not required but are suggested.

Fig. 1
figure 1

Details of 1-dimensional basis functions (based on Friedman 1991)

Full size image

MARS models are resistant to zero- and near-zero variance highly correlated predictors. But this can lead to a significant amount of randomness during the predictor selection process. The split choice between two highly correlated predictors becomes a fortunate chance. Let us consider the following general form of the model, including random variables and random vectors:

$$ Y = f\left(\varvec{X} \right) + \varepsilon,\quad \varvec{X} = \left({X_{1},\quad X_{2}, \ldots,\quad X_{p}} \right)^{T}. $$
(2)

The goal is to construct a set of reflected pairs for each input variables \( x_{j} \left({j = 1,2, \ldots,p} \right) \):

$$ \wp : = \{[x_{j} - \tau]_{+} [\tau - x_{j}]_{+} |\tau \in \{x_{1,j},x_{2,j},x_{3,j},\ldots,x_{N,j} \},\quad j \in \{1,2,\ldots,p\} \}. $$
(3)

Thus, Y can be represented within Eq. (2) by

$$ Y = \theta_{0} + \sum\limits_{m = 1}^{M} {\theta_{m}} T_{m} ({\text{X}}) + \varepsilon, $$
(4)

where Tm are basis functions from ℘ or products of two or more such functions. Interaction basis functions are created by multiplying an existing basis function with a truncated linear function involving a new variable. θ0 and θm are the coefficients estimated by minimizing the residual sum of squares. Furthermore, s may a strand for a selected sign ± 1. The v(j,m) labels the predictor variables and τjm represents values of the corresponding knots (Friedman 1991). Provided the observations represented by these data, the multi-dimensional basis functions look as follows:

$$ T_{m} ({\text{x}}) = \prod\limits_{j = 1}^{{K_{m}}} {\left[{s_{jm} \cdot \left({x_{v(j, m)} - \tau_{jm}} \right)} \right]}. $$
(5)

MARS algorithm is the union of two sub-procedures, named as the forward stepwise and backward stepwise algorithms, represented in Fig. 2.

Fig. 2
figure 2

Flowchart of MARS algorithm

Full size image

As shown in Fig. 2, forward stepwise algorithm produces typically an over-fitting of the data: therefore, a backward deletion procedure is applied afterwards. The backward deletion procedure or backward stepwise algorithm prevents from over-fitting by decreasing the complexity of the model without degrading the fit to the data. The procedure evaluates basis functions (BFs) and detracts from the model such BFs that contribute to the smallest increase in the residual squared error at each stage, producing an optimally estimated model fμ with respect to each number of some complexities of estimation terms, called μ. The optimal value of μ could be calculated with cross-validation according to the number of samples N, but MARS algorithm uses generalized cross-validation (GCV) for decreasing the computational burden. GCV can be defined as follows, and also be called as Lack-of-Fit (LOF):

$$ LOF(f_{\mu}) = GCV(\mu) = \sum\limits_{i = 1}^{N} {\frac{{(Y_{i} - f_{\mu} (\varvec{x}{}_{\varvec{i}}))^{2}}}{{(1 - M(\mu)/N)^{2}}}}. $$
(6)

Here, the dominator is related to some complexity of the estimation. The optimal value of M(μ) can be calculated using the following formula:

$$ M(\mu) = u + d \cdot K. $$
(7)

In Eq. (7), the number of independent basis functions is called u. Forward stepwise algorithm selects K which are the number of knots. The cost of optimal basis is defined with d. A larger M(μ) creates a smaller model with a smaller number of BFs, while a smaller M(μ) creates a larger model with more BFs (Weber et al. 2012). MARS algorithm creates a model which consists of vital non-repetitive basis functions. On the other side, MARS decreases the computational burden and provides ease of processing data. At the same time, the algorithm is very effective in forecasting applications.

1.2 Artificial neural network (ANN)

Neural networks are a branch of the field known as artificial intelligence which also includes case base reasoning, expert systems, and genetic algorithms (Barrow and Crone 2016a, b; Azad et al. 2014). An artificial neural network (ANN), discovered by Warren McCulloch and Walter Pitts, is a software (and also a hardware) simulation of a biological neuron to learn to recognize patterns in group data. An ANN is composed of a number of interconnected processing elements, changing their dynamic state response to external inputs. Neural networks give a better performance for making humanoid activities in fields such as speech processing, image recognition, machine vision, robotic control, forecast, state estimation, etc. (Rosenblatt 1962). ANNs are used for load-forecasting to model underlying physical power systems since the 1990s (Lee et al. 1992; Hippert et al. 2001). Feedforward neural networks, radial basis neural networks, and recurrent neural networks are commonly employed for load forecasting. Back-propagation algorithm is one of the most famous estimation algorithms on neural networks (Rumelhart et al. 1986).

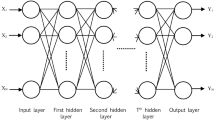
Neural networks occupy a significant place in model classification and learning methods (Rosenblatt 1962). They are generally used for complex data structure applications and include high-dimensional input data applications. In literature, an artificial neuron is a basic and vital part of an artificial neural network is a set of input values (I), associated weights (w), hidden layer function \( f\left(\varvec{x} \right) \) and an output results (Y). The simplest form of a neuron containing input, hidden and output layers is shown in Fig. 3. The number of neurons in the layers can be selected with different values. The input layer shapes the recorded values that are input values to the next layer, which is the hidden layer. Several hidden layers can exist in one neural network. A hidden layer contains transfer functions: sigmoid, threshold, piecewise linear, and Gaussian; they play a key role in learning. The final output layer includes one node for each class. Every iteration ending with an output node takes a value which is assigned to the related node with the highest value.

Fig. 3
figure 3

A simple neuron scheme in an artificial neural network

Full size image

The most critical structure in a neural network is the iterative learning process in which inputs are taken by the network one at a time; the defined weights according to inputs are arranged each time. The process is often repeated since all cases are presented. During this learning phase, the aim is to adjust weights to forecast the correct class label of inputs. Neural networks have a high tolerance to noisy data, which is a significant advantage. The other advantage is the ability to classify patterns on which neural networks have not been trained.

Back propagation algorithm, originally proposed in the 1970s, is the most popular neural network algorithm. But it became very popular after the 1980s (Rumelhart et al. 1986). The back propagation architecture is also shown in Fig. 3. Back propagation architecture, proposing effective nonlinear solutions to ill-defined models not to have clear goals, solution paths, or expected solution, is the most useful and famous architecture for complicated and multi-layered networks. Delta rule placed in this architecture plays a very important role in updating the weights and uses δ learning rate coefficient and γ error coefficient.

The classic back propagation network, where all of the layers are completely connected to the succeeding layers, is typically composed of a neuron which has an input, a hidden and an output layer. The number of hidden nodes in the hidden layer cannot be limited in theory, but it is generally chosen as 1 or 2 for simplicity in real applications. A feed-forward back propagation neural network formed multi-layer perceptron (MLP) is shown in Fig. 4. An MLP consisting of all the neural network properties and requirements is a feedforward artificial neural network model, and input data sets are dependent on a set of appropriate outputs (Özmen and Weber 2014). It uses a supervised learning technique, called backpropagation (Tsoi 1989). Actually, it is a modification of the standard linear perceptron and can distinguish data that are not linearly separable.

Fig. 4
figure 4

A feed-forward back propagation MLP neural network

Full size image

The basis of a training process is the Delta Rule which provides the calculation of the difference between the actual outputs and the desired outputs (Werntges 1990). According to this error, the weights are in proportion to the error times, which are a scaling factor for global accuracy. The weights are identified on the basis of the Delta Rule. This process proceeds until the desired output values are obtained. Training process can be completed as a result. In conclusion related to Delta Rule, we can express that most promising feature of ANN is its ability to learn.

1.3 Linear regression (LR)

Linear regression is the most basic and common predictive model to characterize the relationship between the variables (Vapnik 1998; Seber and Lee 2012). Differently from MARS, data types of the concept are linear. LR can be separated into two groups: simple linear and multiple linear regressions. Multiple linear regressions are represented by the following model:

$$ Y = \varvec{X}^{T}\varvec{\beta}+ \varepsilon . $$
(8)

In this equation, Y is a dependent random variable which can be either a continuous or a categorical value, \( \varvec{X} \) is an independent vector-valued random variable which usually is a continuous term: \( \varvec{\beta} \) consists of coefficient parameter at the input variables and of the intercept parameter. It is analyzed with probability distribution and mainly focuses on a conditional probability distribution with multivariate analysis (Vapnik 1998). In this paper, we focus on a simple linear regression in LR model. Simple linear regression represented in Fig. 5 is the process of prediction which implies a single independent variable; this is a univariate regression analysis as described in Eq. (8) (Papalexopoulos and Hesterberg 1990; Song et al. 2005).

Fig. 5
figure 5

Simple linear regression graph

Full size image

Simple linear regression represents the dependent and independent variables to extend a relationship between two variables, similar to correlation. However, correlation does not distinguish between the dependent and independent variables.

2 Load forecasting using MARS, ANN and LR models

In this paper, the three models assessed by MARS, ANN and LR are proposed for Turkish Electricity System which is shown in Fig. 6. Load data obtained from Turkish Electricity Transmission Company and weather data obtained from Turkish State Meteorological Service are used for LTLF in these models.

Fig. 6
figure 6

Turkish electricity system connections and substations (GENI)

Full size image

The weather data are very important for accuracy and stability of the forecast. In the light of the information, the data used for the models are composed of a 5 years period which addresses hourly load, wind, humidity and temperature information. Two main parts of our models, namely, train and test data periods, are reflected in Fig. 7, together with the kinds of the results, respectively.

Fig. 7
figure 7

Data distribution used underlying the three models

Full size image

The input variables are introduced subsequently:

  • \( x_{1}, x_{2}, \ldots,x_{14} \): lags of electricity demand (such as hourly, daily, weekly, and yearly) (in MW),

  • x15: all national and religious holidays,

  • x16: temperature data of the whole days,

  • x17: relative humidity (in %),

  • x18: wind speed (in m/s),

  • \( x_{19},x_{20}\): weekend.

Input variables carry a high importance in the process of forecasting. In this study, the data of 2 years (2011–2013) have been selected to train data, and the data of 2 years (2013–2015) have been chosen to be test data, in order to let the estimation come as near to reality as possible. All of the data are hourly data, such as the temperature of an hour, the wind of the same hour, etc. In our study, the models are evaluating the same data, and the time factor has been examined in detail because load demand according to time plays an active role in our future power system plans. For example, 1 day load, the previous week’s same day’s load, the previous month’s same day’s load, and the previous year’s same day’s load are dependent on each other deeply. In load forecasting applications, they give nearby information to us about the consumed energy at this day. Input data including these components lead us to a model which is more stable and accurate than a model including only 1 day’s input data.

MARS, ANN and LR models were generated in Salford MARS and MATLAB platforms, respectively. According to these platforms, the basis functions (BFs) of MARS are presented in Table 1.

Table 1 Basis functions obtained from MARS (underlined used for basis functions means that they are appearing in the MARS model)
Full size table

The output function of MARS is shown subsequently as the model:

$$ \begin{aligned} Y & = 0.27906 - 0.59038 \cdot BF_{1} + 0.366955 \cdot BF_{2} - 0.14653 \cdot BF_{3} + 0.00241 \\ & \quad \cdot BF_{4} + 0.00035 \cdot BF_{5} + 8.19874 \cdot BF_{7} + 0.0099 \cdot BF_{8} + 0.00852 \\ & \quad \cdot BF_{9} - 3.75608 \cdot BF_{10} + 1.13678 \cdot BF_{11} + 0.25186 \cdot BF_{12} - 0.45062 \\ & \quad \cdot BF_{13} - 0.07472 \cdot BF_{14} - 0.06809 \cdot BF_{15} + 2.2622 \cdot BF_{17} + 0.0074 \\ & \quad \cdot BF_{18} + 1.5972 \cdot BF_{19} - 0.80938 \cdot BF_{20} + 5.79473 \cdot BF_{21} - 14.7059 \\ & \quad \cdot BF_{22} - 0.00089 \cdot BF_{23} + 0.00036 \cdot BF_{24} - 0.95876 \cdot BF_{25} + 0.51112 \\ & \quad \cdot BF_{27} + 0.43774 \cdot BF_{28} - 0.3393 \cdot BF_{29} + 0.4595 \cdot BF_{30} + 0.91061 \\ & \quad \cdot BF_{31} + 0.00107 \cdot BF_{33} - 0.0036 \cdot BF_{34} + \varepsilon \\ \end{aligned} $$

ANN generates output results in the light of the hidden layer so that the output function for ANN does not occur. The output function of LR is shown in the following model:

$$ \begin{aligned} Y & = 0.07060 + 0.16284 \cdot x_{1} + 0.10330 \cdot x_{6} + 0.512226 \cdot x_{10} + 0.06197 \cdot x_{13} - 0.06162 \cdot x_{15} \\ & \quad - 0.000206 \cdot x_{16} - 0.000241 \cdot x_{17} + 0.001596 \cdot x_{18} - 0.008254 \cdot x_{19} - 0.019441 \cdot x_{20} + \varepsilon. \\ \end{aligned} $$

3 Comparison and evaluation criteria

Table 2 Analysis by evaluation criteria
Full size table

4 Results and comparison

The performance results of three models are represented in Table 3, using the abbreviations from Table 2.

As we may decide from Table 3, the R 2adj value (multiple coefficients of determination) of MARS training 0.907 is closer to 1, and this property is better than the ones for ANN and LR train. The AAE value of MARS being 1% is lower than for the others so that the value of any predicted data has a high reliability. The RMSE and MAPE values of MARS being 1.3 and 3.6% are also lower than the ones of the others; this provides us more accurate results. The r (correlation coefficient) value of MARS is higher than for the other two methods. Large correlation coefficients mean that there is a strong relationship. Stronger relationships will allow us to make more accurate predictions than weaker relationships can. In this comparison, train results of models are used, but test results of the models verify all of the comments, as learned from Table 3. Some of our results are shown in detail in Figs. 8 and 9.

Table 3 Comparison of MARS, ANN and LR results
Full size table
Fig. 8
figure 8

Average absolute error for MARS (red color), ANN (blue color) and LR (green color) based on train data (color figure online)

Full size image
Fig. 9
figure 9

Average absolute error for MARS (red color), ANN (blue color) and LR (green color) based on test data (color figure online)

Full size image

MARS is an adaptive method, which has the capacity to version nonlinearities between variables automatically. GCV criterion of MARS generates equilibrium between flexibility and generalization capability of the MARS model function (Cevik et al. 2017). It is known that the aforementioned characteristics of the method can better be observed with larger dataset like our problem dataset. However, the method was completely verified to be working for our problem.

5 Conclusion and outlook

In this paper, MARS, ANN and LR methods are discussed from an electrical engineering point of view, together with their novel application for the removal of meteorological and time effects on load forecasting applications. The models which we have achieved are not just long-term but also mid- and short-term load forecasting.

The main advantages of Multivariate Adaptive Regression Splines (MARS) are that it is a nonparametric, adaptive extension of decision trees (especially, of Classification and Regression Trees—CART) which is able to produce nonlinear models for regression and classification. MARS can be applied with no assumption about the underlying data distribution. In addition to this advantage, it gives better support for handling of data of mixed-type and missing values, computational scalability, dealing with irrelevant inputs, and interpretability than Linear Regression (LR) (Hastie et al. 2008).

When compared with another commonly method used in the field, Artificial Neural Networks (ANN), MARS is reported to be more computationally efficient (Zhang and Goh 2016). An additional drawback of ANN is that it behaves as models in the form of a ‘black box’ because of hidden layers (Cevik et al. 2017). MARS, like ANN, is also effective in modelling the interactions among variables.

Keeping these qualities in mind, these three powerful methods are also compared according to evaluation criteria, and we obtained the results stated subsequently:

  • Based on the evaluation criteria values of the methods, MARS has nearly a 96–97% accuracy. This result can be trusted for investments. MARS is suitable for high-dimensional applications, and the forecast accuracy increases to 98–99% as the historical data set increases.

  • MARS gives both BFs and an output equation so that our results are more clearly displayed. They are also more stable than ANN results which vary with the training of the network.

Within the light of our preliminary results, MARS seems to be an alternative and, in fact, very competitive tool for STLF, MLTLF, and LTLF, and it can be utilized for other problems related to electrical engineering as well. Future work will apply conic multivariate adaptive regression splines (CMARS) (Weber et al. 2012) and RCMARS (Robust CMARS: the refined version of CMARS by applying robust optimization to further address data uncertainty) (Özmen et al. 2011; Özmen 2016) on larger data sets, including 10 or 20 years of data, and to analyze and compare the method’s performance in detail.