Introduction

In subsurface modeling, several elements such as decision making with imperfect or incomplete data, the importance of the geological setting, and data play an important role in uncertainty modeling (Caers 2011). A major part of uncertainty is dependent on the distribution of subsurface geological and related parameters, resulting from limited samples (Wingle 1997). Increasing accuracy of modeling justifies complementary samples, but in order for these samples to be useful, they should not provide unnecessary and repetitive information. One of the main approaches for designing optimal sampling is geostatistical error management, which is used in many disciplines, such as mining, meteorology, geology, hydrology, soil science, ecology, and environmental science (Myers 1997). Kriging is an efficient geostatistical spatial interpolation method, which gives an unbiased estimation of the random variable with minimum variance (Juang et al. 2008; Lin et al. 2008). The geostatistical estimator, kriging, produces two corresponding values for each estimation: estimated grade and kriging estimation error (Hassanipak and Sharafodin 2004). At unsampled locations, kriging estimation error can be thought of as simply an optimally weighted average of the observations of the surrounding sampled locations (Juang et al. 1999). One approach to geostatistical error management is to minimize the kriging variance that could be reduced by drilling in areas of high error values. The kriging variance is a function of the sample pattern, sample density, the numbers of samples, and their covariance structure. It can be applied for evaluating the accuracy of estimation, selecting new input design samples, and global optimization of computer simulations. However, the kriging variance is independent of data values under the stationary spatial process, which this assumption is often violated in practice (Armstrong 1994; Delmelle 2011). The complementary boreholes are ranked one at a time or a set of them is selected based on minimizing the average kriging variance and the number of complementary boreholes. These techniques have been extended by simulation and optimization algorithms (Chou and Schenk 1983; Gershon et al. 1988; Szidarovszky 1983; Van Groenigen et al. 1999).

Data, which is commonly used in the mining evaluation to determine grade values in the large parts of a mineral deposit, can be obtained through core sampling. Grade distribution of a reserve can be estimated from the data, by kriging. Drilling the optimal additional boreholes can lead to improvement in the quality of grade estimation and the obtained geological information. Based on multiplicative function of grade, error, and thickness; complementary drillings are selected in regions associated with higher estimated productivity and subsequently higher estimated grade, ore thickness, and estimation error (Hassanipak and Sharafodin 2004).

The indicator approach was introduced by Journel (1983) to estimate the spatial distribution of ore and waste zones. Journel (1987, 1989) presents comprehensive literature review of the indicator approach. Thresholds (cutoffs) transform general variables into indicator variables. Indicator variables, which are used to convert qualitative data into quantitative data by assigning a value of 1 or 0, based on the presence or absence of a qualitative feature, or determining the position of a value relative to the selected thresholds (Sinclair and Blackwell 2002). The indicators are implemented to characterize structural analysis of the grade spatial distribution at various thresholds (Vann and Geoval 2003; Vann et al. 2002). The transformed distribution is binary, and so does not include extreme values (Glacken and Blackney 1998; Vann et al. 2002).

Fuzzy sets play an essential role in the solution of realistic problems and the realm of decision analysis, which are applied in many disciplines: artificial intelligence, computer science, control engineering, decision theory, expert systems, logic, etc. (Zimmermann 2001). The fuzzy set theory can provide a calculus for handling the incompleteness, imprecision, uncertainty, and vagueness of the information in database (Zadeh 2008). Since the grade estimation involves error and point threshold sharply separates data into two classes, applying fuzzy interval thresholds rather than sharp (point) thresholds is recommended.

In the present study, both the fuzzy terminology indicator weighted average (IWA) and class membership degree (CMD) are utilized to transform thresholds from crisp number to fuzzy number. IWA represents the fuzzy indicator value of each block based on interval threshold with fuzzy membership function. CMD determines the membership degree of each block allocating to a distinct class. Fuzzy interval thresholds are implemented to calculate the membership degree of each class by determining IWA in a three-dimensional space. In this way, to obtain the objective function, the preference functions for each ore iron (Fe) and gangue phosphorus (P) variables have been determined and kriging variance is multiplied by their weights.

The preference function is a kind of value function that is applied to transform grade to the relative value of ore iron (Fe) and gangue phosphorus (P) variables based on different thresholds. Ore value is calculated by the sum of multiplying CMDs with preference function outputs for Fe and P variables. The objective function is a multiplicative function of kriging variance with the ore value which is the basis for complementary boreholes designing.

Description of the problem and offering solutions

Subsurface modeling requires sufficient information from exploration drilling. However, this process often faces two challenges. First of all, if the number of holes is more than what is needed, part of the gathered data will be redundant, leading to budget waste. On the other hand, if the number of holes is less than what is needed, part of the required information might be missing, which in turn would result in an inaccurate model.

To resolve the problem, this paper presents a novel method for designing an optimal complementary drilling scheme between the primary drilling network. The proposed method calculates the optimal layout of complementary drillings in a three-dimensional space by applying high objective function values, which are related to ore values and kriging variances. This paper briefly describes all the required steps to design a complementary drillings scheme (Fig. 1).

Fig. 1
figure 1

Flowchart of proposed method for designing a complementary drillings scheme

Full size image
  1. Step 1

    Data preparation: After entering the input data, which relate to Fe and P variables from boreholes, statistical summary parameters and the probability distribution of variables are calculated.

  2. Step 2

    Geostatistical modeling: The semivariograms are calculated for Fe and P variables in different directions. Anisotropy model is identified followed by directional variography. Kriging is used for prediction of these variables in three-dimensional space, considering the search space according to anisotropic variogram models.

    Note. Based on the measure of deviation from stationarity, two approaches can be considered. In the homogeneous space, the mean behavior of the entire area represents a spatial variation with assuming local stationarity of the neighboring data samples. In the heterogeneous space, the study area is divided into an optimal number of zones to separately model spatial statistics of each zone, and merge the results of these zones by considering the type of inter-zone relationships (boundaries) (Wingle 1997). In the heterogeneous case, the number of zones, confine of each zone, and type of boundary between zones (sharp, gradational or fuzzy) are determined using geological database. Then, the data samples are assigned to corresponding zone and all steps of the geostatistical modeling (variography, anisotropy modeling, and zonal kriging) are separately computed for each zone (estimation unit).

  3. Step 3

    Interval threshold: Thresholds for input data are defined and converted to interval thresholds by using fuzzy membership functions. IWA is used to calculate the average value of the indicators with different levels of membership degrees.

  4. Step 4

    Ore classification: Blocks are classified based on one threshold for Fe and two thresholds for P (there are two classes for Fe and three classes for P). Combining the existing conditions for Fe and P (indicator Fe and P) generates six classes.

  5. Step 5

    Functional modeling: Interval threshold approach is applied on the kriging estimation of Fe and P variables, and then preference functions of these variables transform grade to a definite scale and express how an increase or decrease in grade translate into the value fluctuation. Ore value for each block is calculated by a multiplicative function of preference output by its corresponding membership degree. The objective function consists of two sub-objectives (maximizing ore value and kriging variance) to locate the positions having high ore and information values.

  6. Step 6

    Designing drilling layout: 3D poles with high objective function values are candidates for complementary drillings; each pole centroid potentially suggests one vertical drilling and the hypothetical line will intersect the pair of pole centroids represent a potential directional borehole. The layout of the feasible complementary borehole map with coordinates, azimuth, and dip parameters is defined based on limitations in length and dip of boreholes. The length and drilling priority of these boreholes are determined by surveying of objective function along drilling axis.

Case study: Choghart iron deposit

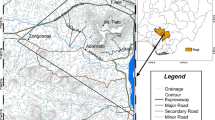
The Choghart iron deposit, the most famous iron mine of Central Iran, is selected as the case study for the proposed method. The Choghart apatite-bearing iron oxide deposit (55° 28′ 2″ E, 31° 42′ 00″ N) is located in the Bafq mining area, 125 km southeast of the city of Yazd (Fig. 2). There are more than 80 identified magnetic anomalies in the Bafq mining area. Choghart is the biggest and the most valuable deposit of its type explored so far in this area (Moor and Modabberi 2003).

Fig. 2
figure 2

Location of Choghart iron deposit in the Bafq mining area of Iran

Full size image

Geology of Choghart

The geometry of the Choghart ore-body is roughly vertical, asymmetric, and pipe-shaped. The basement of Choghart deposit contains metamorphosed Precambrian continental Chapedony Complex and Morad Series that are overlain by volcano-sedimentary units of Eocambrian Esfordi Formation. Different types of volcanic (intrusive and extrusive alkali rhyolites) and metamorphous rocks occur in the vicinity of the deposit. A major component of intrusive rocks is syenitic, but pyroxenite, gabbro, and even granitic patches are also recognized. The intrusive assemblage is encircled by alkali rhyolites (Moor and Modabberi 2003).

Structural features played an important role in the formation of magnetite-apatite deposits. Existing faults lead to a northwest-southeast alteration, displacements, and brecciation of the Choghart deposit. The lower part of this deposit mainly contains massive magnetite accompanied by ancillary minerals which include apatite, pyrite, alkali amphiboles (mainly actinolite and tremolite), calcite, talc, quartz, monazite, davidite, and allanite. Magnetite and apatite are respectively the most abundant ore and gangue at Choghart. The magnetite-apatite and magnetite-silicate ores are the most and least abundant ore types, respectively.

The Choghart iron deposit is classified into different groups according to 45 % threshold for Fe and 1 % and 10 % thresholds for P, respectively: (1) high-grade ore, non-oxidized and low phosphorus; (2) high-grade ore, oxidized and low phosphorus; (3) high-grade ore, non-oxidized and high phosphorus; and (4) high-grade ore, oxidized and high phosphorus (Asghari et al. 2009; Moor and Modabberi 2003; Samani 1988). The geological map of Choghart deposit is presented in Fig. 3.

Fig. 3
figure 3

Geological map of Choghart deposit (Moor and Modabberi 2003)

Full size image

Data sets

The first step in data modeling is studying the elementary statistical parameters. Descriptive statistics are usually used for reviewing and explaining the major features of a data set quantitatively. The statistical summary parameters of Fe and P in the Choghart deposit are presented in Table 1, including maximum, minimum, mean, mode, median, standard deviation (SD), skewness, kurtosis, and 25 and 75 percentiles. Statistical results show that Fe and P mean values are 58 and 0.46 %, respectively. Variation between maximum and minimum values of variables for these data shows a wide range. Histogram of data shows that Fe and P variables are not normally distributed. The normal score transformation was applied on the original data to make the transformed data normally distributed. Figure 4 shows the probability mass function of these variables, using the histogram in the form of the original data and data transferring into standard normal distribution.

Table 1 Descriptive statistical characteristics of Fe and P variables
Full size table
Fig. 4
figure 4

a Fe and P original data histogram, b Fe and P standard normal distribution data histogram

Full size image

One hundred thirty-seven vertical and directional boreholes, with an irregular drilling network, were bored in the Choghart deposit area. Fe and P are variables in a given data set in the isotopic case (i.e., data is available for each variable at all core sampling points). Figure 5 demonstrates the pattern of exploratory boreholes network and distributions of Fe and P in a three-dimensional space.

Fig. 5
figure 5

Location of boreholes and grade distribution in different depth of boreholes a Fe, b P

Full size image

Geostatistical approach

Geostatistical methods are sets of tools that are applied to characterize the spatial variation of regional variables for reserve estimation, classification, simulation, and design of optimal sampling strategies (Hassanipak and Sharafodin 2004). Geostatistical techniques provide the spatial distribution of the variable at unsampled locations, and uncertainty in terms of variance of the conditional distribution. The characterization and evaluation of this spatial variability, is found through calculating the variogram model fitting, anisotropy modeling and geostatistical estimation, such as kriging (Deutsch and Journel 1998; Goovaerts 1997; Sinclair and Blackwell 2002).

Variography

Variogram can be applied in kriging within each of the geological units based on composite data (Keogh et al. 1995). An experimental semivariogram for an interval lag distance class h is represented by Eq. (1):

$$ \gamma (h)=\frac{1}{2N(h)}{\displaystyle \sum_{i=1}^{N(h)}{\left[Z\left(x+h\right)-Z(x)\right]}^2} $$
(1)

where h denotes the lag distance that separates pairs of points; the quantity γ(h) is known as the semivariance at lag h, Z(x) denotes the random variable at the location x; Z(x + h) denotes the random variable at the location (x + h); and N(h) represents the number of pairs separated by the lag distance h (Deutsch and Journel 1998; Webster and Margaret 2007). Due to the volume variance effect, borehole samples need to be composited to an equal length. With regard to modeling of spatial structure, three-dimensional experimental semivariograms of Fe and P were computed for 24 directions, using composite data. For both variables, exponential semivariogram models are fitted in the directions having maximum range and the strongest spatial continuity. These models have the best fits to the empirical semivariogram. The nugget effect of the Fe model is larger than that of P and the semivariogram range of P model is larger than Fe. Figure 6 shows experimental semivariograms with fitting models for Fe and P variables.

Fig. 6
figure 6

Variograms and fitted models for Fe in: a major direction, b semi-major direction, c minor direction, and P in: a major direction, b semi-major direction, c minor direction

Full size image

Anisotropy modeling

Due to the significant role of anisotropy in the estimation process, it should be modeled as accurately as possible (Hassanipak and Sharafodin 2004). In Choghart iron deposit, the geological formations with various rock units and structural features caused the anisotropy of grade distributions. The semivariograms calculated for various directions are used to obtain dimensional and directional properties of the anisotropy ellipsoid and demonstrate the existence of anisotropy and what form it takes. These estimation stages provide a basis for interpreting the causes of spatial variation and for identifying some of the controlling factors and processes (Hekmat et al. 2013; Myers and Journel 1990; Webster and Margaret 2007). In this research, experimental three-dimensional semivariograms were computed in 24 directions based on directional parameters of geological structure and deposit, then the anisotropy factors are defined as the ratio of major range to semi-major range and ratio of major range to minor range. The anisotropy ellipsoids of Fe and P variables are modeled with anisotropy factors, azimuth, plunge, and dip of major range (Table 2). For these variables, search volume represents an almost horizontal ellipsoid with an anisotropy factor (major to minor axis) of about 1.9. Fe and P major axis orientations are 172° and 200°, respectively.

Table 2 Anisotropy ellipsoid parameters of Fe and P variables
Full size table

Ordinary kriging of ore variables

A modified kriging procedure named ordinary kriging was applied. Kriging is used to estimate two values: (1) the value of a random variable at unsampled locations, and (2) the related estimation error (Olea 2009; Webster and Margaret 2007). The estimated value of Z at a block V (Z*(V)) is given by the weighted average of N values of Z (Eq. 2):

$$ {Z}^{*}(V)={\displaystyle \sum_{i=1}^N{\lambda}_iZ\left({x}_i\right)} $$
(2)

where the kriging weights (λ i ) sum to 1. Based on non-bias constraints and minimization of the estimation variance, the ordinary block kriging variance (σ 2obk ) is given by Eq. (3):

$$ {\sigma}_{\mathrm{obk}}^2=2{\displaystyle \sum_{i=1}^n{\lambda}_i\overline{\gamma}\left({x}_i,V\right)}-{\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^n{\lambda}_i{\lambda}_j\gamma }}\left({x}_i-{x}_j\right)-\overline{\gamma}\left(V,V\right) $$
(3)

where \( \overline{\gamma}\left({x}_i,V\right) \) is the average semivariance between data points x i and block V, and \( \overline{\gamma}\left(V,V\right) \) is the average semivariance within V, the within-block variance (Deutsch and Journel 1998; Oliver 2010; Webster and Margaret 2007). The construction of directional variogram models determines the anisotropic ellipsoids which in turn use in the ordinary kriging estimation of the Fe and P variables. Grid dimensions in 2D space were limited by ranges of variograms in two perpendicular directions along a 2D grid (anisotropy modeling) and boreholes layout. The third dimension of the grid (block thickness) is related to mine planning conditions and the ore and waste vertical thickness distributions (Badel et al. 2011; Hekmat et al. 2013). Using this method, the three dimensions of blocks were determined as 20 m × 20 m × 12.5 m. Figure 7 shows the three-dimensional spatial distribution of Fe and P variables.

Fig. 7
figure 7

3D block modeling of grade spatial distribution a Fe, b P

Full size image

Using thresholds of grades to classify deposit

There are different geostatistical techniques that provide ore spatial distribution using a cutoff grade (Vann and Geoval 2003). Geoscience data (such as geological observations and drill core grades) may be interpreted into indicators which are interpolated by geostatistical methods (Marshall and Glass 2012). Fe and P are the most abundant ore and gangue elements at Choghart, respectively, and thresholds of grades were defined for both of the elements. Based on the thresholds, only three values for classes (positive, neutral, or negative) may occur. In Choghart mine, Fe grade is classified with one threshold, 45 %; the Fe quantities with more than 45 % have positive values and Fe quantities with less or equal to 45 % have neutral values. P grade is classified with two thresholds, 1 and 10 %; the P quantities with more than 10 % are positive and P quantities with less or equal to 1 % are neutral. P quantities between 1 and 10 % or equal to 10 % are negative. Choghart mine experts consider a rock with P grade more than 10 % as a valuable phosphorus bearing deposit. Figure 8 shows the three-dimensional distribution of Fe and P classes. The indicators of Fe and P, (I(Fe), I(P)) are defined by Eq. (4):

Fig. 8
figure 8

3D block modeling of indicators (classes spatial distribution) a Fe, b P

Full size image
$$ I\left(\mathrm{F}\mathrm{e}\right)=\left\{\begin{array}{l}1\kern2.25em \mathrm{F}\mathrm{e}\le 45\\ {}2\kern2.25em \mathrm{F}\mathrm{e}>45\end{array}\right. $$
(4.1)
$$ I\left(\mathrm{P}\right) = \left\{\begin{array}{l}1\kern2.25em \mathrm{P}\le 1\\ {}2\kern2.25em 1<\mathrm{P}\le 10\\ {}3\kern2.25em \mathrm{P}>10\end{array}\right. $$
(4.2)

Fuzzy interval threshold definition

Fuzzy set theory is one of the theories which is applied to reason and make rational decisions in an environment of imperfect information. The fuzzy approach can be considered as a tool to present approximate solution of real problems in an efficient way (Zadeh 2008; Zimmermann 2001). A point threshold results in two classes separated by the threshold value as a crisp boundary. However, since error in grade estimation is inevitable, it is necessary to choose a fuzzy interval threshold. We did this by defining fuzzy membership functions instead of a point threshold. A triangular fuzzy number μ i (based on the linear relationship between grade and membership degree) was selected for modeling the interval threshold. Triangular fuzzy number (TFN) has a simple form, yet a high justification membership function and it is most commonly applied in different branches of science such as geosciences (Demicco and Klir 2004; Taboada et al. 2006).

The lower and upper limits of the fuzzy interval threshold are determined based on equal data percentage frequency through both sides of the threshold in a histogram. In this paper, membership functions of Fe and P are determined by 5 % of the data frequency both the lower and upper limits of the threshold, but if the percentage of data frequency is lower than (5 %), the upper limit extends to the maximum of data (Fig. 9). The lower and upper limits of membership around each threshold for both variables are calculated. The decision maker can be modified the percentage of data frequency (lower and upper limits) with regard to conservative and fuzziness degrees.

Fig. 9
figure 9

Histogram of variables with side ranges around threshold a Fe, b P

Full size image

Computing the fuzzy measures IWA and CMD

To define fuzzy interval, membership degree at the exact value of threshold equals 1, and decreases to 0 along the lower and upper limits that could be calculated from equal percentage frequency in the histogram. Figure 10 shows the interval threshold membership function of Fe defined by parameters [42.46; 45; 47.20] and for P defined by parameters [0.85; 1; 1.22] and [6.56; 10; 22.5]. If the data distributions around both limits of cutoff grade are similar, the lower and upper limits will be equal. Interval threshold membership functions of Fe and P are computed by Eq. (5):

Fig. 10
figure 10

Threshold membership function for defining interval threshold a Fe, b P

Full size image
$$ {\mu}_{\mathrm{Fe}}=\left\{\begin{array}{l}1-\frac{\left(45-\mathrm{F}\mathrm{e}\right)}{2.54}\kern1.5em 42.46<\mathrm{F}\mathrm{e}\le 45\\ {}1-\frac{\left(\mathrm{F}\mathrm{e}-45\right)}{2.20}\kern1.5em 45\le \mathrm{F}\mathrm{e}<47.2\end{array}\right. $$
(5.1)
$$ {\mu}_P=\left\{\begin{array}{l}1-\frac{\left(1-\mathrm{P}\right)}{0.15}\kern2.75em 0.85<\mathrm{P}\le 1\\ {}1-\frac{\left(\mathrm{P}-1\right)}{0.22}\kern2.75em 1\le \mathrm{P}<1.22\\ {}1\hbox{-} \frac{\left(10-\mathrm{P}\right)}{3.44}\kern2.75em 6.56<\mathrm{P}\le 10\\ {}1-\frac{\left(\mathrm{P}-10\right)}{12.5}\kern2.5em 10\le \mathrm{P}<22.5\end{array}\right. $$
(5.2)

The fuzzy interval threshold provides the interval indicators for membership degrees (α-cuts) 0.25 to 1 with interval 0.25. Indicator weighted average (IWA) presents the fuzzy indicator value of each block based on interval threshold and membership degree. Figure 11 schematically displays how IWA was calculated for each interval threshold and this can be generalized for each variable with different numbers of interval thresholds. IWA is calculated by the sum of multiplication the indicator values and theirs corresponding membership degrees divided by the sum of membership degrees. The values of IWA for two consecutive classes (C j , and C j+1), n membership degrees (α-cuts), and corresponding grades (G(μ i )) for each threshold are computed using Eq. (6):

Fig. 11
figure 11

Schematic of calculation indicator weighted average by interval threshold

Full size image
$$ \mathrm{I}\mathrm{W}\mathrm{A}{\left[G\left({\mu}_i\right)\right]}_{{C_j}_{+1}}^{C_j}=\frac{{\displaystyle \sum_{i=1}^n{\mu}_i\times I\left[G\left({\mu}_i\right)\right]}}{{\displaystyle \sum_{i=1}^n{\mu}_i}},\ {C}_j\le \mathrm{I}\mathrm{W}\mathrm{A}{\left[G\left({\mu}_i\right)\right]}_{{C_j}_{+1}}^{C_j}\le {C_j}_{+1} $$
(6)

For cases with more than one point (sharp) threshold, the interval threshold with corresponding grade thresholds is generalized around each point threshold. Figure 12 shows the histogram of IWA values for Fe and P variables. Three-dimensional presentation of IWA values for Fe and P variables that were produced from fuzzy boundary instead of the sharp boundary in the transition zone between two classes (Fig. 13). The lower and upper limits of membership have a direct effect on the propagation of the transition zone.

Fig. 12
figure 12

Histogram of indicator weighted average value, a Fe, b P

Full size image
Fig. 13
figure 13

3D block modeling of indicator weighted average value spatial distribution a Fe, b P

Full size image

Class membership degree (CMD) is linear change of the membership degree of each block based on its grade; also ore value is introduced as a linear function of the grade. Hence, the linear relationship is considered between ore value and CMD. In addition, the triangular fuzzy number can be defined CMD value with linear changing of membership degree versus grade. The outputs of IWA have two probable forms: positive integer or rational number between two consecutive positive integers. If IWA is a positive integer (C j , or C j+1 class value), the membership degree of this class (CMD) will be equal 1 and the membership degree of other classes will be equal 0. If IWA is a positive rational number (between C j , and C j+1 class values), the membership degrees of two consecutive positive integer class are computed by considering the relative closeness of rational number two to integers within a range of 0 to 1 (Eq. 7). Figure 14 shows membership degree of each class for different grades of Fe and P.

Fig. 14
figure 14

Variation of membership degree for classes versus grade a Fe, b P

Full size image
$$ \mathrm{C}\mathrm{M}\mathrm{D}=\left\{\begin{array}{l}{C_j}_{+1}-\mathrm{I}\mathrm{W}\mathrm{A}{\left[G\left({\mu}_i\right)\right]}_{{C_j}_{+1}}^{C_j}\kern1.75em C\in {C}_j\\ {}\mathrm{I}\mathrm{W}\mathrm{A}{\left[G\left({\mu}_i\right)\right]}_{{C_j}_{+1}}^{C_j}-{C}_j\kern2.5em C\in {C_j}_{+1}\end{array}\right. $$
(7)

Whenever the CMD varies from 0 to 1, we can compute equivalent grade of each CMD for Fe and P variables with pseudo-defuzzification functions, which are the conversion and interpretation of the membership degrees of the fuzzy number into a specific decision or numerical value in the normalized space. These functions are defined based on the complement of fuzzy interval threshold. If CMD of the sample equals to 1, output grade of pseudo-defuzzification functions and output grade of kriging will be equal (Eq. 8). The relation between CMD and grades of Fe and P is presented in Fig. 15.

Fig. 15
figure 15

Relation between class membership degree and grade for different class a Fe, b P

Full size image
$$ {G}_{\mathrm{Fe}}\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)=\left\{\begin{array}{l}45-2.54\times \left(\mathrm{C}\mathrm{M}\mathrm{D}\right)\kern2.25em 0<\mathrm{C}\mathrm{M}\mathrm{D}<1,\ \mathrm{C}\in 1\\ {}45+2.2\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)\kern3.25em 0<\mathrm{C}\mathrm{M}\mathrm{D}<1,\ \mathrm{C}\in 2\\ {}\mathrm{G}\left(\mathrm{Primary}\right)\kern4.5em \mathrm{C}\mathrm{M}\mathrm{D}=1\end{array}\right. $$
(8.1)
$$ {\mathrm{G}}_{\mathrm{P}}\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)=\left\{\begin{array}{l}1-0.15\times \left(\mathrm{C}\mathrm{M}\mathrm{D}\right)\kern2.5em 0<\mathrm{C}\mathrm{M}\mathrm{D}<1,\ \mathrm{C}\in 1\ \\ {}1+0.22\times \left(\mathrm{C}\mathrm{M}\mathrm{D}\right)\kern2.25em 0<\mathrm{C}\mathrm{M}\mathrm{D}<1,\ \mathrm{C}\in 2,\ 1<\mathrm{I}\mathrm{W}\mathrm{A}\left[\mathrm{G}\left({\mathrm{M}}_i\right)\right]<2\\ {}10-3.44\times \left(\mathrm{C}\mathrm{M}\mathrm{D}\right)\kern2em 0<\mathrm{C}\mathrm{M}\mathrm{D}<1,\ \mathrm{C}\in 2,\ 2<\mathrm{I}\mathrm{W}\mathrm{A}\left[\mathrm{G}\left({\mathrm{M}}_i\right)\right]<3\\ {}10+12.5\times \left(\mathrm{C}\mathrm{M}\mathrm{D}\right)\kern2em 0<\mathrm{C}\mathrm{M}\mathrm{D}<1,\ \mathrm{C}\in 3\\ {}\mathrm{G}\left(\mathrm{Primary}\right)\kern4.25em \mathrm{C}\mathrm{M}\mathrm{D}=1\end{array}\right. $$
(8.2)

Two CMD values occurred in the area of one interval threshold and a corresponding grade is generated for each class in this threshold. When we face more than one threshold, two CMD values are studied and the other CMD values are zero. For this case, second and third classes of P are calculated based on the second interval threshold of P and the first CMD value equals to 0. Figure 16 compared kriging output values with IWA outputs (Eqs. (8.1) and (8.2)) of Fe and P for different classes.

Fig. 16
figure 16

Cross plot of kriging and IWA outputs for different classes a Fe, b P

Full size image

Classifying ore deposit based on fuzzy thresholds

With reference to Eqs. (5.1) and (5.2), for one threshold for Fe and two thresholds for P, there are two classes for Fe and three classes for P. Combining the existing conditions for Fe and P (indicator (Fe, P)) generates six classes as shown in Eq. (9) and class values increase from first class to sixth class (Fig. 17). In Fig. 18, the cross plot of Fe and P variables is presented the distribution of mentioned six classes, although the set of variables is not intrinsically correlated. The spatial distribution of six classes is presented by block model in Fig. 19. The six classes are described as follows:

Fig. 17
figure 17

Schematic illustration for defining six classes based on I(Fe, P)

Full size image
Fig. 18
figure 18

Cross plot of P versus Fe for six classes

Full size image
Fig. 19
figure 19

3D view of spatial distribution of six classes

Full size image

  • 1st class includes the neutral value of Fe and negative value of P.

  • 2nd class includes the neutral value of Fe and neutral value of P.

  • 3rd class includes the neutral value of Fe and positive value of P.

  • 4th class includes the positive value of Fe and negative value of P.

  • 5th class includes the positive value of Fe and neutral value of P.

  • 6th class includes the positive value of Fe and positive value of P.

$$ I\left(\mathrm{F}\mathrm{e},\mathrm{P}\right)=\left\{\begin{array}{l}1\kern2.5em \mathrm{F}\mathrm{e}\le 45\ \mathrm{and}\ 1<\mathrm{P}\le 10\\ {}2\kern2.25em \mathrm{F}\mathrm{e}\le 45\ \mathrm{and}\ \mathrm{P}\le 1\ \\ {}3\kern2.25em \mathrm{F}\mathrm{e}\le 45\ \mathrm{and}\ \mathrm{P}>10\\ {}4\kern2.25em \mathrm{F}\mathrm{e}>45\ \mathrm{and}\ 1<\mathrm{P}\le 10\\ {}5\kern2.25em \mathrm{F}\mathrm{e}>45\ \mathrm{and}\ \mathrm{P}\le 1\ \\ {}6\kern2.25em \mathrm{F}\mathrm{e}>45\ \mathrm{and}\ \mathrm{P}>10\end{array}\right. $$
(9)

In order to determine the CMD of each of these six classes, we used multiplicative functions of corresponding CMD values of Fe and P, with the assumption that CMD for Fe and P are independent. Figure 20 shows a three-dimensional distribution of the membership degrees of the blocks to each class from 1 to 6. For any samples (blocks), six terms of CMD were computed by Eq. (10), however, the quantity of these CMD may be zero or non-zero.

Fig. 20
figure 20

3D presentation and spatial distribution of membership of each class

Full size image
$$ \begin{array}{l}{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_1={\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}(1)}\times {\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}(2)}\\ {}{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_2={\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}(1)}\times {\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}(1)}\\ {}{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_3={\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}(1)}\times {\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}(3)}\\ {}{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_4={\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}(2)}\times {\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}(2)}\\ {}{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_5={\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}(2)}\times {\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}(1)}\\ {}{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_6={\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}(2)}\times {\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}(3)}\end{array} $$
(10)

Functional modeling of Fe and P variables

For each criterion, the preference function translates the difference between the evaluations obtained by two alternatives into a preference degree varying from zero to one (Behzadian et al. 2010). The Preference functions of Fe and P are defined based on ore value fluctuation for different thresholds. These functions transform the grade into the preference degree within a range of 0 to 1, using coefficients 0.01. The Fe preference function (P (G Fe)) has neutral behavior in a range of [0 %; 45 %] and positive value within a range of (45 %; 100 %], the value of which preference function increased from 0.45 to 1 with a constant slope. Neutral part of P preference function (P (G P)) occurs within a range of [0 %; 1 %] and this function has a negative value within a range of (1 %; 10 %] and positive value within a range of (10 %; 100 %]. Eq. (11) presents the preference function of Fe and P variables.

$$ \mathrm{P}\left({G}_{\mathrm{Fe}}\right)=\left\{\begin{array}{l}0\kern4.75em {G}_{\mathrm{Fe}}\le 45\\ {}0.01\times {G}_{\mathrm{Fe}}\kern1.5em 45<{G}_{\mathrm{Fe}}\le 100\end{array}\right. $$
(11.1)
$$ \mathrm{P}\left({G}_{\mathrm{P}}\right)=\left\{\begin{array}{l}0\kern5.25em {G}_{\mathrm{P}}\le 1\\ {}-0.01\times {G}_{\mathrm{P}}\kern1.5em 1<{G}_{\mathrm{P}}\le 10\\ {}0.01\times {G}_{\mathrm{P}}\kern2em 10<{G}_{\mathrm{P}}\le 100\end{array}\right. $$
(11.2)

These preference functions represent different status (positive, neutral and negative) of relative grades and preference degree from each other. In this case, the preference function is determined based on the exact values instead of the value differences and thresholds are determined in the real data domain. Figure 21 shows preference functions of Fe and P variables.

Fig. 21
figure 21

Definition of preference functions of both variables for ore value determination

Full size image

Ore value function

The output of IWA provides CMD and related grades. The preference degrees of Fe and P grades (P (G Fe), P (G P)) of each sample (block) was calculated and multiplicative functions of CMD in preference degree for Fe and P grades were applied in class i (Eq. 12).

$$ \mathrm{F}\mathrm{e}\ \mathrm{value}={\displaystyle \sum_{\mathrm{i}=1}^2{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{Fe}\left(\mathrm{i}\right)}\times \mathrm{P}\left({G}_{\mathrm{Fe}\left(\mathrm{i}\right)}\right)}\mathrm{P}\ \mathrm{value}={\displaystyle \sum_{\mathrm{i}=1}^3{\left(\mathrm{C}\mathrm{M}\mathrm{D}\right)}_{\mathrm{P}\left(\mathrm{i}\right)}\times \mathrm{P}\left({G}_{\mathrm{P}\left(\mathrm{i}\right)}\right)} $$
(12)

In the next stage, weight factors were calculated for Fe and P variables based on the ratio of Fe specific gravity to P specific gravity (because all calculations were performed by volume of block) and the ratio of economic price of Fe to economic price of P (Annels 1996; Rogers and Kanchibotla 2013; Soltani and Hezarkhani 2011). In Choghart mine, the ore value function can be designed based on Fe and P economic values. Finally, ore value was measured by the sum of multiplication Fe weight factor in Fe value and multiplicative P weight factor in P value (Eq. 13). The 3D spatial variation of ore value is shown in Fig. 22.

Fig. 22
figure 22

3D views, a ore value function distribution, b region with large amounts of ore value function, c poles of locations with large amounts of ore value function, d average kriging variance (\( {\overset{\frown }{\sigma}}_{\mathrm{obk}}^2 \) for Fe and P, e objective function distribution, f four poles locations with regard to large amounts of objective function

Full size image
$$ \mathrm{Ore}\ \mathrm{value}={W}_{\mathrm{Fe}}\times \left(\mathrm{F}\mathrm{e}\ \mathrm{value}\right)+{W}_{\mathrm{P}}\times \left(\mathrm{P}\ \mathrm{value}\right)=0.6747\times \left(\mathrm{F}\mathrm{e}\ \mathrm{value}\right)+0.3253\times \left(\mathrm{P}\ \mathrm{value}\right) $$
(13)

Objective function definition

Two concepts were applied in designing complementary drillings. First, large amounts of ore value function were used and centroid of poles (3D center of mass of those large amounts) was selected as a candidate position for complementary drillings. Two poles were selected using this approach (Fig. 22c). Second, ore value function with a kriging variance as a criterion of estimation error was considered. Kriging variance can be used as a criterion for choosing complementary samples (Brus and Heuvelink 2007; Chou and Schenk 1983; Gao et al. 1996; Hossein Morshedy and Memarian 2015; Sinclair and Blackwell 2002; Van Groenigen et al. 1999). Ordinary block kriging variance (σ 2obk ) of each one of Fe and P, as well as their average kriging variance (\( {\overline{\sigma}}_{\mathrm{obk}}^2 \)) was calculated. This average was normalized (\( {\overset{\frown }{\sigma}}_{\mathrm{obk}}^2 \)) within a range of [0; 1] according to Eq. (14).

$$ {\overline{\sigma}}_{\mathrm{obk}}^2=\frac{{\left({\sigma}_{\mathrm{obk}}^2\right)}_{\mathrm{Fe}}+{\left({\sigma}_{\mathrm{obk}}^2\right)}_{\mathrm{P}}}{2} $$
(14.1)
$$ {\overset{\frown }{\sigma}}_{\mathrm{obk}}^2=\frac{{\overline{\sigma}}_{\mathrm{obk}}^2-\mathrm{M}\mathrm{i}\mathrm{n}\left({\overline{\sigma}}_{\mathrm{obk}}^2\right)}{\mathrm{Max}\left({\overline{\sigma}}_{\mathrm{obk}}^2\right)-\mathrm{M}\mathrm{i}\mathrm{n}\left({\overline{\sigma}}_{\mathrm{obk}}^2\right)} $$
(14.2)

The complementary drilling locations were designed on the basis of improving the accuracy of reserve estimation and covering the region with high value of the objective function. As a consequence, objective function was defined by multiplying two factors, namely kriging variance and ore value function, as shown in Eq. (15):

$$ \mathrm{Objective}\ \mathrm{function}={\overset{\frown }{\sigma}}_{\mathrm{obk}}^2\times \kern0.5em \mathrm{Ore}\ \mathrm{value}\ \mathrm{function} $$
(15)

This objective function with two sub-objectives (maximizing kriging variance and ore value) is capable of locating the positions having high ore and information values. Figure 22 illustrates a three-dimensional view of ore value function and large amounts of it and a three-dimensional distribution of the objective function. It also shows the location of poles with the high objective function values.

Designing complementary drillings based on distribution of the objective function outputs

Based on the second concept of the objective function, four poles with larger objective function selected as the candidate and the (x,y,z) coordinates of the poles were extracted (Table 3).

Table 3 Coordinate of selected poles by objective function criteria
Full size table

It is important that we explain two remarks concerning the vertical and directional complementary drillings scheme, considering the coordinates of pole centroids as presented in (Fig. 23):

Fig. 23
figure 23

a Designing vertical drilling based on pole centroid. b Designing directional drilling based on relation of two pole centroids

Full size image
  1. (i)

    Vertical drillings: each pole centroid referred to one potential drilling site. Drilling length was calculated by Euclidean distance from pole’s centroid coordinates to corresponding earth surface coordinates and drilling angle was equal to 90°. In this research, four vertical drillings were selected (Fig. 23a).

  2. (ii)

    Directional drillings: the hypothetical line will intersect double pole centroids representing the potential drilling axis with dip angle (β) and length (L) parameters of drilling, which are displayed in Fig. 23b. There are different cases of double poles, but many of these alternatives are infeasible and not economically justifiable in such mining exploration cases (because of the large drilling length or smaller than 50° drilling dip).

Overall, taking into consideration the two vertical and directional drilling strategies, ten variations may arise. The dip and length of each case were determined. However, only five alternatives from ten cases have commercial justification (considering the constraint dip > 50°) and hence were defined as feasible. In directional drilling, the objective function was modeled along the borehole axis (Table 4).

Table 4 Investigation of status, dimensional and directional properties of ten possible alternatives
Full size table

Difference of the objective function is a suitable tool to model objective function fluctuation along drilling axes. According to the ascending trend and the local maximum of the objective function, the zero value of objective function differential and the acceptable domain of each drilling length, the optimal length of drillings can be defined (Fig. 24).

Fig. 24
figure 24

Defining drilling length, using objective function and it’s changes along drilling length

Full size image

In order to define the priority of feasible exploration drillings, cumulative objective function was used along the length (hypothetical axis) of drilling and cumulative objective function versus length of drilling is plotted in Fig. 25. Maximizing the cumulative objective function in the acceptable domain of each drilling length determined the priority of drillings.

Fig. 25
figure 25

Priority of five feasible alternative drillings with applying cumulative objective function

Full size image

The output of this objective function for five complementary boreholes is shown in Table 5; the dimensional and directional parameters of boreholes are listed with corresponding priority.

Table 5 The collar and survey properties of proposed boreholes with higher priority
Full size table

Figure 26 shows how an arrangement of five extra drillings between the primary drillings led to a reduction in estimation error and improved the accuracy of the category and reserve estimation.

Fig. 26
figure 26

Arrangement of five designed extra drillings between primary drillings network

Full size image

Discussion

The proposed approach (IWA) was compared with indicator kriging (IK), which is a popular geostatistical classification method for evaluating the performance of IWA. IK model of Choghart mine was applied to classify and estimate the probability of Fe and P variables in the mentioned six classes. The confusion matrix is used as the most commonly applicable technique to assess the accuracy of classification analysis. In this matrix, each row represented the instances in an actual class, while each column represented the instances in an estimated class (Aytaç and Barshan 2004; Zapata et al. 2010). As the accuracy measure of classification, correct classification rate (CCR) was calculated by summing the correct decisions given along the diagonal of the confusion matrix and dividing this sum by the total number of tests (Mitchell 2012). The confusion matrices are calculated for the six classes of Choghart deposit based on the classification outputs of IK and IWA method. The CCRs for IK and IWA method are determined 0.622 and 0.756, respectively. With respect to the misclassification error, the ore reserve is affected by the economic effect of ore loss and ore dilution. The economic impact of ore loss is the income lost when ore is sent to the waste dumps and never recovered. The dilution economic effect is imposed on the extra cost of mining and processing waste that is treated as ore. In IK method, the ore loss and ore dilution percent are 20.6 and 17.2 %, while these values for IWA method decrease to 9.4 and 15, respectively. In Fig. 27, the normalized confusion matrices are shown for IK and IWA methods. The lower value of misclassification error and higher value of accuracy (CCR) proves that IWA has better classification performance than IK.

Fig. 27
figure 27

Comparing the normalized confusion matrix between IK and the proposed method

Full size image

Summary and conclusions

Designing complementary drillings between primary drilling network normally use to increase the accuracy of ore reserve modeling and classification. The main goal of this paper was presenting a new method for determining the number, as well as directional and dimensional properties of complementary drillings based on ore value and objective functions, using an interval threshold concept.

In the Choghart iron deposit of central Iran, kriging estimate of Fe and P variables undergo the interval threshold approach by fuzzy membership function instead of point threshold. Based on interval thresholds, IWA and CMD for each block (sample) were computed. Six classes were totally generated, resulting in the existence of one threshold for Fe and two thresholds for P. This study showed that the IWA method has better performance than IK for data classification.

Fe and P preference functions were capable of modeling positive, neutral, and negative values in different ranges of grades. Ore value function depended on CMD values, preference degrees, and weight factors of Fe and P variables. Objective function was defined as a multiplicative function of ore value function and estimation error. Based on large amounts of the objective function, five feasible alternative drillings (four vertical and a single directional) were proposed and their location, dip and azimuth, approximate length and their priority were determined. This process can be applied to improve designing of complementary exploration drillings, for any mineral reserve, with any number of variables and conditions.