3D Design of Optimum Complementary Boreholes by Integrated Analysis of Various Exploratory Data Using a Sequential-MADM Approach

Abstract

Additional and complementary mineral exploration boreholes are often designed to obtain valuable information about mineralized intervals with the least cost. In this research, a new multi-criteria approach is proposed to design the optimum additional directional boreholes in a 3D environment in the second stage of drilling. The proposed algorithm consists of six steps. In the first step, based on the ore deposit type, exploration stage and available exploration data, the main criteria for the selection of the complementary boreholes are identified. In the second step, 3D geological models associated with the identified criteria are prepared. In the third step, a set of 3D candidate complementary boreholes is designed. In the fourth step, scores along the candidate borehole, relevant to various criteria, are estimated. In the fifth step, the candidate boreholes are ranked using a multi-criteria decision-making algorithm and an optimum borehole is selected for further drilling. Finally, information of new borehole is added to the earlier available data and the above steps are repeated to select additional borehole until a stopping condition for drilling is fulfilled. The proposed algorithm is applied at the Dalli Cu–Au porphyry deposit to design optimum boreholes for further drilling. The considered criteria for designing the additional boreholes are based on magnetic susceptibility, logged hydrothermal alteration, mineralized intervals, length of barren rocks, depth of mineralized intervals, Cu and Au grades along the earlier boreholes and trenches, kriging variance and drilling cost. By using the proposed method, four additional boreholes are designed. These boreholes are located in zones of highest uncertainties and highest grades. By drilling these four boreholes, the accuracy of the grade model is improved by 15%. The proposed approach employs all earlier exploration data to improve designing new boreholes in various deposit types and different stages of drilling.

Introduction

Exploration drilling is the most important and expensive activity in a mineral exploration project. Geophysicists mostly use geophysical anomalies associated with mineralization to design exploration boreholes. Geologists may just use specific rock types or alterations to locate boreholes, and geostatistical expert may design boreholes to minimize the estimation error and reduce the uncertainty of grade model. The project investor will mostly consider cost and operational limitations in drilling. It appears that differences in goals may cause contradiction and diversity in designing boreholes. Nevertheless, experienced exploration geologists often use various exploration data and consider cost to design exploration boreholes; however, the objective and criteria for their selection could be different.

Therefore, designing exploration borehole in mineral exploration is a multi-criteria decision-making (MCDM) problem (Abedi et al. 2012). MCDM consist of two main branches, namely multi-attribute decision-making (MADM) and multi-objective decision-making (MODM) methods (Tzeng and Haung 2011). Both of these methods have been used for designing exploratory boreholes (Hassanipak and Sharafodin 2004; Hossein Morshedy and Memarian 2015; Szidarovszky 1983).

Some researchers have considered this problem as multi-objective (Szidarovszky 1983; Hossein Morshedy et al. 2015); but, it has been mostly considered as a one-objective problem and kriging estimation variance (KV) is the most used objective function for analyzing this problem (Gershon 1987). Optimum locations of additional boreholes are determined by optimizing the objective function using an optimization algorithm such as a mathematical optimization method (Scheck and Chou 1983), genetic algorithm (Soltani et al. 2011), spatial simulated annealing (Groenigen et al. 1999; Delmelle and Goovaerts 2009; Soltani-Mohammadi et al. 2012) and particle swarm optimization (Soltani-Mohammadi et al. 2016; Fatehi et al. 2017). Some researchers considered weighted kriging variance as the objective function (Delmelle and Goovaerts 2009; Soltani-Mohammadi et al. 2012; Jafrasteh and Fathianpour 2017). In recent years, beside the kriging variance, the information theorem (Soltani-Mohammadi and Hezarkhani 2013a, b; Soltani and Hezarkhani 2011), conditional simulation (Dirkx and Dimitrakopoulos 2018) and distance function (Safa and Soltani-Mohammadi 2018) have also been used as objective functions for locating in-fill boreholes.

Some researchers considered the borehole locating problem as a MADM problem and solved it through MADM techniques (Hassanipak and Sharafodin 2004; Hossein Morshedy and Memarian 2015); however, they did not mention that this is an MCDM problem. Hossein Morshedy and Memarian (2015) also solved the borehole designing problem using a similar approach that was used by Hassanipak and Sharafodin (2004) with some modification in the search strategy and defining the candidates. They designed 3D candidate boreholes and calculated average grade, ore thickness and the average kriging variance for all candidates. Then, for any borehole, they multiplied these three parameters and finally selected the best additional borehole.

In this research, a new comprehensive approach is proposed to consider different criteria for designing optimum additional directional boreholes. In this proposed method, a set of candidate boreholes are designed and a MADM algorithm is applied to rank and select the best candidate borehole. Three well-known MADM algorithms, namely the technique for order of preference by similarity to ideal solution (TOPSIS), simple additive weighting method (SAW) and weighted product method (WP), have been applied in this proposed approach. The main contribution of this research, in respect to the other published papers in this field of study, is the capability to incorporate all geological, geophysical, grade and uncertainty models, mineralization intervals, local variability, drilling cost and any effective parameters in designing optimum boreholes in 3D space. The proposed approach scans the subsurface and find the dimensional (x, y, z of collar) and directional (azimuth and dip) parameters of optimum boreholes. This proposed approach provides capability for exploration geologists to define various criteria and their importance as a function of deposit type, exploration stage and earlier available data. This approach is applied to the Dalli Cu–Au porphyry deposit in Iran to locate additional 3D boreholes for further drilling. Because boreholes in this proposed approach are selected one by one sequentially by applying MADM algorithm, it is called Sequential-MADM approach.

Methods

The proposed approach for designing optimum additional directional boreholes consists of the following steps:

• (a) Define criteria for selecting optimum boreholes;

• (b) 3D modeling of different geological, geophysical, grade and uncertainty parameters;

• (c) Design a candidate grid and create directional boreholes at each grid node;

• (d) Estimate the different parameters along the candidate boreholes and calculate scores per candidate borehole;

• (e) Rank the candidate boreholes using a MCDM algorithm;

• (f) Add the information of new borehole to the earlier available data and repeat the above steps to select additional borehole until the stopping condition is met.

A simplified flowchart of the proposed approach for designing new optimum borehole is shown in Figure 1. The above-mentioned steps of the proposed approach are discussed in detail in the following sections.

Figure 1

Flowchart of the proposed approach for designing additional boreholes

Exploration Drilling Criteria

Exploration drilling criteria often depend on the type of deposit, available data, stage of exploration and aim of drilling. The importance of each criterion is variable depending on type of deposit and stage of exploration. Several criteria can be used for locating additional exploratory boreholes, some of which are as follows.

• (a) Grade: Boreholes that intersect zones of mineralization with the highest average grade are more interesting (Hassanipak and Sharafodin 2004; Hossein Morshedy and Memarian 2015; Soltani-Mohammadi et al. 2012). In poly-metal deposit, the grade of by-product and penalty elements or components are also important.

• (b) Ore thickness: Boreholes that intersect thick section of zones of mineralization are more favorable (Hassanipak and Sharafodin 2004; Hossein Morshedy and Memarian 2015; Soltani and Hezarkhani 2013).

• (c) Thickness of barren rocks: Boreholes with the lowest intersection of barren rocks are preferred.

• (d) Uncertainty: New boreholes should be located in the uncertain zone of the grade model and sparse sampling area. The uncertainty model is created using geostatistical methods (Scheck and Chou 1983; Groenigen et al. 1999; Soltani-Mohammadi et al. 2012). KV has been usually considered as a measure of uncertainty modeling (Journel and Huijbregts 1978; Webster and Oliver 2007; Chiles and Delfiner 2012; Rossi and Deutsch 2014). Ordinary kriging (OK) is a well-known geostatistical algorithm that estimates the grade of block $v$ by using the surrounding data $z\left( {x_{i} } \right), i = 1, \ldots ,n$ as (Webester and Oliver 2007):

  $$\hat{Z}\left( v \right) = \mathop \sum \limits_{i = 1}^{N} \omega_{i} z\left( {x_{i} } \right)$$

  (1)

  where $\hat{Z}\left( v \right)$ is the estimated grade in block $v$, and $\omega_{i} , i = 1, \ldots ,n$ are OK weights that sum to 1. The OK algorithm calculates simultaneously the estimation variance as:

  $$\text{var} \left[ {\hat{Z}\left( v \right)} \right] = E\left[ {\left\{ {\hat{Z}\left( v \right) - Z\left( v \right)} \right\}^{2} } \right] = 2\mathop \sum \limits_{i = 1}^{N} w_{i} \bar{\gamma }\left( {x_{i} , v} \right) - \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \omega_{i} \omega_{j} \gamma \left( {x_{i} ,x_{j} } \right) - \bar{\gamma }\left( {v , v} \right)$$

  (2)

  where $\gamma \left( {x_{i} ,x_{j} } \right)$ is variogram between samples $x_{i}$ and $x_{j}$, $\bar{\gamma }\left( {x_{i} , v} \right)$ is the average variogram between sample $x_{i}$ and block v, and $\bar{\gamma }\left( {v , v} \right)$ is the average variogram in block v (Webester and Oliver 2007). The KV depends only on the boreholes layout. The highest value of the KV corresponds to the area with sparse drilling, in which the uncertainty of the estimated grade of block model is also higher.

• (e) Geophysical anomalies: Geophysical approaches are widely used for detecting the mineralized zone in most types of mineral deposits (Thoman et al. 2000; John et al. 2010; Hoschke 2010; Holden et al. 2011; Clark 2014; Dentith and Mudge 2014). Boreholes are designed to intersect the interpreted target zone based on geophysical signatures.

• (f) Depth of ore: In some deposits, mineralized zone near the surface are interesting targets for drilling. Therefore, boreholes that can intersect these zones are very important. A similar strategy can also be considered for the depth of ore in the borehole. The initial boreholes should intersect shallower mineralized zones, while, by increasing the number of boreholes, searching for deeper mineralized zones might be more important.

• g) Lithology or alteration: Mineralization often is associated with certain lithologies or hydrothermal alteration zones. Boreholes should be designed so as to intersect favorable host lithology and hydrothermal alteration.

• (h) Drilling cost: By increasing the depth of drilling and decreasing the dip of a borehole, drilling cost is dramatically increased. Therefore, to minimize drilling costs, shallow vertical boreholes are priority. According to drilling companies in Iran, roughly 1% is added to basic drilling cost when the dip of borehole is decreased by about 1º. Usually, when the depth of borehole is increased as D meters, K% of the basic drilling cost is added as a penalty to overall drilling cost. Therefore, drilling cost is calculated by considering two penalties for increasing depth and decreasing dip of borehole.

  $$C = c_{1} \times \left( {1 + \frac{90 - \alpha }{100}} \right) \times L + c_{1} \times \left( {\mathop \sum \limits_{i = 0}^{n - 1} i \times \frac{K}{100} \times D + n \times \frac{K}{100} \times \left( {L - n \times D} \right)} \right)$$

  (3)

  where $n = \frac{L - D}{D} + 1$, $c_{1}$ is basic drilling cost for 1 m, $\alpha$ is dip of borehole and L is final depth of borehole.

• (i) Local variability: In some cases, in particular during detailed exploration stage, monitoring of grade variation is very important. Therefore, a borehole with the highest variance in grade data (local variability) is priority for drilling (Arik 1999; Soltani-Mohammadi et al. 2016; Dirkx and Dimitrakopoulos 2018). This variance depends on the grade of samples in boreholes and is different from the KV that is based on the pattern of boreholes and samples.

The above-mentioned criteria c, f and h are negative (cost) criteria and their lowest values are more favorable, whereas others are positive (benefit) criteria and boreholes with the highest score for these criteria are priority for drilling.

3D Modeling of Geoscience Parameters

To apply the proposed approach, it is important to prepare 3D models of the host lithology and hydrothermal alteration, geophysical signatures, grade and uncertainty. The grade and uncertainty models are prepared by employing OK (Eqs 1 and 2). The host lithological and alteration models can be prepared by using geostatistical approach algorithms or non-geostatistical approach algorithms such as the natural neighborhood (NN) method. In this paper, the NN was used to prepare the 3D alteration model. This method is simple, practical and efficient for modeling categorical variables. The 3D geophysical models are created through 3D data inversion modeling.

Designing Candidate Directional Boreholes for Drilling

Each borehole is specified by spatial parameters of its collar and directional parameters including azimuth and dip. After drilling, core samples are systematically taken and each sample is considered as an interval in the borehole. Designing the candidate boreholes consists of two procedures. First, a regular or scatter grid of the candidate collar is designed. Then, the directional boreholes in each collar location are designed to scan the subsurface. The proposed approach in Hossein Morshedy and Memarian (2015) is used for designing the directional boreholes in this research.

Estimation of Parameters per Borehole

Each borehole is composed of a set of points in 3D space. Based on the initial models, parameters in these points are determined. To estimate these parameters in a borehole, the grade in the borehole is estimated using the nearest neighbor method firstly. By considering the cutoff grade, the length of borehole, the depth of mineralization, the length of mineralized zones and barren rocks in the boreholes are estimated. Then, other parameters including the grade of by-product, uncertainty (KV), host rock and alteration and geophysical signatures in each point are estimated using the nearest neighbor method for a specified length of borehole. Then, the average grade, uncertainty (KV), lithology/alteration and geophysical signatures in each borehole are calculated. By considering the length and dip of a borehole, the drilling cost is calculated by using Eq. 3. The variance of the estimated grade data in the borehole is also calculated. These calculations are applied to all boreholes and the decision matrix is formed as:

$${\text{DM}} = \left[ {\begin{array}{*{20}c} {{\text{BH}}_{ 1} } \\ {{\text{BH}}_{ 2} } \\ {\begin{array}{*{20}c} \vdots \\ {{\text{BH}}_{n} } \\ \end{array} } \\ \end{array} } \right] =\left[ \begin{array}{*{20}l} {\bar{M}_{1} } \hfill & {\overline{{{\text{AKV}}_{1} }} } \hfill & {\text{ML}}_{1} \hfill & {{\text{BRL}}_{1} } \hfill & {G_{1} } \hfill & {A_{1} } \hfill & {D_{1} } \hfill & {C_{1} } \hfill & {V_{1} } \hfill \\ {\bar{M}_{2} } \hfill & {\overline{{{\text{AKV}}_{2} }} } \hfill & {\text{ML}}_{2} \hfill & {{\text{BRL}}_{1} } \hfill & {G_{1} } \hfill & {A_{2} } \hfill & {D_{2} } \hfill & {C_{2} } \hfill & {V_{2} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{M}_{n} } \hfill & {\overline{{{\text{AKV}}_{n} }} } \hfill & {\text{ML}}_{n} \hfill & {{\text{BRL}}_{n} } \hfill & {G_{n} } \hfill & {A_{n} } \hfill & {D_{n} } \hfill & {C_{n} } \hfill & {V_{n} } \hfill \\ \end{array}\right]$$

(4)

where ${\text{BH}}_{i}$ is the name of candidate borehole, $\bar{M}_{i}$ is average grade, $\overline{\text{AKV}}_{i}$ is average of KV, ${\text{ML}}_{i}$ is length of mineralized zone, ${\text{BRL}}_{i}$ is length of barren rocks, $\bar{G}_{i}$ is average of geophysical signatures, $A_{i}$ is hydrothermal alteration score, $D_{i}$ is depth of the mineralized zone, $C_{i}$ is drilling cost and $V_{i}$ is variance of estimated grade in borehole ${\text{BH}}_{i}$. If other parameters such as structures, wall rock lithology and additional geophysical signatures are available, their columns are added to the above matrix.

Ranking of Candidate Boreholes Using MCDM Algorithms

After preparing the above DM, a MADM algorithm is applied to rank the candidate boreholes and select the best one. In this research, three MADM approaches, namely TOPSIS, SAW and WP, were used to rank all 3D candidate boreholes.

TOPSIS

TOPSIS is a simple and well-known ranking method in MCDM that consists of following simple steps (Hwang and Yoon 1981; Lai et al. 1994; Yoon and Hwang 1995; Jahanshahloo et al. 2006; Tzeng and Haung 2011; Pazand et al. 2012; Asadi et al. 2015; Abedi and Norouzi 2016).

• 1. The DM is made and is then is normalized as:

  $${\text{DM}} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {c_{1} } & { c_{2} } & { \begin{array}{*{20}c} \cdots & {c_{j} } & { \begin{array}{*{20}c} \cdots & {c_{n} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \vdots \\ \end{array} } \\ {A_{i} } \\ {\begin{array}{*{20}c} \vdots \\ {A_{m} } \\ \end{array} } \\ \end{array} } & {\left[ {\begin{array}{*{20}c} {g_{11} } & {g_{12} } & \cdots & {g_{1j} } & \cdots & {g_{1n} } \\ {g_{21} } & {g_{22} } & \cdots & {g_{2j} } & \cdots & {g_{2n} } \\ \cdots & \cdots & \cdots & \ldots & \cdots & \ldots \\ {g_{i1} } & {g_{i2} } & \cdots & {g_{ij} } & \cdots & {g_{in} } \\ \cdots & \cdots & \cdots & \ldots & \cdots & \ldots \\ {g_{m1} } & {g_{m2} } & \cdots & {g_{mj} } & \cdots & {g_{mn} } \\ \end{array} } \right]} \\ \end{array}$$

  (5)
  $$r_{ij} = g_{ij} /\sqrt {\mathop \sum \limits_{i = 1}^{m} g_{ij}^{2} } ;\quad i = 1, 2, \ldots , m;\quad j = 1, 2, \ldots , n.$$

  (6)

  where $A_{i}$ is the candidate solution, $c_{j}$ is criterion and $g_{ij}$ is score of the candidate attribute i in criterion j.

• 2. The normalized DM is multiplied by a weight vector (w), which indicates the importance of individual criteria.

  $$v_{ij} = w_{j} r_{ij} ;\quad i = 1, 2, \ldots , m; \quad j = 1, 2, \ldots , n.$$

  (7)

• 3. The positive ideal ($A^{*}$) and negative ideal ($A^{ - }$) solutions are defined, respectively, as the maximum and minimum of criteria in all alternatives.

  $$A^{*} = \left\{ {v_{1}^{*} , \ldots ,v_{n}^{*} } \right\} = \left\{ {\left( {\mathop {\hbox{max} }\limits_{i} v_{ij} |j \in J^{\prime}} \right),(\mathop {\hbox{min} }\limits_{i} v_{ij} |j \in J^{\prime\prime})} \right\}$$

  (8)
  $$A^{ - } = \left\{ {v_{1}^{ - } , \ldots ,v_{n}^{ - } } \right\} = \left\{ {\left( {\mathop {\hbox{min} }\limits_{i} v_{ij} |j \in J^{\prime}} \right),(\mathop {\hbox{max} }\limits_{i} v_{ij} |j \in J^{\prime\prime})} \right\}$$

  (9)

  where $J^{\prime}$ and $J^{\prime\prime}$ are, respectively, the positive criteria and negative criteria.

• 4. Distances of all alternatives to these ideal solutions are calculated.

  $$D_{i}^{*} = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {v_{ij} - v_{j}^{*} } \right)^{2} } ;i = 1, 2, \ldots , m.$$

  (10)
  $$D_{i}^{ - } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {v_{ij} - v_{j}^{ - } } \right)^{2} } ;i = 1, 2, \ldots , m.$$

  (11)

• 5. Finally, the relative closeness of alternatives to ideal solution is calculated using the following equation.

  $$RC = \frac{{D_{i}^{ - } }}{{\left( {D_{i}^{ - } + D_{i}^{ + } } \right)}} , i = 1, 2, \ldots , m.$$

  (12)

Alternatives are ranked according to the RC, and the alternative with the highest RC is considered the best one.

SAW

The SAW method is a simple and may be more applicable MADM method. In this method, the best alternative and candidate are selected as follows (Triantaphyllou 2000):

$$B^{*} = \left\{ {u_{i} \left( x \right) |\mathop {\hbox{max} }\limits_{i} u_{i} \left( x \right)\left| {i = 1, 2, \ldots ,n} \right.} \right\}$$

(13)

where $B^{*}$ is the best candidate, and $u_{i} \left( x \right)$ is the score of the ith candidate and is calculated as (Triantaphyllou 2000):

$$u_{i} \left( x \right) = \mathop \sum \limits_{j = 1}^{n} w_{j} r_{ij} \left( x \right)$$

(14)

where $w_{j}$ is weight of jth criteria and $r_{ij} \left( x \right)$ is normalized score of the ith alternative with respect to jth criterion. In this method, the normalized DM can be calculated using two linear formulas. In one formula, the normalized value of the positive (benefit) criteria and negative (cost) criteria is, respectively, calculated as (Triantaphyllou 2000):

$$r_{ij} \left( x \right) = x_{ij} /x_{j}^{*} ,$$

(15)

$$r_{ij} \left( x \right) = \left( {1/x_{ij} } \right)/\left( {1/x_{j}^{*} } \right),$$

(16)

In the other formula, the normalized benefit and cost criteria are, respectively, calculated as:

$$r_{ij} \left( x \right) = \left( {x_{ij} - x_{j}^{ - } } \right)/\left( {x_{j}^{*} - x_{j}^{ - } } \right)$$

(17)

$$r_{ij} \left( x \right) = \left( {x_{j}^{ - } - x_{ij} } \right)/\left( {x_{j}^{ - } - x_{j}^{*} } \right)$$

(18)

where $x_{ij}$ is score of the ith alternative with respect to jth criterion, $x_{j}^{*}$ and $x_{j}^{ - }$ are, respectively, the maximum and minimum score of all alternatives respect to jth criterion ($x_{j}^{*} = \mathop {\hbox{max} }\limits_{i} x_{ij}$, $x_{j}^{ - } = \mathop {\hbox{min} }\limits_{i} x_{ij}$). In this research, Eqs. 15 and 16 were used to normalize the DM, because they are nonlinear transform equation and are not depend on the data distribution.

WP

The WP is similar to the SAW method with a difference that the scores of an alternative are multiplied. In this method, the final score of the kth alternative is calculated by using the following formula (Triantaphyllou 2000):

$$P\left( {A_{k} } \right) = \mathop \prod \limits_{j = 1}^{n} \left( {r_{ij} } \right)^{{w_{j} }}$$

(19)

where $w_{j}$ is weight of jth criteria and $r_{ij} \left( x \right)$ is normalized score of the ith alternative with respect to jth criterion.

Stopping Criteria

In the proposed approach, the first borehole is selected and added to the previously drilled boreholes. The initial uncertainty (KV) is updated by using the new set of boreholes. If the suggested borehole is drilled rapidly and samples from this borehole are available, they can be used for updating the grade and alteration models and designing the next borehole as well. The selected borehole is removed from the set of candidate boreholes, and the algorithm is repeated to find the next optimum boreholes.

How many boreholes are required to drill? This is an important question in various exploration stages of a certain deposit. To stop the drilling in various stages, some important criteria are considered:

• Estimation error: is the estimated error of the model acceptable? Is the estimated error reduced by adding new boreholes? Variation in the estimated KV before and after drilling the new borehole can be used to answer those questions.

• The resource classes: the mining plan is designed based on the measured resource/reserve and the main part of the resource is assigned to this class and drilling is continued until this criterion is met.

• Financial project restriction: the considered budget for exploration drilling in a project can be also considered as another stopping criterion.

Because the first stopping criterion is more important and in some cases the resource classification comes from the estimation error and the financial restriction is not a big issue in this stage of exploration, in this research, the first stopping criterion is used to determine the number of necessary boreholes.

Case Study at the Dalli Cu–Au Porphyry Deposit

Geology and Mineralization at Dalli Deposit

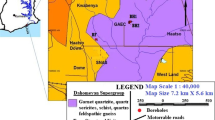
Dalli Cu–Au porphyry deposit is located in the middle section of the Urmia-Dokhtar Magmatic Arc (UDMA) (Fig. 2). Detailed exploration at Dalli deposit delineated two main Cu–Au mineralized porphyry centers (South Hill and North Hill) that are 1.7 km apart (Asadi 2008; Asadi et al. 2015).

Figure 2

1:10,000 scale geological map of Dalli exploration area, showing the main mineralized zones at the South and North porphyry centers along a NE trending structural corridor (Asadi 2008)

The main exposed rocks at Dalli exploration area are Eocene andesitic to basaltic lava flows and andesitic to rhyodacite pyroclastic rocks that have been intruded by Oligo-Miocene intermediate intrusive and sub-volcanic rocks. Quartz-diorite, diorite, porphyritic amphibole–pyroxene andesite and porphyritic andesite dykes and sills are the main intrusive and sub-volcanic rocks in the area. The 1:10,000 geological map of South Hill and North Hill centers is shown in Figure 2.

Hydrothermal alteration and subsequent porphyry disseminated and stockworks mineralization at the Dalli deposit are mostly associated with the intrusion of Oligo-Miocene dioritic to granodioritic rocks into the Eocene andesite and pyroclastic rocks (Asadi et al. 2015). The South Hill is a 190 m × 225 m conical hill with intense potassic alteration surrounded by phyllic, argillic and propylitic alterations (Darabi-Golestan et al. 2013; Asadi et al. 2015). Most of the Cu–Au mineralization occurs as disseminated porphyry in potassic alteration and quartz–hematite–magnetite veins and veinlets (Ayati et al. 2012).

Chalcopyrite, pyrite, bornite, magnetite and native gold are the main minerals in hypogene zone. Gold occurs as free micron-sized grains and inclusions in pyrite, chalcopyrite and quartz. Oxide mineralization includes malachite, azurite, cuprite, Fe oxide (hematite) and Fe hydroxides (goethite and limonite). About eight meters of supergene Cu enrichment are locally present at depth of about 55 m, and are mostly characterized by covellite and chalcocite (Asadi et al. 2015).

Preparing the 3D Models

In this research, the proposed approach was applied to design some new boreholes in the South Hill of the Dalli Cu–Au porphyry deposit. In order to design a few additional boreholes in the second stage of drilling at Dalli, five 3D models, including the Au and Cu grade models, the KV model of Cu, quantified alteration model and magnetic susceptibility model, are prepared.

3D models of Cu–Au grades and KV of Cu were prepared using seven existing boreholes and seven earlier trenches. The depths of the boreholes range from 189 to 550 m, with inclination angles between 50 and 90 degrees (Table 1). Core samples were systematically collected every 1 m along the boreholes and every 2 or 4 m along the trenches. The samples were analyzed by fire assay method for gold and by induced coupled plasma mass spectrometry for 43 other elements at the AMDEL laboratory in Australia. The assay data were transformed into 1-m composite samples to use in 3D modeling. Figure 3 shows the 3D view of the trenches and boreholes.

Table 1 Collar coordinates, depth, dip and azimuth of the initial boreholes

Figure 3

3D view of the initial trenches and boreholes in the south Dalli Cu–Au porphyry deposit

OK method was used to create the Cu–Au grade models and simultaneously the KV of Cu that was considered as an uncertainty model. Before OK, the censored data were replaced by 3/4 of the detection limit of the analysis (Helsel 2005). Outliers were corrected using the Doerffel method (Wellmer 1998), and data were transformed to approximately normal distribution using logarithmic transformation (Davis 2002). Figure 4 shows the histograms of the Cu–Au grade data before and after logarithmic transformation. Variograms in different directions were calculated to define the anisotropy model. However, considerable anisotropy was not observed; therefore, isotropic variogram models were used (Fig. 5). To compute the grade and to estimate the variance, OK was performed with a block size of 10 × 10 × 10 m.

Figure 4

Histograms of Cu and Au in the initial boreholes before (top) and after (bottom) logarithmic transformation

Figure 5

Experimental and theoretical variogram models for log-transformed data (a) Cu and (b) Au

The geological properties of the core samples, including rock type and hydrothermal alteration, were also identified and used to create the 3D lithological alteration model. Potassic, argillic, phyllic, silica and propylitic alteration are the most observed alteration types in the core samples. Potassic alteration is the most important alteration zone in this deposit and Cu–Au mineralization is mostly hosted by this type of alteration. Silicification and phyllic alteration are other two important host alterations. These alterations were scored based on their importance in hosting the mineralization (Table 2). The intensity of the alterations was also defined by experienced exploration geologists. The total score of the alteration ($S_{\text{Alt}}$) was calculated by multiplication of the score of the alteration (Alt) and the score of the alteration intensity (Int) (Eq 20). Then, a 3D alteration model was created using the nearest neighbor (NN) algorithm.

$$S_{\text{Alt}} = {\text{Alt}} \times {\text{Int}}$$

(20)

Table 2 Different alterations zones in South Dalli Cu–Au deposit and assigned scores

Magnetic survey was also implemented over the Dalli deposit, and total magnetic intensity was recorded along profiles with a spacing of 50–100 m and 10 m station intervals. Magnetic survey is a useful method for mapping hydrothermal alteration in copper and gold porphyry deposits. According to Clark (2014), Cu–Au porphyry systems consist of an inner strongly mineralized and magnetic-rich potassic alteration zone surrounded by a shell of magnetic-destructive phyllic zone and an intense propylitic alteration zone, which is also partially magnetic-destructive. Figure 6 shows the alteration zoning model for an Au-rich porphyry Cu deposit and theoretical magnetic profiles over this model (Clark 2014). A symmetric magnetic anomaly is considered in this model. A high magnetic anomaly is considered over the center of the potassic alteration zone that reaches to negative values related to magnetic-destructive phyllic alteration and in the outer zone close to zero value and background (Thoman et al. 2000; John et al. 2010; Hoschke 2010; Holden et al. 2011; Clark 2014).

Figure 6

(a) Variation of magnetic susceptibility in different alterations of an Au-rich Cu porphyry model. (b) Theoretical RTP magnetic responses for different erosion level (Clark 2014)

Figure 7 shows the residual magnetic intensity and the reduced to the pole (RTP) maps for the South Hill Dalli deposit. The locations of initial boreholes and trenches are also shown on the RTP map. Except borehole DH05, other boreholes, which were located on the high magnetic anomaly, intersected the mineralized zone. It also should be mentioned that the potassic alteration zone, which formed the main part of mineralization, is located close to the surface. A high percentage of magnetic minerals are observed in the potassic alteration zone of the Dalli Au-rich Cu porphyry deposit as vein and veinlet. Therefore, the magnetic anomaly can be used for mapping the potassic alteration zone. A 3D magnetic susceptibility model was prepared by inversion of the ground magnetic data and used in designing the optimum boreholes.

Figure 7

Magnetic intensity maps on the South Hill of Dalli. (a) Residual magnetic intensity. (b) Reduced to the magnetic pole overlain by the trenches and boreholes

Figure 8 shows an E–W section of the Cu–Au grade models, KV, the alteration and magnetic susceptibility models. In addition to the modeled parameters, the Cu grade is selected as the main mineralization and by considering the cutoff grade of 0.2 percent, block cells with a grade higher than this value are considered as mineralization zone. Therefore, the ore and barren rock thickness in the boreholes are estimated. The depth of ore body and the final depth of the borehole (length of the borehole) were also calculated.

Figure 8

Vertical sections of the prepared 3D models for designing new optimum boreholes at northing latitude of 3792500 m (UTM zone 39): (a) Cu grade model; (b) Au grade model; (c) kriging variance model; (d) alteration score model; and (e) magnetic susceptibility model

Drilling cost is another criterion that was calculated (Eq 3). The basic drilling cost is about 100$ per 1 m, and about 10% is added to basic drilling cost by increasing the depth of each borehole every 150 m.

Applying the Algorithm

After preparing the necessary 3D models, the proposed approach for designing additional boreholes is implemented. Based on the scatter sampling approach (Hossein Morshedi 2015), an irregular candidate grid node of 10 m × 10 m spacing is defined as the collar location of candidate new boreholes (Fig. 9). The outline of the mineralized zone is specified by integration of different surface and subsurface data (Fatehi and Asadi 2017), and candidate grid nodes located outside of this limit were removed from the analysis. In each grid node, directional boreholes for azimuth within a range of 0–360 degrees with a tolerance of 10 degrees and dip within a range of 50–90 degrees with 5 degrees tolerance are created. Therefore, in each grid node 297 directional boreholes are created. The maximum length considered for the boreholes is 300 m and sampling interval in the borehole 1 m.

Figure 9

Locations of the initial boreholes and the candidate grid nodes

Nine criteria, including average grade of Au (${\bar{M}}_{\text{Au}}$), average grade of Cu (${\bar{M}}_{\text{Cu}}$), average of magnetic susceptibility (${\overline{\text{sus}}}$), average alteration score (${\bar{S}}_{\text{Alt}}$), average estimation KV (${\overline{\text{AKV}} }$), length of mineralization in borehole (ML), length of barren rocks in borehole (BRL), depth of ore body in borehole (D) and drilling cost (C), were defined. Three criteria (BRL), (D) and (C) are negative and the smallest values of these three criteria are favorable, whereas other criteria are positive and their largest values are favorable. In all candidate boreholes, the average values for these nine criteria were estimated and a DM was created. The importance weights of these criteria were defined by experienced exploration geologists (Table 3).

Table 3 Importance weight vectors of different criteria considered for locating additional boreholes at the Dalli Cu–Au deposit

Finally, a MADM algorithm was applied to rank the candidate boreholes. The collar coordinates, azimuths, dips and lengths of borehole were the output of the proposed algorithm. Cu–Au grades were also estimated along the boreholes and were added to the initial boreholes data, and modeling was repeated. The proposed approach was implemented using the same criteria and data in each of the three MADM methods considered here.

Sequential-TOPSIS

The proposed approach was applied by using the TOPSIS method as the ranking algorithm for selecting 10 new boreholes. Figure 10 shows the variation of the average KV after adding new optimum boreholes. The decrease in AKV after adding four new boreholes is considerable, while by adding boreholes 5 and 6 the AKV is slightly decreased. Therefore, at this stage, four additional boreholes (N01, N02, N03 and N04) were suggested for drilling. Figure 11 shows the locations of the additional selected optimum boreholes. The properties of these four new boreholes are also illustrated in Table 4. Additional boreholes were located in the NW zone of the deposit that is due to the higher grade of zones of mineralization, geophysical anomaly and sparse initial drilling data. The additionally proposed boreholes were projected on vertical sections of the Cu–Au grade and KV (Fig. 12). Figure 13 shows the variation of the estimated Cu and Au grade along these new boreholes.

Figure 10

Variation of average kriging variance after adding optimum additional boreholes in the Sequential-TOPSIS method

Figure 11

3D view of initial boreholes and the optimum additional boreholes determined by the Sequential-TOPSIS method

Table 4 Properties of the selected additional boreholes by Sequential-TOPSIS method

Figure 12

Projection of some suggested additional boreholes selected by the Sequential-TOPSIS method on the vertical section of Au (left), Cu (center) and kriging variance (right)

Figure 13

Estimated Cu–Au grade along the additional boreholes suggested by the Sequential-TOPSIS method

Sequential-SAW

The SAW method was the second implemented MADM approach in this research. In this method, the objective function for optimization of additional boreholes is written as:

$$\begin{aligned} & F = w_{{\overline{\text{Cu}} }} \times \overline{\text{Cu}} + w_{{\overline{\text{Au}} }} \times \overline{\text{Au}} + w_{{\overline{\text{Sus}} }} \times \overline{\text{Sus}} + w_{{\overline{\text{ALT}} }} \times \overline{\text{ALT}} \\ & \quad + {\kern 1pt} w_{{\overline{\text{KV}} }} \times \overline{\text{KV}} + w_{\text{ML}} \times {\text{ML}} + w_{\text{GL}} \times {\text{GL}} + w_{D} \times D + w_{C} \times C \\ \end{aligned}$$

(21)

where $w_{i}$ is weight of every criteria (Table 3). In this method, candidate borehole with the highest value of objective function F is selected as the optimum additional boreholes. By using this method, properties of four optimum additional boreholes were specified (Table 5, Fig. 14). The result of Sequential-SAW method is close to the result of Sequential-TOPSIS method; however, there are some small differences between them.

Table 5 Properties of four additional optimum boreholes selected by applying three different MADM methods in the proposed approach

Figure 14

Locations of selected optimum additional boreholes by applying three MADM algorithms to rank the candidate boreholes in the proposed approach

Sequential-WP

The WP was the third implemented MADM algorithm in the proposed approach for ranking the candidate boreholes. In WP method, the objective function is:

$$\begin{aligned} & F = \left( {\overline{\text{Cu}} } \right)^{{w_{{\overline{\text{Cu}} }} }} \times \left( {\overline{\text{Au}} } \right)^{{w_{{\overline{\text{Au}} }} }} \times \left( {\overline{\text{Sus}} } \right)^{{w_{{\overline{\text{Sus}} }} }} \times \left( {\overline{\text{ALT}} } \right)^{{w_{\overline{\text{ALT}}} }} \\ & \quad \times {\kern 1pt} \left( {\overline{\text{KV}} } \right)^{{w_{{\overline{\text{KV}} }} }} \times \left( {\text{ML}} \right)^{{w_{\text{ML}} }} \times \left( {\text{GL}} \right)^{{w_{\text{GL}} }} \times D^{{w_{D} }} \times C^{{w_{C} }} \\ \end{aligned}$$

(22)

In this method, the candidate borehole with the highest value of F is selected as the optimum additional borehole. The directional and dimensional properties of four additional boreholes by using this method were determined (Table 5).

Figure 14 shows the locations of the optimum boreholes by applying three different MADM methods in the proposed approach. All optimum boreholes were located in the NW zone of deposit. The Cu and Au grade in the initial boreholes and trenches as well as the magnetic anomaly in the NW zone of deposit are stronger than in other zones of the deposit; therefore, locating the new optimum boreholes in this zone is logical.

However, the optimum boreholes selected by three approaches in the NW zone are not identical. Different drilling alternatives were selected as optimum additional boreholes by each of the three MCDM methods, indicating their importance. This comparison indicates that by applying each MADM method different result is obtained and is a general issue in MCDM problems.

Discussion

In this research, an innovative approach was used to design the locations of directional boreholes that can be drilled in the different stages of mineral exploration. The proposed approach incorporates different geological, geophysical and initial drilling data to design additional in-fill boreholes. The proposed approach has at least two advantages in respect to the recently similar published papers such as by Dirkx and Dimitrakopoulos (2018), Jafrasteh and Fathianpour (2017) and Safa and Soltani-Mohammadi (2018). One advantage of the proposed approach is consideration of many different criteria, whereas most of the published papers consider just one or a few criteria for designing optimum boreholes. Another advantage is its ability to determine the directional parameters (azimuth and dip) of optimum boreholes as well as their dimensional (collar and length) parameters, whereas other papers just define the collar location of optimum boreholes in 2D area or did not present a specific algorithm for scanning 3D space under surface. Therefore, this approach can be considered as a tool that brings together various experts with different ideas to locate additional in-fill boreholes to make a unique decision. Exploration geologists can prepare 3D models and use them to design the new in-fill boreholes with this proposed algorithm.

The importance weights of drilling criteria, which can be considered by the experts, are considered variable in different stages of exploration. During the preliminary exploration stage, exploration boreholes are sparse; therefore, the weight of surface exploration data, such as geophysical signatures, is often higher than in the detailed exploration stage. In detailed exploration stage, boreholes are drilled to reach an accurate ore deposit model; therefore, boreholes are drilled at locations with the highest uncertainty. Proper assignment of importance weights is so critical because they can largely affect the results. The effect of importance weight is evaluated in the following.

To evaluate the effect of the importance weights of every criterion, 297 directional boreholes were created in a grid node with the coordinate of (437765E, 3792600N) and the proposed algorithm was applied with two different importance weights. In the first example, importance weight of the KV parameter was set to 1 and the importance weight of the other parameters was considered zero. The azimuth and dip of the optimum selected borehole were 340 and 80 degrees, respectively. In another example, the other parameters were also weighted (Table 3) and a borehole with azimuth of 290 and dip of 75 degrees was selected as the optimum borehole. The direction of selected optimum boreholes in these two cases is completely different, indicating the criticality a parameter’s importance weight in this algorithm.

The proposed algorithm was also compared with a simple and well-known GET function approach (Hassanipak and Sharafodin 2004). Because the proposed algorithm considers different criteria for designing the optimum boreholes, it is an advancement of the GET function. The GET function is a multiplicative function of the grade (G), error (E) and thickness (T) of the ore mineralization, thus $f\left( {G, E, T} \right) = G^{\alpha } E^{\beta } T^{\gamma }$ where $\alpha$, $\beta$, $\gamma$ are weighting parameters that indicate the importance of each parameter in designing additional boreholes. In other words, the GET function is the decision function of the WP method. To apply the GET function, the grade and KV models are prepared using a kriging algorithm and initial exploration drilling data. The preparation procedure of these models is explained in "Introduction" section. The importance weights of grade, KV and ore thickness were, respectively, considered as 0.4, 0.4 and 0.2. Figure 15 shows the result of the GET function method. In this map, the area with the highest values is the best location for new drilling. The location of initial and proposed boreholes in "Introduction" section is also indicated on this map. The suggested boreholes by the Sequential-TOPSIS, Sequential-SAW and Sequential-WP methods are located in areas with high values obtained with the GET function.

Figure 15

GET function map overlain by the locations of initial and proposed boreholes in section 3-3

However, the proposed approach in this research has more advantages compared to the GET function (Hassanipak and Sharafodin 2004) in designing new boreholes, thus: (a) because the proposed algorithm considers surface exploratory data to be applicable for designing new boreholes in different stage of drilling; (b) more parameters are used whereas the GET function just consider grade, error and thickness; (c) the effect of new borehole for designing the next boreholes is considered by re-calculating the KV model; (d) the outputs of this proposed approach are directional and dimensional parameters (collar, azimuth and dip), length, estimated grade of the borehole, whereas in the GET function outlines only favorable zones for drilling; and (e) drilling cost is considers whereas the GET function does not take this important parameter into account.

Conclusion

In this research, a new innovative approach for designing optimum complementary boreholes is proposed. This approach incorporates different layers such as geological, geophysical, grade and uncertainty models for locating optimum additional boreholes. The thickness of ore mineralization and barren rocks are other parameters considered for selecting optimum boreholes. Drilling cost was also incorporated, so that this algorithm can determine boreholes with the optimum information and the lowest drilling cost. The proposed algorithm was applied to the exploration area of the South Hill Dalli Cu–Au porphyry deposit to find optimum additional boreholes at the second phase of drilling. The most important results of this research are:

• Designing exploration boreholes is a multi-criteria decision-making problem and different MCDM algorithm can be used for this purpose.

• Results of the different applied MCDM algorithms are strongly similar, but some differences arise due to the nature of MADM methods.

• Based on the available data, nine parameters were defined to design additional boreholes in the second stage of drilling.

• At this stage of drilling, based on the variation of the kriging variance, four additional boreholes were suggested for drilling.

• The proposed approach selects new boreholes sequentially one by one.

• The limitation of this approach is that it is not able to find a group of new boreholes simultaneously, which is an important topic for future research.