Introduction

Freezing is one of the most important processes for preserving product quality and has been widely applied in the food processing industry. Frozen foods are considered to be the next generation of convenience foods, since the global frozen food market is expected to reach USD 307.33 billion by 2020 [1]. The freezing process prevents microbial growth, reduces water activity, and decreases chemical and enzymatic reactions [2]. Therefore, frozen products have longer shelf life and can be transported over long distances. During shipping and storage, one of the risks for frozen products is the potential damage to product quality due to temperature fluctuations. The temperature variations, which are also called freeze-thaw cycles, result in moisture and solute migration and ice recrystallization [3]. These transport and recrystallization phenomena are the primary causes of undesirable quality changes, texture loss, and surface dehydration occurring in the frozen products. For instance, ice recrystallization may increase the crystal size in the final product of ice cream, which would further cause a coarse and icy texture not preferred by consumers. Moisture loss during storage and transportation of frozen potatoes results in dramatic economic losses for food companies and retailers [4].

With the growth of the frozen food supply, there is a demand to reduce product wastage caused by recrystallization and other harmful behaviors during freeze-thaw cycles, such as damage to the texture and taste of frozen products. Therefore, the characteristics of freezing and the effects of temperature fluctuations on frozen foods’ quality have been investigated in several studies [5–7]. The mechanism of nucleation would guide researchers to understand the initialization of ice crystal formation. Furthermore, when freezing temperature drops sufficiently below the glass transition temperature (Tg ), a more stable, rigid, and glassy state can be obtained. It has been shown that foods are most stable if stored in their highly viscous glassy state due to low physicochemical degradation by restricted molecular motion [8]. However, temperature fluctuations may drive a food to a supercooled or molten liquid state above the glass transition temperature, which would rescind the positive effects of mobility restrictions below Tg. In the “Mechanism of Freezing and Experimental Research on Recrystallization” section of this manuscript, experimental results of ice crystallization and recrystallization as a function of temperature fluctuations are presented. The mechanisms of ice crystal formation and propagation are also addressed.

Temperature fluctuations cannot be completely avoided in the frozen food industry because of the fluctuating environmental conditions in food processing plants, storage facilities, shipping containers, and retail stores. The optimum shipping and storage conditions cannot be easily developed by purely experimental designs. Optimizing the freezing process by purely experimental methods is tedious because of the involvement of numerous factors such as the range and time of temperature fluctuations, melting/freezing behavior of different food products and their components, diverse size and shape of packages, and structural and compositional differences in food products. The prediction of quality changes that can occur in frozen food products is crucial for both academic and industrial purposes. The mathematical modeling of heat and mass transfer during freezing allows for improvement in product quality and process design [9]. It also helps food researchers to estimate the refrigeration requirements for freezing systems and allows food engineers to optimize the freezing process. In traditional modeling approaches, heat and mass transfer have been incorporated in the mathematical models. Analytical and numerical methods for heat and mass transfer modeling were introduced in several studies. However, the crystal growth and recrystallization phenomena were not adequately addressed in those models, because most models used only macroscale equations. [10].

The crystal formation and moisture/solute migration exhibit multiscale characteristics [2]. A potato tuber can be used as an example to describe the multiscale characteristics (Fig. 1). The micropores in starch granules, protein bodies, and cell walls can be considered at the microscale (<10 μm) [11]. The whole starch granule, protein bodies, ice crystals, and cell cytoplasm are at the mesoscale (<103 μm), and the tuber tissue is at the macroscale (>1 mm). During freezing, ice crystals begin to form at the crystallization sites where the heterogeneous nucleation starts. This process can be observed in micropores of cell walls and starch granules. Meanwhile, the concentration of solution increases due to solute migration toward unfrozen regions. Vicinal water is adsorbed on the solid polymers in unfrozen regions. At the mesoscale, the vicinal fluid and solid polymers cannot be distinguished from each other and are together labeled as particles. The water migration and diffusion of solutes take place at this scale. At the macroscale, the group of ice crystals, bulk water, and particles consisting of solid polymers and vicinal fluid form a mixture, whose composition can change from region to region. Macrostructure can be visually appealing to consumers and is mainly influenced by the processing conditions, while microstructure is primarily determined by the ingredients [2]. The changes occurring at the microscale can affect the structure at the macroscale. For example, potato tubers under atomic force microscopy were observed to have oblong scratches caused by freeze-thaw cycles [6]. The oblong scratches and rough structure cause expansion of ice in amorphous lamellae or wall channels, which is a microscale characteristic. Therefore, the models that can couple the multiscale phenomena would give a better prediction of transport processes during freezing of food materials. In the “Mathematical Modeling of Food Freezing” section, mathematical models describing the heat and mass transfer during freezing are introduced. Lastly, a hybrid mixture theory (HMT)-based multiscale modeling approach and its suitability for predicting quality changes in foods during freeze-thaw cycles is presented [12, 13].

Fig. 1
figure 1

Multiscale nature of transport processes during freezing of a food material

Full size image

Mechanism of Freezing and Experimental Research on Recrystallization

In general, the freezing process involves ice crystal nucleation, propagation, and maturation. Eventually, if the temperature decreases enough, a frozen product experiences a transition from a liquid/rubbery phase to a solid/glassy phase. The crystalline microstructure plays a crucial role in affecting frozen foods’ texture, appearance, and overall quality. In this section, the mechanisms of ice crystal formation and propagation are summarized, and the results of experimental studies about ice recrystallization are addressed.

Nucleation

Nucleation is the first step in ice formation and it critically affects the crystal size and shape during crystallization. Nucleation starts with a microscopic particle called the nucleus, which can induce the formation and growth of ice crystals. Once a nucleus is in place, other molecules align themselves at the solid-liquid interphase of the nucleation sites. This stage is called crystal growth, in which ice crystals start to mature gradually to a larger diameter by consuming unfrozen water. There are three ways that a nucleus can be created [2, 14]. First, seeding is the simplest way to form a nucleus. When a suspension of the small crystals is added to a supersaturated solution, the solution generally loses its supersaturation and ice crystals are formed around the nuclei and grow in time. The second way to create nuclei is heterogeneous nucleation. Some impurities or different components in a solution, such as biochemicals, starch, and protein bodies, have similar surface properties. Thus, if some particles are present in an unpurified or complex solution, other molecules that have similar surface properties may adsorb on their surface to form a layer to start crystallization. The third type is homogeneous nucleation, which occurs spontaneously without a preferential nucleation site. Homogeneous nucleation can be observed in a very pure system with superheating or supercooling phenomena. For example, pure water freezes at −42 °C rather than at 0 °C (the natural freezing point of water). Therefore, the pure water can remain supercooled as a liquid and eventually exhibits homogeneous nucleation [14]. In food systems, nucleation is primarily heterogeneous due to the presence of impurities.

The rate of nucleation is a function of the amount of supersaturation. During freezing, the number of nuclei increases rapidly when crystallization temperature is achieved (Fig. 2). However, the rate of nucleation decreases with increases in supercooling or supersaturation, since the rising viscosity of the solution prevents the molecules from accumulating and forming nuclei. When a large amount of supersaturation is reached, the nucleation rate becomes approximately zero.

Fig. 2
figure 2

Rate of nucleation as a function of temperature (left) and concentration of solutes (right). When the melting temperature is crossed, the number of nuclei formed rises with increase in supercooling or supersaturation. Then, the rate of nucleation reaches maxima as temperature or concentration increases. While at very low temperature or high concentration which means a large amount of supersaturation, a nucleation rate becomes to zero

Full size image

Glass Transition

Food systems typically develop heterogeneous nucleation, and the solute concentrations are raised through the undercooling process during freezing. The solutes are unlikely to crystallize because of high viscosity from the increasing freeze concentration and low temperature within the food systems. Consequently, non-ideal and non-equilibrium behaviors further dominate the freezing process as the ice content increases and the environmental temperature decreases. A glassy state is defined as a non-equilibrium, amorphous state that has an extremely high viscosity; i.e., 1010–1014 Pas [8]. There are two constraints on the formation of a glassy state. First, water could act as a crystallizable plasticizer, which provides softness and flexibility to crystallize the food. But at higher solute concentrations and with larger quantities of ice, less movable water exists in the frozen food matrix, due to which a glassy state can be achieved [15]. Another crucial constraint for vitrification (glass formation) is that the glass-forming component does not participate in the formation of eutectic mixtures. The eutectic phenomenon is associated with crystallization existing in the components/species of a mixture. Figure 3 illustrates that a mixture (for example, the sucrose solution) crystallizes at a lower temperature than do each component’s melting point, which is called melting point depression. There is a specific point (eutectic point) at which the freezing point depression curves intersect (curves 1 and 2). This intersection is denoted as c in Fig. 3. The temperature at c is the lowest temperature at which the mixture can still remain liquid. However, because of the high viscosities and low temperature during freezing, as well as the faster crystallization rate of water in comparison with solutes, the mixture stays in area d of the phase diagram, where the eutectic phenomenon is rarely able to happen [16, 17]. Therefore, without those constraints mentioned above, when the temperature reaches the glass transition temperature (Tg), a reversible transformation can take place from a rubbery to a brittle glassy state in frozen foods. In a glassy state, the mobility of molecules is restricted and solidification occurs, which results in stability of material structures without any long-range relaxation behavior [18]. Several hypotheses such as free volume, kinetic, and thermodynamic theories attempt to explain the mechanism of glass transition. These theories have been successfully applied to predict glass transition in some practical situations [19]. Free volume theory considers a free volume, where inside segments have a constantly remaining mobility in the glassy state [20]. When the free volume decreases to ∼3% in a material, glass transition is considered to have reached its end and the corresponding temperature is viewed as Tg [21]. However, the free volume theory does not clarify the dynamic nature of glass transition [22]. The kinetic theory assumes glass transition is a dynamic process and includes the effect of heating/cooling rates on glass transition temperatures. Glass transition occurs at a lower temperature when the cooling process decelerates, since more conformational rearrangements are observed in the longer time scale at slow heating/cooling rates [19]. The thermodynamic theory assumes that glass transition acts as a second-order phase change, which means it involves a continuous change in entropy without involving latent heat change. The true equilibrium state of glass transition could be achieved at an infinite observation time. Therefore, according to this theory, a true equilibrium thermodynamic transition is obtained at a temperature 50 °C below the Tg determined by experiments. At that temperature, the conformational entropy of the system is close to zero [23]. Abiad et al. [19] and Roos [24] have presented a detailed discussion of these theories.

Fig. 3
figure 3

General phase diagram for a sucrose solution

Full size image

A state diagram is a supportive tool to present glass transition and the physical states of food components. State diagrams facilitate the study of thermodynamic properties and stability of frozen products [25]. Figure 4 is a typical state diagram providing information on the equilibrium and non-equilibrium phases. The solid (II, III)/liquid (I) phase boundaries and glass transition profile are shown in this figure. When the temperature of a solution is lower than the equilibrium freezing point (Tm), nucleation initiates ice crystal formation and the freeze-concentration process. Hence, the solute concentration continually increases, which further depresses the equilibrium freezing point of the unfrozen phase following the liquidus curve (the arrow near b shows this trend). The temperature of the solution continues to decrease to reach the glass transition point (Tg) during freezing, where the phase transition (from a rubbery to glassy state) occurs. The glass transition line (the arrow near a shows the trend) moves up due to rapid viscosity increase in a non-Arrhenius manner as a function of solute concentration [26]. The glass transition temperature continuously increases by removing water as the plasticizer and the system becomes supersaturated. Thus, the glass transition line is above the position of liquidus curve at a higher solute concentration. The intersection point c of the glass transition line and the extension of liquidus curve is the glass transition temperature corresponding to the maximum-freeze-concentration Tg′. Maximum-freeze-concentration of solute, denoted as Wg′, is reached at Tg′, where no more ice crystals would be formed within the time scale of the measurement [27]. At Tg′, the solute in the glassy state results in a motionless property of the molecules, which is accountable by the remarkable reduction in translational rather than rotational molecular mobility [28]. In Fig. 4, another typical line that a system may follow is marked under equilibrium freezing curve (the arrow near d shows the trend). The system would track this line when extra undercooled water is plasticized during non-equilibrium freezing. A lower glass transition temperature than Tg′ is attained and marked as E on the glass transition line, corresponding to a lower maximum-freeze-concentration Wg. In this condition, food systems may experience various relaxation-recrystallization mechanisms in order to achieve the maximum freeze concentration (Wg′) and reduce the unfrozen water content [8, 29]. The state diagram illustrates how the glass transition and unfrozen matrix affect the stability and quality of a frozen product. State diagrams can also help to determine the optimal storage conditions and suitable temperature and moisture content to process food materials [30].

Fig. 4
figure 4

The state diagram denoting freezing of a water-solute mixture [8]

Full size image

Moisture Migration

Moisture migration is a primary physical change in foods during the freezing process. It causes quality deterioration in frozen products due to factors such as lipid oxidation, enzymatic browning, cell disruption, and recrystallization. Moisture/weight loss from foods, a representative phenomenon of moisture migration, leads to major damage to the food industry’s profitability and is considered a limiting factor for the storage of some frozen foodstuffs, especially meat products [31].

Moisture in frozen foods is lost mainly through evaporation or sublimation driven by both concentration and temperature gradients. These phenomena are likely to follow an Arrhenius-type behavior since they involve a solid to vapor phase change, which is considered the first-order phase transition. In frozen foods, water can simultaneously exist in solid, vapor, liquid, and various types of bound moisture phases, in which diffusion rates would vary. However, due to lack of data, most of the past moisture transport-related modeling studies with frozen foods assumed that moisture movement follows a single-phase diffusion equation with effective diffusivity Dw [32–34].

$$ \frac{\partial \mathrm{W}}{\partial t}=\nabla \cdot \left({\mathrm{D}}_w\nabla W\right) $$
(1)

where W is the concentration of a compound, Dw is the concentration-dependent diffusion coefficient, and t is time.

During the initial stage of freezing, the product undergoes chilling and has a higher temperature than that of the ambient environment. The relative humidity difference between the product surface and the air is also large in the initial stage of freezing. The temperature and humidity gradients significantly affect the rate of weight loss. Hence, it is important to maintain a high relative humidity in the air and increase the chilling/freezing rate. This lowers the surface temperature and minimizes the diffusion of moisture, which further helps to prevent moisture loss at the beginning of the freezing process. During frozen storage, sublimation of water occurs instead of evaporation since ice crystals are formed. The rate of sublimation has a positive correlation with the rise in temperature. Data from several works [35, 36] have indicated that the rate of weight loss doubled for every 7 °C increase in frozen storage temperature. In addition, packaging is also a potential method to prevent the moisture loss, as it has a remarkable effect of decreasing weight loss by more than 50% during frozen storage [33].

Recrystallization

As shown in the phase diagram (Fig. 3), when the ice crystals are formed, the increase in the concentration of solute further depresses the freezing point so that the freezing temperature continuously falls following the liquidus curve. Until the maximum freeze concentration is reached, a portion (10–15%) of unfrozen water is still left in the frozen products. The unfrozen water can diffuse from the serum phase to the crystal surface, causing crystal growth and recrystallization, especially when the temperature fluctuates [3]. Recrystallization contributes to the evolution of crystalline structure and the increase in mean crystal diameter with time. The driving force behind this phenomenon is the minimization of free energy in crystals. The free energy of a crystal is inversely proportional to its radius of curvature. Ostwald ripening, in which large particles absorb smaller ones to grow, is an observed phenomenon of minimizing free energy by increasing the radius of curvature (Fig. 5a). The principal mechanisms of recrystallization are iso-mass, accretive, and migratory recrystallization [34]. Iso-mass recrystallization refers to the change in which crystals gradually convert to spherical and smoother shapes instead of irregular shapes. Since a spherical shape has the smallest surface area for the same given mass, the crystals evolve to a more compact spherical structure due to its lowest surface energy. Accretion is the combination of two smaller ice crystals to form a single and larger one, which starts with a neck formation between the surfaces. Water molecules attach to the neck where the negative curvature has lower surface energy. Eventually, the two crystals merge as the neck becomes planar (Fig. 5b). Migratory recrystallization happens when some smaller crystals melt and move to the surface of larger crystals. The movement or diffusion of the crystals depends on the viscosity of the food materials. Moreover, migratory recrystallization is greatly enhanced by temperature fluctuations that induce variations in ice content. Smaller crystals would completely thaw during warming and migrate into larger crystals during cooling, leading to a gradual growth of the mean crystal size.

Fig. 5
figure 5

a Disproportionation by Ostwald ripening, b accretion of two crystals

Full size image

Instability and temperature fluctuation during freezing also facilitate the ice recrystallization progress and cause critical damage to frozen foods through quality degradation. Recrystallization through thawing and freezing cycles influences the shape, size, and volume of ice crystals, which are the key factors affecting diffusion rates for different compounds moving in and out of the cell interior. Therefore, temperature fluctuations also increase moisture and weight loss in frozen products. Ullah et al. [7] investigated the growth and distribution of ice crystal sizes to determine the frozen food quality. Three freezing cycles were used: from −17 to −16 °C, from −17 to −11 °C, and from −17 to −7 °C. The results show that the pore areas of samples became larger as the temperature fluctuation increased. The total number of pores decreased with the rise in the temperature variation levels, because the solid wall disruption resulted in the merging of smaller pores to form larger ones during the sample thawing and recrystallization. In addition, the starch granule’s surface area in potatoes is enlarged during freezing and thawing cycles [6]. Therefore, the distribution of water molecules changes as the specific surface of granules increases. Some intergranular water and amylose molecules were extracted from the granule pores during freeze-thaw cycles. Also, the low wetting ability of starch resulted from 10 cycles of freezing and thawing, which was caused by damage to the inner structure of granules. Frozen salmon [37], stored beef [38], and other frozen solid foods [39, 40 ] also exhibited a similar trend of larger ice crystal size, smaller total pore numbers, and damage to interstructures due to temperature fluctuations during freezing.

Many foods are frozen quickly to acquire small ice crystals and obtain a freeze-concentrated glassy state using cryogenic freezing techniques. However, recrystallization through temperature fluctuations can offset the advantages of fast freezing. Warming from a glassy state to a rubbery state by increasing the temperature above Tg′ leads to a dramatic increase in intracellular and intercellular diffusion of water and other compounds. This results from not only glass transition but also dilution from melting of small ice crystals [41]. It has been shown that various stabilizers and additives cause an effective deceleration of recrystallization. Regand and Goff [42] discussed that thermodynamic incompatibility between biopolymers and solution heterogeneity (phase separation) inhibited ice crystal growth. It was suggested that these two phenomena promote the water holding ability of ice cream, which is significantly enhanced by the addition of stabilizers and proteins. Therefore, ice recrystallization is reduced, which leads to smaller ice crystal size and distribution in ice cream. They also found that the presence of stabilizers in ice cream actually does not have a significant effect on ice crystal formation or distribution. Other researchers also confirmed that stabilizers do not significantly contribute to the initial freezing properties (nucleation and propagation) of ice cream [5, 43, 44]. However, the stabilizers did retard the growth trend of ice crystals after freeze-thaw cycles during recrystallization [42].

Mathematical Modeling of Food Freezing

The demand for modeling of the freezing process has burgeoned in recent decades, since optimum shipping and storage strategies for frozen foods cannot be developed by purely experimental methods. Food researchers and engineers are interested in exploring freezing time and refrigeration requirements to estimate changes in food products as well as desirable temperature reduction. Through computer simulations, plentiful data can be generated for different refrigeration conditions to compensate for the shortcomings of experimental results [45]. Since numerous factors such as glass transition and melting behavior of foods are involved, a diverse range of shapes and sizes of packages cannot be entirely deliberated by experimental methods. Delgado and Sun [9] noted that most published models predict the cooling process, while only a few models are available for the freezing process. The freezing process is related to a complex situation of heat transfer, which includes the Stefan problem (phase change), removal of both sensible and latent heat, and changes in thermal conductivity, specific heat, and other thermodynamic properties. Mass transfer should also be incorporated in order to obtain physically viable models. Mass transfer also affects heat transfer as energy is carried by moving fluids and solutes. Additionally, phase change occurring in moving fluids influences temperature distribution in frozen products. This section reviews the prediction of freezing time in foods and the models for heat and mass transfer for the freezing process. However, most of the models only explained the physical changes occurring in foods by using a single-scale approach, whereas the recrystallization process as well as moisture and solute migration exhibit multiscale characteristics. A hybrid mixture theory-based multiscale model can be used to couple the microscale changes to mesoscale and macroscale transport mechanisms, which is presented in the last section.

Prediction of Freezing Time in Foods

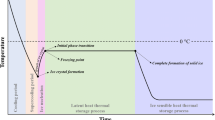
Freezing time is a basic criterion for refrigeration design and a determining condition for the freezing process to reach the final established temperature and control the product quality. The most general definition of freezing time is the time for reducing the initial product temperature to the desired final temperature at the slowest cooling position, which is located at the thermal center of a product [46]. Figure 6a describes the freezing stages of a small water droplet. The process of the droplet cooling down from its initial temperature to its freezing point can be termed as sensible cooling, since the sensible heat is released and the temperature change can be sensed during this stage. When the freezing point is reached, the temperature of the droplet may continue to drop a little because of the supercooling phenomenon. Phase change starts with the formation of nuclei. After supercooling, a large amount of latent heat is released, which increases the temperature of water droplet back to the freezing point and remains for a time in the process region termed as freezing plateau. Once phase change in the water droplet is completed, the temperature continues to fall until the final temperature of the freezing environment is reached. The freezing stages in frozen foods are much more complex than that of pure water since foods contain solutes that cause freezing point depression [47]. Figure 6b shows a characteristic curve of food temperature profile during freezing. The food also experiences supercooling since some water remains liquid during the precooling stage. When the ice crystals start to form, the temperature returns to the freezing point and latent heat begins to be released. However, as the water is freezing into ice crystals, the freezing point is gradually depressed due to increased concentration of solutes in unfrozen domains. As a result, the temperature in the B-C range drops slightly. If one of the solutes in the food becomes supersaturated, the temperature rises are denoted as the range C-D. Once the water and solute crystallization are almost completed, the temperature keeps falling as the sensible heat is removed from the material. Although various stages are not well-defined in frozen foods, the calculation of freezing time still involves solving for prefreezing, phase change, and subcooling periods in many research studies [48].

Fig. 6
figure 6

Distinct stages in the freezing of a a small water droplet and b a food material

Full size image

The prefreezing stage starts from the initial temperature of the frozen product to the point when ice crystals are initially formed. The phase transition does not occur during the prefreezing since the endpoint of temperature in this stage just reaches the freezing point. Therefore, the change in temperature can be described as an unsteady-state heat transfer process, which is a function of time and location in the frozen product [46]. The prefreezing stage can be described by the heat conduction equation:

$$ {\uprho \mathrm{c}}_p\frac{\partial T}{\partial t}=\nabla \cdot \left(\mathrm{k}\nabla \mathrm{T}\right) $$
(2)

where T is the temperature (K), t is the freezing time(s), k is the thermal conductivity (W/m K), ρ is the density (kg/m3), and Cp is the specific heat of the product (J/kg K). This equation shows that the cooling rate of frozen product ∂T/∂t is proportional to its thermal conductivity and inversely proportional to its density and specific heat.

The freezing stage begins when the temperature of food has been cooled to its freezing point. The phase change occurs in this stage, which involves the removal of latent heat. The simplest methods for predicting freezing time are generally related to Plank’s eq. [46]:

$$ {t}_{Plank=}\frac{\rho {L}_f}{T_f-{T}_a}\left(\frac{Pa}{h}+\frac{Qa^2}{k}\right) $$
(3)

or in the form presented by the Biot number [49]:

$$ {t}_{Plank}=\frac{\rho {L}_f a}{2{E}_f h\left({T}_f-{T}_a\right)}\left(1+\frac{B_{if}}{2}\right) $$
(4)

where Ef is the shape factor (1 for a slab, 2 for an infinite cylinder, and 3 for a sphere). Bif is the Biot number, which is defined as

$$ {\mathrm{B}}_{if}=\frac{ha}{2 k} $$
(5)

The Plank equation indicates that freezing time is a function of two groups of factors. One group is related to the product—for example, the latent heat magnitude (Lf), density (ρ), and the thermal conductivity (k) of the frozen product. Additionally, for obtaining an analytical solution, the dimensionless form of Plank’s equation is usually solved for predicting the freezing time of a product with simple geometry, such as an infinite slab or a cylinder or a sphere. The dimension of the product also belongs to this group, which was defined by the product thickness or diameter a and the shape factors using P and Q (Table 1). The second group is related to the process involving the temperature difference between the cooling medium and product (Tf − Ta) and the convective heat transfer coefficient (h). Since Plank’s equation lacks terms for sensible heat and precooling time, it may underestimate the freezing times by 10–40% [9, 50]. More detailed information about the analytical solutions for freezing can be found in the literature [50].

Table 1 P and R values for different geometries in Eq. (3)
Full size table

Salvadori and Mascheroni [51] obtained a simplified analytical method, which is practical to use in industrial calculations and suitable for regular geometries of products. The freezing time t f and thawing time t t can be expressed as the following equations:

$$ {t}_f=\frac{\left({AT}_c+ B\right)\left(\frac{1}{B_i}+ c\right){\left(\frac{T_{c r}-{T}_i}{T_{c r}}\right)}^n{a}^2}{\alpha_0{\left(\frac{T_a-{T}_{c r}}{T_{c r}}\right)}^m} $$
(6)
$$ {t}_t=\frac{\left({AT}_c+ B\right)\left(\frac{1}{B_i}+ c\right){\left(\frac{T_i-{T}_{c r}}{T_{c r}}\right)}^n{a}^2}{\alpha_0{\left(\frac{T_{c r}-{T}_b}{T_{c r}}\right)}^m} $$
(7)

where m, n, c, A, and B factors are dependent on geometric shapes and are tabulated in Table 2. T c is the thermal center temperature, which represents the end point of the freezing/thawing process. T cr is the initial freezing temperature, and T a /T b are the cooling/heating medium temperatures, respectively. Equations (6) and (7) are suitable for foods with a high water content and continuous structure [51].

Table 2 Values of constants of Eqs. (6) and (7)
Full size table

[52] also proposed a graphical method to predict the freezing times of foods with high water content, which was based on dimensionless numbers such as the Fourier, Biot, or Kossovitch numbers. Delgado and Sun [9] reviewed different empirical freezing time prediction methods based on Plank’s equation. They elaborated the modified functions and variables in those equations and illuminated the applicability and limitations of the equations in different geometries.

Numerical techniques can provide more accurate and precise results for nonstandard geometries for modeling freezing time with the help of computers. Numerical methods can also be used to analyze the phase change and variable thermal properties. Numerical methods can also avoid some of the assumptions required for analytic methods. The numerical solution of Eq. (2) can be obtained for one-, two-, or three-dimensional geometries by discretizing the space domain and time variable using techniques such as the finite element method (FEM) and the finite difference method (FDM). The specific heat (cp) in Eq. (2) is considered the apparent specific heat of the food, which includes latent heat effects:

$$ {c}_{app}=\frac{dH}{dT} $$
(8)

The apparent specific heat presents an inherent discontinuity at the freezing point of the product, indicating the removal of latent heat. Figure 7 shows a sharp peak in the specific heat curve around the freezing point [53]. The latent heat would be ignored if the temperature changes across this peak during a large time increment. Therefore, to include latent heat, the enthalpy form of Eq. (2) can be used:

Fig. 7
figure 7

Specific heat of food materials as a function of temperature

Full size image
$$ \uprho \frac{\partial H}{\partial t}=\nabla \cdot \left( k\nabla T\right) $$
(9)

where H is enthalpy.

The FDM and FEM are frequently used in the numerical methods for solving PDEs. FDM is a simple and efficient tool for obtaining the solution for simple geometries. It uses a boundary-fitted square grid with arrayed nodes in the calculation domain. For each node, Eqs. (2) or (9) are discretized with the temperature gradient. [54] successfully predicted the phase change problem during freezing and thawing using FDM based on the Lees scheme for a range of geometries. Ozisik [55] has also discussed the detailed application of FDM in heat transfer [55]. In FEM, the object with irregular geometry is divided into small elements. The adjacent elements share some nodes on their overlapping boundaries. Both FDM and FEM can be used as tools to implement predictive models for the freezing process [56, 57]. The phase change problem and prediction for various thermal properties occurring in freeze-thaw cycles in frozen products can be analyzed using numerical solutions.

Heat and Mass Transfer Models

As mentioned in the “Moisture Migration” section, moisture/solute migration has important implications for weight loss and product quality during the freezing process. Heat transfer is always accompanied by mass transfer since thermal energy is also affected by diffusion of fluids and solutes. With the addition of a transport term, Eq. (9) can be coupled with the mass transfer equation and expressed as

$$ \rho \frac{\partial H}{\partial t}=\nabla \cdot \left( k\nabla T\right)+\nabla \cdot \left({H}_w{\dot{m}}_w\right) $$
(10)

where H w is the enthalpy of the diffusing moisture/solute and \( {\dot{m}}_{w\ } \) is the mass flux, which follows Fick’s law:

$$ {\dot{m}}_w=-{D}_w\nabla W $$
(11)

D w is the diffusivity of moisture/solute and W is its mass concentration. W can be obtained by solving Fick’s second law (Eq. 1). When fast moisture transport and vapor flow are involved, a general transport equation that implements Fickian and Darcian terms can be used as discussed in the following section [13].

HMT and Its Suitability to Model the Freezing Process

In traditional modeling approaches, heat and mass transfer equations have been solved to generate simulation data for the freezing of foods [58]. However, a clear understanding of crystal growth and recrystallization mechanisms was not achieved, since most models only used macroscale equations for weight/moisture loss calculation [10]. Hybrid mixture theory is a powerful method to integrate multiscale mechanisms to estimate physical changes and general transport mechanisms occurring within a food matrix. HMT can also be used to predict a frozen product’s quality changes during the freezing process. The microscale laws of mass, momentum, energy, and entropy balance are volume averaged twice to obtain equations at the mesoscale and macroscales [12, 59]. The microscale balance laws are first averaged over the solid-vicinal fluid domains to achieve the mesoscale equations. The mesoscale equations are further averaged over the solid-fluid mixture and bulk phases to obtain equations at the macroscale. At macroscale, the constitutive theory is formulated to close the system. This involves selecting the dependent and independent variables to describe material behavior. Entropy inequality is exploited to impose restrictions on equations using the Coleman and Noll method [60]. This results in equilibrium, near-equilibrium, and non-equilibrium relations, which are thermodynamically and physically viable. Examples of these relations are the chemical potential equation, near-equilibrium capillary and swelling pressure relations, generalized Darcy’s law, generalized Fick’s law, thermomechanical stress equation, and non-Fickian transport equation. By means of upscaling, the effect of transport mechanisms occurring at the microscale is incorporated into macroscale equations, which are solved for thermomechanical processes. Therefore, the material coefficients showing in the macroscale equations can be easily measured or obtained via macroscale experiments and conventional studies. Solving upscaled equations also saves significant computational time compared to the time needed to solve microscale equations. HMT has successfully explained the thermomechanical behavior of swelling and shrinking porous media like clays [61], expansion of starch during extrusion [62], and drying of corn kernels [63].

Freezing and thawing involve phase changes, crystal growth or decay, moisture and solute migration, and microstructural transformation incorporating multiscale characteristics in the food matrix. HMT can include crystal growth in transport equations via source/sink terms in conservation laws. The transfer of thermodynamic quantities occurring between the phases during freezing or thawing can also be considered via source/sink terms [13]. During freezing or thawing, moisture migrates in both liquid and vapor forms and influences the interactions between different phases (liquid, vapor, and solid). The ice crystals at the nucleation sites grow or melt due to continuous accumulation (or depletion) of water molecules. The growing or shrinking crystals and moving water are also involved in thermomechanical interactions with the surrounding food matrix, which affects the quality of food products. These phenomena can be modeled using the following mass balance and generalized Darcy’s law eqs. [13]:

$$ \frac{D^s\left({\varepsilon}^{\alpha}{\rho}^{\alpha}\right)}{ D t}+\nabla \cdot \left({\varepsilon}^{\alpha}{\rho}^{\alpha}{\boldsymbol{v}}_l^{\alpha, s}\right)-{\varepsilon}^{\alpha}{\rho}^{\alpha}\frac{{\dot{\varepsilon}}^s}{\varepsilon^s}={\sum}^{\beta}{\widehat{e}}^{\alpha}\kern0.75em \mathrm{where}\kern0.5em \alpha, \beta = w, g;\alpha \ne \beta $$
(12)
$$ {\boldsymbol{v}}_l^{\alpha, s}=-\left(\frac{K^{\alpha}}{\mu^{\alpha}}{\varepsilon}^{\alpha}\nabla {p}^{\alpha}+{\varepsilon}^{\alpha}{D}^{\alpha}\nabla {\varepsilon}^{\alpha}+{\varepsilon}^{\alpha}\frac{K^{\alpha}}{\mu^{\alpha}}{B}^{\alpha}\nabla {\dot{\varepsilon}}^{\alpha}\right)\kern0.75em \mathrm{where}\kern0.5em \alpha = w, g $$
(13)

where ε α is the volume fractions of the vapor/ liquid phase, and ε s is the solid phase volume fraction. The material time derivative (D s/Dt) is taken with respect to the solid phase. p α is the physical pressure of water/gas phase in the food matrix. K α is the permeability of the surrounding polymeric matrix, μ α is the dynamic viscosity of the water/gas phase, and B α is the mixture viscosity [13]. The rate of evaporation (or condensation) can be denoted by \( {}^{\beta}{\widehat{e}}^{\alpha} \), which is a source/sink term representing the mass exchange between the α and β phases. This term is absent in the microscale equations but appears in the macroscale equations during the averaging procedure. By applying HMT to the freezing problem, the rates of sublimation \( {}^s{\widehat{e}}^v \) and crystal-growth \( {}^w{\widehat{e}}^s \) terms are expected to rise. The rate of sublimation relation can be used to calculate the weight loss from the frozen product to the atmosphere, and the rate of crystallization relation would provide texture- and structure-related information for the frozen food at a cellular scale. Therefore, the HMT is a powerful method for coupling the microscale changes to mesoscale and macroscale transport mechanisms, to associate the effect of recrystallization happening in the microscale with the phenomenon of moisture loss at meso/macroscales during the freezing process.

Due to the complexity of the involved transport mechanisms and the associated color and microstructural and textural changes in frozen foods, experimental work can be combined with the modeling of solute, moisture, and heat transport processes. For instance, the experimental work can involve quantification of ice crystal size, size distribution, and ice volume fraction by using X-ray microcomputed tomography and scanning electron microscopy of food samples subjected to simulated conditions of temperature fluctuations encountered during industrial storage and shipping. By using quantification data, the relationship between the changes of ice crystal size and corresponding textural damage to the product can be established and implemented in the model. The developed model, in turn, will be applicable to predicting the energy consumption and optimzing the refrigeration conditions. Through numerical simulation of modeling equations and validation of experimental results, the optimal freezing storage and shipping conditions can be determined.

Conclusions

This paper briefly reviewed the mechanism of ice crystal formation and propagation and presented experimental results of ice crystallization and recrystallization to illustrate the effect of temperature fluctuations. Aside from the experimental work used to investigate the phenomena occurring in the freezing process, the mathematical modeling offers complementary information to predict the process of heat and mass transfer during freezing. Analytical and numerical methods combining heat and mass transfer can calculate the cooling time and facilitate the design of refrigeration systems, which involve removal of sensible and latent heat from the product and prediction of weight loss during freezing. Only single-scale mechanisms can be addressed using the traditional models. Thus, the hybrid mixture theory based on multiscale models would allow for predicting not only the transport of moisture, solutes, and heat but also the associated quality changes in the food matrix.