Abstract
Given the complexity in composition and the various environmental conditions to which foods and pharmaceuticals are exposed during processing and storage, stability, functionality, and quality are key attributes that deserve careful attention. Quality and stability of foods and pharmaceuticals are mainly affected by environmental conditions such as temperature, humidity, and time, and for processing conditions (e.g., shear, pressure) under which they may undergo physical and chemical transformations. Glass transition is a key phenomenon which is useful to understand how external conditions affect physical changes on materials. Consequently, theories that predict and describe the glass transition phenomenon are of a great interest not only for the food industry but also it extends to the pharmaceutical and polymer industries. It is important to emphasize that the materials of relevance in these industries are interchangeably sharing similar issues on functionality and their association with the glass transition phenomenon. Development of new materials and understanding the physicochemical behavior of existing ones require a scientific foundation that translates into safe and high-quality foods, improved quality of pharmaceuticals and nutraceuticals with lower risk to patients, and functional efficacy of polymers used in food and medicinal products. This review addresses the glass transition phenomenon from a kinetics and thermodynamics standpoint by presenting existing models that are able to estimate the glass transition temperature. It also explores traditional and novel methods used for the characterization of the glass transition phenomenon.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Although most foods, and in a lesser extent pharmaceutical, are encountered at states that are far from equilibrium, the properties of these materials are commonly determined assuming equilibrium states. However, the glassy state of materials corresponds to a nonequilibrium solid state, in which the molecules forming the material are randomly arranged occupying a volume larger than that of the crystalline state having a similar composition. These glassy materials are referred to as amorphous solids [72, 97, 159, 188]. A glassy material is formed when a melt or liquid having a disordered molecular structure is cooled below its crystalline melting temperature, T m, at a rate sufficiently fast to avoid rearrangement of molecules that may result in crystallization [58, 99]. The glass transition phenomenon was discovered and started to be discussed in publications around 1930s. Donth [54] gives a list of earlier very enlightening quotes of researchers that observed the transition phenomenon covering a period from 1930 to 1958.
Figure 1 schematically illustrates the effect that the cooling paths have on the formation of crystalline and glassy solids. Moreover, different cooling rates may result in glasses having the same chemical composition but, due to the different thermal history, with different structures and properties. Thus, prediction of these properties does not match up with the idea of the equilibrium state in which the properties are uniquely determined by the material itself and its state. The change in the material structure with different heating or cooling rates, and probably with other treatments, results in the formation of glasses with different levels of energy [206]. This energy is computed by the material entropy, enthalpy, or a combination of these two properties, the free energy. Since glassy solids are considered to be in a state of nonequilibrium, the stability of the material is therefore dependent on several factors, which include temperature, water content, molecular weight and, as discussed, the thermal history undergone by the material before reaching the specific glassy state. Many of these factors affect the temperature range at which a glassy solid transitions into a leathery or rubbery state, a range of temperatures known as the glass transition temperature range [71, 103, 158, 179]. The glass transition temperature range of an amorphous material affects its thermomechanical properties [12, 82, 113, 188]. At temperatures below the glass transition range, amorphous solids are stiff and glassy. Upon heating, these solids soften as they exceed their characteristic T g range [188]. At the glass transition range, other physical properties associated with increases in molecular mobility are also significantly affected by and consequently vary accordingly [179]. Unlike plastics and rubbers, plasticized cereals are not brittle at temperatures below their glass transition rather they exhibit limited elasticity. It must be noted that the apparent increase in the elastic modulus observed in these foods is more associated to an increase in their toughness at low temperatures. Glass transition in amorphous solids is a function of temperature, time, composition, molecular weight, and water activity [71, 82, 91, 103, 179–181]. It should be noted that the transition from a glassy state to a rubbery state is a change in the physical state and not a change of phase in the material [58]. Therefore, it can be considered as a kinetic phenomenon instead of one that is described by thermodynamic relationships that are only valid under equilibrium conditions. Many researchers have considered the glass transition phenomenon as a kinetic event [14, 17, 51, 79, 101, 112, 197] as opposed to a thermodynamic transition such as melting. The glass transition phenomenon has been described to have characteristics of a second-order transition [30]. That is, during glass–rubber transition of materials in the glassy state, shift in heat capacity, temperature derivative, and coefficient of expansion can be described by smooth changes in these properties, which is clearly opposed to the observed discontinuities in properties such as enthalpy and volume observed during the course of melting of crystalline materials [188, 206]. It is observed that this change in properties such as heat capacity occurs over a range of temperatures rather than at one fixed temperature [148, 206], and could be explained as the need of additional energy to generate an increase in volume so that a larger motion of molecules is allowed [206].
Schematic of two different cooling paths to produce a solid. Rapid cooling (or quench cooling) leads to the formation of a disordered system, an amorphous solid, whereas a slow cooling rate results in an ordered structure, crystal [99]
For a thermodynamic event, the change in Gibbs free energy, ΔG can be calculated from the changes in enthalpy, ΔΗ, and entropy, ΔS, of the system according to the following equation:
For transitions of the first order, the system exhibits changes in enthalpy and entropy, as well as in heat capacity, C p which are associated to the change in the phase of the system; nonetheless, the two phases may coexist only at the transition temperature [84]. Figure 2 shows how enthalpy and entropy vary as a function of temperature before and after a phase transition such as melting. Both thermodynamic quantities are discontinuous at the phase transition and so it does the material heat capacity, C p [36, 84]. During glass transitions, the system does not show changes in entropy, but continuous changes in heat capacity can be observed (Table 1). As indicated in Table 1 the change of the heat capacity of a material during a glass transition is related to the second-order derivative of the Gibbs free energy, and for that reason, the glass transition is considered to be a second-order event or transition [36, 84, 138]. It should be also noted that although the conformational changes occurring during a glass transition may result in changes of entropy of the system, they are small when compared to the corresponding changes in its enthalpy [188, 198].
Despite the intense debate on the subject, the type of transformation driving the conversion from a liquid to a glass upon cooling (and vice versa upon heating) and whether that transition can be described by equilibrium thermodynamics relationships like those used to describe condensation or crystallization is still unknown [109].
Glass Transition Theories
There are known theories describing the behavior of polymers and other materials near their glass transition temperature range. These theories have been applied to predict glass transition of foods and pharmaceuticals with some success. The major theories include: free-volume, kinetic, and thermodynamic theories. Although all three examine different aspects of the glass transition phenomenon, they can be incorporated to describe a number of systems [188]. In addition to these theories, the typical second-order transition temperature observed during the glass transition event has been characterized either as an iso-viscous [29, 100] or an iso-free volume state [63, 68]. Although not directly related to foods, new models have been developed to describe the mechanical response of polymers and thermoplastic elastomers [13, 170].
Free-Volume Theory
The space within the polymer domain that is available for rotation and translational movements is considered as a free volume that will favor the mobility of macromolecules. It may also be thought of as the excess volume which is occupied by voids [122]. Above the glass transition temperature range, the free volume increases linearly with temperature as does the mobility of the polymeric molecules. When a polymer, above the glass transition temperature range, is cooled, the decreasing free volume reaches a point where there is insufficient space for long-range molecular motions [188]. The free volume can also be defined as the excess volume which can be redistributed freely without energy change [198].
The free-volume theory explains the dependence of the glass transition temperature with pressure, crosslink density, and molecular weight of the system. As pressure increases, the free volume decreases, and to maintain the molecular motion characteristic of the rubbery state, the temperature must be increased, thus resulting in an increased measured glass transition temperature range [59]. An increase in the glass transition temperature can be observed as the crosslink density of polymers increases mainly due to an effective decrease in the free volume [66, 117]. As for the effect of molecular weight on the glass transition temperature, earlier studies have been conducted [59, 102] showing that as the molecular weight of the polymer increases the free volume decreases and thus the glass transition temperature must increase.
A number of models have been proposed to describe the free-volume concept and explain the glass transition phenomenon. Those theories are described in the following sections.
Fox–Flory Equation
Fox and Flory [63] studied the relationship between glass transition and free volume for selected polymers as a function of molecular weight and the polymer relaxation time, which is a parameter strongly affected by the nature and structure of the polymeric material. The free-volume concept can be seen as the volume that the molecules of the material occupy in the liquid, which for polymeric systems is the vast majority of the space of the total volume. However, part of that volume corresponds to the polymer itself and part is the inaccessible volume that is blocked from access by steric effects [163]. The free volume, v f, of a material having an infinite molecular weight at a specific temperature T, above and below the glass transition temperature can be expressed as
where K is a constant related to the free volume of the polymeric system at 0 K, T is the absolute temperature, and α R and α G are the volume expansion coefficients of the material at the rubbery and glassy states, respectively. It was found that below the glass transition temperature T g, the local conformational arrangement of the polymer is independent of temperature and molecular weight, thus having the same free volume. Consequently, the glass transition temperature can be considered as an iso-free-volume state. Close to the glass transition temperature, the volume of the system consists on the free volume of the molecules plus a remaining small fraction of the volume that is free to be used for molecular motion. As the liquid is cooled, its density increases and its free volume decreases which slows the mobility of the molecules [163]. For a given polymer, a second-order transition may occur at a temperature at which the fractional free volume, f, of the system reaches a certain critical value [63, 64, 66] where f is defined as the ratio of the free volume occupied by the molecules to the total volume, \( f = v_{\text{f}} /(v_{\text{f}} + v_{\text{o}} ); \) v o and v f are the volumes of the voids and that occupied by the molecules, respectively.
Assuming that the glass transition of polymers is an iso-free-volume state, Simha and Boyer [177] postulated that the free volume, v f, at T g is constant and can be obtained by the following equation:
where v O,R is the hypothetical volume occupied by the material at the absolute zero temperature (Fig. 3), and v is the total volume given as: v = v f + v o. The labels α R and α G in Fig. 3 are the values of the slopes of the volume–temperature relationship at the rubbery and glass states, respectively which as mentioned above are defined as the volume expansion coefficients of the material at these two states. In addition, a relationship between the coefficients of expansion and the glass transition temperature was derived assuming that at T = T g, the free volume fraction is the same for all polymers:
where K 1 is a constant, or by a different expression as
where K 2 is a constant and α L is the coefficient of volume expansion of the material at the liquid state. Studying a wide variety of polymers covering a wide range of glass temperatures, Simha and Boyer [177] determined K 1 as 0.113 and K 2 as 0.164. Experimental results, however, showed a better agreement when Eq. 4 was used. By considering that the volume expansion coefficient is defined as \( {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 V}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$V$}}(\partial V/\partial T)_{P} \) and using Eq. 4, it can be concluded that the iso-free-volume condition holds and the change in the free volume of the polymer at the glass transition temperature is constant and is equal to 0.113 or 11.3% of the total occupied volume [177].
Schematic of the free volume as a function of temperature calculated by the Simha and Boyer [177] approach
Williams–Landel–Ferry (WLF) Equation
Flow is a form of molecular motion that depends upon the relative volume of molecules in a given free space; in other words, flow requires a critical amount of free volume [55]. Thus, it is possible to find out written in many reports that polymer melt viscosity and free volume are correlated. Earlier studies by Doolittle [55] described a relationship between viscosity of nonassociated pure liquids and free space as
where η is the viscosity, v f/v o is the relative free space for a single substance, and A and B are constants.
Based on the above equation and on the assumption that free volume increases linearly above the glass transition temperature, Williams et al. [203] described the temperature dependence of all mechanical relaxation processes using an empirical function. Accordingly, the ratio α T of any mechanical parameter at a given temperature to its value at a reference temperature T S is a function of the temperature. This ratio can be expressed by the equation:
where T S is the reference temperature chosen to be 50 °C above T g and α T is the ratio of the viscosity at temperature T to the viscosity at the chosen temperature T S, i.e., \( \eta /\eta_{\text{S}} \). Alternatively, if the reference temperature is chosen as T g, then the WLF equation can be written as
However, the WLF equation fails to predict material properties at temperatures 50 °C above T S or 100 °C above T g, i.e., at conditions where the behavior of the material deviates from that associated with the glassy state [203]. The WLF equation assigns the value of 0.025 for the free volume at the glass transition temperature for any polymer, as compared to 0.113 calculated by Simha and Boyer [177]. Thus, it is commonly assumed that the WLF equation describes a universal non-Arrhenius effect of temperature on viscosities and relaxation times around the glass transition region [9]. While for a few synthetic polymeric materials the constants given in Eq. 8 appear to be universal, that does not seem to be the case for many synthetic and natural polymers for which and the equation should be written as
where the parameters C 1 and C 2 are merely fitting parameters and calculated from a linear regression on a plot of \( (T - T_{\text{g}} )/\log \alpha_{T} \) versus (T − T g) [132]. The universality of the WLF equation has been also discussed by Yildiz and Kokini [208], who showed that the parameters C 1 and C 2 in Eq. 9 for foods are not universal and they are highly dependent on conditions such as moisture content and water activity, although these two variable are mutually related by the corresponding moisture isotherms. However, this is not one of the few problems in using the WLF equation. Slade and Levine [181] assumed that T g can be approached by iso-viscosity curves but the type of equation describing the WLF model clearly shows that even for small temperature deviations the viscosity of the material would never be constant for temperatures in the vicinity of T g.
Applications of the WLF equation extend beyond the viscosity ratio and the shift factor, α T, can represent the ratio of any mechanical property [58]. The WLF equation has been considered to describe physical changes in food and biological materials [142, 146, 160, 179, 185]. However, since the WLF equation only fits stiffness–temperature relationships that possess an upward concavity, other equations have been developed to better describe the mechanical behavior of biomaterials at and around their glass transition [148]. For example, the stiffness–temperature relationship of a biomaterial at a constant water activity can be described by the Fermi model as
where Y(T) is the magnitude of stiffness or any other mechanical property, Y s is the magnitude of that parameter at the glassy state, T c is the characteristic temperature, and a is a constant. This equation provides a consistent description of the mechanical behavior at and around the glass transition region where the curve has a downward concavity, whereas at temperatures above the glass transition, the curve shifts to an upward concavity [147, 148], and can also describe a plateau in the vicinity of T g of the measured property. It must be noted that all these equations are empirical and provide a fitting that describes the effects of temperature on the mechanical properties of the material. Thus, assigning physical meaning to parameters involved in these equations that may be associated to mobility and material relaxation phenomenon is not appropriate and should be seen with extreme caution.
In addition to the various approaches to explain the free-volume theory and its applications, experimental studies have been conducted to actually measure the free volume and the free-volume distribution of polymeric systems using a technique called the positron annihilation lifetime spectroscopy (PALS) [43, 106, 115, 211]. The PALS is a microprobe that is capable of determining the holes and free volume in a given material by monitoring the lifetime of a positron, a positive charged electron, and a positronium, Ps—a bound atom consisting of an electron and the positron. These studies estimate that the fraction of free volume vary from 2 to 11% of the total volume [115], which is in agreement to the volume fractions determined using more theoretical approaches [177, 203].
Kinetic Theory
The kinetic theory defines the glass transition temperature as a temperature at which the relaxation times of the molecules present in the system are of the same order of magnitude as the time scale of the experiment. This theory examines the effect of the heating/cooling rate and how the system evolves during the glass transition phenomenon taking into account the respective motions of the empty space and the molecules. Thus, decreasing the time frame of an experiment, i.e., the rate of either heating or cooling would reveal an increase in the glass transition temperature. This phenomenon is clearly illustrated in Table 2 [21], which shows the influence of heating rate on the measured glass transition of polystyrene. Higher heating rates are generally associated with shorter experimental time scales, which would provide less time for potential motion of the molecules and consequently result in higher measurable glass transitions. These results led to conclude that glass transition is a kinetically based phase transformation [51]. The effect of heating rate on T g determination is an important consideration that involves the testing itself as well as a way to evaluate the role of T g on the processing and storage of foods and pharmaceuticals. Typical heating rates used during testing vary between 1 and 10 °C min−1 and although they are of the same order of magnitude than rates used in process like drying by air convection, they may result large compared to characteristic times for other processes like spray drying or expansion during extrusion which could be on the order of milliseconds. The situation changes drastically when storage of food pharmaceutical is considered. In general, these products are stored at temperatures below the T g so mobility is greatly reduced and relevant rates could be of days and even years. However, there are reports that even at temperature well below the glass transition these materials experience molecular reorganization approaching to equilibrium, a phenomenon that is known as physical aging. The phenomenon of physical aging has been investigated for many polymers [86], pharmaceuticals [83], and foods [38, 140].
The WLF equation has served to introduce kinetic aspects on the glass transition phenomenon because it suggests a relationship between the viscosity of the material and the glass transition temperature. That being said and since the viscosity is a time-dependent property, particularly when the physical chemical properties of the material change during storage or processing, one could conclude that glass transition is also a time-dependent phenomenon; in other words, a rate-dependent dynamic transition.
Thermodynamic Theory: Entropy Models
The entropy theory, a thermodynamic approach, is based on the assumption that a glass is a stable state of matter that can be achieved by a thermodynamic second-order transition observable by a significant change in the slope of the energy or entropy versus temperature curves [122]. Without that assumption, the extrapolation of the energy and entropy to temperatures below the glass transition temperature would result in values of energy and entropy for the glassy material falling below that of the corresponding crystal [99]. This phenomenon, referred as the Kauzmann paradox, is contradictory because it presumes that the entropy of an ordered crystal is higher than that of the disordered amorphous glassy solid. This temperature is referred to as the Kauzmann temperature, T k [99, 187, 189]. The Kauzmann paradox was explained by Kauzmann himself assuming that super-cooled liquids crystallize before the Kauzmann temperature. Other explanations to justify this paradox referred to a failure of the extrapolation methodology, and that was the main reason to assume changes on the slope of the energy and entropy versus temperature curves at the glass transition region, which would invalidate the extrapolations.
The theory is mainly based on a lattice model described by Flory [60] for polymeric systems, which describes the number of ways that polymer chains and voids can be arranged in a lattice and calculates the respective thermodynamic properties based on those configurations [122]. However, the theory was not able to solve the Kauzmann paradox. Gibbs and DiMarzio in a series of papers modified Flory theory to explain the glass transition phenomenon including the Kauzmann paradox [47, 48, 72]. They assumed that the relaxation time of the amorphous system is controlled by the configurational entropy. Accordingly, in infinitely slow experiments, the glassy phase will eventually reach an equilibrium state and a glass with entropy slightly higher than that of a crystal will emerge; i.e., glass transition occurs when the configurational entropy, S c, reaches a critical small value very close to zero.
Although the thermodynamic theory has not been directly applied to foods and pharmaceuticals, it has been successful in predicting various phenomena that may be associated to the behavior of these materials. These include the variation of the glass transition temperature as a function of molecular weight [131], cross-link density [43], and plasticizer content [3]. Its applications also extend to predict the glass transition temperature of binary polymer blends as a function of its components mass fractions and individual glass transition temperatures [46, 49].
Evaluation of the Glass Transition Theories and Their Applications
Table 3 provides a summary of the basic theories developed to describe the glass transition phenomenon and lists their applications as well as their limitations. In addition to the glass transition theories discussed earlier, there still exist other approaches which are mentioned briefly. These include the mode-coupling theory (MCT) [17, 79, 112], the random first-order theory [207], and the kinetic Ising model of glass transition [67].
The MCT is a kinetic description of glass dynamics; it predicts a critical temperature, T c, at which the dynamic properties of the material, notably particle motion and relaxation, diverge [17, 79, 112]. This theory anticipates a sharp transition in the viscoelastic properties as well as a change in the relaxation behavior of the glass material near the predicted transition, whereas at temperatures below the transition temperature, the theory anticipates a random freeze of the liquid’s configuration [17, 78, 79, 145].
Conversely, the random first-order transition theory builds on the idea that the configurational entropy is a requirement for motions in glasses as described by Adam and Gibbs [3]. However, the difference between this theory and that proposed by Adam and Gibbs is that the latter did not provide an explanation for the relationship between the rearranging activation energy and the microscopic forces within a unit [207].
As for the kinetic Ising model is concerned, it is a microscopic theory based on a kinetic model that involves cooperative spin–flip rates [67]. This model describes the dynamics of the spin system as a single-flip model allowing only a single spin to change state in a different time increment dt. This model predicts the glass transition temperature through the approximation of the spin relaxation time. It defines a critical temperature below which the system is in equilibrium and the spins are frozen resulting in infinite relaxation times. However, above this critical temperature, the system’s mobility increases and relaxation times decrease. This critical temperature is the glass transition temperature which is predicted without assuming underlying thermodynamic events.
Although the glass transition phenomenon has been studied extensively, it is still a controversial subject and has led to the evolution of computer simulations to further explain the transition process. But, even with these simulations, there still exist two schools of thoughts. One proposes that the transition is a thermodynamic event [186, 205], while the other claims that it is purely dynamical or a kinetic event [101, 167]. One can argue from an experimental point of view that the glass transition phenomenon tends to be kinetically driven, a proof of that is the effect of heating/cooling rate on the measured glass transition (see Table 2). However, the agreement of thermodynamic approaches to predict glass transition experimental results [43, 48, 49, 72, 131] suggests that the glass transition can be defined as a kinetically controlled manifestation of an underlying thermodynamic transition with some unique configuration [44]. A compromising approach has been to consider the glass transition as a mixture of thermodynamics and kinetics events, i.e., a small frozen low-energy state within a larger kinetically frozen state which posses a higher energy [26]. This leaves us to accept the fact that there is still no consensus on the basic aspects governing the glass transition phenomenon.
The Effects of Complex Systems and Additives on Glass Transitions
Foods and pharmaceuticals are mixtures of several polymeric and small size components that may interact altering the glass transition temperatures of the pure components. Such systems then exhibit one or more glass transition temperatures. One major challenge is then to be able to predict the glass transition temperature of such mixtures from their known composition and the glass temperatures of the individual components. For this purpose, many models and equations have been suggested and used on food, pharmaceutical, and polymer systems. Some of these models are based on the ideal mixing assumption [42, 77], while others tend to account for the thermodynamic effects of mixing, taking into consideration the entropy of mixing as well as the interactions developed between various components [10, 42, 76, 107, 150, 170, 171]. More frequently used models are discussed in the next section.
Effect of Amorphous Mixtures
The composition of many foods and pharmaceutical products often can be reduced to two major amorphous components. In such systems, the glass transition temperature is affected by those components, their mass fraction, and the possible interaction that may exist between them. There have been many attempts to model this behavior and predict the resulting glass transition temperature of the composite as a function of several variables such as composition and properties of each component. These proposed models are summarized below [42, 62, 77, 90, 107, 121, 150].
Gordon–Taylor Equation
Gordon and Taylor [77] proposed a model to predict the glass transition temperature of binary polymer blends from the glass transition temperatures of the pure polymers, the mass fraction of the components, and their coefficients of expansion in the glassy and rubbery states. Their theory is based on two major assumptions: (1) ideal volume additivity and (2) the change in volume with temperature are linear. The Gordon–Taylor equation is expressed as
where T g is the glass transition temperature of the mixture, x i is the weight fraction, and T gi is the glass transition temperature of component i, whereas K is a constant that is a function of the coefficient of expansion (α) of the components as they change from the glassy (α G) to the rubbery state (α L). Thus, K is given by the equation:
where V i denotes the specific volume of component i at the corresponding glass transition temperature, and Δα i is given as
The parameter K could be calculated by equations that arise from few approaches. For example, Simha and Boyer [177] proposed alternative relations between the thermal expansivity and the glass transition temperature of materials, which are based on an iso-free-volume state. The first of these equations was given as Eq. 4 but is repeated here as
The second equation (Eq. 5) is based on the assumption that the fractional free volume is constant at T = T g [177]; the equation is repeated here as
With these approximations the parameter K can be calculated as
Studies have shown that the Gordon–Taylor equation appropriately describes the dependence of glass transition temperature with the composition for some specific binary mixtures such as methyl acrylate and acrylonitrile (AN) copolymer (Fig. 4). However, for many systems, the Gordon–Taylor equation fails to describe the dependence of the glass transition with composition of the mixture. This might arise when either the glass transition temperature of the system is higher than the glass temperature of the two components or when the two components have close T g values, e.g., for styrene (S) and AN copolymer (Fig. 5) [149]. In other words, the Gordon–Taylor fails when the composition of the mixture has a negligible effect on the measured T g. The Gordon–Taylor equation as well as other equations to predict T g of multicomponent mixtures that are mentioned below are empirical relationships and must be treated as such. Specifically, all what the Gordon–Taylor relationship demonstrates is an exponential decay curve that can be fitted in more than one way if one is allowed to adjust the parameters, specifically the constant K and the T gs of the pure components. However, T g values are material properties and adjustment to fit the experimental data is not recommended. The assumption of a specific “water glass” at cryogenic temperatures must treated with caution, specifically because water has more than one form at those temperatures. Nevertheless, the relevance of its ‘Tg’, even if it were unique, to food drying at 40–50 °C or higher is yet to be explained.
Measured glass transition temperatures of a mixture of polymers MA/AN. Prediction by the Gordon–Taylor equation is also illustrated [149]
Glass transition temperature of copolymer S/AN showing the observed data points [149]
Mandelkern, Martin, and Quinn Equation
Mandelkern et al. [121] introduced an equation to predict the glass transition temperature of polymer blends. Their prediction model is based on the WLF equation and the assumption that at the glass transition temperature, the ratio of the free volume to the total volume reaches a critical constant value of 0.025 [203]. Based on this assumption, the following equation was obtained:
where R is a parameter given by the following equation: \( R = K \cdot (T_{{{\text{g}}1}} /T_{{{\text{g}}2}} ) \) and K is a constant. This equation is similar to that suggested by Gordon and Taylor [77], but for the special case of R = 1 it reduces to the simple relation also known as the Fox equation [62]:
Couchman–Karasz Equations for Binary and Ternary Systems
Couchman and Karasz [42] proposed a model to predict the glass transition temperature of mixtures based on the assumption that such a transition is a thermodynamic event rather than a second-order transition. In other words, they assumed that the entropy of mixing is a continuous function at the glass transition region, which yields the following equation:
where T gi is the glass transition of the component i in the mixture and x i is the mole fraction concentration of the component i. The change in heat capacity is calculated as
where \( C_{pi}^{\text{L}} \) and \( C_{pi}^{\text{G}} \) are the heat capacities of the component i at the rubbery and glassy state, respectively. This equation was also expanded for ternary polymer systems including a third term as
Another form of expressing Eq. 21 is
where K 1–2 and K 1–3 are constants obtained by dividing Eq. 21 by the term ΔC p1, which is the difference in heat capacity for the first component. The two constants in the above equation can be estimated by the Simha–Boyer [177] rule as
Where ρ ι is the density and T gi is its corresponding glass transition temperature of the component i in the mixture.
Other Models and Equations
Although several models predicting T g-composition profiles have been developed, experimental measurements have shown deviations from them. The majority of these equations are based on either the additivity of the volume [62, 77] or the additivity of the flexible bonds [47, 48, 72]. The observed deviations have been previously addressed and it has been suggested that the entropy of mixing as well as molecular interactions may be contributing factors to the disagreement between the experimental T g values and those predicted by these models [10, 42, 76, 170, 171]. Other models have been suggested by Kwei [107], Schneider [168], and Pinal [150]. Kwei investigated various polymeric systems showing S-shaped T g-composition profiles. Consequently, the proposed model can be written in the following expression [107]:
where k and q are fitting parameters, which are assumed to be dependent on the intermolecular interaction between the components of the polymer mixtures [114, 169].
Schneider [168] expanded the Gordon–Taylor equation into a viral-type expression to include the effects of specific interactions between polymers in the blend. Thus, the modified Gordon–Taylor equation can be written as [168, 171]
where K 1 and K 2 are interaction parameters and x 2C is the corrected weight factor for component “2” with the higher glass transition temperature, T g2, given as
Equation 25 is also referred to as the concentration power equation. Applications of this equation on mixtures where the Gordon–Taylor equation could not be applied have been moderately successful. Figure 6 illustrates the prediction capability of the Fox (Eq. 19) and concentration power equation on mixtures of methyl-methacrylate (MMA) and styrene (S) as well as methyl-methacrylate vinylchloride (VC) mixtures. These models have not been applied to food systems.
Recently, Pinal [150] proposed a new model that includes an additional term in the Couchman–Karasz equation to account for the effect of the entropy of mixing on the glass transition temperature. Hence, the modified Couchman–Karasz equation can be written as [150]
where \( \Updelta C_{{p,{\text{m}}}} \) is the heat capacity difference between the liquid and the crystalline forms of the material and \( \Updelta S_{\text{mix}}^{\text{C}} \) is the configurational entropy of mixing that is accessible to the liquid within the time scale of the experiment. This modified Couchman–Karasz model suggests that the configurational entropy of mixing accessible to the liquid during cooling, \( \Updelta S_{\text{mix}}^{\text{C}} \), causes a shift in the glass transition temperature from the expected value. Figure 7 shows a schematic of this effect using data of a glucose–maltohexaose mixture [143]. The temperature T CK in the graph is calculated by the Couchman–Karasz model while \( \Updelta T_{\text{gm}}^{\text{pred}} \) is calculated using the equation suggested by Pinal [150]:
A graphical representation of the effect of the entropy of mixing on the glass transition temperature of a mixture of glucose and maltohexaose (from [143])
As illustrated in Fig. 7, \( \Updelta T_{\text{gm}}^{\text{pred}} \) is the difference between the predicted Couchman–Karasz temperature and the experimentally measured glass transition temperature, T gm.
Effect of Water and Other Plasticizers
Additives can have two opposite effects on the glass transition temperature of a given material. If an additive lowers the T g of a substance, it is called a plasticizer, whereas if it raises the T g of that substance then it is referred as an antiplasticizer [82, 95]. The antiplasticizer phenomenon has been observed on food materials but it has been associated to a moisture toughening effect [11, 137, 190].
Although water is considered to be the universal plasticizer in foods, any miscible solvent or a low molecular weight additive incorporated in an amorphous system almost invariably will depress its glass transition temperature [111]. The effect of a plasticizer on the glass transition can be explained by two mechanisms: (1) the plasticizer molecules screen off the attractive forces between the material molecules and (2) the plasticizer molecules increase the space between the material molecules, both mechanisms provide a greater free volume and freedom for the molecules to move [11]. In other words, when smaller molecules penetrate the interchain spaces of a given network, the average distance between these chains increase and as a result more free volume is created [68]. Table 4 shows the effect of moisture on the glass transition temperature of selected amorphous low molecular weight carbohydrates [139].
Given the use of sugars in foods and pharmaceutical, in the latter mainly used as excipient, and the role that they have in product formulations, it is important to discuss the glass transition of simple sugars and mixtures and how they compare with the glass transition of larger polymeric materials. Roos [156] determined the glass transition and other thermophysical properties (e.g., melting point, heats of fusion) of anhydrous sugars and the same sugars at different moisture contents. In general, lower glass transitions temperatures were observed, and sugar at different moisture contents were well described by the Gordon–Taylor equation. Glass transition of mixtures of low molecular sugars were also determined and described with the Gordon–Taylor equation with some limited success [172]. While comparing the glass transition of sugars with that of polymeric materials, we can observe that they are significantly lower, which can be explained by studies developed by Flory that demonstrated that glass transition of materials decreases with their molecular weight. In fact, the above-mentioned concept and the associated phenomenon have been used in the development of novel thermoplastic biomaterials by using low molecular sugars to plasticize large molecular weight polymeric materials [192].
Various approaches have been considered to estimate the glass transition temperature of a plasticized polymeric material. All theories and models concerning polymer–plasticizer blends assume that an intimate molecular mixture of the components is attained; otherwise, multiple glass transitions may be observed [90, 102, 151]. The simplest relation between the change in glass transition of a system upon adding a plasticizer is given as [151]
where \( T_{\text{g}}^{\text{p}} \) is the glass transition of the pure substance, m 2 is the mass fraction of the plasticizer, and B is a constant. It must be noted, however, that Eq. 29 is only applicable when low concentrations of plasticizer are used [174]. Kelley and Bueche [102] derived a model suitable for a wider composition of plasticizers and that was based on taking into account the effects of polymer–diluent viscosity and free volume on the glass transition temperature. The expression for this model is given as
where \( \bar{V}_{\text{S}} \) is the volume fraction of the plasticizer and α S and α P are the thermal coefficients of expansion of the plasticizer and the polymer, respectively.
Jenckel and Heusch [90] took into consideration the interactions between the amorphous solid (P) and the added plasticizer (S) by including an interaction term to the weighted glass transition temperature values of the pure components. Thus, expression to calculate T g was written as
where D is the interaction constant.
It has been observed that at higher moisture content, the glass transition temperature decreases with increases in moisture content at a higher rate than that observed at lower water content. This is thought to be due to a larger free volume change created by the molecules of water adsorbed on the polymer, which in turn depend on the chemical nature of the polymer [110].
In addition to the existing models that incorporate water content as a mass fraction, Khalloufi et al. [103] tried to introduce a model that uses water activity instead. The mathematical model using water activity proposed by Khalloufi is given as
where \( A = T_{\text{gs}} \cdot K^{2} \cdot (1 - C), \) \( B = K \cdot [T_{\text{gs}} \cdot (C - 2) + C \cdot M_{0} \cdot T_{\text{gw}} \cdot k], \), \( \alpha = K^{2} \cdot (1 - C), \)and \( \beta = K \cdot [(C - 2) + C \cdot k \cdot M_{0} ]. \)
The Guggenheim–Anderson–de Boer (GAB) model, initially used for the sorption of gases into solid substrates, has been found to be suitable to describe the water adsorption of water in many food materials and is given by the expression:
where M is the moisture content in dry basis; M 0 is an empirical parameter, incorrectly called the monolayer moisture content because water is not associated to solid substrates in the form of a monolayer; and C and K are empirical constants probably related to the energies of interaction between the first and further molecules at the individual sorption sites. If that is the case, C and K would be function of the sorption enthalpies given as [5]
where c 0 and k 0 are two parameters known as entropic accommodation factors while H m, H n, and H l are the molar sorption enthalpies of the monolayer, multilayers, and bulk liquid, respectively. The interpretation of these parameters should be treated with caution, as explained above. The GAB model and the meaning of these parameters may be appropriate for the sorption of gases in solid substrates but are far from reality when the interaction of water and solid substrates is considered. Thus, considering that the absorption of water on solid substrates forms a monolayer may be far of reality due to the polarity of the water molecule and its large size when compared to gas molecules. Regardless of that interpretation, the GAB model provides a good empirical description of water sorption in foods. Thus, its use should be seen as a mere predictive model within the experimentally tested range of moisture contents and not as an extrapolation tool out of that range. Leave alone the interpretation of the model “empirical” parameters in terms of thermodynamic and or physicochemical properties.
Since both water activity and T g are closely related to the moisture content of the sample there have been attempts to combine models that describe these relationships. A combined model that combines the Taylor and the GAB equations to establish a relationship between the water activity, a w, and the glass transition temperature was proposed by Roos [157]. Furthermore, Sablani et al. [164] combined water sorption characteristics and state diagrams for abalone to establish stability criteria of this seafood and found some discrepancies between those based on water activity and T g separately.
In addition to the effects of water, the effects of other additives on the glass transition temperature have been investigated. These studies include the effect of lipids and emulsifiers on the glass transition of gluten [94] and the effect of sugar on the glass transition of gluten and amylopectin [93, 96].
Several reports [8, 108] have assigned equal significance to thermodynamic and kinetic parameters on the stability of foods, being the thermodynamic parameters those associated to the water activity, whereas the kinetic parameters are associated to the glass transition phenomenon. Labuza and Hyman [108] described the phenomenon of water migration in multidomain foods and considered that the driven force for moisture migration is the water activity and not the moisture content of the food domain, which can be calculated from thermodynamics concepts that involves the chemical potential of the water. Although the water activity or driven force for the migration of water is important in this water movement process, the dynamics of the process is closely related to the glass transition characteristic of the food domain because it controls the diffusion of moisture. In general, for domains found within the glassy state, molecular mobility and diffusivity of water are extremely slow so stability during storage should be analyzed considering both water activity (thermodynamic) and glass transition (kinetics) concepts. Similar to the approach proposed by Roos [156] and Al-Muhtaseb et al. [5], Sablani et al. [165] combined the GAB equation, which describes the relationship between moisture content and water activity, with the Gordon–Taylor equation that predicts the glass transition of a mixture of two components to describe the stability of abalone.
Effect of Molecular Weight and Cross-Link Density
The effects of both the molecular weight and cross-link density of the polymers on the glass transition temperature have been studied [21, 63, 65, 66, 74, 211]. It is agreed that increasing the molecular weight, M, or the cross-link density, ρ, for a given polymer will cause a decrease in its specific volume, v, which is inversely proportional to the change in M or in ρ. Consequently, this will cause an increase in the glass transition temperature. Fox and Flory [63, 65] indicated that the general relationship between the glass transition temperature, T g, at a given molecular weight, M, was related to the glass temperature at infinite molecular weight, T g∞ , by
with K being a constant dependent on the material, and α R and α G are the corresponding coefficient of expansion for the rubbery and glassy states, respectively. Fox and Loshaek [66] suggested a simple equation that holds for linear polymers and predicts a linear decrease in the glass transition temperature with the molecular weight of the polymer as indicated by the expression:
In addition, Fox and Loshaek [66] accounted for cross-link density by introducing another term in Eq. 35 to obtain:
where K x is a constant and ρ is the number of cross links per gram.
Yu et al. [211], using the positron annihilation lifetime spectroscopy (PALS) method, studied mono-disperse polystyrene having variable molecular weights ranging from 4,000 to 400,000 Da. They observed that polymers with shorter chains have larger free volumes and thus lower glass transition temperatures. Table 5 shows various values of T g determined by differential scanning calorimetry as a function of molecular weight [211]. Figure 8 shows the effect of molecular weight on the glass transition of polystyrene [21].
The effect of molecular weight variation of the glass transition of polystyrene (from [21])
Similarly, an increase cross-link density is expected to cause an elevation of the glass transition temperature. Although these equations could be applied to foods and biomaterials, no studies applying these models have been found in the literature.
Effect of Pressure
An increase in pressure on an amorphous material causes a decrease in the total free volume. From a thermodynamic standpoint, an increase in pressure on an amorphous system will decrease its entropy. Regardless of the reasoning, both assumptions predict an increase in the glass transition temperature [123]. Assuming correspondence between glass transition and a second-order transition, the effect of pressure on the glass transition temperature was expressed as [18, 19, 141]
where Δ represents the difference between the properties above and below the glass transition, and β and α are the compressibility and expansion coefficients of the material, respectively. Experimental results have shown large deviations from the above equation and therefore other variables were introduced to correct those deviations. Thus, Eq. 37 becomes [19]:
where Z is referred to as the Davies and Jones parameter.
Different experimental approaches have resulted in different values of dT g/dP. Table 6 compares dT g/dP values obtained for polyvinyl acetate (PVAc) using three different experimental approaches. Experiment A involves cooling of the liquid under constant pressure, method B involves heating the glass while under pressure, whereas approach C comprises the cooling of the liquid at constant volume under decreasing pressure [19].
Methods for Measuring Glass Transitions
The glass transition temperatures of amorphous food materials as well as pharmaceuticals can be measured by continuously measuring various physical properties as a function of temperature. These measuremets, which may include specific volume, deformation, conductivity, elasticity, and thermal properties (e.g., heat capacity), can determine the glass transition range by identifying the temperatures where these properties change significantly. Owing to the property measured, methods to characterize glass transition can be classified as calorimetric, thermomechanical, volumetric, and spectroscopic methods [82, 173]. These include differential scanning calorimetry (DSC) [12, 92, 153] and temperature-modulated differential scanning calorimetry (MDSC) [23, 61, 85, 87, 124, 155, 183, 184], dilatometry (DIL) also known as thermomechanical analysis (TMA) [25, 80, 125, 201], dynamic mechanical analysis (DMA) also known as dynamic mechanical thermal analysis (DMTA) [12, 153], inverse gas chromatography (IGC) [6, 75, 133, 134, 136], and nuclear magnetic resonance (NMR) [2, 92, 98, 116, 161, 162], dielectric relaxation spectroscopy (DRS) [4, 56, 57, 135, 139], and other emerging technologies such as oscillatory squeezing flow (OSF) [1], thermal mechanical compression test (TMCT) [25], positron annihilation lifetime spectroscopy (PALS) [43, 89, 104–106, 115, 211], thermally stimulated depolarization current (TSDC) [4, 45, 52, 175, 176, 196], and scanning probe microscopy (SPM) also known as atomic force microscopy (AFM) [88, 126–128]. The assignment of the glass transition can vary significantly depending on the property being measured and the method utilized to determine the glass transition. In general, T gs obtained using various techniques may be different and they are closely associated to how sensitive is the measured property to changes in temperature, specifically around the material glass transition region. The way to determine glass transition may also provide differences in the reported T g values. The glass transition temperature is sometimes reported as the onset temperature where the first changes in the monitored properties are observed, or as the inflection point, midpoint of the steepest slope connecting the onset and offset horizontals. Often during DMA testing, the glass transition is determined as the maximum in the tan δ. Therefore, the glass transition temperature has to be reported along with the technique used as well as the set of test conditions under which it was determined [173]. These methods will be discussed hereafter. Many foods and pharmaceuticals are composed of mixtures of components so it is not possible to define a single glass transition temperature. This and the variability observed in the determination of T g with different methods make the definition of a glass transition temperature range a more reasonable material property definition than a single glass transition temperature.
Differential Scanning Calorimetry
DSC is a technique widely used in the food, pharmaceutical, and the polymer industries to measure heat flow and temperature-dependent specific heat as well as phase transitions [166, 199]. DSC can be used to determine glass transitions, in addition to cold crystallization, crystallization, phase changes, melting, cure kinetics, and other reactions such as oxidative stability. The heat flow is measured as the energy required to maintain a nearly zero temperature difference between the sample and an inert reference material as the two specimen are subject to identical temperature schemes in a cooled or heated environment [118, 199]. A DSC test is considered as a closed thermodynamic process that permits no matter exchange but allows energy to be added or removed from the system [206]. As these events take place at a relatively constant pressure, the total heat transferred, measured by the areas under the peaks, is directly proportional to the change of enthalpy (ΔH) of the sample [166, 188, 206]. DSC reports the phase transitions in the sample as peaks, which are enthalpies absorbed (endotherm) or released (exotherm) during the transition. Endothermic peaks are observed in glass–rubber transitions, melting, denaturation, gelatinization, and evaporation, whereas exothermic peaks or enthalpies are associated to freezing, crystallization, and oxidation processes. Figure 9 shows a conventional DSC scan for a pharmaceutical drug (Indomethacin) in its amorphous and crystalline states, showing the glass transition, crystallization, and melting peaks for both samples.
In addition to the conventional DSC, MDSC is an improvement that increases resolution and sensitivity to detect weak transitions or when two transitions occur within the same temperature range. These improvements over the traditional DSC method are achieved through the application of two simultaneous heating profiles: a linear underlying rate and a sinusoidal modulated rate which can be expressed as:
where T 0 is the initial temperature, q is the heating rate, B is the amplitude of temperature modulation, and ω is the frequency [154, 155].
The linear rate provides the same information as that obtained by the traditional DSC, whereas the sinusoidal modulated rate provides information about the reversing and nonreversing components of the heat flow response [85, 154, 155], the former associated to changes of the heat capacity of the material. In measuring the glass transition temperature, MDSC demonstrates a higher sensitivity than the conventional DSC. Rather than measuring the glass transition temperature as a simple shift in the baseline, MDSC measures T g via analysis of the amplitude of the heat flow oscillation [85, 124, 154, 155]. Consequently, since the glass transition is defined as a change in the heat capacity of the sample, this response is thus correlated to the reversing component of the signal. Conversely, the nonreversing component of the heat signal is associated with kinetically controlled events that are dependent on both temperature and time. It is important to mention that by determining glass transition using DSC it is a good practice to run a thermal gravimetric analysis on the sample prior to running the DSC/MDSC test. This is due to the various reasons summarized as follows [194]: (a) evaporation may appear like melting and may cause hermetic aluminum pans to explode if temperature range exceeds 130 °C, (b) the existence of water/solvent may lower during heating and broaden the glass transition temperature, (c) it is easier to monitor decomposition since DSC does not provide useful data regarding the structure of the material under investigation, and (d) as a guideline, the upper temperature limit of the DSC experiment should not exceed that of 5% weight loss due to decomposition.
An aspect that needs to be discussed when determining thermal transitions of foods and pharmaceuticals, specially using DSC, is related to the structure of the samples. Often these materials, either due to their inherent natural properties or transformations by processing, exhibit both amorphous and crystalline structures. A typical example is starch granules which have crystalline and amorphous structures. A review by Tester et al. [193] describes with large details the structure of starch granules. During gelatinization, water is essential because it acts as a plasticizer favoring gelatinization. The plasticization or mobility-enhancing effect is visualized first in the amorphous zone of the starch which is at the glass state [16]. When the temperature is at the T g of that amorphous zone, a small transition can be detected by DSC measurements. However, at those temperatures, crystalline regions which are contiguous to the amorphous zones start to melt and the energy absorbed during that melting process is significantly larger than the energy associated to the glass transition. As a consequence, the glass transition of these starches is not usually evident using DSC and other techniques should be used.
Thermomechanical Analysis /Dilatometry
As a material passes from the glassy to the rubbery-leathery state, it experiences an increase in its free molecular volume [29, 178, 198, 204, 206]. Thermal expansion and its relation to glass transition have been extensively examined [29, 125, 177, 178, 201, 204, 212]. This has led to new methods and techniques to measure the thermal expansion as a function of temperature to locate the glass transition temperature of various materials.
DIL is thus a thermoanalytical method used for the study and measurement of dimensional changes of samples, shrinkage, and expansion, as a function of temperature. Since these changes may be either linear or volumetric, DIL focuses on direct measurement of volume, density, and linear displacement [125, 204, 212]. The thermal expansivity of the material is then calculated based on the following relationships:
-
Linear coefficient of expansion, β, given as
$$ \beta (T) = {\frac{1}{L}} \cdot \left( {{\frac{\partial L}{\partial T}}} \right)_{\sigma } $$(40) -
Volumetric coefficient of expansion, α, given as
$$ \alpha (T) = {\frac{1}{V}} \cdot \left( {{\frac{\partial V}{\partial T}}} \right)_{P} $$(41)
As a result, dilatometry can be used to measure volumetric expansions, phase transitions as well as determining glass transition temperatures [188, 206]. Conversely, TMA is a technique that measures deformation of a material as a function of temperature under a nonoscillatory load like, for example, compression, tension, flexure, or torsion [118]. Thus, thermodilatometry and TMA are closely related methods that apply similar principles for testing and data collection [31].
TMA technique may be operated using various modes. For example, measurements can be done through penetration mode using probes of different geometries that penetrate the sample or by measuring relaxation/deformation as a compression, tensile, flexural, or torsion force is applied on the sample [31, 118]. Data obtained—like for example sample deformation, volumetric, or linear—is recorded and plotted as a function of temperature. Figure 10 summarizes the results obtained using the dilatometer for poly(cyclohexyl methacrylate) (PCHMA; Fig. 10a) and poly(cyclopentyl methacrylate) (PCPMA; Fig. 10b) [178, 204]. The glass transition temperature can be located as point of change in slope of the specific volume–temperature graphs (Fig. 10a, b), or as the inflection point on the thermal expansivity–temperature graphs (Fig. 10c, d).
a, b Specific volume as a function of temperature for PCPMA and PCHMA, respectively, selecting the glass transition temperature as the point of change in slope. c, d Thermal expansivity of PCPMA and PCHMA, respectively, as a function of temperature showing the glass transition as the inflection point (from [204])
Dynamic Mechanical Analysis
DMA or so-called DMTA is a technique that can provide information about the mechanical and thermomechanical properties of a given material. The DMA applies a sinusoidally oscillating either stress or strain to the sample causing a sinusoidal response, which depending on the applied input will be either the strain or the stress, respectively [129]. The relationship between the stress and the strain of the sample allows the calculation of the sample mechanical modulus often known as “stiffness.” The time shift between the stress and the strain is a measure of the friction generated on polymer molecules when it is deformed. The time shift is used to calculate the viscoelastic properties of the material such as the loss modulus and storage modulus. The DMA also allows various testing modes allowing sweep across temperature or frequency [129] while staying in the linear viscoelastic region of the material under investigation.
Given the nature of the testing technology, the first step in the DMA testing is to prepare tablets loaded and pressed under very high pressures (5000 lbs or more) to avoid the fracture of the samples during measurements. That raises questions as to how the sample material is affected by the sample preparation. An alternative testing setup that may be used is a powder cell, which is available from TA Instruments (New Castle, DE, USA), and can be attached to the dual cantilever clamp on the DMA. The cell allows one to characterize the transitions of powdery materials as temperature changes by observing the peaks changes in the calculated elastic and viscous complex moduli, also called apparent moduli. Since the geometry is not well defined and the material is in a powdery state, these calculated moduli do not provide fundamental measurements of the elastic and viscous nature of the sample, instead they only provide a qualitative assessment of these properties. The use of the powder clamp, however, helps to prevent changes in the material before testing. That is important particularly for active pharmaceutical ingredients which have a structure that can be affected by the extreme pressure utilized to form the tablets. Those implications may also bear a large importance for the testing of food materials whose structure could be affected by the application of high pressure. The DMA is able to detect short-range motion before the glass transition range is attained and hence, the onset of main chain motion [92]. Figure 11 is a typical representation of the glass transition measurement of an amorphous drug using the powder cell with the dual cantilever fixture on the DMA [1].
Dielectric Relaxation Spectroscopy
Each spectroscopic technique is related to a specific property of the sample. For instance, measuring the dielectric response of a given material upon changes in temperature allows the study of its structural characteristics [200]. DRS is a method that is based on the property of a material that responds to an external electrodynamic action. DRS assesses both the magnitude and the time dependence of the sample’s electrical polarization, a property closely related to the sample structural characteristic [182, 200]. Thus, dielectric spectroscopy is capable of measuring the molecular mobility as well as the structural characteristic of a given material over a wide temperature and frequency (10−6–1015 Hz) range [200]. Specifically, dielectric spectroscopy measures the relaxation behavior of the material as it is subject to a temperature ramp over a given polarizing frequency range. Consequently, for amorphous materials, two different relaxation processes can be determined: the principal α-relaxation process, which is associated with the glass–rubber transition in the amorphous region, whereas the secondary β-relaxation process is associated with intramolecular oscillations of small dipolar groups. The principal α-relaxation exhibits a non-Arrhenius temperature-dependent behavior at temperatures above the glass transition temperature and an Arrhenius behavior at temperatures below the glass transition region. However, the β-relaxation can be measured only at higher polarizing frequencies and is described by an Arrhenius temperature-dependent behavior [4, 27, 39, 57] before and after the glass transition. The dielectric response can be expressed of various forms, such as: relaxation times, complex dielectric permittivity, ε*, with real (ε′) and imaginary (ε′′) components, dielectric loss factor, \( \tan \delta = \varepsilon^{\prime \prime } /\varepsilon^{\prime } , \) complex dielectric modulus, \( M^{*} = 1/\varepsilon^{*} \), or absorption conductivity, σ. All these parameters are mutually related and equivalent in the sense of information they provide [4, 200]. Figure 12 shows the variation of tan δ as a function of temperature for amorphous dry d-mannose and for a mixture containing 10% w/w water. As illustrated, these results enable a very visible localization of the glass transition temperature of the material at the temperature where the maximum in the tan δ is observed [139].
The variation of tan δ with temperature at 1 kHz for dry amorphous d-mannose and its 10% w/w water mixture (from [139])
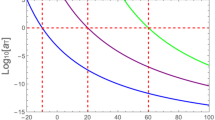
Figure 13 illustrates measured relaxation times in the α-relaxation process as a function of the inverse of the absolute temperature for maltitol [57]. It is clearly observed that there is a change in the dynamics of the principal α-relaxation at the glass transition temperature.
Characteristic relaxation times deduced from dielectric measurements for maltitol, plotted as a function of 1/T (from [57])
Dielectric relaxation spectroscopy has been applied to foods [34, 37, 139], pharmaceuticals [4, 7, 56, 57, 182], and polymers [15, 28, 39, 135] to determine their glass transition temperatures.
Nuclear Magnetic Resonance
NMR spectroscopy provides a powerful tool to study the dynamic and structural features of condensed matter. Pulse NMR has been reported as an alternative method to study the glass transition phenomenon [2, 92, 98, 116, 161, 162]. NMR is able to measure the spin–spin relaxation phenomenon during a glass transition event. It has been reported [2] that the spin–spin relaxation time, T 2, of a rigid component is related to its glass transition. Conversely, spin–lattice relaxation time, T 1, is associated with mobile molecular classes [2, 162]. Figure 14 shows a schematic on the relationship between the NMR relaxation times, T 1 and T 2, and molecular mobility also referred to as the molecular correlation time, τ c [2].
Schematic diagram showing the relationship between the NMR relaxation times, T 1 and T 2, and the molecular correlation time, τ c (from [2])
Applying a pulse NMR, the decay of the pulse signal has two components that can be fitted using the Gaussian and Lorentzian curves of the form [92]:
where h is the signal intensity at time t and h R and h M are proportional to the number of protons in the rigid and the mobile states, respectively. Based on this relationship, Kalichevsky et al. [92] suggested that T 2 is related to the rigid lattice limit temperature, T RLL, which is associated with the glass transition temperature obtained using other calorimetric methods, e.g., DSC. At temperatures below the glass transition, T 2 relaxation time tends to be constant and begins to increase when the temperature approaches the glass transition range due to the increase in molecular mobility. This has been reported by Ruan et al. [162] and Ablett et al. [2]. Figure 15 shows a representative plot of relaxation time versus temperature obtained using pulse NMR for maltodextrin. A change in slope is indicative of the glass transition temperature [162].
T2 relaxation time as a function of temperature for maltodextrin samples [162]
Positron Annihilation Lifetime Spectroscopy
PALS is a microprobe that has been developed to directly determine the local free-volume properties in polymeric materials. Information obtained by PALS contains data about the dimensions, distributions, and concentrations of voids within the material. This is obtained by monitoring the lifetime of positrons and positroniums, Ps, in a given material. A positron is the antiparticle or antimatter of an electron having a charge of +1, whereas a positronium, Ps, is a neutral bound atom consisting of an electron and a positron. The phenomenon in which the electron and positron meet and vanish into other forms of energy is called annihilation. The lifetime of positrons in matter is a function of the electronic environment. In other words, the measured lifetimes are those of a thermal positron in the material under consideration. Since many studies have correlated the glass transition to changes in the free volume, this method has found its way into the polymer industry as a method to measure glass transition phenomenon [43, 89, 104–106, 115, 210].
It is indeed appropriate to mention the theory behind the PALS method. As discussed, a positronium is a bound atom consisting of an electron and the positron. Consequently, there are two types of positronium, Ps: the first is called the ortho-Positronium, o-Ps, where the spins of the two particles are parallel, and the second is called the para-Positronium, p-Ps, where the spins are antiparallel. The o-Ps has a lifetime of 142 ns in vacuum, whereas the p-Ps has a lifetime of 125 ps in vacuum. The o-Ps is mainly the positronium of interest and is monitored to obtain information about holes and the free volume. As has been mentioned, in PALS, the lifetime of these particles, τ, is measured as a function of temperature. The lifetime is inversely proportional to the integral of the positron, ρ +(r), and electron, ρ −(r), densities at the region of investigation and is given as [115]
where K is a constant related to the number of electrons involved in the annihilation. A correlation between the mean o-Ps lifetime and the mean radius of the holes, R, designated as τ 3, can be calculated as
where τ 3 and R are in nanoseconds and Angstroms, respectively, and R 0 is given as R 0 = R + ΔR. ΔR is 1.656 Å obtained from observed o-Ps lifetimes and known as the mean hole radii in porous media. From Eq. 44, the mean free volume hole size can be estimated by simply measuring the o-Ps lifetime. PALS is sensitive to hole sizes ranging between 1 and 10 Å, whereas larger hole sizes lay beyond the detectable region of PALS [115]. As a result of the PALS analysis, plots of τ 3 versus temperature are obtained. Figure 16 illustrated a typical τ 3–temperature plot for polystyrene [115]. As observed, there is a significant change in the slope of the τ 3–temperature curve as the material goes through the glass transition phase. Thus, the glass transition temperature is determined as the inflection point in that curve. The τ 3–temperature curve can be correlated with the rate of increase of the free volume with temperature as the molecular motion within the material intensifies. In addition to the lifetime measurements, PALS measures the intensity of the o-Ps as a function of temperature. However, the variation of the intensity, I 3, with temperature is more complex. It has been reported that the intensity tends to increase at temperatures below T g and then flattens out above the glass transition temperature [115, 120]. Nonetheless, it is valuable to mention that T g values obtained from PALS sometimes tend to be lower than those obtained using other methods such as DMA or DSC. This is attributed to the longer measurement times, about an hour for each temperature, while using the DSC or DMA, data is obtained within seconds or minutes [115, 120].
Mean o-Ps lifetimes for polystyrene as a function of temperature also showing the glass transition temperature which agrees with that determined by DSC (from [115])
Oscillatory Squeezing Flow
The OSF method is a novel technique, which is a modification of that presented by Mert and Campanella [130]. It has been used to measure the thermomechanical properties of powders. This method is based on the same principles and concepts of the well-known rheological technique called squeezing flow [35]. However, the new method has technological improvements. It involves small amplitude oscillations at random frequencies up to 10 kHz. The testing apparatus can be attached to a texture analyzer to control the force or stress exerted by the upper plate on the powder sample.
Details of the experimental setup and the pertinent equations utilized to determine the glass transition of powder systems are given elsewhere [1]. Plots showing normalized stiffness, obtained as the ratio of the stiffness values obtained in an experimental run to the value of the maximum stiffness obtained in that run, as a function of temperature for a pharmaceutical material (indomethacin) is given in Fig. 17 [1]. Values are indicated by triplicate to indicate the reproducibility of the measured T g.
Thermal Mechanical Compression Test
TMCT is a novel technique developed to measure glass transition temperatures by determining changes in either force—force relaxation mode—or monitoring displacement—creep mode [24]. This novel technique consists of a temperature-controlled cell which is attached to a texture analyzer. In the force relaxation mode, a constant deformation/strain is applied to the sample as it is heated. Consequently, changes in the compression force are monitored and recorded as a function of temperature. As the material/powder reaches its transition temperature, the particles will increase in mobility and thus a decrease in the applied compression force is observed [24]. During the creep mode, the deformation of the sample, subjected to a constant force/stress, is recorded while the temperature of the test is changed. As the material transitions from the glassy to the rubbery state, the particles become more mobile and that is reflected by an increase in displacement [24]. This technique shows comparable results with those obtained from traditional methods such as DSC and TMA. Figure 18 shows a typical graph of displacement versus temperature obtained by the TMCT technique. This method has been utilized to determine the glass transition of skim milk, specifically for this case a T g of 59.1 ± 1.6 °C was found and compared to 68.8 ± 0.6 °C as determined by DSC.
Typical heat flow and mechanical behaviors of skim milk powder with 2% (dry basis) moisture content during glass transition (from [25])
Inverse Gas Chromatography
IGC is a gas-phase technique used to characterize the surface and bulk properties of solid materials. IGC may be used to determine batch-to-batch variations, study the surface heterogeneity, or even measure the glass transition temperature of the solid material [6, 134, 136, 209]. Unlike conventional gas chromatography, where the stationary phase serves as a detector for the various gaseous components passing through the column, IGC uses different gaseous solute probes to identify interactions between the solutes and the stationary solid column packing. In other words, in the IGC technique, the packing of the column consists of the testing sample. IGC can be performed in two different modes: infinite dilution [195] and finite solute concentration [53, 195]. When operating IGC in the infinite dilution mode, a small amount of the probe vapor is injected in the column and its retention time and volume are recorded. In this case, the retention volume is independent of the probe concentration and the surface coverage of the adsorbed molecules. This results in a linear adsorption isotherm that can be described by Henry’s law [53, 195]. Conversely, when using the finite solute concentration, a small amount of liquid probe is injected. This leads to the formation of a monolayer of the gas probe on the solid surface. In this case, desorption isotherms can be recorded, which provides an appropriate technique to measure and evaluate heterogeneity of the material surface [53].
Glass transition can be studied using IGC in the infinite dilution mode. The assessment consists of measuring the retention times and the net retention volumes of probes of defined properties passing through the packed chromatography column [40, 75, 133]. The retention times as well as the retention volume are related to the surface interaction and affinity of the probes used for the solid surface [40, 75]. Consequently the retention volume, denoted by V N, can be calculated by the following equation:
where D c is the corrected flow rate of the carrier gas, t R and t 0 are the retention times for the probe and methane, or any other alkane used for the test, respectively. However, to compare different columns and temperatures, the retention volume is normalized to a temperature of 273.15 K (0 °C) and to 1 g of powder. This normalization yields the specific retention volume calculated as
where T is the temperature at which the measurement is being conducted and m is the mass of powder in the column.
In addition, the change in free energy due to adsorption denoted by ΔG ads is a function of the specific retention volume and expressed as
where C is a constant and a function of the reference state of the adsorbed probe, and also depends on the accessible area of the solid. R is the gas constant and T is the measurement absolute temperature.
As the changes of free energy are determined as a function of temperature, this allows the calculation of both the enthalpy and entropy of adsorption as given in Eqs. 48 and 49:
In addition to temperature scans to determine the glass transition temperature, the IGC test provides relative humidity control in the sample column. Consequently, glass transition temperature can be measured at various relative humidity and thus the effect of relative humidity on T g can be studied. Figures 19 and 20 show the plots of \( \ln (V_{\text{N}} /T) \) versus 1/T as well as the location of the glass transition temperature for two amorphous pharmaceutical drugs, Indomethacin and Ketoconazole, respectively. Although this method has not been yet applied to study the glass transition of food materials, it offers some advantages for powder samples, like for example a good control of the relative humidity (water activity) during the test. This type of test provides a tool for evaluating the effect of relative humidity on the glass transition of food samples, a type of measurement that has been an important challenge in this area.
Scanning Probe Microscopy
Scanning probe microscopes (SPMs) are instruments that measure the surface properties of materials. These instruments include atomic force microscopes (AFM) and scanning tunneling microscopes (STM) [20]. Although the initial use of AFM was to provide resolution on 3D surface topographic images, several techniques have been developed to measure other surface properties of materials such as viscoelasticity, mechanical, and thermomechanical properties [22, 50, 70, 81, 126, 127, 144, 152, 191, 202].
Atomic force microscopy is performed by either scanning a sharp tip on the end of a flexible cantilever across the sample surface while maintaining a small constant force, or by simply placing the tip above the sample surface to measure the mechanical properties of that point without scanning. The latter mode is called probing [127]. Some other modes also used to measure surface T g or polymeric material include lateral force microscopy [50, 191], force–distance curves [22], friction force microscopy [81], shear modulation force microscopy [70], scanning local acceleration microscopy [144], and microthermal analysis [152].
Meincken et al. [127] used the atomic force microscope in the stationary noncontact mode for frequency spectroscopy treating the AFM as a nano-DMA. In this method, the response of the material to the oscillating cantilever was measured. As the cantilever oscillates above the polymer surface, it generates a pressure wave and thus excites the underlying molecules. Depending on their degree of freedom and mobility, the molecules respond to this excitation by absorbing energy and hence causing a change in the cantilever resonance frequency. As the temperature can be controlled, this permits to determine the thermal properties of the sample such as the glass transition, melting, or crystallization temperatures [126–128].
Based on this method, the glass transition appears as a plateau in the linearly decreasing frequency curves [127, 128]. Figure 21 shows the glass transition temperature of two different polymers. Measurements using this technique agreed well with values determined using other techniques [128].
AFM data for two different latex polymers showing the plateau locating the glass transition temperature (from [128])
Thermally Stimulated Depolarization Current
Thermally stimulated current (TSC) is a dielectric thermal technique originally developed to investigate ionic motion in crystals [32, 33]. Since then, the technique has evolved into a tool for studying the dynamics and molecular motions/relaxations in semicrystalline and amorphous polymers as well as pharmaceutical powders [45, 52, 69, 73, 119, 175, 176, 196].
In a thermally stimulated depolarizing current (TSDC) experiment, the sample is placed between the electrodes of a parallel plane capacitor under the effect of a DC electric field at a given temperature, T p, for a given period of time, t p [41, 45, 175]. As a result, the dipoles existing in the molecular structure of the material will re-orient to create a certain polarization, P 0. This step is called the polarization step (Fig. 22) [45, 175]. The decay of this polarization follows the Debye model with a single relaxation time, τ, given as
When the sample is cooled or quenched to a temperature, \( T_{\text{p}}^{\prime } \), in the presence of the electric field, the dipolar orientations are retained within the sample. This is called the freeze-in step (Fig. 22). Accordingly, the retained polarization corresponds to the dipolar motions that were activated by the electric field at the polarization temperature and whose relaxation time, \( \tau (T) \), is temperature dependent. In other words, the retained polarization consists of the contribution of all molecular motions that are relatively fast at the selected T P, but become relatively slower than the experimental time at the freeze-in temperature, \( T_{\text{p}}^{\prime } \). The freeze-in phase leaves the sample in a nonequilibrium state where the depolarization is prevented due to kinetic immobility. In the subsequent step, the polarized sample is heated at a constant rate.
where q is the heating rate and T 0 is the initial temperature. As the temperature increases, the molecules become more mobile and return to their equilibrium state. This is the depolarization phase (Fig. 22). During this stage, an electric current, I(T), is generated. This current is recorded as a function of temperature and constitutes the experimental output of a TSDC analysis. In addition to the emitted depolarization current, the temperature-dependent relaxation time can be measured using the TSDC.
The depolarization process is assumed to be a first-order rate process [32, 45] and the emitted current, I(T), can be written as
and
Thus
where P(T) is the polarization at temperature T. T f is the temperature at which the sample is completely depolarized. Plotting τ versus 1/T will produce what is called the relaxation map of a given material. This map contains all the kinetic information related to the different modes of motion including α and β relaxations.
Figure 23 shows the results of a typical TSDC experiment conducted on an amorphous pharmaceutical drug, Indomethacin. The graph shows the current intensity as a function of temperature with a peak in intensity at the glass transition temperature [41].
TSDC data plot showing the current intensity as a function of temperature for Indomethacin (from [41])
Summary
Glass transition has been studied since the early 1950s and yet remains a controversial issue. However, it is agreed that it plays an important role in the stability of food and drugs as well as in polymer manufacturing. This review article is an attempt to explore the theories that have been developed to understand the glass transition phenomenon. These theories have been developed specifically for synthetic polymers; however, in this review, an attempt has been made to extend them to foods and pharmaceuticals. The review also discusses different point of views of the glass transition phenomenon, especially the current controversy concerning whether glass transition can be observed as a thermodynamics or a kinetics event. Although thermodynamics have been used to predict glass transition-related events and properties, kinetics events appear to be the major player in the characteristics of glasses, their formation, and transition. Glass transition temperature can be measured by various techniques which were mainly developed by the synthetic polymer area and are finding yet their way into food and pharmaceutical applications. Table 7 summarizes techniques that have used to characterize glass transition of different systems including polymers, food, and pharmaceutical as well as the corresponding properties, whose changes are determined to determine the glass transition of the material.
The selection of a proper method to evaluate T g is based on the response of interest. In some applications where mechanical properties of polymers are of interest at or around T g, it is more convenient to use DMA, OSF, or TMA; in other applications for instance where material relaxation or conductivity are important parameters, the use of PALS, TSDC, DRS, or even NMR would be more reasonable. If the application involves gas retention then IGC might be a good potential alternative. DSC and MDSC are considered to be the conventional methods to measure glass transition; however, DSCs low sensitivity to changes in the heat capacity of the material at the glass transition, especially when handling strong glasses such as hydroxypropyl methyl cellulose, may show confounding results.
References
Abiad MG (2009) PhD Dissertation. Purdue University, West Lafayette, IN
Ablett S, Darke AH, Izzard MJ, Lillford PJ (1993) Studies of the glass transition in malto-oligomers. In: Blanshard JMV, Lillford PJ (eds) The glassy state in foods. Nottingham University Press, Leicestershire
Adam G, Gibbs JH (1965) On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J Chem Phys 43:139–146
Alie J, Menegotto J, Cardon P, Duplaa H, Caron A, Lacabanne C, Bauer M (2004) Dielectric study of the molecular mobility and the isothermal crystallization kinetics of an amorphous pharmaceutical drug substance. J Pharm Sci 93:218–233
Al-Muhtaseb AH, McMinn WAM, Magee TRA (2002) Moisture sorption isotherm characteristics of food products: a review. Food Bioprod Process 80:118–128
Ambarkhane AV, Pincott K, Buckton G (2005) The use of inverse gas chromatography and gravimetric vapour sorption to study transitions in amorphous lactose. Int J Pharm 294:129–135
Andronis V, Zografi G (1998) The molecular mobility of supercooled amorphous indomethacin as a function of temperature and relative humidity. Pharm Res 15:835–842
Anese M, Shtylla I, Torreggiani D, Maltini E (1996) Water activity and viscosity—relations with glass transition temperatures in model food systems. Thermochim Acta 275(1):131–137
Angell CA (1997) Why C1 = 16–17 in the WLF equation is physical—and the fragility of polymers. Polymer 38:6261–6266
Angell CA, Sare JM, Sare EJ (1978) Glass transition temperatures for simple molecular liquids and their binary solutions. J Phys Chem 82:2622–2629
Attenburrow G, Davies AP (1993) The mechanical properties of cereal based foods in and around the glassy state. In: Blanshard JMV, Lillford PJ (eds) The glassy state in foods. Nottingham University Press, Leicestershire, pp 317–331
Backfolk K, Holmes R, Ihalainen P, Sirvio P, Triantafillopoulos N, Peltonen J (2007) Determination of the glass transition temperature of latex films: comparison of various methods. Polym Test 26:1031–1040
Baeurle SA, Hotta A, Gusev AA (2006) On the glassy state of multiphase and pure polymer materials. Polymer 47:6243–6253
Ball P (1999) Glasses go critical. Nature 399:207
Becker O, Simon GP, Rieckmann T, Forsythe J, Rosu R, Völker S, O’Shea M (2001) Dielectric relaxation spectroscopy of reactively blended amorphous poly(ethylene terephthalate)–poly(ethylene naphthalate) films. Polymer 42:1921–1929
Bemiller JN, Whistler RL (2004) Carbohydrates. In: Fennema OR (ed) Food chemistry, 3rd edn. Marcel Dekker, New York
Bengtzelius U, Gotze W, Sjolander A (1984) Dynamics of supercooled liquids and the glass transition. J Phys C Solid State Phys 17:5915–5934
Bianchi U (1971) Pressure dependence of glass transition temperature in polymers. Rheol Acta 10:213
Bianchi U, Turturro A, Basile G (1967) Pressure effects on glass transition in polymers. II. A study of the factors affecting dTg/dP values. J Phys Chem 71:3555–3558
Binnig G, Quate CF, Gerber C (1986) Atomic force microscope. Phys Rev Lett 56:930–934
Blanchard L-P, Hesse J, Malhotra SL (1974) Effect of molecular weight on glass transition by differential scanning calorimetry. Can J Chem 52:3170–3175
Bliznyuk VN, Assender HE, Briggs GAD (2002) Surface glass transition temperature of amorphous polymers. A new insight with SFM. Macromolecules 35:6613–6622
Boller A, Schick C, Wunderlich B (1995) Modulated differential scanning calorimetry in the glass transition region. Thermochim Acta 266:97–111
Boonyai P, Bhandari B, Howes T (2005) Measurement of glass–rubber transition temperature of skim milk powder by static mechanical test. Dry Technol 23:1499–1514
Boonyai P, Howes T, Bhandari B (2007) Instrumentation and testing of a thermal mechanical compression test for glass-rubber transition analysis of food powders. J Food Eng 78:1333–1342
Bouchaud J-P, Biroli G (2004) On the Adam-Gibbs-Kirkpatrick-Thirumalai-Wolynes scenario for the viscosity increase in glasses. J Chem Phys 121:7347–7354
Boyd RH (1985) Relaxation processes in crystalline polymers: experimental behaviour—a review. Polymer 26:323–347
Boyd RH (1985) Relaxation processes in crystalline polymers: molecular interpretation—a review. Polymer 26:1123–1133
Boyer RF, Spencer RS (1945) Thermal expansion and second-order transition effects in high polymers: part II. Theory. J Appl Phys 16:594–607
Boyer RF, Spencer RS (1946) Second-order transition effects in rubber and other high polymers. In: Mark H, Whitby GS (eds) Scientific progress in the field of rubber and synthetic elastomers. Interscience, New York, pp 1–55
Brown ME (1988) Introduction to thermal analysis: techniques and applications. Chapman and Hall, London
Bucci C, Fieschi R (1964) Ionic thermoconductivity: method for the investigation of polarization in insulators. Phys Rev Lett 12:16–19
Bucci C, Fieschi R, Guidi G (1966) Ionic thermocurrents in dielectrics. Phys Rev 148:816–823
Butler MF, Cameron RE (2000) A study of the molecular relaxations in solid starch using dielectric spectroscopy. Polymer 41:2249–2263
Campanella OH, Peleg M (2002) Squeezing flow viscometry for nonelastic semiliquid foods—theory and applications. Crit Rev Food Sci Nutr 42:241–264
Cengel YA, Boles MA (1994) Thermodynamics: an engineering approach, 2nd edn. McGraw-Hill, New York
Chan RK, Pathmanathan K, Johari GP (1986) Dielectric relaxations in the liquid and glassy states of glucose and its water mixtures. J Phys Chem 90:6358–6362
Chung HJ, Lim ST (2006) Physical aging of amorphous starches (a review). Starch 58(12):599–610
Coburn JC, Boyd RH (1986) Dielectric relaxation in poly (ethylene terephthalate). Macromolecules 19:2238–2245
Comte S, Calvet R, Dodds JA, Balard H (2005) Surface properties of low specific surface powders using inverse gas chromatography. Powder Technol 157:39–47
Correia NT, Ramos JJM, Descamps M, Collins G (2001) Molecular mobility and fragility in indomethacin: a thermally stimulated depolarization current study. Pharm Res 18:1767–1774
Couchman PR, Karasz FE (1978) A classical thermodynamic discussion of the effect of composition on glass-transition temperatures. Macromolecules 11:117–119
Dammert RM, Maunu SL, Maurer FHJ, Neelov IM, Niemel S, Sundholm F, Wästlund C (1999) Free volume and tacticity in polystyrenes. Macromolecules 32:1930–1938
Debenedetti PG, Stillinger FH (2001) Supercooled liquids and the glass transition. Nature 410:259–267
del-Val JJ, Alegria A, Colmenero J, Barandiarán JM (1986) Thermally stimulated depolarization current (TSDC) study of molecular motions in the glass-transition region of polyarylate (PAr). Polymer 27:1771–1776
DiMarzio EA (1990) The glass temperature of polymer blends. Polymer 31:2294–2298
DiMarzio EA, Gibbs JH (1958) Chain stiffness and the lattice theory of polymer phases. J Chem Phys 28:807–813
DiMarzio EA, Gibbs JH (1959) Glass temperature of copolymers. J Polym Sci 40:121–131
DiMarzio EA, Gibbs JH (1963) Molecular interpretation of glass temperature depression by plasticizers. J Polym Sci A Gen Pap 1:1417–1428
Dinelli F, Buenviaje C, Overney RM (2000) Glass transitions of thin polymeric films: speed and load dependence in lateral force microscopy. J Chem Phys 113:2043–2048
Ding X-z, Liu X-h, Wu Q-c, He Y-z (1999) Thermodynamic and kinetic characteristics of glass transition in an amorphous alloy Pd77.5Ni6.~Si16.5. Chin Phys Lett 16:358–360
Diogo HP, Ramos JJM (2008) Slow molecular mobility in the crystalline and amorphous solid states of glucose as studied by thermally stimulated depolarization currents (TSDC). Carbohydr Res 343:2797–2803
Donnet JB, Custodero E, Wang TK, Hennebert G (2002) Energy site distribution of carbon black surfaces by inverse gas chromatography at finite concentration conditions. Carbon 40:163–167
Donth EJ (2001) The glass transition. Springer, New York
Doolittle AK (1951) Studies in Newtonian flow. II. The dependence of the viscosity of liquids on free-space. J Appl Phys 22:1471–1475
Duddu S, Monte PD (1997) Effect of glass transition temperature on the stability of lyophilized formulations containing a chimeric therapeutic monoclonal antibody. Pharm Res 14:591–595
Faivre A, Niquet G, Maglione M, Fornazero J, Jal JF, David L (1999) Dynamics of sorbitol and maltitol over a wide time-temperature range. Eur Phys J B Condens Matter Complex Syst 10:277–286
Ferry JD (1980) Viscoelastic properties of polymers, 3rd edn. Wiley, New York
Ferry JD, Stratton RA (1960) The free volume interpretation of the dependence of viscosities and viscoelastic relaxation times on concentration, pressure, and tensile strain. J Colloid Polym Sci 171:107–111
Flory PJ (1956) Statistical thermodynamics of semi-flexible chain molecules. Proc R Soc Lond A Math Phys Sci 234:60–73
Folmer JCW, Franzen S (2003) Study of polymer glasses by modulated differential scanning calorimetry in the undergraduate physical chemistry laboratory. J Chem Educ 80:813–818
Fox TG (1956) Influence of diluent and of copolymer composition on the glass temperature of a polymer system. Bull Am Phys Soc 1:123
Fox TG, Flory PJ (1950) Second-order transition temperatures and related properties of polystyrene. I. Influence of molecular weight. J Appl Phys 21:581–591
Fox TG, Flory PJ (1951) Intrinsic viscosity relations for polystyrene. J Am Chem Soc 73:1915–1920
Fox TG, Flory PJ (1954) The glass temperature and related properties of polystyrene. Influence of molecular weight. J Polym Sci 14:315–319
Fox TG, Loshaek S (1955) Influence of molecular weight and degree of crosslinking on the specific volume and glass temperature of polymers. J Polym Sci 15:371–390
Fredrickson GH, Andersen HC (1984) Kinetic Ising model of the glass transition. Phys Rev Lett 53:1244–1247
Fujita H, Rishimoto A (1958) Diffusion-controlled stress relaxation in polymers. II. Stress relaxation in swollen polymers. J Polym Sci 28:547–567
Galop M (1997) Characterization of polymers using the thermally stimulated current technique. J Therm Anal 49:107–114
Ge S, Pu Y, Zhang W, Rafailovich M, Sokolov J, Buenviaje C, Buckmaster R, Overney RM (2000) Shear modulation force microscopy study of near surface glass transition temperatures. Phys Rev Lett 85:2340–2343
Genin N, René F (1995) Analyse du Rôle de la Transition Vitreuse dans les Procédés de Conservation Agro-alimentaires. J Food Eng 26:391–408
Gibbs JH, DiMarzio EA (1958) Nature of the glass transition and the glassy state. J Chem Phys 28:373–383
Gil-Zambrano JL, Juhasz C (1981) Thermally stimulated discharge currents in polyvinyl butyral films. J Phys D Appl Phys 14:1661–1670
Glans JH, Turner DT (1981) Glass transition elevation of polystyrene by crosslinks. Polymer 22:1540–1543
Glass AS, Larsen JW (1993) Inverse gas chromatography of glassy polymer surfaces. Macromolecules 26:6354–6358
Goldstein M (1985) Glass temperature mixing relations and thermodynamics. Macromolecules 18:277–280
Gordon M, Taylor JS (1952) Ideal copolymers and the second-order transitions of synthetic rubbers I. Non-crystalline copolymers. J Appl Chem 2:493–500
Gotze W, Sjogren L (1987) The glass transition singularity. Z Phys B Condens Matter 65:415–427
Gotze W, Sjogren L (1992) Relaxation processes in supercooled liquids. Rep Prog Phys 55:241–370
Gugenberger F, Heid R, Meingast C, Adelmann P, Braun M, Wühl H, Haluska M, Kuzmany H (1992) Glass transition in single-crystal C-60 studied by high-resolution dilatometry. Phys Rev Lett 69:3774–3777
Hammerschmidt JA, Gladfelter WL, Haugstad G (1999) Probing polymer viscoelastic relaxations with temperature-controlled friction force microscopy. Macromolecules 32:3360–3367
Hancock BC, Zografi G (1994) The relationship between the glass transition temperature and the water content of amorphous pharmaceutical solids. Pharm Res 11:471–477
Hancock BC, Shamblin SL, Zografi G (1995) Molecular mobility of amorphous pharmaceutical solids below their glass transition temperatures. Pharm Res 12(6):799–806
Haynie DT (2008) Biological thermodynamics, 2nd edn. Cambridge University Press, Cambridge
Hill VL, Craig DQM, Feely LC (1998) Characterisation of spray-dried lactose using modulated differential scanning calorimetry. Int J Pharm 161:95–107
Hutchinson JM (1995) Physical aging of polymers. Prog Polym Sci 20(4):703–760
Hutchinson JM, Montserrat S (1996) The application of modulated differential scanning calorimetry to the glass transition of polymers. I. A single-parameter theoretical model and its predictions. Thermochim Acta 286:263–296
Ihalainen P, Backfolk K, Sirviö P, Peltonen J (2007) Thermal analysis and topographical characterization of latex films by scanning probe microscopy. J Appl Phys 102:029901
Jean YC, Mallon PE, Schrader DM (2003) Introduction to positron and positron chemistry. In: Jean YC, Mallon PE, Schrader DM (eds) Principles and applications of positron & positronium chemistry. World Scientific, Singapore, pp 1–16
Jenckel E, Heusch R (1953) Lowering the freezing temperature of organic glasses with solvents. Kolloid-Z 130:89–105
Kalichevsky MT, Blanshard JMV (1992) A study of the effect of water on the glass transition of 1:1 mixtures of amylopectin, casein and gluten using DSC and DMTA. Carbohydr Polym 19:271–278
Kalichevsky MT, Jaroszkiewicz EM, Ablett S, Blanshard JMV (1992) The glass transition of amylopectin measured by DSC, DMTA and NMR. Carbohydr Polym 18:77–88
Kalichevsky MT, Jaroszkiewicz EM, Blanshard JMV (1992) Glass transition of gluten. 1: gluten and gluten-sugar mixtures. Int J Biol Macromol 14:257–266
Kalichevsky MT, Jaroszkiewicz EM, Blanshard JMV (1992) Glass transition of gluten. 2: The effect of lipids and emulsifiers. Int J Biol Macromol 14:267–273
Kalichevsky MT, Blanshard JMV, Marsh RDL (1993) Applications of mechanical spectroscopy to the study of glassy biopolymers and related systems. In: Blanshard JMV, Lillford PJ (eds) The glassy state in foods. Nottingham University Press, Leicestershire, pp 133–156
Kalichevsky MT, Jaroszkiewicz EM, Blanshard JMV (1993) A study of the glass transition of amylopectin—sugar mixtures. Polymer 34:346–358
Karel M, Anglea S, Buera P, Karmas R, Levi G, Roos Y (1994) Stability-related transitions of amorphous foods. Thermochim Acta 246:249–269
Kaufmann S, Wefing S, Schaefer D, Spiess HW (1990) Two-dimensional exchange nuclear magnetic resonance of powder samples. III. Transition to motional averaging and application to the glass transition. J Chem Phys 93:197–214
Kauzmann W (1948) The nature of the glassy state and the behavior of liquids at low temperatures. Chem Rev 43:219–256
Kauzmann W, Eyring H (1940) The viscous flow of large molecules. J Am Chem Soc 62:3113–3125
Kegel WK (2000) Crystallization in glassy suspensions of colloidal hard spheres. Langmuir 16:939–941
Kelley FN, Bueche F (1961) Viscosity and glass temperature relations for polymer-diluent systems. J Polym Sci 50:549–556
Khalloufi S, El-Maslouhi Y, Ratti C (2000) Mathematical model for prediction of glass transition temperature of fruit powders. J Food Sci 65:842–848
Kim SH, Chung JW, Kang TJ, Kwak S-Y, Suzuki T (2007) Determination of the glass transition temperature of polymer/layered silicate nanocomposites from positron annihilation lifetime measurements. Polymer 48:4271–4277
Kobayashi Y (1991) Quenching of positronium atoms by nitrobenzene in various solutions. J Chem Soc Faraday Trans 87:3641–3645
Kobayashi Y, Haraya K, Kamiya Y, Hattori S (1992) Correlation between the ortho-positronium pick-off annihilation lifetime and the free volume in molecular liquids and polymers. Bull Chem Soc Jpn 65:160–163
Kwei TK (1984) The effect of hydrogen bonding on the glass transition temperature of polymer mixtures. J Polym Sci 22:307–313
Labuza TP, Hyman CR (1998) Moisture migration and control in multi-domain foods. Trends Food Sci Technol 9(2):47–55
Langer J (2007) The mysterious glass transition. Phys Today 60(2):8–9
Lechuga-Ballesteros D, Miller DP, Zhang J (2002) Residual water in amorphous solids: measurement and effects on stability. In: Levine H (ed) Amorphous food and pharmaceutical systems. Athenaeum, Manchester, UK, pp 275–316
Lechuga-Ballesteros D, Miller DP, Zhang J (2002) Residual water in amorphous solids: measurement and effects on stability. In: Levine H (ed) Amorphous food and pharmaceutical systems. Athenaeum, Manchester, UK, pp 1–8
Leutheusser E (1984) Dynamical model of the liquid-glass transition. Phys Rev A 29:2765–2773
Levine H, Slade L (1986) A polymer physico-chemical approach to the study of commercial starch hydrolysis products (SHPs). Carbohydr Polym 6:213–244
Lin AA, Kwei TK, Reiser A (1989) On the physical meaning of the Kwei equation for the glass transition temperature of polymer blends. Macromolecules 22:4112–4119
Liu J, Deng Q, Jean YC (1993) Free-volume distributions of polystyrene probed by positron annihilation: comparison with free-volume theories. Macromolecules 26:7149–7155
Lloyd RJ, Chen XD, Hargreaves JB (1996) Glass transition and caking of spray-dried lactose. Int J Food Sci Technol 31:305–311
Loshaek S (1955) Crosslinked polymers. II. Glass temperatures of copolymers of methyl methacrylate and glycol dimethacrylates. J Polym Sci 15:391–404
Ma C-Y, Harwalkar VR, Maurice TJ (1990) Instrumentation and techniques of thermal analysis in food research. In: Harwalkar VR, Ma C-Y (eds) Thermal analysis of foods. Elsevier, London, pp 1–15
Madani M, Maziad NA, Khafagy RM (2007) Thermally stimulated depolarization current and thermal analysis studies of gamma irradiated lithium-salt/polymer electrolyte blends. J Macromol Sci B Phys 46:1191–1203
Mallon PE (2003) Application to polymer. In: Jean YC, Mallon PE, Schrader DM (eds) Principles and applications of positron & positronium chemistry. World Scientific, Singapore, pp 253–280
Mandelkern L, Martin GM, Quinn FA (1957) Glassy state transitions of poly-(chlorotrifluoroethylene), poly-(vinylidene fluoride) and their copolymers. J Res Natl Bureau Stand 58:137–143
Mansfield ML (1993) An overview of theories of the glass transition. In: Blanshard JMV, Lillford PJ (eds) The glassy state in foods. Nottingham University Press, Leicestershire, pp 103–122
McKinney JE, Goldstein M (1974) PVT relationships for liquid and glassy poly(vinyl acetate). J Res Natl Bureau Stand A Phys Chem 78:331–353
McPhillips H, Craig DQM, Royall PG, Hill VL (1999) Characterisation of the glass transition of HPMC using modulated temperature differential scanning calorimetry. Int J Pharm 180:83–90
Meares P (1957) The second-order transition of polyvinyl acetate. Trans Faraday Soc 53:31–40
Meincken M, Balk LJ, Sanderson RD (2001) Improved sensitivity in the thermal investigation of polymeric nanophases by measuring the resonance frequency shift using an atomic force microscope. Macromol Mater Eng 286:412–420
Meincken M, Graef S, Mueller-Nedebock K, Sanderson RD (2002) Thermal transitions of polymers measured by atomic force microscopy. Appl Phys A Mater Sci Process 74:371–375
Meincken M, Balk LJ, Sanderson RD (2003) Measurement of thermal parameters and mechanical properties of polymers by atomic force microscopy. Surf Interface Anal 35:1034–1040
Menard KP (1999) Dynamic mechanical analysis: a practical introduction. CRC Press, Boca Raton
Mert B, Campanella OH (2008) The study of the mechanical impedance of foods and biomaterials to characterize their linear viscoelastic behavior at high frequencies. Rheol Acta 47:727–737
Misra S, Mattice WL (1993) Atomistic models of amorphous polybutadienes. 3. Static free volume. Macromolecules 26:7274–7281
Morrison FA (2001) Understanding rheology. Oxford University Press, New York
Mukhopadhyay P, Schreiber HP (1993) Inverse gas chromatography for polymer surface characterization above and below Tg. Macromolecules 26:6391–6396
Nastasovic AB, Onjia AE (2008) Determination of glass transition temperature of polymers by inverse gas chromatography. J Chromatogr A 1195:1–15
Neagu E, Pissisz P, Apekisz L, Gomez-Ribellesx JL (1997) Dielectric relaxation spectroscopy of polyethylene terephthalate (PET) films. J Phys D Appl Phys 30:1551–1560
Newell HE, Buckton G, Butler DA, Thielmann F, Williams DR (2001) The use of inverse gas chromatography to study the change of surface energy of amorphous lactose as a function of relative humidity and the processes of collapse and crystallisation. Int J Pharm 217:45–56
Nicholls RJ, Appelqvist IAM, Davies AP, Ingman SJ, Lillford PJ (1995) Glass transitions and the fracture behaviour of gluten and starches within the glassy state. J Cereal Sci 21:25–36
Noel TR, Ring SG, Whittam MA (1993) Relaxations in supercooled carbohydrate liquids. In: Blanshard JMV, Lillford PJ (eds) The glassy state in foods. Nottingham University Press, Leicestershire, pp 173–187
Noel TR, Parker R, Ring SG (2000) Effect of molecular structure and water content on the dielectric relaxation behaviour of amorphous low molecular weight carbohydrates above and below their glass transition. Carbohydr Res 329:839–845
Noel TR, Parker R, Brownsey GF, Farhat IA, MacNaughtan W, Stephen G, Ring SG (2005) Physical aging of starch, maltodextrin, and maltose. J Agric Food Chem 53(22):8580–8585
O’Reilly J (1962) The effect of pressure on glass temperature and dielectric relaxation time of polyvinyl acetate. J Polym Sci 57:429–444
Ollet AL, Parker P (1990) The viscosity of supercooled fructose and its glass transition temperature. J Texture Stud 21:355–362
Orford PD, Parker R, Ring SG (1990) Aspects of the glass transition behaviour of mixtures of carbohydrates of low molecular weight. Carbohydr Res 196:11–18
Oulevey F, Burnham NA, Gremaud G, Kulik AJ, Pollock HM, Hammiche A, Reading M, Song M, Hourston DJ (2000) Dynamic mechanical analysis at the submicron scale. Polymer 41:3087–3092
Paul W (2004) Molecular dynamics simulations of the glass transition in polymer melts. Polymer 45:3901–3905
Peleg M (1992) On the use of the WLF model in polymers and foods. Crit Rev Food Sci Nutr 32:59–66
Peleg M (1994) Mathematical characterization and graphical presentation of the stiffness-temperature-moisture relationship of gliadin. Biotechnol Prog 70:652–654
Peleg M (1994) A model of mechanical changes in biomaterials at and around their glass transition. Biotechnol Prog 10:385–388
Penzel E, Rieger J, Schneider HA (1997) The glass transition temperature of random copolymers: 1. Experimental data and the Gordon-Taylor equation. Polymer 38:325–337
Pinal R (2008) Entropy of mixing and the glass transition of amorphous mixtures. Entropy 10:207–223
Pochan JM, Beatty CL, Pochan DF (1979) Different approach for the correlation of the Tg of mixed amorphous systems. Polymer 20:879–886
Pollock HM, Hammiche A (2001) Micro-thermal analysis: techniques and applications. J Phys D Appl Phys 34:R23–R53
Rahman MS, Al-Marhubi IM, Al-Mahrouqi A (2007) Measurement of glass transition temperature by mechanical (DMTA), thermal (DSC and MDSC), water diffusion and density methods: a comparison study. Chem Phys Lett 440:372–377
Reading M (1993) Modulated differential scanning calorimetry—a new way forward in materials characterization. Trends Polym Sci 1:248–253
Reading M, Luget A, Wilson R (1994) Modulated differential scanning calorimetry. Thermochim Acta 238:295–307
Roos YH (1993) Water activity and physical state effects on amorphous food stability. J Food Process Preserv 16:433–447
Roos YH (1993) Melting and glass transition of low molecular weight carbohydrates. Carbohydr Res 238:39–48
Roos YH (1995) Characterization of food polymers using state diagrams. J Food Eng 24:339–360
Roos YH (2008) The glassy state. In: Aguilera JM, Lillford PJ (eds) Food materials science: principles and practice. Springer, New York, pp 67–81
Roos Y, Karel M (1990) Differential scanning calorimetry study of phase transitions affecting the quality of dehydrated materials. Biotechnol Prog 6:159–163
Ruan RR, Long Z, Song A, Chen PL (1998) Determination of the glass transition temperature of food polymers using low field NMR. Lebensm Wiss Technol 31:516–521
Ruan R, Long Z, Chen P, Huang V, Almaer S, Taub I (1999) Pulse NMR study of glass transition in maltodextrin. J Food Sci 64:6–9
Rubinstein M, Colby RH (2003) Polymer physics. Oxford University Press, New York, p 337
Sablani SS, Kasapis S, Rahman MS, Al-Jabri A, Al-Habsi N (2004) Sorption isotherms and the state diagram for evaluating stability criteria of abalone. Food Res Int 37:915–924
Sablani SS, Kasapis S, Rahman MS (2007) Evaluating water activity and glass transition concepts for food stability. J Food Eng 78:115266–115271
Sahin S, Sumnu SG (2006) Physical properties of foods. Springer, New York
Santen L, Krauth W (2000) Absence of thermodynamic phase transition in a model glass former. Nature 405:550–551
Schneider HA (1989) Glass transition behaviour of compatible polymer blends. Polymer 30:771–779
Schneider HA (1997) Conformational entropy contributions to the glass temperature of blends of miscible polymers. J Res Natl Inst Stand Technol 102:229–248
Schneider HA, DiMarzio EA (1992) The glass temperature of polymer blends: comparison of both the free volume and the entropy predictions with data. Polymer 33:3453–3461
Schneider HA, Rieger J, Penzel E (1997) The glass transition temperature of random. Copolymers: 2. Extension of the Gordon-Taylor equation for asymmetric Tg vs composition curves. Polymer 38:1323–1337
Seo JA, Kim SJ, Kwon HJ, Yang YS, Kim HK, Hwang YH (2006) The glass transition temperatures of sugar mixtures. Carbohydr Res 341:2516–2520
Seyler RJ (ed) (1994) Assignment of the glass transition. ASTM, Philadelphia
Shen MC, Tobolsky AV (1965) Glass transition temperature of polymers. Effect of plasticizer, chain ends and comonomer. In: Platzer NAJ (ed) Advances in chemistry series. American Chemical Society, Washington, DC, pp 27–34
Shmeis RA, Wang Z, Krill SL (2004) A mechanistic investigation of an amorphous pharmaceutical and its solid dispersions, part I: a comparative analysis by thermally stimulated depolarization current and differential scanning calorimetry. Pharm Res 21:2025–2030
Shmeis RA, Wang Z, Krill SL (2004) A mechanistic investigation of an amorphous pharmaceutical and its solid dispersions, part II: molecular mobility and activation thermodynamic parameters. Pharm Res 21:2031–2039
Simha R, Boyer RF (1962) On a general relation involving the glass temperature and coefficients of expansion of polymers. J Chem Phys 37:1003
Simha R, Wilson PS (1973) Thermal expansion of amorphous polymers at atmospheric pressure. II. Theoretical considerations. Macromolecules 6:908–914
Slade L, Levine H (1991) Beyond water activity: recent advances based on an alternative approach to the assessment of food quality and safety. Crit Rev Food Sci Nutr 30:115–360
Slade L, Levine H (1993) Water relationships in starch transitions. Carbohydr Polym 21:105–131
Slade L, Levine H (1995) Water and the glass transition—dependence of the glass transition on composition and chemical structure: special implications for flour functionality in cookie baking. J Food Eng 24:431–509
Smith G, Duffy AP, Shen J, Olliff CJ (1995) Dielectric relaxation spectroscopy and some applications in the pharmaceutical sciences. J Pharm Sci 84:1029–1044
Song M, Hammiche A, Pollock HM, Hourston DJ, Reading M (1995) Modulated differential scanning calorimetry: 1. A study of the glass transition behaviour of blends of poly(methyl methacrylate) and poly(styrene-co-acrylonitrile). Polymer 36:3313–3316
Song M, Hammiche A, Pollock HM, Hourston DJ, Reading M (1996) Modulated differential scanning calorimetry: 4. Miscibility and glass transition behaviour in poly(methyl methacrylate) and poly(epichlorohydrin) blends. Polymer 37:5661–5665
Sopade PA, Halley P, Bhandaria B, D’Arcya B, Doeblerb C, Caffin N (2002) Application of the Williams–Landel–Ferry model to the viscosity–temperature relationship of Australian honeys. J Food Eng 56:67–75
Speedy RJ (1994) On the reproducibility of glasses. J Chem Phys 100:6684–6691
Speedy RJ (2003) Kauzmann’s paradox and the glass transition. Biophys Chem 105:411–420
Sperling LH (2006) Introduction to physical polymer science, 4th edn. Wiley, Hoboken
Stillinger FH (1988) Supercooled liquids, glass transitions, and the Kauzmann paradox. J Chem Phys 88:7818–7825
Suwonsichon T, Peleg M (1998) Instrumental and sensory detection of simultaneous brittleness loss and moisture toughening in three puffed cereals. J Texture Stud 29:255–274
Tanaka K, Taura A, Ge S-R, Takahara A, Kajiyama T (1996) Molecular weight dependence of surface dynamic viscoelastic properties for the monodisperse polystyrene film. Macromolecules 29:3040–3042
Teixeira EM, Da Róz AL, Carvalho AJF, Curvelo AAS (2007) The effect of glycerol/sugar/water and sugar/water mixtures on the plasticization of thermoplastic cassava starch. Carbohydr Polym 69(4):619–624
Tester RF, Karkalas J, Xin Qi X (2004) Review, starch-composition, fine structure and architecture. J Cereal Sci 39:151–165
Thomas L (2008) Use of TGA, DSC and MDSC. TA Instrument Report
Tijburg I, Jagiello J, Vidal A, Papirer E (1991) Inverse gas chromatographic studies on silica: infinite dilution and finite concentration measurements. Langmuir 7:2243–2247
Topić M, Moguš-Milanković A, Katović Z (1991) The study of glass transition in epoxy resin using thermally stimulated depolarization current measurements. Polymer 32:2892–2897
Torquato S (2000) Glass transition: hard knock for thermodynamics. Nature 405:521–523
Turnbull D, Cohen MH (1961) Free-volume model of the amorphous phase: glass transition. J Chem Phys 34:120–125
van der Plaats G (1984) A theoretical evaluation of a heat-flow differential scanning calorimeter. Thermochim Acta 72:77–82
Volkov AA, Prokhorov AS (2003) Broadband dielectric spectroscopy of solids. Radiophys Quantum Electron 46:657–665
Webb SL, Knoche R, Dingwell DB (1992) Determination of silicate liquid thermal expansivity using dilatometry and calorimetry. Eur J Mineral 4:95–104
Weisenhorn AL, Maivald P, Butt HJ, Hansma PK (1992) Measuring adhesion, attraction, and repulsion between surfaces in liquids with an atomic-force microscope. Phys Rev B 45:11226–11232
Williams ML, Landel RF, Ferry JD (1955) The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J Am Chem Soc 77:3701–3707
Wilson PS, Simha R (1973) Thermal expansion of amorphous polymers at atmospheric pressure. I. Experimental. Macromolecules 6:902–908
Woodcock LV (1976) Glass transition in the hard-sphere model. J Chem Soc Faraday Trans 2:1667–1672
Wunderlich B (2005) Thermal analysis of polymeric materials. Springer, Dordrecht
Xia X, Wolynes PG (2000) Fragilities of liquids predicted from the random first order transition theory of glasses. Proc Natl Acad Sci USA 97:2990–2994
Yildiz ME, Kokini JL (2001) Determination of Williams–Landel–Ferry constants for a food polymer system: effect of water activity and moisture content. J Rheol 45(4):903–912
Yla-Maihaniemi PP, Heng JYY, Thielmann F, Williams DR (2008) Inverse gas chromatographic method for measuring the dispersive surface energy distribution for particulates. Langmuir 24:9551–9557
Yu L, Christie G (2001) Measurement of starch thermal transitions using differential scanning calorimetry. Carbohydr Polym 46:179–184
Yu Z, Yahsi U, McGervey JD, Jamieson AM, Simha R (1994) Molecular weight-dependence of free volume in polystyrene studied by positron annihilation measurements. J Polym Sci B Polym Phys 32:2637–2644
Zakin JL, Simha R, Hershey HC (1966) Low-temperature thermal expansivities of polyethylene, polypropylene, mixtures of polyethylene and polypropylene, and polystyrene. J Appl Polym Sci 10:1455–1473
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Abiad, M.G., Carvajal, M.T. & Campanella, O.H. A Review on Methods and Theories to Describe the Glass Transition Phenomenon: Applications in Food and Pharmaceutical Products. Food Eng. Rev. 1, 105–132 (2009). https://doi.org/10.1007/s12393-009-9009-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12393-009-9009-1