1 Introduction

There are numerous examples of real-world manufacturing systems where many production operations are functionally aggregated in a single stage. Relevant examples can be found in the technical textiles’ industry; e.g. the primary operations in a production line that manufactures nonwovens (spunbonded, meltblown, needlepunched, etc.) are filaments extrusion, web formation and consolidation through mechanical, thermal or chemical treatment, winding in rolls and packaging or storage for further processing. Nonetheless, these operations are seamlessly grouped in an integrated production line, i.e. a single manufacturing stage that receives as input polyolefin granules mixed with additives according to the recipe and outputs technical fabrics. From a control point of view, this production stage can be treated as a single “mega machine” and the performance of this machine largely determines the overall performance of the manufacturing system. As a consequence, the task of controlling/managing this machine is of grave importance.

Manufacturing systems of this type have some defining characteristics which are cited hereafter. Due to the volume of production and the size of the equipment, the transition of the manufacturing system from idle to working state requires substantial preparatory activities such as establishing the supply of raw materials, purging of the dies, setting the cooling systems online etc. Consequently, each new production batch entails significant costs. The manufactured products are standardized and easy to store whereas the pressure to meet customer demand is high. As a result, holding costs are low in relation to lost sales costs. The adverse consequences of equipment failures are considerable because of the time/costs needed for conducting repairs and the related productivity drop. Preventive maintenance activities can be undertaken to prevent hard failures but they do not come without the associated costs. Because of the complexity that characterizes manufacturing systems of this type, inspections are needed so as to determine the current deterioration state accurately. Inspections and maintenance actions are preferable to be scheduled when the system is idling in order to increase productivity on one hand, on the other hand most of the times accurate inspection and preventive maintenance are actions that cannot be achieved while the system is producing.

Motivated by the aforementioned type of manufacturing systems, we introduce the Markovian model of a production/inventory system that consists of a single stage. The system produces a single part type to satisfy random demand in the absence of backorders. The manufacturing system experiences deterioration failures and, at the occurrence of such a failure, its state degrades. The system transits from a deterioration stage to another, and if it undergoes a deterioration failure at the last deterioration stage, then it breaks down and ceases to be operational; at that time, a repair is initiated. The deterioration level of the system, with the exception of the situation where the manufacturing facility is broken down, is unknown. The system can be subjected to periodic inspections when the system is idling and at the end of each inspection the current deterioration state of the system can be observed. Since the inspections are not conducted based on a schedule, we can define this inspection policy as an opportunistic one. Based on the observed deterioration of the system, a threshold-type maintenance policy determines whether preventive maintenance should be carried out or not. The manufacturing system operates under an (s, S) production control policy. A special case of the (s, S) mechanism, i.e. the base stock control policy is also considered.

The steady-state probabilities of the investigated system’s states’ are computed numerically. We provide mathematical formulations for multiple criteria that quantify the system’s performance, namely production/inventory/lost sales costs as well as costs related to maintenance, inspections and repairs. The properties of the total cost function in respect to alternative inspection/maintenance/production control policies are studied; based on this analysis a local search procedure is proposed for optimizing the control parameters of the system. The system’s behavior in relation to alternative input parameters is investigated via a series of numerical experiments; the performance of the proposed heuristic procedure is also evaluated. The effect of deterioration failures in a manufacturing system implementing a push type (s, S) production policy, opportunistic inspection and condition based maintenance is studied in order to provide a stochastic model that allows the further investigation of the critical factors affecting the management of such systems. This article investigates, and tries to offer managerial insights, for research questions such as:

  • How do changes in, e.g. production rate and holding cost factors, affect the system’s performance?

  • Which is the best inspection/maintenance/production control policy for a given manufacturing system?

  • In what situations do the costs of inspection/preventive maintenance action counterbalance the related benefits?

  • Why does some control policy outperforms another policy in certain production environments?

  • How should the batch size be set in respect to production cost factors?

  • Which is the best way to set the inventory parameters for a given deteriorating manufacturing system?

  • Which cost components are pivotal in minimizing total cost?

The production/inventory system which is examined in this research has not been addressed in the relevant literature up to now. Analyses of relevant works together with an identification of the literature’s gaps are given in Sect. 2. Section 2 also states the gaps that are addressed by this research and the juxtaposition of this article with existing literature.

The structure of the remainder sections of this article is the following. In Sect. 3 we offer the description of the investigated system and in Sect. 4 we develop the related Markov chain models. Expressions of several performance metrics and the total expected cost function are presented in Sect. 5. The numerical investigation of the cost function’s properties along with the proposed local search procedure is given in Sect. 6. Section 7 contains the numerical experiments and the associated analysis. The paper is concluded with Sect. 8, where some directions for future research are also provided.

2 Related work

This paper studies an integrated production/inspection/maintenance control problem. Integrated or joint optimization problems pertaining to maintenance have been studied extensively over the years (e.g. refer to Zhou et al. 2019; Li and Ma 2017; Xu and Xu 2016; Beheshti-Fakher et al. 2016; Bajestani et al. 2014; Yalaoui et al. 2014; Kang et al. 2018a, b). Relevant literature surveys can be found in the works of Ruschel et al. (2017) and Prajapati et al. (2012). The production/inventory system and the underlying control problem which is studied in this article has not been addressed in the literature up to now. Nonetheless, some of its individual features can be found in existing works. In this section, we categorize publications that are most relevant to this article. Our aim is to show how this article is “positioned” in relation to existing works, demonstrate the gaps in the literature which are addressed by this research and highlight its contribution.

In this paper we examine a single machine system that produces a single part type, similarly to the works of Koutras et al. (2017) and Iravani and Duenyas (2002). To model the manufacturing system in question, the commonly adopted formalism of Markov chains is used (indicatively refer to Cekyay and Ozekici 2012; Rao and Naikan 2009; Liang and Parlikad 2015). We employ the machine deterioration scheme, according to which, the system’s condition is discretized using a number of deterioration stages (Pavitsos and Kyriakidis 2009; Kazaz and Sloan 2013; Xanthopoulos et al. 2015). Apart from the stage where the machine has experienced a hard failure, i.e. is broken down, its current deterioration is only made known by means of periodic inspections (Mousavi et al. 2017; Golmakani and Fattahipour 2011; Soemadi et al. 2014; Lee 2009).

Preventive maintenance activities are authorized on the basis of the current deterioration level of the machine, a scheme widely known as condition-based maintenance (Van and Berenguer 2012; Rausch and Liao 2010; Prajapati and Ganesan 2013; Jiang et al. 2018; Peng et al. 2020; Liu et al. 2020; Raza et al. 2017). Relevant literature surveys regarding optimal management of such systems can be found in the works of Golmakani et al. (2011, 2012, 2014); Shuyuan Gan (2021). When the machine is broken down, repair, i.e. corrective maintenance, activities are undertaken (Zhang and Sun 2018). Regarding the production control component of the joint optimization problem which is addressed in this research, we examine (s, S)—type (Xanthopoulos et al. 2017; Gosavi et al. 2004) and base stock—type (Axsater 2015; Cheng et al. 2011) policies. Production (Axsater 2015; Cheng et al. 2011; Peng and van Houtum 2016), inventory Lee (2009), lost sales (Cheng et al. 2011), inspections, maintenance (Wolter and Helber 2016; Najid et al. 2011) and repair costs are considered in this research.

The primary innovative characteristic of this research is that it studies the combination of deterioration failures with periodic inspection and the implementation of the (s,S) policy. This is what distinguishes the paper from the existing literature; the contribution of this article can be summarized in the following points:

  • A novel model for a deteriorating manufacturing system is introduced.

  • A cost function that incorporates several cost components is formulated.

  • The properties of the cost function are investigated numerically and an efficient heuristic procedure for minimizing total cost is proposed.

  • Alternative productions control policies are compared under the influence of opportunistic periodic inspections and condition based preventive maintenance.

  • For given system configurations, the parameters that govern the production control, inspection and maintenance policies are optimized in respect to the cost function.

3 System description

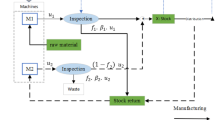
In this section we define the deteriorating manufacturing system controlled by the (s, S) policy that forms the basis of this research. In the remainder of this article, we will refer to this system as (s, S) system for brevity.

The manufacturing system is comprised of a single machine and a finished goods buffer. It manufactures a single type of products. The supply of raw materials is assumed to be infinite, i.e. the machine never starves. The machine manufactures products one-by-one, with no preemption. The processing times are exponentially distributed with mean 1/λp. Manufactured products are stored in the finished goods buffer. The cost of storing one product in the buffer for one time unit is Ch.

Demand for finished goods is stochastic and the demand inter-arrival time is exponential with mean 1/λa. Upon a demand arrival, one unit of the product is requested. If there is available inventory, the demand is satisfied instantly, otherwise the demand is rejected. Rejecting a demand for a finished product costs Ca monetary units.

The machine deteriorates with usage, i.e. when it is working to manufacture products. If the machine is “good-as-new”, then it is considered to be in deterioration stage 0. If the machine is broken-down and under repair, then it is in deterioration stage d + 1. In the case where the current deterioration stage is 0 < i < d + 1, then the machine is deteriorated yet still operational. When operating, the system transits from stage i to stage i + 1 with rate λf, for i = 0, 1,…, d. This type of transition will be referred to as “deterioration failure” in the remainder of this paper. The transition time from one deterioration stage to another is exponential. When in stage d + 1, the machine cannot produce, it is under repair, and it transits to stage 0 (good-as-new) with rate μr. Repair times are exponential and a repair incurs a cost of Cr monetary units.

The system operates under a continuous-review (s, S) control policy which is described by two integer parameters s < S. The level of the finished goods buffer is monitored continuously and, at the time when it drops to s, a new production lot (batch) is initiated. Each production lot has a fixed cost of Cs monetary units. Once the production of a new batch has commenced, the machine manufactures products up to the point where there are S items in the finished goods buffer and then switches to idle state.

In the special case where s = S − 1, the system operates under a base stock, or order-up-to-S, or simply S control policy. A base stock policy is a simple, threshold-type control policy which is characterized by a single parameter, i.e. S: the machine idles as long as the finished goods inventory is greater than or equal to S, and produces otherwise. A manufacturing system controlled by the base stock policy will be called base stock system in the remaining sections of this paper.

3.1 Periodic inspections and preventive maintenance

The model which was defined in Sect. 3 can be extended by considering periodic inspections of the machine’s state and preventive maintenance. In this sub-section we define the additional elements for this extension. This manufacturing system will be referred to as (s, S)—PM system (where PM stands for “preventive maintenance”), in the remainder of this article. Similarly, in the case where s = S − 1, we will refer to a base stock—PM system. Note that all assumptions and conventions used in Sect. 3 apply here as well.

Unless the machine has broken down (i = d + 1), the current deterioration stage is unknown. It is determined by conducting periodic inspections of the manufacturing system. An inspection can only be initiated when the machine is idling. The times between inspections are exponential and, when idling, the system transits to the “under inspection” state with rate λin. The cost for an inspection is Cin and its duration is an exponentially distributed random variable with mean 1/μin. It is noted that the assumption regarding exponential times between inspections/duration of inspections is also adopted in Xanthopoulos et al. (2015), Golmakani and Fattahipour (2011) and Chen et al. (2003) among others.

Upon completion of an inspection, the current deterioration of the machine is established. Based on that information, it can be decided to perform a preventive maintenance or do nothing. A preventive maintenance costs Cm monetary units, has an exponential duration with mean 1/μm and restores the machine to stage 0 (good-as-new). Maintenance decisions are made on the basis of a threshold-type maintenance policy:

$$\begin{gathered} {\text{IF}}\;\,b \le i \le d \hfill \\ \qquad perform \, preventive \, maintenance \hfill \\ {\text{ELSE}} \hfill \\ \qquad do \, nothing \hfill \\ \end{gathered}$$

where d is the number of deterioration stages, i is the current deterioration stage, and b is the parameter of the maintenance policy. It is noted that, when the system transits to deterioration stage d + 1, the machine breaks down and repair actions are initiated immediately. It is reasonable to assume that no inspection is needed to determine the deterioration level at stage d + 1, since the machine does not have the ability to produce at that state.

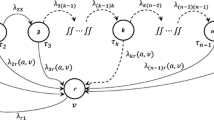
4 Markov chain models

In this section we develop the continuous-time Markov chain model for the (s, S) and (s, S)—PM systems that were defined in Sects. 3 and 3.1, respectively. The state of the system is described by the tuple (i, j, k), where i = 0, 1,…, d + 1 is the deterioration stage of the machine, j = 0, 1,…, S denotes the number of finished products in stock, and k symbolizes the machines state:

$$k = \left\{ {\begin{array}{*{20}c} {0,} & {{\text{if}}} & {{\text{machine}}} & {{\text{is}}} & {{\text{idling}}} \\ {1,} & {{\text{if}}} & {{\text{machine}}} & {{\text{is}}} & {{\text{working}}} \\ {2,} & {{\text{if}}} & {{\text{machine}}} & {{\text{is}}} & {{\text{repaired}}} \\ {3,} & {{\text{if}}} & {{\text{machine}}} & {{\text{is}}} & {{\text{inspected}}} \\ {4,} & {{\text{if}}} & {{\text{machine}}} & {{\text{is}}} & {{\text{maintained}}} \\ \end{array} } \right.$$
(1)

It is noted that the machine is “repaired” when the current deterioration stage is d + 1, i.e. the machine does not have the ability to produce. On the other hand, the machine is “maintained” if it is deteriorated, yet operational. Finally, note that the term “repair” in this article has the same meaning as “corrective maintenance” in some relevant works. The investigated manufacturing system is a discrete-event system, i.e. its state changes only at the occurrence of specific types of events. The only events that can occur in the (s, S) system are “demand arrival”, “production completion”, “deterioration failure” and “repair completion”. All of the aforementioned events can occur in the (s, S)—PM system, in addition to the events “inspection start”, “inspection completion”, and “maintenance completion”. In the following sub-Sects. 4.1 and 4.2, π(i, j, k) symbolizes the steady-state probability of state (i, j, k).

4.1 (s, S) system

In this section we present the balance Eqs. (2–14) that describe the Markov chain model of the deteriorating manufacturing system that was presented in Sect. 3.

Equations (2) and (3) pertain to states where the manufacturing system is idling. For example, Eq. (2) shows that, when in state (i, S, 0), the system exits that state with rate λa (since only the event of demand arrival can occur there). Furthermore, Eq. (2) shows that (i, S, 0) can only be reached from state (i, S − 1, 1), i.e. when the machine is working and the “production completion” event occurs.

Equations (4–11) are related to states were the machine is currently operating to manufacture a new product. For example, Eqs. (4–5) show that the system exits state (i, 0, 1), i = 0, 1,…, d, with rate (λp + λf) since only the events “production completion” and “deterioration failure” can occur in that state. It is reiterated that no backorders are allowed, and since there is no inventory available in state (i, 0, 1), incoming demand is rejected leaving the system state unchanged. Furthermore, Eq. (5) shows that state (0, 0, 1) can be reached from (0, 1, 1) upon occurrence of the “demand arrival” event or from (d + 1, 0, 2) at the completion of a repair activity. The derivation of all equations that pertain to states where the machine is working can be explained in a similar way.

$$\lambda_{a} \pi \left( {i,\;S,\;0} \right)\; = \;\lambda_{p} \pi \left( {i,\;S\; - \;1,\;1} \right),\quad i\; = \;0,\;1,\;2, \ldots .,d$$
(2)
$$\lambda_{a} \pi \left( {i,j, \, 0} \right) \, = \lambda_{a} \pi \left( {i,\;j\; + \;{1},\;0} \right),\quad i\; = \;0,\;{1},\;{2}, \ldots .,d,\quad j\; = \;s\; + \;{1},\;{\text{s}}\; + \;{2}, \ldots ,S\;{-}\;{1}$$
(3)
$$(\lambda_{p} \; + \;\lambda_{f} )\pi \left( {i,\;0,\;{1}} \right)\; = \;\lambda_{a} \pi \left( {i,\;{1},\;{1}} \right)\; + \;\lambda_{f} \pi \left( {i\;{ - }\;{1},\;0,\;{1}} \right),\quad i\; = \;{1},\;{2}, \ldots ,d$$
(4)
$$(\lambda_{p} \; + \;\lambda_{f} )\pi \left( {0,\;0,\;{1}} \right)\; = \; \lambda_{a} \pi \left( {0,\;{1},\;{1}} \right)\; + \;\mu_{r} \pi \left( {d\; + \;{1},\;0,\;{2}} \right)$$
(5)
$$\begin{aligned} (\lambda_{a} \; + \;\lambda_{p} \; + \;\lambda_{f} )\pi \left( {0,\;j,\;{1}} \right)\; = & \;\lambda_{a} \pi \left( {0,\;j\; + \;{1},\;{1}} \right)\; + \;\lambda_{p} \pi \left( {0,\;j\;{-}\;{1},\;{1}} \right)\; + \;\mu_{r} \pi \left( {d\; + \;{1},\;j,\;{2}} \right) ,\\ & j = { 1},{ 2}, \ldots ,s\;{ - }\;{1}\quad {\text{or}}\quad j = s + { 1},s + { 2}, \ldots ,S\;{ - }\;{2} \\ \end{aligned}$$
(6)
$$\begin{aligned} (\lambda_{a} \; + \;\lambda_{p} \; + \;\lambda_{f} )\pi \left( {0,\;s,\;{1}} \right)\; &= \;\lambda_{a} [\pi \left( {0,\;s\; + \;{1},\;{1}} \right)\; + \;\pi \left( {0,\;s\; + \;{1},\;0} \right)]\; + \;\lambda_{p} \pi \left( {0,\;s\;{ - }\;{1},\;{1}} \right) \\ &\quad + \;\mu_{r} \pi \left( {d\; + \;{1},\;s,\;{2}} \right) \\ \end{aligned}$$
(7)
$$(\lambda_{a} \; + \;\lambda_{p} \; + \;\lambda_{f} )\pi \left( {0,\;S\;{ - }\;{1},\;{1}} \right)\; = \;\lambda_{p} \pi \left( {0,\;S\;{ - }\;{2},\;{1}} \right)\; + \;\mu_{r} \pi \left( {d\; + \;{1},\;S\;{ - }\;{1},\;{2}} \right)$$
(8)
$$\begin{aligned} (\lambda_{a} \; + \;\lambda_{p} \; + \;\lambda_{f} )\pi \left( {i,\;s,\;1} \right)\; &= \;\lambda_{a} [\pi \left( {i,\;s\; + \;1,\;1} \right)\; + \;\pi \left( {i,\;s\; + \;1,\;0} \right)]\; + \;\lambda_{p} \pi \left( {i,\;s\;{ - }\;1,\;1} \right)\; + \;\lambda_{f} \pi \left( {i\;{ - }\;1,\;s,\;1} \right), \\ & \quad i\; = \;1,\;2,..,d \\ \end{aligned}$$
(9)
$$\begin{aligned} (\lambda _{a} \; + \;\lambda _{p} \; + \;\lambda _{f} )\pi \left( {i,\;j,\;1} \right)\; = & \;\lambda _{a} \pi \left( {i,\;j\; + \;1,\;1} \right)\; + \;\lambda _{p} \pi \left( {i,\;j\; - \;1,\;1} \right)\; + \;\lambda _{f} \pi \left( {i\; - \;1,\;j,\;1} \right), \\ i\; = & \;1,\;2,..,d,\quad j\; = \;1,\;2, \ldots ,s\; - \;1\quad or\quad i\; = \;1,2,..,d,\quad j\; = \;s\; + \;1, \ldots ,S\; - \;2 \\ \end{aligned}$$
(10)
$$\begin{aligned} (\lambda _{a} \; + \;\lambda _{p} \; + \;\lambda _{f} )\pi \left( {i,\;S\; - \;1,\;1} \right)\; = & \;\lambda _{p} \pi \left( {i,\;S\; - \;2,\;1} \right) \\ + & \;\lambda _{f} \pi \left( {i\; - \;1,\;S\; - \;1,\;1} \right),\;i\; = \;1,\;2, \ldots ,d \\ \end{aligned}$$
(11)
$$\mu_{r} \pi \left( {d\; + \;{1},\;0,\;{2}} \right)\; = \;\lambda_{f} \pi \left( {d,\;0,\;{1}} \right)\; + \;\lambda_{a} \pi \left( {d\; + \;{1},\;{1},\;{2}} \right)$$
(12)
$$\lambda_{a} \; + \;\mu_{r} )\pi \left( {d\; + \;{1},\;j,\;{2}} \right)\; = \;\lambda_{f} \pi \left( {d,\;j,\;{1}} \right)\; + \;\lambda_{a} \pi \left( {d\; + \;{1},\;j\; + \;{1},\;{2}} \right),\;\;j\; = \;{1},\;{2}, \ldots .,S\; - \;{2}$$
(13)
$$(\lambda_{a} \; + \;\mu_{r} )\pi \left( {d\; + \;{1},\;S\;{ - }\;{1},\;{2}} \right)\; = \;\lambda_{f} \pi \left( {d,\;S\; - \;{1},\;{1}} \right)$$
(14)

Finally, Eqs. (12–14) describe the state transitions that can occur in situations where the machine is broken down and under repair. For example, Eq. (13) states that only demand arrival or repair completion can occur in state (d + 1, j, 2), j = 1, 2,…., S − 2. That state can be reached from state (d, j, 1) or from state (d + 1, j + 1, 2) at the occurrence of the “deterioration failure” or “demand arrival” events.

4.2 (s, S)—PM system

In this section we present the balance Eqs. (15–42) that describe the Markov chain model of the deteriorating manufacturing system with inspections and maintenance (Sect. 3.1).

Equations (15–20) describe the state transitions that can occur when the machine is idling. Note that in states with k = 0, there is always available inventory since S > 0 by definition (refer to Sect. 3-system description). Furthermore, recall that inspections can only be initiated when the machine is idling (refer to Sect. 3.1). As a result, the system exits state (i, j, 0) with rate (λa + λin), as stated by (15–20). Next, we explain the derivation of (15); Eqs. (16–20) are derived in a similar way. There are three ways to transit to state (0, S, 0): upon the occurrence of “production completion” in state (0, S − 1, 1) or “inspection completion” is state (0, S, 3) or “maintenance completion” in state (i, S, 4), i = b, b + 1,…, d. This is because, i) the machine switches to idle when the finished goods inventory reaches the threshold S by definition of the (s, S) control policy, ii) the completion of an inspection can never be followed by a maintenance when the machine is good-as-new (i = 0) and, iii) maintenance activities always restore the system to the good-as-new-state. These three ways to transit to state (0, S, 0) are described by the RHS of (15).

Equations (21–32) are related to states were the machine is currently operating to manufacture a new product. When the machine is working (k = 1) and there is available inventory (j ≠ 0) only the events of “production completion”, “demand arrival” and “deterioration failure” can occur thus, the system exits such a state with rate (λa + λp + λf). This situation is described by the LHS of (22–25), (27), (29–32). If there is no inventory, incoming demand is rejected and since the system state is not affected by the occurrence of “demand arrival”, such a state is exited with rate λp + λf (refer to LHS of Eqs. (21), (26), (28)). In the following, we analyze the derivation of the RHS of Eqs. (22) and (29); the rationale of deriving the remaining balance equations for states with k = 1 is similar. Equation (22) shows that, for i = 1, 2, …, b − 1, j = 1, 2, …., s − 1, state (i, j, 1) can be reached either from (i, j + 1, 1), or (i − 1, j, 1), or (i, j − 1, 1), or (i, j, 3) at the occurrence of event “demand arrival”, or “deterioration failure”, or “production completion”, or “inspection completion”, respectively. Note that, upon completion of an inspection, the machine starts to produce if the inventory is less than s (according to the (s, S) control policy) and no maintenance is initiated if the current deterioration is less than b (according to the threshold-type maintenance policy).

The RHS of (29) describes similar state transitions to that of Eq. (22) in respect to the occurrence of the events “demand arrival”, “production completion”, and “inspection completion”. Moreover, it shows that state (0, j, (1), j = 1, 2,…, s − 1, can be reached upon “repair completion” in state (d + 1, j, (2) or “maintenance completion” in state (i, j, 4), i = b, b + 1,…, d.

$$\begin{aligned} (\lambda _{a} + \lambda _{{in}} )\pi \left( {0,S,0} \right) = & \lambda _{p} \pi \left( {0,S - {\mkern 1mu} 1,1} \right) + \mu _{{in}} \pi \left( {0,S,{\mkern 1mu} 3} \right){\mkern 1mu} + \mu _{m} [\pi \left( {b,S,{\mkern 1mu} 4} \right) + \\ + & \pi \left( {b + {\mkern 1mu} 1,S,{\mkern 1mu} 4} \right) + \ldots .. + \pi \left( {d,S,{\mkern 1mu} 4} \right)] \\ \end{aligned}$$
(15)
$$\begin{aligned} (\lambda_{a} + \lambda_{in} )\pi \left( {0,j, \, 0} \right) &= \lambda_{a} \pi \left( {0,j + \, 1, \, 0} \right) + \mu_{in} \pi \left( {0,j, \, 3} \right) + \mu_{m} [\pi \left( {b,j, \, 4} \right) + \pi \left( {b + \, 1,j, \, 4} \right) \\ &\quad + \ldots .. + \pi \left( {d,j, \, 4} \right)],\quad j = s + \, 1,s + \, 2, \, \ldots ..,S - \, 1 \\ \end{aligned}$$
(16)
$$(\lambda_{a} \; + \;\lambda_{in} )\pi \left( {i,\;S,\;0} \right)\; = \;\lambda_{p} \pi \left( {i,\;S\;{-}\;1,\;1} \right)\; + \;\mu_{in} \pi \left( {i,\;S,\;3} \right), \quad i\; = \;1,\;2,\; \ldots ..,b\;{-}\;1$$
(17)
$$\begin{aligned} (\lambda _{a} \; + \;\lambda _{{in}} )\pi \left( {i,\;j,\;0} \right)\; = & \;\lambda _{a} \pi \left( {i,\;j\; + \;1,\;0} \right)\; + \;\mu _{{in}} \pi \left( {i,\;j,\;3} \right), \\ i\; = & \;1,\;2,\; \ldots ..,b\; - \;1,\quad j\; = \;s\; + \;1,\;s\; + \;2,\; \ldots ..,S\; - \;1 \\ \end{aligned}$$
(18)
$$(\lambda_{a} \; + \;\lambda_{in} )\pi \left( {i,\;S,\;0} \right)\; = \;\lambda_{p} \pi \left( {i,\;S\;{-}\;{1},\;{1}} \right), \quad i\; = \;b,\;b\; + \;{1},\; \ldots ..,\;d$$
(19)
$$\begin{aligned} (\lambda _{a} \; + \;\lambda _{{in}} )\pi \left( {i,\;j,\;0} \right)\; = & \;\lambda _{a} \pi \left( {i,\;j\; + \;1,\;0} \right),\quad i\; = \;b,\;b\; + \;1, \ldots ,d, \\ j\; = & \;s\; + \;1,\;s\; + \;2, \ldots ,S\; - \;1 \\ \end{aligned}$$
(20)
$$(\lambda_{p} + \lambda_{f} )\pi \left( {i,0,1} \right) = \lambda_{a} \pi \left( {i,1,1} \right) + \lambda_{f} \pi \left( {i - 1,0,1} \right) + \mu_{in} \pi \left( {i,0,3} \right), \quad i = 1,2, \ldots ,b - 1$$
(21)
$$\begin{aligned} (\lambda _{a} + \lambda _{p} + \lambda _{f} )\pi \left( {i,j,1} \right) = & \lambda _{a} \pi \left( {i,j + 1,1} \right) + \lambda _{f} \pi \left( {i - 1,j,1} \right) + \lambda _{p} \pi \left( {i,j - 1,1} \right) + \mu _{{in}} \pi \left( {i,j,3} \right), \\ i = & 1,2, \ldots ,b - 1,\quad j = 1,{\mkern 1mu} 2, \ldots ,s - 1 \\ \end{aligned}$$
(22)
$$\begin{aligned} (\lambda_{a} + \lambda_{p} + \lambda_{f} )\pi \left( {i,\;s,\;1} \right) & = \lambda_{a} [\pi \left( {i,\;s + 1,\;1} \right)\; + \;\pi \left( {i,\;s\; + \;1,\;0} \right)] \, + \lambda_{p} \pi \left( {i,\;s\; - \;1,\;1} \right) \\ &\quad + \lambda_{f} \pi \left( {i - \, 1,\;s,\;1} \right)\; + \;\mu_{in} \pi \left( {i,\;s,\;3} \right),\quad i = \, 1,\;2, \ldots .,b\; - \;1 \\ \end{aligned}$$
(23)
$$\begin{aligned} (\lambda_{a} + \lambda_{p} + \lambda_{f} )\pi \left( {i,\;j,\;1} \right) &= \lambda_{a} \pi \left( {i,\;j + 1,\;1} \right)\; + \;\lambda_{p} \pi \left( {i,\;j - 1,\;1} \right)\; + \;\lambda_{f} \pi \left( {i\; - \;1,\;j,\;1} \right), \\ i & = \;1,\;2, \ldots .,d,\quad j = s + 1,\;s + \, 2, \ldots .,S\; - \;2\quad {\text{or}}\quad \\ i & = b,\;b\; + \;1, \ldots .,d, \quad j = 1,\;2, \ldots .,s\; - \;1 \\ \end{aligned}$$
(24)
$$(\lambda_{a} + \lambda_{p} + \lambda_{f} )\pi \left( {i,\;S - 1,\;1} \right)\; = \;\lambda_{p} \pi \left( {i,\;S - 2,\;1} \right) + \lambda_{f} \pi \left( {i - 1,\;S - 1,\;1} \right), \quad i = 1,\;2, \ldots ..,d$$
(25)
$$(\lambda_{p} + \lambda_{f} )\pi \left( {i,\;0,\;1} \right) = \lambda_{f} \pi \left( {i - 1,\;0,\;1} \right) + \lambda_{a} \pi \left( {i,\;1,\;1} \right), \quad i = b,\;b + 1, \ldots .,d$$
(26)
$$\begin{aligned} (\lambda _{a} + \lambda _{p} + \lambda _{f} )\pi \left( {i,\;s,\;1} \right) = & \lambda _{a} [\pi \left( {i,\;s + 1,\;1} \right) + \pi \left( {i,\;s + 1,\;0} \right)] \\ + & \lambda _{p} \pi \left( {i,\;s - 1,\;1} \right) + \lambda _{f} \pi \left( {i - 1,\;s,\;1} \right),\quad i = b,\;b + 1, \ldots ,d \\ \end{aligned}$$
(27)
$$\begin{aligned} (\lambda_{p} + \lambda_{f} )\pi \left( {0,\;0,\;1} \right) \, &= \lambda_{a} \pi \left( {0,\;1,\;1} \right) + \mu_{in} \pi \left( {0,\;0,\;3} \right) + \mu_{r} \pi \left( {d + 1,\;0,\;2} \right) \\ &\quad + \mu_{m} [\pi \left( {b,\;0,\;4} \right) + \pi \left( {b + 1,\;0,\;4} \right) + \, \ldots .. + \pi \left( {d,\;0,\;4} \right)] \\ \end{aligned}$$
(28)
$$\begin{aligned} (\lambda _{a} + \lambda _{p} + \lambda _{f} )\pi \left( {0,j,1} \right) = & \lambda _{a} \pi \left( {0,j + 1,1} \right) + \lambda _{p} \pi \left( {0,j - 1,1} \right) + \mu _{{in}} \pi \left( {0,j,3} \right) + \mu _{r} \pi \left( {d + 1,j,2} \right) \\ + & \mu _{m} [\pi \left( {b,j,4} \right) + \pi \left( {b + 1,j,4} \right) + \ldots .. + \pi \left( {d,j,{\mkern 1mu} 4} \right)],\quad j = {\mkern 1mu} 1,{\mkern 1mu} 2, \ldots ,{\mkern 1mu} s - 1 \\ \end{aligned}$$
(29)
$$\begin{aligned} (\lambda_{a} + \lambda_{p} + \lambda_{f} )\pi \left( {0,s,1} \right) &= \lambda_{a} [\pi \left( {0,s + 1,1} \right) + \pi \left( {0,s + 1, \, 0} \right)] + \lambda_{p} \pi \left( {0,s - 1,1} \right) + \mu_{in} \pi \left( {0,s,3} \right) \\ \quad + & \mu_{r} \pi \left( {d + \, 1,s, \, 2} \right) + \mu_{m} [\pi \left( {b,s, \, 4} \right) + \pi \left( {b + 1,s,4} \right) + \ldots . + \pi \left( {d,s, \, 4} \right)] \\ \end{aligned}$$
(30)
$$\begin{aligned} (\lambda _{a} + \lambda _{p} + \lambda _{f} )\pi \left( {0,j,1} \right) = & \lambda _{a} \pi \left( {0,j + {\mkern 1mu} 1,1} \right) + \lambda _{p} \pi \left( {0,j - 1,1} \right) \\ + & \mu _{r} \pi \left( {d + 1,j,{\mkern 1mu} 2} \right),\quad j = s + 1,s + 2, \ldots ,S - 2 \\ \end{aligned}$$
(31)
$$(\lambda_{a} + \lambda_{p} + \lambda_{f} )\pi \left( {0,\;S - 1,\;41} \right) = \lambda_{p} \pi \left( {0,\;S - 2,\;1} \right) + \mu_{r} \pi \left( {d + 1,\;S - 1,\;2} \right)$$
(32)
$$\mu_{r} \pi \left( {d + 1,\;0,\;2} \right) = \lambda_{f} \pi \left( {d,\;0,\;1} \right) + \lambda_{a} \pi \left( {d + 1,\;1,\;2} \right)$$
(33)
$$(\lambda_{a} + \mu_{r} )\pi \left( {d + \, 1,j, \, 2} \right) \, = \lambda_{f} \pi \left( {d,\;j,\;1} \right) + \lambda_{a} \pi \left( {d + 1,j + 1,\;2} \right),\quad j = \, 1,\;2, \, \ldots .,\,S - 2$$
(34)
$$(\lambda_{a} + \mu_{r} )\pi \left( {d + 1,\;S - 1,\;2} \right) = \lambda_{f} \pi \left( {d,\;S - 1,\;1} \right)$$
(35)
$$\mu_{in} \pi \left( {i,\;0,\;3} \right) = \lambda_{a} \pi \left( {i,\;1,\;3} \right),\quad i = \, 0,\;1, \ldots ,\;d$$
(36)
$$(\lambda_{a} + \mu_{in} )\pi \left( {i,\;j,\;3} \right) = \lambda_{a} \pi \left( {i,\;j + 1,\;3} \right),\quad i = 0,\;1, \ldots .,d,\quad j = 1,\;2, \ldots .,s$$
(37)
$$(\lambda_{a} + \mu_{in} )\pi \left( {i,\;j,\;3} \right) = \lambda_{a} \pi \left( {i,\;j + 1,\;3} \right) + \lambda_{in} \pi \left( {i,\;j,\;0} \right),\quad i = 0,1, \ldots .,d,\quad j = s + 1, \ldots ..,S - 1$$
(38)
$$(\lambda_{a} + \mu_{in} )\pi \left( {i,\;S,\;3} \right) = \lambda_{in} \pi \left( {i,\;S,\;0} \right), \quad i = 0,\;1, \ldots ..,d$$
(39)
$$\mu_{m} \pi \left( {i,\;0,\;4} \right) = \mu_{in} \pi \left( {i,\;0,\;3} \right) + \lambda_{a} \pi \left( {i,\;1,\;4} \right),\quad i = b,\;b + 1, \ldots ,d$$
(40)
$$(\mu_{m} + \lambda_{a} )\pi \left( {i,\;S,\;4} \right) = \mu_{in} \pi \left( {i,\;S,\;3} \right), \quad i = b,\;b + 1, \ldots .,d$$
(41)
$$(\mu_{m} + \lambda_{a} )\pi \left( {i,\;j,\;4} \right) = \mu_{in} \pi \left( {i,\;j,\;3} \right) + \lambda_{a} \pi \left( {i,\;j + 1,\;4} \right),\quad i = b,b + 1, \ldots .,d,\quad j = 1,\;2, \ldots .,S - 1$$
(42)

Equations (33)-(35) are associated with states where the manufacturing is undergoing a repair. For example, Eq. (33) shows that when the machine is broken-down (i = d + 1) and there is no available inventory (j = 0) the only event that can cause the system to exit that state is the “repair completion”. Note that, in the absence of finished goods inventory, incoming demand is rejected, and so, the system state does not change. Equation (33) also states that the system transits to state (d + 1, 0, 2) from states (d,0,1) and (d + 1,1,2) with rate λf and λa, respectively.

Equations (36)–(39) describe the state transitions that can occur when the machine is being inspected. For example, the LHS of (38) shows that system exits that particular states with rate (λa + μin), since there is available inventory and the machine is under inspection (no other events can occur besides “demand arrival” and “inspection completion”). The RHS of (38) shows that state (i, j, 3), i = 0, 1,…., d, j = s + 1,….., S − 1 can only be visited from states (i, j + 1, 3) and π(i, j, 0) at the occurrence of “demand arrival” and “inspection start” events (recall from Sect. 3.1 that an inspection can initiated only if the machine is idling at that time).

Finally, Eqs. (40)–(42) pertain to states where the manufacturing system is undergoing a maintenance. For instance, Eq. (40) shows that the only event that can change the current system state is “maintenance completion”, since the finished goods inventory is 0. Moreover, (40) shows that the system transits from states (i, 0, 3) and (i, 1, 4) to (i, 0, 4), i = b, b + 1, …, d, with rates μin and λa, respectively. Recall from Sect. 3.1 that if the current deterioration is found to be greater than b − 1 at an inspection, then maintenance is authorized.

5 Cost function

The steady-state probabilities π(i, j, k) of the two Markov chain models that were described in Sects. 4.1 and 4.2 can be computed by solving the related linear system:

$${{\varvec{\uppi}}}^{T} Q = {\mathbf{0}}$$
(43)

subject to the equality constraint:

$$\sum\nolimits_{i}^{{}} {\sum\nolimits_{j}^{{}} {\sum\nolimits_{k}^{{}} {\pi \left( {i,j,k} \right)} } } = 1$$
(44)

where πT is the row vector of all steady-state probabilities, 0 is a vector with all its elements equal to 0, and Q is the transition rate matrix. Q is a square matrix and its non-diagonal elements are the rates with which the system transits from one state to another. The inner products \({{\varvec{\uppi}}}^{T} Q_{j}\) are equal to 0, where Qj is the j − th column vector of matrix Q. Clearly, the transition rate matrices for both systems that were described in Sects. 4.1 and 4.2 can be straightforwardly found by the respective balance equations.

Having calculated all the steady-state probabilities, we can access the total expected cost of the manufacturing system’s operation which consists of six components: holding costs, production costs, lost sales costs, repair costs, inspection costs, and maintenance costs.

5.1 Cost function of (s, S) system

The total expected cost JsS of the (s, S) system is a function of the average inventory and of the rate with which i) demand is rejected, ii) new production batches are initiated, iii) repairs are conducted.

More specifically, incoming demand is discarded whenever there is no available inventory of finished goods (j = 0), and therefore, the demand rejection rate Ra,sS is written as:

$$R_{a,sS} = \lambda_{a}^{{}} \left[ {\sum\nolimits_{i = 0}^{d} {\pi \left( {i,0,1} \right)} + \pi \left( {d + 1,0,2} \right)} \right]$$
(45)

The production of a new lot (or batch) is initiated whenever the machine is idling and the occurrence of a demand arrival causes the finished goods inventory to drop to the re-order threshold s. Consequently, the rate with which new production lots are initiated is:

$$R_{s,sS} = \lambda_{a} \sum\nolimits_{i = 0}^{d} {\pi \left( {i,s + 1,0} \right)}$$
(46)

A repair is initiated whenever the machine loses its ability to operate, i.e. a “deterioration” failure occurs while in a state with i = d. Therefore, the rate with which “hard failures” occur equals the rate with which repair activities are authorized:

$$R_{r,sS} = \lambda_{f} \sum\nolimits_{j = 0}^{S - 1} {\pi \left( {d,j,1} \right)}$$
(47)

Finally, the average inventory H is obtained by averaging over all possible inventory levels, deterioration stages and machine states:

$$H_{sS} = \sum\nolimits_{i = 0}^{d} {\sum\nolimits_{j = s + 1}^{S} {\left( {j\pi \left( {i,j,0} \right)} \right) + \sum\nolimits_{i = 0}^{d} {\sum\nolimits_{j = 1}^{S - 1} {\left( {j\pi \left( {i,j,1} \right)} \right) + } } } } \sum\nolimits_{j = 1}^{S - 1} {\left( {j\pi \left( {d + 1,j,2} \right)} \right)}$$
(48)

Our goal is to minimize the total expected cost JsS which is a function of all event occurrence rates, control policy parameters etc., and is formulated as:

$$J_{sS} = C_{a} R_{a,sS} + C_{s} R_{s,sS} + C_{r} R_{r,sS} + C_{h} H_{sS}$$
(49)

where Ca is the cost/demand rejection, Ch is the holding cost/finished product/time unit, Cr is the cost/repair and Cs is the production cost/batch.

5.2 Cost function of (s, S)—PM system

The total expected cost JsSPM of the (s, S)—PM system has the additional inspection and maintenance cost components, in relation to the total cost of the (s, S) system.

The derivation of the demand rejection rate Ra,sSPM is similar to that of the (s, S) system:

$$R_{a,sSPM} = \lambda_{a}^{{}} \left[ {\sum\nolimits_{i = 0}^{d} {\left( {\pi \left( {i,0,1} \right) + \pi \left( {i,0,3} \right)} \right)} + \sum\nolimits_{i = b}^{d} {\pi \left( {i,0,4} \right)} + \pi \left( {d + 1,0,2} \right)} \right]$$
(50)

The production of a new batch is started in situations where the machine switches to the “working” state either from “idle”, or “inspected”, or “maintained” state. It follows that the rate of initiating new production lots (batches) can be written as:

$$R_{s,sSPM} = \lambda_{a} \sum\nolimits_{i = 0}^{d} {\pi \left( {i,s + 1,0} \right) + \mu_{in} \sum\nolimits_{i = 0}^{b - 1} {\sum\nolimits_{j = 0}^{s} {\pi \left( {i,j,3} \right) + \mu_{m} \sum\nolimits_{i = b}^{d} {\sum\nolimits_{j = 0}^{s} {\pi \left( {i,j,4} \right)} } } } }$$
(51)

The rate of repairs Rr,sSPM for the (s, S)—PM system equals the analogous rate Rr,sS of the (s, S) system, since the machine can experience a deterioration failure only while working:

$$R_{r,sSPM} = \lambda_{f} \sum\nolimits_{j = 0}^{S - 1} {\pi \left( {d,j,1} \right)}$$
(52)

As stated in Sect. 3.1, inspections of the manufacturing system can be initiated only when the machine is idling thus, the rate with which inspections are authorized is:

$$R_{in,sSPM} = \lambda_{in} \sum\nolimits_{i = 0}^{d} {\sum\nolimits_{j = s + 1}^{S} {\pi \left( {i,j,0} \right)} }$$
(53)

According to the maintenance policy, a preventive maintenance follows an inspection only if the current deterioration stage of the system is found to be greater than or equal to the maintenance threshold b (refer to Sect. 3.1). Therefore, the rate of conducting maintenance actions is:

$$R_{m,sSPM} = \mu_{in} \sum\nolimits_{i = b}^{d} {\sum\nolimits_{j = 0}^{S} {\pi \left( {i,j,3} \right)} }$$
(54)

Finally, the average inventory HsSPM for the (s, S)—PM system can be written as:

$$\begin{aligned} H_{sSPM} &= \sum\nolimits_{j = s + 1}^{S} {\left( {j\sum\nolimits_{i = 0}^{d} {\pi \left( {i,j,0} \right)} } \right) + } \sum\nolimits_{j = 1}^{S - 1} {\left( {j\sum\nolimits_{i = 0}^{d} {\pi \left( {i,j,1} \right)} } \right) + } \sum\nolimits_{j = 1}^{S - 1} {\left( {j\pi \left( {d + 1,j,2} \right)} \right) + } \\ &\quad + \sum\nolimits_{j = 1}^{S} {\left( {j\sum\nolimits_{i = 0}^{d} {\pi \left( {i,j,3} \right)} } \right)} + \sum\nolimits_{j = 1}^{S} {\left( {j\sum\nolimits_{i = b}^{d} {\pi \left( {i,j,4} \right)} } \right)} \\ \end{aligned}$$
(55)

and the total expected cost JsSPM becomes:

$$J_{sSPM} = C_{a} R_{a,sSPM} + C_{s} R_{s,sSPM} + C_{r} R_{r,sSPM} + C_{in} R_{in,sSPM} + C_{m} R_{m,sSPM} + C_{h} H_{sSPM }$$
(56)

where Ca, Ch, Cr, Cs, Cin and Cm are the cost factors of the components of the total cost function (refer to Table 1 for detailed descriptions).

Table 1 Best cost and parameters of examined control policies for varying levels of λp and μr
Full size table

6 Optimization

The control parameters of the (s, S) system are the non-negative integer thresholds s and S. The (s, S)—PM system (refer to Sect. 3.1) has two additional control parameters, namely the threshold b of the maintenance policy and the rate λin at which inspections of the manufacturing system are carried out.

In this section we investigate numerically the properties of the cost function in respect to the aforementioned control parameters. Our aim is to utilize this analysis so as to develop a computationally efficient procedure for finding the control parameter values that minimize the total cost function. For the numerical experiments we consider a system that is described by the following variables: d = 5, λa = 10, λp = 15, λf = 2, μr = 1, μin = 8, μm = 4, Ca = 2, Cs = 3, Cr = 30, Cin = 4, Cm = 6, Ch = 1.

For the (s, S) system, the total cost function in respect to control parameters s and S is depicted on the left side of Fig. 1. It is seen that the cost function is unimodal and that there is a unique minimum for this particular instance at the point (s, S) = (2, 10). The shape of the cost function for the model with inspections and maintenance is shown on the right side of Figs. 1 and 2.

Fig. 1
figure 1

Indicative cost surfaces for the (s, S) system (on the left) and for the (s, S)—PM system (on the right)

Full size image
Fig. 2
figure 2

Indicative cost surfaces for alternative decision variables, for the (s, S)—PM system

Full size image

The visualization of the total cost is difficult in this case due to the fact that there are four decision variables. More specifically, one cannot infer straightforwardly whether the cost function is unimodal or multimodal by simple visual inspection. Nonetheless, one can gain insight on the properties of the function and observe some similarities between the system with inspections/maintenance and the one without. E.g. the cost function exhibits a similar behavior in relation to the variation of parameter S in both cases. Finally, note that, the structure of the cost function for the special cases where the manufacturing system operates under a base stock policy, i.e. s = S − 1 can also be inferred from Figs. 1 and 2.

In light of the numerical investigation of the total cost function, we propose a computationally efficient procedure for obtaining the optimal or near-optimal control parameters s, S and b, λin:

figure a

In steps 1–4 of the procedure, n is the number of decision variables and x is a candidate solution to the optimization problem. For a candidate solution to be feasible the following inequalities must hold: s >  − 1, s < S, λin > 0 and 0 < b < d + 1. These relationships are derived straightforwardly from the system description (Sect. 3). Furthermore, in step 1a of the procedure, bound constraints on the maximum values of S and λin can be defined so as to limit the search to reasonable values for these parameters. In step 3 of the procedure, if some neighbor of x is infeasible, then its associated cost is + ∞.

The proposed search procedure is a local search algorithm with minimal requirements in terms of computational burden. Initially, a feasible, candidate solution is set arbitrarily. Then, the neighborhood of the candidate solution is examined. The neighbor that offers the greatest reduction of the cost function is selected as the next candidate solution. The procedure continues to iterate up to the point where no further improvement can be achieved, in terms of the cost function value.

Provided that the cost function is unimodal and that the steps of the search \({{\varvec{\updelta}}} = \left( {\delta_{1} ,\delta_{2} ,....,\delta_{n} } \right)\) are small enough, the proposed procedure will converge to the optimal solution. If the objective function is multimodal, however, the procedure might get trapped in a local minimum and produce sub-optimal results. In Sect. 7.3, we elaborate on the performance of the proposed procedure and of the cost function’s properties by analyzing an extended set of numerical experiments.

7 Results

In this section, we examine, in terms of total expected cost, the (s, S), base stock, (s, S)—PM and base stock—PM systems. It is reiterated that the (s, S) system is the deteriorating manufacturing system controlled by the (s, S) policy which was described in Sect. 3. The (s, S)—PM system is the system which is subjected to periodic inspections and preventive maintenance activities (refer to Sect. 3.1 for detailed description). Finally, the base stock and base stock—PM systems are the counterparts of the (s, S) and (s, S)—PM systems for s = S − 1 (see also Sects. 3 and 3.1).

The total expected cost for each manufacturing system is obtained by solving the associated Markov chain numerically. The best cost and best control parameters for each system are found by means of the local search procedure that was described in Sect. 6. The parameters of the local search procedure where set as follows: the steps δ1, δ2,… were selected to be 1 and 0.001 for the discrete (b, s, S) and the continuous (λin) decision variables, respectively. The search space for variables S and λin was set to Axsater (2015); Li and Ma 2017) and [0.1, 5] following some pilot experiments that were used to determine the reasonable values for the series of experiments that are reported in this article. All feasible values for decision variables s and b were considered, i.e. d + 1 > b > 0, s > −1 and s < S (or s = S − 1). The initial point for the search was selected at random.

To assess the performance of the alternative control policies, we define initially a “base” instance of the examined manufacturing system: d = 5, λa = 10, λp = 15, λf = 2, μr = 1, Ca = 4, Cs = 3, Cr = 30, Ch = 1 (and μin = 8, μm = 4, Cin = 4, Cm = 6 where applicable).

Using the base instance as a starting point, we examine the behavior of each control policy for various levels of the system parameters λp, μr, Ch, Ca, Cs and Cr by adjusting these parameters one at a time. The best control parameter values for all control policies and all manufacturing system instances are presented in Tables 1, 2 and 3. The associated total expected costs are provided in the aforementioned tables and also presented graphically in Figs. 3, 4 and 5.

Table 2 Best cost and parameters of examined control policies for varying levels of Ch and Ca
Full size table
Table 3 Best cost and parameters of examined control policies for varying levels of Cs and Cr
Full size table
Fig. 3
figure 3

Performance of alternative control policies for various production rates (on the left) and repair rates (on the right)

Full size image
Fig. 4
figure 4

Performance of alternative control policies for various levels of Ch (on the left) and Ca (on the right)

Full size image
Fig. 5
figure 5

Performance of alternative control policies for various levels of Cs (on the left) and Cr (on the right)

Full size image

7.1 Effect of system parameters on total expected cost

From Figs. 4 and 5, it is seen that the total expected cost is an increasing function of the cost factors Ch, Ca, Cs and Cr. The base stock and base stock—PM systems are considerably more sensitive to increases of the cost/batch factor Cs, compared to (s, S) and (s, S)—PM. This is due to the fact that production batches in a system that is controlled by a base stock policy are significantly smaller than the batches of a system controlled by an (s, S) policy. Consequently, in a base stock system, the number of produced batches is higher and additional production costs are incurred.

On the other hand, the base stock and (s, S) systems are significantly more sensitive in respect to the cost/repair factor Cr, in relation to the (s, S)—PM and base stock—PM systems. This can be attributed to the fact that hard failures/repair activities can be prevented by frequently maintaining the manufacturing system and thus, achieving substantial repair cost savings.

A similar argument can explain the increased sensitivity of the base stock and (s, S) systems in terms of the repair rate μr, compared to the (s, S)—PM and base stock—PM systems (refer to Fig. 3). As expected, the total expected cost is observed to be a decreasing function of μr, since the quicker repairs are conducted, the less time is the manufacturing system down. As a result, fewer demands are rejected due to stock-outs and fewer lost sale costs are incurred.

From the left side of Fig. 3, it is seen that the total expected cost is a decreasing function of λp for the (s, S), (s, S)—PM systems but this property does not hold for the base stock-type systems.

This is because, in a manufacturing system controlled by the (s, S) or base stock policy, the increase of the production rate allows for less stock to be held so as to meet demand thus, holding costs are diminished. Nonetheless, in a system controlled by the base stock policy, increasing the production rate causes the size of batches to become even smaller (for a specific demand level). Therefore, total production is split up in additional batches resulting in increased production related costs.

7.2 Performance of alternative control policies

Clearly, the ranking of the alternative control systems is largely affected by the arrival rate, the production rate, the cost parameters of the objective function etc. For example, if the inspection costs are very high, then the base stock and (s, S) systems are more likely to outperform their counterparts that entail inspections and maintenance. Nevertheless, we selected the parameters of all 37 problem instances that comprise this experimental study in such a way so as to simulate realistic situations.

E.g. the cost/repair is significantly higher than the cost/maintenance; the cost/production batch is substantially higher than the holding cost/product/time unit etc. This way, the conclusions drawn from analyzing the experimental results are rendered meaningful and of practical importance.

Our numerical results show that the (s, S)—PM system is superior to all alternative control schemes in all cases. The only situation where the performance of the (s, S)—PM system is comparable to another control policy, i.e. the (s, S) system, is the one where μr = 3.5 (refer to last row of Table 1 and on the right side of Fig. 3). In that case, the repair rate is relatively high and therefore, the benefits of preventive maintenance are counterbalanced by the related inspection/maintenance costs.

In all other cases, the observed superiority of the (s, S)—PM system can be attributed to two factors primarily: (a) increased system availability due to preventive maintenance and (b) low production costs due to large batch sizes.

More specifically, maintenance actions prevent the system from experiencing hard failures and undergoing repairs. As a direct consequence, cost savings related to repair activities are achieved. Another important effect of preventive maintenance is the increase of the manufacturing system’s availability, i.e. the fraction of time that the machine is available to produce. Increased availability means that there is no need to hold excessive inventory to hedge against the demand, and this leads to decreased holding costs. Increased availability also leads to less frequent stock-out phenomena thus, decreased lost sales costs.

The production control policy of the (s, S)—PM results in relatively large batch sizes when compared to order point policies such as base stock. Large batches means fewer batches/decreased production costs and this explains to some extent the superior performance of (s, S)—PM.

From Tables 1, 2 and 3 and Figs. 3, 4 and 5, we can see that the base stock system is outperformed by all other control mechanisms in all cases. The reasons for that can be found on “mirror” arguments that explain the (s, S)—PM system’s favorable performance. For example, when production lot costs are significant, the base stock policy is not advisable because it leads to small, and consequently, many lots.

In this series of experiments, the (s, S) and base stock—PM systems rank second and third, respectively. The (s, S) system is outperformed in all cases by (s, S)—PM but has better performance than base stock—PM in 33 out of 37 cases.

This is an indication that the production related costs largely outweigh other cost components in the evaluation of the total expected cost function. Moreover, examination of Tables 1, 2 and 3 shows that parameter S generally assumes larger values in the (s, S) system compared to the ones of the base stock—PM system. This means that, because of the control policies’ inherent characteristics, the maximum allowed inventory can be set to higher values in the (s, S) system leading to probably decreased lost sales costs.

The base stock—PM system outperforms base stock in all cases as well as the (s, S) system in cases where: i) the repair rate is dramatically lower than the maintenance rate (μr = 0.5) or, ii) the production lot costs are rather negligible (Cs = 1) or, iii) the repair costs are very high (Cr = 42, Cr = 46).

7.3 Evaluation of proposed local search procedure

As stated in Sect. 6, the proposed local search procedure does not come with optimality guarantees. In this section, we assess its usefulness by comparing it with an exhaustive search procedure. More specifically, we compare all results that are presented in Tables 1, 2 and 3 and were produced by the proposed heuristic to the analogous results that were produced by an exhaustive search procedure with the same parameters as the local search: \(S \in \left[ {1,20} \right]\), \(\lambda_{in} \in \left[ {0.1,5} \right]\) and discretized using a step equal to 0.001, search space for s and b includes all feasible values for these variables (refer to second paragraph of Sect. 7 for details).

In 144 out of 4 (manufacturing systems) × 37 (problem instances) = 148 (optimization problems in total) the exhaustive search procedure produced results that were identical to those of the proposed heuristic. The only cases where different results were reported are shown in Table 4.

Table 4 Differences between the proposed local search heuristic and exhaustive search
Full size table

Clearly, the differences between the two solution approaches are rather negligible. The proposed heuristic managed to produce optimal results in the overwhelming majority of cases and marginally sub-optimal results in four cases. Furthermore, the proposed procedure is far more economical compared to the brute-force algorithm n terms of computational cost. It can be argued that it is a very good option for optimizing the examined manufacturing systems, despite the fact that it is not mathematically proven to produce optimal results.

The comparison between the local search procedure and the exhaustive search algorithm gives important insight regarding the properties of the cost function. The two solution approaches gave identical results in respect to the base stock and (s, S) systems. This is an indication that the related total expected cost functions are probably unimodal (see also Sect. 6). On the other hand, by examining the neighborhoods of the solutions presented in the second column of Table 4, it is established that these points are indeed local minima. It follows that the total expected cost functions for the base stock—PM and (s, S)—PM systems are multimodal. This means that there is always a chance for the proposed local search heuristic to get trapped in a local optimum when applied to the two aforementioned systems.

8 Conclusions and directions for future research

Stochastic modelling of deteriorating manufacturing systems, as presented in this paper, provides a useful tool to analyze the behavior of a given system operating under specific production control, inspection, and maintenance policies. Additionally, it identifies how the adjustment of the parameters of each policy is improving its operation as a whole. Several experimental findings of this research can be generalized and provide guidelines for establishing efficient control policies in arbitrary, manufacturing settings.

The experimental results showed that (s, S)—type policies largely outperform base stock − type policies when the costs for starting a new batch are significant and the production rate of the system is relatively high. It was also observed that periodic inspections/preventive maintenance could improve the system’s performance if the repair rate is relatively low and the repair costs are significant. The (s, S)—PM system was found to outperform all alternative control policies in all cases. The base stock system was inferior to all other control policies, in every experiment of this research. The (s, S) system exhibited better performance compared to the base stock—PM in the majority of examined cases.

A straightforward way to extent this paper is to provide additional theoretical results in respect to the total expected cost function. For example, it would be interesting to obtain a closed-form expression for the cost function in respect to control policy parameters. A theoretical analysis of how to optimize the control parameters of the examined production/maintenance policies based on mathematically proven properties of the cost function would also be helpful. Another extension, perhaps more application-oriented, would be to use a similar model as a tool to support investment decisions regarding the initial configuration of the production site. Questions such as the size of the warehouse in relation to the production equipment selected or the comparison between investment and operation cost per produced unit are essential and clearly need to be answered before investing.