Multiperiod optimal emergency material allocation considering road network damage and risk under uncertain conditions

Abstract

Material rescue is a key component of recovery and reconstruction in disaster-affected areas. Scientific and reasonable emergency material allocation (EMA) can improve rescue effects, reduce allocation risks, and minimize the losses due to a disaster. Previous EMA studies have mainly centered on complete or deterministic disaster information, while the impact of uncertain factors affecting material allocation, such as fuzzy random information and road network damage, are generally neglected. Thus, existing material allocation schemes are not fully practically applicable. This paper proposes a multiperiod optimization model for EMA under uncertain conditions with the goals of the shortest time, lowest cost, and lowest risk. A risk measurement method is incorporated into the multiperiod EMA scheme. Deterministic transformation methods of stochastic and fuzzy constrained programming, as well as an improved genetic algorithm (IGA), are applied to solve the proposed model. A computational case based on the LuDian earthquake in China is used to verify the practicability of the proposed model. The results show that the proposed risk measurement method can effectively measure multiperiod transportation risk and path repair risk in the material allocation context. Road conditions also appear to markedly impact the multiperiod allocation of emergency materials. We illustrate the relationship among risk, time, and cost plus a dimension of flexibility in various optimized multiperiod EMA scenarios. A comparative analysis of intelligent algorithms shows that the proposed IGA is the most effective approach to manage large-scale EMA optimization problems as it has higher solving efficiency, better convergence, and stronger stability.

1 Introduction

Large-scale disasters, natural (e.g., earthquakes, floods) and man-made (e.g., terrorist attacks) alike, have caused vast quantities of property damage, injuries, and fatalities in recent years (Ahmadi et al. 2020; Barbarosoǧlu and Arda 2004; Chang et al. 2007; Green et al. 2019; Hu et al. 2016; Huang et al. 2015; Najafi et al. 2013; Qin et al. 2017; Zhao and Liu 2016). Post-disaster emergency management is, to this effect, a vastly challenging issue (MacKenzie and Zobel 2016; Muir et al. 2020; Sarma et al. 2019b; Wu et al. 2017). Post-disaster emergency rescue mainly serves to minimize the casualties, socio-economic losses, and risks associated with a disaster (Rebeeh et al. 2019; Zhang et al. 2018). In this process, material rescue is the key to meeting victims’ basic survival needs and to assist the recovery of the disaster-affected area (Ma et al. 2019). Scientific and reasonable emergency material allocation (EMA) plans can ensure the effective operation and rational use of materials, which limits casualties, reduces the risks of distribution, and improves the overall effectiveness of the rescue (Chen et al. 2020; Guo et al. 2019).

The inherent unpredictability of disasters renders certain information, such as supply, demand, time, and cost, unable to be accurately obtained or updated in a timely manner (Galindo and Batta 2013; Hu et al. 2016). Large-scale disasters tend to damage road networks (Statheropoulos et al. 2015), thereby increasing the risk of material allocation, directly affecting the efficiency and effectiveness of EMA activities, and bringing certain implementation difficulties to the multiperiod EMA process. Decision-making within such a complex environment is characterized by high time-sensitivity, uncertainty, and unpredictability (Ahmadi et al. 2020). Decision support for disaster-relief managers plays a crucial role in effective emergency rescue operations (Amailef and Lu 2013). Traditional methods for solving the EMA problem cannot produce an optimal or even a near-optimal solution in the sufficient time. Intelligent methods (e.g., genetic algorithm), however, can produce high-quality solutions or even optimal solutions within a limited time period (Kyriklidis et al. 2014).

This paper proposes a multiperiod EMA optimization model designed to effectively resolve decision-related problems (e.g., uncertainties, regarding demand, allocation time, and cost of emergency materials, risks in the allocation process, highly urgent timetables). The deterministic transformation methods of stochastic constrained programming and fuzzy constrained programming are analyzed and an improved genetic algorithm (IGA) is utilized to solve the model. The proposed method can help decision-makers to identify the best possible EMA solution in an actual disaster scenario. It serves to provide a high-quality EMA scheme alongside the scientific and effective multiperiod allocation of emergency relief materials.

The main contributions of this work can be summarized as follows.

• A multiperiod EMA model under uncertainty is proposed which simultaneously considers time, cost, and risk as well as trade-offs between these three decision criteria.

• A risk measurement method is designed to measure the path transportation risk and road network repair risk in the multiperiod EMA process, and the impacts of road conditions on the multiperiod EMA are analyzed.

• An IGA method is developed to solve the model so that decision-makers can handily select the best possible EMA strategy.

The remainder of this article is organized as follows. Section 2 reviews the literature relevant to this study. Section 3 presents the notation and model formulation. Section 4 presents the solution algorithm. The LuDian earthquake was taken as a case study to illustrate the applicability and potential advantages of the proposed model as discussed in Sect. 5. Section 6 gives concluding remarks and points out potential future research directions.

2 Literature review

Many previous researchers have investigated material allocation problems in the emergency logistics context, particularly as natural and man-made disasters have increased in frequency and severity in recent years (Caunhye et al. 2012; Farahani et al. 2020; Özdamar and Ertem 2015). As a key link in the emergency response process, EMA is a crucial component of rescue operations (Kemball-Cook and Stephenson 1984; Chen et al. 2020).

Our work centers on three main research topics: (1) decision criteria/objectives in humanitarian EMA operations, (2) EMA optimization models under uncertain decision-making conditions, and (3) solutions to material allocation issues in complex and uncertain contexts.

The decision criteria/objectives in this context involve the allocation of humanitarian materials, which differ from conventional materials in that their primary purpose is to reduce casualties and property losses (Hu et al. 2016; Huang et al. 2015; Galindo and Batta 2013; Sheu 2007). Certain decision criteria/objectives reflecting the efficiency and effectiveness of emergency relief that are usually given priority, include shortest delivery time (Altay 2013; Berkoune et al. 2012; Luan et al. 2020; Yan and Shih 2009), lowest total allocation cost (Barbarosoğlu et al. 2002; Lu and Sun 2020; Özdamar et al. 2004; Wang and Sun 2018; Zahedi et al. 2020), lowest total loss (Wang et al. 2019; Zhang et al. 2017), most reliable path (Miao et al. 2007; Yuan and Wang 2009), or a combination of shortest time and lowest cost (Sheu and Pan 2014; Tzeng et al. 2007; Xu et al. 2020). Altay (2013) proposed a capability-based multi-resource and multi-location EMA model for emergency response operations with the goal of minimizing the total delivery time, i.e., the combined deployment time and response time. Additionally, Wang and Sun (2018) developed an EMA model for natural disaster rescue operations which considers the lowest total allocation cost as an objective; they validated their model on a simulation of the Ya’an earthquake that occurred in China in 2014. Wang et al. (2019) presented a multiperiod model for material allocation to multiple affected locations that minimizes the total loss caused by material shortages. Miao et al. (2007) constructed mathematical reliable path search model and target path-solving algorithm to support transportation networks under the constraints of setting and pseudo-polynomial time. Sheu and Pan (2014) designed a seamless centralized EMA network for large-scale natural disasters emergency logistics operations which targets the minimal operational costs and travel time.

Another important research topic related to our work is EMA optimization models developed under uncertain decision-making conditions. Previous researchers have focused on two uncertain emergency conditions: demand (Beraldi et al. 2004; Beraldi and Bruni 2009; Cheng et al. 2016; Liu et al. 2013; Mete and Zabinsky 2010; Sun et al. 2013; Wang and Sun 2020) and road network conditions (Chen and Ji 2010; Li et al. 2019; Liu et al. 2014; Nolz et al. 2010; Zhang et al. 2019b). Liu et al. (2013) developed a stochastic mixed integer program model for EMA under uncertain demand with the objectives of minimizing the total costs and maximizing the expected completion rate; their model was shown to provide valuable decision support for post-disaster material allocation. Cheng et al. (2016) established an emergency vehicle-routing optimization model considering the stochastic demand for minimizing transportation costs and reducing the losses caused by insufficient or excessive supply in the critical period of a rescue. Wang and Sun (2020) considered the incomplete information acquisition caused by the sudden nature of a disaster. They introduced the interval number to describe the fuzzy uncertainty of emergency material demands, then constructed a multi-type material, multiperiod, and multi-objective model for optimal EMA; they also designed a two-dimensional Euclidean distance objective weighting fuzzy algorithm to solve the model, and validated it based on a case study of the Yushu earthquake. Liu et al. (2014) proposed a robust bi-level programming model for emergency material positioning and allocation model based on the uncertainty of road networks that includes a collaborative allocation strategy for emergency materials combining vertical distribution and horizontal transfer characteristics. Li et al. (2019) presented a post-disaster relief material allocation model based on the road network reliability targeting the shortest path time, smallest material shortage, and highest path reliability.

Many previous researchers have also investigated material allocation issues in complex and uncertain contexts. Uncertainty is the most significant characteristic of the emergency rescue environment (Hu et al. 2016). Approaches to managing this uncertainty mainly include stochastic programming (Mete and Zabinsky 2010; Garrido et al. 2015), fuzzy programming (Sarma et al. 2019a), and robust optimization (Mulvey et al. 1995). Among them, stochastic programming and fuzzy programming are the most commonly used (Rawls and Turnquist 2010; Rennemo et al. 2014; Zhang et al. 2019a). Traditional methods for resolving material allocation problems, such as complete enumeration (Younis and Saad 1996), branch and bound (Weeney and Murphy 1981), integer programming (Elwany et al. 1998), and dynamic programming (Chan et al. 1996), are often used to find exact solutions. However, they are only suitable for small and simple resource allocation problems (Hegazy 1999; Li et al. 2019); their use in large or complex resource allocation problems tends to be computationally infeasible and may result in combinatorial explosions (Geng et al. 2011; Kyriklidis et al. 2014).

Heuristic intelligent methods are preferred for large and complex resource allocation optimization problems (Kyriklidis et al. 2014). Although their effectiveness depends on the problem, their success rate is higher than traditional methods (Hegazy 1999; Leu and Hung 2002) as intelligent search strategies can be used to quickly generate high-quality or optimal solutions (Chan et al. 2005; Leu and Yang 1999). In recent years, heuristic intelligent methods such as genetic algorithm (GA), ant colony algorithm (ACO), simulated annealing algorithm (SAA), and particle swarm optimization (PSO) have been successfully applied to solve resource allocation problems (Leu and Yang 1999; Chen et al. 2007). The GA functions based on the qualities of natural organisms, where the optimal solution is searched by simulating the natural evolution process (Li 2010). The ACO is a probabilistic algorithm used to find an optimal path, inspired by the behavior of ants making pathways as they search for food (Geng et al. 2015). The SAA is derived from the principle of solid annealing. Kirkpatrick introduced annealing into the field of combinatorial optimization as a stochastic optimization algorithm based on the Monte-Carlo iterative solution strategy. Its working concept is the similarity between the annealing process of solid matter in physics and general combinatorial optimization problems (Steinbrunn et al.1997). The PSO is a random search algorithm based on group cooperation that simulates the foraging behavior of birds (Wang and Sun 2018). These intelligent methods have been proven effective in solving material allocation problems (Chen et al. 2019; Huang et al. 2010; Wang et al. 2020). However, they are also known to have problems such as premature convergence and poor exploitation (Kyriklidis et al. 2014). Basic GAs can easily fall into local optimality and precocity. Researchers have attempted to improve the GA by, for example, embedding the steepest descent operator in the GA (Zhao 1997) and optimizing the non-equal probability selection method of the cross position (Zhu et al. 2004). However, these approaches make the algorithm more burdensome to process as they increase its complexity without fundamentally improving it.

The scholars cited above have indeed provided a sound theoretical basis for our work. However, there are still gaps in the EMA literature. There is a lack of EMA research that has simultaneously considered multiperiod time, cost, and risk in the decision-making criteria. Previous EMA problems in uncertain situations usually incorporate only the uncertainty of demand or road networks, while ignoring other factors related to emergency rescue operations. There has been no scientific measurement the risk related to road maintenance and transportation obstacles created by material allocation across a damaged road network. Existing algorithms still show room for improvement in terms of computational efficiency and accuracy as well. Thus, we attempted in this study to develop a multiperiod EMA optimization model that simultaneously captures time, cost, and risk under uncertainty. We explored methods of managing uncertainty in an emergency context and composed an improved solution method for the complex EMA problem to provide decision support for obtaining high-quality or optimal EMA schemes. Our multiperiod EMA optimization model simultaneously captures time, cost, and risk under uncertainty, and measures the risk faced by material allocation via multiperiod risk measurement method. This model allows decision-makers to consider trade-offs between time, cost, and risk in a manner that achieves the multiperiod scientific and optimal allocation of emergency relief materials.

3 Notation and model formulation

3.1 Notation

The settings described here are related to real-world conditions. The sudden and extremely destructive nature of disasters make it impossible to obtain fully accurate information in the process of emergency rescue operations. Material demand and supply, as well as transportation time and risk (particularly as affected by damage to the road network) are highly uncertain. Uncertain information may be input to EMA models as fuzzy interval numbers that are subject to certain distribution rules. Previous researchers have done this successfully. For example, Chen et al. (2014) used triangular fuzzy numbers to represent material demand, transportation time, and cost; Guo et al. (2010) used interval numbers to represent material demand, storage construction costs, and operating costs. In this study, we borrowed from these ideas and set parameters in accordance with our own research questions.

We imposed a normal distribution due to the large amount and significant fluctuations in material demand ($\mathop {\tilde{d}}\nolimits_{{jh}}^{e}$) in the emergency response scenario. Compared with demand, material supply ($\mathop {\tilde{a}}\nolimits_{{ih}}^{e}$) information is easier to obtain, but the information obtained in emergency situations may be relatively inaccurate or arrive at a significant delay, so the supply was set as a triangular fuzzy number. The destruction wreaked by primary disasters plus the impact of secondary disasters render the repair time ($\mathop {\tilde{t}}\nolimits_{{ij}}^{e}$) and repair cost ($\mathop {\tilde{c}rep}\nolimits_{{ij}}^{e}$) of damaged roads, as well as the fixed costs ($\mathop {\tilde{c}fix}\nolimits_{{ij}}^{e}$) and variable costs ($\mathop {\tilde{c}var}\nolimits_{{ijh}}^{e}$) of material transportation, unable to be accurately determined. A disturbance coefficient can be set, however, to express their uncertainty and dynamic variability.

The sets, parameters and variables used in the model formulation are as follows.

$S = \left\{ {\left. i \right|{\text{ }}i = 1,2, \ldots ,m} \right\}$:

Set of all rescue sites (supply points).

$D = \left\{ {\left. j \right|{\text{ }}j = 1,2, \ldots ,n} \right\}$:

Set of all affected locations (demand points).

$H = \left\{ {\left. h \right|{\text{ }}h = 1,2, \ldots ,g} \right\}$:

Set of types of emergency materials.

$E = \left\{ {\left. e \right|{\text{ }}e = 1,2, \ldots ,l} \right\}$:

Set of time periods of EMA.

$\mathop {\tilde{d}}\nolimits_{{jh}}^{e}$:

New demand at affected location $j$ for material $h$ during time period $e$. The demand $\mathop {\tilde{d}}\nolimits_{{jh}}^{e}$ obeys a normal distribution with mean $\mathop E\nolimits_{{\mathop d\nolimits_{{jh}}^{e} }}$ and variance $\mathop {Var}\nolimits_{{\mathop d\nolimits_{{jh}}^{e} }} ^{{\text{2}}}$, $\mathop {\tilde{d}}\nolimits_{{jh}}^{e} \sim N\left( {\mathop E\nolimits_{{\mathop d\nolimits_{{jh}}^{e} }} ,\mathop {Var}\nolimits_{{\mathop d\nolimits_{{jh}}^{e} }} ^{{\text{2}}} } \right)$.

$\mathop {d^{\prime}}\nolimits_{{jh}}^{e}$:

Shortages of material $h$ at affected location $j$ during time period $e$.

$\mathop d\nolimits_{{jh}}^{e}$:

Actual demand for material $h$ at affected location $j$ during period $e$

$\mathop {\tilde{a}}\nolimits_{{ih}}^{e}$:

New supply of material $h$ at rescue sites $i$ during time period $e$ represented by triangular fuzzy numbers, that is, $\mathop {\tilde{a}}\nolimits_{{ih}}^{e} = \left( {\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{L} ,\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{O} ,\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{R} } \right)$; $\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{L}$, $\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{O}$ and $\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{R}$ represent the lowest, the most likely, and the highest predicted supply, respectively.

$\mathop {a^{\prime}}\nolimits_{{ih}}^{e}$:

Inventory of material $h$ at $i$ before the beginning of time period $e$.

$\mathop a\nolimits_{{ih}}^{e}$:

Actual supply (available amount) of $h$ at $i$ during time period $e$.

$\mathop t\nolimits_{{ih}}^{e}$:

Loading time of unit material $h$ at rescue site $i$ during time period $e$.

$\mathop t\nolimits_{{jh}}^{e}$:

Unloading time of the unit material $h$ at $j$ during time period $e$.

$\mathop {\tilde{t}}\nolimits_{{ij}}^{e}$:

Repair time per unit mileage of damaged road from $i$ to $j$ during time period $e$ expressed by uncertain parameters with disturbance coefficient, $\mathop {\tilde{t}}\nolimits_{{ij}}^{e} {\text{ = }}\left[ {\mathop {\dot{t}}\nolimits_{{ij}}^{e} ,{\text{ }}\mathop {\dot{t}}\nolimits_{{ij}}^{e} + \zeta \cdot \mathop {\dot{t}}\nolimits_{{ij}}^{e} } \right]$; $\mathop {\dot{t}}\nolimits_{{ij}}^{e}$ represents the repair time per unit mileage of damaged road, or the minimum nominal repair time in a non-disaster situation, $\zeta \cdot \mathop {\dot{t}}\nolimits_{{ijh}}^{e}$ represents the maximum disturbance value of the repair time per unit path, and the disturbance coefficient $\zeta \cdot \mathop {\dot{t}}\nolimits_{{ijh}}^{e}$ can be determined according to the actual road damage coefficient. In this paper, $\mathop {\tilde{t}}\nolimits_{{ij}}^{e} \sim \left( {\mathop {\dot{t}}\nolimits_{{ij}}^{e} ,\zeta } \right)$ is used to simplify the expression; the minimum nominal repair time of per unit mileage damaged road is $\mathop {\dot{t}}\nolimits_{{ij}}^{e}$ and the maximum disturbance coefficient is $\zeta$ under uncertainty.

$\mathop {tpun}\nolimits_{{jh}}^{e}$:

Time penalty parameter for the shortage of unit material $h$ at affected location $j$ at the end of time period $e$.

$\mathop {\tilde{c}fix}\nolimits_{{ij}}^{e}$:

Fixed cost of transportation from rescue site $i$ to affected location $j$ during time period $e$, $\mathop {\tilde{c}fix}\nolimits_{{ij}}^{e} {\text{ = }}\left[ {\mathop {\dot{c}fix}\nolimits_{{ij}}^{e} ,{\text{ }}\mathop {\dot{c}fix}\nolimits_{{ij}}^{e} + \mathop {\zeta \cdot \dot{c}fix}\nolimits_{{ij}}^{e} } \right]$, which is recorded as $\mathop {\tilde{c}fix}\nolimits_{{ij}}^{e} \sim \left( {\mathop {\dot{c}fix}\nolimits_{{ij}}^{e} ,\zeta } \right)$.

$\mathop {\tilde{c}var}\nolimits_{{ijh}}^{e}$:

Variable cost per unit of allocating material $h$ from $i$ to $j$ during time period $e$, $\mathop {\tilde{c}var}\nolimits_{{ijh}}^{e} = \left[ {\mathop {\dot{c}var}\nolimits_{{ijh}}^{e} ,{\text{ }}\mathop {\dot{c}var}\nolimits_{{ijh}}^{e} + \mathop {\zeta \cdot \dot{c}var}\nolimits_{{ijh}}^{e} } \right]$, recorded as $\mathop {\tilde{c}var}\nolimits_{{ijh}}^{e} \sim \left( {\mathop {\dot{c}var}\nolimits_{{ijh}}^{e} ,\zeta } \right)$.

$\mathop {cpur}\nolimits_{h}^{e}$:

Unit purchase cost of material $h$ during time period $e$.

$\mathop {\tilde{c}rep}\nolimits_{{ij}}^{e}$:

Cost of repairing damaged road unit mileage from $i$ to $j$ during $e$ in case of disaster, $\mathop {\tilde{c}rep}\nolimits_{{ij}}^{e} = \left[ {\mathop {\dot{c}rep}\nolimits_{{ij}}^{e} ,{\text{ }}\mathop {\dot{c}rep}\nolimits_{{ij}}^{e} + \zeta \cdot \mathop {\dot{c}rep}\nolimits_{{ij}}^{e} } \right]$, recorded as $\mathop {\tilde{c}rep}\nolimits_{{ij}}^{e} \sim \left( {\mathop {\dot{c}rep}\nolimits_{{ij}}^{e} ,\zeta } \right)$.

$\mathop {cload}\nolimits_{{ih}}^{e}$:

Unit cost of loading material $h$ at $i$ during time period $e$.

$\mathop {cunload}\nolimits_{{jh}}^{e}$:

Unit cost of uploading material $h$ at $j$ during time period $e$.

$\mathop {cpun}\nolimits_{{jh}}^{e}$:

Penalty cost of shortage unit material $h$ at $j$ at the end of period $e$.

$\mathop {spa}\nolimits_{{ih}}^{{}}$:

Space required to store each unit of material $h$ at rescue point $i$.

$\mathop {Cap}\nolimits_{i}$:

Capacity of emergency rescue point $i$.

$\mathop {Rtra}\nolimits_{{ijh}}^{e}$:

Total path transportation risk of allocating $h$ from $i$ to $j$ during $e$.

$\mathop {\tilde{P}tra}\nolimits_{{ijh}}^{e}$:

Possibility of transportation risk occurring when material $h$ is allocated from $i$ to $j$ during time period $e$. $\mathop {\tilde{P}tra}\nolimits_{{ijh}}^{e} {\text{ = }}\left[ {\mathop {\mathop {Ptra}\nolimits_{{ijh}}^{e} }\nolimits^{ - } ,\mathop {\mathop {Ptra}\nolimits_{{ijh}}^{e} }\nolimits^{ + } } \right]$, where $\mathop {\mathop {\tilde{P}tra}\nolimits_{{ijh}}^{e}}\nolimits^{ - }$ and $\mathop {\mathop {\tilde{P}tra}\nolimits_{{ijh}}^{e} }\nolimits^{{\text{ + }}}$ are the lowest and highest probability, respectively.

$\mathop {Vtra}\nolimits_{{ijh}}^{e}$:

Possibility of large losses caused by transportation risk in the process of allocating material $h$ from $i$ to $j$ during time period $e$.

$\mathop {Ltra}\nolimits_{{ijh}}^{e}$:

Expected degree of damage (loss) due to transportation risk when material $h$ is allocated from $i$ to $j$ during time period $e$. $\mathop {Ltra}\nolimits_{{ijh}}^{e} {\text{ = }}\mathop {ltra}\nolimits_{{ijh}}^{e} \times \mathop x\nolimits_{{ijh}}^{e}$, $\mathop {ltra}\nolimits_{{ijh}}^{e}$ is the loss due to transportation risk when the unit material is allocated from $i$ to $j$ during time period $e$.

$\mathop {Rrep}\nolimits_{{ijh}}^{e}$:

Total path repair risk of allocating material $h$ from $i$ to $j$ during $e$.

$\mathop {\tilde{P}rep}\nolimits_{{ijh}}^{e}$:

Probability of repair risk occurring during repair of damaged road section from $i$ to $j$ during time period $e$. $\mathop {\tilde{P}rep}\nolimits_{{ijh}}^{e} {\text{ = }}\left[ {\mathop {\mathop {Prep}\nolimits_{{ijh}}^{e} }\nolimits^{ - } ,\mathop {\mathop {Prep}\nolimits_{{ijh}}^{e} }\nolimits^{ + } } \right]$,$\mathop {\mathop {\tilde{P}rep}\nolimits_{{ijh}}^{e} }\nolimits^{ - }$ and $\mathop {\mathop {\tilde{P}rep}\nolimits_{{ijh}}^{e} }\nolimits^{{\text{ + }}}$ are, respectively, the minimum and maximum probability.

$\mathop {Vrep}\nolimits_{{ijh}}^{e}$:

Possibility of causing large losses when road repair risk occurs during the allocation of material $h$ from $i$ to $j$ during time period $e$.

$\mathop {Lrep}\nolimits_{{ijh}}^{e}$:

Expected degree of damage (loss) caused by road repair risk when the material $h$ is allocated from $i$ to $j$ during time period $e$. $\mathop {Lrep}\nolimits_{{ijh}}^{e} {\text{ = }}\mathop {lrep}\nolimits_{{ijh}}^{e} \times \mathop x\nolimits_{{ijh}}^{e}$, $\mathop {lrep}\nolimits_{{ijh}}^{e}$ is the loss caused by the road repair risk when the unit material $h$ is allocated from $i$ to $j$ during time period $e$.

$\mathop O\nolimits_{{ij}}^{{}}$:

Total mileage (total distance) from rescue site $i$ to affected location $j$.

$\mathop v\nolimits_{{ij}}^{{}}$:

Speed of vehicle moving from $i$ to $j$ in non-disaster situations.

$\mathop \mu \nolimits_{{ij}}^{e}$:

Penalty coefficient of road mileage from $i$ to $j$ in the case of disaster, $\mathop \mu \nolimits_{{ij}}^{e} \ge {\text{1}}$; a larger $\mathop \mu \nolimits_{{ij}}^{e}$ value indicates more severe road damage. When the road is damaged, assuming that the driving speed is constant, but the time required to traverse the same distance is longer than in a non-disaster case, the transportation time in the case of road damage can be expressed as $\mathop {t^{\prime}}\nolimits_{{ij}}^{e} {\text{ = }}{{\mathop O\nolimits_{{ij}}^{{}} \cdot \mathop \mu \nolimits_{{ij}}^{e} } \mathord{\left/ {\vphantom {{\mathop O\nolimits_{{ij}}^{{}} \cdot \mathop \mu \nolimits_{{ij}}^{e} } {\mathop v\nolimits_{{ij}}^{{}} }}} \right. \kern-\nulldelimiterspace} {\mathop v\nolimits_{{ij}}^{{}} }}$.

$\mathop \delta \nolimits_{{ij}}^{e}$:

Road damage coefficient from $i$ to $j$ during time period $e$ in the case of disaster, $\mathop \delta \nolimits_{{ij}}^{e} \in \left[ {0,1} \right]$; a larger $\mathop \delta \nolimits_{{ij}}^{e}$ value indicates that the road is more severely damaged by the disaster.

$\Pr \left\{ \cdot \right\}$:

Probability that constraint conditions in $\left\{ \cdot \right\}$ hold.

$\rho$:

Confidence level that makes constraints hold.

$M$:

Sufficiently large arbitrary constant.

$\mathop x\nolimits_{{ijh}}^{e}$:

Amount of material $h$ allocated to $j$ from $i$ during time period $e$.

$\mathop y\nolimits_{{ij}}^{e}$:

Binary variable indicating whether materials are allocated to $j$ from $i$ during time period $e$. If so, the value is 1; otherwise, it is 0.

3.2 Risk measurement method for multiperiod EMA

In this study, we utilized the basic formula of risk measurement combined with the multiperiod EMA optimization problem to construct a multiperiod EMA risk measurement method. According to the dictionary of the US Department of Homeland Security (2008), risk can be expressed as:

$$Risk = Threat(T) \times Vulenrability(V) \times Consequense(C)$$

(1)

where “Threat (T)” usually refers to the possibility of an outside entity attempting an attack; “Vulnerability (V)” can be interpreted as the possibility that the attack succeeds and “Consequence (C)” usually represents the expected damage caused by a successful attack, including the direct impact and secondary impact.

Combined with the specific situation faced in the multiperiod EMA after a large-scale disaster, we rewrote the above risk formula as follows:

$$\mathop {Risk}\nolimits^{'} = Probability(P) \times Vulenrability(V) \times Loss(L)$$

(2)

where $P$ represents the possibility of risk occurrence in the EMA process, which can be determined comprehensively by objective environmental factors (e.g., road damage coefficient, route complexity, weather conditions, possibility of secondary disasters) and subjective human factors (e.g., difficulty of road repair, repair time). $V$ indicates the possibility of large losses in the presence of said risk, which is determined by the geographical location, population density, buildings, traffic flow, and value and importance of transportation materials. $L$ refers to the direct and indirect consequences of risks, including economic losses and casualties. Here, economic loss is used to measure the consequences of the risk, which specifically includes the direct economic loss caused to transport vehicles, emergency materials, and rescue personnel and the indirect economic loss caused to surrounding buildings and personnel when the risk occurs.

There are two main sets of necessary information to use Formula (2) to measure the risk. The first involves pre-disaster information, which can save time in subsequent risk measurement; for example, the geographical location, population density, number of buildings, traffic flow, and value of materials transported. The second set must be determined according to the actual disaster situation (e.g., road damage coefficient, difficulty of road repair, repair time, and weather conditions), or alternately, be predicted by a combination of historical cases and the current situation (e.g., the possibility of secondary disasters, direct economic losses, and indirect economic losses). These information can be quickly obtained when historical case support is strong and technical conditions are sufficiently advanced. Considering the diversity and dynamics of disaster scenarios, we propose determining some information (e.g., the possibility of risk occurrence during material transportation and road repair) within a certain range rather than as specific values, thus making the risk measurement method more consistent with actual disaster emergency response scenarios.

We established a measurement method for the overall path risk present in multiperiod EMA in terms of transportation risk and repair risk:

$$Risk = \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\left( {\mathop {Ptra}\nolimits_{{ijh}}^{e} \times \mathop {Vtra}\nolimits_{{ijh}}^{e} \times \mathop {Ltra}\nolimits_{{ijh}}^{e} + \mathop {Prep}\nolimits_{{ijh}}^{e} \times \mathop {Vrep}\nolimits_{{ijh}}^{e} \times \mathop {Lrep}\nolimits_{{ijh}}^{e} } \right)} } } }$$

(3)

where $\mathop {Ptra}\nolimits_{{ijh}}^{e} \times \mathop {Vtra}\nolimits_{{ijh}}^{e} \times \mathop {Ltra}\nolimits_{{ijh}}^{e}$ and $\mathop {Prep}\nolimits_{{ijh}}^{e} \times \mathop {Vrep}\nolimits_{{ijh}}^{e} \times \mathop {Lrep}\nolimits_{{ijh}}^{e}$ represent the transportation risk ($\mathop {Rtra}\nolimits_{{ijh}}^{e}$) and road repair risk ($\mathop {Rrep}\nolimits_{{ijh}}^{e}$) of the multiperiod EMA, respectively. The meaning of these parameters is explained in Sect. 3.1 (“Notation”).

3.3 Model formulation

3.3.1 Objective function

$$\begin{gathered} \min T = \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{e = 1}}^{l} {\left[ {\left( {{{\mathop O\nolimits_{{ij}}^{{}} \cdot \mathop \mu \nolimits_{{ij}}^{e} } \mathord{\left/ {\vphantom {{\mathop O\nolimits_{{ij}}^{{}} \cdot \mathop \mu \nolimits_{{ij}}^{e} } {\mathop v\nolimits_{{ij}} + \mathop {\tilde{t}}\nolimits_{{ij}}^{e} \cdot \mathop \delta \nolimits_{{ij}}^{e} \cdot \mathop O\nolimits_{{ij}}^{{}} }}} \right. \kern-\nulldelimiterspace} {\mathop v\nolimits_{{ij}} + \mathop {\tilde{t}}\nolimits_{{ij}}^{e} \cdot \mathop \delta \nolimits_{{ij}}^{e} \cdot \mathop O\nolimits_{{ij}}^{{}} }}} \right) \cdot \mathop y\nolimits_{{ij}}^{e} } \right]} } } + \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\left( {\mathop t\nolimits_{{ih}}^{e} + \mathop t\nolimits_{{jh}}^{e} } \right) \cdot \mathop x\nolimits_{{ijh}}^{e} } } } } \hfill \\ {\text{ }} + \sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {tpun}\nolimits_{{jh}}^{e} \cdot \mathop {d^{\prime}}\nolimits_{{jh}}^{e} } } } \hfill \\ \end{gathered}$$

(4)

$$\begin{gathered} \min C = \sum_{{j = 1}}^{n} {\sum_{{e = 1}}^{l} {\left\{ {\sum_{{i = 1}}^{m} {\sum_{{h = 1}}^{g} {\left( {\mathop {\tilde{c}var}\nolimits_{{ijh}}^{e} {\text{ + }}\mathop {cpur}\nolimits_{h}^{e} {\text{ + }}\mathop {cload}\nolimits_{{ih}}^{e} + \mathop {cunload}\nolimits_{{jh}}^{e} } \right) \cdot \mathop x\nolimits_{{ijh}}^{e} } } } \right.} } \hfill \\ \left. {{\text{ + }}\sum_{{i = 1}}^{m} {\left( {\mathop {\tilde{c}fix}\nolimits_{{ij}}^{e} + \mathop {\tilde{c}rep}\nolimits_{{ij}}^{e} \cdot \mathop {\mathop \delta \nolimits_{{ij}}^{e} \cdot O}\nolimits_{{ij}}^{{}} } \right) \cdot \mathop y\nolimits_{{ij}}^{e} } + \sum_{{h = 1}}^{g} {\mathop {cpun}\nolimits_{{jh}}^{e} \cdot \mathop {d^{\prime}}\nolimits_{{jh}}^{e} } } \right\} \hfill \\ \end{gathered}$$

(5)

$$\min R = \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {Rtra}\nolimits_{{ijh}}^{e} } } } } {\text{ + }}\sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {Rrep}\nolimits_{{ijh}}^{e} } } } }$$

(6)

The objective function (4) serves to minimize the total time taken to allocate all materials to all affected locations, including the time necessary for regular transportation, damaged road repair, loading at rescue sites, unloading at affected locations, and the temporal cost of any delays. The objective function (5) denotes minimizing the total cost of allocating all materials to all affected locations during all time periods, including the fixed transportation costs, variable allocation costs, procurement costs, road repair costs, loading costs, unloading costs, and penalty costs for material shortages. The objective function (6) serves to minimize the total path risk of EMA during all time periods, including path transportation risk and path repair risk.

3.3.2 Constraints

$$\Pr \left\{ {\sum_{{i = 1}}^{m} {\mathop x\nolimits_{{ijh}}^{e} - \mathop {d^{\prime}}\nolimits_{{jh}}^{{e{\text{ - 1}}}} \le \mathop {\tilde{d}}\nolimits_{{jh}}^{e} } } \right\} \ge \rho \quad \forall j \in D,h \in H,e \in E$$

(7)

$$\mathop a\nolimits_{{ih}}^{{'e}} {\text{ + }}\mathop {\tilde{a}}\nolimits_{{ih}}^{e} {\text{ = }}\sum_{{j = 1}}^{n} {\mathop x\nolimits_{{ijh}}^{e} } + \mathop a\nolimits_{{ih}}^{{'e + 1}} \quad \forall i \in S,h \in H,e \in E$$

(8)

$$\sum_{{i = 1}}^{m} {\sum_{{e = 1}}^{l} {\mathop a\nolimits_{{ih}}^{e} } } \ge \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{e = 1}}^{l} {\mathop x\nolimits_{{ijh}}^{e} } } } \quad \forall h \in H$$

(9)

$$\sum_{{h = 1}}^{g} {\left( {\mathop {a^{\prime}}\nolimits_{{ih}}^{e} {\text{ + }}\mathop {\tilde{a}}\nolimits_{{ih}}^{e} - \sum_{{j = 1}}^{n} {\mathop x\nolimits_{{ijh}}^{e} } } \right) \cdot \mathop {spa}\nolimits_{{ih}}^{{}} } \le \mathop {Cap}\nolimits_{i} \quad \forall i \in S,e \in E$$

(10)

$$\sum_{{h = 1}}^{g} {\mathop x\nolimits_{{ijh}}^{e} } \le M \cdot \mathop y\nolimits_{{ij}}^{e} \quad \forall i \in S,j \in D,e \in E$$

(11)

$$\mathop {Rtra}\nolimits_{{ijh}}^{e} = \mathop {\tilde{P}tra}\nolimits_{{ijh}}^{e} \cdot \mathop {Vtra}\nolimits_{{ijh}}^{e} \cdot \mathop {ltra}\nolimits_{{ijh}}^{e} \cdot \mathop x\nolimits_{{ijh}}^{e} \quad \forall i \in S,j \in D,h \in H,e \in E$$

(12)

$$\mathop {Rrep}\nolimits_{{ijh}}^{e} = \mathop {\tilde{P}rep}\nolimits_{{ijh}}^{e} \cdot \mathop {Vrep}\nolimits_{{ijh}}^{e} \cdot \mathop {lrep}\nolimits_{{ijh}}^{e} \cdot \mathop x\nolimits_{{ijh}}^{e} \quad \forall i \in S,j \in D,h \in H,e \in E$$

(13)

$$\mathop {d^{\prime}}\nolimits_{{jh}}^{e} {\text{ = }}\mathop d\nolimits_{{jh}}^{e} - \sum_{{i = 1}}^{m} {\mathop x\nolimits_{{ijh}}^{e} } \quad \forall j \in D,h \in H,e \in E$$

(14)

$$\mathop d\nolimits_{{jh}}^{e} {\text{ = }}\mathop {\tilde{d}}\nolimits_{{jh}}^{e} {\text{ + }}\mathop {d^{\prime}}\nolimits_{{jh}}^{{e{\text{ - 1}}}} \quad \forall j \in D,h \in H,e \in E$$

(15)

$$\mathop a\nolimits_{{ih}}^{e} = \mathop {\tilde{a^{\prime}}}\nolimits_{{ih}}^{e} + \mathop {a^{\prime}}\nolimits_{{ih}}^{e} \quad \forall i \in S,h \in H,e \in E$$

(16)

$$\mathop y\nolimits_{{ij}}^{e} \in \left\{ {{\text{0,1}}} \right\}\quad \forall i \in S,j \in D,e \in E$$

(17)

$$\mathop x\nolimits_{{ijh}}^{e} \ge {\text{0}}\quad \forall i \in S,j \in D,h \in H,e \in E$$

(18)

$$\mathop {d^{\prime}}\nolimits_{{jh}}^{e} \ge {\text{0}}\quad \forall j \in D,h \in H,e \in E$$

(19)

The demand constraint (7) of EMA ensures that the probability that the amount of material allocated to an affected location in a given period does not exceed the actual demand at this affected location at the confidence level. That is, we do not allow prepositioning of emergency materials before the demand arises. The supply constraint (8) of EMA ensures that the sum of the inventory in the previous period and the latest available quantity in the current period is equal to the sum of the amount of materials allocated to the affected location in the current period and the remaining inventory after allocation at the end of this period. That is, any surplus can be allocated in subsequent periods. Constraint (9) demonstrates ensures that as much need is satisfied as possible; the total amount of available materials at all rescue sites during all periods is equal to or greater than the total amount of materials allocated to all affected locations. That is, the total reserve of emergency materials is greater than the total allocation. Additionally, the inventory capacity constraint (10) ensures that the total inventory of emergency materials at each rescue site cannot exceed its maximum storage capacity at the end of each time period. Constraint (11) defines the logical relationship between the decision variables, indicating whether to allocate materials and repair damage roads. Constraints (12) and (13) give express the total path transportation risk and total path repair risk from the rescue site to the affected location in a given period. Constraint (14) gives the expression of material shortage or unsatisfied material demand in each time period. Constraint (15) gives the expression of the actual material demand at the affected location in each time period, that is, the actual demand equal to the sum of the latest estimated demand of this period and the shortage at the end of the previous period. Finally, constraint (16) is the expression of the actual amount of material available at rescue site in each time period, which is equal to the sum of the inventory before this current period and the latest estimated supply at the current period. Constraint (17) requires that the variables be binary (either 0 or 1). Constraints (18) and (19) are nonnegative to ensure that the decision variables of both the allocated amount and the shortage are nonnegative.

4 Solution method

The proposed model-solution method can be divided into two steps: first, the uncertain parameters (including random numbers and fuzzy numbers) contained in the model are converted into deterministic real numbers, and second, the model is solved via IGA.

4.1 Deterministic transformation of uncertain parameters

4.1.1 Deterministic transformation of stochastic constraint programming

Charnes and Cooper (1959) first proposed the chance constrained programming (CCP) problem, which is generally applicable to cases with random variables in the constraints of the model. The decision must be made before the realization of the random variables. Its basic form is as follows:

$$\min \bar{f}$$

(20)

$${\text{s}}.t.{\text{ }}{\kern 1pt} \quad \Pr \left\{ {f\left( {x,\psi } \right) \ge \bar{f}} \right\} \ge \vartheta$$

(21)

$${\text{Pr}}\left\{ {\mathop g\nolimits_{\omega } \left( {x,\psi } \right) \le 0} \right\} \ge \rho ,\quad 0 \le \rho \le 1,\quad \omega = 1,2, \ldots ,n$$

(22)

where $x$ is the decision variable, $\psi$ is the random variable, $\bar{f}$ is the objective function value (that is, the minimum value of $f\left( {x,\psi } \right)$ when the minimum confidence level is guaranteed to be $\vartheta$), $f\left( {x,\psi } \right)$ is the objective function of the decision variable $x$, i.e., the uncertainty variable, $\mathop g\nolimits_{\omega } \left( {x,\psi } \right)$ is the random constraint function, $\Pr \left\{ \cdot \right\}$ is the probability of the constraint being satisfied in $\left\{ \cdot \right\}$, and $\vartheta$ and $\rho$ represent the confidence levels that can make the objective function and the constraint condition, respectively.

For $\Pr \left\{ {\mathop g\nolimits_{\omega } \left( {x,\psi } \right) \le 0} \right\} \ge \rho ,{\text{ 0}} \le \rho \le {\text{1, }}$ $\omega = 1,2, \ldots ,n{\text{, }}$ we operated the CCP deterministic transformation in two cases for our purposes (Liu et al. 2003).

Lemma 1.

If the function $g\left( {x,\psi } \right){\text{ = }}h\left( x \right) - \psi$, then for any given confidence level $\rho (0 \le \rho \le 1)$, there must be a number $\mathop \lambda \nolimits_{\rho } {\text{ = }}\mathop \Phi \nolimits^{{ - 1}} \left( {{\text{1}} - \rho } \right)$ such that $\Pr \{ \mathop \lambda \nolimits_{\rho } \le \psi \} {\text{ = }}\rho$, and $\Pr \{ g\left( {x,\psi } \right) \le 0\} \ge \rho$ if and only if $h\left( x \right) \le \mathop \lambda \nolimits_{\rho }$, that is, $\Pr \{ h\left( x \right) \le \psi \} \ge \rho$, where $\mathop \Phi \nolimits^{{ - 1}}$ is an inverse function of $\Phi$.

Lemma 2.

Assume that the random distribution vector is $\psi {\text{ = }}(\mathop k\nolimits_{1} ,\mathop k\nolimits_{2} , \ldots ,\mathop k\nolimits_{n} ,b)$ and the form of the random constraint function $g\left( {x,\psi } \right)$ is $g\left( {x,\psi } \right){\text{ = }}\mathop k\nolimits_{{\text{1}}} \mathop x\nolimits_{{\text{1}}} + \mathop k\nolimits_{{\text{2}}} \mathop x\nolimits_{{\text{2}}}$ $+ \cdots + \mathop k\nolimits_{n} \mathop x\nolimits_{n} - b$. If $\mathop k\nolimits_{\omega }$ and $b$ follow a normal distribution and are independent of each other, then for any given confidence level $\rho (0 \le \rho \le 1)$, and $\Pr \{ g\left( {x,\psi } \right) \le 0\} \ge \rho$ if and only if:

$$E\left[ b \right] \ge \sum_{{\omega = 1}}^{n} {E\left[ {\mathop k\nolimits_{\omega } } \right]} \mathop x\nolimits_{\omega } + \mathop \Phi \nolimits^{{ - 1}} \left( \rho \right)\sqrt {\sum_{{\omega = 1}}^{n} {Var\left[ {\mathop k\nolimits_{\omega } } \right]} \mathop x\nolimits_{\omega }^{2} + Var\left[ b \right]}$$

(23)

where $\mathop \Phi \nolimits^{{ - 1}}$ is the inverse of the standard normal distribution function $\Phi$, $E[\mathop k\nolimits_{\omega } ]$ is the expectation, and $Var[\mathop k\nolimits_{\omega } ]$ is the variance.

According to the above definition and lemmas, the constraint (7) of the proposed model can be ultimately transformed into:

$$\sum_{{i = 1}}^{m} {\mathop x\nolimits_{{ijh}}^{e} - \mathop {d^{\prime}}\nolimits_{{jh}}^{{e{\text{ - 1}}}} } \le \mathop \Phi \nolimits^{{ - 1}} \left( {{\text{1}} - \rho } \right) \cdot \mathop {Var}\nolimits_{{\mathop d\nolimits_{{jh}}^{e} }} + \mathop E\nolimits_{{\mathop d\nolimits_{{jh}}^{e} }} \quad \forall j \in D,\quad h \in H,\quad e \in E$$

(24)

4.1.2 Deterministic transformation of fuzzy constraint programming

4.1.2.1 Deterministic transformation of uncertainty parameters with disturbance coefficient in objective function

According to Bertsimas and Sim (2004), we assume that $\tilde{A}$, is the fuzzy uncertain parameter value of the research object, $B$ is its nominal (or minimum) value, and $\zeta$ is a disturbance parameter that fluctuates around the nominal value. The maximum possible disturbance value that deviates from the minimum value $C{\text{ = }}B \times \zeta$. We introduce the optimization constraint level here, $\eta$, which can be set according to the actual situation of the disaster, disaster-affected area, and rescue, $\eta \in \left[ {{\text{0,1}}} \right]$. Let $\eta \ge \frac{{\tilde{A} - B}}{C} = \frac{{\tilde{A} - B}}{{B \times \zeta }}$, then $\tilde{A} \le \eta \times B \times \zeta {\text{ + }}B = B \times \left( {\eta \times \zeta + 1} \right)$.

The objective function (4) can be transformed as follows:

$$\begin{gathered} \min T = \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{e = 1}}^{l} {\left[ {\left( {{{\mathop O\nolimits_{{ij}}^{{}} \cdot \mathop \mu \nolimits_{{ij}}^{e} } \mathord{\left/ {\vphantom {{\mathop O\nolimits_{{ij}}^{{}} \cdot \mathop \mu \nolimits_{{ij}}^{e} } {\mathop v\nolimits_{{ij}}^{{}} }}} \right. \kern-\nulldelimiterspace} {\mathop v\nolimits_{{ij}}^{{}} }}} \right) \cdot \mathop y\nolimits_{{ij}}^{e} + \left( {\eta \cdot \mathop {\bar{t}}\nolimits_{{ij}}^{e} {\text{ + }}\mathop {\dot{t}}\nolimits_{{ij}}^{e} } \right) \cdot \mathop \delta \nolimits_{{ij}}^{e} \cdot \mathop O\nolimits_{{ij}}^{{}} \cdot \mathop y\nolimits_{{ij}}^{e} } \right]} } } \hfill \\ {\text{ }} + \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\left( {\mathop t\nolimits_{{ih}}^{e} + \mathop t\nolimits_{{jh}}^{e} } \right) \cdot \mathop x\nolimits_{{ijh}}^{e} } } } } + \sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {tpun}\nolimits_{{jh}}^{e} \cdot \mathop {d^{\prime}}\nolimits_{{jh}}^{e} } } } \hfill \\ \end{gathered}$$

(25)

Other uncertain parameters $\mathop {\tilde{c}fix}\nolimits_{{ij}}^{e}$, $\mathop {\tilde{c}var}\nolimits_{{ijh}}^{e}$ and $\mathop {\tilde{c}rep}\nolimits_{{ij}}^{e}$ with disturbance coefficients can be deterministically transformed in a similar manner.

4.1.2.2 Deterministic transformation of interval number in objective function

Definition 1:

For any solution $x \in X$ of a general interval linear programming model, define $\beta {\text{ = }}poss(\sum_{{i = 1}}^{n} {\mathop C\nolimits_{i} \mathop x\nolimits_{i} } )$ as the confidence level of $X$ to the objective function $\sum_{{i = 1}}^{n} {\mathop C\nolimits_{i} \mathop x\nolimits_{i} }$; define $\gamma {\text{ = }}poss(\sum_{{i = 1}}^{n} {\mathop W\nolimits_{{ij}} \mathop x\nolimits_{i} } \le \mathop B\nolimits_{j} )$ as the optimization level of $X$ to the constraint condition $\sum_{{i = 1}}^{n} {\mathop W\nolimits_{{ij}} \mathop x\nolimits_{i} } \le \mathop B\nolimits_{j}$, then the solutions $\mathop X\nolimits_{\beta }^{\gamma }$ of the general interval linear programming model with the optimization levels $\beta$ and $\gamma$ can be respectively obtained (Guo et al. 2010).

According to the above transformation for the interval number, under a given constraint optimization level $\beta$, the objective function (6) can be transformed as follows:

$$\begin{gathered} \min R = \left( {{\text{1}} - \beta } \right)\sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {\mathop {Ptra}\nolimits_{{ijh}}^{e} }\nolimits^{ - } \cdot } } } } \mathop {Vtra}\nolimits_{{ijh}}^{e} \cdot \mathop {ltra}\nolimits_{{ijh}}^{e} \cdot \mathop x\nolimits_{{ijh}}^{e} {\text{ + }}\beta \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {\mathop {Ptra}\nolimits_{{ijh}}^{e} }\nolimits^{{\text{ + }}} \cdot } } } } \mathop {Vtra}\nolimits_{{ijh}}^{e} \cdot \mathop {ltra}\nolimits_{{ijh}}^{e} \cdot \mathop x\nolimits_{{ijh}}^{e} \hfill \\ {\text{ }} + \left( {{\text{1}} - \beta } \right)\sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {\mathop {Prep}\nolimits_{{ijh}}^{e} }\nolimits^{ - } \cdot \mathop {Vrep}\nolimits_{{ijh}}^{e} \cdot \mathop {lrep}\nolimits_{{ijh}}^{e} \cdot \mathop x\nolimits_{{ijh}}^{e} } } } } {\text{ + }}\beta \sum_{{i = 1}}^{m} {\sum_{{j = 1}}^{n} {\sum_{{h = 1}}^{g} {\sum_{{e = 1}}^{l} {\mathop {\mathop {Prep}\nolimits_{{ijh}}^{e} }\nolimits^{ + } \cdot \mathop {Vrep}\nolimits_{{ijh}}^{e} \cdot \mathop {lrep}\nolimits_{{ijh}}^{e} \cdot \mathop x\nolimits_{{ijh}}^{e} } } } } \hfill \\ \end{gathered}$$

(26)

4.1.2.3 Deterministic transformation of triangular fuzzy number in constraints

As per the relationship between left and right membership functions (Zhang et al. 2004), under the optimization level $\gamma \in \left[ {{\text{0,1}}} \right]$, the constraints (8) and (10) can be transformed into the following deterministic form:

$$\sum_{{j = 1}}^{n} {\mathop x\nolimits_{{ijh}}^{e} } + \mathop {a^{\prime}}\nolimits_{{ih}}^{{e + 1}} - \mathop {a^{\prime}}\nolimits_{{ih}}^{e} \le \mathop {\left[ {\mathop {\tilde{a}}\nolimits_{{ih}}^{e} } \right]}\nolimits^{R} = \mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{R} + \gamma * \left( {\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{R} - \mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{O} } \right)\quad \forall i \in S,\quad h \in H,\quad e \in E$$

(27)

$$\sum_{{j = 1}}^{n} {\mathop x\nolimits_{{ijh}}^{e} } + \mathop {a^{\prime}}\nolimits_{{ih}}^{{e + 1}} - \mathop {a^{\prime}}\nolimits_{{ih}}^{e} \ge \mathop {\left[ {\mathop {\tilde{a}}\nolimits_{{ih}}^{e} } \right]}\nolimits^{L} = \mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{L} + \gamma * \left( {\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{O} - \mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{L} } \right)\quad \forall i \in S,\quad h \in H,\quad e \in E$$

(28)

$$\mathop {Cap}\nolimits_{i} {\text{ + }}\sum_{{h = 1}}^{g} {\left( {\sum_{{j = 1}}^{n} {\mathop x\nolimits_{{ijh}}^{e} } - \mathop {a^{\prime}}\nolimits_{{ih}}^{e} } \right) \cdot \mathop {spa}\nolimits_{{ih}}^{{}} } \ge \sum_{{h = 1}}^{g} {\left[ {\mathop {\tilde{a}}\nolimits_{{ih}}^{e} } \right]^{L} } \cdot \mathop {spa}\nolimits_{{ih}}^{{}} = \sum_{{h = 1}}^{g} {\left[ {\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{L} + \gamma * \left( {\mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{O} - \mathop {\left[ {\mathop a\nolimits_{{ih}}^{e} } \right]}\nolimits^{L} } \right)} \right]} \cdot \mathop {spa}\nolimits_{{ih}}^{{}} \quad \forall i \in S,\quad e \in E$$

(29)

4.2 Improved genetic algorithm

4.2.1 Basis for method selection

Our multi-objective and multiperiod EMA optimization model involves multiple variables and factors and belongs to the NP-hard problem category. Irregular global or local search spaces as well as multi-peak of objective functions may arise in solving this model (Chan et al. 2005; Chen et al. 2019). Therefore, we sought an intelligent algorithm with strong global search capability and high robustness.

The GAs is a typical intelligent search method which has diverse coding techniques, good versatility, strong search directionality, and fast convergence speed; it has been successfully applied in studies on path optimization, facility location, vehicle scheduling, transportation management and traveling salesman problems (Novoa and Storer 2009). However, it also has poor convergence stability and easy precocity (Kyriklidis et al. 2014). To improve its global optimization ability, it is necessary to increase the randomness of the algorithm and strike the proper balance in the direction of the search (Liu et al. 2018). We introduced the niche technology into the algorithm-solving step to make the IGA meet our solution requirements.

4.2.2 Solution steps and procedures

The flow of the IGA we designed to solve the multiperiod EMA problems is shown in Fig. 1.

Fig. 1

Basic flow of genetic algorithm

4.2.2.1 Step 1 Determine chromosome coding method

Commonly used coding methods include binary coding, symbol coding, real number coding, natural number coding, and matrix coding. Each coding method has its own advantages and disadvantages. We used a hybrid coding method for genetic coding in this study. The rescue sites, disaster affected locations, emergency materials, and emergency periods were coded by symbolic method; the demand quantity of emergency materials was coded by natural number method.

• ① The code of rescue sites is denoted by $\mathop S\nolimits_{1} ,{\text{ }}\mathop S\nolimits_{{\text{2}}} , \ldots ,\mathop {{\text{ }}S}\nolimits_{m}$, the code of disaster affected locations is denoted by $\mathop D\nolimits_{1} ,{\text{ }}\mathop D\nolimits_{{\text{2}}} , \ldots ,\mathop {{\text{ }}D}\nolimits_{n}$, the code of emergency materials is denoted by $\mathop H\nolimits_{1} ,{\text{ }}\mathop H\nolimits_{{\text{2}}} , \ldots ,\mathop {{\text{ }}H}\nolimits_{g}$, and the emergency periods are denoted by $\mathop E\nolimits_{1} ,{\text{ }}\mathop E\nolimits_{{\text{2}}} , \ldots ,\mathop {{\text{ }}E}\nolimits_{l}$. The demand quantity of emergency materials is coded by assuming that there are six disaster-affected locations that need rescue materials. The demand quantity of each affected location is 3, 4, 2, 5, 1, and 2 units of materials. The corresponding genetic code is 342512.

• ② The rescue site completes a material allocation task as a basic gene. For example, $\left( {\mathop S\nolimits_{1} ,{\text{ }}\mathop D\nolimits_{3} ,\mathop {{\text{ }}H}\nolimits_{4} ,\mathop {{\text{ }}E}\nolimits_{5} } \right)$ is the allocation of material $\mathop H\nolimits_{4}$ from the rescue site $\mathop S\nolimits_{1}$ to the disaster affected location $\mathop D\nolimits_{3}$ during the period $\mathop {{\text{ }}E}\nolimits_{5}$.

• ③ The gene segments of all rescue sites are paralleled in sequence from small to large according to the number of rescue sites, thus forming an individual.

4.2.2.2 Step 2 Generate initial population

A certain number of chromosomes is randomly generated. This process is repeated accompanied by screening to form the initial population. Rescue site $\mathop S\nolimits_{i}$ is randomly selected as the starting point of material allocation, then the affected location $\mathop D\nolimits_{j}$ is randomly selected as well as rescue material $\mathop H\nolimits_{g}$ and emergency period $\mathop {{\text{ }}E}\nolimits_{l}$ before combining them into a gene. The steps are repeated to obtain the gene segments of EMA in all emergency periods, and to determine the population size according to the specific complexity of the research problem at hand.

4.2.2.3 Step 3 Construct fitness evaluation function

The fitness function can be regarded as a basic scale for judging the performance of a single chromosome or individual in a population. A larger fitness value is usually considered to have a better effect. First, the chromosomes are rearranged in order from good to bad, that is, from small to large. If the current chromosome is $\mathop V\nolimits_{{\text{1}}} ,{\text{ }}\mathop V\nolimits_{{\text{2}}} ,{\text{ }} \ldots {\text{, }}\mathop V\nolimits_{{pop\_size}}$, the parameter $\lambda \in \left( {0,1} \right)$ is introduced in the process of genetic evolution. An order-based fitness evaluation function can then be obtained:

$$eval\left( {\mathop V\nolimits_{k} } \right) = \lambda \mathop {\left( {1 - \lambda } \right)}\nolimits^{{k - 1}} ,\quad k = 1,{\text{ }}2,{\text{ }} \ldots ,{\text{ }}pop\_size$$

(30)

where $k = 1$ marks the best chromosome and $k = pop\_size$ is the worst.

4.2.2.4 Step 4 Selection

Our approach here is to retain the best individual and improve the roulette to conduct the selection operation of “survival of the fittest”. First, individuals with higher fitness are pre-selected from the offspring individuals. Then, they are directly copied to the next generation by the strategy of reservation so that they can become the candidate parents for the next genetic operation. Second, the parents actually participating in the cross operation are selected according to the improved roulette method; whether they can enter the next generation depends on the calculated fitness value. The steps to this process are as follows.

• ① The cumulative probability for each chromosome $\mathop V\nolimits_{k}$ is calculated.

  $$\left\{ \begin{gathered} \mathop p\nolimits_{k} = 0,{\text{ }}k = 0 \hfill \\ \mathop p\nolimits_{k} = \sum\limits_{{r = 1}}^{k} {eval\left( {\mathop V\nolimits_{r} } \right),{\text{ }}k = 1,{\text{ }}2,{\text{ }} \ldots ,{\text{ }}pop\_size{\text{ }}} \hfill \\ \end{gathered} \right.$$

  (31)

• ② A random number $\sigma$ is randomly generated in the interval $\left( {{\text{0, }}\left. {\mathop p\nolimits_{{pop\_size}} } \right]} \right.$.

• ③ If $\mathop p\nolimits_{{k - 1}} < \sigma < \mathop p\nolimits_{k}$, then the chromosome $k$ (${\text{1 < }}k < pop\_size$) is selected.

• ④ $pop\_size$ for steps ② and ③ is repeated to obtain $pop\_size$ chromosomes.

4.2.2.5 Step 5 Crossover

To increase the diversity of individuals and improve the global optimization ability of the GA, inspired by Ye et al. (2009), we alternated two different crossover algorithms in the process of offspring generation: a multipoint crossover operator and an improved arithmetic crossover operator.

We first randomly selected two parent chromosomes for the crossover operation with a certain probability, then randomly set multiple crossover points at the same position of the two parent chromosomes producing two offspring chromosomes by exchanging multiple gene fragments between the crossover points. We then randomly selected two parent chromosomes $\mathop V\nolimits_{A}^{q}$ and $\mathop V\nolimits_{B}^{q}$ for crossover operations in the $q$ generation population and generated four new offspring individuals via linear combination of the two parent chromosomes:

$$\left\{ \begin{gathered} \mathop V\nolimits_{a}^{{q + 1}} = \partial \cdot \mathop V\nolimits_{B}^{q} + (1 - \partial ) \cdot \mathop V\nolimits_{A}^{q} \hfill \\ \mathop V\nolimits_{b}^{{q + 1}} = \partial \cdot \mathop V\nolimits_{A}^{q} + (1 - \partial ) \cdot \mathop V\nolimits_{B}^{q} \hfill \\ \mathop V\nolimits_{c}^{{q + 1}} = \mathop V\nolimits_{B}^{q} + \partial \cdot (\mathop V\nolimits_{B}^{q} - \mathop V\nolimits_{A}^{q} ) \hfill \\ \mathop V\nolimits_{d}^{{q + 1}} = \mathop V\nolimits_{A}^{q} + \partial \cdot (\mathop V\nolimits_{A}^{q} - \mathop V\nolimits_{B}^{q} ) \hfill \\ \end{gathered} \right.$$

(32)

where $\partial$ is the control parameter between (0, 0.5).

4.2.2.6 Step 6 Mutation

We introduced the mutation operator into the GA to increase the diversity of population and to create local search ability. More new individuals are generated when a larger mutation probability is selected, which increases the global optimization ability but shows down the search. When the mutation probability is too small, the convergence speed is accelerated but it is easy to fall into the local optimal solution. We selected the mutation probability with dynamic adaptive adjustment capability as follows:

$$\mathop \rho \nolimits_{m} = \left\{ \begin{gathered} \mathop \alpha \nolimits_{1} + {{\left( {\mathop g\nolimits_{{\max }} - g} \right)} \mathord{\left/ {\vphantom {{\left( {\mathop g\nolimits_{{\max }} - g} \right)} {\left( {\mathop g\nolimits_{{\max }} - \mathop g\nolimits_{{avg}} } \right){\text{ }},{\text{ }}g \ge \mathop g\nolimits_{{avg}} }}} \right. \kern-\nulldelimiterspace} {\left( {\mathop g\nolimits_{{\max }} - \mathop g\nolimits_{{avg}} } \right){\text{ }},{\text{ }}g \ge \mathop g\nolimits_{{avg}} }} \hfill \\ \mathop \alpha \nolimits_{2} {\text{ }},{\text{ }}g < \mathop g\nolimits_{{avg}} \hfill \\ \end{gathered} \right.$$

(33)

where $\mathop g\nolimits_{{\max }}$ and $\mathop g\nolimits_{{avg}}$ are the maximum fitness and average fitness of the population; $\mathop \alpha \nolimits_{{\text{1}}}$ and $\mathop \alpha \nolimits_{{\text{2}}}$ fall into the interval (0,1) (Wang and Cao 2002).

4.2.2.7 Step 7 Niche technology (niche elimination)

We used niche technology to allow our algorithm to overcome any premature convergence. We selected the offspring individuals produced in the mutation operation and defined the correlation function between any two offspring $\mathop V\nolimits_{A}$ and $\mathop V\nolimits_{B}$ as:

$$f(\mathop V\nolimits_{A} {\text{ }},{\text{ }}\mathop V\nolimits_{B} ) = \left\{ \begin{gathered} 0,{\text{ }}\mathop u\nolimits_{{AB}} \ge U \hfill \\ \min {{(\mathop g\nolimits_{A} {\text{ }},{\text{ }}\mathop g\nolimits_{B} )} \mathord{\left/ {\vphantom {{(\mathop g\nolimits_{A} {\text{ }},{\text{ }}\mathop g\nolimits_{B} )} {2,{\text{ }}\mathop u\nolimits_{{AB}} < U}}} \right. \kern-\nulldelimiterspace} {2,{\text{ }}\mathop u\nolimits_{{AB}} < U}} \hfill \\ \end{gathered} \right.$$

(34)

where $\mathop u\nolimits_{{AB}}$ is the Euclidean distance between $\mathop V\nolimits_{A}$ and $\mathop V\nolimits_{B}$, $\mathop g\nolimits_{A}$ and $\mathop g\nolimits_{B}$ are the fitness of $\mathop V\nolimits_{A}$ and $\mathop V\nolimits_{B}$, and $U$ is a preset distance parameter. When the distance between two individuals is less than the preset value, a penalty function is added to the individual with the smaller fitness value. This not only increases the diversity of the population, but also eliminates the inferior individuals quickly enough to increase the convergence speed of the algorithm.

4.2.2.8 Step 8 Elitism strategy

We compared the individual fitness values of the parent and offspring generated in Step 7. If the optimal value of the population was inferior to the parent, the worst individual in the offspring was replaces with the best individual in the parent population ensure the optimal offspring population value was not worse than that of the previous generation, thus improving the convergence efficiency of the algorithm.

4.2.2.9 Step 9 Termination condition of algorithm

The termination rules of an algorithm should be set according to the actual situation at hand in the process of solving the specific model. In general, an algorithm can be terminated when the fitness value of the current solution does not show any significant improvement or the number of iterations for solving the evolution reaches a certain multiple of the current population size.

5 Computational case

5.1 LuDian earthquake

A magnitude 6.5 earthquake suddenly occurred at 16:40 p.m. China Standard Time on August 3, 2014, in Ludian County, Zhaotong City, Yunnan Province, China (27.1° N, 103.3° E). The maximum intensity was IX with 1,335 aftershocks. As of 15:00 on August 8, a total of 617 individuals had lost their lives, 3,143 were injured, 112 were still missing, and 227,700 were forced to evacuate. The total area of this earthquake showing an intensity of 6 or above reached 10,350 km², affecting 1,088,400 people, across 10 state districts including Yunnan Province, Sichuan Province, and Guizhou Province. The earthquake occurred in a mountainous area where most landforms are alpine valleys. The earthquake caused communication and traffic interruptions that prevented the emergency rescue center from accurately obtaining material demand information of the disaster-affected locations. Damaged roads were difficult to repair due to barrier lakes, narrow operation surfaces, and massive road rolling stones in the Ludian area. The earthquake also caused serious secondary disasters in the subsequent rainy season such as debris flow and landslides, which increased the risk for rescue material transportation and road repair, resulting in a lack of food, medicine, and other emergency materials available for those in the disaster-affected area.

We selected disaster-stricken areas with intensity of 6 or above as emergency material demand points, including Ludian County (LD), Qiaojia County (QJ), Huize County (HZ) and Jinyang County (JY). Kunming (KM) and Chengdu (CD) were selected as rescue sites for EMA. Nutritional biscuits ($\mathop h\nolimits_{{\text{1}}}$) and disinfectant ($\mathop h\nolimits_{{\text{2}}}$) were selected as the required emergency materials. The relevant data for computational case were chosen using a combination of real and hypothetical data, since some disaster data is not published or could not be obtained through official reports. The demand for materials at each affected location and the supply of materials at each rescue site in each period were estimated based on the number of victims at the disaster site and the magnitude of the disaster (Tables 1 and 2). The available capacity at each rescue point and the unit purchase cost are shown in Table 3. Table 4 shows relevant attribute parameters including the loading and unloading time, loading and unloading costs, and storage space of various emergency materials. The nominal fixed and variable transportation costs from rescue sites to the affected locations are shown in Table 5. The average running speed of vehicles in non-disaster situations is 100 km/h. The shortest mileage from each rescue site to each affected location obtained on a Baidu map is shown in Table 6. The time and cost penalty parameters for material shortage at each affected location at the end of each time period are shown in Table 7. In the case of disaster, the nominal repair time and nominal repair cost per unit mileage of damaged road the rescue site to the affected location in each time period are shown in Table 8. The road mileage penalty coefficient and road damage coefficient in each period are shown in Table 9. The possibility of the occurrence of material transportation and road repair risks was estimated according to the intensity of the disaster at the site as well as the terrain, landform, and number of aftershocks. The probability intervals of transportation risks and road repair risks when materials are allocated to the affected location from each rescue site are shown in Tables 10 and 11, respectively. The possibility of large losses occurring and the corresponding economic loss as shown in Tables 12 and 13.

Table 1 Demand for each type of material at each affected location in each time period

Table 2 Supply of each type of materials at each rescue site in each time period

Table 3 Available capacity at each rescue point and unit material purchase cost

Table 4 Related attribute parameters of emergency materials

Table 5 Nominal fixed and unit variable transportation costs, and disturbance coefficient from rescue sites to affected locations (ten thousand Yuan)

Table 6 Shortest distance from rescue sites to affected locations (km)

Table 7 Penalty parameters for unit material shortfall at the end of each time period

Table 8 Repair time, cost and disturbance coefficient from rescue sites (R) to affected locations (A)

Table 9 Road mileage penalty coefficients and road damage coefficients from rescue sites to affected locations in each time period

Table 10 Possibility of transportation risk in each time period

Table 11 Possibility of road repair risk in each time period

Table 12 Possibility of large loss caused by transportation risk and its corresponding economic loss

Table 13 Possibility of large loss caused by road repair risk and its corresponding economic loss

We solved the computational case in MATLAB R2016a on a computer with an Intel(R) Core(TM)1.90 GHz processor with 16.0 GB of RAM. The GA parameters were set as follows: population size $N{\text{ = 50}}$, maximum number of iterations $G{\text{ = 500}}$, parameters $\partial {\text{ = 0}}{\text{.25}}$, $\mathop \alpha \nolimits_{1} {\text{ = 0}}{\text{.7}}$ and $\mathop \alpha \nolimits_{{\text{2}}} {\text{ = 0}}{\text{.3}}$, preset value of minimum Euclidean distance between niche individuals $U{\text{ = 1}}$, optimization levels of deterministic transformation of fuzzy constrained programming were $\gamma = 0.9$, $\beta = 0.9$, and $\eta = 0.{\text{8}}$, and the confidence level of deterministic transformation of stochastic constrained programming $\rho {\text{ = 0}}{\text{.95}}$.

5.2 EMA scheme and analysis

5.2.1 Overall EMA strategy and total time, cost, and risk

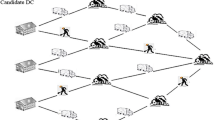
The total allocation time, cost, and risk for the entire emergency period according to the proposed model are 3339 h, 399,960 thousand yuan and 639, respectively. The specific EMA plan is shown in Table 14. The overall EMA network structure is shown in Fig. 2.

Table 14 The overall allocation plan, total time, total cost, and total risk

Fig. 2

Network structure diagram of overall EMA plan

Table 14 and Fig. 2 show the overall EMA from rescue sites to affected locations based on a comprehensive consideration of multiple factors including the distance between the rescue sites and the disaster-affected locations, the fixed and variable costs of transportation, the road damage coefficient and repair time, the possibility of transportation risk and road repair risk, and economic losses. KM allocated materials to all four affected locations including LD, QJ, HZ, and JY. The required emergency materials of LD and JY were mainly supplied from KM. This was expected as the earthquake center was in Yunnan Province. KM, the capital city of Yunnan Province, has certain advantages in geographical location and other respects. CD participated in the allocation of materials to affected locations LD, QJ, and HZ, mainly as emergency materials were in short supply after the disaster and relying on KM alone could not meet the material needs of all the affected locations. CD was required to allocate emergency materials to certain locations to remedy the shortages.

5.2.2 EMA scheme in each period and corresponding time, cost and risk

The time, cost, and risk associated with the allocation of all types of emergency materials in each period are shown in Table 15. The EMA network structure for each period is shown in Fig. 3. The trends of allocation time, cost, and risk in each time period is shown in Fig. 4.

Table 15 EMA scheme, allocation time, cost, and risk in each time period

Fig. 3

Network structure diagram of EMA in each time period

Fig. 4

Time, cost, and risk of EMA in several periods

Table 15, Figs. 3 and 4 together show that the time and risks (transportation and repair) of EMA in each period decreased over the observation period, indicating that rescue activities improve the subjective and objective environment as well as the smoothness of roads over time. The time for emergency materials to be allocated to each affected location was constantly shortened in the post-disaster period as the risk factors of damaged roads were gradually reduced. The cost of EMA increased by a small margin, indicating that reducing the time and risk of material allocation does have certain costs; they can likely be attributed to damaged road repair. Those costs are reduced over time as well until reaching the same level as EMA under non-disaster conditions.

5.2.3 Time, cost, and risk of allocation at each affected location

The specific quantity of emergency materials allocated at each disaster-affected location in each period and the corresponding time, cost, and risk are shown in Table 16. The shortages of materials at each affected location in each period and the corresponding penalty time and penalty cost are shown in Table 17. The time, cost, and risk of allocating materials to each affected location in each period are shown in Figs. 5, 6 and 7.

Table 16 Quantity, time, cost, and risk of allocation at each affected location in each period

Table 17 Shortfalls, penalty time, and penalty costs for EMA at each affected location

Fig. 5

Time for allocating materials to each affected location in each period

Fig. 6

Costs of allocating materials to each affected location in each period

Fig. 7

Path risk of allocating materials to each affected location in each period

As shown in Tables 16 and 17, the rescue sites allocated a certain amount of emergency materials to each affected location according to the situation at hand. The shortages of materials in the previous period were replenished in the subsequent period and the demand of all affected locations for all types of materials was fully met at the end of the emergency period. Figures 5, 6, and 7 shows that the time required for material allocation and the path risk faced are relatively high early on, but the required costs may be relatively low; this can be attributed to the impact of road conditions and secondary disasters in the early stages of disaster. It may take a long time to transport materials from rescue sites to disaster-affected locations. There are many uncertain factors in the process of traversing road networks. The emergency materials are usually limited in the time right after the disaster occurs; the rescue sites may give priority to allocating the limited materials to the nearest disaster-affected locations, which results in relatively low costs. As the rescue continuous, the disaster intensity and road conditions are gradually improved; thus the time and risk of EMA are gradually reduced. However, the costs of damaged road repair may be increased at this time as it is necessary to open the network to farther away disaster-affected areas. The proposed allocation scheme appears to comprehensively incorporate various factors to achieve multiperiod risk reduction and the optimal allocation of emergency materials.

5.3 Verification of IGA effectiveness

To verify the effectiveness of the proposed IGA, we ran 20 random operations on the algorithm while maintaining the same parameters and conditions. The longest computing time (LCT) was 47.23 s, the shortest computing time (SCT) was 32.19 s, and the average computing time (ACT) was 36.31 s, which shows that the IGA can effectively obtain the proper EMA scheme quickly and accurately. The material allocation path was consistent among the 20 generated schemes. The best and the worst total distribution time were 3,339 and 3,361, respectively, with a difference of only 0.65%; the best and worst total allocation costs were 39,996 and 40,512, respectively, with a difference of 1.27%; and the best and worst total path risk values were 639 and 645, respectively, making only a 0.93% difference. The calculation result is relatively stable, thus, the algorithm has strong stability. The convergence trends of the total time function (a), total cost function (b), and total path risk function (c) of the EMA is shown in Fig. 8. After 137 iterations, the value of each objective function began to converge; the IGA thus shows good convergence.

Fig. 8

Convergence trend of total time function (a), total cost function (b), and total path risk function (c)

We also compared our IGA against the basic GA, ACO, SAA and PSO to further validate its effectiveness. GA is a self-adaptive global optimization search algorithm formed by simulating the genetic and evolution process of living beings in the natural environment. It relies on the way the evolution in real-life species works and apply notions of Darwinian theory of evolution in their search for optimality in a solution space (Kyriklidis et al. 2014). It has been successfully applied to problems such as function optimization, combinatorial optimization, vehicle scheduling, and production scheduling (Li and Demeulemeester 2016). ACO is a population-based heuristic random search algorithm proposed by simulating the collective path-finding behavior of ants in nature. It is proposed for solving hard combinatorial optimization problems and was first used on the traveling salesman problem (TSP). It has been successfully applied to other problems such as vehicle routing problem, quadratic assignment problem, and scheduling problem, etc (Bell and McMullen 2004; Yi and Kumar 2007). SAA is derived from the principle of solid annealing, based on the similarity between the solving process of the optimization problem and the physical annealing process. The optimized objective function is equivalent to the internal energy of the metal. The independent variable combination state space of the optimization problem is equivalent to the internal energy state space of the metal. The solution process is to find a combined state that minimizes the objective function value. It has been successfully applied to problems such as production scheduling, control engineering, and combinatorial optimization (e.g., TSP and Knapsack problems) (Sadigh and Asghar 2018). PSO is a random search algorithm based on group cooperation that inspired by the foraging behavior of birds. It regards the search space of the optimization problem as the flight space of birds, and abstracts each bird as a particle. The solution of the optimization problem is equivalent to the food source that birds seek. It has been successfully applied to problems such as function optimization, production scheduling, and resource allocation (Zhao et al. 2017; Wang and Sun 2018). Detailed theoretical results and applications of these algorithms can be found in our referencrs (Goldberg 1989; Dorigo and Blum 2005; Steinbrunn et al. 1997; Kennedy and Eberhart 1995; Geng et al. 2015; Zheng 2019).

We ran the five algorithms 100 times independently. The results are shown in Table 18. The proposed IGA was superior to the GA, ACO, SAA, and PSO in terms of computing time (efficiency), which is crucial in the case of emergency response operations. In addition, the optimal convergence times and relative errors of convergence were also significantly better than other intelligent algorithms. We attribute this the introduction of niche elimination technology. The offspring individuals not only maintain a certain distance and species diversity, but also eliminate individuals with low fitness; this improves the evolution speed and global optimization ability of the algorithm while preventing premature or unstable convergence.

Table 18 Performance comparison of IGA, GA, ACO, SAA, and PSO

6 Conclusions and directions for future research

Effective post-disaster rescue operations are critically dependent on an optimal multiperiod EMA scheme, which should be defined in accordance with real-word disaster relief scenarios. Damaged road networks introduce additional risks and repair costs after a disaster. In this study, we developed a risk measurement method for multiperiod material allocation and road repair under uncertain conditions. This work may provide support for decision-makers tasked with multiperiod risk measurement and management of large-scale EMA problems.

We formulated EMA as a multi-objective programming problem, then built a multiperiod EMA optimization model based on uncertain disaster information. The objective function was to minimize the total delivery time, total costs, and total path risk across the model. Various EMA process-related information was characterized by the random demand, fuzzy supply, fuzzy time, and cost of distribution, as well as the fuzzy repair time and cost of damaged roads. We applied deterministic transformation methods of stochastic and fuzzy constrained programming followed by an IGA to obtain high-quality EMA schemes in accordance with real-world disaster conditions.

Our results may lend several insights into the practice of EMA for multiperiod rescue under uncertain conditions. We provide a risk measurement method for multiperiod EMA that incorporates both transportation risk and road repair risk. We also explored the relationship between time, cost, and risk during EMA. Reductions in the risk and time of material allocation comes at a certain cost. In some cases, the risk can be reduced or eliminated by increasing the allocation cost. We also find that road network conditions have an important impact on the multiperiod EMA. Early on, poor road conditions make the time required for EMA longer and increase the operational risk; as roads are repaired in the middle and late stages of the rescue, the time for EMA is gradually reduced as the overall cost increases due to the cost of the repairs. Additionally, the multiperiod EMA strategy centers on the total efficiency and effectiveness of the entire emergency rescue from the perspective of global optimization. Our strategy prioritizes not only the equity of material allocations among multiple affected locations in the case of initial material shortage, but also the allocation efficiency as the supply gradually increases over time. The strategy also works to minimize the overall risk of the entire emergency period, effectively preventing the “short-sightedness” reflected in the traditional one-period EMA strategy. Heuristic intelligent algorithms can be effectively applied to emergency rescue decision-making. The proposed IGA has significant advantages in terms of solution efficiency, optimization capability, convergence effects, and stability. In practice, it could save valuable time for disaster-relief operations and provide decision support for obtaining high-quality or optimal material allocation schemes. We sought not only to validate the proposed method in conducting this work, but also to emphasize the necessity of considering multiperiod material allocation from the perspective of uncertain disaster information. We also hope to highlight the importance of applying intelligent algorithms to complex resource-allocation optimization problems for the purpose of sustainable disaster relief.

In the future, the realism and complexity of the model could be further improved. An actual disaster rescue environment is extremely complicated. We considered relevant factors as much as possible in constructing our model, but acknowledge that other factors have yet to be taken into account. For example, by considering the living habits of the victims in different areas, real-time traffic conditions could be incorporated and big data technology could be used to analyze the disaster situation. This may allow future researchers to develop a more scientific and effective intelligent algorithm to manage large-scale and complex emergency resource allocation problems. The influence of such factors on the multiperiod EMA of large-scale disaster merits further consideration.