Optimizing a robust tri-objective multi-period reliable supply chain network considering queuing system and operational and disruption risks

Abstract

The closer the supply chain network (SCN) modeling to the real world, the more accurate decisions can be made. In this regard, it is essential to take into account of the factors in the real world such as the formation of the queuing system in the producers of the SCN, and batch transportation and processing (BTP) approaches, as well as the operational and disruption risks. In this research, batch sizes are considered equal to the potential transportation capacity of vehicles. The present paper considers simultaneous optimization of total cost, total time and average total number of commodities dispatched from any echelon of the SCN to the next echelon on a five-echelon multi-period SCN including suppliers, manufacturing plants, assemblers, distribution centers, and customers. To deal with the disruption risk, the reliability of facilities in sending the commodities is computed based on the exponential distribution and is maximized in the third objective function. Additionally, to tackle the operational risk of the problem, we convert the proposed tri-objective mathematical model into the robust mathematical model using Ben-Tal method (ρ-Robust method). Then five multi-objective decision-making (MODM) solution methods are selected to solve the problem. The results of these five methods are compared and the best MODM solution method is selected based on the objective function values and the CPU times. Finally, a novel solution is proposed to find the dominant and dominated objective functions in multi-objective models based on the uncertainty level (⍴) of the model.

1 Introduction

Nowadays, due to the widespread human needs and the existence of competitive markets, there is an urging necessity to meet needs in the best way (i.e., shortest time, lowest cost, and best quality). In this regard, the supply chain management plays an important role in enhancing the customers’ satisfaction.

In other words, there are numerous companies that offer various products and services and there is a fierce competition between them to attract the customers. In this competitive market companies offering appropriate solutions for the customers’ satisfaction will be successful. One of these solutions is that the customers should have access to the necessary commodities with the lowest prices and the distribution centers. This is where the important presentation of appropriate solutions in relation to the SCN comes up. The flows of primary pieces and finished products throughout the SCN should be performed in such a way that the above-mentioned goals are achieved.

In this research, the considered SCN is opened-loop and has five echelon containing suppliers, manufacturing plants, assemblers, distribution centers, and customers. The closer SCN modeling to the real world, the more accurate decisions can be made. In this regard, we attempt to introduce a more realistic model for supply chain network design (SCND) problem by considering the existing factors in the real world such as operational and disruption risks and formation of the queuing system in SCN producers. Our main motivation is to propose a novel model for SCND, unlike the classical supply chain problems.

In the classical supply chain problems, the aim was sending the products from an echelon of SCN to another in order to minimize the total cost. For example, Peidro et al. (2009) proposed a fuzzy mathematical programming model for supply chain planning. The objective function of the model was minimizing variable production cost, overtime cost of the resource, under-time cost of the resource, transport cost, inventory holding cost, and demand backlog cost. In another research, Keyvanshokooh et al. (2015) applied Bender’s decomposition algorithm for designing a closed-loop SCN. The objective function of the model was maximizing profit.

However, the mutual relations between various components of SCN with risk and uncertainty complicate decision-making and necessitate setting new goals (Pasandideh and Akhavan Niaki 2014).

Tang (2006) divided the supply chain risks into operational and disruption risks based on the source of uncertainties (Govindan et al. 2017, Goh et al. 2007; Kleindorfer and Saad 2005; Zhalechian et al. 2018; Ghavamifar et al. 2018, and Sabouhi et al. 2018). In each echelon of SCN, such probable reasons as natural disasters (e.g., adverse weather conditions, earthquakes, and floods) or intentional/unintentional human actions (e.g., war and terrorist attacks) might cause problems in dispatching the needed commodities from an echelon of SCN to the next echelon (Behdani (2013) and Snyder et al. (2016)). These events have undesired effects on the supply chain’s goal and performance. Recently, Govindan et al. (2017) provided a review paper on the SCND under uncertainty and attributed it to the operational and disruption risks. Studies about SCND under disruption risk can be divided into business and non-business supply chains (Govindan et al. 2017). The business supply chain aims to design a supply chain that can perform well even after disruption occurrence. On the other hand, the goal of non-business supply chain, which also known as humanitarian supply chain, is to deliver relief items to the established demand points after disasters.

In the field of non-business supply chains, Noyan (2012) investigated the problem of determining the response facility locations and the inventory levels of the relief supplies at each facility in the presence of uncertainty in demand and the damage level of the disaster network. They considered a risk-averse two-stage stochastic programming model and specified the conditional-value-at-risk (CVaR) as the risk measure. Jabbarzadeh et al. (2012) investigated an integrated SCND problem with multiple distribution centers subjected to various types of disruptions. The problem was formulated as a mixed-integer non-linear programming (MINLP) model, which determined the location of distribution centers and the assignments of customers to distribution centers. They used a scenario-based modeling approach to formulate the disruptions at the distribution centers, in which each scenario specifies the percentage of disruptions for each distribution center. Liu and Guo (2014) proposed a stochastic optimization model for post-disaster relief logistics to guide the strategic planning with respect to the locations of temporary facilities, the mobilization levels of relief supplies, and the deployment of transportation assets with uncertainty on demands. Diabat et al. (2018) presented a bi-objective robust optimization model for the design of supply chains that was resilient to disaster scenarios. The model aimed to minimize the delivery time and cost of products to customers after the occurrence of a disaster while considering possible disruptions in facilities and routes between them. Jabbarzadeh et al. (2018) presented a stochastic robust optimization model for the design of a closed-loop SCN that performs resiliently in the face of disruptions. The proposed model was capable of considering lateral transshipment as a reactive strategy to cope with operational and disruption risks.

It is worth noting that in humanitarian supply chains, the demand for relief supplies has a great deal of uncertainty, depending on the type, magnitude, and location of a disaster. In this regard, reliable SCND models assume a failure probability for a facility or transportation link in the face of disruption as a pre-specified parameter (Govindan et al. 2017). In the context of reliable SCND models, Hatefi and Jolai (2014) investigated facility disruptions in a forward-reverse logistics network design problem. They proposed a mixed integer linear programming (MILP) model with augmented ⍴-robust constraints to control the reliability of the network among disruption scenarios. Pasandideh and Akhavan Niaki (2014) considered the disruption risk in SCN warehouses and computed the reliability of warehouses based on the exponential distribution function. Their model had two objective functions; (1) minimizing total costs consisting of fixed opening costs, transportation costs, and processing costs and (2) maximizing the average total number of products dispatched from warehouses to customers. Hatefi et al. (2015) proposed a credibility-constrained programming model for the reliable design of an integrated forward-reverse logistics network with hybrid facilities under uncertainty and random facility disruptions. To deal with the disruption risk, a novel mathematical model was first developed that integrates the network design decisions in both forward and reverse flows and utilizes reliability concepts to deal with facilities disruption. Yousefi-Babadi et al. (2017) investigated disruption risks in a closed-loop petrochemical SCN. They proposed a multi-objective MINLP model for designing a petrochemical SCN under uncertainty environments, namely disruption risks and less knowledge of parameters. They proposed an objective function that minimized the failure probability of facilities.

Some researchers modeled the uncertainty related to disruptions as a finite set of discrete scenarios. For example, Klibi and Martel (2012) presented a scenario-based SCND approach and proposed two design models using stochastic programming. Furthermore, they discussed risk avoidance and SCN resilience and proposed three design models to improve SCN resilience. Baghalian et al. (2013) developed a stochastic mathematical formulation for designing a network of multi-product supply chain comprising several capacitated production facilities, distribution centers, and retailers in markets under uncertainty. The model considered demand-side and supply-side uncertainties simultaneously. They used a path-based formulation that considered possible disruptions in manufacturers, distribution centers, and their connecting links. In another research, Sadghiani et al. (2015) investigated retail SCND under operational and disruption risks. They first proposed a deterministic multiple set-covering model. Then, they extended the proposed model to a possibilistic scenario-based robust model by scenario generation and disruption profiling to design a robust and resilient retail network.

Furthermore, Tang (2006) and Tang and Tomlin (2008) introduced some mitigation strategies that can be applied to improve supply chains resiliency in the face of risks. The most popular mitigation strategies in the related literature are facility fortification, strategic stock, and sourcing strategy (Govindan et al. 2017). It is worth noting that a few papers such as Hasani and Khosrojerdi (2016); Li and Savachkin (2016), and Snyder et al. (2016) employed mitigation strategies against the disruption risk.

In comparison, in the present research, we consider the disruption risk in all of the SCN facilities containing suppliers, producers, and distributors. Hence, we maximize the reliability of facilities in sending the commodities, as the third objective function. It is of note that this method can be categorized in the field of reliable SCND models.

The operational risks are rooted in the inherent uncertainties of SCN, such as uncertainty in supply, demand, transportation times, and costs (Govindan et al. 2017). The operational risks usually have no influence on the functionality of the supply chain’s elements. However, they affect the operational factors, which are basically assumed to be uncertain. Besides, disruption risks can affect the functionality of the supply chain’s elements (Govindan et al. 2017). Since disruption risk can change the topology of the SCN and increases the reallocation of facilities and customers and the total cost of SCND having an undesired influence on the supply chain’s goal and functionality (Shen et al., 2010). However, operational risks cannot change the topology of SCN and have no influence on the reallocation of facilities and customers. In other words, the impact of operational risks is not high enough to change the goals and functionality of SCN.

Three common approaches exist to deal with operational uncertainty, including stochastic programming, fuzzy programming, and robust programming (Zhalechian et al. 2018). In the stochastic programming method, we should estimate a probability distribution function for any uncertain parameter of the proposed model to deal with the operational risks. Stochastic programming approach has some important drawbacks: (1) in some real cases, estimation of the probability distribution function of uncertain parameters is impossible due to lack of sufficient historical data (Hamidieh et al. 2017), and (2) increase of the number of uncertain parameters can increase the complexity of the model.

Fuzzy programming approach is another method applying experts’ knowledge and incomplete available data to deal with operational risk. This method can adjust the satisfaction level of uncertain parameters based on the decision-makers’ opinion. However, it does not guarantee optimization of the satisfaction levels and reliability of the output results (Hamidieh et al. 2017).

Robust programming method can control the performance of the model and help to solve the deficiencies of the fuzzy programming method (See Ben-Tal and Nemirovski 1998, 2000; Bertsimas and Sim 2004; Inuiguchi and Sakawa 1995; José Alem and Morabito 2012; Mulvey et al. 1995; Pan and Nagi, 2010; Soyster 1973). Robust optimization approach provides a framework to handle the uncertainty of parameters that could immunize the optimal solution for any realization of the uncertainty in a given bounded uncertainty set (Ben-Tal and Nemirovski 2008). Therefore, we select the robust programming approach (Ben-Tal method) to deal with operational risk.

In order to deal with operational risks by robust programming, Hatefi and Jolai (2014) investigated a reliable forward-reverse logistics network design under demand uncertainty. They applied ⍴-Robustness method to cope with the operational risk. Zokaee et al. (2014) presented a robust optimization model for the design of a supply chain facing uncertainty in demand, supply capacity, and major cost data including transportation and shortage cost parameters. To this aim, they first presented a base model for determining the strategic ‘location’ and tactical ‘allocation’ decisions for a deterministic four-tier supply chain. The model was then extended to incorporate uncertainty in key input parameters using a robust optimization approach. Ghodratnama et al. (2015) proposed a novel tri-objective hub location-allocation model and applied a robust and fuzzy goal programming approach to tackle operational risk. Talaei et al. (2016) suggested a bi-objective optimization model for designing a carbon-efficient closed-loop SCN. They proposed a robust fuzzy framework for dealing with the operational risk of the proposed model. Ramezanian and Behboodi (2017) designed a blood SCN with uncertainties in supply and demand. They applied a robust optimization approach to handle operational risk. Zahiri et al. (2017) designed a pharmaceutical SCN with uncertainties in costs and demand. They proposed a novel robust possibilistic optimization approach to deal with operational risk. In this research, the operational uncertainties are considered in such parameters as a set of costs, set of times, and various capacities of facilities.

Heidari-Fathian and Pasandideh (2018) investigated Green-Blood SCND under operational risk. They expressed the uncertainty involved in the nature of supplying the blood by the donors and also the demand for the blood product. Therefore, they applied a robust optimization approach in the model to deal with this type of uncertainty.

Furthermore, to make our SCN modeling more realistic, we pay attention to the formation of the queuing system in the producers of SCN. In the real world, a queuing system usually is formed in the producers of SCN after receiving various commodities. Commodities usually wait in these queues. Therefore, their waiting time and service time (waiting time + processing time) are increased. As a result, the delivery time of final products to customers is increased and customer satisfaction is declined. Computation of waiting time and service time of commodities based on the problem variables is necessary for their entrance in the SCN modeling. Then, we can easily minimize them in objective functions. In this regard, we present a solution to compute the parameters of the formed queuing system in SCN producers based on the batch transportation and processing (BTP) approaches. In other words, the BTP approaches are used to compute the parameters of the formed queuing system in the SCN producers.

Some scholars have attempted to propose more realistic models for SCNs optimization. They applied queuing system concepts in the modeling of SCNs. For this purpose, they usually use two methods for calculating the parameters of the queuing system: (1) Markov process and (2) algebraic relations.

In the field of application of Markov process, Vahdani et al. (2012) proposed a novel robust-M/M/c queuing model to design a reliable network of facilities in a closed-loop supply chain under uncertainty. For this purpose, a mathematical programming model with two objective functions was introduced. The first objective function was to minimize the total costs and the second one was to minimize the expected transportation costs after the failure of facilities of a logistics network (expected failure cost). Vahdani et al. (2013) designed a reliable logistics network considering operational risk and queuing theory. The type of queuing system was M/M/C. They used the proposed method by Torabi and Hassini to tackle the operational risk of the proposed model. In another research, Vahdani and Mohamadi (2015) suggested a bi-objective optimization model for designing closed loop SCN. The type of queuing system was multi-priority M/M/C. They employed the robust optimization method to deal with the operational risk. Yousefi-Babadi et al. (2017) applied the Jackson network and M/M/m/C queuing model for designing a reliable petrochemical SCN.

In the field of algebraic relations application for calculating parameters of the formed queuing system, Ghodratnama et al. (2015) proposed a novel multi-objective hub location-allocation problem with the formation of a queuing system in hubs. Their model consisted of three objective functions; (1) minimizing the total cost, (2) minimizing the total service times and the tardiness and earliness times of the flows, and (3) minimizing the total greenhouse gas.

The distinction of our research with the above-mentioned studies is using the potential capacity of vehicles as the size of input batches to the formed queuing systems in the SCN producers. We also consider two types of risks as follows; (1) disruption risk and (2) operational risk. In fact, our main contribution is combining the operational and disruption risks as well as the queuing system concepts to attain a more realistic model for SCN optimization.

Table 1 presents a number of studies relevant to our research.

Table 1 Review of references

In modeling the SCNs, some important components such as formed queuing system in the producers of the SCN and BTP approaches, as well as the reliability of facilities in sending the commodities, remain neglected. As Table 1 shows, none of the researchers considers the analysis of the formed queuing system in the producers of the SCNs by the BTP approaches under operational and disruption risks. Furthermore, none of the researchers has dealt with the simultaneous optimization of total cost, total time, and reliability of facilities in sending the commodities. It is worth noting that none of the researches compares MODM solution methods by various criteria under uncertainty, and none of them proposes a solution to find the dominant and dominated objectives in multi-objective problems under uncertainty.

To the best of the authors’ knowledge, this is the first study proposing a tri-objective MILP robust optimization model with the BTP approaches, while considering the reliability of facilities and formation of queuing system in the designing of SCN networks. This is also the first paper proposing a robust MILP mathematical model for the simultaneous optimization of total cost, total time and average total number of commodities dispatched from any echelon of the SCN to the next echelon on a five-echelon, multi-period SCN. In this paper, a novel solution is also proposed to find the dominant and dominated objective functions in multi-objective models for the determined weights of objective functions based on the uncertainty level (⍴) of the model for the first time.

The main contributions of this study can be stated as follows:

• We present a novel tri-objective MILP robust mathematical model to optimize a five-echelon multi-period SCN by considering the BTP approaches, formed queuing systems in SCN producers, and the operational and disruption risks.

• Three dimensions of decision-making have been focused on simultaneously as: minimization of total cost, minimization of total time, and maximization of the average total number of commodities dispatched from any echelon of the SCN to the next echelon, since these reduce the total cost of products and product delivery time to the customers and increase the probability of satisfying the needs of customers, respectively.

• We propose a more realistic model for SCN optimization considering operational and disruption risks and queuing system.

• We maximize the reliability of facilities in sending the commodities in the third objective function to tackle the disruption risks.

• We use the ⍴-robust method to cope with the operational risks in the proposed tri-objective model.

• We perform a comparison between five of the MODM solution methods at various levels of ⍴ to determine their best ones to solve the tri-objective robust model.

• We propose a novel solution to find dominant and dominated objectives in multi-objective models for determined weights of objective functions based on the uncertainty level of the model.

The tri-objective model is solved after converting the model into the robust model, using five MODM solution methods as follows:

• LP–metrics method

• Maxi–min method

• Goal–programming method

• Goal–attainment method

• Utility function method

Then, a comparison is drawn between these methods based on the values of the objective functions and CPU times, and the best MODM solution method for solving the problem is introduced.

The present paper is organized as follows: Sect. 2 provides problem characterization and assumptions. In Sect. 3, we discuss the problem and the modeling approach and introduce the tri-objective MILP mathematical model. In Sect. 4, we convert the mathematical model proposed in Sect. 3 to the robust mathematical model. In Sect. 5, we present the solution methods. Section 6 provides the instants characterization. In Sect. 7, the numerical results are reported and a novel solution is presented to find dominant and dominated objectives in multi-objective models under uncertainty. Ultimately, Sect. 8 presents research findings and suggestions for future studies.

2 Problem characterization

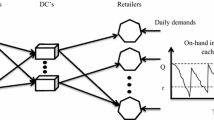
In this research, a multi-period, five-echelon SCN including I suppliers, J manufacturing plants, A assemblers, D distribution centers, M customers, P primary pieces, K semi-finished products, and one type of final product is considered. The network is demonstrated in Fig. 1.

Fig. 1

A multi-period, five-echelon supply chain network configuration

In the real world, transportation of commodities between the SCN facilities is conducted by different vehicles. In this research, the potential transportation capacity of vehicles is considered equal to the batch sizes. Batch sizes cannot exceed volume capacity of the vehicles. In this regard, transportation of pieces from suppliers to manufacturing plants in the SCN is considered with due attention to batch sizes. These batches form a queuing system in each manufacturing plant after delivery by suppliers. In any queuing system, computing the commodities waiting times and service times is highly important to make more accurate decisions.

The main reason to utilize the BTP approaches is that the value of batch size can contribute to computing the parameters of the formed queuing system in SCN producers. Different parameters of the queuing system are computed based on batch sizes in this research. Afterwards, the pieces in the batches are directed to the servers to process them. The above-mentioned processes are repeated in the assemblers for semi-finished products, too. The manufacturing plants produce different semi-finished products and send them to the assemblers, where the final product is produced. Transportation of semi-finished products from manufacturing plants to assemblers in the SCN is considered with due attention to batch size. These semi-finished products form a queuing system in each assembler. Following that, the assemblers dispatch the final product to the distribution centers, where the final product is delivered to the customers. It is worth noting that all the input commodities at any SCN entities are equal to the output commodities and in none of them inventory is allowed. Meanwhile, we define a penalty for unsatisfied demand in the problem modeling to minimize the shortage cost.

2.1 Model assumptions

• Each supplier can supply a number of the required pieces of the final product.

• The supply capacity of any piece is limited by each supplier.

• Each manufacturing plant can produce all the required semi-finished products of the final product (In the proposed model, the manufacturing plants are selected from among the potential ones).

• The production capacity of each manufacturing plant from any type of semi-finished products is limited.

• The production capacity of each assembler is limited.

• The distribution capacity of each distribution center is limited.

• One type of the final product is assembled.

• Transportation of the pieces from suppliers to manufacturing plants in the SCN is addressed with a specific transportation size (potential transportation capacity of vehicles) for each piece and facility, which is known as batch size.

• Transportation of semi-finished products from manufacturing plants to assemblers in the SCN is considered with a specific transportation size (potential transportation capacity of vehicles) for each semi-finished product and facility, which is referred to as batch size.

• The consumption coefficient of each piece in each semi-finished product is equal to one unit.

• The consumption coefficient of each semi-finished product in the final product is equal to one unit.

2.2 Assumptions and problem characterizations aspects

In this research, it is assumed that the suppliers are deterministic and cannot supply all of the required pieces of the final product. Therefore, the supplier selection problem has not been defined. However, the manufacturing plants can produce all the required semi-finished products of the final product and should be selected among potential centers. Assemblers also like the suppliers are deterministic. Distribution centers like the manufacturing plants should be selected among potential locations. Supply, processing, assembling and distributing capacity of facilities are considered limited, since in the real world, a facility cannot have unlimited capacity. In the real world, the transportation of commodities between SCN facilities is performed by vehicles with a specific transportation size (batch size) that we apply it in the supply chain problem modeling.

3 Problem modeling

In this section, the notations, problem definition, and the proposed tri-objective MILP mathematical model are explained.

3.1 Notations

The notations consisting of indices, parameters, and decision variables are as follows:

3.1.1 Indices

i :

Index that is used for a supplier, $i = 1,2, \ldots ,I$

j :

Index that is used for a potential manufacturing plant, $j = 1,2, \ldots ,J$

a :

Index that is used for an assembler, $a = 1,2, \ldots ,A$

d :

Index that is used for a potential distribution center, $d = 1,2, \ldots ,D$

$m$ :

Index that is used for a customer, $m = 1,2, \ldots ,M$

$p$ :

Index that is used for a piece supplied by suppliers, $p = 1,2, \ldots ,P$

$k$ :

Index that is used for a semi-finished product produced by manufacturing Plants, $k = 1,2, \ldots ,K$

$t$ :

Index that is used for a period with a fixed length of τ, $t = 1,2, \ldots ,T$

3.1.2 Parameters

$C_{it}^{p}$ :

Unit supplying cost of piece $p$ by supplier $i$ in period $t$

$C_{jt}^{k}$ :

Unit processing cost of semi-finished product $k$ by manufacturing plant $j$ in period $t$

$C_{at}$ :

Unit assembling cost of final product by assembler $a$ in period $t$

$PC_{jt}^{p}$ :

Unit processing cost of piece $p$ by manufacturing plant in period $t$

$PC_{at}^{k}$ :

Unit processing cost of semi-finished product $k$ by assembler $a$ in period $t$

$PT_{jt}^{p}$ :

Processing time of one unit of piece $p$ by manufacturing plant j in period $t$ (h/unit)

$PT_{at}^{k}$ :

Processing time of one unit of semi-finished product $k$ by assembler a in period $t$ (h/unit)

$TC_{ijt}^{p}$ :

Unit transportation cost of piece $p$ from supplier $i$ to manufacturing plant $j$ in period $t$

$TC_{jat}^{k}$ :

Unit transportation cost of semi-finished product $k$ from manufacturing plant $j$ to assembler $a$ in period $t$

$TC_{adt}$ :

Unit transportation cost of the final product from assembler $a$ to distribution center $d$ in period $t$

$TC_{dmt}$ :

Unit transportation cost of the final product from distribution center $d$ to customer $m$ in period $t$

$T_{i}^{p}$ :

Supply time needed by supplier $i$ to supply one unit of piece $p$ per period (h/unit)

$T_{j}^{k}$ :

Production time needed by manufacturing plant $j$ to produce one unit of semi-finished product $k$ per period (h/unit)

$T_{a}$ :

Assemblage time needed by assembler $a$ to assemble one unit of the final product per period (h/unit)

$V^{p}$ :

Volume of one unit of piece $p$ (m³)

$V^{k}$ :

Volume of one unit of semi-finished product $k$ (m³)

$V$ :

Volume of one unit of the final product (m³)

$TAST_{it}$ :

Total available supply time for supplier $i$ to supply piec in period $t$

$TAPT_{jt}$ :

Total available production time for manufacturing plant $j$ to produce semi-finished products in period $t$

$TAAT_{at}$ :

Total available assemblage time for assembler $a$ to assemble final product in period $t$

$S_{i}$ :

Storage capacity available for supplier $i$ to store pieces in a period (m³)

$S_{j}$ :

Storage capacity available for manufacturing plant $j$ to store commodities (pieces and semi-finished products) in a period (m³)

$S_{a}$ :

Storage capacity available for assembler $a$ to store commodities (semi-finished products and the final products) in a period (m³)

$S_{d}$ :

Storage capacity available for distribution center $d$ to store the final product in a period (m³)

$DD_{mt}$ :

Deterministic demand of the final product by customer $m$ in period $t$

$\lambda_{it}$ :

The parameter of an exponential distribution used for failure rate of supplier $i$ in period t

$\lambda_{jt}$ :

The parameter of an exponential distribution used for failure rate of manufacturing plant $j$ in period $t$

$\lambda_{at}$ :

The parameter of an exponential distribution used for failure rate of assembler $a$ in period $t$

$\lambda_{dt}$ :

The parameter of an exponential distribution used for failure rate of distribution center $d$ in period $t$

$SUC_{j}^{k}$ :

The set-up cost of processing semi-finished product $k$ by manufacturing plant $j$ per period

$SC_{mt}$ :

Unit shortage cost of the final product in supplying the demand of customer $m$ in period $t$

$SUT_{j}^{k}$ :

The set-up time of processing semi-finished product $k$ by manufacturing plant $j$ per period

$TTCA_{i}^{p}$ :

Total transportation capacity available for supplier $i$ to dispatch piece $p$ in a period

$TTCA_{j}^{k}$ :

Total transportation capacity available for manufacturing plant $j$ to dispatch semi-finished product $k$ in a period

$TTCA_{a}$ :

Total transportation capacity available for assembler $a$ to dispatch the final product in a period

$TTCA_{d}$ :

Total transportation capacity available for distribution center $d$ to dispatch the final product in a period

$F_{d}$ :

Fixed cost of selecting a center to establish distribution center $d$

$F_{j}$ :

Fixed cost of selecting a center to establish manufacturing plant $j$

$B_{ijt}^{p}$ :

Batch size of piece $p$ transported from supplier $i$ to manufacturing plant $j$ in period $t$ (potential transportation capacity of the vehicle from supplier $i$ to manufacturing plant $j$)

$B_{jat}^{k}$ :

Batch size of semi-finished product $k$ transported from plant $j$ to assembler $a$ in period $t$ (potential transportation capacity of the vehicle from plant $j$ to assembler $a$)

3.1.3 Decision variables

$X_{ijt}^{p}$ :

Quantity of piece $p$ dispatched by supplier $i$ to manufacturing plant $j$ in period $t$

$X_{jat}^{k}$ :

Quantity of semi-finished product $k$ dispatched by manufacturing plant $j$ to assembler $a$ in period $t$

$X_{adt}$ :

Quantity of the final product dispatched by assembler $a$ to distribution center $d$ in period $t$

$X_{dmt}$ :

Quantity of the final product dispatched by distribution center $d$ to customer $m$ in period $t$

$Y_{d}$ :

1 if distribution center $d$ is established, otherwise 0

$Y_{j}$ :

1 if manufacturing plant $j$ is established, otherwise 0

$W_{it}^{p}$ :

1 if piece $p$ is supplied by supplier $i$ in period $t$, otherwise 0

$X_{it}^{p}$ :

Quantity of piece $p$ supplied by supplier $i$ in period $t$

$X_{jt}^{k }$ :

Quantity of semi-finished product k produced by manufacturing plant j in period $t$

$X_{at}$ :

Quantity of the final product assembled by assembler $a$ in period $t$

$B_{mt}$ :

Shortage quantity of final product for customer $m$ demand in period $t$

$N_{ijt}^{p}$ :

Quantity of batches of piece $p$ dispatched from supplier $i$ to manufacturing plant j in period t

$N_{jat}^{k}$ :

Quantity of batches of semi-finished product $k$ dispatched from manufacturing plant $j$ to assembler $a$ in period $t$

3.2 Problem definition

I suppliers supply P pieces required to produce the final product and then send the pieces to J potential manufacturing plants. Input pieces usually form a queuing system in the selected manufacturing plants.

As it was mentioned previously, to compute some parameters of the queuing system such as waiting times, service times and processing cost of pieces the transportation of commodities from suppliers to manufacturing plants in the SCN is considered with a specific transportation size (potential transportation capacity of vehicles) specified for each piece and facility, which is named batch size.

Afterwards, the pieces are directed to the servers so as to be processed. It is worth mentioning that after receiving the first batch of each piece, the batches continue to enter the manufacturing plants until the total number of pieces in each manufacturing plant does not exceed from its volume capacity. Queuing system formation in the manufacturing plant j is presented in Fig. 2.

Fig. 2

Queuing system formation in the manufacturing plant j

As it is clear in Fig. 2, the total quantity of batches of piece $p$ dispatched from supplier $i$ to manufacturing plant $j$ in period $t$ is equal to:

$$ N_{ijt}^{p} = \frac{{X_{ijt}^{p} }}{{B_{ijt}^{p} }};\quad \forall p,i,j,t $$

(1)

When the first batch of piece $p$ required to produce the semi-finished products in manufacturing plant $j$ in period $t$ is received, the processing of the first input piece $p$ is started. The time required to do this process is equal to $PT_{jt}^{p}$. The second input piece waits until the processing of the first piece $p$ is finished, and then the processing of the second piece $p$ begins immediately. This indicates that the service time, i.e. waiting time + processing time, of second piece $p$ is equal to $2PT_{jt}^{p}$ and it continues until the time required to service the last piece in the batch is equal to $B_{ijt}^{p} .PT_{jt}^{p}$. Therefore, the total time needed to service all the pieces of a batch of piece p dispatched from supplier i to manufacturing plant j in period t is equal to:

$$ PT_{jt}^{p} + 2PT_{jt}^{p} + \cdots + B_{ijt}^{p} PT_{jt}^{p} = \left( {1 + 2 + \cdots + B_{ijt}^{p} } \right)PT_{jt}^{p} = \frac{{B_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2}PT_{jt}^{p} ; \quad \forall p,i,j,t $$

(2)

Owing to the fact that the total number of dispatched batches of piece $p$ from supplier $i$ to manufacturing plant $j$ in period $t$ is equal to $N_{ijt}^{p}$, according to Relation (1), the total service time for all batches of piece $p$ dispatched from supplier i to manufacturing plant $j$ in period $t$ is equal to:

$$ \begin{aligned} N_{ijt}^{p} \frac{{B_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2}PT_{jt}^{p} &= \frac{{X_{ijt}^{p} B_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{{2B_{ijt}^{p} }}PT_{jt}^{p} \hfill \\ &= \frac{{X_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2} PT_{jt}^{p} ;\quad \forall p,i,j,t \hfill \\ \end{aligned} $$

(3)

In addition, the total time required to service all the batches of pieces dispatched from all suppliers to all manufacturing plants in all periods is equal to:

$$ Total\;service\;time = \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \frac{{X_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2}PT_{jt}^{p} ; $$

(4)

Accordingly, Total processing cost of all batches of pieces dispatched from all suppliers to all manufacturing plants in all periods can be calculated as follows:

$$ Total\;processing\;cost = \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} N_{ijt}^{p} B_{ijt}^{p} PC_{jt}^{p} ; $$

(5)

The above-mentioned concepts can be applied to the assemblers as well. Queuing system formation in the assembler a is presented in Fig. 3.

Fig. 3

Queuing system formation in the assembler a

Based on the mathematical formulation obtained for the formed queuing system in the manufacturing plants, the following final relations for formed queuing systems in the assemblers can be defined.

$$ N_{jat}^{k} = \frac{{X_{jat}^{k} }}{{B_{jat}^{k} }}; \quad \forall k,j,a,t $$

(6)

$$ Total\;service\;time = \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \frac{{X_{jat}^{k} \left( {B_{jat}^{k} + 1} \right)}}{2}PT_{at}^{k} ; $$

(7)

$$ Total\;processing\;cost = \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} N_{jat}^{k} B_{jat}^{k} PC_{at}^{k} ; $$

(8)

As noted previously, such probable unforeseen events as adverse weather conditions, delay in delivery by suppliers, sudden increase in prices of raw materials, terrorist attacks, and changes in owners could explain why all produced commodities in facility $q$ do not reach the next echelon (Pasandideh and Akhavan Niaki 2014). These unanticipated events (disruption risks) in facility $q$ in period $t$ follow a Poisson distribution with a mean of $\frac{1}{{\lambda_{qt} }}$. Therefore, the time between two consecutive unforeseen events follows an exponential distribution with a mean of $\lambda_{qt}$. When the interval time between two unforeseen events is represented by $T_{q}$ and the length of the period is considered constant and equal to τ, the reliability of facility $q$ ($R_{q} )$ in sending the commodities to the next echelon in a period is equal to the probability of (Pasandideh and Akhavan Niaki 2014):

$$ R_{q} = p\left( {T_{q} > \tau } \right) = e^{{ - \lambda_{qt} \tau }} ; \quad \forall q = 1,2, \ldots $$

(9)

This means that the reliability of a facility at a time period is equal to the probability of the event that the interval time between two consecutive disruptions exceed the length of the period. In other words, these events do not occur during the period. Thus, the average total number of the products dispatched from a facility of the SCN to the next echelon is obtained through multiplication of this probability in the quantity of the products dispatched from the facility to the next echelon. As a result,

The average quantity of piece $p$ dispatched from supplier $i$ to manufacturing plant $j$ in period $t$ is equal to $e^{{ - \lambda_{it} \tau }} X_{ijt}^{p}$.

The average quantity of semi-finished product $k$ dispatched from manufacturing plant $j$ to assembler $a$ in period $t$ is equal to $e^{{ - \lambda_{jt} \tau }} X_{jat}^{k}$.

The average quantity of the final product dispatched from assembler $a$ to distribution center $d$ in period $t$ is equal to $e^{{ - \lambda_{at} \tau }} X_{adt}$.

The average quantity of the final product dispatched from distribution center $d$ to customer $m$ in period $t$ is equal to $e^{{ - \lambda_{dt} \tau }} X_{dmt}$.

3.3 The proposed tri-objective MILP mathematical model

Based on the above-mentioned relations, the tri-objective MILP mathematical model can be formulated as follows:

$$ \begin{aligned} Min\;Z_{1} & = \mathop \sum \limits_{d = 1}^{D} F_{d} Y_{d} + \mathop \sum \limits_{j = 1}^{J} F_{j} Y_{j} + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} TC_{ijt}^{p} X_{ijt}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} TC_{jat}^{k} X_{jat}^{k} + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 1}^{T} TC_{adt} X_{adt} \\ & \quad + \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 1}^{T} TC_{dmt} X_{dmt} + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{t = 1}^{T} C_{it}^{p} X_{it}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} C_{jt}^{k} X_{jt}^{k} \\ & \quad + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} C_{at} X_{at} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} SUC_{j}^{k} Y_{j} + \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 1}^{T} SC_{mt} B_{mt} \\ & \quad + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} N_{ijt}^{p} B_{ijt}^{p} PC_{jt}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} N_{jat}^{k} B_{jat}^{k} PC_{at}^{k} \\ \end{aligned} $$

(10)

$$ \begin{aligned} Min\;Z_{2} & = \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{t = 1}^{T} T_{i}^{p} X_{it}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} T_{j}^{k} X_{jt}^{k} + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} T_{a} X_{at} \\ & \;\;\; + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \frac{{X_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2}PT_{jt}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} SUT_{j}^{k} Y_{j} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \frac{{X_{jat}^{k} \left( {B_{jat}^{k} + 1} \right)}}{2}PT_{at}^{k} ; \\ \end{aligned} $$

(11)

$$ Max\;Z_{3} = \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{it} \tau }} X_{ijt}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{jt} \tau }} X_{jat}^{k} + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{at} \tau }} X_{adt} + \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{dt} \tau }} X_{dmt} ; $$

(12)

S. t.:

Batch constraints

$$ N_{ijt}^{p} = \frac{{X_{ijt}^{p} }}{{B_{ijt}^{p} }}; \quad \forall p,i,j,t $$

(13)

$$ N_{jat}^{k} = \frac{{X_{jat}^{k} }}{{B_{jat}^{k} }}; \quad \forall k,j,a,t $$

(14)

Available time constraints

$$ \mathop \sum \limits_{p = 1}^{P} T_{i}^{p} X_{it}^{p} \le TAST_{it} ; \quad \forall i,t $$

(15)

$$ \mathop \sum \limits_{k = 1}^{K} T_{j}^{k} X_{jt}^{k} + \mathop \sum \limits_{k = 1}^{K} SUT_{j}^{k} Y_{j} \le TAPT_{jt } Y_{j} ; \quad \forall j,t $$

(16)

$$ T_{a} X_{at} \le TAAT_{at} ; \quad \forall a,t $$

(17)

Flow balance constraints

$$ \mathop \sum \limits_{i = 1}^{I} X_{ijt}^{p} \ge \mathop \sum \limits_{a = 1}^{A} X_{jat}^{k} ; \quad \forall p,k,j,t $$

(18)

$$ \mathop \sum \limits_{j = 1}^{J} X_{jat}^{k} \ge \mathop \sum \limits_{d = 1}^{D} X_{adt} ; \quad \forall k,a,t $$

(19)

$$ \mathop \sum \limits_{a = 1}^{A} X_{adt} \ge \mathop \sum \limits_{m = 1}^{M} X_{dmt} ; \quad \forall d,t $$

(20)

$$ \mathop \sum \limits_{d = 1}^{D} X_{dmt} \ge DD_{mt} ; \quad \forall m,t $$

(21)

$$ \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} X_{ijt}^{1} = \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} X_{ijt}^{2} = \ldots = \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} X_{ijt}^{p} = \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 1}^{T} X_{adt} ; $$

(22)

Storage capacity constraints

$$ \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} V^{p} X_{ijt}^{p} \le S_{j} Y_{j} ; \quad \forall j,t $$

(23)

$$ \mathop \sum \limits_{p = 1}^{P} V^{p} X_{it}^{p} \le S_{i} ; \quad \forall i,t $$

(24)

$$ \mathop \sum \limits_{k = 1}^{K} V^{k} X_{jt}^{k} \le S_{j} Y_{j} ; \quad \forall j,t $$

(25)

$$ \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} V^{k} X_{jat}^{k} \le S_{a} ; \quad \forall a,t $$

(26)

$$ \mathop \sum \limits_{a = 1}^{A} V X_{adt} \le S_{d} Y_{d} ; \quad \forall d,t $$

(27)

$$ V X_{at} \le S_{a} ; \quad \forall a,t $$

(28)

Transportation capacity constraints

$$ \mathop \sum \limits_{j = 1}^{J} X_{ijt}^{p} \le TTCA_{i}^{p} W_{it}^{p} ; \quad \forall p,i,t $$

(29)

$$ \mathop \sum \limits_{a = 1}^{A} X_{jat }^{k} \le TTCA_{j}^{k} Y_{j} ; \quad \forall k,j,t $$

(30)

$$ \mathop \sum \limits_{d = 1}^{D} X_{adt} \le TTCA_{a} ; \quad \forall a,t $$

(31)

$$ \mathop \sum \limits_{m = 1}^{M} X_{dmt} \le TTCA_{d} Y_{d} ; \quad \forall d,t $$

(32)

Shortage constraint

$$ B_{mt} = B_{mt - 1} + DD_{mt} - \mathop \sum \limits_{d = 1}^{D} X_{dmt} ; \quad \forall m,t $$

(33)

Binary and non-negative variables

$$ Y_{d} , Y_{j} , W_{it}^{p} \in \left\{ {0,\left. 1 \right\}} \right.; $$

(34)

$$ X_{ijt}^{p} , X_{jat }^{k} , X_{adt } , X_{dmt} , X_{it}^{p} , X_{jt}^{k} , X_{at} , B_{mt} ,N_{ijt}^{p} ,N_{jat}^{k} \ge 0 ; $$

(35)

We attempt to minimize the following costs in the first objective function (relation 10): the total fixed construction cost of distribution centers, the total fixed construction cost of manufacturing plants, the total transportation cost of pieces dispatched from suppliers to manufacturing plants, the total transportation cost of semi-finished products dispatched from manufacturing plants to assemblers, the total transportation cost of the final product dispatched from assemblers to distribution centers, the total transportation cost of the final product dispatched from distribution centers to customers, the total supply cost of pieces by suppliers, the Total processing cost of semi-finished products by manufacturing plants, the total assembling cost of final product by assemblers, the total set-up cost of manufacturing plants servers, the total shortage cost of the final product for customers’ demands, and the Total processing cost in manufacturing plants and assemblers.

We attempt to minimize the following times in the second objective function (relation 11): the total time required to supply pieces by suppliers, the total time required to produce semi-finished products by manufacturing plants, the total time required to assemble the final product by assemblers, the total time required to process all batches of pieces in manufacturing plants, the total time required to process all batches of semi- finished products in assemblers, and the total set-up time of servers in manufacturing plants.

In the third objective function (relation 12), we attempt to maximize the average total number of commodities dispatched from any echelon of the SCN to the next echelon to deal with disruption risk.

The relation in Eq. (13) is used to compute the optimal number of batches of piece p dispatched from supplier i to manufacturing plant j in period t. The relation in Eq. (14) is also used to compute the optimal number of batches of semi-finished product k dispatched from manufacturing plant j to assembler a in period t. Constraints (15)˗(17) indicate the available times in a period. Constraint (15) states that the total time required to supply the pieces by a supplier in a period cannot exceed the total available supply time in the period. The constraint (16) states that the total time required to produce the semi-finished products and the total time required to set up the servers of a manufacturing plant in a period cannot exceed the total available production time in the period. Constraint (17) states that the total time required to assemble the final product by an assembler in a period cannot exceed the total available assemblage time in the period. Constraints (18)–(21) show the flow balance constraints. Constraint (22) indicates that the consumption coefficient of each piece in the final product is equal to one unit.

Constraints (23)–(28) state the storage capacity constraints. Constraint (23) demonstrates that if a manufacturing plant is constructed, the total volume of all pieces dispatched from all suppliers to the manufacturing plant in a period cannot exceed its storage capacity. Constraint (24) declares that the total volume of all pieces supplied by a supplier in a period cannot exceed its storage capacity. Constraint (25) demonstrates that if a manufacturing plant is constructed, the total volume of all semi-finished products produced by the manufacturing plant cannot exceed its storage capacity. Constraint (26) states that the total volume of all semi-finished products dispatched from the all manufacturing plants to an assembler in a period cannot exceed its storage capacity. Constraint (27) states that if a distribution center is constructed, the total volume of all final products dispatched from all assemblers to the distribution center in a period cannot exceed its storage capacity. Constraint (28) states that the total volume of all final products produced by an assembler in a period cannot exceed its storage capacity.

Constraints (29)–(32) indicate the total available transportation capacity constraints. Constraint (29) states that if a piece is supplied by a supplier in a period, the total pieces dispatched by the supplier to all of the manufacturing plants in the period cannot exceed its total available transportation capacity. Constraint (30) demonstrates that if a manufacturing plant is constructed, the total semi-finished products dispatched by the manufacturing plant to all of the assemblers in a period cannot exceed its total available transportation capacity. Constraint (31) states that the total final products dispatched by an assembler to all of the distribution centers in a period cannot exceed its total available transportation capacity. Constraint (32) states that if a distribution center is constructed, the total final products dispatched by the distribution center to all of the customers in a period cannot exceed its total available transportation capacity.

Equation (33) demonstrates the balance equation for shortages of customers’ demands. Constraints (34) and (35) represent the binary and non-negative variables, respectively.

As the suggested model clearly shows, the proposed tri-objective MILP model creates a competition between the third objective function and the two other objective functions. As the average total number of commodities dispatched from any echelon of SCN to the next echelon (third objective function) increases, the total cost (first objective function) and the total time (second objective function) also increase, while in this model, they are from minimization type. Therefore, it is interesting to find which group will dominate the other one in the competition.

In this paper, a solution is proposed to determine the dominant and dominated objective functions based on the uncertainty level (⍴) in multi-objective models (competitive condition). In the following, first, the proposed tri-objective MILP model is converted to the robust model. Then, the trade-off between objective functions, optimal Pareto front and a solution to determine the dominant and dominated objective functions in the multi-objective model is presented.

4 Robust counterpart mathematical model

To explain the ρ-Robust method, the following basic deterministic MILP model is defined.

$$ \hbox{min} fy + cx $$

(36)

$$ s.t:Tx \ge S $$

(37)

$$ Nx = 0 $$

(38)

$$ Mx \le 0 $$

(39)

$$ Bx \le Ay $$

(40)

$$ y \in \left\{ {0,1} \right\}, x \in R^{ + } $$

(41)

The related uncertain problem can be defined according to Ben-Tal and Nemirovski (1998, 2000) as follows:

$$ \hbox{min} fy + cx $$

$$ s.t:Tx \ge S $$

$$ Nx = 0 $$

$$ Mx \le 0 $$

$$ Bx \le Ay $$

$$ y \in \left\{ {0,1} \right\}, x \in R^{ + } $$

$$ c,S,A \in U $$

(42)

The parameters c, S, and A in the above model vary in a given uncertainty set U. It is worth noting that a vector x is a robust feasible solution to the basic problem if it satisfies all realizations of the constraints from the uncertainty set U. The robust counterpart of basic problem can be defined according to Ben-Tal and Nemirovski (1999) as follows:

$$ \hbox{min} \left\{ {\hat{c}\left( x \right) = \sup \left[ {fy + cx} \right]:Relations\,\left( {37} \right)\,to\,\left( {41} \right) \quad \forall c,S,A \in U} \right\} $$

(43)

Thus, we can mention that an optimal solution to the problem (43) is the optimal robust solution of the basic problem. In other words, a solution satisfies the constraints for all possible realizations of the data and guarantees an optimal objective function value not worse than $\hat{c}\left( x \right)$. It should be mentioned that all binary decision variables are included in the vector y, and all continuous decision variables are included in the vector x.

We consider each of these uncertain parameters to vary in a specified closed bounded box (Ben-Tal et al., 2009); (Pishvaee et al., 2011). The general form of this box is stated as follows:

$$ u_{Box} = \left\{ {\psi \in R^{n} } \right.:\left| {\psi_{t} - \bar{\psi }_{t} } \right| \le \rho G_{t} , t = 1,2, \ldots ,n\} $$

(44)

Where $\bar{\psi }_{t}$ is the nominal value of the $\psi_{t}$ and tth parameter of vector $\psi$, the positive numbers $G_{t}$ represent ‘‘uncertainty scale’’, and $\rho > 0$ is the ‘‘uncertainty level”. A particular case of interest is $G_{t} = \bar{\psi }_{t}$, which corresponds to a simple case where the box contains $\psi_{t}$ whose relative deviation from the nominal data has a size up to $\rho$ (Pishvaee et al., 2011).

As a result, the robust counterpart of the basic model can be formulated as follows:

$$ \hbox{min} z $$

(45)

$$ s.t:fy + cx \le z, \quad \forall c \in u _{Box}^{c} $$

(46)

$$ Tx \ge S \quad \forall S \in u _{Box}^{S} $$

(47)

$$ Nx = 0 $$

$$ Mx \le 0 $$

$$ Bx \le Ay \quad \forall A \in u _{Box}^{A} $$

(48)

$$ y \in \left\{ {0,1} \right\}, x \in R^{ + } $$

Ben-Tal et al. (2005) prove that in this case (closed bounded box), the robust counterpart problem can be converted to a tractable equivalent model where $U_{box}$ is replaced with a finite set $U_{ext}$ consisting of the extreme points of $U_{box}$. To represent the tractable form of the robust basic model, Eqs. (46)–(48) should be converted to their equivalent tractable ones. For Eq. (46), we have:

$$ cx \le z - fy, \quad \forall c \in \left. {u _{Box}^{c} } \right|u _{Box}^{c} = \left\{ {c \in R^{{n_{c} }} } \right.:\left| {c_{t} - \bar{c}_{t} } \right| \le \rho_{c} G_{t}^{c} , t = 1,2, \ldots ,n_{c} \} $$

(49)

The left-hand side of inequality (49) contains the vector of uncertain parameters, while all parameters of the right-hand side are certain. Thus, the tractable form of the above semi-infinite inequality can be written as follows:

$$ \mathop \sum \limits_{t} \left( {\bar{c}_{t} x_{t} + \eta_{t} } \right) \le z - fy, $$

(50)

$$ \rho_{c} G_{t}^{c} x_{t} \le \eta_{t} , \quad \forall t \in \left\{ {1,2, \ldots ,n_{c} } \right\} $$

(51)

$$ \rho_{c} G_{t}^{c} x_{t} \ge - \eta_{t} , \quad \forall t \in \left\{ {1,2, \ldots ,n_{c} } \right\} $$

(52)

In fact, $\eta_{t}$ is the maximum value of the allowed change in the uncertain term of the objective function due to the uncertainty that should be minimized. Similarly, for inequality (47), we have:

$$ Tx \ge S_{i} , \quad \forall i \in \left\{ {1,2, \ldots ,n_{S} } \right\}, \quad \forall S \in \left. {u _{Box}^{S} } \right|u _{Box}^{S} = \left\{ {S \in R^{n} } \right.:\left| {S_{i} - \bar{S}_{i} } \right| \le \rho_{S} G_{i}^{S} , i = 1,2, \ldots ,n_{S} \} $$

(53)

Therefore, it can be rewritten as follows:

$$ Tx \ge \overline{{S_{i} }} + \rho_{S} G_{i}^{S} ,\quad \forall i \in \left\{ {1,2, \ldots ,n_{S} } \right\} $$

(54)

As mentioned previously, a particular case of interest is $G_{i}^{S} = \overline{{S_{i} }}$. Therefore the relation (54) can be rewritten as follows:

$$ Tx \ge \overline{{S_{i} }} \left( {1 + \rho_{S} } \right) $$

(55)

Also, for inequality (48) we have:

$$ Bx \le A_{j} y, \quad \forall j \in \left\{ {1,2, \ldots ,n_{A} } \right\}, \quad \forall A \in \left. {u _{Box}^{A} } \right|u _{Box}^{A} = \left\{ {A \in R^{n} } \right.:\left| {A_{j} - \overline{{A_{j} }} } \right| \le \rho_{A} G_{j}^{A} , j = 1,2, \ldots ,n_{A} \} $$

(56)

Thus, it can be rewritten as follows:

$$ Bx \le \left( {\overline{{A_{j} }} - \rho_{j} G_{j}^{A} } \right)y $$

(57)

As mentioned previously, a particular case of interest is $G_{j}^{A} = \overline{{A_{j} }}$. Therefore the relation (57) can be rewritten as follows:

$$ Bx \le \overline{{A_{j} }} \left( {1 - \rho_{A} } \right)y $$

(58)

Finally, with respect to (50)–(52), (55) and (58) the final form of the robust model can be formulated as follows:

$$ \hbox{min}\,z $$

$$ s.t:\mathop \sum \limits_{t} \left( {\bar{c}_{t} x_{t} + \eta_{t} } \right) \le z - fy $$

$$ \rho_{c} G_{t}^{c} x_{t} \le \eta_{t} , \quad \forall t \in \left\{ {1,2, \ldots ,n_{c} } \right\} $$

$$ \rho_{c} G_{t}^{c} x_{t} \ge - \eta_{t} , \quad \forall t \in \left\{ {1,2, \ldots ,n_{c} } \right\} $$

$$ Tx \ge \overline{{S_{i} }} \left( {1 + \rho_{S} } \right),\quad \forall i \in \left\{ {1,2, \ldots ,n_{S} } \right\} $$

$$ Nx = 0 $$

$$ Mx \le 0 $$

$$ Bx \le \overline{{A_{j} }} \left( {1 - \rho_{A} } \right)y, \quad \forall j \in \left\{ {1,2, \ldots ,n_{A} } \right\} $$

$$ y \in \left\{ {0,1} \right\}, x, \eta_{t} \in R^{ + } $$

To tackle the operational risk of the model, the model proposed in the previous section is converted to the robust model by using ⍴-robustness method. To convert the proposed tri-objective MILP mathematical model into the tri-objective MILP robust mathematical model, the following costs and times are considered as uncertain parameters: fixed construction costs of manufacturing plants and distribution centers, transportation costs, supplying costs of the pieces, processing costs of semi-finished products, assembling costs of the final product, set-up costs, shortage costs, processing costs, supplying times of the pieces, processing times of semi-finished products, assembling times of the final product, processing times, set-up times, total available supply times, total available processing times, total available assemblage times, storage capacities, and total available transportation capacities. According to the above descriptions, the proposed tri-objective MILP robust mathematical model is as follows:

Robust objective functions

$$ Min\;Z_{1} ; $$

(59)

$$ Min\;Z_{2} ; $$

(60)

$$ Max\;Z_{3} ; $$

(61)

$$ \begin{aligned} & Min\mathop \sum \limits_{d = 1}^{D} \left( {\bar{F}_{d} Y_{d} + \eta_{d}^{F} } \right) + \mathop \sum \limits_{j = 1}^{J} \left( {\bar{F}_{j} Y_{j} + \eta_{j}^{F} } \right) + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \left( {\overline{TC}_{ijt }^{p} X_{ijt}^{p} + \eta_{ijt}^{{p^{TC} }} } \right) \\ & + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \left( {\overline{TC}_{jat}^{k} X_{jat}^{k} + \eta_{jat}^{{k^{TC} }} } \right) + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 1}^{T} \left( {\overline{TC}_{adt} X_{adt} + \eta_{adt}^{TC} } \right) \\ & + \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 1}^{T} \left( {\overline{TC}_{dmt} X_{dmt} + \eta_{dmt}^{TC} } \right) + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{t = 1}^{T} \left( {\bar{C}_{it}^{p} X_{it}^{p} + \eta_{it}^{{p^{C} }} } \right) \\ & + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \left( {\bar{C}_{jt}^{k} X_{jt}^{k} + \eta_{jt}^{{k^{C} }} } \right) + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \left( {\bar{C}_{at} X_{at} + \eta_{at}^{C} } \right) \\ & + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \left( {\overline{SUC}_{j}^{k} Y_{j} + \eta_{j}^{{k^{SUC} }} } \right) + \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 1}^{T} \left( {\overline{SC}_{mt} B_{mt} + \eta_{mt}^{SC} } \right) \\ & + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \left( {N_{ijt}^{p} B_{ijt}^{p} \overline{PC}_{jt}^{p} + \eta_{jt}^{{p^{PC} }} } \right) + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \left( {N_{jat}^{k} B_{jat}^{k} \overline{PC}_{at}^{k} + \eta_{at}^{{k^{PC} }} } \right) \le Z_{1} ; \\ \end{aligned} $$

(62)

$$ \begin{aligned} & Min\mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{t = 1}^{T} \left( {\bar{T}_{i}^{p} X_{it}^{p} + \eta_{i}^{{p^{T} }} } \right) + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \left( {\bar{T}_{j}^{k} X_{jt}^{k} + \eta_{j}^{{k^{T} }} } \right) \\ & + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \left( {\bar{T}_{a} X_{at} + \eta_{a}^{T} } \right) + \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \left( {\frac{{X_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2}\overline{PT}_{jt}^{p} + \eta_{jt}^{{p^{PT} }} } \right) \\ & + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} \left( {\frac{{X_{jat}^{k} \left( {B_{jat}^{k} + 1} \right)}}{2}\overline{PT}_{at}^{k} + \eta_{at}^{{k^{PT} }} } \right) + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \left( {\overline{SUT}_{j}^{k} Y_{j} + \eta_{j}^{{k^{SUT} }} } \right) \le Z_{2} ; \\ \end{aligned} $$

(63)

$$ \begin{aligned} & Max\mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{it} \tau }} X_{ijt}^{p} + \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{jt} \tau }} X_{jat}^{k} \\ & + \mathop \sum \limits_{a = 1}^{A} \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{at} \tau }} X_{adt} + \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 1}^{T} e^{{ - \lambda_{dt} \tau }} X_{dmt} \ge Z_{3} ; \\ \end{aligned} $$

(64)

Constraints related to uncertain parameters in objective functions

$$ \rho_{{F_{d} }} G_{d}^{F} Y_{d} \le \eta_{d}^{F} ; \quad \forall d $$

(65)

$$ \rho_{{F_{d} }} G_{d}^{F} Y_{d} \ge - \eta_{d}^{F} ; \quad \forall d $$

(66)

$$ \rho_{{F_{j} }} G_{j}^{F} Y_{j} \le \eta_{j}^{F} ; \quad \forall j $$

(67)

$$ \rho_{{F_{j} }} G_{j}^{F} Y_{j} \ge - \eta_{j}^{F} ; \quad \forall j $$

(68)

$$ \rho_{{TC_{ijt}^{p} }} G_{ijt}^{{p^{TC} }} X_{ijt}^{p} \le \eta_{ijt}^{{p^{TC} }} ; \quad \forall p,i,j,t $$

(69)

$$ \rho_{{TC_{ijt}^{p} }} G_{ijt}^{{p^{TC} }} X_{ijt}^{p} \ge - \eta_{ijt}^{{p^{TC} }} ; \quad \forall p,i,j,t $$

(70)

$$ \rho_{{TC_{jat}^{k} }} G_{jat}^{{k^{TC} }} X_{jat}^{k} \le \eta_{jat}^{{k^{TC} }} ; \quad \forall k,j,a,t $$

(71)

$$ \rho_{{TC_{jat}^{k} }} G_{jat}^{{k^{TC} }} X_{jat}^{k} \ge - \eta_{jat}^{{k^{TC} }} ; \quad \forall k,j,a,t $$

(72)

$$ \rho_{{TC_{adt} }} G_{adt}^{TC} X_{adt} \le \eta_{adt}^{TC} ; \quad \forall a,d,t $$

(73)

$$ \rho_{{TC_{adt} }} G_{adt}^{TC} X_{adt} \ge - \eta_{adt}^{TC} ; \quad \forall a,d,t $$

(74)

$$ \rho_{{TC_{dmt} }} G_{dmt}^{TC} X_{dmt} \le \eta_{dmt}^{TC} ; \quad \forall d,m,t $$

(75)

$$ \rho_{{TC_{dmt} }} G_{dmt}^{TC} X_{dmt} \ge - \eta_{dmt}^{TC} ; \quad \forall d,m,t $$

(76)

$$ \rho_{{C_{it}^{p} }} G_{it}^{{p^{C} }} X_{it}^{p} \le \eta_{it}^{{p^{C} }} ; \quad \forall p,i,t $$

(77)

$$ \rho_{{C_{it}^{p} }} G_{it}^{{p^{C} }} X_{it}^{p} \ge - \eta_{it}^{{p^{C} }} ; \quad \forall p,i,t $$

(78)

$$ \rho_{{C_{jt}^{k} }} G_{jt}^{{k^{C} }} X_{jt}^{k} \le \eta_{jt}^{{k^{C} }} ; \quad \forall k,j,t $$

(79)

$$ \rho_{{C_{jt}^{k} }} G_{jt}^{{k^{C} }} X_{jt}^{k} \ge - \eta_{jt}^{{k^{C} }} ; \quad \forall k,j,t $$

(80)

$$ \rho_{{C_{at} }} G_{at}^{C} X_{at} \le \eta_{at}^{C} ; \quad \forall a,t $$

(81)

$$ \rho_{{C_{at} }} G_{at}^{C} X_{at} \ge - \eta_{at}^{C} ; \quad \forall a,t $$

(82)

$$ \rho_{SUC} G_{j}^{{k^{SUC} }} Y_{j} \le \eta_{j}^{{k^{SUC} }} ; \quad \forall k,j $$

(83)

$$ \rho_{SUC} G_{j}^{{k^{SUC} }} Y_{j} \ge - \eta_{j}^{{k^{SUC} }} ; \quad \forall k,j $$

(84)

$$ \rho_{SC} G_{mt}^{SC} B_{mt} \le \eta_{mt}^{SC} ; \quad \forall m,t $$

(85)

$$ \rho_{SC} G_{mt}^{SC} B_{mt} \ge - \eta_{mt}^{SC} ; \quad \forall m,t $$

(86)

$$ \rho_{{PC_{jt}^{p} }} G_{jt}^{{p^{PC} }} N_{ijt}^{p} B_{ijt}^{p} \le \eta_{jt}^{{p^{PC} }} ; \quad \forall p,i,j,t $$

(87)

$$ \rho_{{PC_{jt}^{p} }} G_{jt}^{{p^{PC} }} N_{ijt}^{p} B_{ijt}^{p} \ge - \eta_{jt}^{{p^{PC} }} ; \quad \forall p,i,j,t $$

(88)

$$ \rho_{{PC_{at}^{k} }} G_{at}^{{k^{PC} }} N_{jat}^{k} B_{jat}^{k} \le \eta_{at}^{{k^{PC} }} ; \quad \forall k,j,a,t $$

(89)

$$ \rho_{{PC_{at}^{k} }} G_{at}^{{k^{PC} }} N_{jat}^{k} B_{jat}^{k} \ge - \eta_{at}^{{k^{PC} }} ; \quad \forall k,j,a,t $$

(90)

$$ \rho_{{PT_{jt}^{p} }} G_{jt}^{{p^{PT} }} \frac{{X_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2} \le \eta_{jt}^{{p^{PT} }} ; \quad \forall p,i,j,t $$

(91)

$$ \rho_{{PT_{jt}^{p} }} G_{jt}^{{p^{PT} }} \frac{{X_{ijt}^{p} \left( {B_{ijt}^{p} + 1} \right)}}{2} \ge - \eta_{jt}^{{p^{PT} }} ; \quad \forall p,i,j,t . $$

(92)

$$ \rho_{{PT_{at}^{k} }} G_{at}^{{k^{PT} }} \frac{{X_{jat}^{k} \left( {B_{jat}^{k} + 1} \right)}}{2} \le \eta_{at}^{{k^{PT} }} ; \quad \forall k,j,a,t $$

(93)

$$ \rho_{{PT_{at}^{k} }} G_{at}^{{k^{PT} }} \frac{{X_{jat}^{k} \left( {B_{jat}^{k} + 1} \right)}}{2} \ge - \eta_{at}^{{k^{PT} }} ; \quad \forall k,j,a,t $$

(94)

$$ \rho_{{T_{i}^{p} }} G_{i}^{{p^{T} }} X_{it}^{p} \le \eta_{i}^{{p^{T} }} ; \quad \forall p,i,t $$

(95)

$$ \rho_{{T_{i}^{p} }} G_{i}^{{p^{T} }} X_{it}^{p} \ge - \eta_{i}^{{p^{T} }} ; \quad \forall p,i,t $$

(96)

$$ \rho_{{T_{j}^{k} }} G_{j}^{{k^{T} }} X_{jt}^{k} \le \eta_{j}^{{k^{T} }} ; \quad \forall k,j,t $$

(97)

$$ \rho_{{T_{j}^{k} }} G_{j}^{{k^{T} }} X_{jt}^{k} \ge - \eta_{j}^{{k^{T} }} ; \quad \forall k,j,t $$

(98)

$$ \rho_{{T_{a} }} G_{a}^{T} X_{at} \le \eta_{a}^{T} ; \quad \forall a,t $$

(99)

$$ \rho_{{T_{a} }} G_{a}^{T} X_{at} \ge - \eta_{a}^{T} ; \quad \forall a,t $$

(100)

$$ \rho_{SUT} G_{j}^{{k^{SUT} }} Y_{j} \le \eta_{j}^{{k^{SUT} }} ; \quad \forall k,j $$

(101)

$$ \rho_{SUT} G_{j}^{{k^{SUT} }} Y_{j} \ge - \eta_{j}^{{k^{SUT} }} ; \quad \forall k,j $$

(102)

Available time constraints

$$ \mathop \sum \limits_{p = 1}^{P} \bar{T}_{i}^{p} \left( {1 + \rho_{{T_{i}^{p} }} } \right) X_{it}^{p} \le \overline{TAST}_{it} \left( {1 - \rho_{TAST} } \right); \quad \forall i,t $$

(103)

$$ \mathop \sum \limits_{k = 1}^{K} \bar{T}_{j}^{k} \left( {1 + \rho_{{T_{j}^{k} }} } \right) X_{jt}^{k} + \mathop \sum \limits_{k = 1}^{K} \overline{SUT}_{j}^{k} \left( {1 + \rho_{SUT} } \right)Y_{j} \le \overline{TAPT}_{jt } (1 - \rho_{TAPT} ) Y_{j} ; \quad \forall j,t $$

(104)

$$ \bar{T}_{a} (1 + \rho_{{T_{a} }} ) X_{at} \le \overline{TAAT}_{at} \left( {1 - \rho_{TAAT} } \right); \quad \forall a,t $$

(105)

Storage capacity constraints

$$ \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{i = 1}^{I} V^{p} X_{ijt}^{p} \le \bar{S}_{j} \left( {1 - \rho_{{S_{j} }} } \right)Y_{j} ; \quad \forall j,t $$

(106)

$$ \mathop \sum \limits_{p = 1}^{P} V^{p} X_{it}^{p} \le \bar{S}_{i} \left( {1 - \rho_{{S_{i} }} } \right); \quad \forall i,t $$

(107)

$$ \mathop \sum \limits_{k = 1}^{K} V^{k} X_{jt}^{k} \le \bar{S}_{j} \left( {1 - \rho_{{S_{j} }} } \right)Y_{j} ; \quad \forall j,t $$

(108)

$$ \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{J} V^{k} X_{jat}^{k} \le \bar{S}_{a} \left( {1 - \rho_{{S_{a} }} } \right); \quad \forall a,t $$

(109)

$$ \mathop \sum \limits_{a = 1}^{A} V X_{adt} \le \bar{S}_{d} \left( {1 - \rho_{{S_{d} }} } \right)Y_{d} ; \quad \forall d,t $$

(110)

$$ V X_{at} \le \bar{S}_{a} \left( {1 - \rho_{{S_{a} }} } \right); \quad \forall a,t $$

(111)

Transportation capacity constraints

$$ \mathop \sum \limits_{j = 1}^{J} X_{ijt}^{p} \le \overline{TTCA}_{i}^{p} \left( {1 - \rho_{{TTCA_{i}^{p} }} } \right) W_{it}^{p} ; \quad \forall p,i,t $$

(112)

$$ \mathop \sum \limits_{a = 1}^{A} X_{jat }^{k} \le \overline{TTCA}_{j}^{k} \left( {1 - \rho_{{TTCA_{j}^{k} }} } \right) Y_{j} ; \quad \forall k,j,t $$

(113)

$$ \mathop \sum \limits_{d = 1}^{D} X_{adt} \le \overline{TTCA}_{a} \left( {1 - \rho_{{TTCA_{a} }} } \right); \quad \forall a,t $$

(114)

$$ \mathop \sum \limits_{m = 1}^{M} X_{dmt} \le \overline{TTCA}_{d} \left( {1 - \rho_{{TTCA_{d} }} } \right) Y_{d} ; \quad \forall d,t $$

(115)

Binary and non-negative variables

$$ Y_{d} , Y_{j} , W_{it}^{p} \in \left\{ {0,\left. 1 \right\}} \right.; \quad \forall d,j,p,i,t $$

(116)

$$ \begin{aligned} & X_{ijt}^{p} , X_{jat }^{k} , X_{adt } , X_{dmt} , X_{it}^{p} , X_{jt}^{k} , X_{at} , , B_{mt} ,N_{ijt}^{p} ,N_{jat}^{k} ,\eta_{ijt}^{{p^{TC} }} ,\eta_{jt}^{{p^{PC} }} ,\eta_{at}^{{k^{PC} }} ,\eta_{it}^{{p^{C} }} ,\eta_{jat}^{{k^{TC} }} ,\eta_{jt}^{{k^{C} }} ,\eta_{adt}^{TC} ,\eta_{at}^{C} ,\eta_{dmt}^{TC} , \hfill \\ & \quad \eta_{j}^{{k^{SUC} }} ,\eta_{d}^{F} ,\eta_{j}^{F} ,\eta_{mt}^{SC} ,\eta_{jt}^{{p^{PT} }} ,\eta_{at}^{{k^{PT} }} ,\eta_{i}^{{p^{T} }} ,\eta_{j}^{{k^{T} }} ,\eta_{a}^{T} ,\eta_{j}^{{k^{SUT} }} \ge 0;\;\quad \forall i,j,a,d,m,p,k,t \hfill \\ \end{aligned} $$

(117)

Unchanged constraints

Constraints (13); (14); (18)–(22); (33).

5 Solution methods

As Sect. 4 indicates, there is a tri-objective MILP robust mathematical model. The ideal solution for the proposed tri-objective robust model should optimize all the objective functions simultaneously considering satisfaction of all constraints. In the real-world environments, there are usually many problems involving conflicting objectives. As a result, a feasible solution cannot optimize all objective functions simultaneously. Therefore, decision-makers should select an effective and preferable solution (Pasandideh and Akhavan Niaki 2014).

Since choosing the appropriate solution method is important for us, five well-known MODM solution methods in the CPLEX solver of GAMS software have been applied to solve the proposed tri-objective MILP robust model. These methods consist of the LP-metrics, maxi-min, goal attainment, goal programming and utility function methods.

To employ the LP-metrics and maxi-min methods, first, the optimal value of each objective function should be obtained separately using the individual optimization method. To employ the goal attainment and goal programming methods, decision-makers should determine a goal value for each objective function. In this research, the mentioned goal values are considered to be equal to the optimal values obtained by individual optimization method. The utility function method does not need any pre-defined goal value.

The individual optimization method optimizes each of the objective functions separately for all primary constraints as follows:

$$ \begin{array}{*{20}c} {\left. {\begin{array}{*{20}c} {Max\;f_{1} } \\ {Max\;f_{2} } \\ . \\ . \\ . \\ {Max\;f_{k} } \\ {s . t:} \\ {All\;constraints} \\ \end{array} } \right\}} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {Max\;f_{1} } \\ {s . t :} \\ {All\;constraints} \\ \end{array} } & {\begin{array}{*{20}c} {Max\;f_{2} } \\ {s . t :} \\ {All\;constraints} \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {\begin{array}{*{20}c} {Max\;f_{k} } \\ {s . t :} \\ {All\;constraints} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} $$

(118)

In the individual optimization method, the optimal solution obtained for each single objective problem is an effective solution for the multi-objective problem and is represented by $f_{i}^{*} \left( { {\text{i}} = 1,2, \ldots {\text{k }}} \right)$ if we have $k$ objective functions. An ideal overall solution is obtained when all the effective solutions are same in terms of all constraints (Pasandideh and Akhavan Niaki 2014).

Finally, using the filtering/displaced ideal solution (DIS) method, we draw a comparison between the five MODM solution methods based on the solution quality and the CPU time values in various levels of $\rho$. In all of these methods, all objective functions are considered from the perspective of maximization type. Minimization type objectives must be converted into a maximization type. These five MODM methods are described below.

5.1 LP-metrics method

The LP-metrics method searches the closest solution to the optimal values of the objective functions (Pasandideh and Akhavan Niaki 2014). In this method, we attempt to minimize the total differences between the values of the objective functions from their optimal values that are obtained by the individual optimization method. To convert the above-mentioned phrase to the scale-less phrase, these differences are divided into the optimal value of each objective function. We indicate the weights of the objective functions by $W_{i}$ in this method $\left( {\mathop \sum \nolimits_{i = 1}^{k} W_{i} = 1} \right)$. The mathematical formulation of the LP-metrics method is as follows:

$$ \begin{aligned} & Min\;Z = \left( {\mathop \sum \limits_{i = 1}^{K} W_{i} \left( {\frac{{f_{i}^{*} - f_{i} }}{{f_{i}^{*} }}} \right)^{p} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \hfill \\ & s . t : \hfill \\ & All\;constraints \hfill \\ \end{aligned} $$

(119)

where $p$ is considered 1 in this research.

5.2 Maxi-min method

The maxi-min method focuses on the weakest objective function (Pasandideh and Akhavan Niaki 2014). As a result, it neglects from the optimization of the other objective functions. This method is aimed at maximizing the minimum of the quantities obtained by dividing the values of the objective functions by their corresponding optimal values obtained by the individual optimization method. We demonstrate the weights of the objective functions by $W_{i} \left( {i = 1,2, \ldots ,k} \right)$ in this method ($\mathop \sum\nolimits_{i = 1}^{k} W_{i} = 1)$. This method can be formulated by the following model:

$$ \begin{aligned} & Max\;Z = Min \left( {\frac{{w_{1} f_{1} }}{{f_{1}^{*} }} , \frac{{w_{2} f_{2} }}{{f_{2}^{*} }} , \ldots ,\frac{{w_{k} f_{k} }}{{f_{k}^{*} }}} \right) \\ & s . t : \\ & All\;constraints \\ \end{aligned} $$

(120)

5.3 Goal programming method

In this method, a goal is considered for each objective function, and the purpose is to achieve this goal. In this regard, for any objective function, a deviation variable from its goal value is considered, and the aim is to minimize this variable. We signify the positive and the negative deviations of the objective functions from their goals by d⁺ and d⁻, respectively. Both of these variables have positive values. In addition, we can consider different weights for deviations (h_i) in accordance with the importance of the objective functions. The mathematical formulation of the goal programming method can be stated as follows:

$$ \begin{aligned} & Min\;Z = \mathop \sum \limits_{i = 1}^{K} h_{i} p_{i} \left( {d_{i}^{ + } , d_{i}^{ - } } \right) \\ & s . t : \\ & All\;constraints \\ & f_{i} - d_{i}^{ + } + d_{i}^{ - } = b_{i} ; \quad \forall i = 1,2, \ldots ,k \\ & d_{i}^{ + } d_{i}^{ - } = 0; \quad \forall i = 1,2, \ldots ,k \\ & d_{i}^{ + } ,d_{i}^{ - } \ge 0; \quad \forall i = 1,2, \ldots ,k \\ \end{aligned} $$

(121)

In this research, the goal values (b_i) are considered to be equal to the optimal values of each objective function (f_i*) obtained by the individual optimization method. In this method, we have:

$$ p_{i} (d_{i}^{ + } ,d_{i}^{ - } ) = \left\{ {\begin{array}{*{20}l} {d_{i}^{ + } } \hfill & {if\;\;f_{i} \,is\,a\,minimization\;objective\;function} \hfill \\ {d_{i}^{ - } } \hfill & {if\;\;f_{i} \,is\,a\,maxmization\;objective\;function} \hfill \\ {d_{i}^{ + } + d_{i}^{ - } } \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

5.4 Goal attainment method

The goal attainment method tries to find a solution that minimizes the highest weighted deviation $\left( Z \right)$ between the individual and the overall objective function values (Pasandideh and Akhavan Niaki 2014). Moreover, in this method the values of the ideal solutions $\left( {b_{i} } \right)$ are considered equal to the optimal values of the objective functions $\left( {f_{i}^{*} } \right)$ obtained by the individual optimization method. This method can be provided in the form of the following model:

$$ \begin{aligned} & Min\; Z \\ & s . t : \\ & All\;constraints \\ & f_{i} + w_{i} Z \ge b_{i} ; \quad \forall i = 1 , 2, \ldots ,k \\ & Z :free \\ \end{aligned} $$

(122)

In addition, in this method after solving the multi-objective model, we have:

$$ If\;Z^* = \left\{ {\begin{array}{*{20}l} {Positive} \hfill & {The\;objective\;functions\;values\;are\;laged\;from\;the\;ideal\;solution\;values} \hfill \\ {Zero} \hfill & {The\;objective\;functions\;values\;are\;equal\;to\;the\;ideal\;solution\;values} \hfill \\ {Negativ} \hfill & {The\;objective\;functions\;values\;are\;exceeded\;from\;the\;ideal\;solution\;values} \hfill \\ \end{array} } \right. $$

The sum of weights $W_{i}$ is equal to 1 in this method ($\mathop \sum \nolimits_{i = 1}^{k} W_{i} = 1$).

5.5 Utility function method

In this method, the objective functions are converted into a unique objective function, and to do this, there are several methods from which we apply the weighted sum method in this research. In this method, the constraints remain unchanged, and new constraints are not added.

$$ \begin{aligned} & Max\;\; Z = u\left( {f_{1} ,f_{2} ,f_{3} , \ldots ,f_{k} } \right) \\ & s.t: \\ & All \;constraints \\ \end{aligned} $$

(123)

Using weighted sum method:

$$ u\left( {f_{1} ,f_{2} ,f_{3} , \ldots ,f_{k} } \right) = w_{1} f_{1} + w_{2} f_{2} + \cdots + w_{k} f_{k} $$

(124)

Moreover, the sum of the weights of the objective functions is equal to 1 in this method. It is worth noting that in all of the above-mentioned five MODM solution methods, the new objective function Z, is none of the previous objective functions defined.

6 Instants characterization

In this section, we provide various test problems of different sizes. Then, based on the objective function values and CPU times, the above-mentioned MODM methods are compared with each other at various levels of uncertainty. To make the comparison between MODM solution methods more reliable, the proposed model should be solved for problems of different sizes. The sizes of test problems are indicated in Table 2.

Table 2 Test problems

In the above table the symbols are:

NOS:

Number of suppliers

NOJ:

Number of manufacturing plants

NOA:

Number of assemblers

NOD:

Number of distribution centers

NOC:

Number of customers

NOP:

Number of pieces

NOW:

Number of semi-finished products

NOT:

Number of periods

It should be noted that the above-mentioned test problems are defined randomly. In other words, there is no relationship between them. We just attempt to increase the size of the problems by increasing the test problem codes.

We generate the parameters of the proposed tri-objective MILP robust model in Sect. 4 randomly based on uniform distributions in pre-specified intervals demonstrated in Table 3.

Table 3 Pre-specified intervals to generate parameters based on uniform distributions

The weights of the objective functions are, $W_{1} = 0.2, W_{2} = 0.2 , W_{3} = 0.6$, and the weights of the deviation variables in the goal programming method are, $h_{1} = 1$, $h_{2} = 1, h_{3} = 10$. Our strategy is to give the greatest importance to maximizing the reliability (third objective function) to minimize the facilities disruption risk, since customer’s demand will not be met if the facilities disruption occurs. It is worth noting that the value of h_i in the goal programming method should be a multiplier of 10. In the other MODM solution methods, the sum of the weights of the objective functions (w_i) should be equal to 1.

7 Numerical results

This section presents multi-objective results and the DIS method, sensitivity analysis, and the proposed solution procedure to find the dominant and dominated objective functions in multi-objective models.

7.1 Multi-objective results and the DIS method

We solve the tri-objective MILP robust mathematical model for various problems of different sizes, using the five MODM methods by the GAMS commercial software on a computer with core (M) i5-CPU 2.40 GH, RAM 6.00 GB. The values of the objective functions and CPU times are given in Table 4.

Table 4 The values of objective functions and CPU time for different MODM methods and various uncertainty levels $\left( \rho \right)$

The CPU time of the individual optimization method is the sum of CPU times obtained from three times running the individual optimization problem for three different objective functions separately.

All values in Table 4 are summarized in Figs. 4, 5 and 6 for the different objective functions and MODM methods and various levels of $\rho$.

Fig. 4

Z₁ values for various levels of ρ and different problem codes and MODM methods

Fig. 5

Z₂ values for various levels of ρ and different problem codes and MODM methods

Fig. 6

Z₃ values for various levels of ρ and different problem codes and MODM methods

The figures above clearly illustrate that the maxi-min method is very sensitive to the objective function weights. Due to the fact that the third objective function values in this method are very close to the individual optimization method values (ideal solution), the first and the second objective function values are very different from those of the individual optimization method. On the other hand, Z₁ and Z₂ values of the other MODM methods are close to the values of the individual optimization method, while Z₃ values are different from them. The CPU time values for different codes and MODM methods and various levels of $\rho$ are summarized in Fig. 7.

Fig. 7

CPU time values for various levels of ρ and different problem codes and MODM methods

The figure above and Table 4 demonstrate that the maxi-min method is the fastest method with a minimum average time of 13.76 s, and the goal attainment method is the slowest method with a maximum average time of 157.756 s. The average values of Z₁, Z₂, and Z₃ and CPU times of different problems code for various levels of $\rho$ and different solution methods are summarized in Table 5 obtained from Table 4. In other words, to obtain the average values of Table 5 for a specific solution method and a certain level of uncertainty, we calculate the average value of all various test problems in Table 4 for the same specific solution method and the same certain level of uncertainty. It means that Table 5 is extracted from Table 4.

Table 5 The average values of objective functions and CPU time for different MODM methods and various levels of $\rho$

According to Table 4, it is clear that no solution is ideal (the objective function values obtained by the individual optimization method have been considered as the ideal solution values) and none of them optimizes all of the objective functions simultaneously. As a result, all of them are effective solutions. In this respect, the displayed ideal solution (DIS) method is used to select the best MODM method to solve the tri-objective MILP robust mathematical model. In this method, a vector (F_i) of the solution is considered for each MODM method and is obtained based on the following four criteria presented in Table 5: the average value of the first objective function, the average value of the second objective function, the average value of the third objective function, and the average value of CPU times. The ideal solution (F*) is specified by determining the minimums in the three rows consisting of the average values of the first objective function and the second objective function and the CPU times as well as determining the maximum in the row consisting of the average of the third objective function value bolded in Table 5.

Following that, the values in Fi are normalized and the direct distance of each of them is computed in the following tables (Pasandideh and Akhavan Niaki 2014). It is worth noting that the maximum differences between criterion values of the solution methods and the ideal solution are used to define the scale-less values of Tables 6, 7, 8 and 9.

Table 6 Criterion scale-less values and direct distances of solution methods ρ = 0

Table 7 Criterion scale-less values and direct distances of solution methods ρ = 0.2

Table 8 Criterion scale-less values and direct distances of solution methods ρ = 0.5

Table 9 Criterion scale-less values and direct distances of solution methods ρ = 0.9

Finally, a solution with a minimum direct distance is selected. The final results are indicated in Tables 6, 7, 8 and 9 for various levels of $\rho$, where the sixth row shows the direct distances of the MODM methods. It is worth noting that the minimum values of direct distances are bolded in Tables 6, 7, 8 and 9.

Based on Table 6, the utility function method (E) with a minimum direct distance of 1.0007 is the best solution method for $\rho = 0$.

Based on Table 7, the utility function method (E) with a minimum direct distance of 1.04506 is the best solution method for $\rho = 0.2$

Based on Table 8, the utility function method (E) with a minimum direct distance of 1.0727 is the best solution method for $\rho = 0.5.$

Based on Table 9, the utility function method (E) with a minimum direct distance of 1.00607 is the best solution method for $\rho = 0.9.$

The results of the DIS method show that to determine the best MODM solution method, in various levels of $\rho$, the utility function method has the minimum direct distance from the optimal values (ideal solution) and is selected as the best MODM solution method to solve the tri-objective MILP robust problem. For instance, the proposed solution for test problem 1 at, $\rho = 0.2$, which is obtained with application of utility function method, is demonstrated in Tables 10 to 15, in detail. The results of solution reveal that among the three potential manufacturing plants and four potential distribution centers, manufacturing plants 1,2, and 3 and distribution center 3 are selected, respectively, to be established with $Z_{1}$ value of 161,884.4, $Z_{2}$ value of 106,284.2, and $Z_{3}$ value of 60.2. It is worth noting that as the results suggest, all pieces can be supplied by all suppliers in this test problem. The value of CPU time is 0.265, and no shortage occurred for none of the customers.

Table 10 Optimal quantity of batches of piece p dispatched from supplier i to manufacturing plant j in period t

Table 10 represents the optimal quantity of batches of five various pieces dispatched from three deterministic suppliers to three selected manufacturing plants in three time periods. Table 11 shows the optimal quantity of the batches of four various semi-finished products dispatched from three selected manufacturing plants to two deterministic assemblers in three time periods. Table 12 shows the optimal quantity of the dispatched final products from two deterministic assemblers to the selected distribution center 3 in three time periods. Finally, Table 13 represents the optimal quantity of the dispatched final products from the selected distribution center 3 to six customers in three time periods. It should be noted that based on Table 13 all the customers demand are fulfilled by selected distribution center 3. Therefore, no gap exists in the context of the fulfillment of the customer’s demand.

Table 11 Optimal quantity of batches of semi-finished product k dispatched from plant j to assembler a in period t

Table 12 Optimal quantity of final products dispatched from assembler a to distribution center d in period t

Table 13 Optimal quantity of final products dispatched from distribution center d to customer m in period t

The queuing system results (service time of commodities) is presented in Tables 14 and 15.

Table 14 Service time of piece p dispatched from supplier i to manufacturing plant j in period t

Table 15 Service time of semi-finished product k dispatched from plant j to assembler a in period t

Table 14 presents the service time values of the five various pieces dispatched from three deterministic suppliers to three selected manufacturing plants in three time periods. Table 15 shows the service time values of the four various semi-finished products dispatched from three selected manufacturing plants to two deterministic assemblers.

7.2 Sensitivity analysis

To learn more regarding the relationship between $Z_{1}$ value (i.e. total cost) and $Z_{2}$ value (i.e. total time), the trade-off between total cost and total time is presented in Fig. 8 for test problem 1 at $\rho = 0.2$, which is obtained by applying utility function method. It is worth noting that the weights of objective functions have been considered to be: {(1,0,0), (0.9,0.1,0), (0.8,0.2,0), …, (0.1,0.9,0), (0,1,0)}. Some of the weights also reach the solutions very close or even equal to each other.

Fig. 8

Trade-off between total cost and total time performed by utility function method

As Fig. 8 shows, the two objective functions are incompatible as an increase in the value of the total cost leads to a decrease in the value of the total time. In the real-world, this rule holds true whenever more costs are spent on the SCNs, the required products are delivered to customers faster. For example, as the transportation costs increase, faster and more vehicles can be utilized and consequently, the required products are delivered to customers faster.

To demonstrate the relationship between $Z_{1}$ value (i.e. total cost) and $Z_{3}$ value (i.e. average total number of commodities dispatched from any echelon of the SCN to the next echelon), the trade-off between total cost and average total number of commodities dispatched from any echelon of the SCN to the next echelon is presented in Fig. 9 for test problem 1 at $\rho = 0.2$, which is obtained by applying utility function method. It is worth noting that the weights of objective functions have been considered to be: {(1,0,0), (0.9,0,0.1), (0.8,0,0.2), …, (0.1,0,0.9), (0,0,1)}. Some of the weights also obtain the solutions very close or equal to each other.

Fig. 9

Trade-off between total cost and average total number of commodities dispatched from any echelon of the SCN to the next echelon performed by utility function method

As Fig. 9 depicts, two objective functions are compatible as an increase in the value of the total cost leads to an increase in the value of the average total number of commodities dispatched from any echelon of the SCN to the next echelon. In the real-world, this rule is also true as more costs (such as costs of transportation and inventory holding) are spent on the SCNs, the average total number of commodities dispatched from any echelon of the SCN to the next echelon increases highly.

To clarify the relationship between $Z_{2}$ value and $Z_{3}$ value, the trade-off between total time and average total number of commodities dispatched from any echelon of the SCN to the next echelon is presented in Fig. 10 for test problem 1 at $\rho = 0.2$, which is obtained by using utility function method. It is worth noting that the weights of objective functions have been considered to be: {(0,1,0), (0,0.9,0.1), (0,0.8,0.2), …, (0,0.1,0.9), (0,0,1)}. Some of the weights also obtain the solutions very close or equal to each other.

Fig. 10

Trade-off between total time and average total number of commodities dispatched from any echelon of the SCN to the next echelon performed by utility function method

Based on Fig. 10, it can be inferred that the two objective functions are compatible since Fig. 10 shows that an increase in the value of the total time leads to an increase in the value of the average total number of commodities dispatched from any echelon of the SCN to the next echelon. This holds true in the real world, since the more time (such as total available supply, production and assembling times) is spent on the SCNs, the average total number of commodities dispatched from any echelon of the SCN to the next echelon increases highly.

Finally, Fig. 11 presents the optimal Pareto front solution for test problem 1 at $= 0.2$, which is obtained via utility function method. It is worth noting that the weights of objective functions have been considered to be: {(1,0,0), (0.8,0.1,0.1), (0.6,0.2,0.2), …. (0.2,0.4,0.4), (0,0.5,0.5), (0,1,0), (0.1,0.8,0.1), (0.2,0.6,0.2), …. (0.4,0.2,0.4), (0.5,0,0.5), (0,0,1), (0.1,0.1,0.8), (0.2,0.2,0.6),…, (0.4,0.4,0.2), (0.5,0.5,0)}. Some of weights also obtain the solutions very close or equal to each other. It is worth noting that all of the above-mentioned MODM solution methods only obtain one solution (non-dominated if the optimality is reached) in every time solved. Therefore, to obtain the Pareto front, we should change the weights of the objective functions and resolve the problem.

Fig. 11

Pareto front obtained by using utility function method

As it was mentioned previously, in the proposed tri-objective MILP robust model, a competition exists between the number of commodities dispatched from each echelon of the SCN to the next echelon (third objective function) and the total cost (first objective function) and total time (second objective function). Since increasing the third objective function leads to increasing the total cost and time while the first and second objective functions are from minimization type. Therefore, the first and second objective functions act against the third objective function. Hence, knowing which group will dominate the other one is of great significance. In other words, we should determine either of the set of first and second objective functions or the third objective function dominates the other.

To answer this question, a solution is proposed to find the dominant and dominated objective functions based on uncertainty level (⍴) in multi-objective models in the following.

7.3 Proposed solution procedure to find the dominant and dominated objective functions in multi-objective models for determined weights of objective functions based on the uncertainty level (⍴) of the model

In this section, we present a three-stage solution procedure as follows:

• 1. Obtain the trend (treatment) of each objective function by increasing the levels of ρ in a non-competitive condition (Individual optimization method) separately. Certainly, there is a general rule for this stage: by increasing the ⍴ value, maximization objective functions have a descending trend and minimization objective functions have an ascending trend. Because by increasing the $\rho$ values, the feasible region of the problem’s solution space decreases and no better solution can be found by the solution method.

• 2. Obtain the trend of each objective function by increasing the levels of ρ in a competitive condition (for example, MODM solution methods).

• 3. Compare the results (objective function trends by increasing the ⍴ value) obtained by the two previous stages in competitive and non-competitive conditions. Any objective function with different trends in the competitive and non-competitive conditions is dominated and controlled by the competitor objective functions.

Accordingly, first, the treatment of Z₁, Z₂, Z₃ values of individual optimization method was obtained by increasing the levels of ρ for different problem codes, while the weights of the objective functions are $W_{1} = 0.2 ,W_{2} = 0.2 , W_{3} = 0.6$, as presented in Fig. 12 (derived from Table 4).

Fig. 12

Trends of Z1, Z2, Z3 values obtained by using individual optimization method by increasing the levels of ρ for different problem codes

Based on Fig. 12 it is clear that for a specific code, by increasing the uncertainty level (ρ), the objective functions values of the individual optimization method do not improve. In other words, according to Fig. 12, it is concluded that by increasing the $\rho$ values, the Z₁ and Z₂ values will not decrease and the Z₃ value will not increase. Because by increasing the $\rho$ values, the feasible region of the problem’s solution space decreases.

Currently, the treatments of three objective functions should be obtained in a competitive condition by the utility function method at various levels of ⍴. Then, two treatments obtained by the individual optimization method and the utility function method are compared. Since by considering the treatments of objective functions in the non-competitive condition, the deviations in the treatments of the objective functions in the competitive condition will be obtained. Each group with a deviation in the competitive condition rather than in non-competitive condition is dominated by the other group, since the dominated group is controlled by the dominant group in terms of attainment of the ideal solutions.

Hence, treatments of Z₁, Z₂, Z₃ values of utility function method by increasing the levels of ρ for different problem codes, while the weights of the objective functions are $W_{1} = 0.2 ,W_{2} = 0.2 , W_{3} = 0.6$ are presented in Fig. 13 (derived from Table 4).

Fig. 13

Trends of Z₁, Z₂, Z₃ values obtained by using utility function method by increasing the levels of ρ for different problem codes

The comparison of the results obtained from two methods indicates that the first and second objective functions have equal treatments in the non-competitive (individual optimization method) and the competitive (utility function method) conditions (please compare Figs. 12 and 13 to each other) and have ascending trends. However, the third objective function treatment is different in competitive and non-competitive conditions. Since in code 2, code 3, code 4, code 5 and code 6, it is expected that as in non-competitive condition, the charts have descending trends, while they have ascending trends (code 1 is infeasible in ⍴ = 0.5 and ⍴ = 0.9). In other words, in these test problems for the third objective function, it is expected that by increasing the uncertainty level (⍴), the obtained solutions are not improved, since by increasing the ⍴ value, the feasible region of the problem’s solution space decreases and no better solution can be found.

Therefore, the first and second objective functions dominate the third objective function and control the obtained solutions by utility function method, although the weight distributions are $W_{1} = 0.2 ,W_{2} = 0.2 , W_{3} = 0.6$. Because, in the proposed tri-objective robust model, a small increase in the third objective function value leads to a large increase in the first and second objective function values while they are from minimization type. However, it is important to note that these results are valid for utility function method. For example, if the maxi-min method is applied, the obtained results will be completely inverse. In other words, the third objective function dominates the two other objective functions (please refer to the maxi-min method in Table 4), since, as it was mentioned previously, the maxi-min method is concentrated on the weakest objective function. This important note indicates the significance of comparing the MODM solution methods.

8 Conclusions and suggestions for future research

In this research, we attempt to propose a realistic model for SCN optimization. In this regard, we concentrate on the formation of the queuing system in the producers of the SCN and BTP approaches, as well as the operational and disruption risks. We maximize the reliability of facilities in sending the commodities in the third objective function to manage the disruption risk and use the ⍴-robust method in order to deal with the operational risk in the proposed tri-objective model. In the present study, a novel tri-objective MILP robust mathematical model was introduced to optimize total cost, total time, and the average total number of commodities dispatched from any echelon of the SCN to the next echelon on a five-echelon multi-period SCN.

The BTP approaches are beneficial to compute the parameters of formed queuing system in the producers of the SCN. It is also useful to compute the optimal quantity of batches transferred from suppliers to producers that can be used in transportation planning.

We compare five of the MODM solution methods at various levels of ⍴ to determine their best ones to solve the proposed tri-objective robust model. Based on the average values of Z₁, Z₂, and Z₃ and CPU time, the utility function method was selected as the best MODM method to solve the proposed mathematical model at various levels of uncertainty.

In fact, the proposed robust tri-objective model leads to a competition between the average total number of commodities dispatched from any echelon of the SCN to the next echelon and total cost and total time. Hence, we propose a novel solution to find dominant and dominated objectives in multi-objective models for determined weights of objective functions based on the uncertainty level of the model. The proposed solution based on uncertainty level and objective functions trends for determined weights of objective functions indicate that the third objective function is dominated by two other objective functions when the model is solved by the utility function method.

Our research is highly beneficial to all companies in the competitive market, since it helps to reduce the total cost and total time of processing the final product and as a result it reduces the prices and delivery times which in turn leads to attracting more customers. Maximizing the facilities reliability is also beneficial for customer satisfaction.

In future studies, other queuing system models such as M/M^(x)/1 model or batch arrival model can be also studied in problem modeling. Furthermore, meta-heuristic algorithms such as NSGA - II and MOPSO can be employed to find Pareto fronts. Some of the model parameters can be also considered as fuzzy parameters. Moreover, instead of the exponential distribution which is assumed to model the reliability of facilities, other probability distributions such as Erlang or Weibull can be considered (Pasandideh and Akhavan Niaki 2014).