Bounded dynamic programming algorithm for the job shop problem with sequence dependent setup times

Abstract

In this paper, the job shop scheduling problem (JSP) with a makespan minimization criterion is investigated. Various approximate algorithms exist that can solve moderate JSP instances within a reasonable time limit. However, only a few exact algorithms are known in the literature. We have developed an exact algorithm by means of a bounded dynamic programming (BDP) approach. This approach combines elements of a dynamic programming with elements of a branch and bound method. In addition, a generalization is investigated: the JSP with sequence dependent setup times (SDST-JSP). The BDP algorithm is adapted for this problem. To the best of our knowledge, the dynamic programming approach has never been applied to the SDST-JSP before. The BDP algorithm can directly be used as a heuristic. Computational results show that the proposed algorithm can solve benchmark instances up to 20 jobs and 15 machines for the JSP. For the SDST-JSP, the proposed algorithm outperforms all the state-of-the-art exact algorithms and the best-known lower bounds are improved for 5 benchmark instances.

1 Introduction

The job shop scheduling problem (JSP) is an important scheduling problem, which is NP-hard. Since the JSP has applications in several areas, the problem and its generalizations have been extensively studied.

Several approximate algorithms have been proposed to tackle the JSP within a reasonable amount of time. Adams et al. (1988) proposed the shifting bottleneck procedure. The tabu search technique has been applied by several researchers, e.g. Nowicki and Smutnicki (1996), Nowicki and Smutnicki (2005), Zhang et al. (2008). The genetic approach has been investigated by Della Croce et al. (1995) and Kurdi (2015). Gonçalves and Resende (2014) presented the biased random-key algorithm. Recently, Peng et al. (2015) presented a powerful hybrid search/path relinking algorithm.

Only a few exact algorithms are known for the JSP. One such algorithm is the branch and bound method (B&B). This method is proposed by several authors (Carlier and Pinson 1989; Brucker et al. 1994; Martin and Shmoys 1996). Carlier and Pinson (1989) proposed the B&B model combined with the concept of immediate selection, which is based on branching on disjunctions. It was the first exact method that solved Fisher and Thompson (1963) $10\times 10$ benchmark instance. Brucker et al. (1994) proposed the B&B based on the disjunctive graph model. The basic scheduling decision is to fix precedence relations between the operations on the same machine. A block approach was used. Gromicho et al. (2012) a corrigendum on this paper by van Hoorn et al. 2016) proposed a dynamic programming (DP) algorithm with the complexity proven to be exponentially lower than exhaustive enumeration. However, computation results show that only $10\times 5$ type benchmark instances were solved by the proposed algorithm. Recently, van Hoorn (2016) provided the bounded dynamic programming algorithm. Thus, the computational time of the previously proposed DP algorithm was drastically decreased for solving benchmark instances. However, the proposed algorithm was able to solve still limited size benchmark instances up to 10 machines and 10 jobs.

Consider now the job shop scheduling problem with sequence dependent setup times (SDST-JSP). This problem is a generalization of the JSP in which setup times occurs when the machine switches between two jobs. This feature significantly changes the nature of the problem. Thus, the problem becomes harder to solve. Within the current literature, the typical approach is to extend the methods that were applied to the classical JSP. We will highlight only the most important papers. Based on the work proposed by Brucker et al. (1994) and Brucker and Thiele (1996) extended the B&B for the general shop problem where SDST-JSP is a special case. They also provided new benchmark instances (denoted by BT96 and named t2-ps01 to t2-ps15). Cheung and Zhou (2001) used a hybrid algorithm that is based on a genetic algorithm and two dispatching rules. The shifting bottleneck approach is extended by Balas et al. (2008). An effective B&B was developed by Artigues and Feillet (2008). This algorithm extends constraint propagation techniques for the SDST-JSP. The lower bound calculation is based on the traveling salesman problem with time windows. The algorithm proposed by Artigues and Feillet (2008) was able to prove the optimality for the first time on two benchmark instances from BT96. Moreover, the lower bound is improved for six instances. The effective hybrid genetic algorithm that hybridizes a genetic algorithm with a local search is reported by González et al. (2008). Empirical results show that the new model outperforms all previous state-of-the-art results improving best-known solutions for 5 benchmark instances of BT96. González et al. (2009) combines a genetic algorithm with a tabu search approach instead of a local search method thus outperforming several empirical results given by González et al. (2008). For both González et al. (2008, 2009), the problem is modeled using the disjunctive graph representation. Grimes and Hebrard (2010) proposed a constraint programming approach that extends the previous model given by Grimes et al. (2009). The model using simple binary disjunctive constraints combines AI strategies with the generic SAT.

In the previous study (Ozolins 2017) we have successfully developed the DP to the blocking flow shop scheduling problem. This problem is another variant of the shop scheduling. Ultimately, this approach outperforms all the known state-of-the-art exact algorithm for the blocking flow shop. This finding suggests that the DP technique can successfully be applied to other variants of the shop scheduling.

Gromicho et al. (2012) proposed the base version of the DP approach for the JSP. In this paper, we improve the DP method for solving the JSP thus increasing the applicability of the DP approach. The novel contribution of our work lies in the SDST-JSP. We extend the DP approach to the SDST-JSP with a makespan objective. As far as we know this is the first time when the DP approach is used for the SDST-JSP.

This paper is organized as follows. In Sect. 2, the JSP is introduced. Basic notations and definitions are given. Section 3 presents the BDP algorithm for the JSP and SDST-JSP cases. Computational results are described in Sect. 4. In Sect. 5, conclusions are given. Finally, “Appendix” is given in the last section.

2 Problem formulation

Basic notations used in the present paper are summarized in Table 1 for a quick reference.

Table 1 Basic notations

Consider the JSP. The processing procedure of a job on a machine is called an operation. Let ${\mathcal {O}}=\{O_{i,k}\mid i=1,\ldots ,n,k=1,\ldots m\}$ denotes the set of operations, partitioned into n jobs $J_1,\ldots ,J_n$ that need to be scheduled on m machines $M_1,\ldots ,M_m$. Let ${\mathcal {J}}=\{J_1,\ldots ,J_n\}$ and ${\mathcal {M}}=\{M_1,\ldots ,M_m\}$ denote the set of jobs and the set of machines, respectively. Each operation $O_{i,k}$ is associated with the specific job $J_i\in {\mathcal {J}}$ and the specific machine $M_{m_{i,k}}\in {\mathcal {M}}$. Hence, $m_{i,k}$ denotes the machine index of operation $O_{i,k}$. Alternatively, this index can be denoted by $M(O_{i,k})$. Each job has to visit all the machines following a specific order. Each machine can process only one job at the same time and each job can be processed by only one machine at the same time. We will study the special case of the JSP where each job has to visit all the machines exactly once.

The processing time of operation $O_{i,k}$ is denoted by $p(O_{i,k})$ or simply by $p_{i,k}$. Alternatively, the processing time associated with a machine $M_k$ and a job $J_j$ can be denoted by $p_j^k$. Denote by $\psi :{\mathcal {O}}\rightarrow {\mathbf {N}}\cup \{0\}$ the schedule. For simplicity, we will also use the notation $\psi _{i,k}$ as an alternative to the notation $\psi (O_{i,k})$. Let

$$\begin{aligned} C_{\max }=\max _{O\in {\mathcal {O}}}\left( \psi (O)+p(O)\right) \end{aligned}$$

be the makespan that corresponds to the schedule $\psi$. The problem can formally be stated as follows.

Definition 1

(Job shop scheduling problem)

$$\begin{aligned} \begin{array}{ll} \underset{\psi }{\text {minimise}} \; C_{\max } &{} \\ {\text{subject}}\,{\text{to:}} &{}\\ C_{\max }\ge \psi _{i,m}+p_{i,m}, &{} i=1,\ldots ,n;\\ \psi _{i,k}+ p_{i,k}\le \psi _{i,k+1}, &{} i=1,\ldots ,n,\; k=1,\ldots ,m-1;\\ \psi _{i,k_1}+p_{i,k_1}\le \psi _{j,k_2}\,{\text {or}}\\ \psi _{j,k_2}+p_{j,k_2}\le \psi _{i,k_1} &{} O_{i,k_1},O_{j,k_2}\in {\mathcal {O}}\,{\text {with}}\,i\ne j \,{\text{and}}\,m_{i,k_1}=m_{j,k_2}. \end{array} \end{aligned}$$

Using the notation given by Graham et al. (1979), the JSP can also be denoted by $J||C_{\max }$.

The JSP can be generalized by defining the setup times $s_{i,j}^k$ between operations $O_{i,k_1},O_{j,k_2}\in {\mathcal {O}}$ on the same machine $M_k\in {\mathcal {M}}$. In addition, an initial setup $s_{0,i}$ is defined for all $i\in \{1,\ldots ,n\}$. This problem is denoted by $J|s_{i,j}^k|C_{\max }$ and can be formalized in the following way.

Definition 2

(Job shop problem with sequence dependent setup times)

$$\begin{aligned} \begin{array}{ll} \underset{\psi }{\text {minimise}} \; C_{\max } &{} \\ {\text{subject}}\,{\text{to:}} &{}\\ C_{\max }\ge \psi _{i,m}+p_{i,m}, &{} i=1,\ldots ,n;\\ \psi _{i,k}+ p_{i,k}\le \psi _{i,k+1}, &{} i=1,\ldots ,n,\; k=1,\ldots ,m-1;\\ \psi _{i,k_1}+p_{i,k_1}+s_{i,j}^k\le \psi _{j,k_2}\,{\text {or}}&{} O_{i,k_1},O_{j,k_2}\in {\mathcal {O}}\,{\text {with}}\\ \psi _{j,k_2}+p_{j,k_2}+s_{j,i}^k\le \psi _{i,k_1} &{} i\ne j \,{\text {and}}\,m_{i,k_1}=m_{j,k_2}\equiv k;\\ \psi _{i,1}\ge s_{0,i} &{} i=1,\ldots ,n. \end{array} \end{aligned}$$

In addition, we assume that setup times satisfy the triangular inequality

$$\begin{aligned} s_{i,j}^k\le s_{i,h}^k+s_{h,j}^k \end{aligned}$$

for all $k\in \{1,\ldots ,m\}$ and for each triplet of distinct jobs $(J_i,J_j,J_h)$.

3 Bounded dynamic programming algorithm

In this section, we will develop the bounded dynamic programming (BDP) approach for solving the JSP. The base version of this approach was proposed by Gromicho et al. (2012). In Sect. 3.1, the complete BDP algorithm will be proposed. The SDST-JSP will be studied in Sect. 3.2. In Sects. 3.3 and 3.4, we will discuss lower bounds for the JSP and SDST-JSP.

3.1 Bounded dynamic programming algorithm formulation

Let T be the sequence of operations. We will further say that T is associated with $G\subset {\mathcal {O}}$ if G contains all the operations that appear in T. Those operations that are not in T are not included in G. We say that T is also associated with $S\subset {\mathcal {J}}$ if S contains those jobs for which all the operations are completed. For example, if we have the job shop instance with 3 jobs and 3 machines and

$$\begin{aligned} T=(O_{3,1},O_{1,1},O_{1,2},O_{2,1},O_{1,3}), \end{aligned}$$

then T is associated with $S=\{J_1\}$ and

$$\begin{aligned} G=\{O_{3,1},O_{1,1},O_{1,2},O_{2,1},O_{1,3}\}. \end{aligned}$$

A no-idle starting time of an operation means that this operation starts directly after the last operation on the same machine or directly after the last operation of the same job. We will further assume that $\psi (O_{i,k})$ stands for this no-idle starting time of operation $O_{i,k}\in G$.

The sequence T is called feasible if

$$\begin{aligned} \psi (T_1)+p(T_1)\le \cdots \le \psi (T_{|G|})+p(T_{|G|}). \end{aligned}$$

In addition, $M(T_g)< M(T_{g+1})$ for those $g\in \{1,\ldots ,|G|-1\}$ for which $\psi (T_g)+p(T_g)=\psi (T_{g+1})+p(T_{g+1})$. From the construction of T it follows that each sequence T can uniquely be associated with the given schedule.

Denote by $C_{\max }(T)$ the maximum completion time among all the operations from T. Let $Succ_i(G)$ denotes the next operation that needs to be scheduled by job $J_i\in {\mathcal {J}}{\setminus } S$. Let $\psi _i(T)$ be the earliest starting time of operation $Succ_i(G)$. A sequence obtained after this insertion is denoted by $T+Succ_i(G)$. In fact, we have

$$\begin{aligned} T+Succ_i(G)=(T_1,\ldots ,T_{|G|},Succ_i(G)). \end{aligned}$$

Denote by $O_{i,l}\in {\mathcal {O}}{\setminus } G$ the new operation that is inserted in T, i.e. $O_{i,l}=Succ_i(G)$. Fix $J_j\in {\mathcal {J}}{\setminus } S$. We explain how to recursively obtain the starting times $\psi _j(T+ O_{i,l})$ from $\psi _j(T)$. Firstly, the makespan is

$$\begin{aligned} C_{\max }(T+ O_{i,l})=\psi _i(T)+p_{i,l}. \end{aligned}$$

The resulting recurrence relation is

$$\begin{aligned} \psi _j(T+ O_{i,l})={\left\{ \begin{array}{ll} C_{\max }(T+ O_{i,l}), &{} m_{i,l}=M(Succ_j(G)),\\ \psi _j(T), &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

Now define the head $r_j(T)$ as the earliest starting time of operation $Succ_j(G)$ such that $T+ Succ_j(G)$ is feasible. These heads $r_j(T)$ are strongly connected with $\psi _j(T)$ and are obtained as follows:

$$\begin{aligned} r_j(T)={\left\{ \begin{array}{ll} \psi _j(T), &{} x_j(T)=1,\\ C_{\max }(T), &{} x_j(T)=0, \end{array}\right. } \end{aligned}$$

where $x_j(T)$ is a binary variable defined as

$$\begin{aligned} x_j(T)={\left\{ \begin{array}{ll} 1, &{} \psi _j(T)+p(Succ_j(G))>C_{\max }(T)\,{\text {or}}\\ &{} \left[ \psi _j(T)+p(Succ_j(G))=C_{\max }(T)\,{\text {and}}\,M(T_{|G|})<M(Succ_j(G))\right] ,\\ 0, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(1)

The variable $x_j(T)$ represents whether the next operation can be added to the end of T without a delay. In fact, $x_j(T)=1$ if and only if

$$\begin{aligned} T+ Succ_j(G)=(T_1,\ldots ,T_{|G|},Succ_j(G)) \end{aligned}$$

is feasible.

Table 2 Processing times and processing orders of an instance

Fig. 1

Example of a schedule

Table 3 The earliest starting times related to Fig. 1

Table 4 Parameters related to the schedule depicted in Fig. 1

In order to understand the basic notations, we give an example. The basic parameters of an instance are given in Table 2. Here each cell contains a pair $(p_i^k,l)$ where l means that the lth operation of job $J_i$ is processed on machine $M_k$.

Figure 1 illustrates the feasible sequence

$$\begin{aligned} T=(O_{3,1},O_{1,1},O_{2,1},O_{1,2}, O_{3,2},O_{2,2},O_{1,3},O_{4,1},O_{1,4}). \end{aligned}$$

This sequence is associated with the set of scheduled jobs $S=\{J_1\}$ and the set of scheduled operations

$$\begin{aligned} G=\{O_{1,1},O_{1,2},O_{1,3},O_{1,4}, O_{2,1},O_{2,2},O_{3,1},O_{3,2},O_{4,1}\}. \end{aligned}$$

The starting times of operations belonging to G are given in Table 3.

The parameters $Succ_j(G),x_j(T),\psi _j(T)$, and $r_j(T)$ are given in Table 4. In addition, $C_{\max }(T)$, the earliest starting times, and the heads are illustrated in Fig. 1. Note that $x_3(T)=0$ since

$$\begin{aligned} \psi _3(T)+p(Succ_3(G))=9+4<C_{\max }(T) \end{aligned}$$

The next definition introduces the complete expansion of a sequence.

Definition 3

Let T be the sequence of operations associated with $G\subset {\mathcal {O}}$. Let

$$\begin{aligned} T^*=(T_1^*,\ldots ,T_{n\cdot m}^*) \end{aligned}$$

be the sequence of operations associated with ${\mathcal {O}}$. We say that $T^*$ is a complete expansion of T if $T_h=T_h^*$ ($h=1,\ldots ,|G|$) and $T^*$ is feasible.

We introduce the weak dominance ‘$\preceq$’ relation as follows.

Definition 4

Let $T^1$ and $T^2$ be two sequences of operations such that both $T^1$ and $T^2$ are associated with $S\subset {\mathcal {J}}$. We say that $T^1$ weakly dominates $T^2$, i.e. $T^1\preceq T^2$ if

$$\begin{aligned} r_i(T^1)\le r_i(T^2) \end{aligned}$$

for all $J_i\in {\mathcal {J}}{\setminus } S$.

When two sequences of operations, namely $T^1$ and $T^2$, are given, then the corresponding starting times will be denoted by $\psi ^1(O)$ and $\psi ^2(O)$, respectively. Hence $O\in {\mathcal {O}}$ belongs to $T^1$ and $T^2$. We are ready to present the theorem related to the weak dominance.

Theorem 1

Let$T^1$and$T^2$be two sequences of operations such that both$T^1$and$T^2$are associated with$G\subset {\mathcal {O}}$. If $T^1$weakly dominates$T^2$, then for all complete expansions of$T^2$there exists a complete expansion of$T^1$such that

$$\begin{aligned} \psi ^1(O)\le \psi ^2(O) \end{aligned}$$

for all$O\in {\mathcal {O}}{\setminus } G$

In other words, Theorem 1 says that $T^2$ can be disregarded if $T^1\preceq T^2$. The Proof of Theorem 1 will be given in Sect. 3.2 for the general case SDST-JSP (Theorem 3) where Theorem 1 is a special case.

The next definition introduces an indirect dominance.

Definition 5

Let T stands for the sequence of operations associated with $G\subset {\mathcal {O}}$ and $S\subset {\mathcal {J}}$. We say that T is indirectly dominated if there exists $M_k\in {\mathcal {M}}$ and $J_j\in {\mathcal {J}}{\setminus } S$ with $M(Succ_j(G))=k$ such that the following two statements hold:

• 1. We have $x_j(T)=0$.

• 2. For all $J_i\in {\mathcal {J}}{\setminus } S{\setminus } J_j$ with $M(Succ_i(G))= k$ we have $r_i(T)\ge \psi _j(T)+p(Succ_j(G))$.

Informally speaking, we can add to T at least one operation $O\in {\mathcal {O}}{\setminus } G$ such that the heads remain the same for $T+O$. Thus, the sequences that are indirectly dominated can be disregarded. The next theorem formalizes this idea.

Theorem 2

LetTbe the sequence of operations associated with$G\subset {\mathcal {O}}$and$S\subset {\mathcal {J}}$. IfTis indirectly dominated, then there exists job$J_j\in {\mathcal {J}}{\setminus } S$such that$x_j(T)=0$and

$$\begin{aligned} r_i(T+Succ_j(G))= r_i(T) \end{aligned}$$

for all$J_i\in {\mathcal {J}}{\setminus } S{\setminus } J_j$.

The Proof of Theorem 2 directly follows from Definition 5. Theorem 2 is formulated in a slightly different way than the one proposed by Gromicho et al. (2012).

Now we investigate the previously studied example, see Fig. 1. Here, $x_3(T)=0$. Moreover,

$$\begin{aligned} r_i(T)\ge \psi _3(T)+p(Succ_3(G))=13 \end{aligned}$$

for $i\in \{3,4\}$. Thus, the schedule depicted in Fig. 1 is indirectly dominated.

We are ready to present the BDP algorithm, see Algorithm 1. This algorithm is similar to the one proposed by van Hoorn (2016). We have reformulated this algorithm using our notation system. Algorithm 1 will also be useful for the SDST-JSP.

Now we briefly describe Algorithm 1. Initially, n sequences of operations are created. Then a loop through stages $t=1$ to $n\cdot m-1$ has been done, see line 1.2. For each stage t we loop through all subsets G with the size t (line 1.3). For each G, we loop through all sequences $T\in Z(G)$. These sequences are expanded with the operations that satisfy requirements given in line 1.5. Function $filter\_ sequences$ (line 1.8) firstly tests whether $T^1$ is indirectly dominated. Then we try to reduce $Z(G^1)$ by keeping only non-dominated sequences of operations. If $T^1$ is not dominated by another sequence from $Z(G^1)$, then we test whether $LB(T^1)<UB$ holds. Finally, if $T^1$ is not discarding, then $T^1$ is included in $Z(G^1)$. If the state space is growing too large, then only H sequences with size $t+1$ are kept (line 1.9). Also, Algorithm 1 becomes the heuristic BDP algorithm. The sorting criterion can be LB values.

In contrast to the previous version of the BDP (van Hoorn 2016), we use function $filter\_ sequences$, see line 1.8. We have two main contribution of this function. Firstly, we use a stronger lower LB than that one used by van Hoorn (2016). This bound will be described in Sect. 3.3. Secondly, if $T^1$ is indirectly dominated, then we do not test whether $T^1\preceq T^2$ for another $T^2$. Thus, we do not need to save $T^1$ if $T^1$ is indirectly dominated.

Algorithm 2 obtains the optimal solution of the JSP. This algorithm is based on Algorithm 1. However, lines 1.9–1.10 are replaced by lines 2.13–2.16. In this case the subproblem (line 2.16) is solved if the state space is growing too large. The parameter H (line 2.13 in Algorithm 2) depends on the computer system requirements.

In summary, the main contributions of Algorithms 1 and 2 are summarized below.

• 1. A stronger lower bound LB is used. This bound is described is Sect. 3.3. It can be expected that more sequences T will be discarded.

• 2. We do not have to save those sequences that are indirectly dominated. Thus, less memory could be required during the run of the BDP algorithm.

• 3. We have included lines 2.13–2.16 in Algorithm 2. Thus, the given algorithm is theoretically able to solve any instance without running out of the given amount of memory.

3.2 Bounded dynamic programming algorithm for the SDST-JSP

Again, let T be the sequence of operations. Throughout this section we will assume that T is associated with $S\subset {\mathcal {J}}$ and $G\subset \mathcal{O}$.

Some additional notations will be introduced. Let $\rho _k(T)$ denotes the job index that corresponds to the last operation completed on machine $M_k\in {\mathcal {M}}$. The completion time of this operation is denoted by $C_k(T)$. If no operation is scheduled on machine $M_k$, then $C_k(T)=0$.

Table 5 Parameters $\rho _k(T)$ and $C_k(T)$ related to the schedule depicted in Fig. 1

Table 5 reports $\rho _k(T)$ and $C_k(T)$ values for the previously studied example (see Table 2 and Fig. 1). In this example we assume that all setup times are equal to 0.

Now we will analyse the transition from T to $T+ O_{i,l}$ where $O_{i,l}\in {\mathcal {O}}{\setminus } G$ is the next operation that job $J_i\in {\mathcal {J}}{\setminus }$ has to schedule. Let $k=m_{i,l}$ denotes the machine index of operation $O_{i,l}$. Firstly, the makespan is equal to

$$\begin{aligned} C_{\max }(T+ O_{i,l})=\psi _i(T)+p_{i,l}. \end{aligned}$$

Secondly, the earliest starting times $\psi _i(T+O_{i,l})$ can be greater than $C_{\max }(T+O_{i,l})$, i.e.

$$\begin{aligned} \psi _i(T+O_{i,l})=\max \left\{ C_{\max }(T+O_{i,l}),C_k(T)+s_{\rho _k(T),i}^k\right\} . \end{aligned}$$

Also, setup times have to be taken into account in order to obtain $\psi _j(T+ O_{i,l})$ for $J_j\in {\mathcal {J}}{\setminus } S{\setminus } \{J_i\}$ with $M(Succ_j(G))=k$. For this case we have

$$\begin{aligned} \psi _j(T+ O_{i,l})=C_{\max }(T+ O_{i,l})+s_{\rho _k(T),j}^k. \end{aligned}$$

The resulting recurrence relation is

$$\begin{aligned} \psi _j(T+ O_{i,l})={\left\{ \begin{array}{ll} \max \left\{ C_{\max }(T+ O_{i,l}), C_k(T)+s_{\rho _k(T),j}^k\right\} , &{} i=j,\\ C_{\max }(T+ O_{i,l})+s_{\rho _k(T),j}^k, &{} M(Succ_j(G))=k,\\ \psi _j(T), &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

where index j is such that $J_j\in {\mathcal {J}}{\setminus } S$.

The heads $r_j(T)$ can be calculated as follows:

$$\begin{aligned} r_j(T)={\left\{ \begin{array}{ll} \psi _j(T), &{} x_j(T)=1,\\ \max \left\{ C_{\max }(T),C_k(T)+s_{\rho _k(T),j}^k\right\} , &{} x_j(T)=0, \end{array}\right. } \end{aligned}$$

where $x_j(T)$ is the binary variable defined in (1). Note that $r_j(T)$ can be greater than $C_{\max }(T)$ due to the setup times.

Let us describe the general heads $r_{j,g}(T)$. These heads represent the earliest starting time of $O_{j,g}\in {\mathcal {O}}{\setminus } G$. Let $k=m_{j,g}$ denotes the machine index of $O_{j,g}$. In general, $r_{j,g}(T)$ can recursively be estimated as follows:

$$\begin{aligned} r_{j,l}(T)&=r_j(T),\\ r_{j,g}(T)&=\max \left\{ r_{j,g-1}(T)+p_{j,g-1}, C_k(T)+s_{\rho _k(T),j}^k\right\} , \quad g=l+1,\ldots ,m, \end{aligned}$$

where index l means that $Succ_j(G)=O_{j,l}$.

Fig. 2

On the left side: the optimal schedule. On the right side: the non-optimal schedule

Fig. 3

On the left side: the optimal schedule. On the right side: the non-optimal schedule

Theorem 1 about the weak dominance cannot directly be applied to the SDST-JSP due to the setup times. Two simple examples are given in Figs. 2 and 3. These examples show that Theorem 1 fails in these cases with unit processing times. The setup times corresponding to Fig. 2 are

$$\begin{aligned} \left( s_{i,j}^1\right) = \begin{pmatrix} 0 &{} 2 &{} 1 &{} 3\\ 2 &{} 0 &{} 2 &{} 3\\ 3 &{} 3 &{} 0 &{} 2\\ 3 &{} 3 &{} 3 &{} 0 \end{pmatrix} \,{\text {and}}\,\left( s_{i,j}^2\right) = \begin{pmatrix} 0 &{} 2 &{} 3 &{} 4\\ 2 &{} 0 &{} 2 &{} 4\\ 4 &{} 4 &{} 0 &{} 2\\ 4 &{} 4 &{} 4 &{} 0 \end{pmatrix}. \end{aligned}$$

For the second example depicted in Fig. 3, we define the setup times as follows:

$$\begin{aligned} \left( s_{i,j}^1\right) = \begin{pmatrix} 0 &{} 3 &{} 2\\ 2 &{} 0 &{} 2\\ 4 &{} 4 &{} 0 \end{pmatrix} \,{\text {and}}\,\left( s_{i,j}^2\right) = \begin{pmatrix} 0 &{} 3 &{} 4\\ 2 &{} 0 &{} 2\\ 4 &{} 4 &{} 0 \end{pmatrix}. \end{aligned}$$

In the first case, we set

$$\begin{aligned} T^1&=(O_{1,1},O_{1,2},O_{2,1},O_{2,2}, O_{3,1},O_{3,2}),\\ T^2&=(O_{2,1},O_{2,2},O_{1,1},O_{1,2}, O_{3,1},O_{3,2}). \end{aligned}$$

Then

$$\begin{aligned} r_4(T^1)=9>r_4(T^2)=8. \end{aligned}$$

However,

$$\begin{aligned} C_{\max }(T^1+ O_{4,1}+ O_{4,2})=11<C_{\max }(T^2+ O_{4,1}+ O_{4,2})=12. \end{aligned}$$

In this case, the problem lies in the fact that the completion times of operation $O_{3,2}$ on the machine $M_2$ differs, i.e. $C_2(T^1)<C_2(T^2)$.

Now we study the example depicted in Fig. 3. In this case, we set

$$\begin{aligned} T^1&=(O_{1,1},O_{1,2},O_{2,1}, O_{2,2}),\\ T^2&=(O_{2,1},O_{2,2},O_{1,1},O_{1,2}). \end{aligned}$$

Then

$$\begin{aligned} r_3(T^1)=7>r_3(T^2)=6 \end{aligned}$$

and

$$\begin{aligned} C_{\max }(T^1+ O_{3,1}+ O_{3,2})=9<C_{\max }(T^2+ O_{3,1}+ O_{3,2})=10. \end{aligned}$$

In this case, $\rho _2(T^1)\ne \rho _2(T^2)$.

Counterexamples in Figs. 2 and 3 show that Theorem 1 cannot be applied to the SDST-JSP. Thus, a stronger dominance rule has to be used. The next definition introduces this rule.

Definition 6

Let $T^1$ and $T^2$ be two sequences of operations such that both $T^1$ and $T^2$ are associated with $G\subset {\mathcal {O}}$ and $S\subset {\mathcal {J}}$. We say that $T^1\preceq T^2$ if the following two statements hold:

• 1. $r_j(T^1)\le r_j(T^2)$ for all $J_j\in {\mathcal {J}}{\setminus } S$.

• 2. Let i denotes the job index for which $i=\rho _k(T^1)$ and let l denotes the index with $k=m_{j,l}$. If $i\ne \rho _k(T^2)$ or $C_k(T^1)>C_k(T^2)$, then

  $$\begin{aligned} C_k(T^1)+s_{i,j}^k\le r_{j,l}(T^2) \end{aligned}$$

  for all $J_j\in {\mathcal {J}}{\setminus } S$.

Note that Definition 6 reduces to Definition 4 if $s_{i,j}^k=0$ for all $i,j\in \{1,\ldots n\}$ and $k\in \{1,\ldots ,m\}$.

Theorem 3

Let$T^1$and$T^2$be two sequences of operations such that both$T^1$and$T^2$are associated with$G\subset {\mathcal {O}}$. If$T^1\preceq T^2$, then for all complete expansions of$T^2$there exists a complete expansion of$T^1$such that

$$\begin{aligned} \psi ^1(O)\le \psi ^2(O) \end{aligned}$$

for all$O\in {\mathcal {O}}{\setminus } G$

Proof

Let $T^4$ denotes the complete expansion of $T^2$. Thus, we have

$$\begin{aligned} T^4=(T_1^2,\ldots ,T_{|G|}^2,T_{|G|+1},\ldots ,T_{n\cdot m}). \end{aligned}$$

Further, let $T^3$ denotes an expansion of $T^1$. We assume that all operations from ${\mathcal {O}}{\setminus } G$ are in the same order as in $T^4$, i.e.

$$\begin{aligned} T^3=(T_1^1,\ldots ,T_{|G|}^1,T_{|G|+1},\ldots ,T_{n\cdot m}). \end{aligned}$$

By reordering operations from $T^3$, we can obtain a feasible sequence of operations.

Let $O_{j,l_1}$ denotes the next operation $T_{|G|+1}$ and let k denotes the machine index of $O_{j,l_1}$. From Condition 1 in Definition 6 it follows that $\psi ^3(O_{j,l_1})\le \psi ^4(O_{j,l_1})$. The same can be stated for all other operations $T_h$ ($h>|G|+1$) for which the following two statements hold:

• $M(T_g)\ne M(T_h)$;

• The job index between operations $T_g$ and $T_h$ are different

for all $g\in \{|G|+1,\ldots ,h-1\}$.

Let $T_h$ ($h>|G|$) denotes the first operation for which there exists previous operation $T_g$ that has to be scheduled on the same machine or by the same job as operation $T_h$. Let $O_{i,l_2}=T_g$ denotes this operation.

Now we will study two cases. For the case $M(T_h)=M(T_g)$, we have

$$\begin{aligned} \psi ^3(T_h)&=\psi ^3(T_g)+p(T_g)+s_{i,j}^k, \end{aligned}$$

(2)

$$\begin{aligned} \psi ^4(T_h)&=\psi ^4(T_g)+p(T_g)+s_{i,j}^k. \end{aligned}$$

(3)

Since $\psi ^3(T_g)\le \psi ^4(T_g)$, it follows from (2)–(3) that $\psi ^3(T_h)\le \psi ^4(T_h)$. For the case $i=j$, we have $O_{i,l_2}=O_{j,l_1-1}$. If no operation from ${\mathcal {O}}{\setminus } G$ has been scheduled on machine $M_k$, then Condition 2 in Definition 6 ensures that $\psi ^3(O_{j,l_1})\le \psi ^4(O_{j,l_2})$ since $\psi ^3(O_{j,l_1-1})\le \psi ^4(O_{j,l_1-1})$. Otherwise, we have

$$\begin{aligned} \rho _k((T_1^3,\ldots ,T_{h-1}^3))= \rho _k((T_1^4,\ldots ,T_{h-1}^4)),\\ C_k((T_1^3,\ldots ,T_{h-1}^3))\le C_k((T_1^4,\ldots ,T_{h-1}^4)), \end{aligned}$$

from which it follows that $\psi ^3(T_h)\le \psi ^4(T_h)$

In summary, we have proved $\psi ^3(T_g)\le \psi ^4(T_g)$ for all $g\in \{|G|+1,\ldots ,h\}$. Hence, $T_h$ is the first operation for which there exists previous operation that has to be scheduled on the same machine or by the same job. By repeating the same steps of the proof, we can recursively prove that $\psi ^4(T_g)\le \psi ^4(T_g)$ for all $g\in \{|G|+1,\ldots ,n\cdot m\}$. By reordering the operations from sequence $T^3$ such that precedence relations among operations remain, we can obtain feasible sequence. This sequence is the complete expansion of $T^3$ such that

$$\begin{aligned} \psi ^3(O)\le \psi ^4(O) \end{aligned}$$

for all $O\in {\mathcal {O}}{\setminus } G$. The proof is completed. $\square$

Definition 5, which introduces the indirect dominance, has to be generalized.

Definition 7

Let T stands for the sequence of operations associated with $G\subset {\mathcal {O}}$ and $S\subset {\mathcal {J}}$. We say that T is indirectly dominated if there exists $M_k\in {\mathcal {M}}$ and $J_j\in {\mathcal {J}}{\setminus } S$ with $M(Succ_j(G))=k$ such that the following two statements hold:

• 1. We have $x_j(T)=0$.

• 2. For all $J_i\in {\mathcal {J}}{\setminus } S{\setminus } J_j$ with $M(Succ_i(G))= k$ we have $r_i(T)\ge \psi _j(T)+p(Succ_j(G))+s_{j,i}^k$.

Theorem 4

LetTbe the sequence of operations associated with$G\subset {\mathcal {O}}$and$S\subset {\mathcal {J}}$. IfTis indirectly dominated, then there exists job$J_j\in {\mathcal {J}}{\setminus } S$such that$x_j(T)=0$and

$$\begin{aligned} r_i(T+Succ_j(G))= r_i(T) \end{aligned}$$

for all$J_i\in {\mathcal {J}}{\setminus } S{\setminus } J_j$.

The Proof of Theorem 4 immediately follows from Definition 7.

3.3 A lower bound for the JSP

Throughout this section we assume that all operations from $G\subset {\mathcal {O}}$ are scheduled. The set of scheduled jobs is denoted by S. Let T denotes the sequence of operations associated with S and G. Let $q_{j,k}$ be a tail, which is defined as a lower bound of the time period between the completion time of operation $O_{j,k}\in {\mathcal {O}}{\setminus } G$ and the optimal makespan $C_{\max }$. The tails $q_{j,k}$ are calculated as follows:

$$\begin{aligned} q_{j,k}=\sum _{h=k+1}^{m}p_{j,h}. \end{aligned}$$

(4)

Let $r_{j,k}(T)$ denotes the earliest starting time of operation $O_{j,k}\in {\mathcal {O}}{\setminus } G$. These starting times can be estimated as follows:

$$\begin{aligned} r_{j,k}(T)=r_j(T)+q_{j,l}-q_{j,k-1}, \end{aligned}$$

(5)

where index l is such that $O_{j,l+1}=Succ_j(G)$ holds.

Fix machine $M_k\in {\mathcal {M}}$. Consider the one-machine scheduling problem with heads $r_{j,l}(T)$ and the corresponding tails where $O_{j,l}\in {\mathcal {O}}$ and $M(O_{j,l})=k$. These heads and tails are defined by (5) and (4) respectively. Let $LB_k(T)$ be the optimal solution of this one-machine sequencing problem. Despite the NP-hardness, the problem can efficiently be solved in practice using the branch and bound method proposed by Carlier (1982). The final lower bound of T is

$$\begin{aligned} LB(T)=\max _{k\in \{1,\ldots ,m\}}LB_k(T). \end{aligned}$$

3.4 A lower bound for the SDST-JSP

Again, we assume that all operations from $G\subset {\mathcal {O}}$ are scheduled and all jobs from $S\subset {\mathcal {J}}$ are completed. Let T stands for the sequence of operations associated with G and S.

The computation of the lower bounds can be reduced to the traveling salesman problem with time windows (TSPTW). Fix machine $M_k\in {\mathcal {M}}$. For the sake of simplicity, denote by $\delta ^k$ the following set:

$$\begin{aligned} \delta ^k=\{i\mid \,{\text {exists}}\,l\,{\text {with}}\,O_{i,l}\in {\mathcal {O}}{\setminus } G\,{\text {and}}\,M(O_{i,l})=k\} \end{aligned}$$

For all $j\in \delta ^k$ define the time windows $[a_j,b_j]$ as follows:

$$\begin{aligned} a_j&= r_{j,l}(T)+p_{j,l},\\ b_j&= UB-q_{j,l}-1, \end{aligned}$$

where l is such that $O_{j,l}\in {\mathcal {O}}{\setminus } G$.

The costs $c_{i,j}$ for $i,j\in \delta ^k$ with $i\ne j$ are defined as

$$\begin{aligned} c_{i,j}=s_{i,j}^k+p_{j,l}, \end{aligned}$$

where l is such that $O_{j,l}\in {\mathcal {O}}{\setminus } G$. The cost $c_{i,j}$ includes both the service time of i and the time needed to travel from i to j. The feasible version of the TSPTW denoted by F-TSPTW asks to find the feasible schedule satisfying time windows constraints. It can be concluded that $LB\ge UB$ if there exists machine $M_k\in {\mathcal {M}}$ such that the solution of F-TSPTW is infeasible.

Obviously, the problem F-TSPTW is NP-hard since it is the generalization of the TSP without the time windows. Similarly as by Artigues and Feillet (2008), we use the dynamic programming algorithm proposed by Feillet et al. (2004). This algorithm solves the elementary shortest path problem with resource constraints (ESPPRC) where TSPTW can be interpreted as a special case of the ESPPRC.

We try to speed up the calculation due to the NP-hardness of the problem F-TSPTW. The general scheme of the algorithm is given in Algorithm 3. The first step in Algorithm 3 is to find a feasible solution of the TSPTW using a time efficiency heuristic (line 3.1). In this paper, we use a variable neighborhood search (VNS) heuristic proposed by Da Silva and Urrutia (2010). Papalitsas et al. (2015) empirically shown that the sorting-based approach is not better than the random-based procedure. However, the VNS algorithm modified by Papalitsas et al. (2015) shows better performance.

If a feasible solution is not found immediately, then the weaker lower bound LB is calculated (line 3.5). We apply the calculation of LB given by Brucker and Thiele (1996). Let $h(\delta ^k)$ be defined as

$$\begin{aligned} h(\delta ^k)=\min _{i\in \delta ^k,\;m_{i,l}=k}r_{i,l}(T)+\sum _{i\in \delta ^k,\;m_{i,l}=k}p_{i,l}+\min _{i\in \delta ^k,\;m_{i,l}=k}q_{i,l}+setup_{\min }(\delta ^k). \end{aligned}$$

(6)

The value $setup_{\min }(\delta ^k)$ in (6) denotes a solution of the TSP with $|\delta ^k|$ vertices and setup times (costs) $s_{i,j}^k$ between those jobs $J_i,J_j$ for which there exists unscheduled operation on machine $M_k$. The values $setup_{\min }(\delta ^k)$ for all $\delta ^k$ can be preprocessing at the beginning of Algorithm 3. Then $h(\delta ^k)$ is calculated for the new $\delta ^k$ that is obtained by deleting one operation from the previous $\delta ^k$. We choose these operations according to the order of non-decreasing heads until $\delta ^k$ is empty. Then we repeat the same procedure but now according to the order of non-decreasing tails. $LB_k$ is obtained by taking the maximum value among all $h(\delta ^k)$ values.

Finally, if the result is not obtained in the previous two steps, then the relaxation of the ESPRC algorithm given by Feillet et al. (2004) has to be solved, see Algorithm 4. The value dist(V, i) denotes the shortest path for a pair (V, i) where $i\in V$ is the current vertex and $V\subset \delta ^k$ is the set of vertices already visited. The sets $\varLambda _i$ and $\varLambda _i^{new}$ consist of the sets V for which $dist(V,i)\ne \infty$. The reachability test (line 4.9 in Algorithm 4) is the same as the one proposed by Artigues and Feillet (2008).

4 Computational results

We implement the BDP algorithm in C++ programming environment and compiled it with Microsoft Visual Studio. Windows 64 bit operating system with 8 GB RAM memory and 2.8 GHz CPU was used. Several sets of benchmark instances are used. The presented computation results will be in two directions: to solve the problem without knowing a lower and upper bound, and the optimality proof by taking UB equals the optimal solution. For the JSP we will only prove the optimality with the aim to show the dimension of benchmark instances that can be solved by the BDP algorithm. For the SDTS-JSP we will try to solve the instances to optimality using two strategies.

Section 4.1 presents computational results for the JSP. In Sect. 4.2, the SDST-JSP is studied.

4.1 Case JSP

In this section, we will analyse how proposed Algorithm 2 works on practice proving the optimality for different benchmark instances. The effectiveness will be analysed in terms of |Z| and CPU times. Hence, |Z| is defined as

$$\begin{aligned} |Z|=\sum _{G\subset {\mathcal {O}}}|Z(G)|. \end{aligned}$$

In other words |Z| is a number of the non-dominated sequences T for which $LB(T)<UB$.

The termination criterion of Algorithm 2 is chosen in the following way. The calculation is interrupted if $|Z|_{t+1}>H$ for the subproblem (line 2.16 in Algorithm 2).

Table 6 The optimality proof for each instance

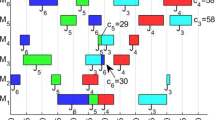
Table 6 shows that the optimality is proven for all $10\times 5,10\times 10,15\times 10,30\times 10$ type benchmark instances. However, the BPP algorithm is able to solve only 5 out of 10 benchmark instances for the case $20\times 10$ and 3 out of 5 instances for the case $15\times 15$. Furthermore, some $20\times 10$ type instances were solved because of the good estimation of the lower bound. Thus, the dominance relation between sequences was not important for those $20\times 10$ type instances as well as for the cases $15\times 5,20\times 5$, and $30\times 10$. Finally, the BDP algorithm is not able to solve any $20\times 15$ type instance as well as instances with a larger dimension. We observe from Table 6 that all $10\times 10$ type instances were solved within a CPU time less than 1 min. CPU times varies from seconds up to 4 h for 15 jobs and 10 machines.

The memory would be overreached for instances la21, la25, and la40 if the termination criterion has not be used (line 2.13 in Algorithm 2).

Table 7 Comparison of CPU times with the previous results of the BDP algorithm

van Hoorn (2016) gives computational results for his version of the BDP algorithm where the optimality was proven only for instances up to 10 jobs. Table 7 compares CPU times with those reported by van Hoorn (2016). We observe that almost all instances were solved significantly faster, except for instances with CPU time zero second. Moreover, van Hoorn algorithm is able to prove the optimality only for instances with a maximum of 10 jobs. It can be concluded that the BDP algorithm proposed in this paper significantly increases the applicability of the BDP approach for solving the classical JSP.

4.2 Case SDST-JSP

Table 11 reports the calculation of UB values whereas Table 8 gives a summary. In this case Algorithm 1 is used where H is taken as 100, 1000, ...  and finally 1,000,000 if it is necessary. Memory requirements of the computer allow us to use $H=10{,}000{,}000$. However, then CPU times would be increased significantly. For larger instances t2-ps11 to t2-ps15, $H=1000$ is the last time window. We start the calculation by setting $H=100$ and $UB=\infty$. Then we try to iteratively improve UB value until no improvement is possible for $H=100$. Then we set $H=1000$ and repeat the same procedure, etc. In Table 8, the three columns with the title ‘Summary’ represent final results obtained for each instance. The calculations are terminated when the optimal value is reached or the maximal H value is reached. The relative percentage deviation (RPD) is calculated as follows:

$$\begin{aligned} RPD=\dfrac{UB_{final}-BKS}{BKS}\times 100 \end{aligned}$$

where BKS denotes the best-known solution previously reported in the literature.

Table 8 Upper bounds: case SDST-JSP

As seen in Table 8, the optimality can be proven within few seconds for small instances of type $5\times 10 \times 5$. CPU times significantly grow for medium instances (named t2-ps06 to t2-ps10). Computational times are huge compared to those obtained by the state-of-the-art heuristic methods, e.g. a genetic algorithm combined with a tabu search or a local search (González et al. 2008, 2009). However, the BDP algorithm is able to reach the optimal value for those instances except for t2-ps08 for which the H value should be increased to obtain the optimal solution. The optimality has not been reached for instances t2-ps11 to t2-ps15 with $n=20$ jobs. However, the proposed algorithm can be applied for improving the best-known lower bounds for harder instances.

Table 9 Lower bounds: case SDST-JSP

The main contribution of the current research for the SDST-JSP is associated with the computational results for large instances. In Table 12 we calculate lower bounds using the following strategy. We start with some initial bound. We replace UB in Algorithm 2 with the current bound. Then we run the BDP algorithm. If the used bound is not lowered after the execution of the algorithm, then it is clear that the lower bound cannot be less than the current value. Thus, the current bound is increased by one for instances t2-ps1 to t2-ps10. For larger instances t2-ps11 to t2-ps15, the increment is taken as five. If the solution is obtained for the current bound, then the previous bound (namely LB$_{\mathrm{fin}}$) is also the optimal value of the given instance. If there exists t with $|Z|_t>3\cdot 10^5$, then the run is terminated. Thus, the optimal solution is not found and the previous bound is taken as the final lower bound of the given instance.

Table 9 gives a summary of lower bounds obtained by the DP. The value $\sum |Z|$ in Table 9 stands for the sum of all |Z| that is obtained for all previous bounds. LB$_{\mathrm{fin}}$ denotes the best lower bound that is found by BDP algorithm. The initial lower bound $LB_0$ is set significantly less in our runs. For the sake of simplicity we report only the final six bounds in Table 12.

As it is shown in Table 12, all small and medium instances t2-ps01 to t2-ps10 are solved to optimally. The best-known lower bounds are improved for all $5\times 20\times 10$ type benchmark instances. However, the proposed algorithm is not able to obtain the optimal solution without overreaching the width $3\cdot 10^{5}$. CPU times varies from less than 1 day to almost 3 days. In practice CPU times below the column ‘LB$_{\mathrm{fin}}$’ can be significantly less than those below the column ‘LB$_{\mathrm{fin}}$+1’ (e.g. the instances t2-ps07 and t2-ps10). On the other hand, for some cases these values can be similar (e.g. the instances t2-ps06 and t2-ps09).

It is interesting to note that a higher |Z| value not always means that a CPU value will be higher. The highest $\sum |Z|$ value is for the instance t2-p14. However, this instance is solved in 8 h that is significantly faster than the time required to solve three other instances, namely t2-ps12, t2-ps13, and t2-ps15.

Now we compare two strategies for solving the SDST-JSP by BDP (see Tables 8 and 9). We have that the first approach is slightly better for small instances in terms of CPU times. For medium instances, the second strategy shows better performance on average. The instance t2-ps06 is solved 200 times faster by the second strategy and for the instance t2-ps07 the optimal solution is not even reached by the first strategy.

Table 10 Comparison versus state-of-the-art exact algorithms: case SDST-JSP

The computational results of the state-of-the-art exact algorithms are summarized in Table 10. BT96, ABF04, AF08, and BDP stand for computational results obtained by Brucker and Thiele (1996), Artigues et al. (2004), Artigues and Feillet (2008), and our BDP approach, respectively. For the BDP we have shown the CPU$_{\mathrm{LB}}$ times for the second strategy, see Tables 9 and 12. The results under AF08 are obtained by similar computer requirements as used in the current work. 2 GHz processor is used for ABF04. Unfortunately, it is difficult to compare our results to those obtained by Brucker and Thiele (1996). Thus, we provide only a rough comparison with BT96. We apply factor 1.5 and 15 for CPU time comparisons with ABF04 and BT96, respectively.

CPU$_{\mathrm{LB}}$ and CPU$_{\mathrm{UB}}$ denote CPU times necessary to obtain LB and UB respectively. Some table cells under column CPU$_{\mathrm{LB}}$ are empty thus meaning that CPU=CPU$_{\mathrm{LB}}$, i.e. LB and UB are obtained in a single run. Artigues and Feillet (2008) uses two slightly different strategies for their branch and bound method. Thus, for each instance the best-obtained results are reported in Table 10.

Table 10 shows that our CPU times outperforms all the state-of-the-art exact algorithms for 10 instances that our approach is able to solve to optimality. The only exception is instance t2-ps06 where the results of AF08 show similar performance. Especially good performance is observed for five smallest BT instances where the BDP algorithm can be competitive even with the heuristic methods. Even using factor 15 for CPU times, the BDP method performs much better than BT96. In fact, for five small instances the average CPU time of the BDP are almost 200 times less than the one of BT96.

All medium instances t2-ps06 to t2-ps10 are solved in a reasonable time limit. This cannot be said about AF08 method, which spends several days to solve the instance t2-ps08. Moreover, the instance t2-ps09 is not solved to optimality since the calculation is terminated after 2 days. On the other hand, our BDP algorithm can solve this instance in 1 h. Lower bounds are improved for all larger instances. Moreover, the CPU times are significantly less than those reported by Artigues and Feillet (2008). The UB-values for large instances are better on average compared to those of AF08. However, the overall performance for obtaining the upper bounds is poor compared to the best-known solutions.

5 Conclusions

In this paper, the bounded dynamic programming (BDP) algorithm that solves the job shop scheduling problem (JSP) is investigated. We developed the BDP algorithm for solving the JSP to optimality. The proposed algorithm is able to prove the optimality for moderate benchmark instances (e.g. 15 jobs and 15 machines, or 20 jobs and 10 machines) thus significantly increasing the applicability of the BDP approach.

The main contribution of the present work is to adapt the BDP algorithm for the JSP with sequence dependent setup times (SDST-JSP). As far as we know this has not been done before. The quality of the BDP algorithm is strongly dependent on the quality of lower bounds (LB). We present the algorithm that calculates an LB. The performance of the BDP is evaluated against 15 benchmark instances proposed by Brucker and Thiele (1996). The comparison among the best-known algorithms shows that the BDP algorithm developed in the current work outperforms all the current state-of-the-art exact methods for the SDST-JSP case. Moreover, we have improved the best-known lower bounds for all 5 unsolved instances given by Brucker and Thiele (1996).

Appendix

See Tables 11 and 12.

Table 11 Calculation of upper bounds: case SDST-JSP

Table 12 Calculation of lower bounds: case SDST-JSP