Geometric Singular Perturbation Approach to Poisson-Nernst-Planck Systems with Local Hard-Sphere Potential: Studies on Zero-Current Ionic Flows with Boundary Layers

Abstract

We examine the dynamics of zero-current ionic flows via Poisson-Nernst-Planck systems with one cation, one anion and boundary layers. To account finite ion size effects in the analysis, we include Bikerman’s local hard-sphere model. Geometric singular perturbation theory is employed in our discussion, together with the specific structures of the model problem, we obtain the existence and local uniqueness result of the problem for zero-current state. More importantly, we are able to derive explicit expressions of the approximation to individual fluxes from the solutions. This allows us to further examine the effect on the zero-current ionic flows with boundary layers from finite ion sizes and diffusion coefficients by further employing regular perturbation analysis. The detailed analysis, particularly, the characterization of the nonlinear interplay between system parameters provides deep insights and better understandings of the internal dynamics of ionic flows through membrane channels.

1 Introduction

Ion channels are pore-forming membrane proteins that allow ions to pass through the channel pore. Ion channels are embedded in cell membranes, which provide a major medium for cells to communicate with each other and with outside environment [1,2,3]. In this way, ion channels control a wide range of biological functions, in particular, many varied functions are necessary for life (see [3] for more discussion). Clinically, malfunctioning channels cause cystic fibrosis, cholera, and many other diseases [4]. Thus, it is significant to explore the mechanism of ion channels.

In general, we study ion channels mainly focusing on two related major topics: structures of ion channels and ionic flow properties. The physical structure of ion channels is defined by the channel shape and the spatial distribution of permanent charges and the polarity of these charges [3, 5]. Thanks to the revolutionary advances of cryo-electro microscopy, which is recognized in the 2018 Nobel Prize, we are able to know the structure of many ion channels. This excellent work enhances the study of permanent charge effects on ionic flows toward a comprehensive understanding of ion channel properties. Once the structure of an open ion channel is given, the main interest is on the study of its electrodiffusion property. A main challenge to study properties of ionic flows through ion channels is to characterize the nonlinear interplay between specific system parameters. Moreover, current experimental techniques are still limited, and the key experimental measurement about ionic flow is the I–V relation defined in (1.7) below [6, 7]. However, it is an input-output type information of an average effect of physical parameters on ionic flows; particularly, it is still impossible to“measure/observe" internal dynamical behaviors of ionic flows. It is not a surprise that to extract coherent properties or to formulate specific characteristic quantities from the experimental measurements that are crucial for classifying general behavior of ionic flows is still challenging. On the other hand, the measurement of I–V relations can still efficiently determine some characteristics of ion channels by employing some well-established methods of the theory of inverse problem [8, 9].

The challenges mentioned above strongly indicates the importance of mathematical models and analysis and numerical simulations as complementary tools to the physiological theory and experiments. Mathematical study might provide deep correspondences from the multiple parameters involved to the internal dynamics and to properties of ion channels, at least for the relatively simple settings adopted in many biological experiments. Recently, there have been some successes in mathematical studies of Poisson-Nernst-Planck (PNP) models for ionic flows through membrane channels. Particularly, for those [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] etc. studied by employing the geometric singular perturbation analysis, interesting phenomena of ionic flows were observed for relatively simple setups.

In this work, we analyze a PNP model with Bikerman’s local hard-sphere component to account for finite ion size effects. Boundary layers are introduced by relaxing the electroneutrality conditions, which is more realistic in the study of ion channel problems. Our main interest is the effect on zero-current ionic flows from finite ion sizes and diffusion coefficients, respectively, which can be mathematically extracted from solutions of the PNP system.

1.1 One-Dimensional Poisson-Nernst-Planck Models

PNP system is a basic macroscopic model for electrodiffusion of charges through ion channels [7, 27,28,29,30,31], etc., which can be derived as a reduced model from molecular dynamics, Boltzmann equations, and variational principles [32,33,34,35], under some further assumptions.

A quasi-one-dimensional steady-state PNP model for a mixtures of n ion species though a single channel reads (first proposed in [36])

$$\begin{aligned} \begin{aligned}&\frac{1}{A(X)}\frac{d}{d X}\left( \varepsilon _r(X)\varepsilon _0A(X)\frac{d \Phi }{d X}\right) =-e\left( \sum _{j=1}^nz_jC_j(X)+Q(X)\right) ,\\&\quad \frac{d{\mathcal {J}}_i}{d X}=0, \quad -{\mathcal {J}}_i=\frac{1}{k_B T}{\mathcal {D}}_i(X)A(X)C_i(X)\frac{d\mu _i}{d X}, \quad i=1,2,\ldots , n, \end{aligned} \end{aligned}$$

(1.1)

where e is the elementary charge, $k_B$ is the Boltzmann constant, T is the absolute temperature; $\Phi (X)$ is the electric potential, Q(X) is the permanent charge density of the channel, $\varepsilon _0(X)$ is the local dielectric coefficient, $\varepsilon _r(X)$ is the relative dielectric coefficient, A(X) represents the area of the cross-section over the point X, n is the number of distinct types of ion species; and for the jth ion species, $C_j$ is the number density, $z_j$ is the valence, $\mu _j$ is the electrochemical potential, ${{{\mathcal {J}}}}_j$ is the number flux density, ${{{\mathcal {D}}}}_j(X)$ is the diffusion coefficient.

The boundary conditions are, for $i=1, 2, \ldots , n$,

$$\begin{aligned} \Phi (0)={\mathcal {V}}, \quad C_i(0)={\mathcal {L}}_i>0; \quad \Phi (l)=0, \quad C_i(l)={\mathcal {R}}_i>0. \end{aligned}$$

(1.2)

For an analysis of the boundary value problem (1.1)–(1.2), we will work on a dimensionless form. Let $C_0$ be a characteristic concentration of the problem, for instance,

$$\begin{aligned} C_0=\max _{1\le i\le n}\Big \{{{{\mathcal {L}}}}_i, {{{\mathcal {R}}}}_i, \sup _{X\in [0,l]}|{\mathcal {Q}}(X)|\Big \}. \end{aligned}$$

Set

$$\begin{aligned} {\mathcal {D}}_0=\max _{1\le i\le n}\left\{ \sup _{X\in [0,l]}{\mathcal {D}}_k(X)\right\} \ \text{ and }\ {\bar{\varepsilon }}_r=\sup _{X\in [0,l]}\varepsilon _r(X). \end{aligned}$$

Let

$$\begin{aligned} \begin{aligned} \varepsilon ^2&=\frac{{\bar{\varepsilon }}_r\varepsilon _0k_BT}{e^2l^2C_0},\quad {\hat{\varepsilon }}_r(x)=\frac{\varepsilon _r(X)}{{\bar{\varepsilon }}_r},\quad x=\frac{X}{l},\quad h(x)=\frac{A(X)}{l^2},\\ D_k(x)&=\frac{{\mathcal {D}}_k(X)}{D_0},\quad Q(x)=\frac{{\mathcal {Q}}(X)}{C_0},\quad \phi (x)=\frac{e}{k_BT}\Phi (X),\quad c_k(x)=\frac{C_k(X)}{C_0},\\ {\hat{\mu }}_k&=\frac{\mu _k}{k_BT},\quad J_k=\frac{{\mathcal {J}}_k}{lC_0D_0}. \end{aligned} \end{aligned}$$

(1.3)

In terms of the new variables, BVP (1.1)–(1.2) becomes, for $k=1,2,\dots , n,$

$$\begin{aligned}&\frac{\varepsilon ^2}{h(x)}\frac{d}{dx}\left( {\hat{\varepsilon }}_r(x)h(x)\frac{d}{dx}\phi \right) =-\sum _{s=1}^n z_sc_s-Q(x),\nonumber \\&\quad \frac{dJ_k}{dx}=0,\quad -J_k=h(x)D_k(x)c_k\frac{d}{dx}{\hat{\mu }}_k \end{aligned}$$

(1.4)

with the following boundary conditions

$$\begin{aligned} \phi (0)=V=\frac{e}{k_BT}{\mathcal {V}},\quad c_k(0)=L_k=\frac{{{{\mathcal {L}}}}_k}{C_0};\quad \phi (1)=0,\quad c_k(1)=R_k=\frac{{{{\mathcal {R}}}}_k}{C_0}. \end{aligned}$$

(1.5)

Very often, the following so-called electroneutrality boundary concentration conditions are imposed to eliminate sharp boundary layers

$$\begin{aligned} \sum _{s=1}^nz_sL_s=\sum _{s=1}^nz_sR_s=0. \end{aligned}$$

(1.6)

For given $V,\ Q(x), L_k'$s and $R_k'$s, if $(\phi (x;\varepsilon ),\ c_k(x;\varepsilon ),\ J_k(\varepsilon ) )$ is a solution of the boundary value problem (1.4)–(1.5), then, the steady rate of flow of charge through a cross-section or current ${\mathcal {I}}$ is

$$\begin{aligned} {\mathcal {I}}={\mathcal {I}}(\varepsilon )=\sum _{s=1}^nz_sJ_s(\varepsilon ). \end{aligned}$$

(1.7)

Our focus will be on the zeroth order approximation (in $\varepsilon$) of $I={\mathcal {I}}(0)$ and $J_k=J_k(0)$. Notice that $J_k$ depends on $V,\ Q(x),\ L_k$’s and $R_k$’s, so does I.

1.2 Excess Potential and a Local Hard-Sphere Model

The electrochemical potential ${\hat{\mu }}_i(x)$ for the ith ion species consists of two components, more precisely, the ideal component $\mu _i^{id}(x)$, and the excess component $\mu _i^{ex}(x)$:

$$\begin{aligned} {\hat{\mu }}_i(x)=\mu _i^{id}(x)+\mu _i^{ex}(x) \end{aligned}$$

with

$$\begin{aligned} \frac{1}{k_BT}\mu _i^{id}(x)=z_i\phi (x)+\ln c_i(x). \end{aligned}$$

(1.8)

We emphasize that the ideal component $\mu _i^{id}(x)$ reflects the interaction between ion particles and the water molecules. The PNP system that just includes the ideal component is the so-called classical PNP (cPNP). The cPNP is the simplest PNP model, which has been studied extensively [6, 22, 36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] and the reference therein. But, many extremely important properties of ion channels, such as selectivity, rely on finite ion sizes critically, especially for those that have the same ion valence but distinct ion size (for example, Na$^{+}$ and K$^+$ ). To examine the effects on ionic flows from the finite ion size, we need to consider ion-specific components of the electrochemical potential in the PNP models. One natural but reasonable way is to have Hard-Sphere (HS) potential models of the excess electrochemical potential. There exist two types of models for hard-sphere potentials: local and nonlocal. Local hard-sphere potential models depends pointwise on ion concentrations while nonlocal hard-sphere models are defined as functionals of ion concentrations (see [17, 54, 55] for more discussions). The PNP type models with finite ion sizes have been studied both computationally and analytically for membrane channels, and have shown great success (see [10, 17, 33, 34, 56,57,58,59,60,61,62,63,64,65,66,67,68,69,70] for example).

In this work, we will take the following local hard-sphere model for $\mu _i^{ex}(X)$ [71]

$$\begin{aligned} \frac{1}{k_BT}\mu _i^{Bik}(x)= -\ln \left( 1-\sum _{j=1}^{n}\nu _jc_j(x)\right) , \end{aligned}$$

(1.9)

where $\nu _i$ is the volume of the ith ion species. We point out that only the Molecular Mean Field treatment led by the authors in [72, 73] includes water as a molecule of defined diameter and also deals successfully with the measurements of activity (i.e., free energy per mole, or chemical potential) of a wide range of ionic solutions including mixtures, in the view of experimentalists.

1.3 Zero-Current Ionic Flows and Reversal Potentials

The zero-current state of ionic flows through membrane channel, a special state among the range of the value for ionic current, is defined to be the moment that there is no net current within a channel. The corresponding membrane potential at zero-current state is called a reversal potential (see [15, 62] for more detailed discussion). The study on zero-current ionic flows is significant for physiology, because one is able to determine which ion species can permeate a particular channel by manipulating ion concentrations from the boundary and determining how the zero-current potential changes, from which the biologists and physiologists are able to identify the selectivity of a specific ion channel [15, 64].

Nernst was one of the first who studied reversal potentials. Specifically, for one charged particle case, he formulated an equation, which now is the Nernst equation for the reversal potential. It then follows a treatment of Mott for electronic conduction in the copper-copper oxide rectifier [46], the Nernst equation was further generalized by Goldman [62], and Hodgkin and Katz [15], the so-called Goldman-Hodgkin-Katz (GHK) equation for reversal potentials involving multiple charged particles.

Recently, in [14], the authors analyzed the cPNP system with nonzero permanent charges, and focused on the existence of reversal potentials and reversal permanent charges that are defined through zero total current for a degenerate case (the two ion species involved in the model have the same diffusion coefficients). Later, in [21], the author extended the work done in [14] to consider the cPNP system with nonuniform diffusion coefficients. The dependence of reversal potentials on channel geometry and diffusion coefficients is mathematically analyzed, which provides rich information of the internal dynamics of ionic flows. In [44], the authors further examine the diffusion coefficients and permanent charge effects on reversal potentials based on the work done in [21], which provides more intuitive illustrations of some analytical results.

However, in [14, 21, 44], the authors ignored the ion sizes. As discussed in Sect. 1.2, the finite ion size plays critical roles in the study of ionic flow properties, particularly, the selectivity phenomena for cations having the same ion valences but distinct finite ion sizes. For this, we include Bikerman’s local hard-sphere electrochemical potential model (1.9) in our PNP system to account for finite ion size effects.

1.4 Electroneutrality Boundary Concentration Conditions Versus Boundary Layers

In the study of ion channel problem, the conditions (1.6) are, in general, enforced at both ends of the channel (see, e.g., [16,17,18,19, 39, 50, 57, 68]). This reduces the difficulty a lot in mathematical analysis of qualitative properties of the system due to the disappearance of the boundary layers (see, e.g., [16, 17, 37, 57, 65]). To examine the boundary layer effects on ionic flows, it is natural to remove the neutral conditions. On the other hand, if those boundary layers reach into the part of the device performing atomic control, they dramatically affect its behavior. Boundary layers of charge are particularly likely to create artifacts over long distances because the electric field spreads a long way [13]. Correspondingly, to get started, we consider the state that is not neutral but close to, which is more realistic in the study of ion channel problems (for this setup, the boundary layers appear). Mathematically, we introduce positive parameters $\sigma$ and $\rho$, and assume

$$\begin{aligned} \left( \sum _{j=1}^kz_jL_j\right) \sigma =- \sum _{j=k+1}^nz_jL_j\ \text{ and }\ \left( \sum _{j=1}^kz_jR_j\right) \rho =-\sum _{j=k+1}^nz_jR_j, \end{aligned}$$

(1.10)

where $z_j>0,\ j=1,2,\cdots , k$ and $z_j<0,\ j=k+1,\cdots , n.$ We are interested in the case when $(\sigma ,\rho )\rightarrow (1,1)$ while $(\sigma ,\rho )=(1,1)$ implies neutral conditions. This is what we did in [51] for the case with $k=1$ and $n=2$ and in [24] for the case with $k=2$ and $n=3$. Compared to previous works under electroneutrality conditions, more rich dynamics are observed. However, in these works, the finite ion size effect is not included, while it is one of our main focuses in current work.

1.5 Problem Setup

We will take the following setting through the rest of the work:

• (A1) We consider two ion species ($n=2$) with $z_1>0$ and $z_2<0$.

• (A2) The permanent charge is set to be zero: $Q(x)=0$.

• (A3) For the electrochemical potential $\mu _i$, we include both the ideal component $\mu _i^{id}$ in (1.8) and the Bikerman’s local hard-sphere potential $\mu _i^{Bik}$ in (1.9).

• (A4) ${\hat{\varepsilon }}_r(x)=1$, $D_i(x)=D_i$ are positive constants, for $i=1,2$.

Under assumptions (A1)–(A4), the boundary value problem (1.4)–(1.5) now reads

$$\begin{aligned} \begin{aligned} \frac{\varepsilon ^2}{h(x)}&\frac{d}{dx}\left( h(x)\frac{d\phi }{dx}\right) =-z_1 c_1-z_2 c_2, \quad \frac{d J_1}{dx}=\frac{d J_2}{dx}=0,\\ \frac{dc_1}{dx}&=-f_1(c_1,c_2;\nu _1,\nu _2)\frac{d\phi }{dx}- \frac{1}{h(x)}g_1\big (c_1,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big ),\\ \frac{dc_2}{dx}&=f_2(c_1,c_2;\nu _1,\nu _2)\frac{d\phi }{dx}- \frac{1}{h(x)}g_2\big (c_2,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big ), \end{aligned} \end{aligned}$$

(1.11)

where

$$\begin{aligned} \begin{aligned} f_1(c_1,c_2; \nu _1,\nu _2)&=(z_1-z_1\nu _1c_1-z_2\nu _2c_2)c_1,\\ f_2(c_1,c_2; \nu _1,\nu _2)&=-(z_2-z_1\nu _1c_1-z_2\nu _2c_2)c_2,\\ g_1\big (c_1,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big )&=\frac{J_1}{D_1}-\left( \nu _1\frac{J_1}{D_1}+\nu _2\frac{J_2}{D_2}\right) c_1,\\ g_2\big (c_2,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big )&=\frac{J_2}{D_2}-\left( \nu _1\frac{J_1}{D_1}+\nu _2\frac{J_2}{D_2}\right) c_2. \end{aligned}\nonumber \\ \end{aligned}$$

Its boundary conditions are, for $i=1,2$,

$$\begin{aligned} \phi (0)=V,\; c_i(0)=L_i; \; \phi (1)=0,\; c_i(1)=R_i. \end{aligned}$$

(1.12)

The rest of the paper is organized as follows. In Sect. 2, under the framework of geometric singular perturbation analysis, we establish the existence and local uniqueness of the solution of the boundary value problem. Meanwhile, noting that the singular orbit of the problem depends regularly on $\nu = \nu _1>0$ small, the diameter of the cation, a regular perturbation analysis is carried out for the singular orbit. Correspondingly, an approximation (in the diameter $\nu$ up to the first order) of the zero-current ionic flow is derived, which allows us to further examine the effects on the zero-current ionic flows from different system parameters, such as finite ion sizes and diffusion coefficients, which is discussed in detail in Sect. 3. In Sect. 4, some concluding remarks are provided. Some proofs are provided in Sect. 5.

2 Dynamical System Framework for (1.11)–(1.12) with Boundary Layers

To get started, we write the system (1.11) as a standard form of a singularly perturbed system. Upon introducing $u=\varepsilon {\dot{\phi }}$ and $\tau =x$, and denoting the derivative with respect to x by overdot, the system (1.11) becomes:

$$\begin{aligned} \begin{aligned} \varepsilon {\dot{\phi }}&=u,\quad \varepsilon {\dot{u}}=-z_1 c_1-z_2 c_2-\varepsilon \frac{h_{\tau }(\tau )}{h(\tau )}u, \\ \varepsilon {\dot{c}}_1&=-f_1(c_1,c_2; \nu _1,\nu _2)u-\frac{\varepsilon }{h(\tau )}g_1\big (c_1,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big ),\\ \varepsilon {\dot{c}}_2&=f_2(c_1,c_2; \nu _1,\nu _2)u-\frac{\varepsilon }{h(\tau )}g_2\big (c_2,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big ),\\ \dot{J}_1=&\dot{J}_2=0,\quad {\dot{\tau }}=1. \end{aligned}\nonumber \\ \end{aligned}$$

(2.1)

System (2.1) is a singularly perturbed system with the singular parameter $\varepsilon$, its phase space is ${\mathbb {R}}^7$ with state variables $(\phi , u, c_1, c_2, J_1, J_2, \tau )$.

For $\varepsilon >0$, the rescaling $x=\varepsilon \xi$ of the independent variable x gives rise to the equivalent fast system,

$$\begin{aligned} \begin{aligned} \phi '&=u,\quad u'=-z_1 c_1-z_2 c_2-\varepsilon \frac{h_{\tau }(\tau )}{h(\tau )}u, \\ c_1'&=-f_1(c_1,c_2; \nu _1,\nu _2)u-\frac{\varepsilon }{h(\tau )}g_1\big (c_1,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big ),\\ c_2'&=f_2(c_1,c_2; \nu _1,\nu _2)u-\frac{\varepsilon }{h(\tau )}g_2\big (c_2,J_1/D_1,J_2/D_2;\nu _1,\nu _2\big ),\\ J'_1&=J'_2=0,\quad \tau '=\varepsilon , \end{aligned}\nonumber \\ \end{aligned}$$

(2.2)

where prime denotes the derivative with respect to the variable $\xi$.

Remark 2.1

For $\varepsilon >0$, the systems (2.1) and (2.2) have exactly the same phase portrait. However, their limiting systems at $\varepsilon =0$ are different. The limiting system of (2.1) is called the limiting slow system, whose orbits are called slow orbits or regular layers. The limiting system of (2.2) is called the limiting fast system, whose orbits are called fast orbits or singular (boundary and/or internal) layers. By a singular orbit of the system (2.1) or (2.2), we mean a continuous and piecewise smooth curve in ${\mathbb {R}}^7$ that is a union of finitely many slow and fast orbits. Very often, limiting slow and fast systems provide complimentary information on state variables. Therefore, the main task of singularly perturbed problems is to patch the limiting information together to form a solution for the entire $\varepsilon >0$ system.

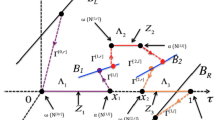
Let $B_L$ and $B_R$ be the subsets of the phase space ${\mathbb {R}}^7$ defined by

$$\begin{aligned} \begin{aligned} B_L&=\left\{ (V, u, L_1, L_2, J_1, J_2, 0)\in {\mathbb {R}}^7: \text {arbitrary}\ u, J_1, J_2 \right\} ,\\ B_R&=\left\{ (0, u, R_1, R_2, J_1, J_2, 1)\in {\mathbb {R}}^7: \text {arbitrary}\ u, J_1, J_2 \right\} , \end{aligned} \end{aligned}$$

(2.3)

where V, $L_1$, $L_2$, $R_1$ and $R_2$ are given in (1.12).

The boundary value problem (1.11) and (1.12) is equivalent to an equivalent connection problem, that is, finding an orbit of (2.1) or (2.2) from $B_L$ to $B_R$.

2.1 Limiting Fast Dynamics and Boundary Layers at $x=0$ and $x=1$

First, we let $\varepsilon \rightarrow 0$ in (2.1) and obtain the so-called slow manifold

$$\begin{aligned} {\mathcal {Z}}=\left\{ u=0, \;z_1 c_1+z_2 c_2=0 \right\} . \end{aligned}$$

(2.4)

Setting $\varepsilon =0$ in (2.2) leads to the limiting fast system,

$$\begin{aligned} \phi '&=u,\quad u'=-z_1 c_1-z_2 c_2, \nonumber \\ c_1'&=-f_1(c_1,c_2; \nu _1,\nu _2)u,\quad c_2'=f_2(c_1,c_2; \nu _1,\nu _2)u, \nonumber \\ J'_1&=J'_2=0,\quad \tau '=0. \end{aligned}$$

(2.5)

We point out that the slow manifold ${\mathcal {Z}}$ is precisely the set of equilibria of the system (2.5), and the dimension of ${\mathcal {Z}}$ is five. By linearizing the system (2.5) at each point in ${\mathcal {Z}}$, one obtains that there are five zero eigenvalues associated to the tangent space of ${\mathcal {Z}}$ and the other two eigenvalues are $\pm \sqrt{z_1^2c_1+z_2^2c_2}$ under the restriction that $c_k$’s are positive. Thus, the slow manifold ${\mathcal {Z}}$ is normally hyperbolic [74]. From the theory of normally hyperbolic invariant manifolds [74], there are six-dimensional stable manifold $W^s({\mathcal {Z}})$ of ${\mathcal {Z}}$ consisting of points approaching ${\mathcal {Z}}$ in forward time, and six-dimensional unstable manifold $W^u({\mathcal {Z}})$ of ${\mathcal {Z}}$ consisting of points approaching ${\mathcal {Z}}$ in backward time.

Let $M_L$ (resp. $M_R$) be the collection of orbits from $B_L$ (resp. $B_R$) in forward (resp. backward) time under the flow of the system (2.5). Then, for a singular orbit connecting $B_L$ and $B_R$, the boundary layer $\Gamma ^0$ must lie in $N_L=M_L\cap W^s({\mathcal {Z}})$ and the boundary layer $\Gamma ^1$ must lie in $N_R=M_R\cap W^u({\mathcal {Z}})$. We first study the limiting fast system (2.5) to understand the two boundary layers and the resulting two landing points $\omega (N_L)$ and $\alpha (N_R)$

Recall that our interest is in the effects on zero-current ionic flows from finite ion size. For small $\nu _1>0$ and $\nu _2>0$, the volumes of ion species, we treat the system (2.5) as a regular perturbation of that with $\nu _1=\nu _2=0$. For convenience, we let

$$\begin{aligned} \nu _1=\nu \ \text{ and }\ \nu _2=\lambda \nu , \end{aligned}$$

(2.6)

where the parameter $\lambda$ is positive, and seek solutions

$$\begin{aligned} \Gamma (\xi ;\nu )=(\phi (\xi ;\nu ), u(\xi ;\nu ), c_1(\xi ;\nu ), c_2(\xi ,\nu ), J_1(\nu ), J_2(\nu ), \tau ) \end{aligned}$$

of the system (2.5) of the form with $i=1,2$

$$\begin{aligned} \begin{aligned} \phi (\xi ;\nu )&=\phi _0(\xi )+\nu \phi _1(\xi )+o(\nu ),\quad u(\xi ,\nu )=u_0(\xi )+\nu u_1(\xi )+o(\nu ),\\ c_i(\xi ,\nu )&=c_{i0}(\xi )+\nu c_{i1}(\xi )+o(\nu ),\quad J_i(\nu )=J_{i0}+\nu J_{i1}+o(\nu ). \end{aligned} \end{aligned}$$

(2.7)

We substitute (2.7) into the system (2.5) and obtain, after careful calculation,

• The zeroth order limiting fast system in $\nu$

  $$\begin{aligned} \begin{aligned} \phi _0'&=u_0,\quad u_0'=-z_1c_{10}-z_2c_{20},\quad c_{10}'=-z_1c_{10}u_0,\quad c_{20}'=-z_2c_{20}u_0,\\ J_{10}'&=J_{20}'=0.\quad \tau '=0. \end{aligned} \end{aligned}$$

  (2.8)

• The first order limiting fast system in $\nu$

  $$\begin{aligned} \phi _1'&=u_1,\quad u_1'=-z_1c_{11}-z_2c_{21},\nonumber \\ c_{11}'&=-z_1u_0c_{11}-z_1c_{10}u_1+(z_1c_{10}+\lambda z_2c_{20})c_{10}u_0,\nonumber \\ c_{21}'&=-z_2u_0c_{21}-z_2c_{20}u_1+(z_1c_{10}+\lambda z_2c_{20})c_{20}u_0,\nonumber \\ J_{11}'&=J_{21}'=0,\quad \tau '=0. \end{aligned}$$

  (2.9)

For the system (2.8) and the system (2.9), one has the following result, which characterizes the boundary layers and the landing points.

Proposition 2.2

Assume that $\nu \ge 0$ is small. Under the condition (1.10) with $k=1$ and $n=2$, that is, $-z_2L_2=(z_1L_1)\sigma$ and $-z_2R_2=(z_1R_1)\rho$, one has

• (i) The zeroth order limiting fast system has three nontrivial first integrals

  $$\begin{aligned} H_1=\ln c_{10}+z_1\phi _0,\quad H_2=\ln c_{20}+z_2\phi _0,\quad H_3=\frac{u_0^2}{2}-c_{10}-c_{20}. \end{aligned}$$

  The first order limiting fast system has three nontrivial first integrals

  $$\begin{aligned} G_1=&\,z_1\phi _1+\frac{c_{11}}{c_{10}}+c_{10}+\lambda c_{20},\\ G_2=&\,z_2\phi _1+\frac{c_{21}}{c_{20}}+ c_{10}+\lambda c_{20},\\ G_3=&\,u_0u_1-c_{11}-c_{21}-\frac{\lambda }{2}c_{20}^2-\frac{1}{2}c_{10}^2-c_{10}c_{20}+\frac{z_2(1-\lambda )}{z_1+z_2}e^{(z_1+z_2)(V-\phi _0)}. \end{aligned}$$

• (ii) The stable manifold $W^s({\mathcal {Z}})$ intersects $B_L$ transversally at points

  $$\begin{aligned} \big (V, u^l_0+u^l_1\nu +o(\nu ), L_1, L_2, J_1(\nu ), J_2(\nu ), 0\big ), \end{aligned}$$

  and the $\omega$-limit set of $N_L=M_L\cap W^s({\mathcal {Z}})$ is

  $$\begin{aligned} \omega (N_L)=\left\{ \big (\phi _0^L+\phi _1^L\nu +o(\nu ), 0, c^L_{i0}+c^L_{i1}\nu +o(\nu ), J_1(\nu ), J_2(\nu ), 0\big )\right\} , \end{aligned}$$

  where $J_i(\nu )=J_{i0}+J_{i1}\nu +o(\nu )$, $i=1,2,$ can be arbitrary, and

  $$\begin{aligned}&\phi _0^L=V-\frac{1}{z_1-z_2}\ln \sigma ,\quad z_1c_{10}^L=-z_2c_{20}^L=(z_1L_1)\sigma ^{\frac{z_1}{z_1-z_2}},\\&u_0^l=sgn(\phi _0^L-V)\sqrt{2\left( L_1+L_2+\frac{z_1-z_2}{z_1z_2}(z_1L_1)\sigma ^{\frac{z_1}{z_1-z_2}}\right) };\\&\phi _1^L=0, \quad z_1c_{11}^L=-z_2c_{21}^L=z_1c_{10}^L(L_1+\lambda L_2-c_{10}^L-\lambda c_{20}^L),\\&u_1^l=\frac{1}{u_0^l}\left( \frac{\lambda }{2}\left( L_2^2-(c_{20}^L)^2 \right) +\frac{1}{2}\left( L_1^2-(c_{10}^L)^2 \right) -c_{10}^Lc_{20}^L-c_{11}^L-c_{21}^L\right. \\&\quad \quad \quad \left. -\frac{z_2(1-\lambda )}{z_1+z_2}e^{(z_1+z_2)(V-\phi _0^L)}\right) . \end{aligned}$$

• (iii) The unstable manifold $W^u({\mathcal {Z}})$ intersects $B_R$ transversally at points

  $$\begin{aligned} \left( 0, u^r_0+u^r_1\nu +o(\nu ), R_1, R_2, J_1(\nu ), J_2(\nu ), 1 \right) , \end{aligned}$$

  and the $\alpha$-limit set of $N_R=M_R\cap W^u({\mathcal {Z}})$ is

  $$\begin{aligned} \alpha (N_R)=\left\{ \left( \phi _0^R+\phi _1^R\nu +o(\nu ), 0, c^R_{i0}+c^R_{i1}\nu +o(\nu ), J_i(\nu ), 1 \right) \right\} , \end{aligned}$$

  where $J_i(\nu )=J_{i0}+J_{i1}\nu +o(\nu )$, $i=1,2,$ can be arbitrary, and

  $$\begin{aligned}&\phi _0^R=-\frac{1}{z_1-z_2}\ln \rho , \quad z_1c_{10}^R=-z_2c_{20}^R=(z_1R_1)\rho ^{\frac{z_1}{z_1-z_2}},\\&u_0^r=-sgn(\phi _0^R)\sqrt{2\left( R_1+R_2+\frac{z_1-z_2}{z_1z_2}(z_1R_1)\rho ^{\frac{z_1}{z_1-z_2}}\right) };\\&\phi _1^R=0, \quad z_1c_{11}^R=-z_2c_{21}^R=z_1c_{10}^R(R_1+\lambda R_2-c_{10}^R-\lambda c_{20}^R),\\&u_1^r=\frac{1}{u_0^r}\left( \frac{\lambda }{2}(R_2^2-(c_{20}^R)^2)+\frac{1}{2}(R_1^2-(c_{10}^R)^2)-c_{10}^Rc_{20}^R-c_{11}^R-c_{21}^R\right. \\&\quad \quad \quad \left. -\frac{z_2(1-\lambda )}{z_1+z_2}e^{-(z_1+z_2)\phi _0^R}\right) . \end{aligned}$$

Proof

We defer the proof to the appendix Sect. 5. $\square$

Remark 2.3

We point out that in Proposition 2.2, the boundary layers are introduced due to the violation of electroneutrality boundary conditions, which is more realistic in the study of ion channel problems. To be specific, if the neutral conditions are enforced at both ends of ion channel, one has $\phi _0^L=V,\ c_{10}^L=L_1,\ c_{20}^L=L_2;\ \phi _0^R=0,\ c_{10}^R=R_1$ and $c_{20}^R=R_2$. In other words, $B_L$ and $B_r$ will totally stay in the slow manifold ${\mathcal {Z}}$, and the boundary layers disappear. To examine the effects on ionic flows from the boundary layers, naturally, one need to relax the neutral conditions.

2.2 Limiting Slow Dynamics and Regular Layer Over (0, 1)

Our focus in this section is to construct the slow orbit $\Lambda$ on the slow manifold ${\mathcal {Z}}$ connecting the two landing points $\omega (N_L)$ and $\alpha (N_R)$ identified in the Proposition 2.2. Note that as $\varepsilon \rightarrow 0$, the system (2.1) loses most information. To remedy this degeneracy, we follow the idea in [13, 18, 19] and make a rescaling $u=\varepsilon p$ and $-z_2c_2=z_1c_1+\varepsilon q$ in system (2.1). In terms of new variables p and q, system (2.1) becomes

$$\begin{aligned} \begin{aligned} {\dot{\phi }}&=p,\quad \varepsilon {\dot{p}}=q-\varepsilon \frac{h_{\tau }(\tau )}{h(\tau )}p,\quad \varepsilon {\dot{q}}=(z_1f_1-z_2f_2)p+\frac{z_1 g_1 +z_2 g_2}{h(\tau )} ,\\ {\dot{c}}_1&=-f_1p-\frac{g_1}{h(\tau )},\quad {\dot{J}}_1={\dot{J}}_2=0,\quad {\dot{\tau }}=1 \end{aligned} \end{aligned}$$

(2.10)

where, for $i=1,2,$

$$\begin{aligned}&f_i=f_i\left( c_1, -\frac{z_1c_1+\varepsilon q}{z_2}; \nu , \lambda \nu \right) ,\\&g_1=g_1\big (c_1, J_1/D_1, J_2/D_2; \nu , \lambda \nu \big ), \\&g_2=g_2\left( -\frac{z_1c_1+\varepsilon q}{z_2}, J_1/D_1, J_2/D_2; \nu , \lambda \nu \right) . \end{aligned}$$

It is also a singular perturbation problem and its limiting slow system is

$$\begin{aligned} \begin{aligned} q&=0, \quad p=-\frac{z_1g_1+z_2g_2}{z_1(z_1-z_2)h(\tau )c_1},\quad {\dot{\phi }}=p,\\ {\dot{c}}_1&=-f_1\left( c_1, -\frac{z_1}{z_2}c_1; \nu , \lambda \nu \right) p-\frac{1}{h(\tau )}g_1\big (c_1, J_1/D_1, J_2/D_2; \nu , \lambda \nu \big ),\\ {\dot{J}}_1&={\dot{J}}_2=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

(2.11)

For system (2.11), the slow manifold is

$$\begin{aligned} {\mathcal {S}}=\bigg \{q=0, \; p=-\frac{z_1 g_1 +z_2 g_2}{z_1(z_1-z_2)h(\tau )c_1}\bigg \}. \end{aligned}$$

Correspondingly, the limiting slow system on ${\mathcal {S}}$ is

$$\begin{aligned} \begin{aligned} {\dot{\phi }}&=p,\quad {\dot{c}}_1= - f_1\left( c_1, -\frac{z_1}{z_2}c_1; \nu , \lambda \nu \right) p-\frac{g_1\big (c_1, J_1/D_1, J_2/D_2; \nu , \lambda \nu \big )}{h(\tau )},\\ {\dot{J}}_1&={\dot{J}}_2=0,\quad {\dot{\tau }}=1, \end{aligned} \end{aligned}$$

(2.12)

where $p=-\frac{z_1 g_1 +z_2 g_2}{z_1(z_1-z_2)h(\tau )c_1}.$

Similarly, for the system (2.12), we look for solutions of (2.12) of the form

$$\begin{aligned} \begin{aligned} \phi (x)&=\phi _0(x)+\phi _1(x)\nu +o(\nu ),\quad c_1(x)=c_{10}(x)+c_{11}(x)\nu +o(\nu ),\\ J_1&=J_{10}+J_{11}\nu +o(\nu ),\quad J_2=J_{20}+J_{21}\nu +o(\nu ), \end{aligned} \end{aligned}$$

(2.13)

which connect $\omega (N_L)$ and $\alpha (N_R)$ given in Proposition 2.2, particularly, for $j=0,1$,

$$\begin{aligned} \left( \phi _j(0), c_{1j}(0)\right) =\left( \phi _j^L, c_{1j}^{L}\right) , \quad \left( \phi _j(1), c_{1j}(1)\right) =\left( \phi _j^{R}, c_{1j}^{R}\right) . \end{aligned}$$

Substituting (2.13) into the system (2.12), we obtain

• The zeroth order limiting slow system in $\nu$:

  $$\begin{aligned} \begin{aligned} \dot{\phi _0}&=-\frac{1}{z_1(z_1-z_2)c_{10}h(\tau )}\left( \frac{z_1J_{10}}{D_1}+\frac{z_2J_{20}}{D_2}\right) ,\\ {\dot{c}}_{10}&=\frac{z_2}{(z_1-z_2)h(\tau )}\left( \frac{J_{10}}{D_1}+\frac{J_{20}}{D_2}\right) ,\quad {\dot{J}}_{10}={\dot{J}}_{20}=0,\quad {\dot{\tau }}=1, \end{aligned} \end{aligned}$$

  (2.14)

• The first order limiting slow system in $\nu$:

  $$\begin{aligned} \begin{aligned} \dot{\phi _1}&=\frac{c_{11}\big (\frac{z_1J_{10}}{D_1}+\frac{z_2J_{20}}{D_2}\big )}{z_1(z_1-z_2)c_{10}^2h(\tau )}-\frac{\frac{z_1J_{11}}{D_1}+\frac{z_2J_{21}}{D_2}}{z_1(z_1-z_2)c_{10}h(\tau )},\\ {\dot{c}}_{11}&=\frac{1}{(z_1-z_2)h(\tau )}\left[ (z_1\lambda -z_2)\left( \frac{J_{10}}{D_1}+\frac{J_{20}}{D_2}\right) c_{10}+z_2\left( \frac{J_{11}}{D_1}+\frac{J_{21}}{D_2}\right) \right] ,\\ {\dot{J}}_{11}&={\dot{J}}_{21}=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

  (2.15)

Recall that our main interest is the qualitative properties of ionic flows at zero-current state, that is (from (1.7)), for small $\nu >0$,

$$\begin{aligned} 0={\mathcal {I}}=&z_1J_1+z_2J_2=z_1J_{10}+z_2J_{20}+\nu (z_1J_{11}+z_2J_{21})+o(\nu ), \end{aligned}$$

which is equivalent to, for small $\nu >0$,

$$\begin{aligned} z_1J_{10}+z_2J_{20}=0\ \text{ and }\ z_1J_{11}+z_2J_{21}=0. \end{aligned}$$

(2.16)

Under the condition (2.16), the system (2.14) and the system (2.15) read

$$\begin{aligned} \begin{aligned} \dot{\phi _0}&=\frac{(D_1-D_2)J_{10}}{(z_1-z_2)D_1D_2c_{10}h(\tau )},\quad {\dot{c}}_{10}=-\frac{(z_1D_1-z_2D_2)J_{10}}{D_1D_2(z_1-z_2)h(\tau )},\\ {\dot{J}}_{10}&={\dot{J}}_{20}=0,\quad {\dot{\tau }}=1, \end{aligned} \end{aligned}$$

(2.17)

and

$$\begin{aligned} \begin{aligned} \dot{\phi _1}&=\frac{(D_2-D_1)J_{10}c_{11}}{(z_1-z_2)D_1D_2c_{10}^2h(\tau )}-\frac{(D_2-D_1)J_{11}}{(z_1-z_2)D_1D_2c_{10}h(\tau )},\\ {\dot{c}}_{11}&=\frac{(z_1\lambda -z_2)(z_2D_2-z_1D_1)J_{10}c_{10}}{z_2(z_1-z_2)D_1D_2h(\tau )}+\frac{(z_2D_2-z_1D_1)J_{11}}{(z_1-z_2)D_1D_2h(\tau )},\\ {\dot{J}}_{11}&={\dot{J}}_{21}=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

(2.18)

For simplicity, in our following discussion, we always assume $D_1\ne D_2$ and introduce

$$\begin{aligned} H(x)=\int _0^x\frac{1}{h(s)}ds. \end{aligned}$$

(2.19)

For the system (2.17), one has

Lemma 2.4

There is a unique solution $(\phi _0(x), c_{10}(x), J_{10}, \tau (x))$ of (2.17) such that

$$\begin{aligned} (\phi _0(0), c_{10}(0), \tau (0))=(\phi _0^L, c_{10}^L, 0)\quad \text {and} \quad (\phi _0(1), c_{10}(1), \tau (1))=(\phi _0^R, c_{10}^R, 1), \end{aligned}$$

where $\phi _0^L, c_{10}^L, \phi _0^R$ and $c_{10}^R$ are given in Proposition 2.2. It is given by

$$\begin{aligned} \begin{aligned} \phi _0(x)&=\phi _0^L-\frac{D_1-D_2}{z_1D_1-z_2D_2}\ln {\frac{c_{10}(x)}{c_{10}^L}},\\ c_{10}(x)&=c_{10}^L-\frac{(z_1D_1-z_2D_2)J_{10}}{D_1D_2(z_1-z_2)}H(x),\quad \tau (x)=x. \end{aligned} \end{aligned}$$

(2.20)

In particular, under the condition (1.10) with $k=1$ and $n=2$, that is, $-z_2L_2=(z_1L_1)\sigma$ and $-z_2R_2=(z_1R_1)\rho$,

$$\begin{aligned} \begin{aligned} J_{10}=\frac{D_1D_2(z_1-z_2)}{(z_1D_1-z_2D_2)H(1)}\left( L_1\sigma ^{\frac{z_1}{z_1-z_2}}-R_1\rho ^{\frac{z_1}{z_1-z_2}}\right) \end{aligned} \end{aligned}$$

(2.21)

under the restriction

$$\begin{aligned} V+\frac{\ln \rho -\ln \sigma }{z_1-z_2}=\frac{D_1-D_2}{z_1D_1-z_2D_2}\Big [\ln R_1-\ln L_1+\frac{z_1}{z_1-z_2}(\ln \rho -\ln \sigma )\Big ]. \end{aligned}$$

Or equivalently,

$$\begin{aligned} J_{10}&=\frac{D_1D_2(z_1-z_2)\big (L_1\sigma ^{\frac{z_1}{z_1-z_2}}-R_1\rho ^{\frac{z_1}{z_1-z_2}}\big )\big (V+\frac{1}{z_1-z_2}(\ln \rho -\ln \sigma )\big )}{(D_1-D_2)\big (\ln R_1-\ln L_1+\frac{z_1}{z_1-z_2}(\ln \rho -\ln \sigma )\big )H(1)}. \end{aligned}$$

Proof

We defer the proof to the appendix Sect. 5.$\square$

For the system (2.18), the following result can be established.

Lemma 2.5

There is a unique solution $(\phi _1(x), c_{11}(x), J_{11}, \tau (x))$ of (2.18) such that

$$\begin{aligned} (\phi _1(0), c_{11}(0), \tau (0))=(\phi _1^L, c_{11}^L, 0)\quad \text {and} \quad (\phi _1(1), c_{11}(1), \tau (1))=(\phi _1^R, c_{11}^R, 1), \end{aligned}$$

where $\phi _1^L, c_{11}^L, \phi _1^R$ and $c_{11}^R$ are given in Proposition 2.2. It is given by

$$\begin{aligned} \phi _1(x)&=\phi _1^L+\frac{D_2-D_1}{z_1D_1-z_2D_2}\left( \frac{c_{11}(x)}{c_{10}(x)}-\frac{c_{11}^L}{c_{10}^L}\right) +\frac{(D_2-D_1)(z_1\lambda -z_2)J_{10}}{z_2(z_1-z_2)D_1D_2}H(x),\\ c_{11}(x)&=c_{11}^L+\frac{z_1\lambda -z_2}{2z_2}(c_{10}^2(x)-(c_{10}^L)^2)+\frac{(z_2D_2-z_1D_1)J_{11}}{D_1D_2(z_1-z_2)}H(x). \end{aligned}$$

In particular, under the condition (1.10) with $k=1$ and $n=2$, that is, $-z_2L_2=(z_1L_1)\sigma$ and $-z_2R_2=(z_1R_1)\rho$,

$$\begin{aligned} J_{11}&=J_{10}\left( \frac{c_{11}^L-c_{11}^R}{c_{10}^L-c_{10}^R}-\frac{z_1\lambda -z_2}{2z_2}(c_{10}^L+c_{10}^R)\right) \\&=J_{10}\bigg [\frac{L_1^2\sigma ^{\frac{z_1}{z_1-z_2}}\big (1-\frac{z_1\lambda }{z_2}\sigma \big )-R_1^2\rho ^{\frac{z_1}{z_1-z_2}}\big (1-\frac{z_1\lambda }{z_2}\rho \big )+\frac{z_1\lambda }{z_2}\big (L_1^2\sigma ^{\frac{2z_1}{z_1-z_2}}-R_1^2\rho ^{\frac{2z_1}{z_1-z_2}}\big )}{L_1\sigma ^{\frac{z_1}{z_1-z_2}}-R_1\rho ^{\frac{z_1}{z_1-z_2}}}\\&\qquad -\frac{z_1\lambda +z_2}{2z_2}\left( L_1\sigma ^{\frac{z_1}{z_1-z_2}}+R_1\rho ^{\frac{z_1}{z_1-z_2}}\right) \bigg ] \end{aligned}$$

under the restriction

$$\begin{aligned} \lambda =\frac{z_2(L_1-R_1)}{z_1(\sigma L_1-\rho R_1)}. \end{aligned}$$

Or equivalently,

$$\begin{aligned} \begin{aligned} J_{11}&=J_{10}\bigg [\frac{(\sigma -\rho )L_1R_1}{\sigma L_1-\rho R_1}+\frac{(1-\sigma )L_1-(1-\rho )R_1}{2(\sigma L_1-\rho R_1)}\left( L_1\sigma ^{\frac{z_1}{z_1-z_2}}+R_1\rho ^{\frac{z_1}{z_1-z_2}}\right) \bigg ]. \end{aligned} \end{aligned}$$

(2.22)

Proof

We defer the proof to the appendix Sect. 5. $\square$

The slow orbit, up to $O(\nu )$,

$$\begin{aligned} \Lambda (x;\nu )=\big (\phi _0(x)+\phi _1(x)\nu , c_{10}(x)+c_{11}(x)\nu , J_{10}+J_{11}\nu , J_{20}+J_{21}\nu , \tau (x)\big ) \end{aligned}$$

(2.23)

given in Lemmas 2.4 and 2.5 connects $\omega (N_L)$ and $\alpha (N_R)$. Let ${\bar{M}}_L$ (resp. ${\bar{M}}_R$) be the forward (resp. backward) image of $\omega (N_L)$ (resp. $\alpha (N_R)$) under the slow flow (2.12) on the five-dimensional slow manifold ${\mathcal {S}}$. The following result can be established.

Proposition 2.6

There exists $\nu _0>0$ small depending on boundary conditions so that, if $0\le \nu \le \nu _0$, then, on the five-dimensional slow manifold ${\mathcal {S}}$, ${\bar{M}}_L$ and ${\bar{M}}_R$ intersects transversally along the unique orbit $\Lambda (x;\nu )$ given in (2.23).

Proof

To see the transversality of the intersection, one may verify that $\omega (N_L)\cdot 1$, the image of $\omega (N_L)$ under the time-one map of the flow of the system (2.12), is transversal to $\alpha (N_R)$ on ${\mathcal {S}}\cap \{\tau =1\}$ for $\nu =0$. For this step, readers may refer to the detailed proof of Proposition 2.3 in the reference [18]. Once this is proved, from the smooth dependence of solutions on the parameter $\nu$, one concludes that there exists $\nu _0>0$ small, such that, if $0\le \nu \le \nu _0,$ then, $\omega (N_L)\cdot 1$ and $\alpha (N_R)$ intersect transversally on ${\mathcal {S}}\cap \{\tau =1\}.$ This completes the proof. $\square$

2.3 Existence of Solutions Near the Singular Orbit

From Sects. 2.1 and 2.2, we have constructed a unique singular orbit on [0,1] that connects $B_L$ to $B_R$. It consists of two boundary layer orbits $\Gamma ^0$ from the point

$$\begin{aligned} \left( V, u_0^l+u_1^l\nu +o(\nu ), L_1, L_2, J_{10}+J_{11}\nu +o(\nu ), J_{20}+J_{21}\nu +o(\nu ), 0 \right) \in B_L \end{aligned}$$

to the point

$$\begin{aligned} \left( \phi ^L, 0, c_1^L, c_2^L, J_1, J_2, 0 \right) \in \omega (N_L) \subseteq {\mathcal {Z}} \end{aligned}$$

and $\Gamma ^1$ from the point

$$\begin{aligned} \left( \phi ^R, 0, c_1^R, c_2^R, J_1, J_2, 1 \right) \in \alpha (N_R) \subseteq {\mathcal {Z}} \end{aligned}$$

to the point

$$\begin{aligned} \left( 0,u_0^r+u_1^r\nu +o(\nu ), R_1, R_2, J_{10}+J_{11}\nu +o(\nu ), J_{20}+J_{21}\nu +o(\nu ), 1 \right) \in B_R, \end{aligned}$$

and a regular layer $\Lambda$ on ${\mathcal {Z}}$ connecting the two landing points $(\phi ^L, 0, c_1^L, c_2^L, J_1, J_2, 0) \in \omega (N_L)$ and $(\phi ^R, 0, c_1^R, c_2^R, J_1, J_2, 1) \in \alpha (N_R)$ of the boundary layers.

We now focus on the existence of a solution of the system (1.11)–(1.12), which is close to the singular orbit constructed above. To be specific, it is a union of two boundary layers and one regular layer, that is, $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$. The proof of the result is similar to that in [13, 18, 19] and the main tool to be employed is the Exchange Lemma [75, 76] of the geometric singular perturbation theory.

Theorem 2.7

Let $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$ be the singular orbit of the connecting problem system (2.1) associated to $B_L$ and $B_R$ in (2.3). Then, for $\varepsilon >0$ small and $\nu >0$ small, the corresponding boundary value problem (1.11)–(1.12) has a unique smooth solution near the singular orbit $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$.

Proof

Let $\nu _0>0$ be as in Proposition 2.6. For $0\le \nu \le \nu _0$, define $u^l=u_0^l+u_1^l\nu ,$ $J_1(\nu )=J_{10}+J_{11}\nu$ and $J_2(\nu )=J_{20}+J_{21}\nu$. Fix $\delta >0$ small to be determined. Let

$$\begin{aligned} B_L(\delta )=\left\{ (V, u, L_1, L_2, J_1, J_2, 0)\in {\mathbb {R}}^7: |u-u^l|<\delta , |J_i-J_i(\nu )|<\delta \right\} , \end{aligned}$$

a neighborhood of $\Gamma ^0\cap B_L=\left\{ \left( V,u_0^l, L_1, L_2, J_1, J_2,0 \right) \right\}$ in $B_L$.

For $\varepsilon >0$, define $M^0(\varepsilon )$ to be the forward trace of $B_L(\delta )$ under the flow of the system (2.1). We will claim that $M^0(\varepsilon )$ and $B_R$ intersects transversally close to the point $\Gamma ^1\cap B_R=\{(0, u_0^r, R_1, R_2, J_1, J_2, 1)\}.$

As for the evolution of $M^0(\varepsilon )$, it will start near the point $(V, u_0^l, L_1, L_2, J_1, J_2, 0)$, follow the singular layer $\Gamma ^0$ to the slow manifold ${\mathcal {Z}}$, move along the regular layer $\Lambda$, and then leave the vicinity of ${\mathcal {Z}}$ along the singular layer $\Gamma ^1$ toward the point $(0, u_0^r, R_1, R_2, J_1, J_2, 1)\in B_R.$

The exchange lemma [75, 76], etc is applied along the stage described above to track the evolution. It indicates that, near $\Gamma ^1$, $M^0(\varepsilon )$ is $C^1 O(\varepsilon )$-close to $W^u(\alpha (N_R)\cdot (-\rho ,\rho ))$ for some $\rho >0$ independent of $\varepsilon$, if

• (i) $M^0(0)$ intersects $W^s({\mathcal {Z}})$ transversally along $\Gamma ^0$ established in Proposition 2.2;

• (ii) The vector field on ${\mathcal {Z}}$ is not tangent to $\omega (N_L)$ at $(\phi ^L, 0, c_{1}^L, c_{2}^L, J_{1}, J_{2}, 0)\in {\mathcal {Z}}$, which follows from ${\dot{\tau }}=1$ in (2.11).

Note that the latter is transversal to $B_R$ near the point $(0, u_0^r, R_1, R_2, J_1, J_2, 1).$ One has $M^0(\varepsilon )$ intersects $B_R$ transversally near $(0, u_0^r, R_1, R_2, J_1, J_2, 1).$ Note also that $\dim M^0(\varepsilon )=\dim B_L+1=4$ and $\dim B_R=3$. Correspondingly, $\dim (M^0(\varepsilon )\cap B_R)=\dim M^0(\varepsilon )+\dim B_R-7=0;$ that is, the intersection near $(0, u_0^r, R_1, R_2, J_1, J_2, 1),$ is a singleton. This completes the proof. $\square$

3 Qualitative Properties of Zero-Current Ionic Flows

In this section, we will examine the qualitative properties of the zero-current ionic flows through membrane channels from different directions, more precisely, we will study the effects on ionic flows from finite ion sizes and diffusion coefficients with boundary layers.

To get started, we comment that under zero-current state $I=z_1J_1+z_2J_2=0$, we have $J_1=-(z_2/z_1)J_2$, thereby, for convenience in our following study, we introduce $J^{zc}$ as $J^{zc}=J_1=-(z_2/z_1)J_2,$ and call it the zero-current ionic flow. Corresponding, one has $J_0^{zc}$ corresponding to $J_{10}$ in (2.21), the zeroth order in $\nu$ and $J_1^{zc}$ corresponding to $J_{11}$ in (2.22), the first order term in $\nu$.

On the other hand, as we discussed in the introduction, in this work, we will also consider the effects from the boundary layers due to the violation of the electroneutrality boundary conditions in terms of the two positive parameters $\sigma$ and $\rho$. More precisely, we will study the case as $(\sigma ,\rho )\rightarrow (1,1)$, a state that is not neutral but close to (recall that $(\sigma ,\rho )=(1,1)$ indicates electroneutrality condition). Mathematically, we view it as a regular perturbation to the neutral condition. We expand the zero-current ionic flow at $(\sigma ,\rho )=(1,1)$ up to the first order term and neglect higher order terms. To be specific, we rewrite $J^{zc}=J^{zc}(V;\nu ;\sigma ,\rho )$ as

$$\begin{aligned} J^{zc}&=J^{zc}(V;\nu ;1,1)+\frac{\partial J^{zc}}{\partial \sigma }(V;\nu ;1,1)(\sigma -1)+\frac{\partial J^{zc}}{\partial \rho }(V;\nu ;1,1)(\rho -1). \end{aligned}$$

(3.1)

3.1 Ion Size Effects on Zero-Current Ionic Flows

To examine the finite ion size effects on the zero-current ionic flow $J^{zc}$, we employ regular perturbation analysis and expand it along the small parameter $\nu$ at $\nu =0$. To be specific, from (3.1), one has

$$\begin{aligned} J^{zc}&=J_0^{zc}(V;0;1,1)+\frac{\partial J_0^{zc}}{\partial \sigma }(V;0;1,1)(\sigma -1)+\frac{\partial J_0^{zc}}{\partial \rho }(V;0;1,1)(\rho -1)\\&\quad +\nu \left( J_1^{zc}(V;0;1,1)+\frac{\partial J_1^{zc}}{\partial \sigma }(V;0;1,1)(\sigma -1)+\frac{\partial J_1^{zc}}{\partial \rho }(V;0;1,1)(\rho -1)\right) \\&\quad + o(\nu ), \end{aligned}$$

where, with $f_0(L_1,R_1)=\frac{L_1-R_1}{\ln L_1-\ln R_1},$

$$\begin{aligned} \begin{aligned} J_0^{zc}(V;0;1,1)&=\frac{D_1D_2(z_1-z_2)f_0(L_1,R_1)V}{(D_2-D_1)H(1)},\\ \frac{\partial J_0^{zc}}{\partial \sigma }(V;0;1,1)&=-\frac{D_1D_2}{(D_2-D_1)H(1)}\left( \frac{z_1\big (f_0(L_1,R_1)-L_1\big )V}{\ln L_1-\ln R_1}+f_0(L_1,R_1)\right) ,\\ \frac{\partial J_0^{zc}}{\partial \rho }(V;0;1,1)&=\frac{D_1D_2}{(D_2-D_1)H(1)}\left( \frac{z_1\big (f_0(L_1,R_1)-R_1\big )V}{\ln L_1-\ln R_1}+f_0(L_1,R_1)\right) ,\\ J_1^{zc}(V;0;1,1)=&\,0,\\ \frac{\partial J_1^{zc}}{\partial \sigma }(V;0;1,1)&=-\frac{D_1D_2(z_1-z_2)L_1f_0(L_1,R_1)}{2(D_2-D_1)H(1)}V,\\ \frac{\partial J_1^{zc}}{\partial \rho }(V;0;1,1)&=-\frac{D_1D_2(z_1-z_2)R_1f_0(L_1,R_1)}{2(D_2-D_1)H(1)}V. \end{aligned} \end{aligned}$$

(3.2)

For convenience, we introduce ${\bar{J}}_0^{zc}={\bar{J}}_0^{zc}(V;\sigma ,\rho )$ and ${\bar{J}}_1^{zc}={\bar{J}}_1^{zc}(V;\sigma ,\rho )$ defined as follows

$$\begin{aligned} \begin{aligned} {\bar{J}}_0^{zc}&=J_0^{zc}(V;0;1,1)+\frac{\partial J_0^{zc}}{\partial \sigma }(V;0;1,1)(\sigma -1)+\frac{\partial J_0^{zc}}{\partial \rho }(V;0;1,1)(\rho -1),\\ {\bar{J}}_1^{zc}&=J_1^{zc}(V;0;1,1)+\frac{\partial J_1^{zc}}{\partial \sigma }(V;0;1,1)(\sigma -1)+\frac{\partial J_1^{zc}}{\partial \rho }(V;0;1,1)(\rho -1). \end{aligned} \end{aligned}$$

(3.3)

Clearly, ${\bar{J}}_1^{zc}(V;\sigma ,\rho )$ is the leading term that contains finite ion size effects, and its our main interest in the following discussion.

Remark 3.1

We point out that for $(\sigma ,\rho )=(1,1)$ corresponding to the electroneutrality boundary conditions, the leading term ${\bar{J}}_1^{zc}$ vanishes, and the finite ion size effects on ionic flows crucial for the study of the selectivity property of ion channels cannot be characterized. This further indicates that it is necessary to relax the neutral conditions and consider the state close to neutral, a more realistic biological setup (see also [24, 51, 56] for more discussions related to boundary layers).

We first define two critical potentials $V_0^c$ and $V_1^c$, which are essential for our following discussion.

Definition 3.2

We define two critical potentials $V_0^c$ and $V_1^c$ by ${\bar{J}}_0^{zc}(V_0^c)=0$ and ${\bar{J}}_1^{zc}(V_1^c)=0.$ Particularly,

$$\begin{aligned} V_0^c=\frac{(\sigma -\rho )(\ln L_1-\ln R_1)(L_1-R_1)}{R_1f(L_1, R_1;\sigma ,\rho )}\ \text{ and }\ V_1^c=0, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} f(L_1,R_1;\sigma ,\rho )&=(z_1-z_2)\left( \frac{L_1}{R_1}-1\right) (\ln L_1-\ln R_1)+z_1\Big [(\sigma -1)\frac{L_1}{R_1}-(\rho -1)\Big ]\\&\quad \times (\ln L_1-\ln R_1)+z_1(\rho -\sigma )\left( \frac{L_1}{R_1}-1\right) . \end{aligned}\end{aligned}$$

(3.4)

For the function $f(L_1,R_1;\sigma ,\rho )$, the following result can be established.

Lemma 3.3

Assume $x=L_1/R_1>1$ and $(\sigma ,\rho )\rightarrow (1,1)$. One has $f(L_1,R_1;\sigma ,\rho )>0$.

Proof

With $x=L_1/R_1$, one has

$$\begin{aligned} f(L_1,R_1;\sigma ,\rho )&=f(x;\sigma ,\rho )\\&=(z_1-z_2)(x-1)\ln x+z_1\big [(\sigma -1)x-(\rho -1)\big ] \ln x\\&\quad +z_1(\rho -\sigma )(x-1). \end{aligned}$$

Direct calculation yields

$$\begin{aligned} f'(x;\sigma ,\rho )&=(z_1-z_2)\ln {x}+(z_1-z_2)\left( 1-\frac{1}{x}\right) +z_1(\sigma -1)\ln {x}\\&\quad +z_1\left( (\sigma -1)-\frac{\rho -1}{x}\right) +z_1(\rho -\sigma ),\\ f''(x;\sigma ,\rho )&=\frac{z_1\rho -z_2+(z_1\sigma -z_2)x}{x^2}. \end{aligned}$$

Note that $f''(x;\sigma ,\rho )>0$ for $x>0$. Hence, the function $f(x;\sigma ,\rho )$ is concave up for $x\in (0, \infty )$. Together with $f'(1;\sigma ,\rho )=0$, one can conclude that $x=1$ is the unique critical point of the function $f(x;\sigma ,\rho )$ for $x>0$. Therefore, the function $f(x;\sigma ,\rho )$ attains its absolute minimum at $x=1$. Note also that $f(1;\sigma ,\rho )=0$. One has $f(x;\sigma ,\rho )>0$ for $x>1$. $\square$

It follows directly from Lemma 3.3 that

Lemma 3.4

Assume $(\sigma ,\rho )\rightarrow (1,1)$. One has $V_0^c>V_1^c$ if $\sigma >\rho$; and $V_0^c<V_1^c$ if $\sigma <\rho$.

3.1.1 Ion Size Effects on $J^{zc}$

In this part, we analyze the sign of ${\bar{J}}_1^{zc}$, which provides the information of the finite ion size effects on the zero-current ionic flow $J^{zc}$. Note that ${\bar{J}}_1^{zc}$ is linear in the potential V. We first consider $\frac{\partial {\bar{J}}_1^{zc}}{\partial V}(V;x; \sigma ,\rho )$ with $x=L_1/R_1$. Careful calculation gives

$$\begin{aligned} \begin{aligned} \frac{\partial {\bar{J}}_1^{zc}}{\partial V}(V;x;\sigma ,\rho )&=\frac{D_1D_2}{D_1-D_2}\frac{z_1-z_2}{2H(1)}\frac{x-1}{\ln {x}}R_1^2F(x;\sigma ,\rho ), \end{aligned} \end{aligned}$$

(3.5)

where

$$\begin{aligned} F(x;\sigma ,\rho )=(\sigma -1)x+(\rho -1). \end{aligned}$$

For the function $F(x;\sigma ,\rho )$, one has the following result, which is crucial for our subsequent analysis.

Lemma 3.5

Assume $1<x<\rho /\sigma$. One has

• (i) $F(x;\sigma ,\rho )>0$ if one of the following conditions holds

  • (i1) $\sigma \rightarrow 1^{+},\ \rho \rightarrow 1^{+}$ and $\sigma <\rho$;

  • (i2) $\sigma \rightarrow 1^{-},\ \rho \rightarrow 1^{+}, \ \sigma +\rho <2$ and $\frac{\sigma +\rho }{\sigma \rho }<2$;

  • (i3) $\sigma \rightarrow 1^{-},\ \rho \rightarrow 1^{+},\ \sigma +\rho <2$ and $\frac{\sigma +\rho }{\sigma \rho }>2$ for $x<\frac{1-\rho }{\sigma -1}$.

• (ii) $F(x;\sigma ,\rho )<0$ if one of the following conditions holds

  • (ii1) $\sigma \rightarrow 1^{-}, \ \rho \rightarrow 1^{+}$ and $\sigma +\rho >2$;

  • (ii2) $\sigma \rightarrow 1^{-},\ \rho \rightarrow 1^{+},\ \sigma +\rho <2$ and $\frac{\sigma +\rho }{\sigma \rho }>2$ for $\frac{1-\rho }{\sigma -1}<x$;

  • (ii3) $\sigma \rightarrow 1^{-},\ \rho \rightarrow 1^{-}$ and $\sigma <\rho$.

Proof

The proof is straightforward calculus argument, and we omit it here. $\square$

Our main result then follows.

Theorem 3.6

Assume $1<x<\rho /\sigma$ for $(\sigma ,\rho )\rightarrow (1,1)$ with $\rho >\sigma$. For $\varepsilon >0$ small and $\nu >0$ small, one has

• (i) For $D_1>D_2$,

  • (i1) If $F(x; \sigma , \rho )>0$, then, ${\bar{J}}_1^{zc}(V)>0$ for $V>V_1^c$ and ${\bar{J}}_1^{zc}(V)<0$ for $V<V_1^c$; that is, ion sizes enhances the zero-current ionic flow $J^{zc}(V)$ if $V>V_1^c$ and reduces the zero-current ionic flow $J^{zc}(V)$ for $V<V_1^c$.

  • (i2) If $F(x; \sigma , \rho )<0$, then, ${\bar{J}}_1^{zc}(V)>0$ for $V<V_1^c$ and ${\bar{J}}_1^{zc}(V)<0$ for $V>V_1^c$; that is, ion sizes enhances the zero-current ionic flow $J^{zc}(V)$ if $V<V_1^c$ and reduces the zero-current ionic flow $J^{zc}(V)$ for $V>V_1^c$.

• (ii) For $D_1<D_2$,

  • (ii1) If $F(x; \sigma , \rho )>0$, then, ${\bar{J}}_1^{zc}(V)>0$ for $V<V_1^c$ and ${\bar{J}}_1^{zc}(V)<0$ for $V>V_1^c$; that is, ion sizes enhances the zero-current ionic flow $J^{zc}(V)$ if $V<V_1^c$ and reduces the zero-current ionic flow $J^{zc}(V)$ for $V>V_1^c$.

  • (ii2) If $F(x; \sigma , \rho )<0$, then, ${\bar{J}}_1^{zc}(V)>0$ for $V>V_1^c$ and ${\bar{J}}_1^{zc}(V)<0$ for $V<V_1^c$; that is, ion sizes enhances the zero-current ionic flow $J^{zc}(V)$ if $V>V_1^c$ and reduces the zero-current ionic flow $J^{zc}(V)$ for $V<V_1^c$.

Proof

From (3.5), the sign of $\frac{\partial {\bar{J}}_1^{zc}(V;x;\sigma ,\rho )}{\partial V}$ is determined by $\frac{F(x;\sigma ,\rho )}{D_1-D_2}$ since the factor $\frac{D_1D_2(z_1-z_2)(x-1)}{2H(1)\ln x}R_1^2>0.$ Taking the statement (i) for example. With $D_1>D_2$, the sign of $\frac{\partial {\bar{J}}_1^{zc}(V;x;\sigma ,\rho )}{\partial V}$ is uniquely determined by the sign of $F(x;\sigma ,\rho )$. And the result follows directly. $\square$

The result in Theorem 3.6 indicates the sensitive dependence of the zero-current ionic flow property on the diffusion coefficients, which will be further analyzed in Sect. 3.2.

3.1.2 Ion Size Effects on $\left| J^{zc}\right|$, the Magnitude of $J^{zc}$

The discussion in the Sect. 3.1.1 provide information of the relative finite ion size effects on the zero-current ionic flows since ${\bar{J}}_0^{zc}(V)$ and ${\bar{J}}_1^{zc}(V)$ have different sign. We now focus on the ion size effects on the magnitude of zero-current ionic flow $J^{zc}$, namely $|J^{zc}(V)|$, equivalent to analyzing ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)$ for small $\nu >0$.

With $x=L_1/R_1$, careful calculation gives

$$\begin{aligned} \begin{aligned} \frac{\partial {\bar{J}}_0^{zc}}{\partial V}(x;\sigma ,\rho )&=\frac{D_1D_2}{D_2-D_1}\frac{1}{H(1)}\frac{R_1}{(\ln {x})^2}f(x;\sigma ,\rho ), \end{aligned} \end{aligned}$$

(3.6)

where f is given in (3.4).

From Lemma 3.4, together with (3.6), we establish the following result.

Theorem 3.7

Assume $x=L_1/R_1>1$ and $(\sigma ,\rho )\rightarrow (1,1)$. One has

• (i) If $D_1>D_2$, then, ${\bar{J}}_0^{zc}>0$ (resp. ${\bar{J}}_0^{zc}<0$) for $V<V_0^c$ (resp. $V>V_0^c$).

• (ii) If $D_1<D_2$, then, ${\bar{J}}_0^{zc}>0$ (resp. ${\bar{J}}_0^{zc}<0$) for $V>V_0^c$ (resp. $V<V_0^c$).

We now state our main result related to the finite ion size effects on the magnitude of the zero-current ionic flow $J^{zc}(V)$.

Theorem 3.8

Assume $1<x<\rho /\sigma$ and $(\sigma ,\rho )\rightarrow (1,1)$ with $\rho >\sigma$. For small $\varepsilon >0$ and small $\nu >0$, one has

• (i) For $D_1>D_2$,

  • (i1) If $F(x; \sigma , \rho )>0$, then, ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)<0$ for either $V<V_0^c$ or $V>V_1^c$; and ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)>0$ for $V_0^c<V<V_1^c$. Equivalently, ion size effects reduce $\left| J^{zc}\right|$ for $V<V_0^c$ or $V>V_1^c$, while enhance $\left| J^{zc}\right|$ for $V_0^c<V<V_1^c$;

  • (i2) If $F(x; \sigma , \rho )<0$, then, ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)>0$ for either $V<V_0^c$ or $V>V_1^c$; and ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)<0$ for $V_0^c<V<V_1^c$. Equivalently, ion size effects enhance $\left| J^{zc}\right|$ for $V<V_0^c$ or $V>V_1^c$, while reduce $\left| J^{zc}\right|$ for $V_0^c<V<V_1^c$.

• (ii) For $D_1<D_2$,

  • (ii1) If $F(x; \sigma , \rho )>0$, then, ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)<0$ for either $V<V_0^c$ or $V>V_1^c$; and ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)>0$ for $V_0^c<V<V_1^c$. Equivalently, ion size effects reduce $\left| J^{zc}\right|$ for $V<V_0^c$ or $V>V_1^c$ while enhance $\left| J^{zc}\right|$ for $V_0^c<V<V_1^c$;

  • (ii2) If $F(x; \sigma , \rho )<0$, then, ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)>0$ for either $V<V_0^c$ or $V>V_1^c$; and ${\bar{J}}_0^{zc}(V){\bar{J}}_1^{zc}(V)<0$ for $V_0^c<V<V_1^c$. Equivalently, ion size effects enhance $\left| J^{zc}\right|$ for $V<V_0^c$ or $V>V_1^c$, while reduce $\left| J^{zc}\right|$ for $V_0^c<V<V_1^c$.

Proof

The result follows directly from Lemma 3.4, Theorem 3.6 and Theorem 3.7. $\square$

To end the discussion of the finite ion size effects on ionic flows, we point out that, for the terms ${\bar{J}}_0^{zc}$ and ${\bar{J}}_1^{zc}$, and the critical potentials $V_0^c$ and $V_1^c$, interesting scaling laws in boundary concentrations are observed, which actually provides efficient ways to control the finite ion size effects on the zero-current ionic flows.

Lemma 3.9

Treating ${\bar{J}}_0^{zc}$, ${\bar{J}}_1^{zc}$, $V_0^c$ and $V_1^c$ as functions of the boundary concentrations $L_1$ and $R_1$, one has

• (i) ${\bar{J}}_0^{zc}$ is homogeneous of degree one in $(L_1, R_1)$, that is, for any $s>0$,

  $$\begin{aligned} {\bar{J}}_0^{zc}(V; sL_1,sR_1)=s{\bar{J}}_0^{zc}(V; L_1, R_1); \end{aligned}$$

• (ii) ${\bar{J}}_1^{zc}$ is homogeneous of degree two in $(L_1, R_1)$, that is, for any $s>0$,

  $$\begin{aligned} {\bar{J}}_1^{zc}(V; sL_1,sR_1)=s^2{\bar{J}}_1^{zc}(V; L_1, R_1); \end{aligned}$$

• (iii) $V_0^c$ and $V_1^c$ are homogeneous of degree zero in $(L_1, R_1)$, that is, for any $s>0$,

  $$\begin{aligned} V_0^c(sL_1, sR_1)=V_0^c(L_1, R_1)\ \text{ and }\ V_1^c(sL_1, sR_1)=V_1^c(L_1, R_1). \end{aligned}$$

Proof

Note that $f_0(sL_1, sR_1)=sf_0(L_1,R_1)$ for $s>0$. The statements follow (3.2) and (3.3) directly. $\square$

3.2 Effects on Zero-Current Flows from Diffusion Coefficients

Diffusion coefficients play critical roles in the study of the qualitative properties of the zero-current ionic flows through ion channels, and we further examine their effects on ionic flows in this part. For convenience, we rewrite ${\bar{J}}_0^{zc}$ and ${\bar{J}}_1^{zc}$ as ${\bar{J}}_0^{zc}(V; D_1,D_2)$ and ${\bar{J}}_1^{zc}(V; D_1,D_2)$ to emphasize the dependence of the zero-current ionic flows on the diffusion coefficients.

The following results can be established.

Theorem 3.10

Assume $x=L_1/R_1>1$ and $(\sigma ,\rho )\rightarrow (1,1)$. One has

• (i) ${\bar{J}}_0^{zc}$ increases (resp. decreases) in the diffusion coefficient $D_1$ if $V>V_0^c$ (resp. $V<V_0^c$);

• (ii) ${\bar{J}}_0^{zc}$ increases (resp. decreases) in the diffusion coefficient $D_2$ if $V<V_0^c$ (resp. $V>V_0^c$).

Proof

Careful calculation gives, with $x=L_1/R_1,$

$$\begin{aligned} \frac{\partial {\bar{J}}_0^{zc}(V;D_1,D_2)}{\partial D_1}&=\left( \frac{D_2}{D_2-D_1}\right) ^2\frac{R_1}{H(1)\ln x}\left( \frac{f(x)}{\ln {x}}V+(x-1)(\rho -\sigma )\right) \\&=\left( \frac{D_2}{D_2-D_1}\right) ^2\frac{R_1f(x)}{H(1)\ln ^2 x}(V-V_0^c),\\ \frac{\partial {\bar{J}}_0^{zc}(V;D_1,D_2)}{\partial D_2}&=-\left( \frac{D_1}{D_2-D_1}\right) ^2\frac{R_1}{H(1)\ln x}\left( \frac{f(x)}{\ln {x}}V+(x-1)(\rho -\sigma )\right) \\&=-\left( \frac{D_2}{D_2-D_1}\right) ^2\frac{R_1f(x)}{H(1)\ln ^2 x}(V-V_0^c), \end{aligned}$$

where f(x) is given in (3.4) and $V_0^c$ is defined in Definition 3.2. Statements (i) and (ii) then follows directly. $\square$

Theorem 3.11

Assume $1<x=L_1/R_1<\rho /\sigma$ and $(\sigma ,\rho )\rightarrow (1,1)$ with $\rho >\sigma$. One has

• (i) For $F(x;\sigma ,\rho )>0$,

  • (i1) ${\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_1$ if $V<V_1^c$ (resp. $V>V_1^c$);

  • (i2) ${\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_2$ if $V>V_1^c$ (resp. $V<V_1^c$).

• (ii) For $F(x;\sigma ,\rho )<0$,

  • (ii1) ${\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_1$ if $V>V_1^c$ (resp. $V<V_1^c$);

  • (ii2) ${\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_2$ if $V<V_1^c$ (resp. $V>V_1^c$).

Proof

The argument is similar to that in Theorem 3.10, and we omit it here. $\square$

We comment that, from the analysis in Theorems 3.10 and 3.11, the effects on ${\bar{J}}_0^{zc}$ and ${\bar{J}}_1^{zc}$, respectively, from the diffusion coefficients $D_1$ and $D_2$ are opposite. The critical roles of the potentials $V_0^c$ and $V_1^c$ identified in the Definition 3.2 are further demonstrated in these results.

We now examine the effects on $|J^{zc}|$, the magnitude of $J^{zc}$ (equivalent to ${\bar{J}}_0^{zc}{\bar{J}}_1^{zc}$) from the diffusion coefficients from small finite ion sizes. To be specific, we consider the monotonicity properties of $|J^{zc}|$ in terms of $D_1$ and $D_2$, respectively, which is characterized in the following result.

Theorem 3.12

Assume $1<x=L_1/R_1<\rho /\sigma$ and $(\sigma ,\rho )\rightarrow (1,1)$ with $\rho >\sigma$. Assume further that $D_1>D_2$. One has

• (i) For $F(x;\sigma ,\rho )>0$,

  • (i1) ${\bar{J}}_0^{zc}{\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_1$ if either $V<V_0^c$ or $V>V_1^c$ (resp. $V_0^c<V<V_1^c$);

  • (i2) ${\bar{J}}_0^{zc}{\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_2$ if $V_0^c<V<V_1^c$ (resp. either $V<V_0^c$ or $V>V_1^c$ ).

• (ii) For $F(x;\sigma ,\rho )<0$,

  • (ii1) ${\bar{J}}_0^{zc}{\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_1$ if $V_0^c<V<V_1^c$ (resp. either $V<V_0^c$ or $V>V_1^c$);

  • (ii2) ${\bar{J}}_0^{zc}{\bar{J}}_1^{zc}$ increases (resp. decreases) in the diffusion coefficients $D_2$ if either $V<V_0^c$ or $V>V_1^c$ (resp. $V_0^c<V<V_1^c$).

Remark 3.13

Similar result as that in the Theorem 3.12 can be obtained for the case with $D_1<D_2$. Meanwhile, we would like to demonstrate that the monotonicity of the zero-current ionic flow $J^{zc}$ in the diffusion coefficients sensitively depends on the nonlinear interplay among the system parameters, especially the ratio of the boundary layer parameters $\rho /\sigma$, the order of $D_1$ and $D_2$, the ratio of the boundary concentrations $L_1/R_1$, and the critical potentials $V_0^c$ and $V_1^c$. This indicates again the complexity of the qualitative properties of the ionic flow through membrane channel. The rigorous mathematical analysis based on the PNP model in current work should provide some insights and better understanding of the mechanism of ionic flows through membrane channels.

4 Concluding Remarks

In this work, we analyze the Poisson-Nernst-Planck model with particular interest in the zero-current ionic flows through a membrane channel. The model problem includes one cation and one anion. Bikerman’s local hard-sphere model is included to characterize the ion size effects. By employing the geometric singular perturbation theory, we obtain the existence and local uniqueness result. Particularly, from the solutions of the limiting PNP system, we are able to obtain explicit expressions of the approximation of the zero-current ionic flow $J^{zc}$, the starting point of our analysis on ionic flow properties.

The qualitative properties of the zero-current ionic flows is our main interest, which is analyzed from two directions: effects from finite ion sizes and effects from diffusion coefficients. Detailed analysis along each direction is provided, from which one can better understand the mechanism of ionic flows through membrane channels, particularly the internal dynamics of ionic flows, which are non-intuitive and cannot be detected by current technology. We would also like to demonstrate that our studies on the ionic flow properties is under the assumption that the two ends (very often, people call them baths) connected by the ion channel are not neutral, but close to (that is, $(\sigma ,\rho )\rightarrow (1,1)$ but not equal to 1 simultaneously). This is a more realistic setup in the study of ion channel problem, but the mathematical analysis is more channeling due to the appearance of two boundary layers. Among others, we find

• (i) The sign of the leading term ${\bar{J}}_1^{zc}$ that contains the finite ion size effects depends sensitively on the interplays among system parameters, such as the diffusion coefficients $(D_1,D_2)$, the boundary concentrations $(L_1,R_1)$, and the boundary layers in terms of $(\sigma , \rho )$ through the critical potentials $V_0^c$ and $V_1^c$;

• (ii) The monotonicity of ${\bar{J}}_k^{zc}$ for $k=0,1$ on the diffusion coefficient $D_1$ is opposite to that on the diffusion coefficient $D_2$ (see Theorems 3.10 and 3.11);

• (iii) Under electronuetrality boundary conditions (i.e. $(\sigma ,\rho )=(1,1)$), the leading term ${\bar{J}}_1^{zc}$ that contains finite ion size effects vanishes (see Remark 3.1), and the finite ion size effects, which is crucial in the study of the selectivity property of ion channels, cannot be characterized. This also indicates the setup (including the boundary layers) in current work is necessary.

To end this section, we comment that

• (I) as a first step to investigate the qualitative properties of zero-current ionic flows through membrane channels, the setup in current work does not include the permanent charge due to the complicity of the analysis, and surely this will have some limitations in the study of ion channel problems. Particularly, when the adjacent regions of permanent charges have opposite signs, very likely, they will produce complex and therefore useful effects, just as they do in the PN junctions of bipolar transistors. We will focus on the case with nonzero permanent charges in our future projects.

• (II) the boundary layers we considered in this work are located at the ends of the channel. A brief illustration is provided in the Remark 2.3. One may also refer to [13] for more detailed discussion.

5 Appendix: Proofs of Some Results

5.1 Proof of Proposition 2.2

Statement (i) can be checked directly. Statements (ii) and (iii) are derived based on the first integrals obtained from the first statement, and the arguments are similar. Here we briefly provide a proof for the second statement. The second statement consists of three parts: (a) the intersection of the stable manifold $W^s({\mathcal {Z}})$ and the set $B_L$; (b) the transversality of the intersection stated in (a); and (c) the characterization of the landing point $\omega (N_L)$.

For the part (a), it is clear since $\dim W^s({\mathcal {Z}})=6$ and $\dim B_L=3$, while the state variables are in the phase space ${\mathbb {R}}^7$.

For the part (b), via the first integrals obtained in the statement (i), one is able to consider the tangent space of the stable manifold $W^s({\mathcal {Z}})$ and the set $B_L$ at the intersection point, from which linearly independent vectors that span the whole phase space ${\mathbb {R}}^7$ can be identified, and this establishes the transversality of the intersection. The calculation is tedious but straightforward, and we skip the details here.

For the part (c), we will just show the derivation of the variables $\phi _0^L,\ c_{10}^L,\ c_{20}^L$ and $u_0^l$ associated to the zeroth order (in $\nu$) limiting fast system. The discussion for the variables $\phi _1^L,\ c_{11}^L,\ c_{12}^L$ and $u_1^l$ is similar. Let $z(\xi )=(\phi _0(\xi ), u_0(\xi ), c_{10}(\xi ), c_{20}(\xi ), J_{10}(\xi ), J_{20}(\xi ), \tau (\xi ))$ be a solution of the system (2.8) with $z(0)\in B_L$ and $z(\xi )\in W^s({\mathcal {Z}})$. Then, one has $J_{10}(\xi )=J_{10},\ J_{20}(\xi )=J_{20},\ \tau (\xi )=0$ for all $\xi$,

$$\begin{aligned} z(\xi )\rightarrow z(\infty )=(\phi _0^L, 0, c_{10}^L, c_{20}^L, J_1, J_2, 0)\in {\mathcal {Z}} \end{aligned}$$

for some $\phi _0^L,\ c_{10}^L$ and $c_{20}^L$ with $z_1c_{10}^L=-z_2c_{20}^L,$ and

$$\begin{aligned} \phi _0(0)=V,\ c_{10}(0)=L_1,\ c_{20}(0)=L_2. \end{aligned}$$

Using the integrals $H_1$ and $H_2$ in the statement (i), one has

$$\begin{aligned} \ln c_{10}(\xi )+z_1\phi _0(\xi )=\ln L_1+z_1V\ \text{ and }\ \ln c_{20}(\xi )+z_2\phi _0(\xi )=\ln L_2+z_2V, \end{aligned}$$

from which we get

$$\begin{aligned} c_{10}(\xi )=L_1e^{z_1(V-\phi _0(\xi ))}\ \text{ and }\ c_{20}(\xi )=L_2e^{z_2(V-\phi _0(\xi ))}. \end{aligned}$$

(5.1)

Let $\xi \rightarrow \infty$, one has

$$\begin{aligned} c_1^L=L_1e^{z_1(V-\phi _0^L)}\ \text{ and }\ c_2^L=L_2e^{z_2(V-\phi _0^L)}. \end{aligned}$$

Recall that $z_1c_{10}^L=-z_2c_{20}^L$ and $-z_2L_2=(z_1L_1)\sigma .$ We obtain

$$\begin{aligned} \phi _0^L=V-\frac{1}{z_1-z_2}\ln \sigma . \end{aligned}$$

It follows that

$$\begin{aligned} c_{10}^L=\frac{1}{z_1}(z_1L_1)^{\frac{-z_2}{z_1-z_2}}(-z_2L_2)^{\frac{z_1}{z_1-z_2}}=\frac{1}{z_1}(z_1L_1)\sigma ^{\frac{z_1}{z_1-z_2}}\ \text{ or }\ z_1c_{10}^L=(z_1L_1)\sigma ^{\frac{z_1}{z_1-z_2}}. \end{aligned}$$

Similarly,

$$\begin{aligned} -z_2c_{20}^L=(z_1L_1)\sigma ^{\frac{z_1}{z_1-z_2}}. \end{aligned}$$

Note that $\phi _0''=-z_1c_{10}-z_2c_{20}$. The system (5.1) indicates that $\phi _0$ satisfies the Hamiltonian equation

$$\begin{aligned} \phi _0''+z_1L_1e^{z_1(V-\phi _0)}+z_2L_2e^{z_2(V-\phi _0)}=0 \end{aligned}$$

with $\phi _0(0)=V$ and $\phi _0(\xi )\rightarrow \phi _0^L$ as $\xi \rightarrow \infty .$ The corresponding Hamiltonian is

$$\begin{aligned} H(\phi _0,u_0)=\frac{u_0^2}{2}-L_1e^{z_1(V-\phi _0)}-L_2e^{z_2(V-\phi _0)}. \end{aligned}$$

In terms of $\phi _0$ and $u_0=\phi _0'$, the equation reads

$$\begin{aligned} \phi _0'=u_0,\quad u_0'=-z_1L_1e^{z_1(V-\phi _0)}-z_2L_2e^{z_2(V-\phi _0)}. \end{aligned}$$

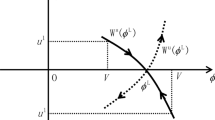
The Hamiltonian system has a unique equilibrium $(\phi _0^L,0)$ with $\phi _0^L$ given above, and it is easy to verify that the equilibrium is a saddle point of the system. If $W^s(\phi _0^L)$ is the stable manifold of $(\phi _0^L,0)$, then it is the restriction of $W^s({\mathcal {Z}})$ to the $(\phi _0,u_0^l)$-plane. To have $(V,u_0^l)\in W^s(\phi _0^L)$, one need $H(\phi _0^L,0)=H(V,u_0^l)$, from which the expression for $u_0^l$ follows. The sign of $u_0^l$ is determined by which stable branch of $W^s(\phi _0^L)$ the solution approaches the equilibrium.

5.2 Proof of Lemma 2.4

Taking the integral for the second equation in (2.17) from 0 to x, together with the initial value $c_{10}(0)=c_{10}^L$, one has

$$\begin{aligned} c_{10}(x)-c_{10}^L&=-\frac{(z_1D_1-z_2D_2)J_{10}}{D_1D_2(z_1-z_2)}\int _0^x\frac{1}{h(s)}ds, \end{aligned}$$

which gives

$$\begin{aligned} c_{10}(x)=c_{10}^L-\frac{(z_1D_1-z_2D_2)J_{10}}{D_1D_2(z_1-z_2)}H(x). \end{aligned}$$

(5.2)

Again, from the $c_{10}$-equation in (2.17), one has

$$\begin{aligned} \frac{1}{h(\tau )}=\frac{D_1D_2(z_1-z_2){\dot{c}}_{10}}{(z_2D_2-z_1D_1)J_{10}}. \end{aligned}$$

Substituting the above relation into the $\phi _0$-equation in (2.17), and integrating it from 0 to x, we have

$$\begin{aligned} \phi _0(x)-\phi _0^L&=\frac{(D_1-D_2)J_{10}}{(z_1-z_2)D_1D_2}\cdot \frac{D_1D_2(z_1-z_2)}{(z_2D_2-z_1D_1)J_{10}}\int _{0}^{x} \frac{{\dot{c}}_{10}}{c_{10}} ds\\&=-\frac{D_1-D_2}{z_1D_1-z_2D_2}\ln {\frac{c_{10}(x)}{c_{10}^L}}, \end{aligned}$$

which gives

$$\begin{aligned} \phi _0(x)=\phi _0^L-\frac{D_1-D_2}{z_1D_1-z_2D_2}\ln {\frac{c_{10}(x)}{c_{10}^L}}. \end{aligned}$$

(5.3)

Evaluating (5.2) and (5.3) at $x=1$, together with $\phi _0(1)=\phi _0^R$ and $c_{10}(1)=c_{10}^R$, one has

$$\begin{aligned} \phi _0^R&=\phi _0^L-\frac{D_1-D_2}{z_1D_1-z_2D_2}\ln {\frac{c_{10}^R}{c_{10}^L}}\quad \text{ and }\quad c_{10}^R=c_{10}^L-\frac{(z_1D_1-z_2D_2)H(1)}{D_1D_2(z_1-z_2)}J_{10}, \end{aligned}$$

from which, together with the relation $-z_2L_2=(z_1L_1)\sigma$ and $-z_2R_2=(z_1R_1)\rho$, we obtain

$$\begin{aligned} J_{10}&=\frac{D_1D_2(z_1-z_2)(c_{10}^L-c_{10}^R)}{(z_1D_1-z_2D_2)H(1)}=\frac{D_1D_2(z_1-z_2)\left( L_1\sigma ^{\frac{z_1}{z_1-z_2}}-R_1\rho ^{\frac{z_1}{z_1-z_2}}\right) }{(z_1D_1-z_2D_2)H(1)} \end{aligned}$$

(5.4)

with

$$\begin{aligned} \phi _0^L-\phi _0^R=\frac{D_1-D_2}{z_1D_1-z_2D_2}(\ln c_{10}^R-\ln c_{10}^L) \end{aligned}$$

(5.5)

equivalent to

$$\begin{aligned} V+\frac{\ln \rho -\ln \sigma }{z_1-z_2}=\frac{D_1-D_2}{z_1D_1-z_2D_2}\Big [\ln R_1-\ln L_1+\frac{z_1}{z_1-z_2}(\ln \rho -\ln \sigma )\Big ]. \end{aligned}$$

Or equivalently, one has

$$\begin{aligned} J_{10}=\frac{D_1D_2(z_1-z_2)\left( L_1\sigma ^{\frac{z_1}{z_1-z_2}}-R_1\rho ^{\frac{z_1}{z_1-z_2}}\right) \left( V-\frac{1}{z_1-z_2}\ln \frac{\sigma }{\rho }\right) }{(D_2-D_1)\left( \ln L_1-\ln R_1+\frac{z_1}{z_1-z_2}\ln \frac{\sigma }{\rho }\right) H(1)}. \end{aligned}$$

5.3 Proof of Lemma 2.5

Note that, with the ${\dot{c}}_{10}$-equation in the system (2.17), the ${\dot{c}}_{11}$-equation in the system (2.18) can be written as

$$\begin{aligned} {\dot{c}}_{11}=\frac{z_1\lambda -z_2}{z_2}c_{10}{\dot{c}}_{10}+\frac{(z_2D_2-z_1D_1)J_{11}}{(z_1-z_2)D_1D_2}\frac{1}{h(\tau )}. \end{aligned}$$

Taking the integration for 0 to x, together with $c_{11}(0)=c_{11}^L$, one has

$$\begin{aligned} c_{11}(x)=c_{11}^L+\frac{z_1\lambda -z_2}{2z_2}\big (c_{10}^2(x)-(c_{10}^L)^2\big )+\frac{(z_2D_2-z_1D_1)J_{11}}{(z_1-z_2)D_1D_2}H(x). \end{aligned}$$

(5.6)

Similarly, for the $\phi _1$-equation, one has

$$\begin{aligned} \phi _1(x)&=\phi _1^L+\frac{(D_2-D_1)J_{10}}{(z_1-z_2)D_1D_2}\int _0^x\frac{c_{11}(s)}{c_{10}^2(s)h(s)}ds\\&\quad -\frac{(D_2-D_1)J_{11}}{(z_1-z_2)D_1D_2}\int _0^x\frac{1}{c_{10}(s)h(s)}ds. \end{aligned}$$

From the ${\dot{c}}_{10}$-equation in (2.17), one has

$$\begin{aligned} \frac{1}{h(s)}=-\frac{D_1D_2(z_1-z_2)}{(z_1D_1-z_2D_2)J_{10}}{\dot{c}}_{10}(s). \end{aligned}$$

It follows that

$$\begin{aligned}&\int _0^x\frac{c_{11}(s)ds}{c_{10}^2(s)h(s)}\\&=-\frac{D_1D_2(z_1-z_2)}{(z_1D_1-z_2D_2)J_{10}}\int _0^x\frac{c_{11}(s){\dot{c}}_{10}(s)}{c_{10}^2(s)}ds\\&=\frac{D_1D_2(z_1-z_2)}{(z_1D_1-z_2D_2)J_{10}}\left[ \frac{c_{11}(x)}{c_{10}(x)}-\frac{c_{11}^L}{c_{10}^L}-\int _0^x\frac{{\dot{c}}_{11}(s)}{c_{10}(s)}ds\right] \\&=\frac{D_1D_2(z_1-z_2)}{(z_1D_1-z_2D_2)J_{10}}\left( \frac{c_{11}(x)}{c_{10}(x)}-\frac{c_{11}^L}{c_{10}^L}\right) +\frac{z_1\lambda -z_2}{z_2}H(x)+\frac{J_{11}}{J_{10}}\int _0^x\frac{1}{h(s)c_{10}(s)}ds, \end{aligned}$$

where, a similar argument gives

$$\begin{aligned} \int _0^x\frac{1}{c_{10}(s)h(s)}ds=&\frac{(z_1-z_2)D_1D_2}{(z_2D_2-z_1D_1)J_{10}}\big (\ln c_{10}(x)-\ln c_{10}^L\big ). \end{aligned}$$

Together, we get the expression for $\phi _1(x)$. Evaluating both the $c_{11}(x)$-equation and the $\phi _1(x)$-equation at $x=1$ yields

$$\begin{aligned} \begin{aligned} c_{11}^R&=c_{11}^L+\frac{z_1\lambda -z_2}{2z_2}\left( (c_{10}^R)^2-(c_{10}^L)^2\right) +\frac{(z_2D_2-z_1D_1)J_{11}}{(z_1-z_2)D_1D_2}H(1),\\ \phi _1^R&=\phi _1^L+\frac{D_2-D_1}{z_1D_1-z_2D_2}\left( \frac{c_{11}^R}{c_{10}^R}-\frac{c_{11}^L}{c_{10}^L}\right) +\frac{(D_2-D_1)(z_1\lambda -z_2)J_{10}}{z_2(z_1-z_2)D_1D_2}H(1). \end{aligned} \end{aligned}$$

(5.7)

The first equation in (5.7), together with $J_{10}$ in (5.4) and (5.5), gives

$$\begin{aligned} J_{11}&=J_{10}\left( \frac{c_{11}^L-c_{11}^R}{c_{10}^L-c_{10}^R}-\frac{z_1\lambda -z_2}{2z_2}\left( c_{10}^L+c_{10}^R\right) \right) \\&=J_{10}\bigg [\frac{L_1^2\sigma ^{\frac{z_1}{z_1-z_2}}\big (1-\frac{z_1\lambda }{z_2}\sigma \big )-R_1^2\rho ^{\frac{z_1}{z_1-z_2}}\big (1-\frac{z_1\lambda }{z_2}\rho \big )+\frac{z_1\lambda }{z_2}\big (L_1^2\sigma ^{\frac{2z_1}{z_1-z_2}}-R_1^2\rho ^{\frac{2z_1}{z_1-z_2}}\big )}{L_1\sigma ^{\frac{z_1}{z_1-z_2}}-R_1\rho ^{\frac{z_1}{z_1-z_2}}}\\&\quad -\frac{z_1\lambda +z_2}{2z_2}\left( L_1\sigma ^{\frac{z_1}{z_1-z_2}}+R_1\rho ^{\frac{z_1}{z_1-z_2}}\right) \bigg ]. \end{aligned}$$

The restriction on $J_{11}$ is actually the second equation in (5.7). Careful calculation leads to the equivalent one given by $\lambda =\frac{z_2(L_1-R_1)}{z_1(\sigma L_1-\rho R_1)}.$