Dynamics of Classical Poisson–Nernst–Planck Systems with Multiple Cations and Boundary Layers

Abstract

We study a quasi-one-dimensional classical Poisson–Nernst–Planck model for ionic flow through a membrane channel with two positively charged ion species (cations) and one negatively charged, and with zero permanent charges. We treat the model problem as a boundary value problem of a singularly perturbed differential system. Under the framework of the geometric singular perturbation theory, together with specific structures of this concrete model, the existence of solutions to the boundary value problem is established and, for a special case that the two cations have the same valences, we are able to derive approximations of the individual fluxes and the I–V (current–voltage) relation explicitly, from which, our two main focuses in this work, boundary layer effects on ionic flows and competitions between two cations, are analyzed in great details. Critical potentials are identified and their roles in characterizing these effects are studied. Nonlinear interplays among physical parameters, such as boundary concentrations and potentials, diffusion coefficients and ion valences, are characterized, which could potentially provide efficient ways to control and affect some biological functions. Numerical simulations are performed, and numerical results are consistent with our analytical ones.

1 Introduction

Ion channels are large cylindrical shaped, hollow proteins embedded in cell membranes that regulates the movement of charged particles (mainly $\hbox {Ca}^{++}$, $\hbox {Na}^{+}$, $\hbox {K}^{+}$ and $\hbox {Cl}^{-}$) and establish communication between the cell and its external environment. And hence, they are able to control a wide range of biological functions. The study of ion channels consists of two related major topics: structures of ion channels and ionic flow properties. Our main focus in this work is exclusively on open channels with given structures. With a given structure of an open channel, the main interest is to understand its electrodiffusion property.

Electrodiffusion, the diffusion of electric charge, plays a central role in a wide range of important technological devices and physical phenomena [15, 16, 18, 45, 62, 63, 74]: semiconductors controls the migration and diffusion of quasi-particles of charge in transistors and integrated circuits [71, 78, 82], properties of electrolytic solutions and thin films [6, 11, 16, 17, 20, 27], all of biology occurs in solutions of ions and charged organic molecules in water [3, 19, 35, 81]. It is the goal of technology (and much of physical science and biological processes) to control these electorodiffusive systems to produce useful behavior.

Beyond general electrodiffusion phenomena for electrolytic solutions in bulks or near charged walls, ionic flows through membrane channels have more specifics; namely, the study of ionic flows has to take into considerations of global constraints, including the boundary conditions (boundary concentrations and boundary potentials) in addition to protein structures. As demonstrated by the celebrated works [36,37,38,39,40] of Hodgkin and Huxley for neurons consisting of a population of ion channels and by the works in the volume Single-Channel Recording ([73] edited by B. Sakmann and E. Neher) and many other works afterwards, the properties of ion channels depend in an extremely rich way on different regions of boundary concentrations and boundary potentials. It is exactly the global constraints and the internal structures of membrane channels that make the relevant electrodiffusion properties specific for ion channel problems.

A basic continuum model for electrodiffusion is the Poisson–Nernst–Planck (PNP) system, a reduced model that treats the medium (aqueous within which ions are migrating) as a dielectric continuum. The channel is assumed to be narrow so that it can be effectively viewed as a one-dimensional line segment [0, l] where l, typically in the range of $10-20$ nanometers, is the length of the channel whose endpoints are the baths that the channel links. A quasi-one-dimensional steady-state PNP model for ion flows of n ion species through a single channel is (see [58, 65])

$$\begin{aligned} \begin{aligned}&\frac{1}{A(X)}\frac{d}{d X}\left( \varepsilon _r(X)\varepsilon _0A(X)\frac{d \Phi }{d X}\right) =-e\bigg (\sum _{j=1}^nz_jC_j(X)+Q(X)\bigg ),\\&\frac{d {\mathcal {J}}_i}{dX}=0, \quad -{\mathcal {J}}_i=\frac{1}{k_BT}{{\mathcal {D}}}_i(X)A(X)C_i(X)\frac{d\mu _i}{dX}, \quad i=1,2,\cdots , n, \end{aligned} \end{aligned}$$

(1.1)

where e is the elementary charge, $k_B$ is the Boltzmann constant, T is the absolute temperature; $\Phi$ is the electric potential, Q(X) is the permanent charge of the channel, $\varepsilon _r(X)$ is the relative dielectric coefficient, $\varepsilon _0$ is the vacuum permittivity; A(X) is the area of cross-section of the channel over the point $X\in [0,l]$. For the ith ion species, $C_i$ is the concentration (number of ith ions per unit volume), $z_i$ is the valence (number of charges per particle) that is positive for cations and negative for anions, $\mu _i$ is the electrochemical potential, ${\mathcal {J}}_i$ is the flux density, and ${{\mathcal {D}}}_i(X)$ is the diffusion coefficient.

For system (1.1), we impose the following boundary conditions (see, [24] for justification), for $k=1,2,\cdots , n$,

$$\begin{aligned} \Phi (0)={{\mathcal {V}}}, \ \ C_i(0)={{\mathcal {L}}}_i>0; \quad \Phi (l)=0, \ \ C_i(l)={{\mathcal {R}}}_i>0. \end{aligned}$$

(1.2)

The electrochemical potential $\mu _k$ is the sum of the ideal component

$$\begin{aligned} \mu _k^{id}(X)=z_ke \Phi (X)+k_BT\ln \frac{C_k(X)}{C_0} \end{aligned}$$

(1.3)

with some characteristic number density $C_0$, and the excess component $\mu _k^{ex}(X)$.

The PNP system can be derived as a reduced model from molecular dynamics [76], from Boltzmann equations [4], and from variational principles [41,42,43]. More sophisticated models have also been developed. Coupling PNP and Navier-Stokes equations for aqueous motions has also been proposed (see, e.g. [10, 21, 22, 28, 33, 79]). Reviews of various models for ion transport and comparisons among the models can be found in [12, 44, 72, 85]. While these sophisticated systems can model the physical problem more accurately, it is a great challenge to examine their dynamics analytically and even computationally. Focusing on key features of the biological system, the PNP system is an appropriate model for analysis and numerical simulations of ionic flows.

The simplest PNP system is the classical Poisson–Nernst–Planck (cPNP) system that includes the ideal component $\mu _k^{id} (X)$ in (1.3) only. The ideal component $\mu _k^{id}$ contains contributions by considering ion particles as point charges and ignoring the ion-to-ion interaction. For a wide range of purposes, the classical PNP models have been studied numerically and analytically to a great extent (see, e.g., [1, 4, 5, 7, 8, 24, 25, 47, 54,55,56, 58, 60, 67, 73, 75, 83, 84, 87, 88]). Very often, in the studies of ion channel problems, the so-called electroneutrality boundary conditions are enforced at both ends of the channel (see, e.g., [5, 13, 46, 47, 55,56,57, 59, 87]). This greatly reduces the difficulty in examining the qualitative properties of ionic flows because, under the assumption of electroneutrality boundary concentrations, the boundary layers disappear in the study of PNP model for membrane channels (see, e.g., [1, 13, 47, 48, 57, 86]). Accordingly, in order to study the effect on ionic flows from boundary layers, one should remove the neutral conditions on boundary concentrations. On the other hand, if those boundary layers reach into the part of the device performing atomic control, they dramatically affect its behavior. In particular, boundary layers of charge are likely to create artifacts over long distances because the electric field spreads a long way.

In [88], we examined the classical PNP system with two ion species, one positively charged and one negatively charged. More rich dynamics of ionic flows were observed due to the existence of boundary layers. However, ions are crowded and more ion species should be included to obtain a more realistic model and to better understand the dynamics of ionic flows. In this work, as a natural extension, we will study the cPNP model with three ion species, two positively charged and one negatively charged to further examine the important role, in which the boundary layer plays. Of particular interest are

• (I) effects of boundary layers on both individual fluxes and I–V relations based on system (1.1)–(1.2).

• (II) Competitions between two cations with boundary layers, which is closely related to selectivity phenomena, a popular topic in the study of ion channel problem.

We would like to comment that due to the additional cation involved in the system, it becomes very challenging to derive approximate solutions (in $\varepsilon$) to the limiting system, in particular, for the limiting slow system. To overcome this difficulty, we further assume that the two cations have the same valences, together with the specific structures of the system, we are able to obtain the solutions of the limiting systems explicitly, from which both the I–V relations and the individual fluxes can be extracted. This is critical for one to characterize the two most important biological properties of interest: permeation and selectivity. In addition, the competition between two cations that is closely related to the selectivity phenomenon of ion channels is carefully analyzed under the existence of boundary layers. This is one of our main contributions, and also the novelty of this work compared to the one done in [88].

The framework for the analysis is a geometric singular perturbation theory [24, 56]. In Sect. 2, we set up our problem with further assumptions. In Sect. 3, following the same outline as in [55, 56, 58, 60], the existence and uniqueness of solutions of the singularly perturbed system are established. Our main results are in Sect. 4, which consists of three subsections. To examine the qualitative properties of ionic flows with boundary layer effects, we further assume that the two cations have the same valences (such as $\hbox {Na}^{+}$ and $\hbox {K}^{+}$) so that the zeroth order (in $\varepsilon$) explicit expressions of the individual fluxes can be obtained (see Lemma 4.1). In particular, we assume $-z_3L_3=\sigma (zL_1+zL_2)$ and $-z_3R_3=\rho (zR_1+zR_2)$, where $\sigma$ and $\rho$ are some positive constants not equal to 1 simultaneously since $(\sigma ,\rho )=(1,1)$ implies electroneutrality boundary conditions. Our main interest is to analyze the qualitative properties of ionic flows as $(\sigma ,\rho )\rightarrow (1,1)$, namely the boundary layer effects on ionic flows. In Sect. 4.1, we study the boundary layer effects on ionic flows in terms of both individual fluxes and the total flow rate of charges, while in Sect. 4.2, we focus on the competitions between two cations with boundary layers. It turns out that under some further restrictions on the boundary concentrations and diffusion coefficients, the ion channel will prefer one cation over the other determined by the boundary potential (see Theorems 4.10, 4.11 and 4.12). In both subsections, critical potentials are identified and their roles in characterizing the effects on ionic flows are carefully discussed. Numerical simulations are performed in Sects. 4.3 to further examine the boundary layer effects, and our numerical results are consistent with our analytical ones.

2 Problem Set-Ups

For simplicity, we make the following assumptions:

• (A1). We consider three ion species ($n=3$) with $z_1>0$, $z_2>0$ and $z_3<0$.

• (A2). We assume the permanent charge $Q(X)=0$ over the whole interval [0, 1].

• (A3). For $\mu _k$, we only include the ideal component $\mu _k^{id}$ as in (1.3).

• (A4). We assume the relative dielectric coefficient and the diffusion coefficient to be constants, that is, $\varepsilon _r(X)=\varepsilon _r$ and $D_i(X)=D_i$.

In the sequel, we will assume (A1)–(A4). We first make a dimensionless rescaling following [30]. Set $C_0=\max \{{{\mathcal {L}}}_i, {{\mathcal {R}}}_i:i=1,2\}$ and let

$$\begin{aligned} \begin{aligned} \varepsilon ^2=&\frac{ {\varepsilon }_r\varepsilon _0k_BT}{e^2l^2C_0},\quad x=\frac{X}{l},\quad h(x)=\frac{A(X)}{l^2}, \quad D_i=lC_0 {{\mathcal {D}}}_i;\\ \phi (x)=&\frac{e}{k_BT}\Phi (X), \quad c_i(x)=\frac{C_i(X)}{C_0}, \quad J_i=\frac{{{\mathcal {J}}}_i}{D_i};\\ V=&\frac{e}{k_BT}{{\mathcal {V}}}, \quad L_i=\frac{{{\mathcal {L}}}_i}{C_0}; \quad R_i=\frac{{{\mathcal {R}}}_i}{C_0}. \end{aligned} \end{aligned}$$

(2.1)

The BVP (1.1)–(1.2) then reads

$$\begin{aligned} \begin{aligned}&\frac{\varepsilon ^2}{h(x)}\frac{d}{dx}\left( h(x)\frac{d}{dx}\phi \right) =-(z_1c_1+z_2c_2+z_3c_3),\\&\frac{d c_1}{d x}+z_1c_1\frac{d \phi }{dx}=- \frac{J_1}{h(x)},\quad \frac{d c_2}{d x}+z_2c_2\frac{d \phi }{dx}=- \frac{J_2}{h(x)},\\&\frac{d c_3}{d x}+z_3c_3\frac{d \phi }{dx}=- \frac{J_3}{h(x)},\quad \frac{d J_k}{dx}=0, \end{aligned}\end{aligned}$$

(2.2)

with the boundary conditions, for $i=1,2,3,$

$$\begin{aligned} \phi (0)=V,\ \ c_i(0)=L_i>0; \ \ \phi (1)=0,\ \ c_i(1)=R_i>0. \end{aligned}$$

(2.3)

For ion channels, an important characteristic is the I–V (current-voltage) relation. Given a solution of the boundary value problem (BVP) (1.1)–(1.2), the current is

$$\begin{aligned} \mathcal{I}=\sum _{k=1}^nz_k \mathcal{J}_k=\sum _{k=1}^nz_kD_kJ_k, \end{aligned}$$

(2.4)

where $z_k\mathcal{J}_k$ is the individual flux of charge of the kth ion species. For fixed boundary concentrations $L_k$’s and $R_k$’s, $\mathcal{J}_k$’s depend on V only and formula (2.4) provides a dependence of the current $\mathcal{I}(V;\varepsilon )$ on the voltage V.

With the assumption that $\varepsilon$ is small, system (2.2) together with the boundary condition (2.3) will be treated as a singular boundary value problem. We comment that in our following discussion, we take $h(x)=1$ over the whole interval [0, 1]. This is because for ion channels with zero permanent charge, the variable h(x) contributes through an average, explicitly through the factor $\frac{1}{\int _0^1h^{-1}(x)dx}$ (see [57] for example), which does not affect our analysis of the qualitative properties of the ionic flows.

3 Geometric Singular Perturbation Approach to System (2.2)–(2.3)

Denote the derivative with respect to x by overdot and introduce $u=\varepsilon {\dot{\phi }}$ and $\tau =x$. We rewrite system (2.2) into the following standard form for singularly perturbed system, the so-called slow system:

$$\begin{aligned} \begin{aligned} \varepsilon {\dot{\phi }}=&u,\quad \varepsilon {\dot{u}}=-z_1c_1-z_2c_2-z_3c_3, \quad \varepsilon {\dot{c}}_1=-z_1c_1u-\varepsilon J_1,\\ \varepsilon {\dot{c}}_2=&-z_2c_2 u-\varepsilon J_2,\quad \varepsilon {\dot{c}}_3=-z_3c_3 u-\varepsilon J_3,\quad \dot{J}_k=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

(3.1)

We will treat system (3.1) as a singularly perturbed system with $\varepsilon$ being the singular parameter, whose phase space is ${\mathbb {R}}^9$ with state variables $(\phi , u, c_1, c_2, c_3, J_1, J_2, J_3, \tau )$.

For $\varepsilon >0$, under the rescaling $x=\varepsilon \xi$ of the independent variable, one gets the so-called fast system with prime denoting the derivative about the variable $\xi$,

$$\begin{aligned} \begin{aligned} \phi '=&u,\quad u'=-z_1c_1-z_2c_2-z_3c_3, \quad c_1'=-z_1c_1u-\varepsilon J_1,\\ c_2'=&-z_2c_2u-\varepsilon J_2,\quad c_3'=-z_3c_3u-\varepsilon J_3,\quad J'_k=0,\quad \tau '=\varepsilon . \end{aligned} \end{aligned}$$

(3.2)

We comment that for $\varepsilon >0$, slow system (3.1) and fast system (3.2) have exactly the same phase portrait. However, their limiting systems at $\varepsilon =0$ are different. The limiting system of (3.1) is called the limiting slow system, whose orbits are called slow orbits or regular layers. The limiting system of (3.2) is the limiting fast system, whose orbits are called fast orbits or singular (boundary and/or internal) layers. Under this context, we define a singular orbit of system (3.1) or (3.2) to be a continuous and piecewise smooth curve in ${\mathbb {R}}^9$ that is a union of finitely many slow and fast orbits. Very often, limiting slow and fast systems provide complementary information on state variables. Accordingly, the main task is to patch the limiting information together to form a solution for the entire $\varepsilon >0$ system.

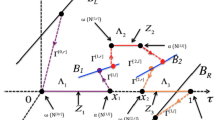
Let $B_L$ and $B_R$ be the subsets of the phase space ${\mathbb {R}}^9$ defined by

$$\begin{aligned} \begin{aligned} B_L=&\{(V, u, L_1, L_2, L_3, J_1, J_2, J_3, 0)\in {\mathbb {R}}^9: \text {arbitrary}\ u, J_1, J_2, J_3\},\\ B_R=&\{(0, u, R_1, R_2, R_3, J_1, J_2, J_3,1)\in {\mathbb {R}}^9: \text {arbitrary}\ u, J_1, J_2, J_3\}. \end{aligned} \end{aligned}$$

(3.3)

Then the original boundary value problem is equivalent to a connecting problem, namely, finding a solution of (3.1) or (3.2) from $B_L$ to $B_R$ (see, for example, [49]).

3.1 Geometric Construction of Singular Orbits

We will construct a singular orbit on [0, 1] connecting $B_L$ to $B_R$ [24, 55, 56]. In general, such an orbit will include two boundary layers and a regular layer.

3.1.1 Limiting Fast Dynamics and Boundary Layers

Setting $\varepsilon =0$ in (3.1), we get the so-called slow manifold

$$\begin{aligned} {\mathcal {Z}}=\{u=0, \;z_1c_1+ z_2c_2+z_3c_3=0\}. \end{aligned}$$

(3.4)

Setting $\varepsilon =0$ in (3.2), we get the limiting fast system

$$\begin{aligned} \begin{aligned} \phi '=&u,\quad u'=-z_1c_1-z_2c_2-z_3c_3, \quad c'_1=-z_1c_1u,\\ c'_2=&-z_2c_2u, \quad c'_3=-z_3c_3u,\quad J'_k= 0,\quad \tau '=0. \end{aligned} \end{aligned}$$

(3.5)

Observe that the slow manifold ${{\mathcal {Z}}}$ is the set of equilibria of (3.5). We have [5, 56, 57]

Lemma 3.1

For the limiting fast system (3.5), the slow manifold ${\mathcal {Z}}$ is normally hyperbolic.

We denote the stable (resp. unstable) manifold of ${\mathcal {Z}}$ by $W^s({\mathcal {Z}})$ (resp. $W^u({\mathcal {Z}})$). Let $M_L$ (resp. $M_R$) be the collection of orbits from $B_L$ (resp. $B_R$) in forward (resp. backward) time under the flow of system (3.5). Then, for a singular orbit connecting $B_L$ to $B_R$, the boundary layer at $x=0$ must lie in $N_L=M_L\cap W^s({\mathcal {Z}})$ and the boundary layer at $x=1$ must lie in $N_R=M_R\cap W^u({\mathcal {Z}})$. In this part, we will determine the boundary layers $N_L$ and $N_R$, and their landing points $\omega (N_L)$ and $\alpha (N_R)$ on the slow manifold ${{\mathcal {Z}}}$. The regular layer, which is determined by the limiting slow system in § 3.1.2, will lie in ${{\mathcal {Z}}}$ and connect the landing points $\omega (N_L)$ at $x=0$ and $\alpha (N_R)$ at $x=1$.

Proposition 3.2

• (i) System (3.5) has the following first integrals

  $$\begin{aligned} H_1=&c_1e^{z_1\phi },\quad H_2=c_2e^{z_2\phi },\quad H_3=c_3e^{z_3\phi },\quad H_4=\frac{u^2}{2}-c_1-c_2-c_3,\\ H_5=&J_1,\quad H_6=J_2,\quad H_7=J_3,\quad H_8=\tau . \end{aligned}$$

• (ii) Let $\Gamma ^0\subset N_L$ be a boundary at $x=0$. Assume $\Gamma ^0$ is the orbit of the solution $z(\xi )=(\phi (\xi ), u(\xi ), c_1(\xi ), c_2(\xi ), c_3(\xi ), J_1, J_2, J_3, 0)$ with $z(0)\in B_L$ and $\lim _{\xi \rightarrow +\infty }z(\xi )=z(+\infty )\in \mathcal{Z}.$ Then, $\phi (\xi )$ is determined by the Hamiltonian system

  $$\begin{aligned} \phi ''+z_1L_2e^{-z_1(\phi -V)}+z_2L_2e^{-z_2(\phi -V)}+z_3L_3e^{-z_3(\phi -V)}=0 \end{aligned}$$

  together with $\phi (+\infty )=\phi ^L$, where $\phi ^L$ is the unique solution of

  $$\begin{aligned} z_1L_2e^{-z_1(\phi -V)}+z_2L_2e^{-z_2(\phi -V)}+z_3L_3e^{-z_3(\phi -V)}=0; \end{aligned}$$

  $u(\xi )=\phi '(\xi )$ with $u(0)=u^{l}$ and $u(+\infty )=0$, where

  $$\begin{aligned} u^{l}=sgn(\phi ^L-V)\left( \sum _{k=1}^3 2L_k(1-e^{z_k(V-\phi ^L)})\right) ^{\frac{1}{2}}, \end{aligned}$$

  where sgn is the sign function; and

  $$\begin{aligned} c_k(\xi )=L_ke^{-z_k(\phi (\xi )-V)} \end{aligned}$$

  with $c_k(0)=L_k$ and $c_k^L:=c_k(+\infty )=L_ke^{-z_k(\phi ^L-V)}$. The stable manifold $W^s({\mathcal {Z}})$ intersects $B_L$ transversally at points $\big (V, u^l,L_1,L_2, L_3, J_1, J_2, J_3, 0\big ),$ and the $\omega$-limit set of $N_L=M_L \bigcap W^s({\mathcal {Z}})$ is

  $$\begin{aligned} \omega (N_L)=\big \{(\phi ^L, 0, c_{1}^L, c_{2}^L, c_3^L, J_1, J_2, J_3, 0)\big \}. \end{aligned}$$

• (iii) Let $\Gamma ^1\subset N_R$ be a boundary at $x=1$. Assume $\Gamma ^1$ is the orbit of the solution $z(\xi )=(\phi (\xi ), u(\xi ), c_1(\xi ), c_2(\xi ), c_3(\xi ), J_1, J_2, J_3, 0)$ with $z(0)\in B_R$ and $\lim _{\xi \rightarrow -\infty }z(\xi )=z(-\infty )\in \mathcal{Z}.$ Then, $\phi (\xi )$ is determined by the Hamiltonian system

  $$\begin{aligned} \phi ''+z_1R_1e^{-z_1(\phi -0)}+z_2R_2e^{-z_2(\phi -0)}+z_3R_3e^{-z_3(\phi -0)}=0 \end{aligned}$$

  together with $\phi (-\infty )=\phi ^R$, where $\phi ^R$ is the unique solution of

  $$\begin{aligned} z_1R_1e^{-z_1(\phi -0)}+z_2R_2e^{-z_2(\phi -0)}+z_3R_3e^{-z_3(\phi -0)}=0; \end{aligned}$$

  $u(\xi )=\phi '(\xi )$ with $u(0)=u^{r}$ and $u(-\infty )=0$, where

  $$\begin{aligned} u^{r}=sgn(\phi ^R-0)\left( \sum _{k=1}^3 2R_k(1-e^{z_k(0-\phi ^R)})\right) ^{\frac{1}{2}}, \end{aligned}$$

  where sgn is the sign function; and

  $$\begin{aligned} c_k(\xi )=R_ke^{-z_k(\phi (\xi )-0)} \end{aligned}$$

  with $c_k(0)=R_k$ and $c_k^R:=c_k(-\infty )=R_ke^{-z_k(\phi ^R-0)}$. The unstable manifold $W^u({\mathcal {Z}})$ intersects $B_R$ transversally at points $\big (0, u^r,R_1,R_2, R_3, J_1, J_2, J_3, 1\big ),$ and the $\alpha$-limit set of $N_R=M_R \bigcap W^u({\mathcal {Z}})$ is

  $$\begin{aligned} \omega (N_R)=\big \{(\phi ^R, 0, c_{1}^R, c_{2}^R, c_3^R, J_1, J_2, J_3, 1)\big \}. \end{aligned}$$

Proof

Statement (i) can be checked directly. We provide a detailed proof for statement (ii). We assume $z(\xi )=(\phi (\xi ), u(\xi ), c_1(\xi ), c_2(\xi ), c_3(\xi ), J_1(\xi ), J_2(\xi ), J_3(\xi ), \tau (\xi ))$ is a solution of the limiting fast system (3.5) from $B_L$ to $\mathcal{Z}$; namely, $z(\xi )\in N_L$. It follows that $J_k(\xi )=J_k$ are some constants and $\tau (\xi )=0$. Notice that $z(0)\in B_L$ and $\lim _{\xi \rightarrow +\infty }z(\xi )=z(+\infty )\in \mathcal{Z}.$ One has $\phi (0)=V,\ c_k(0)=L_k, \ u(+\infty )=0,$ and $z_1c_1(+\infty )+z_2c_2(+\infty )+z_3c_3(+\infty )=0.$ Define $u(0)=u^l$. By the integrals in statement (i), we get

$$\begin{aligned}\ln c_k(\xi )+z_k\phi (\xi )=\ln L_k+z_kV.\end{aligned}$$

Hence,

$$\begin{aligned} c_k(\xi )=L_ke^{-z_k(\phi (\xi )-V)}. \end{aligned}$$

(3.6)

Now the first two equations in the limiting fast system (3.5) read

$$\begin{aligned} \phi '=u,\quad u'=-z_1L_1e^{-z_1(\phi -V)}-z_2L_2e^{-z_2(\phi -V)}-z_3L_3e^{-z_3(\phi -V)}, \end{aligned}$$

(3.7)

which is a Hamiltonian system with a Hamiltonian function given by

$$\begin{aligned} H(\phi , u)=\frac{1}{2}u^2-z_1L_1e^{-z_1(\phi -V)}-z_2L_2e^{-z_2(\phi -V)}-z_3L_3e^{-z_3(\phi -V)}. \end{aligned}$$

Not difficult to see that the above Hamiltonian function is exactly the integral $H_4$ in statement (i) with the relation (3.6). The equilibria of (3.7) are given by

$$\begin{aligned} u=0,\ z_1L_1e^{-z_1(\phi -V)}+z_2L_2e^{-z_2(\phi -V)}+z_3L_3e^{-z_3(\phi -V)}=0. \end{aligned}$$

(3.8)

We now claim that $\phi ^L$ is the unique solution of the second equation in (3.8). To get started, we let

$$\begin{aligned} f(\phi )=z_1L_1e^{-z_1(\phi -V)}+z_2L_2e^{-z_2(\phi -V)}+z_3L_3e^{-z_3(\phi -V)}. \end{aligned}$$

(3.9)

It is easy to see that

$$\begin{aligned} f'(\phi )=-z_1^2L_1e^{-z_1(\phi -V)}-z_2^2L_2e^{-z_2(\phi -V)}-z_3^2L_3e^{-z_3(\phi -V)}<0, \end{aligned}$$

which implies that $f(\phi )$ is a decreasing function. Note that in our set-up, $z_1>0,\ z_2>0,\ z_3<0$ and $L_k$’s are positive, one has $f(\phi )\rightarrow -\infty$ as $\phi \rightarrow +\infty$ and $f(\phi )\rightarrow +\infty$ as $\phi \rightarrow -\infty$. Correspondingly, (3.8) has a unique solution.

Let $c_k(+\infty )=c_k^L$, then, from (3.6), one has

$$\begin{aligned} c_k^L=L_ke^{-z_k(\phi ^L-V)}. \end{aligned}$$

Evaluating the integral $H_4$ in Statement (i) at $\xi =0$ and $\xi \rightarrow +\infty$, we have

$$\begin{aligned} \frac{1}{2}u(0)-L_1-L_2-L_3=-L_1e^{-z_1(\phi ^L-V)}-L_2e^{-z_2(\phi ^L-V)}-L_3e^{-z_3(\phi ^L-V)}, \end{aligned}$$

which gives the expression for $u^l$. The choice of the sign can be determined from the phase portrait sketched in Fig. 1.

Fig. 1

The phase portrait for the Hamiltonian system (3.7). The sign of $u^l$ agrees with the sign of $(\phi ^L-V)$

Finally, we claim that the expressions under the square root in $u^l$ and $u^r$ are non-negative. We just provide the proof for the expression in $u^l$. Let

$$\begin{aligned} F(\phi )=L_1\left( 1-e^{z_1(V-\phi )}\right) +L_2\left( 1-e^{z_1(V-\phi )}\right) +L_1\left( 1-e^{z_1(V-\phi )}\right) . \end{aligned}$$

Notice that $F'(\phi )=f(\phi )$ and $F''(\phi )=f'(\phi )$ where $f(\phi )$ is defined in (3.9). Since $f'(\phi )<0$, one has $F(\phi )$ is concave down. Together with $F'(\phi ^L)=f(\phi ^L)=0$, one has $F(\phi ^L)$ is the unique maximal value of $F(\phi )$, and particularly, $F(\phi ^L)\ge F(V)=0.$ This completes the proof. $\square$

3.1.2 Limiting Slow Dynamics and Regular Layers

We now construct the regular layer $\Lambda$ on ${\mathcal {Z}}$ connecting $\omega (N_L)$ and $\alpha (N_R)$. Notice that, for $\varepsilon =0$, system (3.1) loses most information. To remedy this degeneracy, we follow the idea in [5, 24, 55,56,57] and rescale system (3.1) by setting

$$\begin{aligned} u=\varepsilon p,\quad -z_3 c_3=z_1c_1+z_2c_2+\varepsilon q. \end{aligned}$$

(3.10)

Via the new variables, system (3.1) becomes

$$\begin{aligned} \begin{aligned} {\dot{\phi }}=&p,\quad \varepsilon {\dot{p}}=q, \\ \varepsilon {\dot{q}}=&\left( (z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2-\varepsilon z_3q \right) p+z_1J_1 +z_2J_2+z_3J_3,\\ {\dot{c}}_1=&- zc_1 p-J_1,\quad {\dot{c}}_2=-zc_2p-J_2,\quad {\dot{J}}_k=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

(3.11)

It is again a singular perturbation problem and its limiting slow system is

$$\begin{aligned} \begin{aligned} {\dot{\phi }}=&p,\quad q=0, \quad p=-\frac{z_1 J_1+z_2J_2+z_3J_3}{(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2},\\ {\dot{c}}_1=&- z_1c_1p-J_1, \quad {\dot{c}}_2=- z_2c_2p-J_2,\quad {\dot{J}}_k=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

(3.12)

For system (3.12), the slow manifold is

$$\begin{aligned} {\mathcal {S}}=\bigg \{q=0, \; p=-\frac{z_1 J_1+z_2J_2+z_3J_3}{(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2}\bigg \}. \end{aligned}$$

Therefore, the limiting slow system on ${\mathcal {S}}$ is

$$\begin{aligned} \begin{aligned} {\dot{\phi }}=&-\frac{z_1 J_1+z_2J_2+z_3J_3}{(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2},\\ {\dot{c}}_1=&\frac{z_1 J_1+z_2J_2+z_3J_3}{(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2}z_1c_1-J_1, \\ {\dot{c}}_2=&\frac{z_1 J_1+z_2J_2+z_3J_3}{(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2}z_2c_2-J_2, \quad {\dot{J}}_k=0,\quad {\dot{\tau }}=1. \end{aligned} \end{aligned}$$

(3.13)

Notice that, on ${\mathcal {S}}$ where $q=0$, one has from (3.10),

$$\begin{aligned} z_1c_1+z_2c_2=-z_3c_3, \end{aligned}$$

which yields

$$\begin{aligned} (z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2=&z_1^2c_1+z_2^2c_2-z_3(z_1c_1+z_2c_2)\\ =&z_1^2c_1+z_2^2c_2+z_3^2c_3>0 \end{aligned}$$

since $c_k$’s are concentrations of ion species and we are only interested in solutions with $c_k>0$ for $k=1,2,3.$

Multiply $(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2$ on the right-hand side of system (3.13), the system reads, in terms of a new independent variable, say y,

$$\begin{aligned} \begin{aligned} \frac{d\phi }{dy}=&-(z_1 J_1+z_2J_2+z_3J_3),\\ \frac{dc_1}{dy}=&\big (z_1 J_1+z_2J_2+z_3J_3\big )z_1c_1-J_1\big ((z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2\big ), \\ \frac{dc_2}{dy}=&\big (z_1 J_1+z_2J_2+z_3J_3\big )z_2c_2-J_2\big ((z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2\big ), \\ {\dot{J}}_k=&0,\quad \frac{d\tau }{dy}=(z_1-z_3)z_1c_1+(z_2-z_3)z_2c_2. \end{aligned} \end{aligned}$$

(3.14)

Observe that the equations for $c_1$ and $c_2$ form a linear system

$$\begin{aligned} \left( \begin{array}{cccc} \frac{dc_1}{dy} \\ \frac{dc_2}{dy} \end{array} \right) =\left( \begin{array}{cccc} z_1\sum _{k=1}^3z_kJ_k+z_1(z_3-z_1)J_1 &{} z_2(z_3-z_2)J_1\\ z_1(z_3-z_1)J_2 &{} z_2\sum _{k=1}^3z_kJ_k+z_2(z_3-z_2)J_2 \end{array} \right) \left( \begin{array}{cccc} c_1 \\ c_2 \end{array} \right) . \end{aligned}$$

By the variation of parameter formula, together with the initial condition $(\phi ^L, c_1^L, c_2^L, J_1, J_2, J_3, 0)\in \omega (N_L)$, we obtain the solution of system (3.14)

$$\begin{aligned} \begin{aligned} \phi (y)=&\phi ^L-y(z_1J_1+z_2J_2+z_3J_3),\\ C(y)=&e^{Ay}C^L,\\ \tau =&(z_1-z_3)z_1\int _0^yc_1(s)ds+(z_2-z_3)z_2\int _0^yc_2(s)ds, \end{aligned} \end{aligned}$$

(3.15)

where $C(y)=(c_1(y),c_2(y)^{T}\ C^L=(c_1^L, c_2^L)^{T}$, and

$$\begin{aligned} A=\left( \begin{array}{cccc} z_1\sum _{k=1}^3z_kJ_k+z_1(z_3-z_1)J_1 &{} z_2(z_3-z_2)J_1\\ z_1(z_3-z_1)J_2 &{} z_2\sum _{k=1}^3z_kJ_k+z_2(z_3-z_2)J_2 \end{array} \right) . \end{aligned}$$

Note that we are seeking for solution of (3.14) lying on $\Lambda$ from $\omega (N_L)$ to $\alpha (N_R).$ We suppose $\tau (y_0)=1$ for some $y_0$ which is necessarily positive, and necessarily, $\phi (0)=\phi ^R$ and $C(y_0)=C^R=(c_1^R, c_2^R)^{T}$. We now evaluate (3.15) and get

$$\begin{aligned} \begin{aligned} \phi ^R=&\phi ^L-y_0(z_1J_1+z_2J_2+z_3J_3),\\ C^R=&e^{Ay_0}C^L,\\ 1=&(z_1-z_3)z_1\int _0^{y_0}c_1(s)ds+(z_2-z_3)z_2\int _0^{y_0}c_2(s)ds, \end{aligned} \end{aligned}$$

(3.16)

Observe that

$$\begin{aligned} (z_1(z_1-z_3), z_2(z_2-z_3))=\frac{1}{z_3(J_1+J_2+J_3)}(z_1-z_3,z_2-z_3)A. \end{aligned}$$

System (3.16) is then equivalent to

$$\begin{aligned} \begin{aligned} \phi ^R=&\phi ^L-y_0(z_1J_1+z_2J_2+z_3J_3),\\ C^R=&e^{Ay_0}C^L,\\ J_1+J_2+J_2=&\frac{(z_1-z_3, z_2-z_3)(C^L-C^R)}{z_3}. \end{aligned} \end{aligned}$$

(3.17)

We comment that there are 4 unknowns $J_1, J_2, J_3$ and $y_0$, and 4 equations. Theoretically, there should have at least one solution. Of course, the solution may not be unique. Based on our discussion, associate to each solution, a singular orbit $\Gamma ^0\cup \Lambda \cup \Gamma ^1$ over the interval [0, 1] is able to be constructed.

The slow orbit

$$\begin{aligned} \Lambda (x)=\big (\phi (x), c_{1}(x), c_2(x), J_{1}, J_{2}, J_3, \tau (x)\big ) \end{aligned}$$

(3.18)

given in (3.15) connects $\omega (N_L)$ and $\alpha (N_R)$. Let ${\bar{M}}_L$ (resp., ${\bar{M}}_R$) be the forward (resp., backward) image of $\omega (N_L)$ (resp., $\alpha (N_R)$) under the slow flow (3.13). One has the following result whose proof can be established by a similar argument as those in [48, 56, 57, 60].

Proposition 3.3

On the seven-dimensional slow manifold ${{\mathcal {S}}}$, ${\bar{M}}_L$ and ${\bar{M}}_R$ intersect transversally along the unique orbit $\Lambda (x)$ given in (3.18).

3.2 Existence of Solutions Near the Singular Orbit

We have constructed a unique singular orbit on [0,1] that connects $B_L$ to $B_R$. It consists of two boundary layer orbits $\Gamma ^0\cup \Gamma ^1$ and a regular layer $\Lambda$ with $\Gamma ^0$ from the point $(V, u^l, L_1,L_2, L_3,J_{1}, J_{2}, J_3, 0) \in B_L$ to the point $(\phi ^L, 0, c_1^L, c_2^L, c_3^L, J_1, J_2,J_3, 0) \in \omega (N_L) \subset {\mathcal {Z}},$ and $\Gamma ^1$ from the point $(\phi ^R, 0, c_1^R, c_2^R, c_3^R,J_1, J_2, J_3,1) \in \alpha (N_R) \subset {\mathcal {Z}}$ to the point $(0, u^r, R_1, R_2, R_3,J_1, J_2, J_3,1) \in B_R,$ and $\Lambda \subset {\mathcal {Z}}$ connecting the two landing points $(\phi ^L, 0, c_1^L, c_2^L, c_3^L,J_1, J_2, J_3,0) \in \omega (N_L)$ and $(\phi ^R, 0, c_1^R, c_2^R, c_3^R,J_1, J_2, J_3,1) \in \alpha (N_R)$ of the two boundary layers.

We now establish the existence of a solution to (2.2)–(2.3) near the singular orbit constructed above which is a union of two boundary layers and one regular layer $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$. The proof follows the same line as that in [24, 48, 55,56,57] and the main tool used is the Exchange Lemma (see, for example [49,50,51, 80]) of geometric singular perturbation theory.

Theorem 3.4

Let $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$ be the singular orbit of the connecting problem for (3.1) associated with $B_L$ and $B_R$ in (3.3). Then, for $\varepsilon >0$ small, the boundary value problem (2.2)–(2.3) has a unique smooth solution near the singular orbit.

Proof

Fix $\delta >0$ small to be determined. Define

$$\begin{aligned} B_L(\delta )=\left\{ (V, u, L_1, L_2, L_3, J_1, J_2, J_3, 0)\in {\mathbb {R}}^9: |u-u^l|<\delta , |J_i-J_i(\nu )|<\delta \right\} . \end{aligned}$$

For $\varepsilon >0$, let $M_L(\varepsilon ,\delta )$ be the forward trace of $B_L(\delta )$ under the flow of system (3.1) or equivalently of system (3.2) and let $M_R(\varepsilon )$ be the backward trace of $B_R$. To prove the existence and uniqueness statement, it suffices to show that $M_L(\varepsilon ,\delta )$ intersects $M_R(\varepsilon )$ transversally in a neighborhood of the singular orbit $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$. The latter will be established by an application of the Exchange Lemma.

Note that $\dim B_L(\delta )$=4. It is obvious that the vector field of the fast system (3.2) is not tangent to $B_L(\delta )$ for $\varepsilon \ge 0$, it follows that $\dim M_L(\varepsilon ,\delta )$=5. We next apply the Exchange Lemma to track $M_L(\varepsilon ,\delta )$ in the vicinity of $\Gamma ^0 \bigcup \Lambda \bigcup \Gamma ^1$. Under the conditions

• (i) the transversality of the intersection $B_L(\delta ) \bigcap W^s({\mathcal {Z}})$ along $\Gamma ^0$ in Proposition 3.2 implies the transversality of the intersection $M_L(0,\delta ) \bigcap W^s({\mathcal {Z}})$;

• (ii) we have also established that $\dim \omega (N_L)=\dim N_L-1=3$ in Proposition 3.2 and that the limiting slow flow is not tangent to $\omega (N_L)$ in Sect. 3.1.2;

the Exchange Lemma [49,50,51, 80] states that there exist $\rho >0$ and $\varepsilon _1>0$ such that, if $0<\varepsilon \le \varepsilon _1$, then $M_L(\varepsilon ,\delta )$ will first follow $\Gamma ^0$ toward $\omega (N_L) \subset {\mathcal {Z}}$, then follow the trace of $\omega (N_L)$ in the vicinity of $\Lambda$ toward $\{\tau =1\}$, leave the vicinity of ${\mathcal {Z}}$, and, upon exiting, a portion of $M_L(\varepsilon ,\delta )$ is $C^1$ $O(\varepsilon )$-close to $W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))$ in the vicinity of $\Gamma ^1$. Note that $\dim W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))=\dim M_L(\varepsilon ,\delta )=5$.

It remains to show that $W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))$ intersects $M_R(\varepsilon )$ transversally since $M_L(\varepsilon ,\delta )$ is $C^1$ $O(\varepsilon )$-close to $W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))$. Recall that, for $\varepsilon =0$, $M_R$ intersects $W^u(\mathcal{Z})$ transversally along $N_R$ (Proposition 3.2); in particular, at $\gamma _1:=\alpha (\Gamma ^1)\in \alpha (N_R)\subset \mathcal{Z}$, we have

$$\begin{aligned} T_{\gamma _1}M_R=T_{\gamma _1}\alpha (N_R)\oplus T_{\gamma _1}W^u(\gamma _1)\oplus \text{ span }\{V_s\}, \end{aligned}$$

where, $T_{\gamma _1}W^u(\gamma _1)$ is the tangent space of the one-dimensional unstable fiber $W^u(\gamma _1)$ at $\gamma _1$ and the vector $V_s\not \in T_{\gamma _1}W^u(\mathcal{Z})$ (the latter follows from the transversality of the intersection of $M_R$ and $W^u(\mathcal{Z})$). Also,

$$\begin{aligned} T_{\gamma _1}W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))=T_{\gamma _1}(\omega (N_L)\cdot 1)\oplus \text{ span }\{V_{\tau }\}\oplus T_{\gamma _1}W^u(\gamma _1), \end{aligned}$$

where the vector $V_{\tau }$ is the tangent vector to the $\tau$-axis as a result of the interval factor $(1-\delta _1,1+\delta _1)$. From Proposition 3.3, $\omega (N_L)\cdot 1$ and $\alpha (N_R)$ are transversal on $\mathcal{Z}\cap \{\tau =1\}$. Therefore, at $\gamma _1$, the tangent spaces $T_{\gamma _1}M_R$ and $T_{\gamma _1}W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))$ contain seven linearly independent vectors: $V_s$, $V_{\tau }$, $T_{\gamma _1}W^u(\gamma _1)$ and the other four from $T_{\gamma _1}(\omega (N_L)\cdot 1)$ and $T_{\gamma _1}\alpha (N_R)$; that is, $M_R$ and $W^u(\omega (N_L) \times (1-\delta _1,1+\delta _1))$ intersect transversally. We thus conclude that, there exists $0<\varepsilon _0\le \varepsilon _1$ such that, if $0<\varepsilon \le \varepsilon _0$, then $M_L(\varepsilon ,\delta )$ intersects $M_R(\varepsilon )$ transversally.

For uniqueness, note that the transversality of the intersection $M_L(\varepsilon ,\delta ) \cap M_R(\varepsilon )$ implies $\dim (M_L(\varepsilon ,\delta ) \cap M_R(\varepsilon ))=\dim M_L(\varepsilon ,\delta )+\dim M_R(\varepsilon )-9=1$. Thus, there exists $\delta _0>0$ such that, if $0<\delta \le \delta _0$, the intersection $M_L(\varepsilon ,\delta ) \cap M_R(\varepsilon )$ consists of precisely one solution near the singular orbit $\Gamma ^0 \cup \Lambda \cup \Gamma ^1$. $\square$

4 Qualitative Properties of Ionic Flows: Case Studies

We would like to point out, for the PNP system with three ion species, two positively charged and one negatively charged, an explicit solution to the limiting slow system (the zeroth order approximation in $\varepsilon$) cannot be obtained explicitly if $z_1\ne z_2.$ However, the capability of constructing such an explicit solution, from which one can derive the approximated individual flux explicitly in terms of boundary conditions and other physical parameters, is crucial for us to further examine the qualitative properties of ionic flows. For this purpose, we assume that the two positively charged ion species have the same valences, that is, $z_1=z_2>0$. Of particular interest in this work are

• (I) Effects on ionic flows from boundary layers in terms of both individual fluxes and the total flow rate of charges;

• (II) Competitions between two cations (positively charged ion species) with boundary layers.

Note that, under electroneutrality boundary conditions, two boundary layers disappear. Therefore, to examine the boundary layer effects on ionic flows, a first step is to examine the ionic flow properties of interest without assuming electroneutrality conditions in boundary concentrations but close to the neutral state. More precisely, we assume

$$\begin{aligned} -z_3L_3=\sigma (z L_1+z L_2) \quad \text{ and }\quad -z_3R_3=\rho (z R_1+z R_2), \end{aligned}$$

(4.1)

for some positive constants $\sigma$ and $\rho$, which are not both equal to 1 and study the case as $(\sigma ,\rho )\rightarrow (1,1)$ since $(\sigma ,\rho )=(1,1)$ in (4.1) implies electroneutrality conditions on boundary concentrations.

To get started, we first obtain the explicit approximations of the individual fluxes $J_1,\ J_2$ and $J_3$, and expand $J_{k},\ k=1,2,3,$ at the point $(\sigma ^*,\rho ^*)=(1,1)$ up to the first order (we neglect higher order terms).

Lemma 4.1

Under the assumption $z_1=z_2:=z$, from (3.17), one has the zeroth order (in $\varepsilon$) approximations of the individual fluxes

$$\begin{aligned} J_{1}=&\frac{c_1^L+c_2^L-c_1^R-c_2^R}{\ln (c_1^L+c_2^L)-\ln (c_1^R+c_2^R)}\frac{\ln (c_1^L+c_2^L)-\ln (c_1^R+c_2^R)e^{z(\phi ^R-\phi ^L)}}{c_1^L+c_2^L-(c_1^R+c_2^R)e^{z(\phi ^R-\phi ^L)}}(c_1^L-c_1^Re^{z(\phi ^R-\phi ^L)}),\\ J_{2}=&\frac{c_1^L+c_2^L-c_1^R-c_2^R}{\ln (c_1^L+c_2^L)-\ln (c_1^R+c_2^R)}\frac{\ln (c_1^L+c_2^L)-\ln (c_1^R+c_2^R)e^{z(\phi ^R-\phi ^L)}}{c_1^L+c_2^L-(c_1^R+c_2^R)e^{z(\phi ^R-\phi ^L)}}(c_2^L-c_2^Re^{z(\phi ^R-\phi ^L)}),\\ J_3=&-\frac{z}{z_3}\frac{c_1^L+c_2^L-c_1^R-c_2^R}{\ln (c_1^L+c_2^L)-\ln (c_1^R+c_2^R)}\left( \ln (c_1^L+c_2^L)-\ln (c_1^R+c_2^R)e^{z_3(\phi ^R-\phi ^L)}\right) . \end{aligned}$$

Proposition 4.2

Assume conditions (4.1). For $\phi ^L,\ \phi ^R,\ c_k^L$ and $c_k^R$ defined in Proposition 3.2, one has

$$\begin{aligned} \phi ^L=&V-\frac{\ln \sigma }{z-z_{3}},\ \ c_1^L=L_1\sigma ^{\frac{z}{z-z_{3}}},\ \ c_2^L=L_2\sigma ^{\frac{z}{z-z_{3}}};\\ \phi ^R=&-\frac{\ln \rho }{z-z_{3}},\ \ c_1^R=R_1\rho ^{\frac{z}{z-z_{3}}},\ \ c_2^R=R_2\rho ^{\frac{z}{z-z_{3}}}. \end{aligned}$$

Furthermore, as $(\sigma ,\rho )\rightarrow (1,1),$ up to the first order, one has

$$\begin{aligned} \begin{aligned} \mathcal{J}_1(V;\sigma ,\rho )=&D_1f_{1}(L_1,L_2, R_1,R_2;V)g(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})\left( L_{1}-R_{1}e^{-zV}\right) ,\\ \mathcal{J}_2(V;\sigma ,\rho )=&D_2f_{1}(L_1,L_2, R_1,R_2;V)g(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})\left( L_{2}-R_{2}e^{-zV}\right) ,\\ \mathcal{J}_3(V;\sigma ,\rho )=&-\frac{z}{z_3}D_3f_{2}(L_1,L_2, R_1,R_2;V)g(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})\\&\times \left( L_{1}+L_{2}-(R_{1}+R_{2})e^{-z_{3}V}\right) , \end{aligned} \end{aligned}$$

(4.2)

where $f_1=f_{1}(L_{1},L_{2},R_{1},R_{2};V),\ f_2=f_{2}(L_{1},L_{2},R_{1},R_{2};V)$ and $g=(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})$ are defined by

$$\begin{aligned} \begin{aligned} f_{1}=&\frac{\ln \left( L_{1}+L_{2}\right) -\ln \left( R_{1}+R_{2}\right) +zV}{(L_{1}+L_{2})-(R_{1}+R_{2})e^{-zV}} ,\\ f_{2}=&\frac{\ln \left( L_{1}+L_{2}\right) -\ln \left( R_{1}+R_{2}\right) +z_{3}V}{(L_{1}+L_{2})-(R_{1}+R_{2})e^{-z_{3}V}},\\ g=&f_0(L_1,L_2,R_1,R_2)+\frac{z}{z-z_{3}}g_0(\sigma ,\rho ;L_1,L_2,R_1,R_2),\\ \end{aligned} \end{aligned}$$

(4.3)

where

$$\begin{aligned} \begin{aligned} f_0=&\frac{\left( L_{1}+L_{2}\right) -\left( R_{1}+R_{2}\right) }{\ln (L_{1}+L_{2})-\ln (R_{1}+R_{2})},\\ g_0=&\frac{\big (L_{1}+L_{2}-f_{0}\big )(\sigma -1)}{\ln \left( L_{1}+L_{2}\right) -\ln \left( R_{1}+R_{2}\right) } -\frac{\big (R_{1}+R_{2}-f_{0}\big )(\rho -1)}{\ln \left( L_{1}+L_{2}\right) -\ln \left( R_{1}+R_{2}\right) }. \end{aligned} \end{aligned}$$

(4.4)

The following result can be easily established.

Lemma 4.3

The functions $f_0, \ f_1$ and $f_2$ defined in (4.3) and (4.4) are positive. In particular, $f_0\rightarrow R_1+R_2>0$ as $L_1+L_2\rightarrow R_1+R_2,$ $f_1\rightarrow \frac{e^{zV}}{R_1+R_2}>0$ as $L_1+L_2\rightarrow (R_1+R_2)e^{-zV}$, and $f_2\rightarrow \frac{e^{z_3V}}{R_1+R_2}>0$ as $L_1+L_2\rightarrow (R_1+R_2)e^{-z_3V}$.

Additionally, for the function g defined in (4.3), one has

Lemma 4.4

Assume $L_1+L_2\ne R_1+R_2$. One has $g(\sigma ,\rho ;L_1,L_2,R_1,R_2)>0$ as $(\sigma ,\rho )\rightarrow (1,1)$.

Proof

Without loss of generality, we assume $L_1+L_2> R_1+R_2$. Rewrite g as $g(\sigma ,\rho ;L_1,L_2,R_1,R_2)=(R_1+R_2)h(x)$ where, with $x=\frac{L_1+L_2}{R_1+R_2}>1,$

$$\begin{aligned} h(x)=&\frac{z-z_{3}}{z}(x-1)+(\sigma -1)x+(\rho -\sigma )\frac{x-1}{\ln x}+1-\rho =\frac{h_1(x)}{\ln x}, \end{aligned}$$

with

$$\begin{aligned} h_1(x)=(\sigma -\frac{z_3}{z})x\ln x+(\rho -\sigma )(x-1)+(\frac{z_{3}}{z}-\rho )\ln x. \end{aligned}$$

Note that $h_1(1)=0$,

$$\begin{aligned} h_1'(x)= & {} (\sigma -\frac{z_3}{z})\ln x+\sigma -\frac{z_3}{z}+\rho -\sigma +\frac{\frac{z_3}{z}-\rho }{x}\Longrightarrow h_1'(1)=0.\\ h_1''(x)= & {} \frac{\sigma -\frac{z_3}{z}}{x}-\frac{\frac{z_3}{z}-\rho }{x^2}=\frac{(\sigma -\frac{z_3}{z})x+(\rho -\frac{z_3}{z})}{x^2}, \end{aligned}$$

from which $h_1''(x)>0$ for all $x>1$. It follows that $h_1'(x)$ is increasing for all $x>1$. Together with $h_1'(1)=0,$ we have $h_1'(x)>0$ for all $x>1$, which implies that $h_1(x)$ is increasing for all $x>1$. Note that $h_1(1)=0$, one can conclude that $h_1(x)>0$ for all $x>1.$ Thus, $h(x)>0$ for all $x>1$, and hence $g(\sigma ,\rho ;L_1,L_2,R_1,R_2)>0$ for $L_1+L_2>R_1+R_2$. $\square$

Similar arguments lead to the following two lemmas about $g_{0}(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})$ defined in (4.4), which are crucial for our further discussion on qualitative properties of ionic flows. For convenience, we define a function p(x), with $x=\frac{L_1+L_2}{R_1+R_2}$, by

$$\begin{aligned} p(x)=(\sigma -1)x\ln x+(\rho -\sigma )(x-1)+(1-\rho )\ln x. \end{aligned}$$

Lemma 4.5

$g_{0}(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})>0$ under one of the following conditions

• (i) $(\sigma ,\rho )\rightarrow (1^+,1^+)$,

• (ii) $L_1+L_2>R_1+R_2$ and $(\sigma ,\rho )\rightarrow (1^{+},1^{-})$ with $\sigma +\rho >2$,

• (iii) $L_1+L_2>R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{-},1^{+})$ with $\sigma +\rho >2$, and $1<\frac{L_1+L_2}{R_1+R_2}<x_1^{*}$, where $x_1^{*}$ is the unique root of $p(x)=0$ on the interval $(1,+\infty )$,

• (iv) $L_1+L_2>R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{+},1^{-})$ with $\sigma +\rho <2$, and $\frac{L_1+L_2}{R_1+R_2}>x_2^{*}$, where $x_2^{*}$ is the unique root of $p(x)=0$ on the interval $(1,+\infty )$,

• (v) $L_1+L_2<R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{-},1^{+})$ with $\sigma +\rho >2$, and $0<\frac{L_1+L_2}{R_1+R_2}<1$,

• (vi) $L_1+L_2<R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{+},1^{-})$ with $\sigma +\rho >2$, and $x_{1*}<\frac{L_1+L_2}{R_1+R_2}<1$, where $x_{1*}$ is the unique root of $p(x)=0$ on the interval (0, 1),

• (vii) $L_1+L_2<R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{-},1^{+})$ with $\sigma +\rho <2$, and $0<\frac{L_1+L_2}{R_1+R_2}<x_{2*}$, where $x_{2*}$ is the unique root of $p(x)=0$ on the interval (0, 1).

Lemma 4.6

$g_{0}(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})<0$ under one of the following conditions

• (i) $(\sigma ,\rho )\rightarrow (1^-,1^-)$,

• (ii) $L_1+L_2>R_1+R_2$ and $(\sigma ,\rho )\rightarrow (1^{-},1^{+})$ with $\sigma +\rho <2$,

• (iii) $L_1+L_2>R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{-},1^{+})$ with $\sigma +\rho >2$, and $\frac{L_1+L_2}{R_1+R_2}>{\tilde{x}}_1^{*}$, where ${\tilde{x}}_1^{*}$ is the unique root of $p(x)=0$ on the interval $(1,+\infty )$,

• (iv) $L_1+L_2>R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{+},1^{-})$ with $\sigma +\rho <2$, and $1<\frac{L_1+L_2}{R_1+R_2}<{\tilde{x}}_2^{*}$, where ${\tilde{x}}_2^{*}$ is the unique root of $p(x)=0$ on the interval $(1,+\infty )$,

• (v) $L_1+L_2<R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{+},1^{-})$ with $\sigma +\rho <2$, and $0<\frac{L_1+L_2}{R_1+R_2}<1$,

• (vi) $L_1+L_2<R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{+},1^{-})$ with $\sigma +\rho >2$, and $0<\frac{L_1+L_2}{R_1+R_2}<{\tilde{x}}_{1*}$, where ${\tilde{x}}_{1*}$ is the unique root of $p(x)=0$ on the interval (0, 1),

• (vii) $L_1+L_2<R_1+R_2$, $(\sigma ,\rho )\rightarrow (1^{-},1^{+})$ with $\sigma +\rho >2$, and ${\tilde{x}}_{2*}<\frac{L_1+L_2}{R_1+R_2}<1$, where ${\tilde{x}}_{2*}$ is the unique root of $p(x)=0$ on the interval (0, 1).

4.1 Boundary Layer Effects on Ionic Flows

To examine the effects from boundary layers, we first introduce $J_{k}^{EN}$ (resp. $I^{EN}$) to denote the individual flux (resp. the total flux of charge) with electroneutrality boundary conditions, and $J_{k}$ (resp. I) to denote the individual flux (resp. the total flux of charge) without electroneutrality boundary conditions. To investigate the boundary layer effect on ionic flows, which is equivalent to the effects from the violation of electroneutrality boundary concentrations under our setups, we define four functions $\mathcal{E}_k(V;\sigma ,\rho )=\mathcal{E}_k(V;\sigma ,\rho ;L_1,L_2,R_1,R_2),\ k=1,2,3$ and $\mathcal{E}_t(V;\sigma ,\rho )=\mathcal{E}_{t}(V; \sigma ,\rho ; L_1,L_2,R_1,R_2)$ as follows:

$$\begin{aligned} \begin{aligned} \mathcal{E}_{1}(V;\sigma ,\rho )=&J_{1}(V; \sigma ,\rho )-J_{1}^{EN}(V; 1,1)\\ =&\frac{z}{z-z_{3}}f_{1}(L_1,L_2,R_1,R_2;V)g_{0}(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})\left( L_{1}-R_{1}e^{-zV}\right) ,\\ \mathcal{E}_{2}(V;\sigma ,\rho )=&J_{2}(V; \sigma ,\rho )-J_{2}^{EN}(V; 1,1)\\ =&\frac{z}{z-z_{3}}f_{1}(L_1,L_2,R_1,R_2;V)g_{0}(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2})\left( L_{2}-R_{2}e^{-zV}\right) ,\\ \mathcal{E}_{3}(V;\sigma ,\rho )=&J_{3}(V; \sigma ,\rho )-J_{3}^{EN}(V; 1,1)\\ =&\frac{-z^{2}}{z_{3}(z-z_{3})}\left( \ln (L_1+L_2)-\ln (R_1+R_2)+ z_3V\right) g_{0}(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2}),\\ \mathcal{E}_{t}(V;\sigma , \rho )=&I(V; \sigma ,\rho )-I^{EN}(V; 1,1)\\ =&\frac{z^{2}}{z-z_3}g_0(\sigma ,\rho ;L_{1},L_{2},R_{1},R_{2}){\tilde{f}}_1(L_1,L_2,R_1,R_2;D_1,D_2;V), \end{aligned} \end{aligned}$$

(4.5)

where

$$\begin{aligned} {\tilde{f}}_1=&f_1(L_1,L_2,R_1,R_2;V)\left( D_1L_1+D_2L_2-(D_1R_1+D_2R_2)e^{-zV}\right) \\&-D_3\left( \ln (L_1+L_2)-\ln (R_1+R_2)+ z_3V\right) . \end{aligned}$$

We first identify four critical potentials which play important role in characterizing boundary layer effects on ionic flows by

$$\begin{aligned} \mathcal{E}_1(V_{1}^b;\sigma , \rho )=0,\ \mathcal{E}_2(V_{2}^b;\sigma , \rho )=0,\ \mathcal{E}_3(V_{3}^b;\sigma , \rho )=0\ \text{ and }\ \mathcal{E}_{t}(V_t^b;\sigma , \rho )=0 \end{aligned}$$

from which one gets

$$\begin{aligned} \begin{aligned} V_{1}^b=&\frac{\ln R_1-\ln L_1}{z},\ V_{2}^b=\frac{\ln R_2-\ln L_2}{z},\ V_{3}^b=\frac{\ln (R_1+R_2)-\ln (L_1+L_2)}{z}, \end{aligned} \end{aligned}$$

(4.6)

and $V_t^b$ is the unique zero of ${\tilde{f}}_1$ (see the proof in Proposition 4.7).

The following monotonicity results can be established.

Proposition 4.7

Under conditions (4.1) and one of the conditions in Lemma 4.5, for small $\varepsilon >0$, one has

• (i) $\mathcal{E}_1(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_1(V;\sigma ,\rho )<0$) for $V>V_{1}^b$ (resp. $V<V_{1}^b$). Furthermore, $\mathcal{E}_1(V;\sigma ,\rho )$ is increasing in the potential V, that is, the boundary layer effects on the individual flux $J_1$ becomes stronger as $V>V_{1}^b$ becomes larger.

• (ii) $\mathcal{E}_2(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_2(V;\sigma ,\rho )<0$) for $V>V_{2}^b$ (resp. $V<V_{2}^b$). Furthermore, $\mathcal{E}_2(V;\sigma ,\rho )$ is increasing in the potential V, that is, the boundary layer effects on the individual flux $J_2$ becomes stronger as $V>V_{2}^b$ becomes larger.

• (iii) $\mathcal{E}_3(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_3(V;\sigma ,\rho )<0$) for $V<V_{3}^b$ (resp. $V>V_{3}^b$). Furthermore, $\mathcal{E}_3(V;\sigma ,\rho )$ is decreasing in the potential V, that is, the boundary layer effects on the individual flux $J_3$ becomes weaker as $V>V_{3}^b$ becomes larger.

• (iv) $\mathcal{E}_t(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_t(V;\sigma ,\rho )<0$) for $V>V_{t}^b$ (resp. $V<V_{t}^b$), where $V_{t}^b$ is a unique potential, such that $\mathcal{E}_t(V_{t}^b;\sigma ,\rho )=0$. Furthermore, $\mathcal{E}_t(V;\sigma ,\rho )$ is increasing in the potential V, that is, the boundary layer effects on the total flux I becomes stronger as $V>V_{t}^b$ becomes larger.

Proof

From Eq. (4.5), a direct calculation gives

$$\begin{aligned} \frac{d\mathcal{E}_1}{dV}(V;\sigma ,\rho )=&\frac{z^{2}}{z-z_{3}}\frac{e^{-zV}}{(L_1+L_2-(R_1+R_2)e^{-zV})^2}g_0 {\bar{h}}(V;L_1,L_2,R_1,R_2), \end{aligned}$$

where

$$\begin{aligned}&{\bar{h}}(V;L_1,L_2,R_1,R_2)=L_1(L_1+L_2)e^{zV}-R_1(R_1+R_2)e^{-zV}+z(L_2R_1-L_1R_2)V\\&\quad +(L_2R_1-L_1R_2)(\ln (L_1+L_2)-\ln (R_1+R_2))-L_1(R_1+R_2)-R_1(L_1+L_2). \end{aligned}$$

It is easy to check that ${\bar{h}}(V;L_1,L_2,R_1,R_2)>0$ for $V\ne \frac{1}{z}\ln \frac{R_1+R_2}{L_1+L_2}$. Recall that $g_{0}>0$ under one of the conditions in Lemma 4.5. Then statement (i) follows. Statement (ii) can be established similarly and Statement (iii) is obviously. Statement (iv) can be obtained by the facts

$$\begin{aligned} \lim _{V\rightarrow -\infty }\mathcal{E}_t(V;\sigma ,\rho )= & {} -\infty , \quad \lim _{V\rightarrow \infty }\mathcal{E}_t(V;\sigma ,\rho )=\infty ,\\ \mathcal{E}_t(V;\sigma ,\rho )= & {} z(D_{1}\mathcal{E}_1(V;\sigma ,\rho )+D_{2}\mathcal{E}_2(V;\sigma ,\rho ))+z_{3}D_{3}\mathcal{E}_3(V;\sigma ,\rho ), \end{aligned}$$

and statements (i), (ii) and (iii). $\square$

Proposition 4.8

Under conditions (4.1) and one of the conditions in Lemma 4.6, for small $\varepsilon >0$, one has

• (i) $\mathcal{E}_1(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_1(V;\sigma ,\rho )<0$) for $V<V_{1}^b$ (resp. $V>V_{1}^b$). Furthermore, $\mathcal{E}_1(V;\sigma ,\rho )$ is decreasing in the potential V, that is, the boundary layer effects on the individual flux $J_1$ becomes weaker as $V>V_{1}^b$ becomes larger.

• (ii) $\mathcal{E}_2(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_2(V;\sigma ,\rho )<0$) for $V<V_{2}^b$ (resp. $V>V_{2}^b$). Furthermore, $\mathcal{E}_2(V;\sigma ,\rho )$ is decreasing in the potential V, that is, the boundary layer effects on the individual flux $J_2$ becomes weaker as $V>V_{2}^b$ becomes larger.

• (iii) $\mathcal{E}_3(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_3(V;\sigma ,\rho )<0$) for $V>V_{3}^b$ (resp. $V<V_{3}^b$). Furthermore, $\mathcal{E}_3(V;\sigma ,\rho )$ is increasing in the potential V, that is, the boundary layer effects on the individual flux $J_3$ becomes stronger as $V>V_{3}^b$ becomes larger.

• (iv) $\mathcal{E}_t(V;\sigma ,\rho )>0$ (resp. $\mathcal{E}_t(V;\sigma ,\rho )<0$) for $V<V_{t}^b$ (resp. $V>V_{t}^b$), where $V_{t}^b$ is a unique potential, such that $\mathcal{E}_t(V_{t}^b;\sigma ,\rho )=0$. Furthermore, $\mathcal{E}_t(V;\sigma ,\rho )$ is decreasing in the potential V, that is, the boundary layer effects on the total flux I becomes weaker as $V>V_{t}^b$ becomes larger.

4.2 Competitions Between Cations with Boundary Layers

We now consider the competition between two positively charged ion species with boundary layer effects, which is closely related to selectivity phenomena. For convenience, we define $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ as

$$\begin{aligned} \begin{aligned} \mathcal{E}_{1,2}(V;\sigma ,\rho )=&D_{1} \left( J_1(V;\sigma ,\rho )-J_1^{EN}(V;1,1)\right) -D_{2}\left( {J}_2(V;\sigma ,\rho )-J_2^{EN}(V;1,1)\right) \\ =&\frac{z}{z-z_{3}}f_1(L_1,L_2,R_1,R_2;V) g_{0}(L_1,L_2,R_1,R_2;\sigma ,\rho )\\&\times \left( D_1L_1-D_2L_2-(D_1R_1-D_2R_2)e^{-zV}\right) . \end{aligned} \end{aligned}$$

(4.7)

It follows directly from (4.7) that

Proposition 4.9

Under condition (4.1) and one of the conditions stated in Lemma 4.6, one has

• (i) if $D_1R_1-D_2R_2=0$, then $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ and $D_1L_1-D_2L_2$ have the opposite sign;

• (ii) if $D_1R_1-D_2R_2>0$ and $D_1L_1-D_2L_2\le 0$, then $\mathcal{E}_{1,2}(V;\sigma ,\rho )>0$ for all V;

• (iii) if $D_1R_1-D_2R_2<0$ and $D_1L_1-D_2L_2\ge 0$, then $\mathcal{E}_{1,2}(V;\sigma ,\rho )<0$ for all V;

• (iv) if $(D_1R_1-D_2R_2)(D_1L_1-D_2L_2)>0$, then $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ has the opposite sign as that of $(D_1R_1-D_2R_2)(V-V_d)$ where

  $$\begin{aligned} V_d=\frac{1}{z}\ln \frac{D_1R_1-D_2R_2}{D_1L_1-D_2L_2}. \end{aligned}$$

  (4.8)

Proof

The result follows directly from Lemmas 4.3 and 4.6. $\square$

We next study the monotonicity of $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ with respect to the potential V for fixed boundary concentrations.

Theorem 4.10

Under condition (4.1), one of the conditions stated in Lemma 4.6, and $\frac{D_1}{D_2}>\frac{R_2}{R_1},$ for small $\varepsilon >0$, one has

• (i) For $\frac{D_1}{D_2}>\frac{L_2}{L_1}$, $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ is decreasing in potential V, and $\mathcal{E}_{1,2}(V;\sigma ,\rho )=0$ has a unique solution $V_d$ defined in (4.8);

• (ii) For $\frac{D_1}{D_2}<\frac{L_2}{L_1}$, $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ decreases in the potential V if $V<V_1^d$ and increases in V if $V>V_1^d$, where $V_1^d$ is uniquely defined by $\frac{d\mathcal{E}_{1,2}}{dV}(V_1^d;\sigma ,\rho )=0$.

Proof

We only provide a detailed proof for the first statement. A similar argument leads to statement (ii) directly. From (4.7), we obtain

$$\begin{aligned} \begin{aligned} \frac{d\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV}=&\frac{z g_{0}}{(L_1+L_2-(R_1+R_2)e^{-zV})^{2}}\bigg [(D_1 L_1-D_2 L_2-(D_1 R_1-D_2 R_2)e^{-zV})\\&\quad \times (L_1+L_2-(R_1+R_2)e^{-zV})+e^{-zV}(\ln (L_1+L_2)-\ln (R_1+R_2)+zV)\\&\quad \times (R_1 L_1-L_1 R_2)(D_1+D_2)\bigg ]. \end{aligned} \end{aligned}$$

Further,

$$\begin{aligned} \begin{aligned}&\frac{d^{2}\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV^{2}}=-\frac{z^{2} g_{0}e^{-2zV}(R_1 L_2-L_1 R_2)(D_1+D_2)}{(L_1+L_2-(R_1+R_2)e^{-zV})^{3}}H(V;L_1,L_2,R_1,R_2), \end{aligned} \end{aligned}$$

(4.9)

where $H=H(V;L_1,L_2,R_1,R_2)$ is given by

$$\begin{aligned} \begin{aligned} H=&(L_1+L_2) e^{zV}(zV+\ln (L_1+L_2)-\ln (R_1+R_2)-2)\\&+(R_1+R_2)(zV+\ln (L_1+L_2)-\ln (R_1+R_2)+2). \end{aligned} \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned}&\frac{d H}{dV}=z(L_1+L_2) e^{zV}(zV+\ln (L_1+L_2)-\ln (R_1+R_2)-1) +z(R_1+R_2),\\&\frac{d^{2} H}{dV^{2}}=z^{2}(L_1+L_2) e^{zV}(zV+\ln (L_1+L_2)-\ln (R_1+R_2)). \end{aligned} \end{aligned}$$

Therefore, if $V>V_{3}^b=\frac{1}{z}\ln \left( \frac{R_1+R_2}{L_1+L_2}\right)$, $\frac{d^{2} H}{dV^{2}}>0$, that is, $\frac{d H}{dV}$ is increasing on $V\in (V_{3}^b,+\infty )$. Note that $\frac{d H}{dV}\rightarrow 0$ as $V\rightarrow V_{3}^b$. and hence, for $V>V_{3}^b$, we have $\frac{d H}{dV}>0$, which implies that H is increasing on $V\in (V_{3}^b,+\infty )$. It follows from $H\rightarrow 0$ as $V\rightarrow V_{3}^b$ that $H>0$ on the interval $(V_{3}^b,+\infty )$. Similarly, one can prove that $H<0$ on the interval $(-\infty , V_{3}^b)$.

From the above analysis and (4.9), we conclude that $\frac{d^{2}\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV^{2}}>0$ (resp. $\frac{d^{2}\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV^{2}}<0$) if $\frac{R_{1}}{R_{2}}<\frac{L_{1}}{L_{2}}$ (resp. $\frac{R_{1}}{R_{2}}>\frac{L_{1}}{L_{2}}$). Either way, one has $\frac{d\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV}$ is monotone. Note that, under the conditions $\frac{D_1}{D_2}>\frac{R_2}{R_1}$ and $\frac{D_1}{D_2}>\frac{L_2}{L_1}$,

$$\begin{aligned} \lim _{V\rightarrow -\infty }\frac{d\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV}<0\ \text{ and }\ \lim _{V\rightarrow \infty }\frac{d\mathcal{E}_{1,2}(V;\sigma ,\rho )}{dV}<0. \end{aligned}$$

Therefore, one has $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ is decreasing in potential V and the uniqueness of solutions of $\mathcal{E}_{1,2}(V;\sigma ,\rho )=0$ follows immediately from

$$\begin{aligned}\lim _{V\rightarrow -\infty }\mathcal{E}_{1,2}(V;\sigma ,\rho )=-\infty ,\ \text{ and }\ \lim _{V\rightarrow \infty }\mathcal{E}_{1,2}(V;\sigma ,\rho )=+\infty . \end{aligned}$$

$\square$

Similarly, one has

Theorem 4.11

Under condition (4.1), one of the conditions stated in Lemma 4.6, and $\frac{D_1}{D_2}<\frac{R_2}{R_1},$ for small $\varepsilon >0$, one has

• (i) For $\frac{D_1}{D_2}<\frac{L_2}{L_1}$, $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ increases in potential V, and $\mathcal{E}_{1,2}(V;\sigma ,\rho )=0$ has a unique solution $V_d$ defined as in Lemma 4.8;

• (ii) For $\frac{D_1}{D_2}>\frac{L_2}{L_1}$, $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ increases in the potential V if $V<V_2^d$ and decreases in V if $V>V_2^d$, where $V_2^d$ is uniquely defined by $\frac{d\mathcal{E}_{1,2}(V_2^d;\sigma ,\rho )}{dV}=0$.

Theorem 4.12

Under condition (4.1) and one of the conditions stated in Lemma 4.6, for small $\varepsilon >0$, one has

• (i) For $\frac{D_1}{D_2}=\frac{L_2}{L_1}$, $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ increases (resp. decreases) in the potential V if $\frac{D_1}{D_2}<\frac{R_2}{R_1}$ (resp. $\frac{D_1}{D_2}>\frac{R_2}{R_1}$).

• (ii) For $\frac{D_1}{D_2}=\frac{R_2}{R_1}$, $\mathcal{E}_{1,2}(V;\sigma ,\rho )$ increases (resp. decreases) in the potential V if $\frac{D_1}{D_2}<\frac{L_2}{L_1}$ (resp. $\frac{D_1}{D_2}>\frac{L_2}{L_1}$).

We comment that the significance of Theorems 4.10, 4.11 and 4.12 is that as the potential V changes under different nonlinear interplays of $(D_1, D_2),\ (\sigma , \rho )$, $(L_1, L_2)$ and $(R_1, R_2)$, the ion channel will eventually prefer one cation (positively charged ion species) over the other. More precisely, the individual flux of one cations becomes stronger as the potential changes compared to the other. For example, in Theorem 4.10, the individual flux $\mathcal{J}_1$ becomes stronger as the potential decreases under the condition $\frac{D_1}{D_2}>\frac{L_2}{L_1}$ and some conditions stated in Lemma 4.6. In other words, the ionic flow through membrane channels with given protein structures can be controlled through boundary potentials while boundary concentrations and diffusion coefficients satisfy certain conditions. This could potentially provide an efficient way to control and affect some biological functions.

4.3 Numerical Simulations

To further examine the boundary layer effects on ionic flows of interest, we conduct the following three numerical experiments to system (2.2)–(2.3) with small $\varepsilon >0$.

• (i) Numerically detect the so-called reversal potential $V_0$ (resp. $V_0^{EN}$) for the total flow rate of charges, namely, the potential that satisfies $I(V_0)=0$ (resp. $I^{EN}(V_0^{EN})=0$), with (resp. without) boundary layers (see Fig. 2);

• (ii) Numerically investigate the difference of the individual fluxes and I–V relations with/without boundary layers, that is, ${\mathcal {E}}_k(V;\sigma ,\rho )=J_{k}(V;\sigma ,\rho )-J_k^{EN}(V;1,1)$ and ${\mathcal {E}}_t(V;\sigma ,\rho )=I(V;\sigma ,\rho )-I^{EN}(V;1,1)$ (see Fig. 3).

• (iii) Numerically study the competitions between two cations with boundary layers, that is, ${\mathcal {E}}_{1,2}(V;\sigma ,\rho )=D_1{\mathcal {E}}_1(V,\sigma ,\rho )-D_2{\mathcal {E}}_2(V;\sigma ,\rho )$ (see Fig. 4).

To be specific, in our numerical simulations, we take

$$\begin{aligned} L_1=20, \ L_2=8; \sigma =1.02,\ \rho =0.95;\ z_1=z_2=1,\ z_3=-1, \varepsilon =0.001 \end{aligned}$$

and distinct values for $(D_1, D_2, D_3)$ and $(R_1, R_2)$ illustrated in Figures 2, 3 and 4.

Fig. 2

Reversal potentials of the total flow rate of charges. The left figure shows the reversal potential without electroneutrality boundary conditions while the right one identifies the reversal potential with neutral boundary conditions

Fig. 3

Difference of individual fluxes ${\mathcal {E}}_k(V;\sigma ,\rho ))=J_k(V;\sigma ,\rho )-J_k^{EN}(V;\sigma ,\rho )$ and total flow rate of charges ${\mathcal {E}}_t(V;\sigma ,\rho )=I(V;\sigma ,\rho )-I^{EN}(V;\sigma ,\rho )$ under different set-ups

Fig. 4

Competitions $E_{1,2}(V;\sigma ,\rho )={\mathcal {E}}_{1,2}(V;\sigma ,\rho )$ between cations under different set-ups. Upper left figure corresponds to the first statement in Theorem 4.10, Upper right one corresponds to the first statement in Theorem 4.11, Lower left one corresponds to the first statement in Theorem 4.12 and lower right one corresponds to the second statement in Theorem 4.12

To end this section, we comment that the choice of above parameters corresponds to case (iv) in Lemma 4.6 with ${\tilde{x}}_2^*=18.4580$, and other cases can be studied in a similar way. It turns out that our numerical results are consistent with the analytical ones (see Proposition 4.8 and Theorems 4.10, 4.11 and 4.12 for details). Taking the upper left figure in Figure 3 for example, our numerical result shows clearly that ${\mathcal {E}}_1(V;\sigma ,\rho )>0$ (resp. ${\mathcal {E}}_1(V;\sigma ,\rho )<0$) for $V>V_1^b$ (resp. $V<V_1^b$), where $V_1^b$ is defined as that in (4.6) but for small $\varepsilon$; furthermore, due to the fact that $\frac{d{\mathcal {E}}_1(V;\sigma ,\rho )}{dV}<0$, one has ${\mathcal {E}}_1(V;\sigma ,\rho )$ is decreasing in V. This corresponds to the first statement in Proposition 4.8. In particular, in our first numerical experiment, we identified two critical potentials, $V_0$, the reversal potential of the total flow rate of charges with boundary layers, and $V_0^{EN}$, the one without boundary layers. Under our set-ups, $V_0>V_0^{EN}$, and the dynamics of the total flow rate of charges over the interval $(V_0^{EN}, V_0)$ are quite different, more precisely, $I(V)<0$ on $(V_0^{EN}, V_0)$ while $I^{EN}>0$ over $(V_0^{EN}, V_0)$. The difference is caused by the violation of electroneutrality boundary conditions, which produces totally different dynamics of ionic flows. This again indicates the interest and significance of the study of effects on ionic flows from boundary layers. More careful analysis along this direction for more realistic PNP type models, such as the PNP system for more ion species with nonzero permanent charges and finite ion sizes, will be carried out in our future studies.