Stability and Perturbations of Generalized Heteroclinic Loops in Piecewise Smooth Systems

Abstract

We investigate a class of planar piecewise smooth systems with a generalized heteroclinic loop (a closed curve composed of hyperbolic saddle points, generalized singular points and regular orbits). We give conditions for the stability of the generalized heteroclinic loop and provide some sufficient conditions for the maximum number of limit cycles that bifurcate from the heteroclinic connection. The discussions rely on the approximation of the Poincaré map, which is constructed near the generalized heteroclinic loop. To obtain it, we introduce the Dulac map and use Melnikov method. By analyzing the fixed point of the Poincaré map, we get the number of limit cycles, which can be produced from the generalized heteroclinic loop. As applications to our theories, we give an example to show that two limit cycles can appear.

1 Introduction

Piecewise smooth (abbreviated as PWS) systems are frequently encountered in applied science and engineering, such as control theory, mechanical engineering, power electronic circuits and so on (see for instance [4, 8, 14, 19, 30] and the references given there). For the details about the fundamental theory of PWS systems, we refer to the monographs [9, 13, 22, 27].

As known in [2, 6], studying bifurcations of limit cycles is one of main problems in smooth systems. This problem in PWS systems has attracted considerable attentions in the past tens of years. Hopf bifurcation and periodic bifurcation for Filippov systems have been studied in [1, 7, 11, 12, 18, 23, 24]. Homoclinic bifurcation for PWS systems was investigated in [5, 23, 24]. Attentions also have been paid to limit cycles bifurcate from heteroclinic loops. In this respect, bifurcations of limit cycles in planar PWS systems with two zones, which are separated by a straight line and contain two real saddles in each zones, were studied, for example, in [3, 20, 26] for PWS linear systems, in [15] for PWS Hamiltonian systems. Recently, heteroclinic bifurcation in PWS systems with multiple zones was considered in [25, 29]. Liang, Han and Zhang [24] in 2013 once studied bifurcation of limit cycles from generalized homoclinic loops, which have generalized singular points on the switching manifold. We remark that generalized singular points are also referred to as sliding points (see for instance [9, 13]). In this work, we are concerned with a planar PWS system defined in two domains which are separated by a switching manifold and assume that the system has a generalized heteroclinic loop, which has a real saddle in one subsystem and a generalized singular point on the switching manifold.

More precisely, we assume that the plane is divided into

$$\begin{aligned}&{\varOmega }_{+}=\{x=(x_1,x_2)^T\in {\mathbb {R}}^2: x_2>0\},\\&{\varOmega }_{-}=\{x=(x_1,x_2)^T\in {\mathbb {R}}^2: x_2<0\} \end{aligned}$$

with the switching maniflold

$$\begin{aligned}&{\varOmega }_0=\{x=(x_1,x_2)^T\in \,{\mathbb {R}}^{2}: x_2=0\}. \end{aligned}$$

Consider a planar PWS system in the form

$$\begin{aligned} \quad \dot{x}=f_{+}(x)+\varepsilon g_{+}(x):=F_+(x, \varepsilon ),\quad&x \in {{\varOmega }}_{+}, \end{aligned}$$

(1a)

$$\begin{aligned} \quad \dot{x}=f_{-}(x)+\varepsilon g_{-}(x):=F_-(x, \varepsilon ),\quad&x \in {{\varOmega }}_{-}, \end{aligned}$$

(1b)

where

$$\begin{aligned} f_{\pm }(x) = \begin{pmatrix} p^{\pm }(x)\\ q^{\pm }(x) \end{pmatrix},\quad g_{\pm }(x) = \begin{pmatrix} j^{\pm }(x)\\ k^{\pm }(x) \end{pmatrix} \end{aligned}$$

with $p^{\pm }, q^{\pm }, j^{\pm }, k^{\pm } \in C^{n}({{\varOmega }}_{\pm }\cup {\varOmega }_0, {\mathbb {R}}^2)$ ($n\ge 3$) and $|\varepsilon |<\varepsilon _0\ll 1$ for some $\varepsilon _0>0$. When $\varepsilon =0$, the system is reduced to

$$\begin{aligned} \dot{x}=f_{+}(x),\quad&x \in {{\varOmega }}_{+}, \end{aligned}$$

(2a)

$$\begin{aligned} \dot{x}=f_{-}(x),\quad&x \in {{\varOmega }}_{-}. \end{aligned}$$

(2b)

As indicated in [18], the generalized singular point of system (2) is a point $P\in {\varOmega }_0$ satisfying $q^{+}(P)q^{-}(P)\le 0$. We define a closed curve ${\varGamma }$ as a generalized heteroclinic loop if it consists of at least one generalized singular point on ${\varOmega }_0$ and one singular point in ${\varOmega }_{\pm }$. We assume system (2) satisfies the following hypotheses:

(H) :

The system (2) has a counterclockwise generalized heteroclinic loop ${\varGamma }$, which has a hyperbolic saddle point $S\in {\varOmega }_-$ and a generalized singular point $P\in {\varOmega }_0$ satisfying

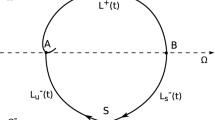
$$\begin{aligned} p^{+}(P)<0, \quad q^{+}(P)=0, \quad q^{+}_{x_1}(P)<0, \quad q^{-}(P)>0. \end{aligned}$$

(3)

Besides the point P, the generalized heteroclinic loop ${\varGamma }$ intersects ${\varOmega }_0$ at the other point Q, which is a crossing point satisfying $q^{+}(Q)<0$ and $q^{-}(Q)<0$. See Fig. 1.

Fig. 1

The generalized heteroclinic loop ${\varGamma }$ of the unperturbed system (2)

Without loss of generality, in what follows we always assume that the generalized singular point P is at the origin point.

The aim of this paper is to study the stability and perturbations of the generalized heteroclinic loop ${\varGamma }$. Among various approaches for determining the number of limit cycles bifurcate from periodic orbits, homoclinic loops or heteroclinic loops in smooth systems, the Melnikov method is treated as one of the efficient techniques (see [16, 28]). In the recent decades, the efforts in extending this method to PWS system have been made, see for instance in [5, 12, 15, 22, 24, 25, 29]. We will use the Melnikov method and introduce the Dulac map in a small neighborhood of S to estimate the Poincaré map, from which we get stability of ${\varGamma }$. By analyzing zeros of the successor function of the perturbed system in the neighborhood of ${\varGamma }$, which will be defined in Sect. 3, we can obtain the number of limit cycles bifurcate from the generalized heteroclinic loop ${\varGamma }$.

The present paper is built up as follows. Some necessary preparations are presented in Sect. 2. We construct the Poincaré map near the generalized heteroclinic loop and give conditions for stability of it in Sect. 3. Section 4 is devoted to perturbations of the generalized heteroclinic loop. As applications of main results, an example is given in the final section.

2 Preliminaries

We firstly introduce some notations used repeatedly below. Let $\langle a, b\rangle =a^T b$, $\Vert a \Vert =\sqrt{\langle a, a\rangle }$, $a\wedge b=a_1 b_2-a_2 b_1$ and $a^{\bot }=(-a_2, a_1)^T$ for $a=(a_1, a_2)^T$, $b=(b_1, b_2)^T$ in ${\mathbb {R}}^2$. The vector n is given by $n=(0,1)^T$. $\mathrm{div}\, X$ and DX respectively denote the divergence and the Jacobian matrix of a smooth vector field $X(x)=(X_1(x), X_2(x))^T$.

Let real constants $\lambda ^-$ and $\lambda ^+$ with $\lambda ^-<0<\lambda ^+$ be the eigenvalues of the matrix $Df_-(S)$ and $\lambda _0=-\lambda ^-/\lambda ^+>0$. The stable and unstable manifolds of the hyperbolic saddle point S are respectively denoted by ${\varGamma }_s$ and ${\varGamma }_u$, the branch of ${\varGamma }$ in ${\varOmega }_{+}$ is defined by ${\varGamma }_0$. See Fig. 1. As the solution defined in [13, 18], we define ${\varGamma }_s:=\{\gamma _s(t): t\in [t_Q, +\infty )\}$, ${\varGamma }_u:=\{\gamma _u(t): t\in (-\infty , t_P)\}$ and ${\varGamma }_0:=\{\gamma _0(t): t\in (t_P,t_Q]\}$, furthermore, $\gamma _s(t_Q)=\gamma _0(t_Q)=Q$, $\lim _{t\rightarrow t_P^-}\gamma _u(t)=P$ and $\lim _{t\rightarrow t_P^+}\gamma _0(t)=P$. Note that $S\in {\varOmega }_-$ is a hyperbolic saddle point, then subsystem (1b) has a hyperbolic saddle point $S_\varepsilon$ near the point S for sufficiently small $|\varepsilon |$. Let $\lambda ^-(\varepsilon )$ and $\lambda ^+(\varepsilon )$ with $\lambda ^-(\varepsilon )<0<\lambda ^+(\varepsilon )$ be the eigenvalues of the matrix $DF_-(S_\varepsilon ,\varepsilon )$. Under the perturbation, ${\varGamma }_s$ (resp., ${\varGamma }_u$) becomes ${\varGamma }_s^\varepsilon$ (resp., ${\varGamma }_u^\varepsilon$), the stable (resp., unstable) manifold of $S_\varepsilon$.

In order to approximate the Poincaré map, which will be constructed below, we introduce the Dulac map in the following. As known in [21], there exists a local $C^{n-1}$ diffeomorphism $T_{\varepsilon }$, which transforms subsystem (1b) into the following normal form:

$$\begin{aligned} \dot{u}=\lambda ^+(\varepsilon ) u(1+h_1(u,v, \varepsilon )),\quad \dot{v}=\lambda ^-(\varepsilon ) v(1+h_2(u,v, \varepsilon )), \end{aligned}$$

(4)

where $h_i(u, v, \varepsilon )=uvh_{i0}(u, v, \varepsilon )$ with $h_{i0}\in C^{n-2}$ for $i=1, 2$. For sufficiently small $\rho$, we take two sections of form

$$\begin{aligned} l^{'}_1=\{(u, v)^T \ | \ v=\rho ,~0\le u\le \rho \},\quad l^{'}_2=\{(u, v)^T \ | \ u=\rho ,~0\le v\le \rho \}, \end{aligned}$$

then the flow of system (4) induces the Dulac map ${\mathcal {D}}_0:={\mathcal {D}}_0(\cdot \, ,\varepsilon )$ from $l^{'}_1$ to $l^{'}_2$: ${\mathcal {D}}_0(\cdot \, , \varepsilon ): [0,\rho ] \rightarrow [0,\rho ].$ See Fig. 2.

Fig. 2

The Dulac map ${\mathcal {D}}_0$ of system (4) near the hyperbolic sadddle

Let the sections $l_1$ and $l_2$ cross ${\varGamma }_s$ and ${\varGamma }_u$ at the points $A_s:=T_0^{-1}((0, \rho )^T)$ and $B_u:=T_0^{-1}((\rho ,0)^T)$ along the vectors

$$\begin{aligned} n_{A_s}:=\frac{f^\perp _-(A_s)}{||f_-(A_s)||}, \quad n_{B_u}:=\frac{f^\perp _-(B_u)}{||f_-(B_u)||}, \end{aligned}$$

respectively. Then for sufficiently small $|\varepsilon |$, the section $l_1$ (resp., $l_2$) can intersect ${\varGamma }_s^{\varepsilon }$ (resp., ${\varGamma }_u^{\varepsilon }$) transversally at $A_s^{\varepsilon }:=A_s+a^s(\varepsilon ) n_{A_s}$ (resp., $B_u^{\varepsilon }:=B_u+b^u(\varepsilon ) n_{B_u}$). Given that $A:=A_s+an_{A_s}$ for some small $a>a^s(\varepsilon )$, then the flow of subsystem (1b) from A crosses $l_2$ at $B:=B_u+bn_{B_u}$, which induces the Dulac map ${\mathcal {D}}:={\mathcal {D}}(\cdot \, ,\varepsilon )$, that is, $b={\mathcal {D}}(a,\varepsilon )$. The expression of the Dulac map ${\mathcal {D}}$ can be obtained by [17, Lemma 3.5, p.302] and [17, Lemma 3.8, p.308]. The compendium of them is shown in the following lemma.

Lemma 1

([17]) Let the notations be given above. Then for sufficiently small $|\varepsilon |$, the following assertions hold:

• (i) Let $\lambda (\varepsilon )=-\lambda ^-(\varepsilon )/\lambda ^+(\varepsilon )>0$. Then for any $k\in (0, \lambda _0/(1+\lambda _0))$, we have

  $$\begin{aligned} {\mathcal {D}}_0(u, \varepsilon )= & {} \rho ^{1-\lambda (\varepsilon )}u^{\lambda (\varepsilon )} (1+\varphi _0(u, \varepsilon )),\\ \frac{\partial {\mathcal {D}}_0}{\partial u}(u, \varepsilon )= & {} \lambda (\varepsilon ) \rho ^{1-\lambda (\varepsilon )}u^{\lambda (\varepsilon )-1}(1+\varphi _1(u, \varepsilon )), \end{aligned}$$

  where $\varphi _0(u, \varepsilon )=o(u^k)$, $\varphi _1(u,\varepsilon )=o(u^k)$ and $u\frac{\partial \varphi _{0}}{\partial u}=o(u^k)$.

• (ii) Let $\beta _1=\Vert T^{-1}_0((1,0)^T)-P_0\Vert$, $\beta _2=\Vert T^{-1}_0((0,1)^T)-P_0\Vert$. Then there exist $C^{n-1}$ functions

  $$\begin{aligned} W_1(u,\rho , \varepsilon )= & {} a^s(\varepsilon )+M_1(\rho , \varepsilon )u+O(u^2),\\ W_2(u,\rho , \varepsilon )= & {} b^u(\varepsilon )+M_2(\rho , \varepsilon )u+O(u^2), \end{aligned}$$

  such that if $a(\varepsilon )=W_1(u,\rho , \varepsilon )$, then ${\mathcal {D}}(a(\varepsilon ), \varepsilon ) =W_2({\mathcal {D}}_0(u, \varepsilon ), \rho , \varepsilon )$, furthermore, $M_i(\rho , 0)\rightarrow \beta _i\sin \theta$ as $\rho \rightarrow 0$, $i=1,2$, where $\theta$ is the angle between eigenvectors of $\lambda ^+$ and $\lambda ^-$.

3 Stability of Generalized Heteroclinic Loops

To get the stability of the generalized heterocinic loop ${\varGamma }$ with the assumption (H), we will construct the Poincaré map near ${\varGamma }$ and analyze the properties of the successive function. Precisely, we take $l_1$ as the Poincaré section, where $l_1$ is the same as defined in Sect. 2. Let $A=A_s+\delta n_{A_s}\in l_1$ for sufficiently small $\delta >0$. Then the flow of subsystem (1b) starting from A intersects $l_2$ at $B:=B_u+{\mathcal {D}}(\delta ,0) n_{B_u}$. As stated in Lemma 1, we can have the fact that if $\delta$ is small, so is ${\mathcal {D}}(\delta ,0)$. Then by the continuous dependency on initial values, for sufficiently small $\delta$ the flow starting from B intersects the switching manifold ${\varOmega }_0$ at C and D successively. The flow returns to the Poincaré section $l_1$ for the first time at $E:=A_s+h(\delta ) n_{A_s}$. See Fig. 3. Let $t_X$ be the time, when the flow reaches X, $X=A, B, C, D, E$. Then we can define the map ${\mathcal {P}}$ from $l_1$ to itself by ${\mathcal {P}}(A)=E$, which is called the Poincaré map.

Fig. 3

The Poincaré map near the generalized heteroclinic loop ${\varGamma }$

To approximate the Poincaré map, we need to make some preparations. Due to the assumption (H), the orbit ${\varGamma }_0$ of subsystem (2a) intersects ${\varOmega }_0$ at exactly two points P and Q, furthermore, $q^{+}(Q)<0$ and (3) holds. Suppose that the orbit $\widetilde{{\varGamma }}_0$ of subsystem (2a) crosses the point $\widetilde{P}=(-d,0)^T$ for sufficiently small $d>0$, then by the continuous dependency on initial value, $\widetilde{{\varGamma }}_0$ intersects ${\varOmega }_0$ at $\widetilde{Q}=Q+(\widetilde{d},0)^T$ and $x_2$-axis at $\widetilde{T}=(0,-d_0)^T$ if the domain of subsystem (2a) is extended to ${\mathbb {R}}^2$. See Fig. 4. Then the following result gives the relationship between d and $\widetilde{d}$.

Fig. 4

The flow of system (2a) with the initial value near the generalized singular point P

Lemma 2

Let notations be given above. Then for sufficiently small d, we have

$$\begin{aligned} \widetilde{d}=\frac{q^+_{x_1}(P)}{2q^+(Q)}\exp \,\left( \int ^{t_Q}_{t_P} \mathrm{div}\, f_+(\gamma _0(s))d s\right) d^2+O(d^3). \end{aligned}$$

(5)

Proof

Since subsystem (2a) satisfies (3), then near the point $P=(0,0)^{T}$,

$$\begin{aligned} \frac{d x_2}{d x_1} = \frac{q^+_{x_1}(P)}{p^+(P)}x_1+ \frac{q^+_{x_2}(P)}{p^+(P)}x_2+ \varphi (x_1,x_2), \end{aligned}$$

(6)

where $\varphi (x_1,x_2)$ is the high order term of $x_1$ and $x_2$. Consider Eq. (6) with the initial value $x_2(0)=-d_0$, then

$$\begin{aligned} d_0=\frac{q^+_{x_1}(P)}{2 p^+(P)}d^2 +\frac{q^+_{x_2}(P)}{p^+(P)}\int ^{-d}_{0} x_2 d x_1 + \int ^{-d}_{0} \varphi (x_1,x_2) d x_1, \end{aligned}$$

(7)

note that $x_2(-d)=0$ and through partial integration, we can obtain

$$\begin{aligned} \int ^{-d}_{0} x_2 d x_1=-\int ^{-d}_{0} x_1 \left( \frac{q^+_{x_1}(P)}{p^+(P)}x_1+ \frac{q^+_{x_2}(P)}{p^+(P)}x_2+ \varphi (x_1,x_2)\right) d x_1=O(d^3),\nonumber \\ \end{aligned}$$

(8)

and it is clear that for sufficiently small d,

$$\begin{aligned} \int ^{-d}_{0} \varphi (x_1,x_2) d x_1 =O(d^3). \end{aligned}$$

(9)

From (7) to (9) it follows that

$$\begin{aligned} d_0=\frac{q^+_{x_1}(P)}{2 p^+(P)}d^2 + O(d^3). \end{aligned}$$

(10)

Therefore, in order to obtain the relationship between d and $\widetilde{d}$, it is only necessary to get the function of $\widetilde{d}$ in $d_0$.

Let $x_{0}^{+}(t; t_{0}, X)$ be the solution of (2a) with $x_{0}^{+}(t_{0})= X$ for any $X\in {{\varOmega }}_{+}\bigcup {{\varOmega }}_{0}$. By the $C^n$ dependency on initial values, for sufficiently small $d_0$, we can expand $x_{0}^{+}(t; t_{P}, \widetilde{T})$ as

$$\begin{aligned} x_{0}^{+}(t; t_{P}, \widetilde{T}) =\gamma _0(t)+{\varPsi }_1(t; P)(\widetilde{T}-P)+O(\Vert \widetilde{T}-P\Vert ^{2}), \end{aligned}$$

(11)

where ${\varPsi }_1(t; P)$ satisfies the variational equation

$$\begin{aligned} \dot{\varPsi }_1(t; P)=Df_+(\gamma _0(t)){\varPsi }_1(t; P),\quad {\varPsi }_1(t_P; P)=I. \end{aligned}$$

Assume that $x_{0}^{+}(t_{\widetilde{Q}}; t_P, \widetilde{T})=\widetilde{Q}\in {\varOmega }_0$, then from the $C^n$ dependency on initial values it follows that

$$\begin{aligned} t_{\widetilde{Q}}=t_{Q}+\tau _1+O(\Vert \widetilde{T}-P\Vert ^{2}), \end{aligned}$$

(12)

where $\tau _1=O(\Vert \widetilde{T}-P\Vert )$. Note that $n^T Q=n^T \widetilde{Q}=0$, substituting (12) into (11) yields

$$\begin{aligned} \tau _1= -\frac{n^T{\varPsi }_1(t_Q; P)(\widetilde{T}-P)}{n^T f_+(Q)}. \end{aligned}$$

(13)

If we plug (12) and (13) back into (11), we get

$$\begin{aligned} \widetilde{Q}=Q+\frac{f_+(Q)\wedge [{\varPsi }_1(t; P)(\widetilde{T}-P)]}{q^+(Q)}n^\perp +O(\Vert \widetilde{T}-P\Vert ^{2}). \end{aligned}$$

(14)

Take $\omega (t; P):=f_+(\gamma _0(t))\wedge [{\varPsi }_1(t; P)(\widetilde{T}-P)]$, we can check that $\omega (t; P)$ satisfies

$$\begin{aligned} \frac{d}{d t} \omega (t; P)=\mathrm{div}\, f_+(\gamma _0(t)) \omega (t; P), \quad \omega (t_P; P)=-d_0 p^+(P), \end{aligned}$$

which yields

$$\begin{aligned} \omega (t_Q; P)=-d_0 p^+(P)\exp \,\left( \int ^{t_Q}_{t_P} \mathrm{div}\, f_+(\gamma _0(s)) d s\right) . \end{aligned}$$

(15)

Consequently, from (14) and (15) it follows that

$$\begin{aligned} \widetilde{d}= & {} \frac{p^+(P)}{q^+(Q)} \exp \,\left( \int ^{t_Q}_{t_P} \mathrm{div}\, f_+(\gamma _0(s)) d s\right) d_0+O(d_0^{2}). \end{aligned}$$

(16)

Then, substituting (10) into (16) yields (5). Thus the proof is complete. $\square$

Lemma 3

Suppose that $\delta$ and $\rho$ are sufficiently small, then we have

$$\begin{aligned} h(\delta )=K_1(\rho ){\mathcal {D}}^2(\delta ,0)+O({\mathcal {D}}^3(\delta ,0)), \end{aligned}$$

(17)

where

$$\begin{aligned} K_1(\rho )= & {} -\frac{q^+_{x_1}(P)q^-(Q)}{2q^+(Q)(q^-(P))^2} \left( -\frac{\lambda ^2_+\beta _1^2}{\lambda _- \beta _2}\rho +O(\rho ^2)\right) \exp (H(\rho )),\\ H(\rho )= & {} 2\int ^{t_P}_{t_{B_u}} \mathrm{div}\, f_-(\gamma _u(\tau ))d \tau +\int ^{t_Q}_{t_P} \mathrm{div}\, f_+(\gamma _0(\tau ))d \tau +\int ^{t_{A_s}}_{t_Q} \mathrm{div}\, f_-(\gamma _s(\tau )) d \tau . \end{aligned}$$

Proof

By the similar method used to obtain the formula (14), we can obtain

$$\begin{aligned} C= & {} P+\frac{f_-(B_u)\wedge (B-B_u)}{f_-(P) \wedge n^\perp } \exp \,\left( \int ^{t_P}_{t_{B_u}} \mathrm{div}\, f_-(\gamma _u(\tau ))d \tau \right) n^\perp \nonumber \\&+O(\Vert B-B_u\Vert ^{2}), \end{aligned}$$

(18)

$$\begin{aligned} E= & {} A_s+\frac{f_-(Q) \wedge (D-Q)}{f_-(A_s) \wedge n_{A_s}} \exp \,\left( \int ^{t_{A_s}}_{t_Q} \mathrm{div}\, f_-(\gamma _s(\tau )) d \tau \right) n_{A_s} \nonumber \\&+O(\Vert D-Q\Vert ^{2}), \end{aligned}$$

(19)

and it is clear to check that

$$\begin{aligned} f_-(B_u)\wedge (B-B_u)=\Vert f_-(B_u)\Vert \Vert B-B_u\Vert ,\quad f_-(A_s) \wedge n_{A_s}=\Vert f_-(A_s)\Vert . \end{aligned}$$

From (5), (18) and (19), we can obtain

$$\begin{aligned} h(\delta )=-\frac{q^+_{x_1}(P)q^-(Q)}{2q^+(Q)(q^-(P))^2} \frac{\Vert f_-(B_u)\Vert ^2}{\Vert f_-(A_s)\Vert } {\mathcal {D}}^2(\delta ,0) \exp (H(\rho ) ) +O({\mathcal {D}}^3(\delta ,0)). \end{aligned}$$

(20)

By [5, Lemma 3], we have the fact that

$$\begin{aligned} \ \Vert f_-(A_s)\Vert= & {} -\rho \lambda _-\beta _2+O(\rho ^2), \end{aligned}$$

(21)

$$\begin{aligned} \Vert f_-(B_u)\Vert= & {} \rho \lambda _+\beta _1+O(\rho ^2). \end{aligned}$$

(22)

Then, substituting (21) and (22) into (20) yields (17). Therefore, the proof is now complete. $\square$

Theorem 1

Suppose that system (2) has a generalized heteroclinic loop ${\varGamma }$ with the assumption (H). Given that $\lambda _0\ne 1/2$, then ${\varGamma }$ is asymptotically stable if $\lambda _0>1/2$, unstable if $\lambda _0<1/2$.

Proof

For sufficiently small $\delta$, using result (ii) in Lemma 1, we can obtain

$$\begin{aligned} u= & {} \frac{\delta }{M_1(\rho , 0)}(1+O(\delta )), \end{aligned}$$

(23)

$$\begin{aligned} {\mathcal {D}}(\delta ,0)= & {} M_2(\rho , 0){\mathcal {D}}_0(u, 0)+O\left( {\mathcal {D}}^2_0(u, 0)\right) , \end{aligned}$$

(24)

thus from (23), (24) and result (i) in Lemma 1, it follows that

$$\begin{aligned} {\mathcal {D}}(\delta ,0)= & {} \rho ^{1-\lambda _0}\frac{M_2(\rho , 0)}{M_1^{\lambda _0}(\rho , 0)}\left( 1+o\left( \delta ^{k_0}\right) \right) \delta ^{\lambda _0} +O\left( \delta ^{2\lambda _0}\right) \nonumber \\= & {} K_2(\rho )\left( 1+o\left( \delta ^{k_0}\right) \right) \delta ^{\lambda _0} +O\left( \delta ^{2\lambda _0}\right) , \end{aligned}$$

(25)

where the constant $k_0\in (0, \lambda _0/(1+\lambda _0))$,

$$\begin{aligned} K_2(\rho ) = (\rho \sin \theta )^{1-\lambda _0}\frac{\beta _2}{\beta _1^{\lambda _0}}(1+\varphi (\rho )), \end{aligned}$$

and the function $\varphi (\rho )$ with $\varphi (\rho )\rightarrow 0$ as $\rho \rightarrow 0$. Take sufficiently small $\rho$ fixed, substituting (25) into (17) yields

$$\begin{aligned} h(\delta )=K_1(\rho )K_2^2(\rho )(1+o(\delta ^{k_0}))\delta ^{2\lambda _0} +O\left( \delta ^{3\lambda _0}\right) . \end{aligned}$$

Consequently, for sufficiently small $\delta >0$, we have

$$\begin{aligned} \frac{h(\delta )}{\delta }=K_1(\rho )K_2^2(\rho )(1+o(\delta ^{k_0})) \delta ^{2\lambda _0-1}+O\left( \delta ^{3\lambda _0-1}\right) . \end{aligned}$$

(26)

If $\lambda _0>1/2$, from (26) it follows that $h(\delta )/\delta \rightarrow 0$ as $\delta \rightarrow 0$. Thus the generalized heteroclinic loop ${\varGamma }$ is asymptomatically stable.

If $\lambda _0<1/2$, from (26) we have

$$\begin{aligned} \frac{h(\delta )}{\delta }=\left( K_1(\rho )K_2^2(\rho )(1+o(\delta ^{k_0})) +O\left( \delta ^{\lambda _0}\right) \right) \delta ^{2\lambda _0-1}, \end{aligned}$$

where $K_1(\rho )K_2^2(\rho )> 0$, $k_0>0$ and $\lambda _0>0$. Then we have that $h(\delta )/\delta \rightarrow +\infty$ as $\delta \rightarrow 0$. Thus the generalized heteroclinic loop ${\varGamma }$ is unstable. Therefore, the proof is now complete. $\square$

4 Perturbations of Generalized Heteroclinic Loops

We assume that ${\varGamma }_s^\varepsilon$ (resp., ${\varGamma }_u^\varepsilon$), the stable (resp., unstable) manifold of $S_\varepsilon$, intersects ${\varOmega }_0$ at $Q_\varepsilon ^-$ (resp., $P_\varepsilon ^-$). Under the condition (3) in (H), we will prove that there exists a generalized singular point $P_\varepsilon ^+\in {\varOmega }_0$ of system (1) near P. The flow of subsystem (1a) starting from $P_\varepsilon ^+$ crosses ${\varOmega }_0$ transversally at point $Q_\varepsilon ^+$. The next lemma will give the locations of $P_\varepsilon ^\pm$ and $Q_\varepsilon ^\pm$.

Lemma 4

Suppose that system (2) has a generalized heteroclinic loop ${\varGamma }$ with the assumption (H), then for sufficiently small $|\varepsilon |$, system (1) has a generalized singular point $P_\varepsilon ^+\in {\varOmega }_0$, furthermore,

$$\begin{aligned} P^+_{\varepsilon } := P+\delta _1^+(\varepsilon )n^{\perp }= & {} P+ \frac{k^+(P)}{q_{x_1}^+(P)} n^\perp \varepsilon + O(\varepsilon ^2),\\ P^-_{\varepsilon } := P+\delta _1^-(\varepsilon )n^{\perp }= & {} P+\frac{M_{u}}{q^-(P)} n^{\perp }\varepsilon +O(\varepsilon ^2),\\ Q^-_{\varepsilon } := Q+\delta _2^-(\varepsilon )n^{\perp }= & {} Q-\frac{M_{s}}{q^-(Q)} n^{\perp }\varepsilon +O(\varepsilon ^2),\\ Q^+_{\varepsilon } := Q+\delta _2^+(\varepsilon )n^{\perp }= & {} Q+ \left\{ \frac{k^+(P)q^+(P)}{q_{x_1}^+(P)q^+(Q)}+\frac{M_0}{q^+(Q)}\right\} \\&\times \exp \,\left( \int _{t_P}^{t_Q}\mathrm{div}\, f_+(\gamma _0(\tau )) d \tau \right) n^\perp \varepsilon + O(\varepsilon ^2), \end{aligned}$$

where

$$\begin{aligned} M_{u}:= & {} \int _{-\infty }^{t_P} f_-(\gamma _u(\tau ))\wedge g_{-}(\gamma _u(\tau )) \exp \,\left( -\int _{t_P}^{\tau }\mathrm{div}\, f_-(\gamma _u(s)) d s\right) d \tau ,\\ M_{s}:= & {} \int _{t_Q}^{+\infty } f_-(\gamma _s(\tau ))\wedge g_{-}(\gamma _s(\tau )) \exp \,\left( -\int _{t_Q}^{\tau }\mathrm{div}\, f_-(\gamma _s(s)) d s\right) d \tau ,\\ M_{0}:= & {} \int _{t_P}^{t_Q} f_+(\gamma _0(\tau ))\wedge g_{+}(\gamma _0(\tau )) \exp \,\left( -\int _{t_P}^{\tau }\mathrm{div}\, f_+(\gamma _0(s)) d s\right) d \tau . \end{aligned}$$

Proof

We define a function $\psi (\delta ,\varepsilon ):=q^+(-\delta ,0)+\varepsilon k^+(-\delta ,0)$. Clearly, the function $\psi$ is continuously differentiable in $\delta$ and $\varepsilon$. Note that $\psi (0,0)=q^+(P)=0$ and $\psi _\delta (0,0)=-q_{x_1}^+(P)>0$, using the implicit function theorem yields that there exists a unique $C^n$ function

$$\begin{aligned} \delta _1^+(\varepsilon )=\frac{k^+(P)}{q_{x_1}^+(P)}\varepsilon + O(\varepsilon ^2) \end{aligned}$$

(27)

satisfying $\psi (\delta _1^+(\varepsilon ),\varepsilon )=0$ for small $|\varepsilon |$ . We can take $P^+_{\varepsilon }=(-\delta _1^+(\varepsilon ),0)^{T}\in {\varOmega }_0$, which satisfies $q^+(P^+_{\varepsilon })+\varepsilon k^+(P^+_{\varepsilon })=0$. Thus, the point $P^+_{\varepsilon }$ is a generalized singular point of system (1). Note that $n^{\bot }=(-1,0)^{T}$, then we prove the existence and location of $P^+_{\varepsilon }$.

From [5, Lemma 5], we can obtain the expressions of $P^-_{\varepsilon }$ and $Q^-_{\varepsilon }$. As follows, we only carry out the proof for $Q^+_{\varepsilon }$.

We define $x^+_\varepsilon (t; t_0, X)$ to be the solution of (1a) with $x^+_\varepsilon (t_0)=X$ for any $X\in {{\varOmega }}_{+}\bigcup {{\varOmega }}_{0}$. Using (27) and the $C^n$ dependency on initial values and parameters yields that for sufficiently small $|\varepsilon |$, we can write $x^+_\varepsilon (t; t_P, P_{\varepsilon }^+)$ as

$$\begin{aligned} x^+_\varepsilon (t; t_P, P_{\varepsilon }^+)= \gamma _0(t)+\alpha (t)\varepsilon +O(\varepsilon ^2), \end{aligned}$$

(28)

where $\alpha =\frac{\partial x^+_\varepsilon }{\partial \varepsilon }|_{\varepsilon =0}$. Note that $x^+_\varepsilon$ is $C^n$ with respect to $(t,\varepsilon )$ for $t\in {\mathbb {R}}$ and sufficiently small $|\varepsilon |$, then we have

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial x^+_\varepsilon }{\partial \varepsilon }|_{\varepsilon =0}\right)= & {} \frac{\partial ^2 x^+_\varepsilon }{\partial t \partial \varepsilon } |_{\varepsilon =0} =\frac{\partial ^2 x^+_\varepsilon }{\partial \varepsilon \partial t} |_{\varepsilon =0} =\frac{\partial }{\partial \varepsilon }\left( f_{+}(x^+_\varepsilon ) +\varepsilon g_{+}(x^+_\varepsilon )\right) |_{\varepsilon =0}\nonumber \\= & {} \left( Df_{+}(x^+_\varepsilon )\frac{\partial x^+_\varepsilon }{\partial \varepsilon } +g_{+}(x^+_\varepsilon )+\varepsilon Dg_{+}(x^+_\varepsilon ) \frac{\partial x^+_\varepsilon }{\partial \varepsilon }\right) |_{\varepsilon =0}\nonumber \\= & {} Df_+(\gamma _0(t))\alpha (t)+g_+(\gamma _0(t)), \end{aligned}$$

(29)

where the first equality follows from the result in [10, Exercise 3211.1] and the others can be easily checked. Letting $t=t_P$ in (28) and using (29) yield that $\alpha$ satisfies

$$\begin{aligned} \dot{\alpha }(t) = Df_+(\gamma _0(t))\alpha (t)+g_+(\gamma _0(t)), \quad \alpha (t_P) = \frac{k^+(P)}{q_{x_1}^+(P)} n^{\perp }. \end{aligned}$$

Assume that $x_{\varepsilon }^{+}(t_{Q^+_{\varepsilon }}; t_P, P_{\varepsilon }^+)=Q^+_{\varepsilon }\in {\varOmega }_0$, from the $C^n$ dependency on initial values and parameters it follows that $t_{Q^+_{\varepsilon }}$ can be expanded as

$$\begin{aligned} t_{Q^+_{\varepsilon }}=t_Q+T_{1}\varepsilon +O(\varepsilon ^2). \end{aligned}$$

(30)

Note that $n^T Q^+_{\varepsilon }=n^T Q=0$, by substituting (30) into (28), we can obtain

$$\begin{aligned} T_{1} = -\frac{n^T\alpha (t_Q)}{n^T f_+(Q)}. \end{aligned}$$

(31)

Thus, substituting (30) and (31) into (28) yields

$$\begin{aligned} Q^+_{\varepsilon } = Q+\frac{f_+(Q)\wedge \alpha (t_Q)}{n^T f_+(Q)}n^{\perp }\varepsilon +O(\varepsilon ^2). \end{aligned}$$

(32)

To get the expansion of $Q^+_{\varepsilon }$, it is only necessary to obtain $f_+(Q)\wedge \alpha (t_Q)$. We define $\zeta (t):=f_+(x^+_0(t; t_P, P))\wedge \alpha (t)$, and we can check that $\zeta (t)$ satisfies

$$\begin{aligned} \dot{\zeta }(t) = \mathrm{div}\, f_+(\gamma _0(t))\zeta (t)+f_+(\gamma _0(t))\wedge g_+(\gamma _0(t)), \quad \zeta (t_P) = \frac{k^+(P)n^T f_+(P)}{q_{x_1}^+(P)}, \end{aligned}$$

which implies

$$\begin{aligned} \zeta (t_Q)= \left\{ \frac{k^+(P) n^T f_+(P)}{q_{x_1}^+(P)} +M_0\right\} \exp \,\left( \int _{t_P}^{t_Q}\mathrm{div}\, f_+(\gamma _0(\tau )) d \tau \right) . \end{aligned}$$

(33)

Then, from (32) and (33) we can obtain the expression of $Q^+_{\varepsilon }$. Therefore, the proof is now complete. $\square$

Consider the following sets:

$$\begin{aligned} V_1(\varepsilon ):= & {} \{\varepsilon \in {\mathbb {R}}: |\varepsilon |\le \varepsilon _0\, , \delta _2^-(\varepsilon )\ge \delta _2^+(\varepsilon )\},\\ V_2(\varepsilon ):= & {} \{\varepsilon \in {\mathbb {R}}: |\varepsilon |\le \varepsilon _0\, , \delta _2^-(\varepsilon )< \delta _2^+(\varepsilon )\}, \end{aligned}$$

where $\delta _2^\pm (\varepsilon )$ are defined in Lemma 4. Clearly, if $\varepsilon \in V_1(\varepsilon )$, then $Q^+_{\varepsilon }$ is at the right side of $Q^-_{\varepsilon }$, otherwise, $Q^+_{\varepsilon }$ is at the left side of $Q^-_{\varepsilon }$. See Fig. 5.

Take $l_i$, $i=1, 2$, to be the sections as those defined in Sect. 2. We assume that the flow of subsystem (1b) starting from $Q^+_\varepsilon$ intersects $l_1$ for the first time at $\overline{A}_\varepsilon :=A_s+\overline{a}(\varepsilon )n_{A_s}$. Let $A_\varepsilon := A_s+\delta n_{A_s}$ with $\delta >\max \{a^s(\varepsilon ),\overline{a}(\varepsilon )\}$. The forward flow of system (1) from $A_\varepsilon$ intersects $l_2$ and ${\varOmega }_0$ at $B^1_\varepsilon$ and $C^1_\varepsilon$ respectively, the backward flow crosses ${\varOmega }_0$ at $B^2_\varepsilon$ and $C^2_\varepsilon$ in order. See Fig. 5. Then we can define the Poincaré map ${\mathcal {P}}(\cdot \, ,\varepsilon )$ in the form ${\mathcal {P}}(C^2_\varepsilon , \varepsilon )=C^1_\varepsilon$. Let

$$\begin{aligned} \Vert A_\varepsilon -A_s^\varepsilon \Vert =d_{1\varepsilon },&\Vert B^1_\varepsilon -B_u^\varepsilon \Vert =d_{2\varepsilon },&\Vert C^1_\varepsilon -P^-_\varepsilon \Vert =d_{3\varepsilon }, \\ \Vert A_\varepsilon -\overline{A}_\varepsilon \Vert =\delta _{1\varepsilon },&\Vert B^2_\varepsilon -Q^+_\varepsilon \Vert =\delta _{2\varepsilon },&\Vert C^2_\varepsilon -P^+_\varepsilon \Vert =\delta _{3\varepsilon }. \end{aligned}$$

Clearly, $d_{1\varepsilon }\ge \delta _{1\varepsilon }$ if $\varepsilon \in V_1(\varepsilon )$, $d_{1\varepsilon }<\delta _{1\varepsilon }$ if $\varepsilon \in V_2(\varepsilon )$.

Fig. 5

The generalized heteroclinic loop under perturbations

Theorem 2

Suppose that system (2) has a generalized heteroclinic loop ${\varGamma }$ with the assumption (H). If $\lambda _0>1$, then there exists a neighborhood U of ${\varGamma }$ such that for sufficiently small $|\varepsilon |$, system (1) has at most one limit cycle in U. If $0<\lambda _0\le 1$ and $\lambda _0\ne 1/2$, then there exists a neighborhood U of ${\varGamma }$ such that for sufficiently small $|\varepsilon |$, system (1) has at most two limit cycles in U.

Proof

As stated above, we have

$$\begin{aligned} d_{1\varepsilon }=\delta -a^s(\varepsilon ), \quad d_{2\varepsilon }={\mathcal {D}}(\delta ,\varepsilon )-b^u(\varepsilon ), \end{aligned}$$

(34)

where $a^s(\varepsilon )$ and $b^u(\varepsilon )$ satisfy $A_s^{\varepsilon }=A_s+a^s(\varepsilon ) n_{A_s}$ and $B_u^{\varepsilon }=B_u+b^u(\varepsilon ) n_{B_u}$, respectively, and the Dulac map ${\mathcal {D}}$ is defined in Sect. 2. Then from (34) and Lemma 1, we have

$$\begin{aligned} u= & {} \frac{d_{1\varepsilon }}{M_1(\rho ,\varepsilon )}(1+O(d_{1\varepsilon }))\nonumber ,\\ {\mathcal {D}}_0(u, \varepsilon )= & {} \frac{\rho ^{1-\lambda (\varepsilon )}}{M_1^{\lambda (\varepsilon )} (\rho ,\varepsilon )} (1+o(d^{k_0}_{1\varepsilon }))d^{\lambda (\varepsilon )}_{1\varepsilon } +O(d_{1\varepsilon }^{2\lambda (\varepsilon )}), \end{aligned}$$

(35)

where $k_0\in (0, \lambda _0/(1+\lambda _0))$ is fixed. Then from (34), (35) and result (ii) in Lemma 1 it follows

$$\begin{aligned} d_{2\varepsilon }=\frac{M_2(\rho ,\varepsilon )\rho ^{1-\lambda (\varepsilon )}}{M_1^{\lambda (\varepsilon )}(\rho ,\varepsilon )} (1+o(d^{k_0}_{1\varepsilon }))d^{\lambda (\varepsilon )}_{1\varepsilon } +O(d_{1\varepsilon }^{2\lambda (\varepsilon )}). \end{aligned}$$

(36)

By the same argument used in the proof of (14), we have

$$\begin{aligned} d_{3\varepsilon }= & {} K_{1\varepsilon }d_{2\varepsilon }+O(d^2_{2\varepsilon }), \end{aligned}$$

(37)

$$\begin{aligned} \delta _{2\varepsilon }= & {} K_{2\varepsilon }\delta _{1\varepsilon }+O(\delta ^2_{1\varepsilon }), \end{aligned}$$

(38)

where

$$\begin{aligned} K_{1\varepsilon }= & {} \frac{F_-(B_u^\varepsilon ,\varepsilon )\wedge n_{B_u}}{F_-(P^-_\varepsilon ,\varepsilon )\wedge n^{\bot }} \exp \,\left( \int ^{t_{P^-_\varepsilon }}_{t_{B_u^\varepsilon }} \mathrm{div}\, F_-(x^-_\varepsilon (s; t_{B_u^\varepsilon },B_u^\varepsilon ), \varepsilon )d s\right) ,\\ K_{2\varepsilon }= & {} -\frac{F_-(\overline{A}_\varepsilon ,\varepsilon )\wedge n_{A_s}}{F_-(Q^+_\varepsilon ,\varepsilon )\wedge n^{\bot }} \exp \,\left( \int ^{t_{Q^+_\varepsilon }}_{t_{\overline{A}_\varepsilon }} \mathrm{div}\, F_-(x^-_\varepsilon (s; t_{\overline{A}_\varepsilon },\overline{A}_\varepsilon ),\varepsilon )d s\right) . \end{aligned}$$

As stated in Lemma 2, we have

$$\begin{aligned} \delta _{2\varepsilon } = K_{3\varepsilon }\delta _{3\varepsilon }^2+O(\delta _{3\varepsilon }^3), \end{aligned}$$

(39)

where

$$\begin{aligned} K_{3\varepsilon }= & {} \frac{q^+_{x_1}(P^+_\varepsilon )+\varepsilon k_{x_1}^+(P^+_\varepsilon )}{2q^+(Q^+_\varepsilon )+2\varepsilon k^+(Q^+_\varepsilon )} \exp \,\left( \int ^{t_{Q^+_\varepsilon }}_{t_{P^+_\varepsilon }} \mathrm{div}\, F_+(x^+_\varepsilon (s; t_{P^+_\varepsilon },P^+_\varepsilon ),\varepsilon )d s\right) . \end{aligned}$$

Furthermore, we can check the fact that as $\varepsilon \rightarrow 0$,

$$\begin{aligned} K_{1\varepsilon }\rightarrow & {} \frac{\Vert f_-(B_u)\Vert }{q^{-}(P)}\exp \,\left( \int ^{t_{P}}_{t_{B_u}}\mathrm{div}\, f_-(\gamma _u(\tau )) d\tau \right) ,\\ K_{2\varepsilon }\rightarrow & {} -\frac{\Vert f_-(A_s)\Vert }{q^{-}(Q)}\exp \,\left( \int ^{t_{Q}}_{t_{A_s}}\mathrm{div}\, f_-(\gamma _s(\tau )) d\tau \right) ,\\ K_{3\varepsilon }\rightarrow & {} \frac{q^+_{x_1}(P)}{2q^+(Q)}\exp \,\left( \int ^{t_{Q}}_{t_{P}} \mathrm{div}\, f_+(\gamma _0(\tau )) d\tau \right) . \end{aligned}$$

Therefore, from (36) to (39) it follows that

$$\begin{aligned} d_{3\varepsilon }= & {} N_1(\varepsilon )(1+o(d^{k_0}_{1\varepsilon }))d^{\lambda (\varepsilon )}_{1\varepsilon } +O(d_{1\varepsilon }^{2\lambda (\varepsilon )}), \end{aligned}$$

(40)

$$\begin{aligned} \delta _{3\varepsilon }= & {} N_2(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }^{\frac{1}{2}}, \end{aligned}$$

(41)

where

$$\begin{aligned} N_1(\varepsilon )=\frac{K_{1\varepsilon } M_2(\rho ,\varepsilon ) \rho ^{1-\lambda (\varepsilon )}}{M_1^{\lambda (\varepsilon )}(\rho ,\varepsilon )} \ \text{ and } \ N_2(\varepsilon )=K^{\frac{1}{2}}_{2\varepsilon }K^{\frac{1}{2}}_{3\varepsilon }. \end{aligned}$$

In order to get the number of limit cycles bifurcate from ${\varGamma }$, we take sufficiently small $\rho >0$ fixed and consider the function $h(\delta ,\varepsilon )$, which satisfies

$$\begin{aligned} h(\delta ,\varepsilon )n^{\bot }= & {} {\mathcal {P}}(C^2_\varepsilon , \varepsilon ) -C^2_\varepsilon =C^1_\varepsilon -C^2_\varepsilon \nonumber \\= & {} (C^1_\varepsilon -P^-_\varepsilon )+(P^-_\varepsilon -P^+_\varepsilon ) +(P^+_\varepsilon -C^2_\varepsilon )\nonumber \\= & {} (d_{3\varepsilon }+\varphi (\varepsilon )-\delta _{3\varepsilon })n^{\bot }, \end{aligned}$$

(42)

where the function $|\varphi (\varepsilon )|=\Vert P^-_\varepsilon -P^+_\varepsilon \Vert$ only depends on the parameter $\varepsilon$. From (40) to (42) it follows that

$$\begin{aligned} \frac{\partial }{\partial \delta }h(\delta , \varepsilon )= & {} \lambda (\varepsilon ) N_1(\varepsilon )d^{\lambda (\varepsilon )-1}_{1\varepsilon } \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) \\&-\frac{N_2(\varepsilon )}{2}\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }^{-\frac{1}{2}}. \end{aligned}$$

Suppose that $\lambda _0>1$, then for sufficiently small $|\delta |+|\varepsilon |$, we have $\lambda (\varepsilon )-1>0$ and $\frac{\partial h}{\partial \delta }(\delta , \varepsilon )<0$. Therefore, if $\lambda _0>1$, then there exists a neighborhood U of ${\varGamma }$ such that for sufficiently small $|\varepsilon |$, system (1) has at most one limit cycle in U.

The proof of the case $0<\lambda _0\le 1$ and $\lambda _0\ne 1/2$ will be divided into two different cases, which rely on the relative location between $Q^+_\varepsilon$ and $Q^-_\varepsilon$.

Case (i) Suppose that $\varepsilon \in V_1(\varepsilon )$, that is, $Q^-_\varepsilon$ is at the left side of $Q^+_\varepsilon$ (see Fig. 5a). Note that $\frac{\partial h}{\partial \delta }(\delta , \varepsilon ) =0$ is equivalent to

$$\begin{aligned} \lambda (\varepsilon ) N_1(\varepsilon ) \delta _{1\varepsilon }^{\frac{1}{2}}d^{\lambda (\varepsilon )-1}_{1\varepsilon } \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) -\frac{N_2(\varepsilon )}{2}\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) =0.\nonumber \\ \end{aligned}$$

(43)

Suppose that $\lambda _0>1/2$, we can rewrite (43) as

$$\begin{aligned} \lambda (\varepsilon ) N_1(\varepsilon ) d^{\lambda (\varepsilon )-\frac{1}{2}}_{1\varepsilon } \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) (\delta _{1\varepsilon }^{\frac{1}{2}}d_{1\varepsilon }^{-\frac{1}{2}}) =\frac{N_2(\varepsilon )}{2}\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) .\nonumber \\ \end{aligned}$$

(44)

Since $\varepsilon \in V_1(\varepsilon )$, we have $d_{1\varepsilon }\ge \delta _{1\varepsilon }$. Thus, for $\varepsilon \in V_1(\varepsilon )$,

$$\begin{aligned} \delta _{1\varepsilon }^{\frac{1}{2}}d_{1\varepsilon }^{-\frac{1}{2}}\le 1, \quad d_{1\varepsilon }^{\lambda (\varepsilon )-^{\frac{1}{2}}} \rightarrow 0, \quad \text{ as } |\delta |+|\varepsilon |\rightarrow 0. \end{aligned}$$

(45)

Therefore, from (44) and (45) we can get the result that for sufficiently small $|\delta |+|\varepsilon |$ and $\varepsilon \in V_1(\varepsilon )$, $h(\delta , \varepsilon )$ has at most one zero.

Suppose that $0<\lambda _0<1/2$, note that $\frac{\partial h}{\partial \delta }(\delta , \varepsilon ) =0$ is equivalent to

$$\begin{aligned} (\lambda (\varepsilon ) N_1(\varepsilon ))^{-2}d^{2-2\lambda (\varepsilon )}_{1\varepsilon } \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) =4N_2^{-2}(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }. \end{aligned}$$

Let

$$\begin{aligned} h_1(\delta ,\varepsilon )=d^{2-2\lambda (\varepsilon )}_{1\varepsilon } \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) -N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }, \end{aligned}$$

where $N(\varepsilon )=4\lambda ^2(\varepsilon )N_1^2(\varepsilon )N_2^{-2}(\varepsilon )$. Since

$$\begin{aligned} \frac{\partial }{\partial \delta }h_1(\delta , \varepsilon )= & {} d^{1-2\lambda (\varepsilon )}_{1\varepsilon } \left( 2-2\lambda (\varepsilon )+o(d^{k_0}_{1\varepsilon }) +O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) \nonumber \\&-N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) , \end{aligned}$$

and $2-2\lambda (\varepsilon )>0$, $1-2\lambda (\varepsilon )<0$ for sufficiently small $|\varepsilon |$, then for sufficiently small $|\delta |+|\varepsilon |$, $h_1(\delta , \varepsilon )$ has at most one zero. Therefore, by Rolle’s Theorem, $h(\delta ,\varepsilon )$ has at most two zeros for sufficiently small $|\delta |+|\varepsilon |$.

Case (ii) Suppose that $\varepsilon \in V_2(\varepsilon )$, that is, $Q^+_\varepsilon$ is at the left side of $Q^-_\varepsilon$ (see Fig. 5b).

Suppose that $0<\lambda _0<1/2$, the condition $\varepsilon \in V_2(\varepsilon )$ implies $d_{1\varepsilon } < \delta _{1\varepsilon }$. Thus for $\varepsilon \in V_2(\varepsilon )$,

$$\begin{aligned} \delta _{1\varepsilon }^{\frac{1}{2}}d_{1\varepsilon }^{-\frac{1}{2}}> 1, \quad d_{1\varepsilon }^{\lambda (\varepsilon )-\frac{1}{2}} \rightarrow +\infty , \quad \text{ as } |\delta |+|\varepsilon |\rightarrow 0. \end{aligned}$$

(46)

Therefore, from (44) and (46) it follows that $h(\delta , \varepsilon )$ has at most one zero for sufficiently small $|\delta |+|\varepsilon |$ and $\varepsilon \in V_1(\varepsilon )$.

Suppose that $1/2<\lambda _0\le 1$, set $\alpha (\varepsilon ):=2-2\lambda (\varepsilon )$, $\omega (\delta ,\varepsilon ):=(d_{1\varepsilon }^{\alpha (\varepsilon )}-1)/\alpha (\varepsilon )$ for $\alpha (\varepsilon )\ne 0$ and $\omega (\delta ,\varepsilon ):=\ln d_{1\varepsilon }$ for $\alpha (\varepsilon )=0$, then we can rewrite $h_1(\delta ,\varepsilon )$ as

$$\begin{aligned} h_1(\delta ,\varepsilon )= (\alpha (\varepsilon )\omega (\delta ,\varepsilon )+1) \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) -N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }. \end{aligned}$$

Suppose that $|\delta _0|+|\varepsilon |$ is sufficiently small and $h_1(\delta _0,\varepsilon )=0$, then

$$\begin{aligned} (\alpha (\varepsilon )\omega (\delta _0,\varepsilon )+1) \left( 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) =N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }, \end{aligned}$$

note that

$$\begin{aligned} N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) \delta _{1\varepsilon }\rightarrow 0, \quad 1+o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon }) \rightarrow 1, \text{ as } |\delta |+|\varepsilon | \rightarrow 0, \end{aligned}$$

then for sufficiently small $|\delta _0|+|\varepsilon |$, there exists a constant $\mu$ such that

$$\begin{aligned} 0>\mu >\alpha (\varepsilon )\omega (\delta _0,\varepsilon )\ge -1. \end{aligned}$$

(47)

We define the function

$$\begin{aligned} h_2(\delta ,\varepsilon ):= & {} d_{1\varepsilon }^{2\lambda (\varepsilon )-1} \frac{\partial }{\partial \delta }h_1(\delta , \varepsilon )\\= & {} \alpha (\varepsilon )+o(d^{k_0}_{1\varepsilon }) +O(d^{\lambda (\varepsilon )}_{1\varepsilon }) -N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) d_{1\varepsilon }^{2\lambda (\varepsilon )-1}, \end{aligned}$$

then the zeros of $\frac{\partial }{\partial \delta }h_1(\delta , \varepsilon )$ are equivalent to those of $h_2(\delta ,\varepsilon )$. Since for any $\nu >0$,

$$\begin{aligned} d^{\nu }_{1\varepsilon }\omega \rightarrow 0, \text{ as } |\delta |+|\varepsilon |\rightarrow 0, \end{aligned}$$

and

$$\begin{aligned} h_2(\delta ,\varepsilon )\omega= & {} \alpha (\varepsilon )\omega + \left( o(d^{k_0}_{1\varepsilon })+O(d^{\lambda (\varepsilon )}_{1\varepsilon })\right) \omega \nonumber \\&-N(\varepsilon )\left( 1+O(\delta _{1\varepsilon }^{\frac{1}{2}})\right) d_{1\varepsilon }^{2\lambda (\varepsilon )-1}\omega , \end{aligned}$$

(48)

then for a small $\varepsilon$ fixed, from (47) and (48) we have that $h_2(\delta _0,\varepsilon )$ has the same sign as $\alpha (\varepsilon )$, where $\delta _0$ is a zero of $h_1(\delta ,\varepsilon )$. Therefore, $h_1(\delta ,\varepsilon )$ has at most one zeros for sufficiently small $|\delta |+|\varepsilon |$. Consequently, using Rolle’s Theorem yields that $h(\delta ,\varepsilon )$ has at most two zeros. Therefore, the proof is now complete. $\square$

5 An Example

Consider a planar PWS system in the form

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_1= -1,\\ \dot{x}_2= -3x_1^2-4x_1+2\varepsilon _1(x_1+1), \end{array}\right. \qquad (x_1,x_2)^T\in {{\varOmega }}_{+}, \end{aligned}$$

(49)

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_1=x_1+4x_2+5+\varepsilon _2(x_1+1),\\ \dot{x}_2=4x_1+x_2+5+2\varepsilon _2(x_2+1), \end{array}\right. \qquad (x_1,x_2)^T\in {{\varOmega }}_{-}, \end{aligned}$$

(50)

where $\varepsilon _1$ and $\varepsilon _2$ are small parameters, ${\varOmega }_{\pm }$ and ${\varOmega }_0$ are the same as defined in the general system (1).

When $\varepsilon _1=\varepsilon _2=0$, we can check that the unperturbed system has a generalized heteroclinic loop ${\varGamma }$, which has a generalized singular point P at the origin, a hyperbolic saddle point at $S=(-1,-1)^T$ and the other intersection between ${\varGamma }$ and $x_1$-axis is point $Q=(-2,0)^T$. The branches of ${\varGamma }$ are in the following form

$$\begin{aligned} {\varGamma }_u= & {} \{(x_1,x_2)^T\in {\mathbb {R}}^2: x_2=x_1\,, x_1\in (-1,0)\},\\ {\varGamma }_0= & {} \{(x_1,x_2)^T\in {\mathbb {R}}^2: x_2=x_1^3+2x_2^2\,, x_1\in [-2,0)\},\\ {\varGamma }_s= & {} \{(x_1,x_2)^T\in {\mathbb {R}}^2: x_2=-x_1-2\,, x_1\in [-2,-1)\}. \end{aligned}$$

It is clear that $\lambda ^-=-3$, $\lambda ^+=5$ and $\lambda _0=3/5>1/2$. Then from Theorem 1 it follows that ${\varGamma }$ is asymptomatically stable.

When $0<\varepsilon _1\ll 1$ and $\varepsilon _2=0$, there are no changes in subsystem (50). The flow of subsystem (49) starting from $P=(0,0)^T$ exactly crosses the point Q. Substituting $(x_1,x_2)=(0,0)$ into (50) yields $(\dot{x}_1,\dot{x}_2)=(-1,2\varepsilon _1)$. Therefore, a new homoclinic loop ${\varGamma }_{\varepsilon _1}$ appears. Since $\lambda ^++\lambda ^- = 2>0$, then by [5, Theorem 1], we can obtain that the homoclinic loop ${\varGamma }_{\varepsilon _1}$ is unstable. Thus, a stable limit cycle appears if $0<\varepsilon _1\ll 1$ and $\varepsilon _2=0$.

When $0<\varepsilon _2 \ll \varepsilon _1 \ll 1$, S is also the hyperbolic saddle point of subsystem (50). But ${\varGamma }_s$ and ${\varGamma }_u$ change to be ${\varGamma }^\varepsilon _s$ and ${\varGamma }^\varepsilon _u$ respectively, which are in the form

$$\begin{aligned} {\varGamma }^\varepsilon _s= & {} \{(x_1,x_2)^T\in {\mathbb {R}}^2: x_2+1=k_-(x_1+1) \,, x_2\in (-1,0)\},\\ {\varGamma }^\varepsilon _u= & {} \{(x_1,x_2)^T\in {\mathbb {R}}^2: x_2+1=k_+(x_1+1)\,, x_2\in (-1,0)\}, \end{aligned}$$

where $k_{\pm }=(\varepsilon _2\pm \sqrt{64+\varepsilon _2^2})/8$. We can check that ${\varGamma }^\varepsilon _u$ and ${\varGamma }^\varepsilon _s$ intersect ${\varOmega }_0$ at $P_\varepsilon ^-=(-1-k_-,0)^T$ and $Q_\varepsilon ^-=(-1-k_+,0)^T$ respectively, where $-1-k_-<0$ and $-1-k_+<-2$. Thus, the homoclinic loop ${\varGamma }_{\varepsilon _1}$ breaks and from [5, Theorem 2] it follows that another one limit cycle appears. As known in Theorem 2, the perturbed system has at most two limit cycles near the generalized heteroclinic loop. Therefore, there are only two limit cycles in the perturbed system under the condition $0<\varepsilon _2\ll \varepsilon _1\ll 1$.