Exact Solutions in Invariant Manifolds of Some Higher-Order Models Describing Nonlinear Waves

Abstract

In this paper, we study the exact traveling wave solutions for five high-order nonlinear wave equations using the dynamical system approach. Based on Cosgrove’s work and the dynamical system method, infinitely many soliton solutions and quasi-periodic solutions are presented in an explicit form. We show the existence of uncountably infinite many double-humped solitary wave solutions. We discuss the parameters range as well as geometrical explanation of soliton solutions.

1 Introduction

Usually, nonlinear wave equations are used to describe the nonlinear physical phenomena in a lot of areas, such as fluid mechanics, plasma physics, optical fibers, solid state physics, et al. Some high-order nonlinear equations play an important role in these models. How to find exact travelling wave solutions for these models? In this paper, we considered the following five equations.

1. The Olver Equation

In [7], by constructing meromorphic solutions in terms of the Weierstrass elliptic function, the authors found some new exact solutions for the Olver equation [16] (and also see [17]):

$$\begin{aligned} \eta _t+\eta _z+q_1\eta _{zzzzz}+q_2\eta ^2\eta _z+q_3\eta \eta _{zzz}+q_4\eta _z\eta _{zz}+q_5\eta _{zzz}+q_6\eta \eta _z=0. \end{aligned}$$

(1)

This unidirectional model describes long, small amplitude waves in shallow water. It can take the wave velocity or, alternatively, the surface elevation as the principal variable, i.e., $\eta$ gives a surface elevation, z is the horizontal coordinate, and coefficients $q_i, i=1, \ldots , 6$ are real constants, depending on surface tension.

Equation (1) contains six arbitrary constant coefficients and four nonlinear terms. We assume that $q_1q_2q_3\ne 0$. Then, letting $\eta =v(z,t)-\frac{q_6}{2q_2}$, Eq. (1) becomes

$$\begin{aligned}&v_t+\left( 1-\frac{q_6^2}{4q_2}\right) v_z+q_1v_{zzzzz}+q_2v^2v_z+q_3vv_{zzz}\nonumber \\&\quad +\,q_4v_zv_{zz}+\left( q_5-\frac{q_3q_6}{2q_2}\right) v_{zzz}=0. \end{aligned}$$

(2)

Consider traveling wave solution $v(z,t)=v(x-ct)=\phi (\xi )$. We have

$$\begin{aligned}&\left( 1-c-\frac{q_6^2}{4q_2}\right) \phi _{\xi }+q_1\phi _{\xi \xi \xi \xi \xi }+q_2\phi ^2\phi _{\xi }+q_3\phi \phi _{\xi \xi \xi }\nonumber \\&\qquad +\,q_ 4\phi _{\xi }\phi _{\xi \xi }+\left( q_5-\frac{q_3q_6}{2q_2}\right) \phi _{\xi \xi \xi }=0. \end{aligned}$$

(3)

Integrating Eq. (3) once we obtain

$$\begin{aligned}&\left( 1-c-\frac{q_6^2}{4q_2}\right) \phi +q_1\phi _{\xi \xi \xi \xi }+\frac{1}{3}q_2\phi ^3+q_3\phi \phi _{\xi \xi }+\frac{1}{2}(q_4-q_3)(\phi _{\xi })^2\nonumber \\&\qquad +\left( q_5-\frac{q_3q_6}{2q_2}\right) \phi _{\xi \xi }+\beta _1=0, \end{aligned}$$

(4)

where $\beta _1$ is an integration constant.

Considering the cases of $q_1q_2>0$ and $q_1q_2<0$, respectively, under some special parametric conditions, [7] gave some Weierstrass elliptic function solutions of Eq. (4).

It is different from [7] and [17], in this paper, we use the method of dynamical systems to find the exact solutions of Eq. (4). We make the transformation $y=-\left( \frac{q_5}{q_3}-\frac{q_6}{2q_2}\right) -\phi ,$ then Eq. (4) becomes the following 4-order equation:

$$\begin{aligned} y^{\prime \prime \prime \prime }=c_1yy^{\prime \prime }+c_2(y^{\prime })^2-c_3y^3+c_4y^2+\alpha y+\beta , \end{aligned}$$

(5)

where

$$\begin{aligned} c_1= & {} \frac{q_3}{q_1}, \ \ \ c_2=\frac{1}{2q_1}(q_4-q_3),\ \ \ c_3=\frac{q_2}{3q_1}, \ \ \ c_4=-\frac{q_2}{q_1}\left( \frac{q_5}{q_3}-\frac{q_6}{2q_2}\right) ,\nonumber \\ \alpha= & {} -\frac{q_2}{q_1}\left( \frac{q_5}{q_3}-\frac{q_6}{2q_2}\right) ^2-\frac{1}{q_1}\left( 1-c-\frac{q_6^2}{4q_2}\right) ,\nonumber \\ \beta= & {} \frac{\beta _1}{q_1}-\frac{q_2}{3q_1}\left( \frac{q_5}{q_3}-\frac{q_6}{2q_2}\right) ^3-\frac{1}{q_1}\left( 1-c- \frac{q_6^2}{4q_2}\right) \left( \frac{q_5}{q_3}-\frac{q_6}{2q_2}\right) . \end{aligned}$$

(6)

For some given $c_j, j=1-5$, Eq. (5) has a form of Cosgrove’s higher-order Painleve equations (see [5]), i.e., the forms F-III, F-IV, F-V and F-VI. Therefore, we can obtain exact solutions of $y(\xi )$ for these integrable systems by using the method of dynamical systems. Thus, we have

$$\begin{aligned} \eta (\xi )=\phi (\xi )-\frac{q_6}{2q_2}=-\frac{q_5}{q_3}-y(\xi ). \end{aligned}$$

(7)

Formula (7) gives rise to the exact traveling wave solution of Olver Eq. (1). In order to know exact $y(\xi )$, we should consider the following four cases.

• (1) The case $c_1=15, c_2=\frac{45}{4}, c_3=15, c_4=0$ i.e., $q_2=45q_1, q_3=15q_1, q_4=\frac{45}{2}q_1, q_6=6q_5$ and $q_1, q_5$ are arbitrary constants. In this case, Eq. (5) becomes the form F-III:

  $$\begin{aligned} y^{\prime \prime \prime \prime }=15yy^{\prime \prime }+\frac{45}{4}(y^{\prime })^2-15y^3+\alpha y+\beta , \end{aligned}$$

  (8)

• (2) The case $c_1=30, c_2=0, c_3=60, c_4=0$ i.e., $q_2=180q_1, q_3=q_4=30q_1, q_6=12q_5$ and $q_1, q_5$ are arbitrary constants. In this case, Eq. (5) becomes the form F-IV:

  $$\begin{aligned} y^{\prime \prime \prime \prime }=30yy^{\prime \prime }-60y^3+\alpha y+\beta , \end{aligned}$$

  (9)

• (3) The case $c_1=20, c_2=10, c_3=40, c_4=0$ i.e., $q_2=120q_1, q_3=20q_1, q_4=40q_1, q_6=12q_5$ and $q_1, q_5$ are arbitrary constants. In this case, Eq. (5) becomes the form F-V:

  $$\begin{aligned} y^{\prime \prime \prime \prime }=20yy^{\prime \prime }+10(y^{\prime })^2-40y^3+\alpha y+\beta , \end{aligned}$$

  (10)

• (4) The case $c_1=18, c_2=9, c_3=24, c_4=\tilde{\alpha }, \alpha =\frac{1}{9}\tilde{\alpha }^2$ i.e., $q_2=72q_1, q_3=18q_1, q_4=36q_1$ and $q_1, q_5$ are arbitrary constants, $q_6$ depends on $q_1, q_5, c$. In this case, Eq. (5) becomes the form F-VI:

  $$\begin{aligned} y^{\prime \prime \prime \prime }=18yy^{\prime \prime }+9(y^{\prime })^2-24y^3+\tilde{\alpha } y^2+\frac{1}{9}\tilde{\alpha }^2y+\beta , \end{aligned}$$

  (11)

2. A Higher Order KdV-BBM Long Wave Equation

In [15], the authors considered the following higher order KdV-BBM long wave equation:

$$\begin{aligned}&u_t+u_x-\frac{1}{6}u_{xxt}+\delta _1u_{xxxxt}+\delta _2u_{xxxxx}\nonumber \\&\quad +\left( \frac{3}{4}u^2+\gamma (u^2)_{xx}-\frac{1}{12}u_x^2-\frac{1}{4}u^3\right) _x=0. \end{aligned}$$

(12)

Substituting $u(x,t)=u(x-ct)=u(\xi )$ into (12) and integrating obtained result once, we have

$$\begin{aligned}&\hat{\alpha } u_{\xi \xi \xi \xi }+\frac{c}{6}u_{\xi \xi } +\left( 2\gamma -\frac{1}{12}\right) u_{\xi }^2+2\gamma uu_{\xi \xi }\nonumber \\&\quad =\frac{1}{4}u^3 -\frac{3}{4}u^2-(1-c)u+g=0, \end{aligned}$$

(13)

where $\hat{\alpha }=\delta _2-c\delta _1$ and g is an integral constant. Making the transformation $u=\frac{1}{2\gamma }\left( y-\frac{c}{6}\right) ,$ Eq. (13) becomes Eq. (5), where

$$\begin{aligned} c_1= & {} \frac{1}{-\hat{\alpha }},\quad c_2=\frac{24\gamma -1}{48\gamma \hat{\alpha }},\quad c_3=\frac{1}{16\gamma ^2\hat{\alpha }},\quad \ c_4=\frac{1}{\gamma \hat{\alpha }}\left( \frac{3}{8}+\frac{c}{32\gamma }\right) ,\\ \alpha= & {} \frac{1}{\hat{\alpha }}\left( 1-c-\frac{c}{8\gamma }-\frac{c^2}{192\gamma ^2}\right) ,\quad \beta =\frac{1}{\hat{\alpha }} \left( -2\gamma g-\frac{c(c-1)}{6}+\frac{c^2}{96\gamma }+\frac{c^3}{3456\gamma ^2}\right) . \end{aligned}$$

Similar to the Eq. (4), we can reduce the parameters in Eq. (5), such that it become the above forms (8)–(11).

3. The (2+1)-Dimensional B-Type Kadomtsev–Petviashvili Equation

[6] investigate the following (2+1)-dimensional B-type Kadomtsev–Petviashvili equation:

$$\begin{aligned}&u_t+u_{xxxxx}-5(u_{xxy}+\partial ^{-1}_x u_{yy})\nonumber \\&\quad +\,15(u_xu_{xx}+uu_{xxx}-uu_y-u_x\partial _x^{-1}u_y)+45u^2u_x=0, \end{aligned}$$

(14)

where $\partial _x^{-1}$ is the inverse operator of $\partial _x.$

Substituting $u(x,t)=u(x+ay-ct)=u(\xi )$ into (14) and integrating obtained result once, we have

$$\begin{aligned} -cu+u_{\xi \xi \xi \xi }-5(au_{\xi \xi }+a^2u)+15(uu_{\xi \xi }-au^2)+15u^3+g=0. \end{aligned}$$

(15)

Let $u=\frac{1}{3}a-2y.$ Then, (15) becomes

$$\begin{aligned} y^{\prime \prime \prime \prime }=30yy^{\prime \prime }-60y^3+(c+10a^2)y+\left( \frac{1}{2}g-\frac{25}{18}a^2-\frac{1}{6}ca\right) . \end{aligned}$$

(16)

Equation (16) is F-IV form.

4. The (2+1)-Dimensional Sawada–Kotera Equation

[2] and [14] discussed the (2+1)-dimensional Sawada–Kotera equation:

$$\begin{aligned}&u_t+\frac{1}{9}\left( u_{xxxx}+5u_{xy}+5uu_{xx}+\frac{5}{3}u^3\right) _x\nonumber \\&\quad +\,\frac{5}{9}\left( 2uu_y+u_x\partial _x^{-1}u_y-\partial _x^{-1}u_{yy}\right) =0. \end{aligned}$$

(17)

Substituting $u(x,t)=u(x+ay-ct)=u(\xi )$ into (17) and integrating obtained result once, we get

$$\begin{aligned} u_{\xi \xi \xi \xi }-9cu+5(a+u)u_{\xi \xi }+\frac{5}{3} u^3+5au^2+5a(1-a)u+g=0, \end{aligned}$$

(18)

where g is an integral constant. Making the transformation $u=-(a+6y),$ we obtain the following F-IV form:

$$\begin{aligned} y^{\prime \prime \prime \prime }=30yy^{\prime \prime }-60y^3+(9c-5a+10a^2)y+\left( \frac{1}{6}g+\frac{3}{2}ca-\frac{5}{6}a^2+\frac{25}{18}a^2\right) . \end{aligned}$$

(19)

5. A Sixth Order Solitary Wave Equation

By using Hirita’s bilinear operator, [4] derived the following sixth order equation:

$$\begin{aligned} u_{tt}=2u_{xx}-15(uu_{xx})_{xx}+15(u^3)_{xx}+3(u^2)_{xx}-u_{xxx}+u_{xxxxxx}. \end{aligned}$$

(20)

Substituting $u(x,t)=u(x-ct)=u(\xi )$ into (20) and integrating obtained result twice, we see that

$$\begin{aligned} u_{\xi \xi \xi \xi }=(1+15u)u_{\xi \xi }-3u^2-15u^3-(2-c^2)u+g, \end{aligned}$$

(21)

where g is an integral constant. Making the transformation $u=2y-\frac{1}{15},$ we obtain the following F-IV form:

$$\begin{aligned} y^{\prime \prime \prime \prime }=30yy^{\prime \prime }-60y^3+\left( c^2-\frac{9}{5}\right) y+\left( \frac{1}{2} g-\frac{c^2}{30}+\frac{14}{225}\right) . \end{aligned}$$

(22)

For the above five models, the authors of the above references did not give all possible exact travelling wave solutions. In this paper, by using the method of dynamical systems (see [8,9,10,11,12,13] ), we discuss the exact solution families of Eq. (9) (i.e., the form F-IV). We see from (16), (19) and (22) that we can choose the integral constant g such that $\beta =0$ in Eq. (9).

This paper is organized as follows. In Sect. 2, we consider the exact solutions in the invariant manifold of the saddle-saddle type of equilibrium points of system (23) corresponding to the form F-IV. We show that it is different from three-order wave equation (like KdV equation), high-order wave equations have uncountably infinite many double-humped solitary wave solutions. In Sect. 3, we discuss the exact solutions in the invariant manifold of the center-saddle type of equilibrium points of system (23). In Sect. 4, we investigate the exact solutions in the invariant manifold of the center-center type of equilibrium points of system (23). Sect. 5 state some simple conclusions.

2 The Exact Solutions in the Invariant Manifold of the Saddle–Saddle

Let $x_1=y,\ x_2=x_1^{\prime }=y^{\prime },\ x_3=x_2^{\prime }=y^{\prime \prime },\ x_4=x_3^{\prime }=y^{\prime \prime \prime }.$ Equation (9) is equivalent to the system

$$\begin{aligned} x_1^{\prime }=x_2,\ \ x_2^{\prime }=x_3,\ \ x_3^{\prime }=x_4,\ \ x_4^{\prime }=30x_1^2x_3-60x_1^3+\alpha x_1+\beta , \end{aligned}$$

(23)

which has the following first integrals:

$$\begin{aligned} \varPhi _1(x_1,x_2,x_3,x_4)= & {} x_4^2-12x_4x_1x_2-24x_1x_3^2+12x_3x_2^2+120x_3x_1^3\nonumber \\&-\,144x_1^5-2\alpha x_1x_3+\alpha x_2^2+4\alpha x_1^3 \end{aligned}$$

(24)

and

$$\begin{aligned} \varPhi _2(x_1,x_2,x_3,x_4)= & {} x_1x_4^2-21x_1^2x_3^2+120x_1^4x_3+7\alpha x_1^4-\frac{1}{12}\alpha x_3^2-\frac{1}{12}\alpha ^2x_1^2\nonumber \\&-\,180x_1^6-9x_2^4+\frac{1}{3}x_3^3-18x_1^2x_2x_4+36x_1x_2^2x_3-x_2x_3x_4\nonumber \\&+\,\frac{1}{6}\alpha x_2x_4-2\alpha x_1^2x_3+\frac{1}{1296}\alpha ^3. \end{aligned}$$

(25)

For given two constants $K_1$ and $K_2$, the two level sets defined by $\varPhi _1(x_1,x_2,x_3,x_4)=K_1$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_2$ determine two three-dimensional invariant manifolds of system (23). Their intersection is a two-dimensional manifold.

Notice that when $\beta =0$ under the transformation $(x_1,x_2,x_3,x_4)\rightarrow (x_1,-x_2,x_3,-x_4)$ and $t\rightarrow -t$, system (25) is invariant. This symmetry is important for the persistence of homoclinic orbits under some small perturbation (see [18]).

We take $\alpha =60p^2, \beta =0\ (p>0).$ Then, system (23) has three equilibrium points for which $E_1(-\,p,0,0,0)$ is a center–center with the eigenvalues $\pm \, \lambda _1 i\equiv \pm \, [(15+\sqrt{15})p]^{\frac{1}{2}} i, \pm \,\lambda _2 i\equiv \pm \,[(15-\sqrt{15})p]^{\frac{1}{2}} i;$$E_2(0,0,0,0)$ is a center-saddle with the eigenvalues $\pm \, \lambda _1 i\equiv \pm \, (15)^{\frac{1}{4}}\sqrt{2p} i, \pm \, \lambda _2\equiv \pm \,(15)^{\frac{1}{4}}\sqrt{2p}$ and $E_3(p,0,0,0)$ is a hyperbolic equilibrium point (saddle–saddle) with the eigenvalues $\pm \,\lambda _1\equiv \pm \,[(15+\sqrt{105})p]^{\frac{1}{2}}, \pm \,\lambda _2\equiv \pm \,[(15-\sqrt{105})p]^{\frac{1}{2}}.$

Corresponding to (24) and (25), we have

$$\begin{aligned} K_{11}= & {} \varPhi _1(-\,p,0,0,0)=-96p^5,\ \ \ \ \ K_{21}=\varPhi _2(-\,p,0,0,0)=\frac{320}{3}p^6.\\ K_{12}= & {} \varPhi _1(0,0,0,0)=0,\ \ \ \ \ K_{22}=\varPhi _2(0,0,0,0)=\frac{500}{3}p^6.\\ K_{13}= & {} \varPhi _1(p,0,0,0)=96p^5,\ \ \ \ \ K_{23}=\varPhi _2(p,0,0,0)=\frac{320}{3}p^6. \end{aligned}$$

In this section, we first consider the solutions of system (23) in the invariant manifold of the equilibrium point $E_3(p,0,0,0)$. In fact, the two level set $(L_1)$ and $(L_2)$ defined by $\varPhi _1(x_1,x_2,x_3,x_4)=K_{13}$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_{23}$ pass through the equilibrium point $E_3$. By using the method given by [5], we know that in the intersection of $(L_1)$ and $(L_2)$, there exist solutions of (23) as follows:

$$\begin{aligned} y(\xi )= & {} x_1(\xi )=\frac{1}{2}\left[ (U(\xi )+V(\xi ))^{\prime } +(U(\xi )+V(\xi ))^2-U(\xi )V(\xi )+A_3\right] ,\nonumber \\ \end{aligned}$$

(26)

where $U(\xi )$ and $V(\xi )$ are defined by inversion of the following two hyper-elliptic integrals:

$$\begin{aligned} I_1\equiv & {} \int _{\infty }^U\frac{dt}{\sqrt{P_3(t)}}+\int _{\infty }^V\frac{dt}{\sqrt{P_3(t)}}=\hat{C}_1,\ \nonumber \\ \quad I_2\equiv & {} \int _{\infty }^U\frac{t dt}{\sqrt{P_3(t)}}+\int _{\infty }^V\frac{t dt}{\sqrt{P_3(t)}}=\hat{C}_2+\xi , \end{aligned}$$

(27)

and

$$\begin{aligned} P_3(t)=(t^2+A_3)^3-\alpha (t^2+A_3)+B_3t+\frac{1}{3}\beta , \end{aligned}$$

(28)

$B_3^2=\frac{4}{3}K_{13}=\frac{512}{3}p^5, A_3=-\frac{64K_{23}}{9B_3^2}=-\frac{40}{9}p$ and $\hat{C}_1$ and $\hat{C}_2$ are integral constants.

Under the parameter conditions of this section, we have

$$\begin{aligned} P_3(t)= & {} t^6-\frac{40}{3}p t^4+\frac{1060}{27}p^2t^2+\frac{16\sqrt{6}}{3}p^{\frac{5}{2}}t+\frac{800}{729}p^3 \nonumber \\= & {} \frac{1}{729}(9t^2+18\sqrt{6p}t+50p)(9t^2-9\sqrt{6p}t-4p)^2\nonumber \\= & {} (t-r_1)(t+r_2)[(t+r_3)(t+r_4)]^2, \end{aligned}$$

(29)

where $r_1=\frac{1}{2}\left( \frac{1}{3}\sqrt{70}+\sqrt{6}\right) \sqrt{p},\ r_2=\frac{1}{2}\left( \frac{1}{3}\sqrt{70}-\sqrt{6}\right) \sqrt{p},\ r_3=\left( \sqrt{6}-\frac{2}{3}\right) \sqrt{p}, r_4=\left( \sqrt{6}+\frac{2}{3}\right) \sqrt{p}.$ We notice that

$$\begin{aligned}&\int ^U\frac{dt}{\sqrt{P_3(t)}}=-\frac{1}{(r_1+r_2)\lambda _1}\nonumber \\&\quad \times \,\ln \left( \frac{\lambda _1^2+e_1(U-r_1)+\lambda _1\sqrt{(U-r_1)^2+2e_1(U-r_1) +\lambda _1^2}}{\frac{1}{2}(U-r_1)}\right) \nonumber \\&\qquad +\,\frac{1}{(r_1+r_2)\lambda _2} \ln \left( \frac{\lambda _2^2+e_2(U+r_2)+\lambda _2\sqrt{(U+r_2)^2+2e_2(U+r_2) +\lambda _2^2}}{\frac{1}{2}(U+r_2)}\right) ,\nonumber \\ \end{aligned}$$

(30)

and

$$\begin{aligned}&\int ^U\frac{t dt}{\sqrt{P_3(t)}}=-\frac{r_1}{(r_1+r_2)\lambda _1} \nonumber \\&\quad \times \,\ln \left( \frac{\lambda _1^2+e_1(U-r_1)+\lambda _1\sqrt{(U-r_1)^2+2e_1(U-r_1) +\lambda _1^2}}{\frac{1}{2}(U-r_1)}\right) \nonumber \\&\qquad -\,\frac{r_2}{(r_1+r_2)\lambda _2} \ln \left( \frac{\lambda _2^2+e_2(U+r_2)+\lambda _2\sqrt{(U+r_2)^2+2e_2(U+r_2) +\lambda _2^2}}{\frac{1}{2}(U+r_2)}\right) ,\nonumber \\ \end{aligned}$$

(31)

where $\lambda _1^2=r_1^2+r_1r_3+r_1r_4+r_3r_4=(15+\sqrt{105})p, \lambda _2^2=r_2^2-r_2r_3-r_2r_4+r_3r_4=(15-\sqrt{105})p, e_1=\frac{1}{2}(2r_1+r_3+r_4) =\frac{4}{3}\sqrt{6p}+r_1, e_2=\frac{1}{2}(-2r_2+r_3+r_4)=\frac{4}{3}\sqrt{6p}-r_2.$

Hence, by using two integral formulas given by (27), we obtain

$$\begin{aligned}&\frac{\left( \lambda _1^2+e_1U_1+\lambda _1\sqrt{U_1^2+2e_1U_1+\lambda _1^2}\right) \left( \lambda _1^2+e_1V_1+\lambda _1\sqrt{V_1^2+2e_1V_1+\lambda _1^2}\right) }{U_1V_1}\nonumber \\&\quad =\tilde{C}_1e^{-\omega _1\xi }, \end{aligned}$$

(32)

and

$$\begin{aligned}&\frac{\left( \lambda _2^2+e_2U_2+\lambda _2\sqrt{U_2^2+2e_2U_2+\lambda _2^2}\right) \left( \lambda _2^2+e_2V_2+\lambda _2\sqrt{V_2^2+2e_2V_2+\lambda _2^2}\right) }{U_2V_2}\nonumber \\&\quad =\tilde{C}_2e^{-\omega _2\xi }, \end{aligned}$$

(33)

where $\omega _1=\frac{1}{2}\left( 1+\frac{r_1}{r_2}\right) \lambda _1, \omega _2=\frac{1}{2}\left( 1+\frac{r_2}{r_1}\right) \lambda _2, \ U_1=U(\xi )-r_1, \ V_1=V(\xi )-r_1, U_2=U(\xi )+r_2, \ V_2=V(\xi )+r_2, \tilde{C}_1$ and $\tilde{C_2}$ are two integral constants.

To get the exact explicit parametric representations of $U(\xi )$ and $V(\xi )$ from (32) and (33), let

$$\begin{aligned} (\lambda _1^2+e_1V_1+\lambda _1\sqrt{V_1^2+2e_1V_1+\lambda _1^2}=a_1,\ \ \lambda _2^2+e_2U_2+\lambda _2\sqrt{U_2^2+2e_2U_2+\lambda _2^2}=a_2, \end{aligned}$$

where $a_1$ and $a_2$ are two constants given by (45) below. Thus, (32) and (33) imply that

$$\begin{aligned} U(\xi )= & {} U_a(\xi )=r_1- \frac{2C_1\lambda _1^2}{2e_1C_1-C_1^2e^{-\omega _1\xi }-(e_1^2-\lambda _1^2)e^{\omega _1\xi }}\nonumber \\= & {} r_1-\frac{\frac{\lambda _1^2}{C_1}}{\frac{e_1}{C_1}-\cosh _{q_1}(-\omega _1\xi )},\nonumber \\ V(\xi )= & {} V_a\equiv r_1+V_{10}=r_1+\frac{a_1e_1+\sqrt{a_1^2e_1^2-(a_1^2-2\lambda _1^2a_1)(e_1^2-\lambda _1^2)}}{e_1^2-\lambda _1^2}, \end{aligned}$$

(34)

where $C_1=\frac{V_{10}\tilde{C}_1}{a_1}, q_1=\frac{e_1^2-\lambda _1^2}{C_1^2}, \cosh _q(\xi )=\frac{1}{2}(e^{\xi }+qe^{-\xi })$ is generalized hyperbolic function defined by [13] and

$$\begin{aligned} V(\xi )= & {} V_b(\xi )=-r_2-\frac{2C_2\lambda _2^2}{2e_2C_2-C_2^2e^{-\omega _2\xi }-(e_2^2-\lambda _2^2)e^{\omega _2\xi }}\nonumber \\= & {} -r_2-\frac{\frac{\lambda _2^2}{C_2}}{\frac{e_2}{C_2}-\cosh _{q_2}(-\omega _2\xi )},\nonumber \\ U(\xi )= & {} U_b\equiv -r_2+U_{20}=-r_2+\frac{a_2e_2+\sqrt{a_2^2e_2^2-(a_2^2-2\lambda _2^2a_2)(e_2^2-\lambda _2^2)}}{e_2^2-\lambda _2^2},\qquad \end{aligned}$$

(35)

where $C_2=\frac{U_{20}\tilde{C}_2}{a_2}, q_2=\frac{e_2^2-\lambda _2^2}{C_2^2}.$ We see from (34) and (35) that

$$\begin{aligned} U_a^{\prime }(\xi )=\frac{2C_1\lambda _1^2\omega _1\left[ C_1^2e^{-\omega _1\xi }-(e_1^2-\lambda _1^2)e^{\omega _1\xi }\right] }{\left[ 2e_1C_1-C_1^2e^{-\omega _1\xi }-(e_1^2-\lambda _1^2)e^{\omega _1\xi }\right] ^2}=\frac{\frac{\lambda _1^2\omega _1}{C_1}\sinh _{q_1}(-\omega _1\xi )}{\left[ \frac{e_1}{C_1}-\cosh _{q_1}(-\omega _1\xi )\right] ^2}\quad \end{aligned}$$

(36)

and

$$\begin{aligned} V_b^{\prime }(\xi )=\frac{2C_2\lambda _2^2\omega _2\left[ C_2^2e^{-\omega _2\xi }-(e_2^2-\lambda _2^2)e^{\omega _2\xi }\right] }{\left[ 2e_2C_2-C_2^2e^{-\omega _2\xi }-(e_2^2-\lambda _2^2)e^{\omega _2\xi }\right] ^2}=\frac{\frac{\lambda _2^2\omega _2}{C_2}\sinh _{q_2}(-\omega _2\xi )}{\left[ \frac{e_2}{C_2}-\cosh _{q_2}(-\omega _2\xi )\right] ^2}.\quad \end{aligned}$$

(37)

Therefore, we know from (26) that system (23) has the following three classes of exact solutions:

$$\begin{aligned} x_1(\xi )= & {} y(\xi )=x_{11}(\xi )=\frac{1}{2}\left[ U_a^{\prime }(\xi )+(U_a(\xi )+V_a)^2-U_a(\xi )V_a-\frac{40p}{9}\right] ,\quad \end{aligned}$$

(38)

$$\begin{aligned} x_1(\xi )= & {} y(\xi )=x_{12}(\xi )=\frac{1}{2}\left[ V_b^{\prime }(\xi )+(V_b(\xi )+U_{b})^2-V_b(\xi )U_b-\frac{40p}{9}\right] ,\quad \end{aligned}$$

(39)

$$\begin{aligned} x_1(\xi )= & {} y(\xi )=x_{13}(\xi )\nonumber \\= & {} \frac{1}{2}\left[ U_a^{\prime }(\xi )+V_b^{\prime }(\xi )+(U_a(\xi )+V_b(\xi ))^2)-U_a(\xi )V_b(\xi )-\frac{40p}{9}\right] . \end{aligned}$$

(40)

Letting $\xi \rightarrow \pm \,\infty ,$ we have from (38), (39) and (40) that

$$\begin{aligned}&x_{11}(\xi )\rightarrow \frac{1}{2}\left[ 3r_1^2+3r_1V_{10}+V_{10}^2-\frac{40p}{9}\right] \equiv x_{11}(\pm \,\infty ), \end{aligned}$$

(41)

$$\begin{aligned}&x_{12}(\xi )\rightarrow \frac{1}{2}\left[ 3r_2^2-3r_2U_{20}+U_{20}^2-\frac{40p}{9}\right] \equiv x_{12}(\pm \,\infty ) \end{aligned}$$

(42)

and

$$\begin{aligned} x_{13}(\xi )\rightarrow \frac{1}{2}\left[ (r_1-r_2)^2+r_1r_2-\frac{40p}{9}\right] =p. \end{aligned}$$

(43)

Now, we take

$$\begin{aligned} x_{11}(\pm \,\infty )=x_{12}(\pm \,\infty )=p. \end{aligned}$$

(44)

It is easy to see from (41) and (42) that (44) gives rise to two equations with respect to $a_1$ and $a_2$ which imply two solutions $a_1$ and $a_2$ as follows:

$$\begin{aligned} a_1= & {} \frac{p}{9}\left( 2\sqrt{7461\sqrt{105}+82787}+\left( 413+27\sqrt{105}\right) \right) , \nonumber \\ a_2= & {} \frac{p}{9}\left( 9\sqrt{105}+65-6\sqrt{85\sqrt{105}-465}\right) . \end{aligned}$$

(45)

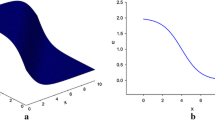
Obviously, three solutions $x_{11}(\xi )$, $x_{12}(\xi )$, and $x_{13}(\xi )$ of (23) with $\beta =0$, given by (38), (39) and (40), respectively, depend on integral constants $C_1$ or $C_2$ or both. When $C_1>0$ and $C_2>0$ these three solutions have singularities at some points where the denominators of $U_a(\xi )$ and $V_b(\xi )$ are equal to zeros. However, when we choose the two constants $C_1<0$ and $C_2<0,$ (38), (39) and (40) give rise to infinitely many smooth soliton solutions. For some fixed pairs $(C_1, C_2),$ we have the graphs of $x_{13}(\xi )$, decaying to a non-zero constant p (See Fig. 1a, b).

(a) $C_1=C_2=-2,$ a double-humped wave profile of $x_{13}(\xi ).$ (b) $C_2=-2, C_1\in (-\,5,-\,1),$ infinitely many double-humped soliton solutions. (c) $C_1=-2, C_2\in (-\,5,-\,1),$ infinitely many double-humped soliton solutions.

Fig. 1

The infinitely many soliton solutions defined by (40) when $p=1$

To sum up, we have proved the following conclusion.

Theorem 1

• (i) Equation (9) with $\beta =0$ has a two-dimensional global homoclinic manifold to the hyperbolic equilibrium point $E_3(p,0,0,0)$ laying in the intersection of $\varPhi _3(x_1,x_2,x_3,x_4)=K_{13}$ and $\varPhi _4(x_1,x_2,x_3,x_4)=K_{23},$ in which the flow of (9) is defined by $(x_{13}(\xi ),x_{13}^{\prime }(\xi ),x_{13}^{\prime \prime }(\xi ),x_{13}^{\prime \prime \prime }(\xi )),$ where $x_{13}(\xi )$ is given by (40).

• (ii) Taking $C_1<0, C_2<0$ in $x_{11}(\xi ), x_{12}(\xi )$ and $x_{13}(\xi )$, then (38), (39) and (40) give rise to uncountably infinite many solton solutions of Eq. (9). Especially, (40) defined a family of double-humped solutions.

3 Exact Solitary Wave Solution and Quasi-Periodic Solutions in the Invariant Manifold of the Saddle-Center

In this section, we investigate the solutions on the intersection of level manifolds $\varPhi _1(x_1,x_2,x_3,x_4)=K_{12}=0$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_{2}.$ By using the result in [3] cited by [5], we know that

$$\begin{aligned} y=x_1(\xi )=U(\xi )+V(\xi ), \end{aligned}$$

(46)

where U and V are defined by

$$\begin{aligned} (U^{\prime })^2= & {} 4U^3-5p^2U+\frac{1}{6}\sqrt{K_2},\nonumber \\ (V^{\prime })^2= & {} 4V^3-5p^2V-\frac{1}{6}\sqrt{K_2}. \end{aligned}$$

(47)

Taking $K_2=K_{22},$ then we have

$$\begin{aligned} (U^{\prime })^2= & {} 4U^3-5p^2U+\frac{15\sqrt{15}}{27}p^3=\left( U-\frac{\sqrt{15}}{6}p\right) ^2\left( 4U+\frac{4\sqrt{15}}{3}p\right) ,\nonumber \\ (V^{\prime })^2= & {} 4V^3-5p^2V-\frac{15\sqrt{15}}{27}p^3=\left( V+\frac{\sqrt{15}}{6}p\right) ^2\left( 4V-\frac{4\sqrt{15}}{3}p\right) . \end{aligned}$$

(48)

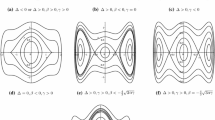
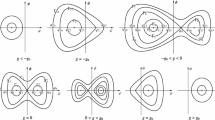
Notice that in the $(U,\dot{U})-$phase plane and $(V,\dot{V})-$phase plane, the two equations defined by (48) determine two cubic algebraic curves shown in Fig. 2a, b, respectively. Clearly, the first equation of (48) gives rise to a homoclinic orbit, while the second equation gives rise to an open curve and a point $(V,\dot{V})=\left( -\frac{\sqrt{15}}{6}p,0\right)$.

Fig. 2

The phase curves defined by (48) a$(U,\dot{U})$-phase plane for $p>0$. b$(V,\dot{V})$-phase plane for $p>0$.

Thus, by using (48) to do integrate, we obtain the following results.

• (1) Corresponding to the homoclinic orbit in Fig. 2a, we have its parametric representation

  $$\begin{aligned} U(\xi )=U_{o1}(\xi )=\frac{\sqrt{15}}{2}p\left[ \tanh ^2(\omega \xi )-\frac{2}{3}\right] , \end{aligned}$$

  where $\omega =\frac{1}{2}(2\sqrt{15}p)^{\frac{1}{2}}=\frac{1}{2}\lambda _2.$

• (2) Corresponding to the stable manifold and the unstable manifold in the right of the saddle $\left( \frac{\sqrt{15}p}{6},0\right)$ in Fig. 2a, we have the parametric representation

  $$\begin{aligned} U(\xi )=U_{o2}(\xi )=\frac{\sqrt{15}}{2}p\left[ \text {ctnh}^2(\omega \xi )-\frac{2}{3}\right] . \end{aligned}$$

• (3) Corresponding to the equilibrium point $\left( \frac{\sqrt{15}p}{6},0\right)$ in Fig. 2a, we have its parametric representation

  $$\begin{aligned} U(\xi )=U_{o3}(\xi )=\frac{\sqrt{15}p}{6}. \end{aligned}$$

• (4) Corresponding to the point $\left( -\frac{\sqrt{15}}{6}p,0\right)$ in Fig. 2b, we have its parametric representation

  $$\begin{aligned} V(\xi )=V_{o1}(\xi )=-\frac{\sqrt{15}}{6}p. \end{aligned}$$

• (5) Corresponding to the open curve passing through the point $\left( \frac{\sqrt{15}p}{3},0\right)$ in Fig. 2b, we have the parametric representation

  $$\begin{aligned} V(\xi )=V_{o2}(\xi )=\frac{\sqrt{15}p}{2}\left[ \text {tan}^2(\omega \xi )+\frac{2}{3}\right] . \end{aligned}$$

Therefore, as some intersection curves of two level manifolds $\varPhi _1(x_1,x_2,x_3,x_4)=0$ and $\varPhi _2(x_1,x_2,x_3,x_4)=\frac{500}{3}p^6$, we obtain the following exact explicit non-trivial parametric representations of the solutions of Eq. (9):

$$\begin{aligned} y= & {} x_1(\xi )=U_{o1}(\xi )+V_{o1}(\xi )\nonumber \\= & {} -\frac{\sqrt{15}p}{6} +\frac{\sqrt{15}p}{2}\left[ \tanh ^2(\omega \xi )-\frac{2}{3}\right] = -\omega ^2\text {sech}^2(\omega \xi ),\nonumber \\ y= & {} x_1(\xi )=U_{o2}(\xi )+V_{o1}(\xi )\nonumber \\= & {} -\frac{\sqrt{15}p}{6}+\frac{\sqrt{15}p}{2}\left[ \text {ctnh}^2(\omega \xi )-\frac{2}{3}\right] = \omega ^2\text {csch}^2(\omega \xi ),\nonumber \\ y= & {} x_1(\xi )=U_{o3}(\xi )+V_{o2}(\xi )\nonumber \\= & {} \frac{\sqrt{15}p}{6}+\frac{\sqrt{15}p}{2}\left[ \tan ^2(\omega \xi )+\frac{2}{3}\right] = \omega ^2\text {sec}^2(\omega \xi ), \nonumber \\ y= & {} x_1(\xi )=U_{o1}(\xi )+V_{o2}(\xi )\nonumber \\= & {} \frac{\sqrt{15}p}{2}\left[ \tanh ^2(\omega \xi )+\tan ^2(\omega \xi )\right] , \nonumber \\ y= & {} x_1(\xi )=U_{o2}(\xi )+V_{o2}(\xi )\nonumber \\= & {} \frac{\sqrt{15}p}{2}\left[ \text {ctnh}^2(\omega \xi )+\tan ^2(\omega \xi )\right] . \end{aligned}$$

(49)

In (49), the first solution just gives rise to a solitary wave solution of Eq. (9) which corresponds to the homoclinic orbit to center-saddle $E_2(0,0,0,0)$.

We next consider the intersection of two level manifolds $\varPhi _1(x_1,x_2,x_3,x_4)=0$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_2$ where $K_2<K_{22}$ and $0\le |K_2-K_{22}|\le \delta$ with $\delta >0$ sufficiently small such that in the $(U,\dot{U})$-phase plane and $(V,\dot{V})$-phase plane, there exists respectively a closed branch of the curves defined by (47). For example, taking $K_2=K_{2b}=\frac{320}{3}p^6$ in (47), we have

$$\begin{aligned} (U^{\prime })^2= & {} 4U^3-5p^2U+\frac{4\sqrt{15}}{9}p^3,\nonumber \\ (V^{\prime })^2= & {} 4V^3-5p^2V-\frac{4\sqrt{15}}{9}p^3. \end{aligned}$$

(50)

In the $(U,\dot{U})$-phase plane and $(V,\dot{V})$-phase plane, the two equations defined by (50) determine two cubic algebraic curves which are shown in Fig. 3a, b, respectively. Obviously, two equations of (50) give rise to an open curve and a closed curve, respectively.

Fig. 3

The phase curves defined by (50) a$(U,\dot{U})$-phase plane for $p>0$. b$(V,\dot{V})$-phase plane for $p>0$.

In the two cases, we have from (50) that

$$\begin{aligned} (U^{\prime })^2= & {} 4U^3-5p^2U+\frac{1}{6}\sqrt{K_2}=4(r_1-U)(r_2-U)(U-r_3),\nonumber \\ (V^{\prime })^2= & {} 4V^3-5p^2V-\frac{1}{6}\sqrt{K_2}=4(z_1-V)(z_2-V)(V-z_3). \end{aligned}$$

(51)

where when $K_2\rightarrow K_{22},\ r_1, r_2\rightarrow \frac{\sqrt{15}p}{6},\ r_3\rightarrow -\frac{\sqrt{15}p}{3},\ z_2,z_3\rightarrow -\frac{\sqrt{15}p}{6},\ z_1\rightarrow \frac{\sqrt{15}p}{3},\ r_1-r_3\rightarrow \frac{\sqrt{15}p}{2},\ z_1-z_3\rightarrow \frac{\sqrt{15}p}{2}.$

By using (51), we obtain

$$\begin{aligned} U(\xi )= & {} U_p(\xi )=r_3+(r_2-r_3)\text {sn}^2(\sqrt{r_1-r_3}\xi ,k_1)=r_3+R_d\text {sn}^2(\varOmega _1\xi ,k_1),\\ V(\xi )= & {} V_p(\xi )=z_3+(z_2-z_3)\text {sn}^2(\sqrt{z_1-z_3}\xi ,k_2)=z_3+Z_d\text {sn}^2(\varOmega _2\xi ,k_2), \end{aligned}$$

where $k_1=\sqrt{\frac{r_2-r_3}{r_1-r_3}},\ k_2=\sqrt{\frac{z_2-z_3}{z_1-z_3}},\ R_d=r_2-r_3,\ Z_d=z_2-z_3,\ \varOmega _1=\sqrt{r_1-r_3},\ \varOmega _2=\sqrt{z_1-z_3}, \text {sn}(\cdot ,k)$ is Jacobin elliptic function (see [1]). It is easy to see that when $K_2\rightarrow K_{22},\ U_p(\xi )\rightarrow U_o(\xi ),\ V_p(\xi )\rightarrow V_o(\xi ).$

Hence, we have

$$\begin{aligned} y=x_1(\xi )=r_3+z_3+R_d\text {sn}^2(\varOmega _1\xi ,k_1)+Z_d\text {sn}^2(\varOmega _2\xi ,k_2). \end{aligned}$$

(52)

This parametric representation gives rise to a family of quasi-periodic wave solutions of Eq. (9).

To sum up, we have proved the following conclusion.

Theorem 2

• (i) Equation (9) has a solitary wave solution given by the first equation of (49) and other exact solutions given by other equations of (49). Geometrically, they lie in the intersection of two level manifolds $\varPhi _1(x_1,x_2,x_3,x_4)=0$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_{22}$ of system (23).

• (ii) There exists a family of quasi-periodic solutions of system (23) with the parametric representation given by (52). Geometrically, they lie in the intersection of two families of level manifolds $\varPhi _1(x_1,x_2,x_3,x_4)=0$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_2$ of system (23) where $K_2\in (K_{22}-\delta , K_{22}).$

4 Exact Periodic Wave Solutions and Quasi-Periodic Wave Solutions in the Invariant Manifold of the Center–Center

In this section, we discuss the flow related the equilibrium point $E_1$. In this case, instead of $P_3(t)$ in (29), we have

$$\begin{aligned} P_1(t)=t^6+\frac{40}{3}p t^4+\frac{1060}{27}p^2t^2+\frac{16\sqrt{6}}{3}(-\,p)^{\frac{5}{2}}t-\frac{800}{729}p^3 \end{aligned}$$

(53)

Clearly, by the parameter transformation $p\rightarrow -p$, the polynomial $P_1(t)$ becomes $P_3(t)$. Therefore, we have from (34) and (35) that

$$\begin{aligned} U_{a1}(\xi )=r_1+ \frac{C_1\lambda _1^2}{2e_1C_1-C_1^2e^{-i\omega _1\xi }-(e_1^2+\lambda _1^2)e^{i\omega _1\xi }}, \end{aligned}$$

(54)

and

$$\begin{aligned} V_{b1}(\xi )=-r_2+ \frac{C_2\lambda _2^2}{2e_2C_2-C_2^2e^{-i\omega _2\xi }-(e_2^2+\lambda _2^2)e^{i\omega _2\xi }}. \end{aligned}$$

(55)

Taking the real parts and imaginary parts, respectively, we obtain

$$\begin{aligned} U_{a1r}(\xi )=r_1+\frac{C_1\lambda _1^2[2e_1C_1-(C_1+e_1^2+\lambda _1^2)\cos (\omega _1\xi )]}{[2e_1C_1-(C_1^2+e_1^2 +\lambda _1^2)\cos (\omega _1\xi )]^2+(C_1^2-e_1^2-\lambda _1^2)^2\sin ^2(\omega _1\xi )}\nonumber \\ \end{aligned}$$

(56)

and

$$\begin{aligned} U_{a1i}(\xi )= & {} -\frac{C_1\lambda _1^2[(C_1^2-e_1^2-\lambda _1^2)\sin (\omega _1\xi )]}{[2e_1C_1-(C_1+e_1 +\lambda _1^2)\cos (\lambda _1\xi )]^2+(C_1^2-e_1^2-\lambda _1^2)^2\sin ^2(\omega _1\xi )}; \end{aligned}$$

(57)

$$\begin{aligned} \nonumber \\ \\ V_{b1r}(\xi )= & {} -r_2+\frac{C_2\lambda _2^2[2e_2C_2-(C_2+e_2^2+\lambda _2^2)\cos (\omega _2\xi )]}{[2e_2C_2-(C_2+e_2 +\lambda _2^2)\cos (\omega _2\xi )]^2+(C_2^2-e_2^2-\lambda _2^2)^2\sin ^2(\omega _2\xi )}\nonumber \\ \end{aligned}$$

(58)

and

$$\begin{aligned} V_{b1i}(\xi )=-\frac{C_2\lambda _2^2[(C_2^2-e_2^2-\lambda _2^2)\sin (\omega _2\xi )]}{[2e_2C_2-(C_2^2+e_2^2 +\lambda _2^2)\cos (\omega _2\xi )]^2+(C_2^2-e_2^2-\lambda _2^2)^2\sin ^2(\omega _2\xi )}.\nonumber \\ \end{aligned}$$

(59)

Thus, similar to (40), system (23) has the following solutions:

$$\begin{aligned} x_1(\xi )= & {} y(\xi )=\frac{1}{2}\left[ U_{a1r}^{\prime }(\xi )+V_{b1r}^{\prime }(\xi )+(U_{a1r}(\xi )\right. \nonumber \\&\left. +\,V_{b1r}(\xi ))^2)-U_{a1r}(\xi )V_{b1r}(\xi ) -\frac{40p}{9}\right] \end{aligned}$$

(60)

and

$$\begin{aligned} x_1(\xi )= & {} y(\xi )=\frac{1}{2}\left[ U_{a1i}^{\prime }(\xi )+V_{b1i}^{\prime }(\xi )+(U_{a1i}(\xi )\right. \nonumber \\&\left. +\,V_{b1i}(\xi ))^2)-U_{a1i}(\xi )V_{b1i}(\xi ) -\frac{40p}{9}\right] . \end{aligned}$$

(61)

Generally, $\omega _1$ and $\omega _2$ are unreduced. Hence, (60) and (61) give rise to two families of quasi-periodic solutions of system (23) for any real number pair $(C_1,C_2)$.

We see from the above discussion, the following conclusion holds.

Theorem 3

• (i) There exist two families of quasi-periodic solutions of system (23) with the parametric representation given by (60) and (61). Geometrically, they lie in the intersection of two families of level manifolds $\varPhi _1(x_1,x_2,x_3,x_4)=K_{11}$ and $\varPhi _2(x_1,x_2,x_3,x_4)=K_{21}$ of system (23).

• (ii) Letting $C_1=0, C_2\ne 0$ or $C_2=0, C_1\ne 0$, then there exist two families of periodic solutions of system (23) given by (60) and (61). These solutions lie in the center manifold of the equilibrium $E_1$ of system (23) given by $M_1=\{(x_1,x_2,x_3,x_4)\in R^4 | \varPhi _1(x_1,x_2,x_3,x_4)=K_{11}, \varPhi _2(x_1,x_2,x_3,x_4)=K_{21}\}$.

5 Conclusion

In Sects. 2, 3 and 4 of this paper, we obtain the exact solutions in the invariant manifolds of the three equilibrium points of system (23) with $\beta =0.$ Under determined parameter conditions, these results give rise to the exact travelling wave solutions for above five nonlinear wave equations mentioned in introduction. We find that the high-order nonlinear equations have uncountably infinite many double-humped soliton solutions.

When $\beta \ne 0$, to get exact solutions, the calculation is very complicated.