Nonlinear wave solutions and their relations for the modified Benjamin–Bona–Mahony equation

Abstract

In this paper, we use the bifurcation method of dynamical systems to investigate the nonlinear wave solutions of the modified Benjamin–Bona–Mahony equation. These nonlinear wave solutions contain periodic wave solutions, solitary wave solutions, periodic blow-up wave solutions, kink wave solutions, unbounded wave solutions and blow-up wave solutions. Some previous results are extended.

1 Introduction

The Benjamin–Bona–Mahony (BBM) equation

$$\begin{aligned} u_{t}+u_{x}+uu_{x}-u_{xxt}=0, \end{aligned}$$

(1)

which was first derived to describe an approximation for surface long waves in nonlinear dispersive media [1]. The equation can also characterize the hydromagnetics waves in cold plasma, acoustic waves in enharmonic crystals and acoustic-gravity waves in compressible fluids [2, 3].

Yusufoglu [4] investigate the modified Benjamin–Bona–Mahony (MBBM)

$$\begin{aligned} u_{t}+u_{x}+a u^{2}u_{x}+u_{xxt}=0. \end{aligned}$$

(2)

Yusufoglu used the exp-function method to obtain generalized solitonary solutions of Eq. (2). When $a=1$, Eq. (2) becomes the equation

$$\begin{aligned} u_{t}+u_{x}+u^{2}u_{x}+u_{xxt}=0, \end{aligned}$$

(3)

which was studied in [5–8]. Daghan et al. [5] obtained some traveling wave solutions of Eq. (3) by using $(\frac{G^{\prime }}{G})$-expansion method. Abbasbandy and Shirzadi [6] used the first integral method to obtain two real exact solutions and two complex exact solutions of Eq. (3). Yusufoglu and Bekir [7] obtained the solitons solutions, periodic solutions and complex solutions of Eq. (3) by using the tanh and sine–cosine methods. Noor et al. [8] used the exp-function method to construct some soliton solutions of Eq. (3).

The aim of this paper is to investigate the nonlinear wave solutions and their phase portraits for Eq. (2) by using the bifurcation method and qualitative theory of dynamical systems [9–16]. Through some special phase orbits, we obtain many smooth periodic wave solutions, periodic blow-up solutions, solitary wave solutions, kink wave solutions, unbounded wave solutions and blow-up wave solutions.

The remainder of this paper is organized as follows. In Sect. 2, we present our main results. Section 3 gives the derivation for our main results. A short conclusion will be given in Sect. 4.

2 Main results

In this section, we state our main results. To relate conveniently, let

$$\begin{aligned}&\alpha =-\frac{a}{c},\qquad \beta =-\frac{c-1}{c}, \end{aligned}$$

(4)

$$\begin{aligned}&g_{0}=\frac{2|\beta |}{3}\sqrt{\frac{\beta }{\alpha }}, \end{aligned}$$

(5)

$$\begin{aligned}&\xi =x-ct. \end{aligned}$$

(6)

Proposition 1

For given positive constants $c$ and $g_{0}$, (2) has the following periodic wave solutions when $\alpha >0$.

(1) If $g=0$, we get four periodic wave solutions

$$\begin{aligned}&u_{1}(x,t)=\frac{a_{1}+b_{1}\mathrm{sn}^{2}(\omega _{1}\xi ,k_{1})}{c_{1}+d_{1}\mathrm{sn}^{2}(\omega _{1}\xi ,k_{1})}, \end{aligned}$$

(7)

$$\begin{aligned}&u_{2}(x,t)=\sqrt{\varphi _{4}^{2}-\left( 2\varphi _{4}^{2}-\frac{6\beta }{\alpha }\right) \mathrm{sn}^{2}\left( \varphi _{4}\sqrt{\frac{\alpha }{6}}\xi , k_{2}\right) },\nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}&u_{3_{\pm }}(x,t)=\pm \varphi _{6}\mathrm{cn}\left( \sqrt{\frac{\alpha }{3}\varphi _{6}^{2} -\beta }\xi ,\varphi _{6}\sqrt{\frac{\alpha }{2\alpha \varphi _{6}^{2}-6\beta }}\right) ,\nonumber \\ \end{aligned}$$

(9)

where

$$\begin{aligned}&a_{1}=\varphi _{1}\left( -\varphi _{1}+\sqrt{\frac{6\beta }{\alpha }-\varphi _{1}^{2}}\right) ,\quad \nonumber \\&b_{1}=\varphi _{1}\left( \varphi _{1}+\sqrt{\frac{6\beta }{\alpha }-\varphi _{1}^{2}}\right) , \end{aligned}$$

(10)

$$\begin{aligned}&c_{1}=-\varphi _{1}+\sqrt{\frac{6\beta }{\alpha } -\varphi _{1}^{2}},\qquad d_{1}=-\varphi _{1}-\sqrt{\frac{6\beta }{\alpha } -\varphi _{1}^{2}},\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned}&\omega _{1}=\frac{-\varphi _{1}\sqrt{\alpha }+\sqrt{6\beta -\alpha \varphi _{1}^{2}}}{2\sqrt{6}},\qquad k_{1}\!=\!\frac{\varphi _{1}\!+\!\sqrt{\frac{6\beta }{\alpha }\!-\!\varphi _{1}^{2}}}{\varphi _{1}\!-\!\sqrt{\frac{6\beta }{\alpha }\!-\!\varphi _{1}^{2}}},\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned}&-\sqrt{\frac{6\beta }{\alpha }}<\varphi _{1} <-\sqrt{\frac{3\beta }{\alpha }},\qquad k_{2}=\sqrt{2-\frac{6\beta }{\alpha \varphi _{4}^{2}}}, \end{aligned}$$

(13)

$$\begin{aligned}&\sqrt{\frac{3\beta }{\alpha }}\!<\!\varphi _{4}\!<\!\sqrt{\frac{6\beta }{\alpha }}, \qquad \varphi _{5}<\!-\!\sqrt{\frac{6\beta }{\alpha }}, \qquad \varphi _{6}\!>\!\sqrt{\frac{6\beta }{\alpha }}.\nonumber \\ \end{aligned}$$

(14)

And two solitary wave solutions

$$\begin{aligned} u_{4_{\pm }}(x,t)=\pm \sqrt{\frac{6\beta }{\alpha }} \mathrm{sech}\sqrt{\beta }\xi , \end{aligned}$$

(15)

(2) If $-g_{0}<g<0$, we get six periodic wave solutions

$$\begin{aligned}&u_{5}(x,t)\nonumber \\&\quad =\frac{A_{1}\varphi _{10}+\varphi _{11}B_{1} \!+\!(A_{1}\varphi _{10}\!-\!\varphi _{11}B_{1})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{1}B_{1}}{6}}\xi ,k_{3}\!\right) }{A_{1}\!+\!B_{1}\!+\!(A_{1}\!-\!B_{1})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{1}B_{1}}{6}}\xi ,k_{3}\!\right) },\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}&u_{6}(x,t)\nonumber \\&\quad =\frac{-2\gamma _{1}+\eta _{1}\delta _{1} +\eta _{1}\sqrt{\mu _{1}}\cos \left( \sqrt{\frac{\alpha \gamma _{1}}{6}}\xi \right) }{\delta _{1}+\sqrt{\mu _{1}} \cos \left( \sqrt{\frac{\alpha \gamma _{1}}{6}}\xi \right) }, \end{aligned}$$

(17)

$$\begin{aligned}&u_{7}(x,t)\nonumber \\&\quad =\frac{\varphi _{14}(\varphi _{17}-\varphi _{15}) +\varphi _{17}(\varphi _{15}-\varphi _{14})\mathrm{sn}^{2}(\omega _{2}\xi ,k_{4})}{\varphi _{17}-\varphi _{15} +(\varphi _{15}-\varphi _{14})\mathrm{sn}^{2}(\omega _{2}\xi ,k_{4})}, \end{aligned}$$

(18)

$$\begin{aligned}&u_{8}(x,t)\nonumber \\&\quad =\frac{\varphi _{17}(-\varphi _{16}+\varphi _{14}) -\varphi _{14}(\varphi _{17}-\varphi _{16})\mathrm{sn}^{2}(\omega _{2}\xi ,k_{4})}{-\varphi _{16}+\varphi _{14} -(\varphi _{17}-\varphi _{16})\mathrm{sn}^{2}(\omega _{2}\xi ,k_{4})},\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned}&u_{9}(x,t)\nonumber \\&\quad =\frac{A_{2}\varphi _{18}+\varphi _{19}B_{2} \!+\!(A_{2}\varphi _{18}\!-\!\varphi _{19}B_{2})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{2}B_{2}}{6}}\xi ,k_{5}\!\right) }{A_{2}+B_{2}+(A_{2}-B_{2})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{2}B_{2}}{6}}\xi ,k_{5}\right) },\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned}&u_{10}(x,t)\nonumber \\&\quad =\frac{A_{2}\varphi _{18}\!+\!\varphi _{19}B_{2} \!-\!(A_{2}\varphi _{18}\!-\!\varphi _{19}B_{2})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{2}B_{2}}{6}}\xi ,k_{5}\!\right) }{A_{2}\!+\!B_{2}\!-\!(A_{2}\!-\!B_{2})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{2}B_{2}}{6}}\xi ,k_{5}\right) },\nonumber \\ \end{aligned}$$

(21)

where

$$\begin{aligned} A_{1}&= \sqrt{\left( \varphi _{11}-\frac{c_{1}+\overline{c}_{1}}{2}\right) ^{2} -\frac{(c_{1}-\overline{c}_{1})^{2}}{4}},\nonumber \\ B_{1}&= \sqrt{\left( \varphi _{10}-\frac{c_{1}+\overline{c}_{1}}{2}\right) ^{2} -\frac{(c_{1}-\overline{c}_{1})^{2}}{4}}, \end{aligned}$$

(22)

$$\begin{aligned} A_{2}&= \sqrt{\left( \varphi _{19}-\frac{c_{2}+\overline{c}_{2}}{2}\right) ^{2} -\frac{(c_{2}-\overline{c}_{2})^{2}}{4}},\nonumber \\ B_{2}&= \sqrt{\left( \varphi _{18}-\frac{c_{2}+\overline{c}_{2}}{2}\right) ^{2} -\frac{(c_{2}-\overline{c}_{2})^{2}}{4}}, \end{aligned}$$

(23)

$$\begin{aligned} k_{3}&= \sqrt{\frac{(\varphi _{11}-\varphi _{10})^{2} -(A_{1}-B_{1})^{2}}{4A_{1}B_{1}}},\nonumber \\ k_{4}&= \sqrt{\frac{(\varphi _{17}-\varphi _{16})(\varphi _{15} -\varphi _{14})}{(\varphi _{17}-\varphi _{15})(\varphi _{16}-\varphi _{14})}}, \end{aligned}$$

(24)

$$\begin{aligned} \omega _{2}&= \frac{\sqrt{\alpha (\varphi _{17}-\varphi _{15})(\varphi _{16} -\varphi _{14})}}{2\sqrt{6}},\nonumber \\ k_{5}&= \sqrt{\frac{(\varphi _{19}-\varphi _{18})^{2}-(A_{2} -B_{2})^{2}}{4A_{2}B_{2}}}, \end{aligned}$$

(25)

$$\begin{aligned} \gamma _{1}&= \frac{1}{\alpha }\left( 12\beta -3\alpha \varphi _{9}\left( \varphi _{9} +\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}}\right) \right) ,\nonumber \\ \delta _{1}&= -2\varphi _{9}+2\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}}, \end{aligned}$$

(26)

$$\begin{aligned} \mu _{1}&= 4\varphi _{9}\left( \varphi _{9}+\sqrt{\frac{12\beta }{\alpha } -3\varphi _{9}^{2}}\right) ,\nonumber \\ \eta _{1}&= \frac{1}{2}\left( -\varphi _{9}+\sqrt{\frac{12\beta }{\alpha } -3\varphi _{9}^{2}}\right) , \end{aligned}$$

(27)

$c_{1}$, $\overline{c}_{1}$, $c_{2}$ and $\overline{c}_{2}$ are complex numbers. And two solitary wave solutions

$$\begin{aligned}&u_{11_{\pm }}(x,t)=\varphi _{9}\nonumber \\&\quad +\frac{6\beta -\alpha \varphi _{9}^{2}}{2\alpha \varphi _{9}\pm \sqrt{6\alpha \beta -2\alpha ^{2}\varphi _{9}^{2}}\cosh \left( \sqrt{\beta -\alpha \varphi _{9}^{2}}\xi \right) },\nonumber \\ \end{aligned}$$

(28)

(3) If $g=-g_{0}$, we get two periodic wave solutions as follows

$$\begin{aligned}&u_{12}(x,t)\nonumber \\&\quad =\frac{A_{3}\varphi _{22}+\varphi _{23}B_{3}\!+\!(A_{3}\varphi _{22}\!-\! \varphi _{23}B_{3})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) }{A_{3}\!+\!B_{3}\!+\!(A_{3}\!-\!B_{3})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) },\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned}&u_{13}(x,t)\nonumber \\&\quad =\frac{A_{4}\varphi _{24}+\varphi _{25}B_{4}\!+\!(A_{4}\varphi _{24}\!-\! \varphi _{25}B_{4})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{4}B_{4}}{6}}\xi ,k_{7}\!\right) }{A_{4}+B_{4}+(A_{4}-B_{4})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{4}B_{4}}{6}}\xi ,k_{7}\right) },\nonumber \\ \end{aligned}$$

(30)

where

$$\begin{aligned} A_{3}&= \sqrt{\left( \varphi _{23}-\frac{c_{3}+\overline{c}_{3}}{2}\right) ^{2}-\frac{(c_{3}-\overline{c}_{3})^{2}}{4}},\nonumber \\ B_{3}&= \sqrt{\left( \varphi _{22}-\frac{c_{3}+\overline{c}_{3}}{2}\right) ^{2} -\frac{(c_{3}-\overline{c}_{3})^{2}}{4}}, \end{aligned}$$

(31)

$$\begin{aligned} A_{4}&= \sqrt{\left( \varphi _{25}-\frac{c_{4}+\overline{c}_{4}}{2}\right) ^{2}-\frac{(c_{4}-\overline{c}_{4})^{2}}{4}},\nonumber \\ B_{4}&= \sqrt{\left( \varphi _{24}-\frac{c_{4}+\overline{c}_{4}}{2}\right) ^{2} -\frac{(c_{4}-\overline{c}_{4})^{2}}{4}}, \end{aligned}$$

(32)

$$\begin{aligned} k_{6}&= \sqrt{\frac{(\varphi _{23}-\varphi _{22})^{2}-(A_{3}-B_{3})^{2}}{4A_{3}B_{3}}},\quad \nonumber \\ k_{7}&= \sqrt{\frac{(\varphi _{25}-\varphi _{24})^{2}-(A_{4}-B_{4})^{2}}{4A_{4}B_{4}}}, \end{aligned}$$

(33)

$c_{3}$, $\overline{c}_{3}$, $c_{4}$ and $\overline{c}_{4}$ are complex numbers. And a solitary wave solution

$$\begin{aligned} u_{14}(x,t)=\frac{\sqrt{\beta }(-9+2\beta \xi ^{2})}{\sqrt{\alpha }(3+2\beta \xi ^{2})}. \end{aligned}$$

(34)

Proposition 2

For given positive constants $c$ and $g_{0}$, (2) has the following periodic wave solution when $\alpha <0$.

(1) $g=0$, we get two periodic wave solutions

$$\begin{aligned}&u_{15_{\pm }}(x,t)\nonumber \\&=\pm \sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\mathrm{sn}\left( \widetilde{\varphi }_{4}\sqrt{-\frac{\alpha }{6}}\xi , \frac{1}{\widetilde{\varphi }_{4}}\sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\right) ,\nonumber \\ \end{aligned}$$

(35)

six periodic blow-up wave solutions

$$\begin{aligned} u_{16_{\pm }}(x,t)&= \pm \frac{\widetilde{\varphi }_{4}}{\mathrm{sn}\left( \widetilde{\varphi }_{4}\sqrt{-\frac{\alpha }{6}}\xi , \frac{1}{\widetilde{\varphi }_{4}}\sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\right) }, \end{aligned}$$

(36)

$$\begin{aligned} u_{17_{\pm }}(x,t)&= \pm \sqrt{\frac{6\beta }{\alpha }}\sec \left( \sqrt{-\beta }\xi \right) , \end{aligned}$$

(37)

$$\begin{aligned} u_{18_{\pm }}(x,t)&= \pm \sqrt{\frac{6\beta }{\alpha }}\csc \left( \sqrt{-\beta }\xi \right) , \end{aligned}$$

(38)

two kink wave solutions

$$\begin{aligned} u_{19_{\pm }}(x,t)=\pm \sqrt{\frac{3\beta }{\alpha }}\tanh \left( \sqrt{-\frac{\beta }{2}}\xi \right) , \end{aligned}$$

(39)

and two unbounded wave solutions

$$\begin{aligned} u_{20_{\pm }}(x,t)=\pm \sqrt{\frac{3\beta }{\alpha }}\coth \left( \sqrt{-\frac{\beta }{2}}\xi \right) , \end{aligned}$$

(40)

(2) If $0<g<g_{0}$, we get four periodic blow-up wave solutions

$$\begin{aligned}&u_{21}(x,t)\nonumber \\&\quad =\frac{(-\widetilde{\varphi }_{11}+\widetilde{\varphi }_{9})\widetilde{\varphi }_{8} +(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})\widetilde{\varphi }_{9}\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) }{-\widetilde{\varphi }_{11}+\widetilde{\varphi }_{9}+(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) },\nonumber \\ \end{aligned}$$

(41)

$$\begin{aligned}&u_{22}(x,t)\nonumber \\&\quad =\frac{(\widetilde{\varphi }_{10}-\widetilde{\varphi }_{8})\widetilde{\varphi }_{11} -(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})\widetilde{\varphi }_{10}\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) }{\widetilde{\varphi }_{10}-\widetilde{\varphi }_{8}-(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) },\nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned}&u_{23_{\pm }}(x,t)\nonumber \\&\quad =\frac{2\gamma _{2}+\eta _{2}\delta _{2}\pm \eta _{2}\sqrt{\mu _{2}}\cos (\sqrt{\frac{\alpha \gamma _{2}}{6}}\xi )}{\delta _{2}\pm \sqrt{\mu _{2}}\cos (\sqrt{\frac{\alpha \gamma _{2}}{6}}\xi )}, \end{aligned}$$

(43)

a periodic wave solution

$$\begin{aligned}&u_{24}(x,t)\nonumber \\&\quad =\frac{(-\widetilde{\varphi }_{10}+\widetilde{\varphi }_{8})\widetilde{\varphi }_{9} +(\widetilde{\varphi }_{10}-\widetilde{\varphi }_{9})\widetilde{\varphi }_{8}\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) }{-\widetilde{\varphi }_{10}+\widetilde{\varphi }_{8}+(\widetilde{\varphi }_{10}-\widetilde{\varphi }_{9})\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) },\nonumber \\ \end{aligned}$$

(44)

where

$$\begin{aligned} \omega _{3}&= \sqrt{\frac{-\alpha (\widetilde{\varphi }_{11}-\widetilde{\varphi }_{9}) (\widetilde{\varphi }_{10}-{\widetilde{\varphi }}_{8})}{2\sqrt{6}}},\nonumber \\ k_{8}&= \sqrt{\frac{(\widetilde{\varphi }_{10}-\widetilde{\varphi }_{9}) (\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})}{(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{9})(\widetilde{\varphi }_{10}-\widetilde{\varphi }_{8})}}, \end{aligned}$$

(45)

$$\begin{aligned} \gamma _{2}&= \frac{12\beta -3\alpha \widetilde{\varphi }_{7}^{2}-3\sqrt{3}\widetilde{\varphi }_{7} \sqrt{4\alpha \beta -\alpha ^{2}\widetilde{\varphi }_{7}^{2}}}{\alpha },\quad \nonumber \\ \delta _{2}&= \frac{2\left( \alpha \widetilde{\varphi }_{7}+\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right) }{\alpha }, \end{aligned}$$

(46)

$$\begin{aligned} \mu _{2}&= \frac{4\widetilde{\varphi }_{7}\left( \alpha \widetilde{\varphi }_{7}-\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right) }{\alpha },\quad \nonumber \\ \eta _{2}&= \frac{1}{2\alpha }\left( -\alpha \widetilde{\varphi }_{7}-\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right) . \end{aligned}$$

(47)

a blow-up wave solution

$$\begin{aligned}&u_{25}(x,t)\nonumber \\&\quad =\widetilde{\varphi }_{7}\!+\!\frac{6\beta -6\alpha \widetilde{\varphi }_{7}^{2}}{2\alpha \widetilde{\varphi }_{7}\!+\!\sqrt{6\alpha \beta \!-\!2\alpha ^{2}\widetilde{\varphi }_{7}^{2}} \cosh \left( \sqrt{\beta \!-\!\alpha \widetilde{\varphi }_{7}^{2}}\xi \right) },\nonumber \\ \end{aligned}$$

(48)

and a solitary wave solution

$$\begin{aligned}&u_{26}(x,t)\nonumber \\&\quad =\widetilde{\varphi }_{7}\!+\!\frac{6\beta \!-\!6\alpha \widetilde{\varphi }_{7}^{2}}{2\alpha \widetilde{\varphi }_{7}\!-\!\sqrt{6\alpha \beta \!-\!2\alpha ^{2}\widetilde{\varphi }_{7}^{2}} \cosh \left( \sqrt{\beta \!-\!\alpha \widetilde{\varphi }_{7}^{2}}\xi \right) }.\nonumber \\ \end{aligned}$$

(49)

(3) If $g=g_{0}$, we get three blow-up wave solutions

$$\begin{aligned} u_{27}(x,t)&= -\sqrt{\frac{\beta }{\alpha }}\frac{9-2\beta \xi ^{2}}{3+2\beta \xi ^{2}}, \end{aligned}$$

(50)

$$\begin{aligned} u_{28}(x,t)&= \frac{6\sqrt{-6\alpha }-\beta \sqrt{\alpha \beta }\xi ^{3}}{6\alpha \xi +\alpha \beta \xi ^{3}}, \end{aligned}$$

(51)

$$\begin{aligned} u_{29}(x,t)&= -\frac{6\sqrt{-6\alpha }+\beta \sqrt{\alpha \beta }\xi ^{3}}{6\alpha \xi +\alpha \beta \xi ^{3}}, \end{aligned}$$

(52)

and a periodic wave solution

$$\begin{aligned}&u_{30}(x,t)\nonumber \\&\quad =\frac{-A_{5}\widetilde{\varphi }_{17}\!+\!B_{5}\widetilde{\varphi }_{18}\!+\!(A_{5} \widetilde{\varphi }_{17}\!+\!\widetilde{\varphi }_{18}B_{5})\mathrm{cn}\left( \! \sqrt{\frac{-\alpha A_{5}B_{5}}{6}}\xi ,k_{9}\!\!\right) }{-A_{5}+B_{5}+(A_{5}+B_{5})\mathrm{cn}\left( \sqrt{\frac{-\alpha A_{5}B_{5}}{6}}\xi ,k_{9}\right) },\nonumber \\ \end{aligned}$$

(53)

where

$$\begin{aligned} A_{5}&= \sqrt{\left( \widetilde{\varphi }_{18}-\frac{c_{5}+\overline{c}_{5}}{2}\right) ^{2} -\frac{(c_{5}-\overline{c}_{5})^{2}}{4}},\nonumber \\ B_{5}&= \sqrt{\left( \widetilde{\varphi }_{17}-\frac{c_{5}+\overline{c}_{5}}{2}\right) ^{2}-\frac{(c_{5} -\overline{c}_{5})^{2}}{4}}, \end{aligned}$$

(54)

$$\begin{aligned} k_{9}&= \sqrt{\frac{(A_{5}+B_{5})^{2}-(\widetilde{\varphi }_{18}-\widetilde{\varphi }_{17})^{2}}{4A_{5}B_{5}}}, \end{aligned}$$

(55)

$c_{5}$ and $\overline{c}_{5}$ are conjugate complex numbers.

Proposition 3

For these solutions, the following are their relations.

• (1) When $\varphi _{1}$ and $\varphi _{5}$ tend to $\varphi _{7}$, the periodic wave solutions $u_{1}$ and $u_{3_{-}}$ tend to solitary wave solution $u_{4_{-}}$, that is

  $$\begin{aligned} \lim \limits _{\varphi _{1} \rightarrow \varphi _{7}}{u_{1}(x,t)}=\lim \limits _{\varphi _{5} \rightarrow \varphi _{7}}{u_{3_{-}}(x,t)}=u_{4_{-}}(x,t).\nonumber \\ \end{aligned}$$

  (56)

• (2) When $\varphi _{4}$ and $\varphi _{6}$ tend to $\varphi _{8}$, the periodic wave solutions $u_{2}$ and $u_{3_{+}}$ tend to solitary wave solution $u_{4_{+}}$, that is

  $$\begin{aligned} \lim \limits _{\varphi _{4} \rightarrow \varphi _{8}}{u_{2}(x,t)}=\lim \limits _{\varphi _{6} \rightarrow \varphi _{8}}{u_{3_{+}}(x,t)}=u_{4_{+}}(x,t).\nonumber \\ \end{aligned}$$

  (57)

• (3) When $\varphi _{11}$ tends to $\varphi _{13}$, the periodic wave solutions $u_{5}$ and $u_{7}$ tend to periodic wave solution $u_{6}$, that is

  $$\begin{aligned} \lim \limits _{\varphi _{11} \rightarrow \varphi _{13}}{u_{5}(x,t)}=\lim \limits _{\varphi _{11} \rightarrow \varphi _{13}}{u_{7}(x,t)}=u_{6}(x,t).\nonumber \\ \end{aligned}$$

  (58)

• (4) When $\varphi _{17}$ and $\varphi _{19}$ tends to $\varphi _{21}$, the periodic wave solution $u_{7}$ and $u_{9}$ tend to solitary wave solution $u_{11_{-}}$, that is

  $$\begin{aligned} \lim \limits _{\varphi _{17} \rightarrow \varphi _{21}}{u_{7}(x,t)} =\lim \limits _{\varphi _{19} \rightarrow \varphi _{21}}{u_{9}(x,t)}=u_{11_{-}}(x,t).\nonumber \\ \end{aligned}$$

  (59)

• (5) When $\varphi _{17}$ and $\varphi _{19}$ tends to $\varphi _{21}$, the periodic wave solution $u_{8}$ and $u_{10}$ tend to solitary wave solution $u_{11_{+}}$, that is

  $$\begin{aligned} \lim \limits _{\varphi _{17} \rightarrow \varphi _{21}}{u_{8}(x,t)}=\lim \limits _{\varphi _{19} \rightarrow \varphi _{21}}{u_{10}(x,t)}=u_{11_{+}}(x,t).\nonumber \\ \end{aligned}$$

  (60)

• (6) When $\varphi _{22}$ and $\varphi _{24}$ tends to $\varphi _{26}$, the periodic wave solution $u_{12}$ and $u_{13}$ tend to solitary wave solution $u_{14}$, that is

  $$\begin{aligned} \lim \limits _{\varphi _{22} \rightarrow \varphi _{26}}{u_{12}(x,t)}=\lim \limits _{\varphi _{24} \rightarrow \varphi _{26}}{u_{13}(x,t)}=u_{14}(x,t).\nonumber \\ \end{aligned}$$

  (61)

• (7) When $\widetilde{\varphi }_{4}$ tends to $\varphi _{+}$, the periodic wave solution $u_{15_{\pm }}$ tends to kink wave solution $u_{19_{\pm }}$, that is

  $$\begin{aligned} \lim \limits _{\widetilde{\varphi }_{4} \rightarrow \varphi _{+}}{u_{15_{\pm }}(x,t)}=u_{19_{\pm }}(x,t).\nonumber \\ \end{aligned}$$

  (62)

• (8) When $\widetilde{\varphi }_{4}$ tends to $\varphi _{+}$, the periodic wave solution $u_{16_{\pm }}$ tends to unbounded wave solution $u_{20_{\pm }}$, that is

  $$\begin{aligned} \lim \limits _{\widetilde{\varphi }_{4} \rightarrow \varphi _{+}}{u_{16_{\pm }}(x,t)}=u_{20_{\pm }}(x,t). \end{aligned}$$

  (63)

• (9) When $\widetilde{\varphi }_{11}$ tends to $\widetilde{\varphi }_{7}$, the periodic wave solution $u_{21}$ tends to blow-up wave solution $u_{25}$, that is

  $$\begin{aligned} \lim \limits _{\widetilde{\varphi }_{11} \rightarrow \widetilde{\varphi }_{7}}{u_{21}(x,t)}=u_{25}(x,t). \end{aligned}$$

  (64)

• (10) When $\widetilde{\varphi }_{10}$ tends to $\widetilde{\varphi }_{7}$, the periodic wave solution $u_{24}$ tends to solitary wave solution $u_{26}$, that is

  $$\begin{aligned} \lim \limits _{\widetilde{\varphi }_{10} \rightarrow \widetilde{\varphi }_{7}}{u_{24}(x,t)} =u_{26}(x,t). \end{aligned}$$

  (65)

3 The derivation of main results

In this section, we will give the derivations for our main results.

3.1 Planar system and phase portraits

For given positive constant wave speed $c$, substituting $u=\varphi (\xi )$ with $\xi =x-ct$ into the MBBM equation (2), it follows that

$$\begin{aligned} -c\varphi ^{\prime }+\varphi ^{\prime }+a\varphi ^{2}\varphi ^{\prime } -c\varphi ^{\prime \prime \prime }=0. \end{aligned}$$

(66)

Integrating (66) once, we have

$$\begin{aligned} (-c+1)\varphi +\frac{a}{3}\varphi ^{3}-c\varphi ^{\prime \prime }=g_{1}, \end{aligned}$$

(67)

where $g_{1}$ is integral constant.

Letting $\phi =\varphi ^{\prime }$, we get the following planar system

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi ,\\ \frac{\mathrm{d}\phi }{\mathrm{d}\xi }=-\frac{\alpha }{3}\varphi ^{3}+\beta \varphi +g, \end{array}\right. \end{aligned}$$

(68)

where $\alpha =-\frac{a}{c}, \beta =-\frac{c-1}{c}$ and $g=-\frac{g_{1}}{c}$.

Obviously, the above system (68) is a Hamiltonian system with Hamiltonian function

$$\begin{aligned} H(\varphi ,\phi )=\phi ^{2}+\frac{\alpha }{6}\varphi ^{4}-\beta \varphi ^{2}-2g\varphi . \end{aligned}$$

(69)

Now, we consider the phase portraits of system (68). Set

$$\begin{aligned} f_{0}(\varphi )=-\frac{\alpha }{3}\varphi ^{3}+\beta \varphi , \end{aligned}$$

(70)

$$\begin{aligned} f(\varphi )=-\frac{\alpha }{3}\varphi ^{3}+\beta \varphi +g. \end{aligned}$$

(71)

Obviously, $f_{0}(\varphi )$ has three zero points, $\varphi _{-}, \varphi _{0}$ and $\varphi _{+}$, which are given as follows

$$\begin{aligned} \varphi _{-}=-\sqrt{\frac{3\beta }{\alpha }},\qquad \varphi _{0}=0,\qquad \varphi _{+}=\sqrt{\frac{3\beta }{\alpha }}. \end{aligned}$$

(72)

It is easy to obtain two extreme points of $f_{0}(\varphi )$ as follows:

$$\begin{aligned} \varphi _{-}^{*}=-\sqrt{\frac{\beta }{\alpha }},\qquad \varphi _{+}^{*}=\sqrt{\frac{\beta }{\alpha }}. \end{aligned}$$

(73)

Letting

$$\begin{aligned} g_{0}=|f_{0}(\varphi _{-}^{*})|=|f_{0}(\varphi _{+}^{*})|= \frac{2|\beta |}{3}\sqrt{\frac{\beta }{\alpha }}, \end{aligned}$$

(74)

then it is easily seen that $g_{0}$ is the extreme values of $f_{0}(\varphi )$.

Let $(\varphi _{i}, 0)$ be one of the singular points of system (68), then the characteristic values of the linearized system of system (68) at the singular points $(\varphi _{i}, 0)$ are

$$\begin{aligned} \lambda _{\pm }=\pm \sqrt{f'(\varphi _{i})}. \end{aligned}$$

(75)

From the qualitative theory of dynamical systems, we therefore know that

• (i) If $f'(\varphi _{i})>0,\quad (\varphi _{i}, 0)$ is a saddle point.

• (ii) If $f'(\varphi _{i})<0,\quad (\varphi _{i}, 0)$ is a center point.

• (iii) If $f'(\varphi _{i})=0,\quad (\varphi _{i}, 0)$ is a degenerate saddle point.

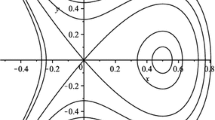
Therefore, we obtain the phase portraits of system (68) in Figs. 1 and 2.

Fig. 1

The phase portraits of system (68) when $\alpha >0$

Fig. 2

The phase portraits of system (68) when $\alpha <0$

3.2 The derivation of Proposition 1

In this section, we will obtain the explicit expressions of solutions for the MBBM equation (2) when $\alpha >0$.

(1) If $g=0$, we set

$$\begin{aligned} \sqrt{\frac{3\beta }{\alpha }}<\varphi _{4}<\sqrt{\frac{6\beta }{\alpha }},\qquad \varphi _{6}>\sqrt{\frac{6\beta }{\alpha }}. \end{aligned}$$

(76)

(i) From the phase portrait, we see that there are two closed orbits $\varGamma _{1}$ and $\varGamma _{1}^{*}$ passing the points $(\varphi _{1},0)$, $(\varphi _{2},0)$, $(\varphi _{3},0)$ and $(\varphi _{4},0)$. In $(\varphi ,\phi )$-plane the expressions of the closed orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi -\varphi _{1})(\varphi -\varphi _{2})(\varphi -\varphi _{3}) (\varphi _{4}-\varphi )},\nonumber \\ \end{aligned}$$

(77)

where $\varphi _{1}=-\varphi _{4}$, $\varphi _{2}=-\sqrt{\frac{6\beta }{\alpha }-\varphi _{4}^{2}}$ and $\varphi _{3}=\sqrt{\frac{6\beta }{\alpha }-\varphi _{4}^{2}}$.

Substituting (77) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{1}$ and $\varGamma _{1}^{*}$,   we have

$$\begin{aligned}&\pm \int _{\varphi _{1}}^{\varphi }\frac{1}{\sqrt{(\varphi _{4}-s)(\varphi _{3}-s)(\varphi _{2}-s)(s-\varphi _{1}) }}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s, \end{aligned}$$

(78)

$$\begin{aligned}&\pm \int _{\varphi _{4}}^{\varphi }\frac{1}{\sqrt{(s-\varphi _{1})(s-\varphi _{2}) (s-\varphi _{3})(\varphi _{4}-s)}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(79)

From (78), (79) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we obtain the periodic wave solutions $u_{1}(x,t)$ as (7) and $u_{2}(x,t)$ as (8).

(ii) From the phase portrait, we see that there are a closed orbit $\varGamma _{2}$ passing the points $(\varphi _{5},0)$ and $(\varphi _{6},0)$. In $(\varphi ,\phi )$-plane the expressions of the closed orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi _{6}-\varphi )(\varphi -\varphi _{5})(\varphi -\varphi _{5}^{*})(\varphi -\overline{\varphi }_{5}^{*})},\nonumber \\ \end{aligned}$$

(80)

where $\varphi _{5}=-\varphi _{6}$, $\varphi _{5}^{*}=i\sqrt{\varphi _{6}^{2}-\frac{6\beta }{\alpha }}$ and $\overline{\varphi }_{5}^{*}=-i\sqrt{\varphi _{6}^{2}-\frac{6\beta }{\alpha }}$.

Substituting (80) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along the orbit $\varGamma _{2}$,   we have

$$\begin{aligned}&\pm \int _{\varphi _{5}}^{\varphi }\frac{1}{\sqrt{(\varphi _{6}-s)(s-\varphi _{5})(s-\varphi _{5}^{*}) (s-\overline{\varphi }_{5}^{*})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s, \end{aligned}$$

(81)

$$\begin{aligned}&\pm \int _{\varphi _{6}}^{\varphi }\frac{1}{\sqrt{(\varphi _{6}-s)(s-\varphi _{5})(s-\varphi _{5}^{*}) (s-\overline{\varphi }_{5}^{*})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(82)

From (81), (82) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we obtain the periodic wave solutions $u_{3_{\pm }}(x,t)$ as (9).

(iii) From the phase portrait, we see that there are two symmetric homoclinic orbits $\varGamma _{3}$ and $\varGamma _{3}^{*}$ connected at the saddle point $(0,0)$. In $(\varphi ,\phi )$-plane, the expressions of the homoclinic orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\varphi \sqrt{(\varphi -\varphi _{7})(\varphi _{8}-\varphi )}, \end{aligned}$$

(83)

where $\varphi _{7}=-\sqrt{\frac{6\beta }{\alpha }}$ and $\varphi _{8}=\sqrt{\frac{6\beta }{\alpha }}$.

Substituting (83) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along the orbits $\varGamma _{3}$ and $\varGamma _{3}^{*}$, we have

$$\begin{aligned} \pm \int _{\varphi _{7}}^{\varphi }\frac{1}{\varphi \sqrt{(s-\varphi _{7})(\varphi _{8}-s)}}\mathrm{d}s =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s, \end{aligned}$$

(84)

$$\begin{aligned} \pm \int _{\varphi _{8}}^{\varphi }\frac{1}{\varphi \sqrt{(s-\varphi _{7})(\varphi _{8}-s)}}\mathrm{d}s =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(85)

From (84), (85) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we obtain the solitary wave solutions $u_{4_{\pm }}(x,t)$ as (15).

(2) If $-g_{0}<g<0$, we set the middle solution of $f(\varphi )=0$ be $\varphi _{9}(0<\varphi _{9}<\sqrt{\frac{\beta }{\alpha }})$. then we can get another two solutions of $f(\varphi )=0$ as follows:

$$\begin{aligned} \varphi _{9}^{*}=\frac{1}{2}\left( -\varphi _{9}-\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}}\right) , \end{aligned}$$

(86)

$$\begin{aligned} \varphi _{9}^{\star }=\frac{1}{2}\left( -\varphi _{9}+\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}}\right) . \end{aligned}$$

(87)

(i) From the phase portrait, we see that there are a closed orbit $\varGamma _{4}$ passing the points $(\varphi _{10},0)$ and $(\varphi _{11},0)$. In $(\varphi ,\phi )$-plane, the expressions of the closed orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi _{11}-\varphi )(\varphi -\varphi _{10})(\varphi -c_{1})(\varphi -\overline{c}_{1}) },\nonumber \\ \end{aligned}$$

(88)

where $\varphi _{12} <\varphi _{10}<\varphi _{9}^{*}<\varphi _{13}$, $c_{1}$ and $\overline{c}_{1}$ are conjugate complex numbers.

Substituting (88) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{4}$, we have

$$\begin{aligned}&\pm \int _{\varphi _{10}}^{\varphi }\frac{1}{\sqrt{(\varphi _{11}-s)(s-\varphi _{10})(s-c_{1}) (s-\overline{c}_{1})}}\mathrm{d}s\nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(89)

From (89) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a periodic wave solution $u_{5}(x,t)$ as (16).

(ii) From the phase portrait, we note that there is a special orbit $\varGamma _{5}$, which has the same hamiltonian with that of $(\varphi _{9}^{\star },0)$. In $(\varphi ,\phi )$-plane the expressions of the orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi -\varphi _{9}^{\star })^{2}(\varphi -\varphi _{12})(\varphi _{13}-\varphi )}, \end{aligned}$$

(90)

where

$$\begin{aligned} \varphi _{12}&= \frac{1}{2}\left( \varphi _{9}-\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}}\right. \nonumber \\&\qquad \qquad \left. -2\sqrt{\varphi _{9} (\varphi _{9}+\,\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}})}\right) ,\end{aligned}$$

(91)

$$\begin{aligned} \varphi _{13}&= \frac{1}{2}\left( \varphi _{9}-\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}}\right. \nonumber \\&\qquad \qquad \left. +\,2\sqrt{\varphi _{9} (\varphi _{9}+\,\sqrt{\frac{12\beta }{\alpha }-3\varphi _{9}^{2}})}\right) . \end{aligned}$$

(92)

Substituting (90) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{5}$, it follows that

$$\begin{aligned}&\pm \int _{\varphi _{12}}^{\varphi }\frac{1}{\sqrt{(\varphi _{13}-s)(s-\varphi _{9}^{\star })^{2}(s-\varphi _{12}) }}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(93)

From (93) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a periodic wave solution $u_{6}(x,t)$ as (17).

(iii) From the phase portrait, we note that there are two orbits $\varGamma _{6}$ and $\varGamma _{6}^{*}$ passing the points $(\varphi _{14},0)$, $(\varphi _{15},0)$, $(\varphi _{16},0)$ and $(\varphi _{17},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi -\varphi _{14})(\varphi -\varphi _{15})(\varphi -\varphi _{16}) (\varphi _{17}-\varphi )},\nonumber \\ \end{aligned}$$

(94)

where $\varphi _{20}<\varphi _{14}<\varphi _{12}<\varphi _{15}<\varphi _{9}<\varphi _{16}<\varphi _{9}^{\star }<\varphi _{17}<\varphi _{21}$.

Substituting (94) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{6}$ and $\varGamma _{6}^{*}$, we have

$$\begin{aligned}&\pm \int _{\varphi _{14}}^{\varphi }\frac{1}{\sqrt{(\varphi _{17}-s)(\varphi _{16}-s)(\varphi _{15}-s)(s-\varphi _{14}) }}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s, \end{aligned}$$

(95)

$$\begin{aligned}&\pm \int _{\varphi _{17}}^{\varphi }\frac{1}{\sqrt{(\varphi _{17}-s)(s-\varphi _{16})(s-\varphi _{15})(s-\varphi _{14}) }}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(96)

From (95), (96) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get two periodic wave solutions $u_{7}(x,t)$ as (18) and $u_{8}(x,t)$ as (19).

(iv) From the phase portrait, we note that there is a special orbit $\varGamma _{7}$ passing the points $(\varphi _{18},0)$ and $(\varphi _{19},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbit are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi _{19}-\varphi )(\varphi -\varphi _{18})(\varphi -c_{2})(\varphi -\overline{c}_{2})},\nonumber \\ \end{aligned}$$

(97)

where $\varphi _{18}<\varphi _{20}<\varphi _{21}<\varphi _{19}$, $c_{2}$ and $\overline{c}_{2}$ are conjugate complex numbers.

Substituting (97) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating it along $\varGamma _{7}$, we have

$$\begin{aligned}&\pm \int _{\varphi _{18}}^{\varphi }\frac{1}{\sqrt{(\varphi _{19}-s)(s-\varphi _{18})(s-c_{2}) (s-\overline{c}_{2})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(98)

From (98) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a periodic wave solution $u_{9}(x,t)$ as (20).

If $\varphi (\xi )$ is a traveling wave solution, then $\varphi (\xi +q)$ is a traveling wave solution too. Taking $q=2K$ and noting that $\mathrm{cn}(u+2K)=-\mathrm{cn}u$, we get a periodic wave solution $u_{10}(x,t)$ as (21).

(v) From the phase portrait, we note that there are two homoclinic orbits $\varGamma _{8}$ and $\varGamma _{8}^{*}$ connected at the saddle point $(\varphi _{9},0)$. In $(\varphi ,\phi )$-plane the expressions of the orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi -\varphi _{9})^{2}(\varphi -\varphi _{20})(\varphi _{21}-\varphi )}, \end{aligned}$$

(99)

where

$$\begin{aligned} \varphi _{20}&= -\varphi _{9}-\sqrt{\frac{6\beta }{\alpha }-2\varphi _{9}^{2}}, \end{aligned}$$

(100)

$$\begin{aligned} \varphi _{21}&= -\varphi _{9}+\sqrt{\frac{6\beta }{\alpha }-2\varphi _{9}^{2}}. \end{aligned}$$

(101)

Substituting (99) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{8}$ and $\varGamma _{8}^{*}$, it follows that

$$\begin{aligned}&\pm \int _{\varphi _{20}}^{\varphi }\frac{1}{\sqrt{(s-\varphi _{9})^{2} (s-\varphi _{20})(\varphi _{21}-s)}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s, \end{aligned}$$

(102)

$$\begin{aligned}&\pm \int _{\varphi _{21}}^{\varphi }\frac{1}{\sqrt{(s-\varphi _{9})^{2} (s-\varphi _{20})(\varphi _{21}-s)}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(103)

From (102), (103) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get two solitary wave solutions $u_{11_{\pm }}(x,t)$ as (28).

(3) If $g=-g_{0}$, we will consider two kinds of orbits.

(i) From the phase portrait, we note that there is a special orbit $\varGamma _{9}$ passing the points $(\varphi _{22},0)$ and $(\varphi _{23},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbit are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi _{23}-\varphi )(\varphi -\varphi _{22})(\varphi -c_{3})(\varphi -\overline{c}_{3}) },\nonumber \\ \end{aligned}$$

(104)

where $-\sqrt{3\alpha }<\varphi _{22}<-2\sqrt{\frac{\alpha }{3}}<\varphi _{23}<\sqrt{\frac{\alpha }{3}}$, $c_{3}$ and $\overline{c}_{3}$ are conjugate complex numbers.

Substituting (104) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating it along $\varGamma _{9}$, we have

$$\begin{aligned}&\pm \int _{\varphi _{22}}^{\varphi }\frac{1}{\sqrt{(\varphi _{23}-s)(s-\varphi _{22})(s-c_{3}) (s-\overline{c}_{3})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(105)

From (105) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a periodic wave solutions $u_{12}(x,t)$ as (29).

(ii) From the phase portrait, we note that there is a special orbit $\varGamma _{10}$ passing the points $(\varphi _{24},0)$ and $(\varphi _{25},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbit are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi _{25}-\varphi )(\varphi -\varphi _{24})(\varphi -c_{4}) (\varphi -\overline{c}_{4})},\nonumber \\ \end{aligned}$$

(106)

where $\varphi _{24}<-\sqrt{3\alpha }<\sqrt{\frac{\alpha }{3}}<\varphi _{25}$, $c_{4}$ and $\overline{c}_{4}$ are conjugate complex numbers

Substituting (106) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{10}$, we have

$$\begin{aligned}&\pm \int _{\varphi _{24}}^{\varphi }\frac{1}{\sqrt{(\varphi _{25}-s)(s-\varphi _{24})(s-c_{4}) (s-\overline{c}_{4})}}\,\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(107)

From (107) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a periodic wave solutions $u_{13}(x,t)$ as (30).

(iii) From the phase portrait, we see that there is a homoclinic orbit $\varGamma _{11}$, which passes the degenerate saddle point $(\varphi _{+}^{*},0)$ for system (68). In $(\varphi ,\phi )$-plane, the expressions of the homoclinic orbit are given as

$$\begin{aligned} \phi =\pm \sqrt{\frac{\alpha }{6}}\sqrt{(\varphi _{+}^{*}-\varphi )^{3}(\varphi -\varphi _{26})}, \end{aligned}$$

(108)

where

$$\begin{aligned} \varphi _{26}=-3\sqrt{\frac{\beta }{\alpha }}. \end{aligned}$$

(109)

Substituting (108) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\varGamma _{11}$, it follows that

$$\begin{aligned}&\pm \int _{\varphi _{26}}^{\varphi }\frac{1}{(s-\varphi _{+}^{*})\sqrt{(s-\varphi _{+}^{*}) (\varphi _{26}-s)}}\mathrm{d}s \nonumber \\&\quad =\sqrt{\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(110)

From (110) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a solitary wave solution $u_{14}(x,t)$ as (34).

Thus, the derivation of Proposition 1 has been finished.

3.3 The derivation of Proposition 2

In this section, we will obtain the explicit expressions of solutions for the MBBM equation (2) when $\alpha <0$.

(1) If $g=0$, we will consider three kinds of orbits.

(i) From the phase portrait, we note that there are three special orbits $\widetilde{\varGamma }_{1}^{*}$, $\widetilde{\varGamma }_{1}$ and $\widetilde{\varGamma }_{1}^{\star }$ passing the points $(\widetilde{\varphi }_{1},0),(\widetilde{\varphi }_{2},0)$, $(\widetilde{\varphi }_{3},0)$ and $(\widetilde{\varphi }_{4},0)$. In $(\varphi ,\phi )$-plane the expressions of the orbit are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\widetilde{\varphi }_{1})(\varphi -\widetilde{\varphi }_{2}) (\varphi -\widetilde{\varphi }_{3})(\varphi -\widetilde{\varphi }_{4})},\nonumber \\ \end{aligned}$$

(111)

where $\widetilde{\varphi }_{1}=-\widetilde{\varphi }_{4}, \widetilde{\varphi }_{2}=-\sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}, \widetilde{\varphi }_{3}=\sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}$ and $\sqrt{\frac{3\beta }{\alpha }}<\widetilde{\varphi }_{4}<\sqrt{\frac{6\beta }{\alpha }}$.

Substituting (111) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\widetilde{\varGamma }_{1}^{*}$, $\widetilde{\varGamma }_{1}$ and $\widetilde{\varGamma }_{1}^{\star }$, we have

$$\begin{aligned}&\pm \int _{0}^{\varphi }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{1})(s-\widetilde{\varphi }_{2}) (s-\widetilde{\varphi }_{3})(s-\widetilde{\varphi }_{4})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s, \end{aligned}$$

(112)

$$\begin{aligned}&\pm \int _{\varphi }^{\infty }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{1})(s-\widetilde{\varphi }_{2}) (s-\widetilde{\varphi }_{3})(s-\widetilde{\varphi }_{4})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(113)

From (112), (113) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get two periodic wave solutions $u_{15_{\pm }}(x,t)$ as (35) and two periodic blow-up solutions $u_{16_{\pm }}(x,t)$ as (36).

(ii) From the phase portrait, we note that there are two special orbits $\widetilde{\varGamma }_{3}$ and $\widetilde{\varGamma }_{3}^{*}$, which have the same hamiltonian with that of the center point $(0,0)$. In $(\varphi ,\phi )$-plane, the expressions of these two orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\varphi \sqrt{(\varphi -\widetilde{\varphi }_{5})(\varphi -\widetilde{\varphi }_{6})}, \end{aligned}$$

(114)

where $\widetilde{\varphi }_{5}=-\sqrt{\frac{6\beta }{\alpha }}$ and $\widetilde{\varphi }_{6}=\sqrt{\frac{6\beta }{\alpha }}$.

Substituting (114) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along the two orbits $\widetilde{\varGamma }_{3}$ and $\widetilde{\varGamma }_{3}^{*}$, it follows that

$$\begin{aligned}&\pm \int _{\widetilde{\varphi }_{6}}^{\varphi }\frac{1}{s\sqrt{(s-\widetilde{\varphi }_{5}) (s-\widetilde{\varphi }_{6})}}\mathrm{d}s=\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s, \end{aligned}$$

(115)

$$\begin{aligned}&\pm \int _{\varphi }^{+\infty }\frac{1}{s\sqrt{(s-\widetilde{\varphi }_{5}) (s-\widetilde{\varphi }_{6})}}\mathrm{d}s=\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s.\nonumber \\ \end{aligned}$$

(116)

From (115), (116) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get four periodic blow-up solutions $u_{17_{\pm }}(x,t)$ and $u_{18_{\pm }}(x,t)$ as (37) and (38).

(iii) From the phase portrait, we see that there are two heterclinic orbits $\widetilde{\varGamma }_{2}$ and $\widetilde{\varGamma }_{2}^{*}$ connected at saddle points $(\varphi _{-},0)$ and $(\varphi _{+},0)$. In $(\varphi ,\phi )$-plane, the expressions of the heterclinic orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\varphi _{-})^{2}(\varphi -\varphi _{+})^{2}}. \end{aligned}$$

(117)

Substituting (117) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along the heterclinic orbits $\widetilde{\varGamma }_{2}$ and $\widetilde{\varGamma }_{2}^{*}$, it follows that

$$\begin{aligned}&\pm \int _{0}^{\varphi }\frac{1}{(s-\varphi _{-}) (\varphi _{+}-s)}\mathrm{d}s=\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s, \end{aligned}$$

(118)

$$\begin{aligned}&\pm \int _{\varphi }^{+\infty }\frac{1}{(s-\varphi _{-}) (s-\varphi _{+})}\mathrm{d}s=\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(119)

From (118), (119) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get two kink wave solutions $u_{19_{\pm }}(x,t)$ as (39) and two unbounded solutions $u_{20_{\pm }}(x,t)$ as (40).

(2) If $0<g<g_{0}$, we set the largest solution of $f(\varphi )=0$ be $\widetilde{\varphi }_{7}\left( \sqrt{\frac{\beta }{\alpha }}<\widetilde{\varphi }_{7}<\sqrt{\frac{3\beta }{\alpha }}\right)$, then we can get another two solutions of $f(\varphi )=0$ as follows:

$$\begin{aligned} \widetilde{\varphi }_{7}^{*}&= \frac{1}{2\alpha }\left( -\alpha \widetilde{\varphi }_{7} +\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right) , \end{aligned}$$

(120)

$$\begin{aligned} \widetilde{\varphi }_{7}^{\star }&= \frac{1}{2\alpha }\left( -\alpha \widetilde{\varphi }_{7} -\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right) . \end{aligned}$$

(121)

(i) From the phase portrait, we note that there are three special orbits $\widetilde{\varGamma }_{4}^{*}$, $\widetilde{\varGamma }_{4}$ and $\widetilde{\varGamma }_{4}^{\star }$ passing the points $(\widetilde{\varphi }_{8},0),(\widetilde{\varphi }_{9},0)$, $(\widetilde{\varphi }_{10},0)$ and $(\widetilde{\varphi }_{11},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbit are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\widetilde{\varphi }_{8})(\varphi -\widetilde{\varphi }_{9}) (\varphi -\widetilde{\varphi }_{10})(\varphi -\widetilde{\varphi }_{11})},\nonumber \\ \end{aligned}$$

(122)

where $\widetilde{\varphi }_{14}<\widetilde{\varphi }_{8}<\widetilde{\varphi }_{12}<\widetilde{\varphi }_{13}<\widetilde{\varphi }_{9} <\widetilde{\varphi }_{7}^{\star }<\widetilde{\varphi }_{10}<\widetilde{\varphi }_{7}<\widetilde{\varphi }_{11}<\widetilde{\varphi }_{15}$.

Substituting (122) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\widetilde{\varGamma }_{4}^{*}$, $\widetilde{\varGamma }_{4}$ and $\widetilde{\varGamma }_{4}^{\star }$, we have

$$\begin{aligned}&\int _{\varphi }^{\widetilde{\varphi }_{8}}\frac{1}{\sqrt{(\widetilde{\varphi }_{11}-s)(\widetilde{\varphi }_{10}-s) (\widetilde{\varphi }_{9}-s)(\widetilde{\varphi }_{8}}-s)}\,\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }, \end{aligned}$$

(123)

$$\begin{aligned}&\int _{\widetilde{\varphi }_{11}}^{\varphi }\frac{1}{\sqrt{(\widetilde{\varphi }_{11}-s)(\widetilde{\varphi }_{10}-s) (s-\widetilde{\varphi }_{9})(s-\widetilde{\varphi }_{8})}}\,\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }, \end{aligned}$$

(124)

$$\begin{aligned}&\int _{\widetilde{\varphi }_{9}}^{\varphi }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{11})(s-\widetilde{\varphi }_{10}) (s-\widetilde{\varphi }_{9})(s-\widetilde{\varphi }_{8})}}\,\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }. \end{aligned}$$

(125)

From (123), (124), (125) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get two periodic blow-up wave solutions $u_{21}(x,t)$, $u_{22}(x,t)$ as (41), (42) and a periodic wave solution $u_{24}(x,t)$ as (44).

(ii) From the phase portrait, we see that there are a homoclinic orbit $\widetilde{\varGamma }_{5}$, which passes the saddle point $(\widetilde{\varphi }_{7},0)$, and a spacial orbit $\widetilde{\varGamma }_{6}$ passing the point $(\widetilde{\varphi }_{12},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\widetilde{\varphi }_{7})^{2}(\varphi -\widetilde{\varphi }_{12}) (\varphi -\widetilde{\varphi }_{13})}, \end{aligned}$$

(126)

where

$$\begin{aligned} \widetilde{\varphi }_{12}&= \frac{-\alpha \widetilde{\varphi }_{7} +\sqrt{6\alpha \beta -2\alpha ^{2}\widetilde{\varphi }_{7}^{2}}}{\alpha }, \end{aligned}$$

(127)

$$\begin{aligned} \widetilde{\varphi }_{13}&= \frac{-\alpha \widetilde{\varphi }_{7} -\sqrt{6\alpha \beta -2\alpha ^{2}\widetilde{\varphi }_{7}^{2}}}{\alpha }. \end{aligned}$$

(128)

Substituting (126) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along the orbits, it follows that

$$\begin{aligned}&\pm \int _{\varphi }^{\infty }\dfrac{1}{\sqrt{(s-\widetilde{\varphi }_{7})^{2} (s-\widetilde{\varphi }_{12})(s-\widetilde{\varphi }_{13})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(129)

$$\begin{aligned}&\pm \int _{\widetilde{\varphi }_{13}}^{\varphi }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{7})^{2} (s-\widetilde{\varphi }_{12})(s-\widetilde{\varphi }_{13})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(130)

From (129), (130) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a blow-up solution $u_{25}(x,t)$ as (48) and a solitary wave solution $u_{26}(x,t)$ as (49).

(iii) From the phase portrait, we see that there are two special orbits $\widetilde{\varGamma }_{7}$ and $\widetilde{\varGamma }_{7}^{*}$, which have the same hamiltonian with that of the center point $(\widetilde{\varphi }_{7}^{\star },0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\widetilde{\varphi }_{7}^{\star })^{2}(\varphi -\widetilde{\varphi }_{14}) (\varphi -\widetilde{\varphi }_{15})}, \end{aligned}$$

(131)

where

$$\begin{aligned} \widetilde{\varphi }_{14}&= \frac{1}{2\alpha }\left( \alpha \widetilde{\varphi }_{7} +\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right. \nonumber \\&\left. +\,2 \sqrt{\alpha \widetilde{\varphi }_{7}(\alpha \widetilde{\varphi }_{7} -\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}})}\right) ,\nonumber \\ \end{aligned}$$

(132)

$$\begin{aligned} \widetilde{\varphi }_{15}&= \frac{1}{2\alpha }\left( \alpha \widetilde{\varphi }_{7} +\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}}\right. \nonumber \\&\left. -\,2 \sqrt{\alpha \widetilde{\varphi }_{7}(\alpha \widetilde{\varphi }_{7} -\sqrt{12\alpha \beta -3\alpha ^{2}\widetilde{\varphi }_{7}^{2}})}\right) .\nonumber \\ \end{aligned}$$

(133)

Substituting (131) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along the orbits, it follows that

$$\begin{aligned}&\pm \int _{\widetilde{\varphi }_{14}}^{\varphi }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{7}^{\star })^{2} (s-\widetilde{\varphi }_{14})(s-\widetilde{\varphi }_{15})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s, \end{aligned}$$

(134)

$$\begin{aligned}&\pm \int _{\widetilde{\varphi }_{15}}^{\varphi }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{7}^{\star })^{2} (s-\widetilde{\varphi }_{14})(s-\widetilde{\varphi }_{15})}}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\,\mathrm{d}s. \end{aligned}$$

(135)

From (134), (135) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get two periodic blow-up wave solutions $u_{23_{\pm }}(x,t)$ as (43).

(3) If $g=g_{0}$, we will consider two kinds of orbits.

(i) From the phase portrait, we see that there are two orbits $\widetilde{\varGamma }_{8}$ and $\widetilde{\varGamma }_{8}^{*}$, which have the same hamiltonian with the degenerate saddle point $(\varphi _{+}^{*},0)$. In $(\varphi ,\phi )$-plane the expressions of these two orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\varphi _{+}^{*})^{3}(\varphi -\widetilde{\varphi }_{16})}, \end{aligned}$$

(136)

where

$$\begin{aligned} \widetilde{\varphi }_{16}=-3\sqrt{\frac{\beta }{\alpha }}. \end{aligned}$$

(137)

Substituting (136) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along these two orbits $\widetilde{\varGamma }_{8}$ and $\widetilde{\varGamma }_{8}^{*}$, it follows that

$$\begin{aligned}&\pm \int _{\varphi }^{+\infty }\frac{1}{\sqrt{(s-\varphi _{+}^{*})^{3}(s -\widetilde{\varphi }_{16})}}\mathrm{d}s=\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s,\nonumber \\ \end{aligned}$$

(138)

$$\begin{aligned}&\pm \int _{\widetilde{\varphi }_{16}}^{\varphi }\frac{1}{\sqrt{(s-\varphi _{+}^{*})^{3}(s -\widetilde{\varphi }_{16})}}\mathrm{d}s=\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s.\nonumber \\ \end{aligned}$$

(139)

From (138), (139) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get three blow-up solutions $u_{27}(x,t))$, $u_{28}(x,t)$ and $u_{29}(x,t)$ as (50), (51) and (52).

(ii) From the phase portrait, we see that there are two special orbits $\widetilde{\varGamma }_{9}$ and $\widetilde{\varGamma }_{9}^{*}$ passing the points $(\widetilde{\varGamma }_{17},0)$ and $(\widetilde{\varGamma }_{18},0)$. In $(\varphi ,\phi )$-plane, the expressions of the orbits are given as

$$\begin{aligned} \phi =\pm \sqrt{-\frac{\alpha }{6}}\sqrt{(\varphi -\widetilde{\varphi }_{18})(\varphi -\widetilde{\varphi }_{17})(\varphi -c_{5}) (\varphi -\overline{c}_{5})},\nonumber \\ \end{aligned}$$

(140)

where $\widetilde{\varphi }_{17}<\widetilde{\varphi }_{16}<\widetilde{\varphi }_{+}^{*}<\widetilde{\varphi }_{18}$, $c_{5}$ and $\overline{c}_{5}$ are conjugate complex numbers.

Substituting (140) into $\frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=\phi$ and integrating them along $\widetilde{\varGamma }_{9}$ and $\widetilde{\varGamma }_{9}^{*}$, we have

$$\begin{aligned}&\pm \int _{\widetilde{\varphi }_{18}}^{\varphi }\frac{1}{\sqrt{(s-\widetilde{\varphi }_{18})(s-\widetilde{\varphi }_{17})(s-c_{5}) (s-\overline{c}_{5}) }}\mathrm{d}s \nonumber \\&\quad =\sqrt{-\frac{\alpha }{6}}\int _{0}^{\xi }\mathrm{d}s. \end{aligned}$$

(141)

From (141) and noting that $u=\varphi (\xi )$ and $\xi =x-ct$, we get a periodic wave solutions $u_{30}(x,t)$ as (53).

Thus, we obtain the results given in Proposition 2.

3.4 The derivation of Proposition 3

In this section, we will give that the solitary wave solutions, periodic wave solutions, kink wave solutions, blow-up wave solutions and unbounded solutions can be obtained from the limits of the smooth periodic wave solutions or periodic blow-up solutions.

(1) Letting $\varphi _{1}\rightarrow \varphi _{7}$, it follows that $a_{1}\rightarrow -\frac{6\beta }{\alpha }$, $b_{1}\rightarrow \frac{6\beta }{\alpha }$, $c_{1}\rightarrow \sqrt{\frac{6\beta }{\alpha }}$, $d_{1}\rightarrow \sqrt{\frac{6\beta }{\alpha }}$, $\omega _{1}\rightarrow \frac{\sqrt{\beta }}{2} k_{1}\rightarrow 1$ and $\mathrm{sn}(\omega _{1}\xi ,1)=\tanh (\omega _{1}\xi )$, and we have

$$\begin{aligned}&\lim \limits _{\varphi _{1} \rightarrow \varphi _{7}}{u_{1}(x,t)}=\lim \limits _{\varphi _{1} \rightarrow \varphi _{7}}{\frac{a_{1}+b_{1}\mathrm{sn}^{2}(\omega _{1}\xi ,k_{1})}{c_{1}+d_{1}\mathrm{sn}^{2}(\omega _{1}\xi ,k_{1})}}\nonumber \\&\quad =\frac{-\frac{6\beta }{\alpha }+\frac{6\beta }{\alpha }\tanh ^{2}\left( \frac{\sqrt{\beta }}{2}\xi \right) }{\sqrt{\frac{6\beta }{\alpha }}+\sqrt{\frac{6\beta }{\alpha }}\tanh ^{2}\left( \frac{\sqrt{\beta }}{2}\xi \right) }\nonumber \\&\quad =-\sqrt{\frac{6\beta }{\alpha }}\frac{1-\tanh ^{2}\left( \frac{\sqrt{\beta }}{2}\xi \right) }{1+\tanh ^{2}\left( \frac{\sqrt{\beta }}{2}\xi \right) }\nonumber \\&\quad =-\sqrt{\frac{6\beta }{\alpha }}\mathrm{sech}\left( \sqrt{\beta }\xi \right) =u_{4_{-}}(x,t).\nonumber \\\end{aligned}$$

(142)

$$\begin{aligned}&\lim \limits _{\varphi _{5} \rightarrow \varphi _{7}}{u_{3_{-}}(x,t)}=\lim \limits _{\varphi _{5} \rightarrow \varphi _{7}} \varphi _{5}\mathrm{cn}\nonumber \\&\qquad \times \left( \sqrt{\frac{\alpha }{3}\varphi _{5}^{2}\!-\!\beta }\xi ,-\varphi _{5} \sqrt{\frac{\alpha }{2\alpha \varphi _{5}^{2}\!-\!6\beta }}\right) \nonumber \\&\quad = -\sqrt{\frac{6\beta }{\alpha }}\mathrm{cn}\left( \sqrt{\beta }\xi ,1\right) \nonumber \\&\quad = -\sqrt{\frac{6\beta }{\alpha }}\mathrm{sech}\left( \sqrt{\beta }\xi \right) =u_{4_{-}}(x,t).\nonumber \\ \end{aligned}$$

(143)

Therefore, the hyperbolic solitary wave solution $u_{4_{-}}(x,t)$ is the limit of the elliptic function periodic wave solutions $u_{1}(x,t)$ and $u_{3_{-}}(x,t)$. Their limiting process are in Figs. 3 and 4.

Fig. 3

The limiting process of $u_{1}$ tends to $u_{4_{-}}$ when $\varphi _{1}$ tends to $\varphi _{7}$

Fig. 4

The limiting process of $u_{3_{-}}$ tends to $u_{4_{-}}$ when $\varphi _{5}$ tends to $\varphi _{7}$

(2) Letting $\varphi _{4}\rightarrow \varphi _{8}$, it follows that $k_{2}\rightarrow 1$ and $\mathrm{sn}\left( \varphi _{4}\sqrt{\frac{\alpha }{6}}\xi ,1\right) =\tanh (\sqrt{\beta }\xi )$, and we have

$$\begin{aligned}&\lim \limits _{\varphi _{4} \rightarrow \varphi _{8}}{u_{2}(x,t)}\nonumber \\&\quad =\lim \limits _{\varphi _{4} \rightarrow \varphi _{8}} {\sqrt{\varphi _{4}^{2}-(2\varphi _{4}^{2}-\frac{6\beta }{\alpha }) \mathrm{sn}^{2}\left( \varphi _{4}\sqrt{\frac{\alpha }{6}}\xi , k_{2}\right) }}\nonumber \\&\quad =\sqrt{\frac{6\beta }{\alpha }-\frac{6\beta }{\alpha }\tanh ^{2}\left( \sqrt{\beta }\xi \right) } =\sqrt{\frac{6\beta }{\alpha }}\mathrm{sech}\left( \sqrt{\beta }\xi \right) \nonumber \\&\quad =u_{4_{+}}(x,t). \end{aligned}$$

(144)

$$\begin{aligned}&\lim \limits _{\varphi _{6} \rightarrow \varphi _{8}}{u_{3_{+}}(x,t)}\nonumber \\&\quad =\lim \limits _{\varphi _{6} \rightarrow \varphi _{8}} {\varphi _{6}\mathrm{cn}\left( \sqrt{\frac{\alpha }{3}\varphi _{6}^{2}-\beta }\xi ,\varphi _{6}\sqrt{\frac{\alpha }{2\alpha \varphi _{6}^{2}-6\beta }}\right) }\nonumber \\&\quad =\sqrt{\frac{6\beta }{\alpha }}\mathrm{cn}\left( \sqrt{\beta }\xi ,1\right) =\sqrt{\frac{6\beta }{\alpha }}\mathrm{sech}\left( \sqrt{\beta }\xi \right) \nonumber \\&\quad =u_{4_{+}}(x,t). \end{aligned}$$

(145)

Therefore, the hyperbolic solitary wave solution $u_{4_{+}}(x,t)$ is the limit of the elliptic function periodic wave solutions $u_{2}(x,t)$ and $u_{3_{+}}(x,t)$. Their limiting process are in Figs. 5 and 6.

Fig. 5

The limiting process of $u_{2}$ tends to $u_{4_{+}}$ when $\varphi _{4}$ tends to $\varphi _{8}$

Fig. 6

The limiting process of $u_{3_{+}}$ tends to $u_{4_{+}}$ when $\varphi _{6}$ tends to $\varphi _{8}$

(3) Letting $\varphi _{11}\rightarrow \varphi _{13}-0$, it follows that $c_{1}\rightarrow \varphi _{9}^{\star }, \quad \overline{c}_{1}\rightarrow \varphi _{9}^{\star },$ $k_{3}\rightarrow 0,\varphi _{10}\rightarrow \varphi _{12}+0, A_{1}\rightarrow \varphi _{13}-\varphi _{9}^{\star }$ and $B_{1}\rightarrow \varphi _{12}-\varphi _{9}^{\star }$, and we have

$$\begin{aligned}&\lim \limits _{\varphi _{11} \rightarrow \varphi _{13}}{u_{5}(x,t)}=\lim \limits _{\varphi _{11} \rightarrow \varphi _{13}}\nonumber \\&\quad {\frac{A_{1}\varphi _{10}\!+\!\varphi _{11}B_{1}\!+\!(A_{1}\varphi _{10}\!-\! \varphi _{11}B_{1})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{1}B_{1}}{6}}\xi ,k_{3}\!\right) }{A_{1}+B_{1}+(A_{1}-B_{1})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{1}B_{1}}{6}}\xi ,k_{3}\right) }}\nonumber \\&\quad =\frac{-2\gamma _{1}+\eta _{1}\delta _{1}+\eta _{1}\sqrt{\mu _{1}}\cos \left( \sqrt{\frac{\alpha \gamma _{1}}{6}}\xi \right) }{\delta _{1}+\sqrt{\mu _{1}}\cos \left( \sqrt{\frac{\alpha \gamma _{1}}{6}}\xi \right) }\nonumber \\&\quad =u_{6}(x,t). \end{aligned}$$

(146)

Therefore, the trigonometric function periodic wave solution $u_{6}(x,t)$ is the limit of the elliptic function periodic wave solution $u_{5}(x,t)$. The limiting process is in Fig. 7.

Fig. 7

The limiting process of $u_{5}$ tends to $u_{6}$ when $\varphi _{11}$ tends to $\varphi _{13}$

(6) Letting $\varphi _{22}\rightarrow \varphi _{26}$, it follows that $\varphi _{23}\rightarrow \varphi _{+}^{*},\quad c_{3}\rightarrow \varphi _{+}^{*},\quad \overline{c}_{3}\rightarrow \varphi _{+}^{*},$ $A_{3}\rightarrow 0, \quad B_{3}\rightarrow 4\sqrt{\frac{\beta }{\alpha }}$ and $\mathrm{cn}\left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) \rightarrow \mathrm{cn}(0,k_{6})=1$, and we have

$$\begin{aligned}&\lim \limits _{\varphi _{22} \rightarrow \varphi _{26}}{u_{12}(x,t)} =\lim \limits _{\varphi _{22} \rightarrow \varphi _{26}}\nonumber \\&\quad {\frac{A_{3}\varphi _{22}+\varphi _{23}B_{3}+(A_{3}\varphi _{22} -\varphi _{23}B_{3})\mathrm{cn} \left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) }{A_{3}+B_{3} +(A_{3}-B_{3})\mathrm{cn}\left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) }}\nonumber \\&\quad =\lim \limits _{A_{3} \rightarrow 0} {\frac{A_{3}\varphi _{22}+\varphi _{23}B_{3}\!+\!(A_{3}\varphi _{22} \!-\!\varphi _{23}B_{3})\mathrm{cn}\left( \!\sqrt{\frac{\alpha A_{3}B_{3}}{6}} \xi ,k_{6}\!\right) }{A_{3}+B_{3}+(A_{3}-B_{3})\mathrm{cn} \left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) }}\qquad \nonumber \\&\quad =\lim \limits _{A_{3} \rightarrow 0}{\frac{2\sqrt{6\alpha A_{3}B_{3}} \left( \varphi _{22} \!+\!\varphi _{22}\chi _{1}\right) \!-\!\alpha B_{3}(A_{3}\varphi _{22}\!-\!B_{3}\varphi _{23}) \xi \chi _{2}\chi _{3}}{2\sqrt{6\alpha A_{3}B_{3}}\left( 1+\chi _{1}\right) -\alpha B_{3}(A_{3}-B_{3})\xi \chi _{2}\chi _{3}}}\nonumber \\&\quad =\frac{\sqrt{\beta }(-9+2\beta \xi ^{2})}{\sqrt{\alpha }(3+2\beta \xi ^{2})} =u_{14}(x,t). \end{aligned}$$

(147)

where $\chi _{1} \!=\! \mathrm{cn}\left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right) \!,\chi _{2}\!=\!\mathrm{dn}\!\Bigg (\sqrt{\frac{\alpha A_{3}B_{3}}{6}}\!\xi , k_{6}\!\Bigg )\!,\chi _{3}\!=\!\mathrm{sn}\left( \sqrt{\frac{\alpha A_{3}B_{3}}{6}}\xi ,k_{6}\right)$.

Therefore, the fractional function solitary wave solution $u_{14}(x,t)$ is the limit of the elliptic function periodic wave solution $u_{12}(x,t)$. The limiting process is similar to that in Fig. 3.

(7) Letting $\widetilde{\varphi }_{4}\rightarrow \varphi _{+}+0$, it follows that $\sqrt{\frac{6\beta }{\alpha }\!-\!\widetilde{\varphi }_{4}^{2}}\rightarrow \sqrt{\frac{3\beta }{\alpha }}$,   $\frac{1}{\widetilde{\varphi }_{4}}\sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\rightarrow 1$ and $\mathrm{sn}\left( \sqrt{-\frac{\beta }{2}}\xi ,1\right) =\tanh \left( \sqrt{-\frac{\beta }{2}}\xi \right)$, and we have

$$\begin{aligned}&\lim \limits _{\widetilde{\varphi }_{4} \rightarrow \varphi _{+}}{u_{15_{\pm }}(x,t)}=\lim \limits _{\widetilde{\varphi }_{4} \rightarrow \varphi _{+}} \pm \sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\mathrm{sn}\nonumber \\&\quad \left( \widetilde{\varphi }_{4}\sqrt{-\frac{\alpha }{6}}\xi , \frac{1}{\widetilde{\varphi }_{4}} \sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\right) \nonumber \\&\quad =\pm \sqrt{\frac{3\beta }{\alpha }}\tanh \left( \sqrt{-\frac{\beta }{2}}\xi \right) \nonumber \\&\quad =u_{19_{\pm }}(x,t). \end{aligned}$$

(148)

Therefore, the kink wave solutions $u_{19_{\pm }}(x,t)$ are the limit of the elliptic function periodic wave solutions $u_{15_{\pm }}(x,t)$. Their limiting process are in Figs. 8 and 9.

Fig. 8

The limiting process of $u_{15_{+}}$ tends to $u_{19_{+}}$ when $\widetilde{\varphi }_{4}$ tends to $\varphi _{+}$

Fig. 9

The limiting process of $u_{15_{-}}$ tends to $u_{19_{-}}$ when $\widetilde{\varphi }_{4}$ tends to $\varphi _{+}$

(8) Letting $\widetilde{\varphi }_{4}\rightarrow \varphi _{+}+0$, it follows that $\frac{1}{\widetilde{\varphi }_{4}}\sqrt{\frac{6\beta }{\alpha }\!-\!\widetilde{\varphi }_{4}^{2}}\rightarrow 1$ and $\mathrm{sn}\left( \sqrt{-\frac{\beta }{2}}\xi ,1\!\right) \!=\!\tanh \left( \!\sqrt{-\frac{\beta }{2}}\xi \!\right)$, and we have

$$\begin{aligned}&\mathop {\lim }\limits _{\widetilde{\varphi }_{4} \rightarrow \varphi _{+}}{u_{16_{\pm }}(x,t)}\nonumber \\&\quad =\mathop {\lim }\limits _{\widetilde{\varphi }_{4} \rightarrow \varphi _{+}} {\pm \frac{\widetilde{\varphi }_{4}}{\mathrm{sn}\left( \widetilde{\varphi }_{4}\sqrt{-\frac{\alpha }{6}}\xi , \frac{1}{\widetilde{\varphi }_{4}}\sqrt{\frac{6\beta }{\alpha }-\widetilde{\varphi }_{4}^{2}}\right) }}\nonumber \\&\quad =\pm \sqrt{\frac{3\beta }{\alpha }}\coth \left( \sqrt{-\frac{\beta }{2}}\xi \right) =u_{20_{\pm }}(x,t). \end{aligned}$$

(149)

Therefore, the unbounded wave solutions $u_{20_{\pm }}(x,t)$ are the limit of the elliptic function periodic wave solutions $u_{16_{\pm }}(x,t)$. Their limiting process are in Figs. 10 and 11.

Fig. 10

The limiting process of $u_{16_{+}}$ tends to $u_{20_{+}}$ when $\widetilde{\varphi }_{4}$ tends to $\varphi _{+}$

Fig. 11

The limiting process of $u_{16_{-}}$ tends to $u_{20_{-}}$ when $\widetilde{\varphi }_{4}$ tends to $\varphi _{+}$

(9) Letting $\widetilde{\varphi }_{11}\rightarrow \widetilde{\varphi }_{7}-0$, it follows that $\widetilde{\varphi }_{8}\rightarrow \widetilde{\varphi }_{12}-0,\widetilde{\varphi }_{9}\rightarrow \widetilde{\varphi }_{13}+0,\widetilde{\varphi }_{10}\rightarrow \widetilde{\varphi }_{7}+0$, $k_{8}\rightarrow 1,\omega _{3}\rightarrow \frac{\sqrt{\beta -\alpha \widetilde{\varphi }_{7}^{2}}}{2}$ and $\mathrm{sn}(\omega _{3}\xi ,1)\rightarrow \tanh (\omega _{3}\xi )$, and we have

$$\begin{aligned}&\lim \limits _{\widetilde{\varphi }_{11} \rightarrow \widetilde{\varphi }_{7}}{u_{21}(x,t)}\nonumber \\&\quad =\lim \limits _{\widetilde{\varphi }_{11} \rightarrow \widetilde{\varphi }_{7}} {\frac{(-\widetilde{\varphi }_{11}+\widetilde{\varphi }_{9})\widetilde{\varphi }_{8} +(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})\widetilde{\varphi }_{9}\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) }{-\widetilde{\varphi }_{11}+\widetilde{\varphi }_{9}+(\widetilde{\varphi }_{11}-\widetilde{\varphi }_{8})\mathrm{sn^{2}}\left( \omega _{3}\xi ,k_{8}\right) }}\nonumber \\&\quad =\frac{(-\widetilde{\varphi }_{7}+\widetilde{\varphi }_{13})\widetilde{\varphi }_{12}+ (\widetilde{\varphi }_{7}-\widetilde{\varphi }_{12}) \widetilde{\varphi }_{13}\tanh ^{2}(\omega _{3}\xi )}{-\widetilde{\varphi }_{7}+\widetilde{\varphi }_{13} +(\widetilde{\varphi }_{7}-\widetilde{\varphi }_{12}) \tanh ^{2}(\omega _{3}\xi )}\nonumber \\&\quad =\widetilde{\varphi }_{7}+\frac{6\beta -6\alpha \widetilde{\varphi }_{7}^{2}}{2\alpha \widetilde{\varphi }_{7}+\sqrt{6\alpha \beta -2\alpha ^{2}\widetilde{\varphi }_{7}^{2}} \cosh \left( \sqrt{\beta -\alpha \widetilde{\varphi }_{7}^{2}}\xi \right) }\nonumber \\&\quad =u_{25}(x,t). \end{aligned}$$

(150)

Therefore, the blow-up wave solution $u_{25}(x,t)$ is the limit of the periodic blow-up wave solution $u_{21}(x,t)$. The limiting process is in Fig. 12.

Fig. 12

The limiting process of $u_{21}$ tends to $u_{25}$ when $\widetilde{\varphi }_{4}$ tends to $\widetilde{\varphi }_{7}$

Similarly, we can derive the others cases. This has proved Proposition 3.

Remark 1

One may find that we only consider the case when $g\le 0$ in Proposition 1(when $g\ge 0$ in Proposition 2). In fact, we may get exactly the same solutions in the opposite case.

Remark 2

By comparing with the solutions of Refs. [4–7], most of my results are new. After checking over those solutions carefully, when $a=1$, we find that my results (15), (37) and (38), exactly the same as those results (5.19), (5.16), (5.17), (5.20), (5.21) given in Ref. [7]. When $a=1$ and $c=\frac{\alpha }{1-2\alpha ^{2}}$, we find that my results (39) and (40), exactly the same as those results (5.6) given in Ref. [7]. To our knowledge, we believe that many other solutions are new.

4 Conclusions

In this paper, I have obtained many traveling wave solutions for the MBBM equation (2) by employing the bifurcation method and qualitative theory of dynamical systems. The traveling wave solutions have been given in Propositions 1 and 2. On the other hand, in Proposition 3, we prove that the solitary wave solutions, periodic wave solutions, kink wave solutions, blow-up wave solutions and unbounded solutions can be obtained from the limits of the smooth periodic wave solutions or periodic blow-up solutions. The method can be applied to many other nonlinear evolution equations, and we believe that many new results wait for further discovery by this method.