Abstract
In this paper, we discuss a neutral delay predator–prey model with Hassel–Varley type functional response and impulse is investigated. By using Mawhin coincidence degree theory, we obtain some sufficient conditions for the existence of positive periodic solutions. We extend some known work.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The predator–prey model was first introduced by Lotka and Volterra, and then the traditional predator–prey models have been extensively studied [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Many models have been established to describe the relationships between species and the outer environment and the connections between species. In 1969, Hassell and Varley proposed a predator–prey model (HV, for short), in which the functional response dependents on the predator density in different way [1]. In Ref. [2], Wang considered the periodicity to a non-autonomous predator–prey model with HV functional response and delay in the prey specific growth term
Recently, the neutral differential equation with delay has been widely studied and the applications in mathematical ecology will continue to be one of the dominant themes due to its universal existence and importance [3, 4]. Many excellent results have been done for the predator–prey model with neutral and delays. For example, Zhang and Zheng [5] considered the following neutral delay predator–prey model with Holling type II functional response
On the other side, in population dynamics, perturbations occur in a more-or-less fashion for many reasons. For example, mating habits, hunting, harvesting, birth, etc. This perturbation bring sudden change to the model. To describe the mathematical ecology systems more realistically, it need to consider the impulse term. In the recent years, impulsive differential equations have been extensively studied [6, 7]. By applying impulsive differential equations theory, many authors investigated the mathematical ecology systems with impulse [8,9,10,11]. However there are few papers discussing the impulse neutral differential systems.
Motivated by the above work, in this paper, we study the following neutral delay predator–prey model with HV type functional response and impulse
with initial condition
where x and y represent prey and predator densities at time t, respectively. \(a(t),~b(t),~c(t),~ d(t),~ r(t),~ \tau (t),\) \(\sigma _1(t)\) are continuous nonnegative T-periodic functions. m, \(\rho ~\hbox {and }\gamma \) are positive constants, \(\sigma _2\) is a small positive constant. \(\theta _{ik} >-1, ~i=1,2,~ k \in N^{+}={1,~2,~\ldots }\) . Furthermore, \( \sigma := \max \nolimits _{t\in [0,T]} \{ \tau (t), ~ \sigma _1(t),~\sigma _2 \}\).
By using the Mawhin coincidence theory, we establish some criteria to guarantee the existence of positive periodic solutions of systems (1.1) and (1.2). Our results show that the impulsive neutral delay model (1.1) and (1.2) preserve the original periodicity without the neutral term and impulse under appropriate periodic impulse perturbations. From Theorem 3.1 of this paper, we can easily see that the condition \([A_3]\) of Theorem 3.1 in paper [2] could be removed.
2 Preliminaries
Definition 2.1
\((x(t),y(t))^{T}\in C([-\sigma ,+\infty ),(0,+\infty ),(0,+\infty ))\) is said to be a solution of the initial value problem (1.1) and (1.2) on \([-\sigma ,+\infty )\) if
-
(i)
x(t), y(t) are absolutely continuous on each interval \((0,t_{1}]\) and \((t_{k},t_{k+1}],k\in N^{+};\)
-
(ii)
for any \(t_{k},~k\in N^{+}, ~(x(t_{k}^{+}),y(t_{k}^{+}))^{T}\) and \((x(t_{k}^{-}),y(t_{k}^{-}))^{T}\) exist and \((x(t_{k}^{-}),y(t_{k}^{-}))^{T}=(x(t_{k}),y(t_{k}))^{T};\)
-
(iii)
\((x(t),y(t))^{T}\) satisfies (1.1) and (1.2) for almost everywhere (a.e.) in \([0,\infty )\backslash \{t_{k}\}\) and satisfies \(x(t^{+}_{k})-x(t_{k})=\theta _{1k}x(t_{k}),~ y(t^{+}_{k})-y(t_{k})=\theta _{2k}y(t_{k}), \) for \(t=t_{k},~k\in N^{+}.\)
We make the following assumptions
- \({[H_{1}]}\) :
-
\(0<t_{1}<t_{2}<\cdots<t_{k}<\cdots \) are fixed points and \(\lim \nolimits _{k\rightarrow \infty }t_{k}=+\infty ;\)
- \({[H_{2}]}\) :
-
\(\{\theta _{ik}\}\) are real sequences such that \(\theta _{ik}>-1\) and \(\prod \nolimits _{0<t_{k}<t}(1+\theta _{ik}),~i=1,2\) are T-periodic functions.
Under the assumptions \([H_{1}]~\hbox {and}~[H_{2}]\), we consider the following system
with initial condition
where
Lemma 2.1
Suppose that \([H_{1}]~\hbox {and}~[H_{2}]\) hold, then
-
(i)
if \((N_1(t),N_2(t))^{T}\) is a solution of (2.1) and (2.2), then \((x(t),y(t))^{T}\) is a solution of (1.1) and (1.2), where
$$\begin{aligned} x(t)=\prod _{0<t_{k}<t}(1+\theta _{1k})N_1(t),\quad y(t)=\prod _{0<t_{k}<t}(1+\theta _{2k})N_2(t); \end{aligned}$$ -
(ii)
if \((x(t),y(t))^{T}\) is a solution of (1.1) and (1.2), then \((N_1(t),N_2(t))^{T}\) is a solution of (2.1) and (2.2), where
$$\begin{aligned} N_1(t)=\prod _{0<t_{k}<t}(1+\theta _{1k})^{-1}x(t),\quad N_2(t)=\prod _{0<t_{k}<t}(1+\theta _{2k})^{-1}y(t). \end{aligned}$$
Proof
(i) It is easy to see that \(x(t)=\prod \nolimits _{0<t_{k}<t}(1+\theta _{1k})N_1(t),~~y(t)=\prod \nolimits _{0<t_{k}<t}(1+\theta _{2k})N_2(t)\) are absolutely continuous on every interval \((t_{k},t_{k+1}]\). For any \(t\ne t_{k},~k\in N^{+}\), one has
On the other hand, for any \(t=t_{k},~k\in N^{+}\), we have
and
Thus we obtain
From (2.2)–(2.6), we know that \((x(t),~y(t))^{T}\) is a solution of (1.1) and (1.2).
(ii) Since \( \displaystyle { x(t)=\prod \nolimits _{0<t_{k}<t}(1+\theta _{1k})N_1(t),~~y(t)=\prod \nolimits _{0<t_{k}<t}(1+\theta _{2k})N_2(t)}\) are absolutely continuous on every interval \((t_{k},t_{k+1}],~k\in N^{+}\). According to definition 2.1, \(\forall ~ k\in N^{+},\) we have
and
which implies that \(N_1(t),~N_2(t)\) are continuous on \([-\sigma ,+\infty ).\) It is easy to prove that \(N_1(t),~N_2(t)\) are absolutely continuous on \([-\sigma ,+\infty ).\)
Similar to the proof of the case (i), we could show that
are the solutions of systems (2.1) and (2.2). The proof of Lemma 2.1 is completed.
From Lemma 2.1, we only study the existence of positive periodic solutions of systems (2.1) and (2.2) and obtain the existence of positive periodic solutions of systems (1.1) and (1.2).
In order to present sufficient conditions for guaranteeing the existence of positive periodic solutions for the systems (2.1) and (2.2), we introduce the coincidence degree theorem.
Let X and Y be two Banach spaces, \(L: \hbox {D}omL\subset X \rightarrow Y\) is a linear map, and \(N: X \rightarrow Y\) is a continuous map. If \( \text{ dim } \text{ Ker }L=\hbox {codim Im}L<+\infty \) and \( \text{ I }mL\in Y\) is closed, then we call the operator L is a Fredholm operator with index zero. And if L is a Fredholm operator with index zero and there exist continuous projections \( P: X\rightarrow X\) and \(Q: Y\rightarrow Y\) such that \( \hbox {Im}P= \hbox {Ker}L\), \( \hbox {Im}L=\hbox {Ker}Q= \hbox {Im}(I-Q)\), then \(L|_{DomL\cap KerP}: (I-P)X\rightarrow \hbox {Im}L\) has an inverse function, we set it as \(K_{p}\). Assume \(\Omega \in X\) is any open set, if \(QN({{\overline{\Omega }}})\) is bounded and \(K_{p}(I-Q)N({{\overline{\Omega }}})\in X\) is relative compact, then we say \(N\in {{\overline{\Omega }}}\) is L-compact.
Lemma 2.2
[17] Let X and Y be both Banach spaces, \(L:\hbox {Dom}L\subset X \rightarrow Y\) be a Fredholm operator with index zero, \(\Omega \in Y\) be an open bounded set, and \(N: {{\overline{\Omega }}}\rightarrow X\) be L-compact on \({{\overline{\Omega }}}\). If all the following conditions hold
- \({[C_{1}]}\) :
-
\(Lx\ne \lambda Nx\), for \(x\in {\partial \Omega }\cap \hbox {Dom}L, \lambda \in (0,1)\);
- \({[C_{2}]}\) :
-
\(Nx\not \in \hbox {ImL}\), for \(x\in \partial \Omega \cap \hbox {Ker}L\);
- \({[C_{3}]}\) :
-
deg\(\{JQN,\Omega \cap \hbox {Ker}L, 0 \}\ne 0\), where \(J: \hbox {Im}Q\rightarrow \hbox {KerL}\) is an isomorphism;
then the equation \(Lx=Nx\) has at least one solution on \({{\overline{\Omega }}}\cap \hbox {Dom}L\).
Lemma 2.3
[18, 19] If \( \tau \in C^{1}(R,R) \) with \( \tau (t+T)=\tau (t)\) and \( \tau '(t)<1 \) for \( t \in [0,T]\), then the function \( \delta (t)=t-\tau (t) \) has a unique inverse \( \delta ^{-1}(t)\) satisfying \( \delta \in C(R,R)\) with \( \delta ^{-1}(s+T)=\delta ^{-1}(s)+T \) for \( s\in [0,T] \).
For convenience, we denote
where f is a nonnegative T-periodic continuous function.
3 Main Results
Theorem 3.1
Assume that \([H_{1}],~[H_{2}]\) and the following conditions hold
- \({[H_{3}]}\) :
-
\( \tau '(t)<1\);
- \({[H_{4}]}\) :
-
\( 1>\delta e^{R}\), where R is defined in the proof;
- \({[H_{5}]}\) :
-
\( M{{\overline{r}}}>{{\overline{C}}},~ \frac{ e^{R}A^{M}}{{{\overline{d}}}M}>\theta ,~ \frac{{{\overline{A}}}}{{{\overline{d}}}}>\theta .\)
Then systems (1.1) and (1.2) have at least one T-periodic solution.
Proof
It is not difficult to see that the solution of system (2.1) remains positive for all \(t\in R\). Let
Then system (2.1) can be reformulated in the following form
In order to apply Lemma 2.2 to study the existence of positive periodic solutions to above system, set
and denote
Then X and Y are both Banach spaces when they are endowed with the norms \(\Vert \cdot \Vert \) and \(|\cdot |_{\infty }\), respectively.
Define operators L, P and Q as follows, respectively
where \(\hbox {Dom}L=\{z|z\in X: z(t)\in C^{1}(R,R^{2})\}\), and define \(N: X\rightarrow Y\) by the form
where
Then \(\hbox {Ker} L=R^{2}, \hbox {and} ~ \hbox {Im}L=\{z\in Y: \int _{0}^{T} z(t)dt=0\} \hbox { is closed in } Y\). Furthermore, \(\dim \hbox {Ker}L=\hbox {codim Im}L \), and P, Q are both continuous projections satisfying
So L is a Fredholm operator with index zero, which implies that L has a unique inverse. Define \(K_{p}:\hbox {Im} L\rightarrow \hbox {Ker}P\cap \hbox {Dom}L\) being the inverse of L. By simply calculating, one has
Therefore
where \(\Lambda ^{*}_1(z,t)=r(t)-B(t)e^{u(t-\tau (t))}-\frac{C(t)e^{v(t)}}{ M e^{\gamma v(t)}+ \theta e^{u(t)} }. \) Then we obtain
Obviously, it is not difficult to check by the Lebesgue convergence theorem that QN and \(K_{p}(I-Q)N\) are both continuous. By using Arzela-Ascoli Theorem, we know that operator \(K_{p}(I-Q)N({{\overline{\Omega }}})\) is compact and \(QN({{\overline{\Omega }}})\) is bounded for any open set \(\Omega \in X\). So \(N\in \Omega \) is L-compact on \({{\overline{\Omega }}}\).
Corresponding to operator equation \(Lz=\lambda Nz\) for \(\lambda \in (0,1),\) we have
Assume that \((u(t),~v(t))^{T}\in X\) is a T-period solution of (3.2) for a certain \(\lambda \in (0,~1)\). Integrating (3.2) over the interval [0, T], we obtain
In view of Lemma 2.3 and \([H_3]\), one has
It follows from (3.3) that
which implies
where \( P=\frac{B(\delta ^{-1}(s))}{1-\tau '(\delta ^{-1}(s))} .\)
Multiplying both sides of the second equation of (3.2) by \(e^{\gamma v(t)}\), and integrating them from \(0 ~\hbox {to}~ T\), we have
which leads to
Then
Now we prove by the following two cases: \(v(t)\ge 0\) and \(v(t)< 0\).
Case 1 If \(v(t)\ge 0\), then \( e^{\gamma v(t)} \ge 1.\) Together with (3.6) yields
which implies that there exists \( \xi _1 \in [0,T]\) such that \( v(\xi _1)\le \frac{ln U_2}{\gamma }, \) therefore
Thus there exists \( \eta _1\in [0,T]\) such that \( u(\eta _1)\le \)max\( \{ |lnU_1|,~ |ln\frac{Md^{L}}{A^{M}}| \} .\)
Case 2 If \(v(t)< 0\), then \( e^{\gamma v(t)}<1 .\) According to (3.3), we have
which implies
Again from (3.4), one has \( U_1> \frac{1}{T}\int ^{T}_{0} e^{u(t)} dt >L_1 .\) So there exists \( \eta _2 \in [0,T]\) such that \( u(\eta _2) \le \max \big \{ | lnU_1 |,~ | lnL_1 | \big \}. \) We can choose \( \eta \in [0,T] \) such that \( u(\eta ) \le \hbox {max} \{ | ln U_1|,~| lnL_1 |,~| ln\frac{Md^{L}}{A^{M}} | \}:=W_1.\)
By the mean value theorem of differential calculus, we have
In view of (3.3) and Lemma 2.3, one has
where \( E(t)=\frac{B(\delta ^{-1}(t))}{1-\tau '(\delta ^{-1}(t))}. \) Thus
There exists \( \zeta _3\in [0,T] \) such that
Since \(\int ^{T}_{0}r(t)dt>0, ~r^{M}>0\), we obtain \( u(\zeta _3)<ln\frac{2r^{M}}{E^{L}} \) and \( u(\zeta _3-\tau (\zeta _3))<\frac{2r^{M}}{B^{L}}. \) Therefore
which implies that \(u(t)<R. \)
By the mean value theorem of differential calculus, we see that there exists \(\xi _{1}\in [0,T]\) such that
Thus
which implies that
It is easy to see that
According to the second equation of (3.2), one has
By the mean value theorem of differential calculus, there exists \(\zeta \in [0,T]\) such that
which yields that
It is not difficult to see that \(\int ^{T}_{0}|v'(t)|dt<2{{\overline{d}}}T,\) thus
In view of (3.2), we get
Now it is easy to see that
\(M_5\) is independent of \(\lambda .\) Set \( M^{*}=M_5+1 \), and take \(\Omega =\{ z=(u,v)^{T}:z<M^{*} \} \). It is clear that \( \Omega \) verifies the condition \([C_1]\) in Lemma 2.2.
When \(z=(u,v)^{T}\in \partial \Omega \cap \hbox {KerL}=\partial \Omega \cap R^{2},~z=(u,v)^{T}\) is a constant vector in \(R^{2}\) with \( ||z||=M^{*}\), we have
This prove that condition \([C_{2}]\) in Lemma 2.2 is satisfied.
Finally, we will show that condition \([C_{3 }]\) in Lemma 2.2 holds.
Define the homotopy \(\phi :~\hbox {Dom}L\times [0,1]\rightarrow X\) by
where \(\mu \in [0,1]\) is a parameter. When \((u,v)^{T}\in \partial \Omega \cap \hbox {Ker}L=\partial \Omega \cap R^{2},~(u,v)^{T}\) is a constant vector in \(R^{2}\) with \(\Vert (u,v)^{T}\Vert =W.\) We will show that when \((u,v)^{T}\in \partial \Omega \cap \hbox {Ker}L\), \(\phi ((u,v)^{T},\mu )\ne 0.\) The following algebraic equation
has a unique solution \((u^{*},v^{*})^{T},\) which satisfy \(e^{u^{*}}=\frac{{{\overline{r}}}}{{{\overline{B}}}},~ e^{\gamma v^{*}}=\frac{{{\overline{r}}}}{M{{\overline{B}}}}\big (\frac{{{\overline{A}}}}{{{\overline{d}}}}-\theta \big ) .\) Define the homomorphism \(J: \hbox {Im} Q \rightarrow \hbox {Ker}L\), \(Jz \equiv z\), a direct calculation shows that
Therefore, we have verified all the requirements of Mawhin coincidence theorem in \(\Omega \) and the system (3.1) has at least one positive T-periodic solution. Then, by Lemma 2.2, we derive that systems (1.1) and (1.2) have at least one positive T-periodic solution. This completes the proof. \(\square \)
Remark 3.1
In (1.1) and (1.2), if \( \rho =\theta _{ik}=0, ~i=1,2,~ k \in N^{+}\), then the model discussed in [2] is a special case of (1.1) and (1.2). From the proof of our main result, we know that the condition \([A_3]\) of Theorem 3.1 in [2] could be removed. So our main result generalized Theorem 3.1 in [2].
Remark 3.2
In (1.1) and (1.2), if \( \tau (t)=\sigma _1,~\sigma _1(t)=\sigma _2,~\gamma =1,~ \theta _{1k}=\theta _{2k}=0, \) we can obtain that the model in [7] is a special case of (1.1) and (1.2).
4 Example
Considering the following neutral delay predator–prey model with HV-type functional response and impulse
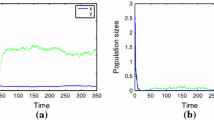
It is easy to calculate \( \tau '(t)=\frac{cost}{2}<1,~ \theta <1, ~,R>24 \pi , ~\delta e^{R}\ll 1,~{{\overline{r}}}=6,~{{\overline{C}}}=2\theta , ~M=4\theta , ~{{\overline{d}}}=3, ~{{\overline{A}}}=10\theta ,~ A^{M}>11 . \) We can check that all the conditions of Theorem 3.1 hold, then the system has at least one \(2\pi -\)periodic solution.
References
Hassell, M., Varley, G.: New inductive population model for insect parasites and its bearing on biological control. Nature 223, 1133–1136 (1969)
Wang, K.: Periodic solutions to a delayed predator-prey model with Hassell–Varley type functional response. Nonlinear Anal. Real World Appl. 12, 137–145 (2011)
Kuang, Y.: On neutral delay logistic Gauss-type predator-prey systems. Dyn. Stab. Syst. 6, 173–189 (1991)
Kuang, Y.: Delay Differential Equations with Applications in Population Dynamics. Academic Press, Boston (1993)
Zhang, F., Zheng, C.: Positive periodic solutions for the neutral ratio-dependent predator–prey model. Comput. Math. Appl. 61, 2221–2226 (2011)
Samoikleno, A.M., Perestyuk, N.A.: Impulsive Differential Equations. World Scientific, Singapore (1995)
Zavalishchhin, S.T., Sesekin, A.N.: Dynamic Impulse Systems, Theory and Applications. Kluwer Academic Publishers Group, Dordrecht (1997)
Huo, H.: Existence of positive periodic solutions of a neutral delay Lotka–Volterra system with impulses. Comput. Math. Appl. 48, 1833–1846 (2004)
Dai, B., Su, H., Hu, D.: Periodic Solution of a delayed ratio-dependent predator–prey model with monotonic functional response and impulse. Nonlinear Anal. 70, 126–134 (2009)
Wang, Q., Dai, B.: Existence of positive periodic solutions for a neutral population model with delays and impulse. Nonlinear Anal. 69, 3919–3930 (2008)
Du, Z., Feng, Z.: Periodic solutions of a neutral impulsive predator–prey model with Beddington–DeAngelis functional response with delays. J. Comput. Appl. Math. 258, 87–98 (2014)
Lv, Y., Du, Z.: Existence and global attractivity of a positive periodic solution to a Lotka–Volterra model with mutual interference and Holling III type functional response. Nonlinear Anal. Real World Appl. 12, 3654–3664 (2011)
Du, Z., Lv, Y.: Permanence and almost periodic solution of a Lotka–Volterra model with mutual interference and time delays. Appl. Math. Model. 37(3), 1054–1068 (2013)
Terry, A.J.: Predator–prey models with component Allee effect for predator reproduction. J. Math. Biol. 71, 1325–1352 (2015)
Ducrot, A., Langlais, M.: A singular reaction–diffusion system modelling prey–predator interactions: invasion and co-extinction waves. J. Differ. Equ. 253, 502–532 (2012)
Fan, M., Kuang, Y.: Dynamics of a nonautonomous predator–prey system with the Beddington–DeAngelis functional response. J. Math. Anal. Appl. 295, 15–39 (2004)
Gaines, R.E., Mawhin, J.L.: Coincidence Degree and Nonlinear Differential Equations. Springer, Berlin (1977)
Lu, S.: On the existence of positive periodic solutions to a Lotka–Volterra cooperative population model with multiple delays. Nonlinear Anal. 68, 1746–1753 (2008)
Lu, S.: On the existence of positive periodic solutions for neutral functional differential equation with multiple deviating arguments. J. Math. Anal. Appl. 280, 321–333 (2003)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is supported by the Natural Science Foundation of China (Grant No. 11471146), and partially supported by PAPD of Jiangsu Province.
Rights and permissions
About this article
Cite this article
Chen, X., Du, Z. Existence of Positive Periodic Solutions for a Neutral Delay Predator–Prey Model with Hassell–Varley Type Functional Response and Impulse. Qual. Theory Dyn. Syst. 17, 67–80 (2018). https://doi.org/10.1007/s12346-017-0223-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12346-017-0223-6