Project portfolio selection and scheduling under a fuzzy environment

Abstract

The problem of integrated project portfolio selection and scheduling (PPSS) is among the most important and highly pursed subjects in project management. In this study, a mathematical model and algorithm are designed specifically to assist decision makers decide which projects are to be chosen and when these projects are to be undertaken. More specifically, the PPSS problem is first formulated as a nonlinear multi-objective model with simultaneous consideration of benefit and risk factors. Due to the complexity and uncertainty involved in most real life situations, fuzzy numbers are incorporated into the model, which can provide decision makers with more flexibility. Then, an inverse modeling based multi-objective evolutionary algorithm using a Gaussian Process is presented to obtain the Pareto set. Finally, an illustrative example is used to demonstrate the high efficacy of the foregoing approach, which can provide decision makers with valuable insights into the PPSS process. The proposed algorithm is found to be more effective compared with two other popular algorithms.

1 Introduction

Project portfolio selection and scheduling (PPSS) strives to choose appropriate projects from a given set of competing alternatives and make an overall development plan. Obviously, excellent project systems are regarded as critical to organizations as poorly selected projects are often dysfunctional and may even compromise other projects [1]. However, decision makers (DMs) often face a difficult tradeoff during a project management process. On the one hand, they cannot afford to develop an indiscriminately large number of projects subject to scarce resources, such as money, manpower, and equipments. On the other hand, they need to develop the right types of projects to maximize their contributions. Therefore, there is a great demand for an overall plan for the selection and scheduling of multiple projects to form an effective and efficient portfolio solution.

The PPSS process, however, is difficult to carry out for DMs, as they may have to take into account extensive data as well as conflicting criteria. Another issue in the problem is associated with the uncertainty of the decision-making environment. In most real-life situations, it is often difficult or even impossible, for DMs to provide complete and precise information regarding project management problems due to complexity, time pressure or limited expertise. Fuzzy set theory was proposed to handle this, because it can provide DMs with more freedom to represent uncertainty and flexibility regarding information [2, 3]. Some authors have focused on PPSS problem under a fuzzy environment. In general, a great deal of attention in the literature has been devoted to the selection, ranking, or scheduling problem in various fields, under both crisp and fuzzy environments. The common approaches toward the problem can be classified into three categories: multi-criteria decision making (MCDM), mathematical programming models, and intelligent optimization algorithms. Please refer to Sect. 2 for a detailed literature review.

Normally, the PPSS problem consists of selecting the appropriate projects from a given set of alternatives and scheduling their development time under various constraints. One of the main goals is to maximize the project benefits to the highest possible extent. Meanwhile, uncertainties may arise in the development of the selected projects. The risk of some projects’ failure to provide desired benefits is another important factor that cannot be overlooked. In other words, various criteria need to be considered throughout the PPSS process. Thus, the PPSS problem could be treated as a multi-objective optimization problem which is NP-hard in nature. In the currently existing studies, two solutions are mostly applied in solving the foregoing problems. The first one focuses on transforming multi-objective problems into a single objective. The key limitation is that each optimization run finds only one single solution and knowledge of the problem is required to solve it. However, the PPSS problem may consist of contradictory objectives (like benefit and risk). Quite often, these objectives contradict each other. That is, the larger benefit often means a higher corresponding risk. An increment in one feature could be done at the cost of the other. Therefore, it is unreasonable to mix these objectives into one objective. The second approach uses population based multi-objective optimizing algorithms to search for a set of Pareto optimal solutions.

Although research has been carried out in the PPSS field, several issues remain to be elucidated. First, most existing studies focused only one the selection or scheduling of project portfolios. However, it makes more sense to take into account the selection and scheduling of project portfolios simultaneously. Next, benefit is mostly treated as the main objective in the evaluation of various solutions whereas risk is seldom considered, which may cause unreasonable or ineffective solutions to be recommended [1]. In addition, most existing studies used crisp values in the PPSS modeling and solving process, which is difficult or impossible in real life situations. Thus, incorporating uncertainties regarding information in the decision making process is more realistic and natural. Last, most algorithms proposed to tackle the PPSS problem often entail great computational costs, especially when the number of objectives is large [4].

To address all the aforesaid research void, a quantitative mathematical model and an inverse modeling based multi-objective evolutionary algorithm (IMMOEA) are proposed in this paper to solve the PPSS problem. First, the PPSS problem is formulated as an optimization problem with new objectives under fuzzy constraints. Then, a novel algorithm, named IMMOEA, is used and modified to solve the model in order to obtain the Pareto set. Comparable experiments are also executed to verify its effectiveness. To the best of our knowledge, this is the first time that such an algorithm has been designed specifically for solving the PPSS problem within a fuzzy environment.

The rest of the paper is organized as follows. In Sect. 2, a brief review of different methods developed for the project portfolio selection and/or scheduling problem is presented. Subsequently, the PPSS problem is briefly described and a quantitative model is designed having appropriate constraints and formulations. The proposed algorithm for solving the PPSS problems is then explained in detail in Sect. 4. In Sect. 5, an illustrative example is studied to verify the algorithm’s feasibility and practicality. Comparative studies are carried out to demonstrate its usefulness and efficacy. Finally, conclusions and suggestions are made in Sect. 6.

2 Literature review

To date, a great deal of attention in the literature has been devoted to tackling the evaluation, selection or scheduling of project portfolios in various fields. In general, DMs need to evaluate project portfolios and execute the selection (scheduling) process based on certain criteria or try to find the most appropriate set of solutions that can better meet their special requirements. To sum up, all these methods used to tackle this area can be classified into three categories: (1) MCDM methods, (2) mathematical programming models, and (3) intelligent optimization algorithms. In the following part, this paper reviews and analyzes some popular and representative methods adopted in existing studies for each category mentioned above as explained in the following three paragraphs.

Within different MCDM methods, Analytic Hierarchy Process (AHP) and Analytic Network Process (ANP) are two of the most widely used approaches in the literature. For both methods, the relative importance for a given set of projects should be determined. Some other distance-based approaches, like TOPSIS, VIKOR or outranking methods, like ELECTRE, PROMETHEE, are also used to evaluate and select an appropriate set of projects. For example, Vetschera and de Almeida [5] studied the use of PROMETHEE outranking methods for portfolio selection problems. Likewise, Tavana et al. [6] combined Data Envelopment Analysis (DEA), the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), and linear Integer Programming (IP) for the screening, ranking, and selecting of appropriate project portfolios in a fuzzy environment. Recently the use of hybrid methods combining two or more techniques has recently received more attention. Overall, numerous approaches can be applied to solve MCDM problems associated with project portfolio selection or scheduling [7, 8].

In the second category, researchers have proposed different mathematical programming models based on reality and solved the models to obtain appropriate solutions. Hassanzadeh et al. [9] developed a multi-objective integer programming model with imprecise information both in objectives and constraints for use with Research and Development (R&D) project portfolio selection problems. Schaeffer and Cruz-Reyes [10] proposed a mathematical model framework for portfolio optimization in which projects were allowed to be divided into different tasks and dependencies within tasks could be handled as well. Sefair et al. [11] developed a mean-semivariance project portfolio selection model and used the model in the oil and gas industry. Chen et al. [12] formulated a mixed integer linear programming model considering multiple concurrent projects with the objective of minimizing the total tardiness of all projects. In summary, researchers have been focusing on proposing various models to represent the real world situations and trying to solve the associated models to obtain appropriate solutions [13,14,15,16].

As for the third category, some intelligent optimization algorithms have been designed to tackle the complexity of the problem, especially as the number of projects grows. Yassine et al. [17] proposed two new genetic algorithm approaches for scheduling project activities under a multi-project, resource-constrained, and iterative environment. Xiong et al. [18] addressed the problem of R&D project selection associated with resource allocation and activity scheduling by using a cooperative coevolutionary multi-objective algorithm to obtain high-quality solutions. Kumar et al. [19] proposed three meta-heuristics for the solution of project portfolio selection and scheduling problem. The performance of the proposed algorithms has been found to be promising in terms of quality and convergence. Overall, the advantage of using intelligent optimization algorithms in the PPSS problem is their high efficiency in finding appropriate solutions.

Despite the considerable amount of research in the PPSS field, more comprehensive quantitative model under uncertainty and corresponding algorithms are needed to conduct selection and scheduling processes. Thus, an improved scientific model and algorithm for making reasonable decisions for the PPSS problem could prove to be very useful.

3 Problem formulation

In this section, the mathematical model about the PPSS problem is proposed. First, common notations used throughout this paper are listed. Then, the portfolio definition, objectives, and constraints are given with explanations in the following subsections.

3.1 Notations

In this section, some common notations used in the model formulation are explained (Table 1).

Table 1 Notations used in this paper

3.2 Portfolio definition

In the PPSS problem, a DM or organization needs to select one or more projects from a set of I candidate projects and subsequently schedule the starting time of each selected project within a time of period of length T under various constraints. Thus, the associated decision variables, $x_{it}$, can be defined as

$$ x_{it} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\,project\,i\,starts\;at\;time{\kern 1pt} \,t} \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

(1)

where $i = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2, \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} I$ and ${\kern 1pt} t = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2, \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} T.$

In this situation, any vector $x = \{ x_{11} ,{\kern 1pt} x_{12} , \ldots ,x_{1T} ;x_{21} ,x_{22} ,{\kern 1pt} \ldots ,x_{2T} ; \ldots ,x_{I1} ,x_{I2} , \ldots ,x_{IT} \}$ with a length of $I \cdot T$ variables, denotes a portfolio. Note that the duration of each project $d_{i} (i = 1,2, \ldots ,I)$, where $d_{i}$ can be a time unit such as months or years, is given. Hence, in this study, we focus on the starting period of each project if it is chosen.

For example, a DM in an armament company may have a budget to develop some new weapons to meet the capability requirements of military operations over the next 5 years. Ten possible candidate types of weapons are under consideration. However, only a small set of weapons (projects) can be chosen and developed due to budget constraints. In this case, there are altogether $2^{I \cdot T} = 2^{10 \times 5} = 2^{50}$ vectors or solutions. Then, the vector $x = \{ 0,{\kern 1pt} 0,1,0,{\kern 1pt} 0;1,0,{\kern 1pt} 0,0,0; \ldots ,0,{\kern 1pt} 0,0,0,0\}$ is an example of a profile. It denotes that the first weapon is chosen in the third year, the second weapon is selected in the first year, and the last weapon is not chosen. However, DMs need to evaluate different portfolios based on appropriate criteria under various constraints.

Note that each project can provide corresponding benefits during its duration. In addition, these projects have specific resource requirements in different periods and may possess risks that should be taken into account when they arise. Normally, higher benefits for a project mean more resources are needed and the risks are greater. In general, benefits, resource requirements, and risks are time-dependent.

3.3 Objectives

Different portfolios need to be evaluated by the DMs based on a set of criteria over T time periods. There are two main types of criteria: benefit type such as profits and market shares, for which one desires higher values, and cost type like risks which one wishes to minimize.

To begin with, consider the first type of criterion. Assume that there are Q kinds of benefits that DMs want to maximize simultaneously. Each benefit is represented by an objective function. For a specific time period, each benefit contains two main components. On the one hand, for each feasible portfolio, the individual contributions of the selected projects based on their implementation periods, should be considered. On the other hand, synergies may exist between certain projects, which will result in additional positive or negative effects [20]. Let $c_{q,i,k + 1 - t}$ be the value of benefit q provided by project i in period k. Note that in period k, the implementation time of that project is $k + 1 - t$ if it is selected (starts) at time t.

Based on the foregoing discussion, the time-dependent objective function associated with benefit q in period k is defined as

$$ F_{qk} (x) = \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {c_{q,i,k + 1 - t} \cdot x_{it} } } + \sum\limits_{j = 1}^{J} {g_{jk} (x)a_{qjk} } \quad q = 1,2,{\kern 1pt} \ldots ,Q,k = 1,2, \ldots ,T , $$

(2)

where the double summation term on the left denotes the sum of the benefit value that each individual project can provide, and the summation on the right represents the sum of the benefit value arising from the interactions between certain projects. Note that $g_{jk}$ represents whether synergy j comes into effect in period k, and it takes value 1 if synergy j is activated and 0 otherwise. In other words, only when the portfolio contains all the projects that belong to the set $A_{j} (j = 1,2, \ldots ,J)$ in period k ($k = 1,2, \ldots ,T$), is $g_{jk} (x)$ instrumental.

Then, each benefit value q that a portfolio x can provide throughout entire periods should be aggregated as

$$ F_{q} (x) = \sum\limits_{k = 1}^{T} {\left( {\sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {c_{q,i,k + 1 - t} \cdot x_{it} } } + \sum\limits_{j = 1}^{J} {g_{jk} (x)a_{qjk} } } \right)} = \sum\limits_{k = 1}^{T} {F_{qk} (x)} \,q = 1,2, \ldots ,Q, $$

(3)

Now consider the second type of criterion, mainly associated with risk of failure. Throughout the entire process, there exist some probabilities that projects may fail to provide corresponding benefits due to various causes (such as technology, cost, organization), which is also an important factor that needs to be considered. Herein, we assume that failure or success of a project does not affect other projects. This does not contradict interactions between projects in terms of providing benefits. For example, a reconnaissance plane and an attack plane, working together, can assist in identifying and destroying certain targets more easily. However, the former does not affect the attack ability of the latter, whereas the latter does not affect the detection ability of the former.

In this study, the term risk specifically stands for the probability of failing to provide certain benefits arising from internal factors (e.g. equipment aging or malfunction) throughout this paper. In addition, we assume that once a project fails to provide certain benefits, it can no longer provide benefits later on. In this case, if a portfolio works as planned and provides proper benefits in period k, then all the projects in this portfolio must work properly in the previous period k-1. Thus, we consider only the risk value of a given portfolio throughout the entire period T. In this reason, the total risk objective associated benefit q for a given portfolio x can be formulated as

$$ R_{q} (x) = 1 - \prod\limits_{i = 1}^{I} {\left( {\prod\limits_{t = 1}^{{d_{i} }} {(1 - r_{qit} )} } \right)^{{\sum\limits_{t = 1}^{T} {x_{it} } }} \quad } q = 1,2, \ldots ,Q, $$

(4)

where $r_{qit}$ denotes the probability of project i failing to provide benefit q in implementation period t, d_i is the duration of project i.$\prod\nolimits_{t = 1}^{{d_{i} }} {(1 - r_{qit} )}$ denotes the probability of project i working properly throughout its lifecycle. $\sum\nolimits_{t = 1}^{T} {x_{it} }$ represents the selection status of project i. It takes value 1 if project i is selected and 0 otherwise. $\prod\nolimits_{i = 1}^{I} {\left( {\prod\nolimits_{t = 1}^{{d_{i} }} {(1 - r_{qit} )} } \right){\kern 1pt}^{{\sum\limits_{t = 1}^{T} {x_{it} } }} }$ denotes the probability that all the selected projects work as planned and provide proper benefits throughout the entire period. This process can be treated as a series system with $\sum\nolimits_{i = 1}^{I} {\sum\nolimits_{t = 1}^{T} {x_{it} } }$ elements. Thus, the whole formula represents the probability of having at least one project failing to provide benefit q throughout the entire period.

Then, different portfolios can be evaluated based on their values associated with these two criteria. DMs always want to select appropriate portfolios with greater benefit values while having lower risk values at the same time. However, as mentioned above, the larger benefit often means a higher corresponding risk. That is, an increment in one feature could be done at the cost of the other. Therefore, it is unreasonable to mix these objectives into one objective.

3.4 Constraints

PPSS is a complicated process consisting of choosing the most appropriate projects and scheduling their starting times. It often takes place under a limited development time and constrained resources throughout the entire decision-making process. In most real-life situations, some parameters cannot be fully known due to a lack of knowledge, time pressure or limited expertise in the problem domain, in which case there exists uncertainty. To handle this, special attention is paid to the uncertainty on parameters in the resource constraints in this study. Next, some preliminaries on fuzzy set theory are first given in the following subsections. Subsequently, different constraints in conformity with real-life situations are proposed.

3.4.1 Fuzzy resource constraints

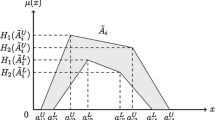
To begin with, the definition of a triangular fuzzy number (TFN) is given as displayed in Fig. 1. A TFN $\tilde{a}$ on R can be expressed as a triplet $(a,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,\bar{a})$ when its membership function $\mu_{{\tilde{a}}} (x):R \to [0,1]$ is equal to

$$ \mu_{{\tilde{a}}} (x) = \left\{ {\begin{array}{*{20}l} 0 \hfill &\quad {x \le a - \underline{a} ,} \hfill \\ {1 - \frac{a - x}{{\underline{a} }},} \hfill &\quad {a - \underline{a} < x \le a,} \hfill \\ {1 - \frac{x - a}{{\bar{a}}},} \hfill &\quad {a < x \le a + \bar{a},} \hfill \\ 0 \hfill &\quad {x > a + \bar{a},} \hfill \\ \end{array} } \right., $$

(5)

where $a$ is deemed as the middle value, and $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}$ and $\bar{a}$ are the left and right spreads from $a$, respectively.

Fig. 1

A triangular fuzzy number

Based on the forgoing definition, fuzzy numbers are used in this study to model uncertainty. Hence, the constraint associated with each resource spent on all the selected projects in each period is given as

$$ R\tilde{I}_{uk} \le \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {r\tilde{s}_{u,i,k + 1 - t} \cdot x_{it} \le R\tilde{S}_{uk} } } \;u = \{ 1,{\kern 1pt} 2, \ldots ,U\} ,k = \{ 1,2, \ldots ,T\}, $$

(6)

where $r\tilde{s}_{u,i,k + 1 - t}$ means the fuzzy amount of resource u needed by project i in period k if it is selected at time t, also denoted as a triplet $(rs_{u,i,k + 1 - t} ,\underline{rs}_{u,i,k + 1 - t} ,\overline{rs}_{u,i,k + 1 - t} )$. $R\tilde{I}_{uk}$ and $R\tilde{S}_{uk}$ are the fuzzy minimum and maximum amount of resources that DMs can provide in period k for resource u, also expressed as $(RI_{uk} ,\underline{RI}_{uk} ,\overline{RI}_{uk} )$ and $(RS_{uk} ,\underline{RS}_{uk} ,\overline{RS}_{uk} )$, respectively. In general, the amount of resource in each period should not vary a lot.

Moreover, synergies between certain projects can also consume some resources. In this situation, extra resources are needed in order to come into effect and provide corresponding benefits. Using the same logic as was applied in the first objective function, the resource constraint should be modified as

$$ \begin{aligned} & R\tilde{I}_{uk} \le \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {r\tilde{s}_{u,i,k + 1 - t} \cdot x_{it} + \sum\limits_{j = 1}^{J} {g_{jk} (x)\tilde{h}_{ujk} } \le } } R\tilde{S}_{uk} {\kern 1pt} , \\ & \quad u = \{ 1,2, \ldots ,U\} ,\quad k = \{ 1,2, \ldots ,T\} , \\ \end{aligned} $$

(7)

where the double summation term denotes the sum of all the selected projects’ individual resource requirements associated with resource u in period k, and the summation on the right part represents the amount of resource u needed by all the activated synergies in period k. In addition, given that resources may not be fully utilized at the end of each period, we assume that the remaining resources would not be used again at the next time point.

To tackle the TFNs used in the above constraint, the comparison method [21] is used, for which main idea is to enable a comparison between two fuzzy numbers using $\alpha$-cuts without creating extra elements. Specifically, given a TFN, $\tilde{a} = (a,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,\bar{a})$, set a confidence level $\alpha \in [0,1]$. Then, the triangular fuzzy intervals under $\alpha$-cut, as shown in Fig. 2, can be expressed in mathematical form as

$$ \tilde{a}_{\alpha } = \{ x\left| {\mu_{{\tilde{a}}} (x) \ge \alpha } \right.\} = [a_{\alpha }^{L} ,a_{\alpha }^{R} ] = [a - (1 - \alpha )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,a + (1 - \alpha )\bar{a}] $$

(8)

Fig. 2

Triangular fuzzy intervals under $\alpha$-cut

Given two TFNs $\tilde{a} = (a,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,\bar{a})$ and $\tilde{b} = (b,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ,\bar{b})$, $\tilde{a} \le \tilde{b}$ at the confidence level $\alpha \in [0,1]$, if the following two conditions are satisfied:

$$ a + (1 - \beta )\bar{a} \le b + (1 - \beta )\bar{b} $$

(9)

$$ a - (1 - \beta )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \le b - (1 - \beta )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} $$

(10)

for all $\beta \in [\alpha ,1].$

Thus, given a confidence level $\alpha_{u} \in [0,1]$ for resource u, the resource constraint (7), as mentioned above, can be transformed into the following two parts, shown as

$$ \begin{aligned} & RI_{uk} + (1 - \beta_{u} )\overline{RI}_{uk} \le \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {(rs_{u,i,k + 1 - t} + (1 - \beta_{u} )\overline{rs}_{u,i,k + 1 - t} ) \cdot x_{it} + \sum\limits_{j = 1}^{J} {g_{jk} (x) \cdot (h_{ujk} + (1 - \beta_{u} )\bar{h}_{ujk} )} } } \\ {\kern 1pt} & \quad \le RS_{uk} + (1 - \beta_{u} )\overline{RS}_{uk} u = \{ 1,2, \ldots ,U\} ,k = \{ 1,2, \ldots ,T\} , \\ \end{aligned} $$

(11)

$$ \begin{aligned} & RI_{uk} - (1 - \beta_{u} )\underline{RI}_{uk} \le \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {(rs_{u,i,k + 1 - t} - (1 - \beta_{u} )\underline{rs}_{u,i,k + 1 - t} ) \cdot x_{it} + \sum\limits_{j = 1}^{J} {g_{jk} (x) \cdot (h_{ujk} - (1 - \beta_{u} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{h}_{ujk} )} } } \\ {\kern 1pt} & \quad \le RS_{uk} - (1 - \beta_{u} )\underline{RS}_{uk} \,u = \{ 1,2, \ldots ,U\} ,k = \{ 1,2, \ldots ,{\kern 1pt} T\} , \\ \end{aligned} $$

(12)

where $\beta_{u} \in [\alpha_{u} ,1]$, constraint (11) is obtained based on constraint (9) and constraint (12) is obtained based on constraint (10), both of which denote the constraint associated with resource u in period k.

3.4.2 Other constraints

• (1) Constraints on synergies between projects

  As mentioned above, $g_{jk}$ represents whether synergy j comes into effect in period k. It takes value 1 only when the portfolio x contains all the projects simultaneously belonging to the set $A_{j}$ in period k so that synergy j can be activated. Based on above, $g_{jk} (x)$ can be represented in mathematical form as

  $$ g_{jk} (x) = \prod\limits_{{i \in A_{j} }} {\sum\limits_{{t{\kern 1pt} = {\kern 1pt} \hbox{max} {\kern 1pt} (1,{\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} } } \quad j = 1,2, \ldots ,J,k = 1,2, \ldots ,T, $$

  (13)

  where $d_{i}$ denotes the duration of the ith project as before, $\sum\nolimits_{{t = \hbox{max} {\kern 1pt} (1,{\kern 1pt} {\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} }$ takes value 1 if project i exists in a portfolio in period k, $k - d_{i} + 1$ is the earliest starting time for project i so that it is still executed in period k. In case that $k - d_{i} + 1$ is smaller than 1, which is meaningless, t takes the maximum of 1 and $k - d_{i} + 1$. In other words, this constraint ensures that the function $g_{jk} (x)$ takes value 1 only when the portfolio x verifies the synergy j.

• (2) Constraints on the simultaneous execution of projects

  Sometimes, DMs may impose restrictions on the number of projects that can be carried out at the same time in a certain period k. In this case, lower and upper bounds are defined as $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} (k)$ and $\bar{n}(k){\kern 1pt} .$

  $$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} (k) \le \sum\limits_{i = 1}^{I} {\sum\limits_{{t{\kern 1pt} = {\kern 1pt} \hbox{max} {\kern 1pt} (1,{\kern 1pt} {\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} } } \le \bar{n}(k),\quad k = 1,2, \ldots ,T , $$

  (14)

  where $\sum\nolimits_{{t{\kern 1pt} = {\kern 1pt} \hbox{max} {\kern 1pt} (1,{\kern 1pt} {\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} }$ takes value 1 if project i is executed in period k, and 0 otherwise.

• (3) Constraints about uniqueness

  Each project can at most be executed only once. However, DMs may demand that certain projects must be executed. For a particular project, this restriction can be implemented by setting its lower bound $NL_{i}$ as 1. Otherwise, $NL_{i}$ equals 0.

  $$ NL_{i} \le \sum\limits_{t = 1}^{T} {x_{it} \le 1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \in \{ 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} I\} $$

  (15)

  Notice that the above constraint on the lower bound permits them to have a value of 1 when certain projects must be implemented.

• (4) Constraints about the starting period

  This constraint ensures that the starting periods of certain projects are within the given intervals if chosen by using the following inequality:

  $$ \upsilon_{i} \sum\limits_{t = 1}^{T} {x_{it} } \le \sum\limits_{t = 1}^{T} {t \cdot x_{it} \le \omega_{i} } \quad i \in \{ 1,2, \ldots ,I\} , $$

  (16)

  where $\upsilon_{i}$ and $\omega_{i}$ are the lower and upper bounds associated with the starting time for project i.

• (5) Constraints about precedence

  Like other project scheduling problems, in some cases there may exist some precedent constraints among certain projects. For example, suppose that project i must be executed prior to project m. Then, it can be expressed in a mathematical form as

  $$ \sum\limits_{t = 1}^{T} {t \cdot x_{it} \le } \sum\limits_{t = 1}^{T} {t \cdot x_{mt} } \quad 1 \le i,m \le I $$

  (17)

In summary, this PPSS model can be formulated with the objectives given in Eqs. (3) and (4), subject to the constraints provided in constraints (11)–(17) inclusive.

4 An inverse modeling-based multi-objective evolutionary algorithm

The classic PPSS problem is very complex. Several factors regarding benefit, risk, and resource constraints need to be considered simultaneously. Furthermore, additional constraints associated with time, the interrelationships between different projects, make the problem more complicated. Traditional mathematical programming methods are inefficient or limited in the application. In contrast, multi-objective evolutionary algorithms (MOEAs) have proven to be highly efficient in solving this kind of problem. However, unlike most MOEAs that store non-dominated solutions during the search, the IMMOEA proposed by Cheng et al. [22] uses Gaussian process based inverse modeling to create new solutions, which has exhibited robust search performance on a variety of multi-objective optimization test problems. Accordingly, the existing IMMOEA is used and modified in this paper to handle the new PPSS problem.

4.1 Overview of the proposed IMMOEA

Model-based algorithms have been demonstrated to be very effective in approximating the Pareto front for multi-objective problems [23]. A new model based algorithm with regard to IMMOEA is introduced in this section to obtain the Pareto solutions. Its main idea lies in mapping non-dominated solutions from the objective space (OS) to the decision space (DS) based on some constructed inverse models [22]. To the best of the authors’ knowledge, there is no prior study using IMMOEA to solve the multi-objective PPSS problem under uncertainty.

Figure 3 displays an overview of the proposed IMMOEA, for which the pseudo code is given in Algorithm 1 [22] for the PPSS problem. To begin with, an initial population is generated, which is then partitioned into different groups based on some reference vectors (item 4 in Algorithm 1). Note that DMs’ preferences can be incorporated in the initialization process by setting certain constraints on the values used to encode various projects. The population is then evaluated by estimating each solution’s objectives and constraints. Herein, objectives refer to the benefits and risks of different PPSS solutions, whereas constraints refer to the extent to which different constraint limits are exceeded. As traditional IMMOEA focuses on solving optimization problems without considering the constraints. Thus, the penalty function is used to address various constraints associated with the PPSS problem. More specifically, the penalty function f is defined as

$$ \begin{aligned} f & = \sum\limits_{u = 1}^{U} {\sum\limits_{k = 1}^{T} {\hbox{max} \left( {0,R\tilde{I}_{uk} - \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {r\tilde{s}_{u,i,k + 1 - t} \cdot x_{it} } } - \sum\limits_{j = 1}^{J} {g_{jk} (x)\tilde{h}_{ujk} } } \right)} } \\ & \quad + \sum\limits_{u = 1}^{U} {\sum\limits_{k = 1}^{T} {\hbox{max} \left( {0,\sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{k} {r\tilde{s}_{u,i,k + 1 - t} \cdot x_{it} + \sum\limits_{j = 1}^{J} {g_{jk} (x)\tilde{h}_{ujk} } } } - R\tilde{S}_{uk} } \right)} } \\ & \quad + \sum\limits_{k = 1}^{T} {\hbox{max} \left( {0,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} (k) - \sum\limits_{i = 1}^{I} {\sum\limits_{{t{\kern 1pt} = {\kern 1pt} \hbox{max} {\kern 1pt} (1,{\kern 1pt} {\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} } } } \right)} + \sum\limits_{k = 1}^{T} {\hbox{max} \left( {0,\sum\limits_{i = 1}^{I} {\sum\limits_{{t{\kern 1pt} = {\kern 1pt} \hbox{max} {\kern 1pt} (1,{\kern 1pt} {\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} } } - \bar{n}(k)} \right)} \\ & \quad + \sum\limits_{i = 1}^{I} {\hbox{max} \left( {0,NL_{i} - \sum\limits_{t = 1}^{T} {x_{it} } } \right) + \sum\limits_{i = 1}^{I} {\hbox{max} \left( {0,\sum\limits_{t = 1}^{T} {x_{it} - 1} } \right)} } \\ & \quad {\kern 1pt} + \sum\limits_{i = 1}^{I} {\hbox{max} \left( {0,\upsilon_{i} \sum\limits_{t = 1}^{T} {x_{it} } - \sum\limits_{t = 1}^{T} {t \cdot x_{it} } } \right) + \sum\limits_{i = 1}^{I} {\hbox{max} \left( {0,\sum\limits_{t = 1}^{T} {t \cdot x_{it} - } \omega_{i} } \right)} } \\ & \quad + \sum\limits_{i = 1}^{I} {\sum\limits_{m = 1}^{I} {\hbox{max} \left( {0,\sum\limits_{t = 1}^{T} {t \cdot x_{it} } - \sum\limits_{t = 1}^{T} {t \cdot x_{mt} } } \right)} ,} \\ \end{aligned} $$

(18)

where each part in Eq. (18) denotes the extent to which the corresponding limit is exceeded in terms of the minimum resource constraint, the maximum resource constraint, the simultaneous execution of projects, the uniqueness of projects, the starting periods, and the precedence of projects, respectively. Taking the first term $\sum\nolimits_{u = 1}^{U} {\sum\nolimits_{k = 1}^{T} {\hbox{max} \left( {0,R\tilde{I}_{uk} - \sum\nolimits_{i = 1}^{I} {\sum\nolimits_{t = 1}^{k} {r\tilde{s}_{u,i,k + 1 - t} \cdot x_{it} } } - \sum\nolimits_{j = 1}^{J} {g_{jk} (x)\tilde{h}_{ujk} } } \right)} }$ as an example, for each resource u in each period k, the resource used in total cannot be lower than the fuzzy minimum amount of resource $R\tilde{I}_{uk}$, otherwise, the corresponding penalty is $R\tilde{I}_{uk} - \sum\nolimits_{i = 1}^{I} {\sum\nolimits_{t = 1}^{k} {r\tilde{s}_{u,i,k + 1 - t} \cdot x_{it} } } - \sum\nolimits_{j = 1}^{J} {g_{jk} (x)\tilde{h}_{ujk} }$. Conversely, the corresponding penalty function is 0, meaning that no violation of the constraint is triggered. The same logic applies to the other constraints. Then, the penalty value is incorporated into the objective value of each solution. The greater (smaller) is the new benefit (risk) value, the better is the individual (solution).

Fig. 3

Overview of IMMOEA based on [22]

Then, a selection procedure is carried out within each group to make up the parents of each group (item 5 in Algorithm 1). Next, a Gaussian process (GP) based inverse model is designed with regard to the generation of offspring in each group. Finally, the offspring and their parents are put together to form a new combined population. Some details of IMMOEA are provided as in Sects. 4.2–4.4 inclusive.

4.2 Partitioning the combined population

As illustrated in Algorithm 1, the combined population is first divided into several partitions. To begin with, S uniform reference vectors $\vec{v}_{s}$ are generated for a problem having m objectives [24]. More precisely, a set of S uniformly distributed points $\vec{w}_{s} = (w_{s}^{1} ,w_{s}^{2} , \ldots ,w_{s}^{m} ),s = 1,2, \ldots ,S$ are first generated, where each of the weight vectors $w_{s}^{i}$ selects a value from $\left\{ {\frac{0}{H},\frac{1}{H}, \ldots ,\frac{H}{H}} \right\}$, $\sum\nolimits_{i = 1}^{m} {w_{s}^{i} } = 1$, and H is a parameter controlling the number of vectors. After that, the uniformly distributed reference vector $\vec{v}_{s}$ can be obtained by mapping $\vec{w}_{s}$ from the unit hyperplane to a unit hypersphere as

$$ \vec{v}_{s} = \frac{{\vec{w}_{s} }}{{||\vec{w}_{s} ||}}s = 1,2, \ldots ,S $$

(19)

Once the reference vectors have been obtained, the total combined population is then partitioned into S subpopulations. This step is done by comparing their relative positions in the OS between each individual solution with the predefined reference vectors mentioned above [22]. More specifically, consider an arbitrary solution x_i as an example, which is assigned to reference vector $\vec{v}_{s}$ under the condition that the angle between its position with that of $\vec{v}_{s}$ is the minimum among all the reference vectors by calculating the sine function value of their angles using

$$ s_{i} = \mathop {\text{argmin} }\limits_{s = 1, \ldots ,S} \left( {\frac{{\vec{x}_{i} }}{{||\vec{x}_{i} ||}}{\kern 1pt} {\kern 1pt} \times \vec{v}_{s} } \right) $$

(20)

4.3 Inverse modeling

Let X denote a set of the decision vectors (i.e., PPSS solutions as defined in Eq. (1)) and Y denote a set of objective objectives associated with benefits and risks, both of which represent the current parent population. To generate the offspring $X^{0}$, a group of generated objective vectors $Y^{0}$ in the OS is mapped back to the DS using $P(X\left| Y \right.)$ associated with the Bayes’ Theorem [22]. Herein, $P(X\left| Y \right.)$ is the conditional probability distribution, which can be estimated by a probabilistic inverse model mapping Y back to X. In fact, $P(Y\left| X \right.)$ is the priori knowledge, i.e., the objectives functions mapping X to Y.

$$ P(X^{0} ) = \frac{{P(X\left| Y \right.)P(Y^{0} )}}{P(Y\left| X \right.)}, $$

(21)

In general, the probabilistic inverse model $P(X\left| Y \right.)$ is decomposed into $m \times n$ univariate models $P(x_{i} \left| {f_{j} } \right.)$. Note that m equals $2 \cdot Q$ (associated with Q benefits and Q risks) and n equals $I \cdot T$ (length of the decision variable) as mentioned in Sect. 3. However, it is very hard or impossible to estimate the inverse model for a problem with m objectives and n variables, especially those associated with large-scale optimization problems. In this reason, random grouping technology [25] is used for the building of multiple inverse models. Each univariate model takes only one single objective and one decision variable into account. More specifically, a total of m groups of inverse models are built for a problem having m objectives, where the jth objective $f_{j}$ would be treated as the input variable in group j, and L variables are randomly picked as well. As can be seen, the total number of inverse models now decreases from $m \times n$ to $m \times L$, where L is much smaller than n.

Assume that $N_{t}$ pairs of data are needed for training L GP models. Then, $T_{j,i}$ is denoted as the specific training data set used for training $P(x_{i} \left| {f_{j} } \right.)$ in the jth group as

$$ T_{j,i} = [f_{j} ,x_{i} ], $$

(22)

where $f_{j} = [f_{j}^{1} , \ldots ,f_{j}^{{N_{t} }} ]^{T}$ and $x_{i} = [x_{i}^{1} , \ldots ,x_{i}^{{N_{t} }} ]^{T}$, $f_{j}^{h}$ is the jth objective value of the hth individual, and $x_{i}^{h}$ is the ith decision variable of the hth individual.

The inverse mapping $P(x_{i} \left| {f_{j} } \right.)$ can be assumed to be a latent function $g( \cdot )$, represented by a number of arbitrary function variables $g = \{ g_{1} ,g_{2} , \ldots ,g_{{N_{t} }} \}$, which follows a joint Gaussian distribution [26]:

$$ P(g\left| {f_{j} } \right.) = N(\bar{g},C), $$

(23)

where $N(\bar{g},C)$ represents the multivariate Gaussian distribution, $\bar{g}$ denotes the mean vector, and C is the covariance matrix. $P(g\left| {f_{j} } \right.)$ stands for the conditional probability associated with the training data $f_{j}$. In order to decrease the computational burden of training a GP model, the mean function $\mu (f_{j} )$ which calculates the mean value of all the training data, is usually set to 0 by means of subtracting certain offset from $T_{j,i}$. Thus, Eq. (23) can be transformed to

$$ P(g\left| {f_{j} } \right.) = N(0,C) $$

(24)

A linear covariance function is used in this study for saving computational cost as

$$ C(f_{j}^{p} ,f_{j}^{q} ) = (f_{j}^{p} )^{T} f_{j}^{q} $$

(25)

Assume that $x_{i} = g(f_{j} ) + \varepsilon$ is affected by white noise $\varepsilon \sim N(0,(\sigma_{n} )^{2} Z)$. Then, a proper noise model can be expressed as

$$ P(x_{i} \left| g \right.) = N(g,(\sigma_{n} )^{2} Z) , $$

(26)

where Z is an identity matrix. Thus, the following equality associated with the marginal likelihood is obtained:

$$ P(x_{i} |f_{j} ) = \int {P(x_{i} |g)P(g|f_{j} )dg = } N(0,C + (\sigma_{n} )^{2} Z) . $$

(27)

Based on (27), given a test input $f_{j,*}$, a Bayesian inference can be utilized to achieve the corresponding output $x_{i,*}$. The following equation is used to obtain the mean and variance, correspondingly.

$$ \begin{aligned} & \mu_{j,i} = C_{*}^{T} (C + (\sigma_{n} )^{2} Z)^{ - 1} x_{i} \\ & (\sigma_{j,i} )^{2} = C_{**} - C_{*}^{T} (C + (\sigma_{n} )^{2} Z)^{ - 1} C_{*} , \\ \end{aligned} $$

(28)

where $C_{**} = [c(f_{j}^{1} ,f_{j}^{1} ), \ldots ,c(f_{j}^{{N_{t} }} ,f_{j}^{{N_{t} }} )]$ is composed of all the covariance values between each pairs of elements among $f_{j}$, and $C_{*} = [c(f_{j,*}^{1} ,f_{j}^{1} ), \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} c(f_{j,*}^{{N_{t} }} ,f_{j}^{{N_{t} }} )]$ consists of the covariance values between each pair of elements associated with the test input $f_{j,*}$ and that of the training data $f_{j}$. In this way, the inverse model $P(x_{i} \left| {f_{j} } \right.)$ is then transformed into a set of normal distributions as shown in Eq. (28).

In this study, the following equation is used to sample the input points $f_{j,*}$ as

$$ f_{j,*} = \left\{ {\frac{{\left[ {f_{j}^{\hbox{min} } - 0.5\xi_{j} ,{\kern 1pt} f_{j}^{\hbox{max} } + 0.5\xi_{j} } \right]}}{{N_{s} }}} \right\}, $$

(29)

where $N_{s}$ is the sample size, which is usually set to $N_{t}$, $f_{j}^{\hbox{max} }$ and $f_{j}^{\hbox{min} }$ are the maximum and minimum values, respectively, associated with objective j in $f_{j}$, and $\xi_{j} = f_{j}^{\hbox{max} } - f_{j}^{\hbox{min} } .$

4.4 Reproduction

Once the inverse models have been obtained, the test input points $f_{j,*}$ can be mapped to the DS $x_{i,*}$ by means of adding the mean values $\mu_{j,i} = (\mu_{{_{j,i} }}^{1} ,\ldots,\mu_{{_{j,i} }}^{{N_{s} }} )$ with white noise $z \sim (N(0,(\sigma_{j,i}^{1} )^{2} ), \ldots ,N(0,(\sigma_{j,i}^{{N_{s} }} )^{2} ))$ using

$$ x_{i,*} = \mu_{j,i} (f_{j,*} ) + z_{j,i} , $$

(30)

where $\mu_{{_{j,i} }}^{1} ,\ldots ,\mu_{{_{j,i} }}^{{N_{s} }}$ and $(\sigma_{j,i}^{1} )^{2} , \ldots ,(\sigma_{j,i}^{{N_{s} }} )^{2}$ are the outputs associated with a trained GP model in Eq. (28). After that, replace the current values $x_{i} = {\kern 1pt} (x_{i}^{1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i}^{{N_{s} }} )$ of each subpopulation with the new generated solutions $x_{i,*} = (x_{i,*}^{1} , \ldots ,x_{i,*}^{{N_{s} }} )$. Then, a new combined population is formed by integrating the offspring individuals produced by each subpopulation with their parents. A new round is initiated until the termination condition is satisfied. For more details, please refer to [22, 27].

5 Illustrative example

Assume that an investor has a budget to renovate some of the projects over the next five years. However, due to limited resources (mainly associated with money, in thousands of monetary units), only a set of projects can be selected. Two objectives are taken into account as maximizing benefits (in thousands of monetary units) and minimizing risks under various constraints. The main values of the projects associated with benefits that each project can provide and the risks that each project may possess in failing to provide benefits in different periods are given in Tables 2 and 3, respectively. In general, the risk values increase as time goes by. Next, portfolios are evaluated based on the two objectives under the conditions of satisfying various constraints.

Table 2 Benefit values of projects

Table 3 Risk values of projects

Regarding the first objective for each portfolio, the sum of all the benefit values that each individual project can provide is

$$ \sum\limits_{k = 1}^{5} {\sum\limits_{i = 1}^{10} {\sum\limits_{t = 1}^{k} {c_{1,i,k + 1 - t} \cdot x_{it} } } } , $$

(31)

where the values for $c_{1,i,k + 1 - t}$ are given as tabulated in Table 2.

Moreover, additional benefit (0.7, in this case) can be expected arising from the interactions between Projects 4 and 6. Therefore, the benefit value throughout the entire period should be aggregated as

$$ Max\,F(x) = \sum\limits_{k = 1}^{5} {\sum\limits_{i = 1}^{10} {\sum\limits_{t = 1}^{k} {c_{1,i,k + 1 - t} \cdot x_{it} } } } + \sum\limits_{k = 1}^{5} {0.7g_{1k} (x} ), $$

(32)

where $g_{1k} (x)$ equals 1 if the fourth and sixth projects exist simultaneously in period k. Otherwise, it takes a value of 0, where $A_{1} = \{ 4,6\}$, and $g_{1k} = \prod\nolimits_{{i \in A_{1} }} {\sum\nolimits_{{t = \hbox{max} {\kern 1pt} (1,{\kern 1pt} k - d_{i} + 1)}}^{k} {x_{it} } ,\quad k = 1,2, \ldots ,5} .$

Regarding the second objective for each portfolio, the probability of failure associated with projects should be expected to increase as time passes. The risk value corresponding to the second objective is formulated as

$$ Min\;R(x) = 1 - \prod\limits_{i = 1}^{10} {\left( {\prod\limits_{t = 1}^{{d_{i} }} {(1 - r_{1it} )} } \right)^{{\sum\limits_{t = 1}^{5} {x_{it} } }} ,} $$

(33)

where the probabilities for each project to become invalid in different periods $r_{1it}$ are given as tabulated in Table 3.

As for the resources, the fuzzy estimated amount of resources required for each project in different periods $r\tilde{s}_{1it}$ are given in Table 4. The fuzzy amount of resource for the synergy $\tilde{h}_{11k}$, as well as the fuzzy minimum and maximum amount of resources available in different periods are also given.

Table 4 Fuzzy resource coefficients for projects

As mentioned above, the remaining resource at the end of each year will not be re-used in the next year. Based on constraint (7), the set of constraints on resources in each year can be obtained as

$$ \begin{aligned} k & = 1:\tilde{0} \le 2\tilde{5}x_{11} + 4\tilde{2}x_{21} + 2\tilde{4}x_{31} + 4\tilde{0}x_{41} + 1\tilde{5}x_{51} + 3\tilde{0}x_{61} + 4\tilde{5}x_{71} + 5\tilde{0}x_{81} + 1\tilde{8}x_{91} + 3\tilde{2}x_{10,1} + 1\tilde{5}g_{11} \le {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\tilde{0}0 \\ k & = 2:\tilde{0} \le 3\tilde{2}x_{11} + 2\tilde{5}x_{12} + 4\tilde{2}x_{22} + 3\tilde{7}x_{31} + 2\tilde{4}x_{32} + 4\tilde{5}x_{41} + 4\tilde{0}x_{42} + 1\tilde{8}x_{51} + 1\tilde{5}x_{52} + 2\tilde{4}x_{61} + 3\tilde{0}x_{62} \\ & \quad + 4\tilde{5}x_{72} + 4\tilde{3}x_{81} + 5\tilde{0}x_{82} + 2\tilde{3}x_{91} + 1\tilde{8}x_{92} + 3\tilde{6}x_{10,1} + 3\tilde{2}x_{10,2} + 1\tilde{5}g_{12} \le {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\tilde{2}0 \\ k & = 3:\tilde{0} \le 3\tilde{2}x_{12} + 2\tilde{5}x_{13} + 4\tilde{2}x_{23} + 4\tilde{0}x_{31} + 3\tilde{7}x_{32} + 2\tilde{4}x_{33} + 4\tilde{8}x_{41} + 4\tilde{5}x_{42} + 4\tilde{0}x_{43} + 1\tilde{8}x_{52} + 1\tilde{5}x_{53} \\ & \quad + 1\tilde{8}x_{52} + 1\tilde{5}x_{53} + 2\tilde{4}x_{62} + 3\tilde{0}x_{63} + 4\tilde{5}x_{73} + 5\tilde{2}x_{81} + 4\tilde{3}x_{82} + 5\tilde{0}x_{83} + 3\tilde{4}x_{91} + {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\tilde{3}x_{92} + 1\tilde{8}x_{93} \\ & \quad + 4\tilde{6}x_{10,1} + 3\tilde{6}x_{10,2} + 3\tilde{2}x_{10,3} + 1\tilde{5}g_{13} \le {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\tilde{3}0 \\ k & = 4:\tilde{0} \le 3\tilde{2}x_{13} + 2\tilde{5}x_{14} + 4\tilde{2}x_{24} + 3\tilde{5}x_{31} + 4\tilde{0}x_{32} + 3\tilde{7}x_{33} + 2\tilde{4}x_{34} + 4\tilde{8}x_{42} + 4\tilde{5}x_{43} + 4\tilde{0}x_{44} + 1\tilde{8}x_{53} \\ & \quad + 1\tilde{5}x_{54} + 2\tilde{4}x_{63} + 3\tilde{0}x_{64} + 4\tilde{5}x_{74} + 2\tilde{0}x_{81} + 5\tilde{2}x_{82} + 4\tilde{3}x_{83} + 5\tilde{0}x_{84} + 4\tilde{5}x_{91} + 3\tilde{4}x_{92} + 2\tilde{3}x_{93} \\ & \quad + 1\tilde{8}x_{94} + 4\tilde{6}x_{10,2} + 3\tilde{6}x_{10,3} + 3\tilde{2}x_{10,4} + 1\tilde{5}g_{14} \le {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\tilde{1}5 \\ k & = 5:\tilde{0} \le 3\tilde{2}x_{14} + 2\tilde{5}x_{15} + 4\tilde{2}x_{25} + 4\tilde{2}x_{31} + 3\tilde{5}x_{32} + 4\tilde{0}x_{33} + 3\tilde{7}x_{34} + 2\tilde{4}x_{35} + 4\tilde{8}x_{43} + 4\tilde{5}x_{44} + 4\tilde{0}x_{45} \\ & \quad + 1\tilde{8}x_{54} + 1\tilde{5}x_{55} + 2\tilde{4}x_{64} + 3\tilde{0}x_{65} + 4\tilde{5}x_{75} + 2\tilde{0}x_{82} + 5\tilde{2}x_{83} + 4\tilde{3}x_{84} + 5\tilde{0}x_{85} + 4\tilde{0}x_{91} + 4\tilde{5}x_{92} \\ & \quad + 3\tilde{4}x_{93} + 2\tilde{3}x_{94} + 1\tilde{8}x_{95} + 4\tilde{6}x_{10,3} + 3\tilde{6}x_{10,4} + 3\tilde{2}x_{10,5} + 1\tilde{5}g_{15} \le {\kern 1pt} {\kern 1pt} {\kern 1pt} 9\tilde{5} \\ \end{aligned} $$

(34)

where $g_{11} = x_{41} \cdot x_{61} ,g_{12} = \left( {\sum\nolimits_{t = 1}^{2} {x_{4t} } } \right) \cdot \left( {\sum\nolimits_{t = 1}^{2} {x_{6t} } } \right),g_{13} = \left( {\sum\nolimits_{t = 1}^{3} {x_{4t} } } \right) \cdot \left( {\sum\nolimits_{t = 2}^{3} {x_{6t} } } \right),g_{14} = \left( {\sum\nolimits_{t = 2}^{4} {x_{4t} } } \right) \cdot \left( {\sum\nolimits_{t = 3}^{4} {x_{6t} } } \right)$ and $g_{15} = \left( {\sum\nolimits_{t = 3}^{5} {x_{4t} } } \right) \cdot \left( {\sum\nolimits_{t = 4}^{5} {x_{6t} } } \right)$, denoting whether the synergy takes place in the corresponding period. In general, the left side of (34) represents the fuzzy minimum amount of resources available in each period, whereas the right side limits the fuzzy maximum amount of resources available in each period. This set of constraints ensures that the resources used for a portfolio x in each period are within the given intervals.

Fuzzy constraints have to be transferred to crisp values for comparison. As mentioned above, a parameter $\alpha = 0.9$ is given, which can also be deemed as a confidence level. Suppose that the resources required for each project can increase or decrease both by 25% of their middle values, whereas the resource available in each year can increase or decrease by up to 20% and 30%, respectively. Thus, the above constraint on resources (34) should be transferred to two parts based on (11) and (12) for comparison. Next, some additional constraints are given by DMs by taking some real life situations and individual preferences into consideration.

DMs determined that at least two projects, whereas five projects at most, can be executed simultaneously in the second and third years. Thus, the following two inequalities are obtained using constraint (14):

$$ \begin{aligned} 2 & \le \sum\limits_{t = 1}^{2} {x_{1t} } + \sum\limits_{t = 2}^{2} {x_{2t} } + \sum\limits_{t = 1}^{2} {x_{3t} } + \sum\limits_{t = 1}^{2} {x_{4t} } + \sum\limits_{t = 1}^{2} {x_{5t} } \\ & \quad + \sum\limits_{t = 1}^{2} {x_{6t} } + \sum\limits_{t = 2}^{2} {x_{7t} } + \sum\limits_{t = 1}^{2} {x_{8t} } + \sum\limits_{t = 1}^{2} {x_{9t} } + \sum\limits_{t = 1}^{2} {x_{10,t} } \le 5{\kern 1pt} \\ \end{aligned} $$

(35)

$$ \begin{aligned} 2 & \le \sum\limits_{t = 2}^{3} {x_{1t} } + \sum\limits_{t = 3}^{3} {x_{2t} } + \sum\limits_{t = 1}^{3} {x_{3t} } + \sum\limits_{t = 1}^{3} {x_{4t} } + \sum\limits_{t = 2}^{3} {x_{5t} } \\ & \quad + \sum\limits_{t = 2}^{3} {x_{6t} } + \sum\limits_{t = 3}^{3} {x_{7t} } + \sum\limits_{t = 1}^{3} {x_{8t} } + \sum\limits_{t = 1}^{3} {x_{9t} } + \sum\limits_{t = 1}^{3} {x_{10,t} } \le 5{\kern 1pt} \\ \end{aligned} $$

(36)

DMs found that Project 6 must be selected and scheduled, whereas there are no mandatory constraints on other projects.

$$ 0 \le \sum\limits_{t = 1}^{5} {x_{it} \le 1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,3,4,5,7,8,9,10 $$

(37)

$$ 1 \le \sum\limits_{t = 1}^{5} {x_{6t} \le 1} \Rightarrow \sum\limits_{t = 1}^{5} {x_{6t} = 1} $$

(38)

Some limitations on the starting periods of each project are given if selected:

$$ \begin{aligned} & \sum\limits_{t = 1}^{5} {t \cdot x_{1t} \le 3} ,3\sum\limits_{t = 1}^{5} {x_{3t} } \le \sum\limits_{t = 1}^{5} {t \cdot x_{3t} \le 4} ,\sum\limits_{t = 1}^{5} {t \cdot x_{5t} \le 3} \\ & 2\sum\limits_{t = 1}^{5} {x_{6t} } \le \sum\limits_{t = 1}^{5} {t \cdot x_{6t} \le 3} ,\sum\limits_{t = 1}^{5} {x_{8t} } \le \sum\limits_{t = 1}^{5} {t \cdot x_{8t} \le 4} ,3\sum\limits_{t = 1}^{5} {x_{9t} } \le \sum\limits_{t = 1}^{5} {t \cdot x_{9t} \le 5} \\ \end{aligned} $$

(39)

As Project 3 can provide Project 8 with some additional support, the former one should be scheduled earlier before project 8 if chosen. Thus, a new constraint about precedence is given as

$$ \sum\limits_{t = 1}^{5} {t \cdot x_{3t} \le } \sum\limits_{t = 1}^{5} {t \cdot x_{8t} } $$

(40)

The bi-objective optimization model is now built with the objectives contained in (32) and (33), subject to the constraints (34)–(40). Then, IMMOCA is used to solve it using Matlab Version R2016a. Additionally, two other traditional multi-objective optimization algorithms, namely a multi-objective evolutionary algorithm based on decomposition (MOEA/D) [28] and non-dominated sorting genetic algorithm II (NSGA-II) [29], are also independently used to solve the problem under the same constraints for comparison purposes. MOEA/D decomposes a multi-objective optimization problem into a number of scalar optimization sub-problems and optimizes them simultaneously, whereas NSGA-II uses a fast non-dominated sorting procedure and an elitist-preserving approach to create a diverse Pareto-optimal front.

Three metrics, namely convergence (γ), diversity (Δ) and Generational Distance (GD), are calculated to measure the results of the aforementioned three different algorithms. More specifically, convergence (γ) is used to evaluate the accuracy of approximating the obtained results to the global Pareto-optimal front. If γ equals 0, it means that the obtained Pareto set is the actual Pareto set. Diversity (Δ) is used to evaluate the diversity among the obtained non-dominated solutions using Eq. (41), where n is the number of solutions, $h_{i}$ is the distance between two adjacent solutions, $\bar{h}$ is the average value of $h_{i}$, $h_{f}$ and $h_{1}$ are distances between extreme solutions and boundary solutions, respectively. According to this metric, the smaller the diversity, the better is the diverse set of the obtained solution.

$$ \Delta = \frac{{h_{f} + h_{1} + \sum\nolimits_{i = 1}^{n - 1} {|h_{i} - \bar{h}|} }}{{h_{f} + h_{1} + (n - 1)\bar{h}}}. $$

(41)

GD is used to describe the distance between the obtained Pareto set and the true Pareto set using (42), where $dist_{i}^{{}}$ is the shortest distance between the ith Pareto set and the true Pareto set. This one is used to evaluate not only convergence, but also diversity. In the following equation, a lower value is better.

$$ GD = \frac{{\sqrt {\sum\nolimits_{i = 1}^{n} {dist_{i}^{2} } } }}{n} $$

(42)

There are two major objectives in this example, listed as benefit and risk. The former one illustrates the sum of all the overall benefit values that a portfolio solution can provide in a given period, and the latter one represents the probability of having at least one project failing to provide its expected benefit throughout the entire period.

In what follows, set the population size at Pop = 100, the total number of generations at MaxGen = 500, and the random group size L = 3. Then, each algorithm is independently executed 10 times and its best results are recorded as shown in Fig. 4.

Fig. 4

The best results of three algorithms

As shown in Fig. 4, the bottom-left points of IMMEOA, MOEA/D, and NSGA-II are (2.35, 0.32), (3.35, 0.40), and (4.85, 0.53), respectively. The top-right points of these three algorithms are (10.50, 0.79), (9.30, 0.70), and (10.55, 0.81), respectively. It is obvious that the Pareto set obtained by IMMOEA has the longest distribution curve among the three, followed by MOEA/D and NSGA-II. Hence, the Pareto set obtained by IMMOEA contains more portfolio solutions.

In most situations, the exact Pareto set is not known, and consequently, it is necessary to propose a reference set for the calculation of the above three metrics. To this aim, the above three algorithms are independently executed 10 times, and the best Pop non-dominated solutions are taken as the reference set. Moreover, Pop * 10 solutions are obtained for each algorithm. Then, the best, worst, mean, and standard deviation (std) among these solutions for each algorithm are recorded, as tabulated in Table 5. For all of the three metrics, a lower value is better.

Table 5 Statistical comparisons among three different algorithms

As can be seen, the worst occurs with NSGA-II for all different measures for the three metrics compared with that of IMMOEA and MOEA/D, though the best value in convergence is not the worst. IMMOEA has the smallest mean value of the convergence metric, which means that IMMOEA has the best convergence. As for the diversity metric, IMMOEA also outperforms the others, followed by MOEA/D and NSGA-II. The best, worst, and mean values of GD for these measures having the smallest values are also recorded for IMMOEA, which in a way indicates the good convergence and diversity of IMMOEA. Moreover, Table 6 displays the average time for each round of these different algorithms. Note that the efficiency of IMMOEA is more superior to the other algorithms. Therefore, IMMOEA stands out from the other two algorithms regarding convergence and diversity, which means that it can produce more robust solutions in a shorter time.

Table 6 Average computation time (t) among the three different algorithms (in seconds)

After obtaining the Pareto set by IMMOEA, we continue the process to obtain a compromise solution using the TOPSIS approach [30], for which the criteria are benefit and risk. The main idea of this MCDM approach lies in selecting the most appropriate alternative that is the nearest to the positive ideal solution, while farthest from the negative ideal one as well. Set the relative importance of these two criteria as 0.6 and 0.4, for the benefit criterion and risk criterion, respectively. Note that various algorithms and methodologies, especially preferences based multi-objective optimization, have been designed in recent decades to obtain a representative subset of the Pareto front or even certain compromise solutions [31].

Details of the compromise solution are shown in Table 7. The symbol of “√” indicates the starting time of its corresponding project. As shown in Table 7, six out of ten projects are chosen to be developed throughout the given period. More specifically, Projects 1 and 5 are selected to be developed in the first year, whereas Project 8 is developed in the second year, Projects 4 and 6 in the third year, and Project 2 in the fourth year. Taking the duration of each project into consideration, the numbers of projects existing in each year are 2, 3, 3, 4, and 2, respectively. Note that Projects 4 and 6 occur simultaneously in the third and fourth years. Thus, additional benefit can be raised from the interactions between them.

Table 7 Details of the compromise solution

As mentioned above, fuzzy numbers are used in this model, and the confidence level $\alpha$ is utilized to transform them into precise values. It is logical to think that different efficient frontiers can be obtained at different confidence levels given by DMs. Thus, we continue the experiment using IMMOEA at different confidence levels for comparison purposes, while the other parameters used in the algorithm remain the same. The algorithm is re-executed 10 times at each value of $\alpha$ to get a $100 \times 10$ Pareto sets. However, some of the solutions are the same, the number of unique Pareto solutions under different circumstances need to be identified. After that, TOPSIS approach is used to get the compromise solutions under each circumstance, whose values associated with the two objectives are listed in Table 8. The solution number of each Pareto set varies each other. The statistical results are shown in Table 8.

Table 8 Statistical data at different confidence levels

It is apparent that when $\alpha$ equals 1, the fuzzy resource constraints are transformed into precise values. As $\alpha$ decreases, the number of total unique solutions under different confidence levels decreases as well. The variation range of the compromise solutions at different confidence levels is [10.30, 13.85] associated with the benefit value, and [0.77, 0.92] for the risk value. Actually, the compromise solutions obtained at different confidence levels are quite similar. For example, the corresponding compromise solutions are the same when $\alpha$ equals 0.8, 0.4, and 0.3. The same situation occurs when $\alpha$ is equal to 0.6 and 0.2. However, the unique solution number obtained when $\alpha$ equals 0.2 is lower than that of 0.6. In fact, as $\alpha$ decreases, the fuzzy resource constraints become more and more restrictive. Thus, the unique solution numbers should decrease as well. Note that the efficient Pareto solutions obtained at a higher confidence level are also feasible for any lower confidence level. Therefore, some of the solutions may be a part of different Pareto frontiers even under different confidence levels.

6 Conclusions

PPSS is an important strategic problem having significant impacts on the running efficiency of organizations. In this paper, a mathematical PPSS model is constructed as a bi-objective optimization problem under a fuzzy environment. As an extension to existing studies, the model focuses on maximizing various solutions’ overall benefits and lowering the risk values simultaneously. Specific resource limitations and DMs’ preferences are taken into account. To address the uncertainties regarding information, fuzzy numbers are also incorporated into the model, enabling DMs with more flexibility.

A hybrid algorithm called IMMOEA is used and modified to obtain the Pareto set, which is the first time that such an algorithm has been used to solve the PPSS problem. Three algorithms are employed in an example and different metrics are used simultaneously to compare their efficacy. The results show that IMMOEA outperforms MOEA/D and NSGA-II with respect to diversity, spread, and convergence. NSGA-II is the worst compared with the other two algorithms used in this study. Finally, details regarding the corresponding compromise solution are determined. Certain conclusions and suggestions are proposed based on the calculations. Hence, this research can provide project managers with additional insights into this PPSS procedure.

In future studies, the authors will consider projects with multiple activity relationships, various constraints, and even dynamic events occurring during the project execution time. These challenges will certainly contribute to the expansion of this methodology for tackling a broader range of problems.