A combined constraint handling framework: an empirical study

Abstract

This paper presents a new combined constraint handling framework (CCHF) for solving constrained optimization problems (COPs). The framework combines promising aspects of different constraint handling techniques (CHTs) in different situations with consideration of problem characteristics. In order to realize the framework, the features of two popular used CHTs (i.e., Deb’s feasibility-based rule and multi-objective optimization technique) are firstly studied based on their relationship with penalty function method. And then, a general relationship between problem characteristics and CHTs in different situations (i.e., infeasible situation, semi-feasible situation, and feasible situation) is empirically obtained. Finally, CCHF is proposed based on the corresponding relationship. Also, for the first time, this paper demonstrates that multi-objective optimization technique essentially can be expressed in the form of penalty function method. As CCHF combines promising aspects of different CHTs, it shows good performance on the 22 well-known benchmark test functions. In general, it is comparable to the other four differential evolution-based approaches and five dynamic or ensemble state-of-the-art approaches for constrained optimization.

1 Introduction

In the real-world applications, constrained optimization problems (COPs) are very common and important. The COPs can be generally expressed by the following formulations:

$$\begin{aligned} \hbox {Minimize}&\quad f\left( \vec {x}\right) \\ \hbox {Subject to:}&\quad g_j \left( \vec {x}\right) \le 0,{\begin{array}{ll} &{}\quad {j=1,\ldots ,l} \\ \end{array} }\\&\quad h_j \left( \vec {x}\right) =0,{\begin{array}{ll} &{}\quad {j=l+1,\ldots ,m} \\ \end{array} } \end{aligned}$$

where $\vec {x}=(x_1 ,\ldots ,x_n )$ is the decision variable. The decision variable is bounded by the decision space S which is defined by the constraints:

$$\begin{aligned} L_i \le x_i \le U_i , \quad {1\le i\le n} \end{aligned}$$

(1)

l is the number of inequality constraints and $m-l$ is the number of equality constraints.

The evolutionary algorithms (EAs) are essentially unconstraint search techniques [1] and can be mainly used to generate solutions. Equivalently, choosing the better solutions among the parent and offspring populations, especially for the COPs is another important research area in optimization, which leads to the development of various constrained optimization evolutionary algorithms (COEAs) [2,3,4] The three most frequently used constraint handling techniques (CHTs) in COEAs are based on the concept of penalty functions, biasing feasible over infeasible solutions and multiobjective optimization [3, 5,6,7].

Penalty function method is generic and applicable to any type of constraints. It constructs a fitness evaluation by adding an amount of constraint violation to an objective function. The fine tuning of penalty parameters, which helps to balance the objective and constraint violation, is the key point.

Methods which compare separately the objective functions and constraint violations were also developed. For example, Deb [5] proposed a feasibility-based rule to pair-wise compare individuals:

• (1) Any feasible solution is preferred to any infeasible solution.

• (2) Among two feasible solutions, the one having better objective function value is preferred.

• (3) Among two infeasible solutions, the one having smaller constraint violation is preferred.

Meanwhile, multiobjective optimization technique which considers the objective function and constraint violation at the same time has been employed to handle constraints [3, 7].

Besides these basic CHTs, some other concepts like cooperative coevolution [8, 9] and ensemble [10, 11] have also been proposed. These methods employed different subpopulations and evolve parallel. Normally, the population size of these methods changes with the evolution process. Thus, it can be seen as a dynamic adjustment process.

Taking ensemble of constraint handling techniques (ECHT) [11] as an example, it utilizes multiple subpopulations. Each subpopulation corresponds to one CHT with its own offspring. And the parent population of one CHT will compete with all the offspring populations so that every function call can be utilized effectively.

The evolution process will inevitably experiences three different situations in solving COPs [12], and consequently, some dynamic approaches were developed.

Zhang et al. [13] proposed a dynamic stochastic selection (DSS) within the framework of multimember DE (DSS_MDE). Another adaptive penalty formulation was introduced by Tessema and Yen [14].It uses the number of feasible individuals to determine the amount of penalty added to infeasible individuals.

Wang et al. [12] proposed an adaptive tradeoff model (ATM). To satisfy the different requirements in corresponding situations, different tradeoff schemes during different situations of a search process are designed. Based on it, an improved ATM with each constraint violation first normalized was proposed by Wang and Cai [15]. It was combined with ($\upmu +\uplambda$)-DE to form the framework of ($\upmu +\uplambda$)-CDE. In this approach, a constraint-handling mechanism is designed in each situation based on the characteristics of the current population. To overcome the drawbacks of ($\upmu +\uplambda$)-CDE, an improved version of ($\upmu +\uplambda$)-CDE, named ICDE, was presented by Jia et al. [16]. ICDE consists of an improved ($\upmu +\uplambda$)-differential evolution (IDE) and a novel archiving-based adaptive tradeoff model (ArATM). Especially, the hierarchical non-dominated individual selection scheme is utilized and an individual archiving technique is proposed to maintain the diversity of the population in the infeasible situation. In the semi-feasible situation, the feasibility proportion of the population is used to convert the objective function of each individual.

Among all of these aforementioned methods, the problem characteristics are rarely considered. But as Michalewicz summarized [17], it seems that Evolutionary Algorithms, in the broad sense of this term, provide just a general framework on how to approach complex problems. All their components, from the initialization, through variation operators and selection methods, to constraint-handling methods, might be problem-specific. From this, we believe it is essential to design a general framework from the aspect of problem characteristics.

Besides, there are already some computational time complexity analyses of EAs [18, 19] that emphasize the relationship between algorithmic features and problem characteristics. As Yao presented [20], analyzing the relationship between problem characteristics and algorithmic features will shed light on the essential question of when to use which algorithm in solving a difficult problem instance class. And he introduced EA-hard and EA-easy problem instance classes. These classes are based on the functional relationship between the mean number of generations (i.e., the mean first hitting time) and the problem size (in terms of dimensionality). But as he also pointed out, it is still unclear what the relationship is between the optimization time and the problem size for different EAs on different problems. Though a lot of theoretical analysis was obtained, Yao did not give the specific relationship between algorithms and problems.

Additionally, some researchers have emphasized the importance of the relationship between problem characteristics and algorithms, and have tried to realize some simple combination of algorithm variants, although the results are not satisfactory. For example, Tsang and Kwan [21] pointed out the need to map constraint satisfaction problems to algorithms and heuristics. But they did not give an exact relationship between them. Mezura-Montes et al. [22] proposed a simple combination of two DE variants (i.e., DE/rand/1/bin and DE/best/1/bin) based on the empirical analysis of four DE variants. Gibbs et al. [23] identified the relationship between the optimal number of GA generations and the problem characteristics, through quantifying different problem characteristics of unconstrained problems.

Recently, some researchers have made some beneficial attempt on the use of information during the evolutionary process, and got some good results. It is noted that, in the course of the information use, the relationship between diversity and convergence, exploration and exploitation should be well handled.

Wang et al. [24] proposed the strategy of incorporating objective function information into the Deb’s feasibility-based rule, and achieved an effective balance between constraints and objective function in constrained optimization. The paper also presented some new replacement mechanisms and mutation strategy to better exploit the information of individuals with good objective function values.

Qiu et al. [25] developed some adaptive cross-generation differential evolution operators for multi-objective optimization. This mechanism utilized the swarm information between neighbor generations from the aspect of objective spaces into two mutation operators, so as to achieve the good balance between convergence and diversity. This paper also presented a new parameter adaptation mechanism to self-adapt the individuals’ associate parameters.

Elsayed and Sarker [26] presented a general differential evolution framework for big data optimization. Three sub-swarms were employed to correspond to a variant respectively. During the evolutionary process, the performance information of each variant was recorded, and an exponential curve was fitted to predict the future performance of each variant.

Feng et al. [27] proposed an evolutionary memetic search, which can learn and evolve knowledge meme across different but related problem domains. It was realized on two combination optimization problems, capacitated vehicle routing problem (CVRP) and capacitated arc routing problem (CARP).

Other methods concerning the problem characteristics were also reported [28]. As presented in [28], a method to construct the relationship between problems and algorithms as well as constraint handling techniques from the qualitative and quantitative point of view was proposed. In the paper, the problem characteristics were also summarized systematically.

Unlike the aforementioned methods, in this work, we try to study the features of different CHTs (i.e., penalty function method, multiobjecitve optimization technique and Deb’s feasibility-based rule) and get the corresponding relationship between problem characteristics and CHTs in different situations. A combined constraint handling framework (CCHF) is proposed based on the corresponding relationship.

The rest of this paper is organized as follows. Section 2 briefly introduces DE. Section 3 gives the detail analysis of the relationship among three CHTs (i.e., multi-objective optimization technique and penalty function method, Deb’s feasibility-bases rule and penalty function method). The comparison of different CHTs in different situations is analyzed in Sect. 4. Based on this, Sect. 5 presents a detailed description of the proposed CCHF. The experimental results and the comparison with some state-of-the-art methods are given in Sect. 6. Finally, Sect. 7 concludes this paper and provides some possible paths for future research.

2 Differential evolution (DE)

DE, which was proposed by Storn and Price, is a simple and efficient EA. The mutation, crossover and selection operations are introduced in DE. The first two operations are used to generate a trial vector to compete with the target vector while the third one is used to choose the better one for the next generation. Several variants of DE have been proposed [29]. DE/rand/1/bin was adopted in this paper as the search algorithm.

The population of DE consists of NP n-dimensional real-valued vectors

$$\begin{aligned} \vec {x}_i =\left\{ {x_{i,1} ,x_{i,2} ,\ldots ,x_{i,n} } \right\} , \quad {i=1,2,\ldots ,\textit{NP}} \end{aligned}$$

(2)

The three operations are defined as follows.

2.1 Mutation operation

Taking into account each individual $\vec {x}_i$ (named a target vector), a mutant vector $\vec {v}_i =\{ {v_{i,1} ,v_{i,2} ,\ldots ,v_{i,n} } \}$ is defined as

$$\begin{aligned} \vec {v}_i =\vec {x}_{r1} +F\cdot \left( \vec {x}_{r2} -\vec {x}_{r3}\right) \end{aligned}$$

(3)

where r1, r2 and r3 are randomly selected from [1, NP] and satisfying: $r1\ne r2\ne r3\ne i$ and F is the scaling factor.

In this paper, if $v_{i,j}$ violates the boundary constraint, it will be reset as follows [9]:

$$\begin{aligned} v_{i,j} =\left\{ {\begin{array}{ll} \min \left\{ {U_j ,2L_j -v_{i,j} } \right\} ,&{}\quad \,if\,{v_{i,j} <L_j } \\ \max \left\{ {L_j ,2U_j -v_{i,j} } \right\} ,&{}\quad if\,{v_{i,j} >U_j} \\ \end{array}} \right. \end{aligned}$$

(4)

2.2 Crossover operation

A trial vector $\vec {u}_i$ is generated through the crossover operation on the target vector $\vec {x}_i$and the mutant vector $\vec {v}_i$

$$\begin{aligned} u_{i,j} =\left\{ {\begin{array}{ll} v_{i,j} &{}\quad { if }\,rand_j \le C_r\quad {or }\,{j=j_{ rand}} \\ x_{i,j} &{}\quad { otherwise} \\ \end{array}} \right. \end{aligned}$$

(5)

where $i=1,2,\ldots ,\textit{NP},j=1,2,\ldots ,n, j_{rand}$ is a randomly chosen integer within the range [1, n], $rand_j$ is the $j\hbox {th}$ evaluation of a uniform random number generator within [0,1], and $C_r$ is the crossover control parameter. The introduction of $j=j_{rand}$ can guarantee the trial vector $\vec {u}_i$ is different from its target vector $\vec {x}_i$.

2.3 Selection operation

Selection operation is realized by comparing the trial vector $\vec {u}_i$ against the target vector $\vec {x}_i$ and the better one will be preserved for the next generation.

$$\begin{aligned} \vec {x}_i =\left\{ {\begin{array}{ll} {\vec {u}_i }&{}\quad \,{ if }\,{f\left( \vec {u}_i\right) \le f\left( \vec {x}_i\right) }\\ {\vec {x}_i }&{}\quad { otherwise} \\ \end{array}} \right. \end{aligned}$$

(6)

3 Systematic analysis of CHTs

3.1 Definitions

Unlike the single optimization solution in single-objective optimization problem, there are often a set of the optimization solutions in multiobjective optimization problem. Thereby it is necessary to introduce some essential definitions regarding the multiobjective optimization [30]. These definitions are mostly from the aspect of variables.

Definition 1

(Pareto dominance) A multiobjective minimization problem with m decision variables (parameters) and n objectives can be formulated as follows:

$$\begin{aligned} \hbox {Minimize}&\quad \vec {y}=\vec {f}\left( \vec {x}\right) =\left( f_1 \left( \vec {x}\right) ,\ldots ,f_n \left( \vec {x}\right) \right) \nonumber \\ \hbox {where}&\quad \vec {x}=(x_1 ,\ldots ,x_m )\in X\nonumber \\&\quad \vec {y}=(y_1 ,\ldots ,y_n )\in Y \end{aligned}$$

(7)

and where $\vec {x}$ is decision vector, X is parameter space, $\vec {y}$ is objective vector, and Y is objective space. A decision vector $\vec {a}\in X$ is said to dominate a decision vector $\vec {b}\in X$, denoted as $\vec {a}\prec \vec {b}$, if and only if

$$\begin{aligned}&\forall i\in \left\{ {1,\ldots ,n} \right\} ,f_i \left( \vec {a}\right) \le f_i \left( \vec {b}\right) \quad \hbox { and}\quad \nonumber \\&\quad \exists j\in \left\{ {1,\ldots ,n} \right\} ,f_j \left( \vec {a}\right) <f_j \left( \vec {b}\right) \end{aligned}$$

(8)

Definition 2

(Pareto optimality) The decision vector $\vec {a}$ is said to be nondominated regarding a set $X^{\prime }\subseteq X$ if and only if there is no vector in $X{\prime }$ which dominates $\vec {a}$, as

$$\begin{aligned} \lnot \exists \vec {a}^{\prime }\in X^{\prime },\vec {a}^{\prime }\prec \vec {a} \end{aligned}$$

(9)

Besides, the decision vector $\vec {a}$ is Pareto-optimal if and only if $\vec {a}$ is nondominated regarding X.

Definition 3

(Pareto optimal set) The set $X^{\prime }$ is called a global Pareto-optimal set if and only if $\forall \vec {a}^{\prime }\in X^{\prime }, \lnot \exists \vec {a}\in X,\vec {a}\prec \vec {a}^{\prime }$. We can define it as

$$\begin{aligned} \rho ^{{*}}=\left\{ {\vec {a}^{\prime }\in X^{\prime }\left| {\lnot \exists \vec {a}\in X,\vec {a}\prec \vec {a}^{\prime }} \right. } \right\} \end{aligned}$$

(10)

The Pareto optimal set is a set of parameters and the corresponding set of objective vectors is denoted as “Pareto-optimal front”.

3.2 Systematic analysis of penalty function method and multiobjective optimization technique

As the aforementioned definitions in multiobjective optimization technique can be described in the form of penalty function method, the relationship between them can be analyzed as follows.

For the given $\lambda ,\delta >0$, let the evaluation function L in the penalty function method as

$$\begin{aligned} L\left( \vec {x}_i ,\lambda ,\delta \right) =f\left( \vec {x}_i\right) +\lambda G\left( \vec {x}_i ,\delta \right) \quad i=1,2,\ldots ,\textit{NP} \end{aligned}$$

(11)

where $\vec {x}_i$ is the NP n-dimensional real-valued vectors of the population as defined in (2), $\lambda$ is the penalty parameter, $\delta$ is the tolerance value for the equality constraints, f is the objective function and G is the real-valued penalty function.

As $\delta$ can be supposed as a constant, the effect of $\lambda$ is mainly concerned. The formula (11) can be transformed as

$$\begin{aligned} L\left( \vec {x}_i ,\lambda \right) =f\left( \vec {x}_i\right) +\lambda G\left( \vec {x}_i\right) \quad i=1,2,\ldots ,\textit{NP} \end{aligned}$$

(12)

Given two population members, $\vec {x}_s$ and $\vec {x}_t$, where s and t are randomly selected from [1, NP] and satisfying: $s\ne t$, the difference between their evaluation function values is:

$$\begin{aligned} \Delta \left( \vec {x}_s ,\vec {x}_t ,\lambda \right)= & {} L\left( \vec {x}_s ,\lambda \right) -L\left( \vec {x}_t ,\lambda \right) \nonumber \\= & {} \left[ f\left( \vec {x}_s\right) +\lambda G\left( \vec {x}_s\right) \right] -\left[ f\left( \vec {x}_t\right) +\lambda G\left( \vec {x}_t\right) \right] \nonumber \\= & {} \left[ f\left( \vec {x}_s\right) -f\left( \vec {x}_t\right) \right] +\lambda \left[ G\left( \vec {x}_s\right) -G\left( \vec {x}_t\right) \right] \nonumber \\ \end{aligned}$$

(13)

We define $\Delta f_{st} =f(\vec {x}_s )-f(\vec {x}_t ),\Delta G_{st} =G(\vec {x}_s )-G(\vec {x}_t )$, then formula (13) can be written as:

$$\begin{aligned} \Delta \left( \vec {x}_s ,\vec {x}_t ,\lambda \right) =\Delta f_{st} +\lambda \cdot \Delta G_{st} \end{aligned}$$

(14)

According to the definition, $\Delta f_{st} \ne \pm \infty$ and $\Delta G_{st} \ne \pm \infty$.

The multiobjective optimization technique converts a COP into a biobjective or multiobjective optimization problem, for the sake of clarity, let $\vec {f}(\vec {x})=(\vec {f}_1 (\vec {x}),\vec {f}_2 (\vec {x}))=(f(\vec {x}),G(\vec {x}))$

By employing the aforementioned definitions and the form of penalty function, we obtain the following conclusions:

Theorem 1

$\vec {x}_s \prec \vec {x}_t \Leftrightarrow \forall \lambda >0,L\left( \vec {x}_s ,\lambda \right) <L\left( \vec {x}_t ,\lambda \right)$.

Proof

As mentioned above, $\forall \lambda >0,L(\vec {x}_s ,\lambda )<L(\vec {x}_t ,\lambda )$ is equal to $\forall \lambda >0,\Delta f_{st} +\lambda \cdot \Delta G_{st} <0$.

The sufficient condition can be easily proved.

From the definition of dominance, if$\vec {x}_s \prec \vec {x}_t$, then $\Delta f_{st} \le 0$, $\Delta G_{st} \le 0$, and $\Delta f_{st}$ and $\Delta G_{st}$ can’t be equal to 0 simultaneously.

The conclusion $\forall \lambda >0,\Delta f_{st} +\lambda \cdot \Delta G_{st} <0$ is obtained.

Next, we prove the necessary condition.

From $\forall \lambda >0,\Delta f_{st} +\lambda \cdot \Delta G_{st} <0$, we can conclude:

$$\begin{aligned} \Delta G_{st} <-\frac{\Delta f_{st} }{\lambda } \end{aligned}$$

(15)

Let us define $A=-\frac{\Delta f_{st} }{\lambda }$, then $\Delta G_{st} <A$.

For the different properties of $\Delta f_{st}$, there are three different cases.

• (1) $\Delta f_{st} >0$: in this case, $A<0$, $\Delta G_{st}<A<0$. When $\lambda \rightarrow 0^{+}$, then $A\rightarrow -\infty$, and $\Delta G_{st} =-\infty$, which contradicts the previous assumption.

• (2) $\Delta f_{st} =0$: in this case, A=0, $\Delta G_{st} <0$.

• 3) $\Delta f_{st} <0$: in this case, $A>0$, $\Delta G_{st} <A$. When $\lambda \rightarrow +\infty$, then $A\rightarrow 0^{+}$, and $\Delta G_{st} \le 0$,

In general, $\Delta f_{st} \le 0, \Delta G_{st} \le 0$, and $\Delta f_{st}$ and $\Delta G_{st}$ are not equal to 0 simultaneously. So the conclusion $\vec {x}_s \prec \vec {x}_t$ is obtained.

Likewise, we can get two related theorems as follows.

Theorem 2

$\vec {x}_s$ nondominates $\vec {x}_t \Leftrightarrow \exists \lambda >0,L(\vec {x}_s ,\lambda )\ge L(\vec {x}_t ,\lambda )$.

Proof

As mentioned above, $\exists \lambda >0,L(\vec {x}_s ,\lambda )\ge L(\vec {x}_t ,\lambda )$ is equal to $\exists \lambda >0,\Delta f_{st} +\lambda \cdot \Delta G_{st} \ge 0$

$\vec {x}_s$ nondominates $\vec {x}_t$

$\Leftrightarrow \exists i,f_i (\vec {x}_s )>f_i (\vec {x}_t )$ or $\forall i,f_i (\vec {x}_s )=f_i (\vec {x}_t )$ (where $i=1,2$) $\Leftrightarrow f(\vec {x}_s )>f(\vec {x}_t )$ or $G(\vec {x}_s )>G(\vec {x}_t )$, or $f(\vec {x}_s )=f(\vec {x}_t )$ and $G(\vec {x}_s )=G(\vec {x}_t )$.

Let us first prove the sufficient condition.

From the definition of nondominated, if $\vec {x}_s$ nondominates $\vec {x}_t$, then $\Delta f_{st} >0$, or$\Delta G_{st} >0$, or $\Delta f_{st} =\Delta G_{st} =0$.

Then four cases are listed as follows.

• (1) $\Delta f_{st}>0, \Delta G_{st} >0$: in this case, $\Delta f_{st} +\lambda \cdot \Delta G_{st} \ge 0$ holds for $\forall \lambda >0$.

• (2) $\Delta f_{st} >0,\Delta G_{st} \le 0$: if $\Delta G_{st} =0$, then the inequality $\Delta f_{st} +\lambda \cdot \Delta G_{st} \ge 0$ holds; else suppose$\frac{\Delta f_{st} }{-\Delta G_{st} }=\eta \ge \lambda >0$, then the inequality holds.

• (3) $\Delta f_{st} \le 0,\Delta G_{st} >0$: suppose $\frac{-\Delta f_{st} }{\Delta G_{st} }=\eta \ge \lambda >0$, then the inequality holds.

• (4) $\Delta f_{st} =\Delta G_{st} =0$: the conclusion $\Delta f_{st} +\lambda \cdot \Delta G_{st} \ge 0$is obtained.

Next, we prove the necessary condition.

The main aim is to find out the relationship of $\Delta f_{st}$ and $\Delta G_{st}$ under the conditions.

For the different properties of $\Delta G_{st}$, there are three different cases.

• (1) $\Delta G_{st} >0$: in this case, $\lambda \ge -\frac{\Delta f_{st} }{\Delta G_{st} }=\eta$ holds for any $\Delta f_{st}$, and in this situation, $\vec {x}_s$ nondominates $\vec {x}_t$ (as cases 1 and 3 in the previous part);

• (2) $\Delta G_{st} =0$: in this case,$\Delta f_{st} \ge 0$, then $\vec {x}_s$ nondominates $\vec {x}_t$ (as cases 2 and 4 in the previous part);

• (3) $\Delta G_{st} <0$: in this case, $\lambda \le -\frac{\Delta f_{st} }{\Delta G_{st} }=\eta , \Delta f_{st} >0$, then $\vec {x}_s$ nondominates $\vec {x}_t$ (as case 2 in the previous part).

In general, $\Delta G_{st} >0$, or $\Delta G_{st} =0$ and $\Delta f_{st} \ge 0$, or $\Delta G_{st} <0$ and $\Delta f_{st} >0$. So the conclusion $\vec {x}_s$ nondominates $\vec {x}_t$ is obtained.

To expand the individuals to a set, then Theorem 3 is obtained.

Theorem 3

$$\begin{aligned} \rho ^{*}= & {} \left\{ {\vec {x}_s \in X^{\prime }|\lnot \exists \vec {x}_t \in X,\vec {x}_t \prec \vec {x}_s } \right\} \\\Leftrightarrow & {} \left\{ {\vec {x}_s \in X^{\prime }|\forall \vec {x}_t \in X,\exists \lambda >0,L\left( \vec {x}_t ,\lambda \right) \ge L\left( \vec {x}_s ,\lambda \right) } \right\} \end{aligned}$$

3.3 Systematic analysis of penalty function method and Deb’s feasibility-based rule

As analyzed in [31], Deb’s feasibility-based rule corresponds to one special case of penalty function method when penalty parameter is large enough (i.e., larger than $\lambda _{\max }$) for the following reason:

• (1) For the feasible situation, both methods have the same effect on ranking due to the fact that only objective function values are used for ranking.

• (2) For the infeasible and semi-feasible situations, when $\lambda >\lambda _{\max }$, the two methods have the same effect on ranking the whole population. While, when $\lambda <\lambda _{\max }$, these two methods present different effect on ranking. Here, $\lambda _{\max }$ is determined by the current solutions.

Fig. 1

The corresponding rule for penalty parameter $\lambda$

Table 1 Details of the benchmark functions

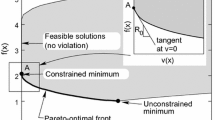
The general results can be illustrated in Fig.1, where A_1, A_2, B_1, B_2 are four rules for comparing feasible and infeasible solutions. A_1, B_1 stands for Deb’s feasibility-based rule.

4 Comparison of different CHTs in different situations

To fully compare the effect of different CHTs on different situations, two experiments, will be carried out. One is under the infeasible situation while the other one is under the semi-feasible situation. All our experiments are based on the benchmark functions in [32]. The details of these benchmark functions and the classifications (which takes some idea from [22]) are presented in Tables 1 and 2 respectively.

Table 2 Classification of benchmark functions based on the number of decision variables and the type of objectives and constraints

To make fair comparison, all CHTs will be compared under the same circumstance (i.e., with the same initial solutions and the same setting of DE).

The average method (which divides the range of each independent variable equally) is adopted to generate the initial solutions. 15 out of 22 benchmark functions are in the infeasible situation. As the rest seven benchmark functions are not enough to analyze the characteristics of CHT in the semi-feasible situation, we adopt the other 15 benchmark functions with the semi-feasible situation. Deb’s feasibility-based rule is applied to the 15 benchmark functions to get at least a feasible solution (i.e., semi-feasible situation).

Therefore, 15 and 22 benchmark functions are used in experiment 1 and experiment 2 respectively for comparison. The experimental results are listed in Tables 3 and 4.

Table 3 Comparison of different CHTs in infeasible situation

Table 4 Comparison of different CHTs in semi-feasible situation

The Deb’s feasibility-based rule [5] and multi-objective optimization technique without any variants [12] are used here.

4.1 Comparison under infeasible situation

In this situation, both Deb’s feasibility-based rule and multiobjective optimization technique can always find the feasible solutions. This is because that these two methods take the constraint violation as a metric for evaluation (i.e., comparing the constraint violation directly).

Multi-objective optimization technique shows a better performance in g03, g05, g15, g16, g17, g21 and g23 while Deb’s feasibility-based rule performs better in g06, g07 and g18. They show similar performance in other functions.

Considering the problem characteristics, it indicates that if equality constraints are involved, multiobjective optimization technique is preferred; otherwise, Deb’s feasibility-based rule is preferred.

4.2 Comparison under semi-feasible situation

In this experiment, multiobjective optimization technique performs better than Deb’s feasibility-based rule in most test functions, especially in g03, g05, g06, g10 and g14. However, it performs worse than Deb’s feasibility-based rule in g08.

All these two CHTs have the same or similar performance in g04, g07, g08, g09, g12, g16, g18, g19 and g24 with the known optimal value reached. It is worthy noting that multiobjective optimization technique needs less fitness evaluations (FES) comparing with Deb’s feasibility-based rule.

It also should be pointed out that these two CHTs can not find the optimal solutions in g13, g21 and g23.

Considering the problem characteristics, Deb’s feasibility-based rule performs better in solving problems with inequality constraints and the nonlinear objective function’s type; multiobjective optimization technique performs better in the other types of problems.

4.3 General conclusion

We can conclude that different CHTs can solve different problems effectively in corresponding situations. These conclusions can be generalized as follows.

• (1) For the infeasible situation, Deb’s feasibility-based rule and multiobjective optimization technique can effectively solve problems with only inequality constraints and the others respectively.

• (2) For the semi-feasible situation, Deb’s feasibility-based rule and multiobjective optimization technique can effectively solve problems with inequality constraints with nonlinear objective function and the other types of problems respectively.

• (3) For the feasible situation, these CHTs have the same performance as there is no constraint violation considered.

This conclusion forms a good basis for combining promising aspects of different CHTs on different problems into a new approach, as demonstrated in next section.

5 Combined constraint handling framework (CCHF)

As mentioned in Sect. 4, different CHTs have different effects on solving different problems in different situations. Based on this, a generalized CCHF is proposed.

Fig. 2

Illustration of the basic idea

The basic idea of the combining strategy, the framework of CCHF and the implementation of the corresponding CHT choosing are illustrated in Figs. 2, 3 and 4 respectively.

As shown in Fig. 2, in the infeasible and semi-feasible situation, both Deb’s feasibility-based method and multiobjective method are ready in the CHT pools. During an evolution, the problem characteristics will determine which CHT will be adopted, as shown in Fig. 4. After choosing the corresponding CHT, the population will be ranked and the best NP individuals will be selected to form the next population.

It is important to note that as to the multiobjective method, different pareto front levels will be used to help select the best individuals.

Fig. 3

Framework of CCHF

Fig. 4

Implementation of the corresponding CHT choosing

It should be pointed out that CCHF can also be seen as an ensemble method, in which the problem characteristics and different situations are considered when designing the corresponding relationship. This makes it different from other ensemble methods, such as ECHT [11], DECV [22], and other methods based on these three situations, such as ICDE [16], CMODE [7].

Table 5 Results of CCHF, including best, median, worst, mean and standard deviation values

6 Experimental study

6.1 Experimental settings

As mentioned in Sect. 4, 22 benchmark functions [32] were used in our experiment. The details of these benchmark functions are reported in Table 1, where n is the number of decision variables, $\rho ={| F|}/{|S|}$ is the estimated ratio between the feasible region and the search space, LI, NI, LE, NE is the number of linear inequality constraints, nonlinear inequality constraints, linear equality constraints and nonlinear equality constraints respectively, a is the number of active constraints at the optimal solution and $f(\vec {x}^{{*}})$ is the objective function value of the best known solution. These benchmark functions are also classified into different groups as shown in Table 2.

The parameters in DE are set as follows [7]: the population size (NP) is set to 100; the scaling factor (F) is randomly chosen between 0.5 and 0.6, and the crossover control parameter (Cr) is randomly chosen between 0.9 and 0.95. The same settings of these CHTs were used as in Sect. 4 to keep consistency.

6.2 Experimental results

Twenty-five independent runs were performed for each test function using $5\times 10^{5}$ FES at maximum, as suggested by Liang et al. [32]. Additionally, the tolerance value $\delta$ for the equality constraints was set to 0.0001.

Fig. 5

Convergence graph for g01–g04

Table 5 lists the results of CCHF, including best, median, worst, mean, standard deviation values, the feasible rate (the percentage of runs where at least one feasible solution is found in MAX_FES, denoted as FR), the success rate (the percentage of runs where the algorithm finds a solution that satisfies the success condition, denoted as SR). Here, the success condition is $f(\vec {x})-f(\vec {x}^{*})\le 0.0001$ and $f(\vec {x})$ is feasible. The results show that CCHF can always find feasible solutions in all functions, but it can not get the known optimal values in g13, g17, g21 and g23. The mainly reason is that this CCHF takes the simplest form of the CHTs. And the main purpose of CCHF is to illustrate the practicability of the idea.

Fig. 6

Convergence graph for g05–g08

The convergence graphs of $\log (f(\vec {x})-f(\vec {x}^{{*}}))$ over FES at the best run are plotted in Figs. 5, 6, 7, 8, 9 and 10. Since test functions g13, g17, g21 and g23 can not reach the optimal value, their convergence graphs are plotted in Fig. 10.

As shown in Figs. 5, 6, 7, 8 and 9, all test functions (except g02 and g08), can reach the error accuracy level with −20 with <2 $\times$ 10$^{5}$ FES. The test functions g02 and g08 can reach the error accuracy level with −15. It is also important to note that g11 and g12 can reach the optimal value at the first generation.

As to Fig. 10, these test functions can not get the optimal values, with the error accuracy level with −1 to −3. The main reason is also the simple form of CHTs.

Fig. 7

Convergence graph for g09–g12

Fig. 8

Convergence graph for g14–g16

Fig. 9

Convergence graph for g18, g19, and g24

Fig. 10

Convergence graph for g13, g17, g21, and g23

6.3 Comparison with some state-of-the-art approaches

In this part, five latest “dynamic” or “ensemble” approaches: COMDE [33], DECV [22], DSS-MDE [13], ATMES [12], and ECHT [11], are selected to compare with CCHF.

Table 6 presents the statistically results of t test (h values) for the different approaches. Numerical values −1, 0, 1 represent that CCHF is inferior to, equal to and superior to other approaches respectively.

Table 6 Comparison of CCHF with state-of-the-art “dynamic” or “ensemble” approaches

CCHF performs better than the other five approaches in g01, g02, g07 and g10, and it presents a worse performance in g06 and g13 than the other five approaches. All the six approaches have the same or similar performance in g04, g08 and g12.

As for g03 and g09, CCHF performs similar with DSS-MDE and ECHT-EP, DSS-MDE, COMDE and DECV, but superior than the other algorithms. As for g05 and g11, CCHF performs similar with COMDE and ATMES, ATMES and DECV respectively, but inferior to the other approaches.

Overall, CCHF is superior to, equal to and inferior to other approaches in 25, 25 and 15 cases, respectively out of the 65 cases. The worse cases are mainly from g06 and g13.

Therefore, CCHF shows a comparable overall performance with the other five approaches. This also verifies the effectiveness of the proposed method in solving COPs.

7 Conclusion

In this paper, a CCHF, which combines promising aspects of different CHTs in different situations with consideration of problem characteristics, was proposed, implemented, and validated. The presented work is distinguished in three scientific contributions. First, the relationship between problem characteristics and CHTs, and the relationship between different CHTs were analyzed; second, the CCHF was developed based on the analysis; third, the 22 benchmark functions collected on constrained real-parameter optimization were utilized to verify the effectiveness of the newly developed CCHF.

The results show that CCHF is comparable to the other five dynamic or ensemble state-of-the-art approaches for constrained optimization, especially when considering that CCHF is simple and easy to realize due to adoption of only the basic CHTs without any variants in this framework.

The problem characteristics summarized in this paper are based on the benchmark functions, but as Z. Michalewicz concluded [17], there is no comparison in terms of complexity between real-world problems and toy problems, and real-world applications usually require hybrid approaches where an ‘evolutionary algorithm’ is loaded with non-standard features, so how to apply these conclusions to the real-world problems is still challenging and will be our future work.