Swarm based mean-variance mapping optimization for convex and non-convex economic dispatch problems

Abstract

In power system generation, the economic dispatch (ED) is used to allocate the real power output of thermal generating units to meet the required load demand so as the total cost of thermal generating units is minimized. This paper proposes a swarm based mean-variance mapping optimization $(\hbox {MVMO}^{S})$ for solving the ED problems with convex and nonconvex objective functions. The proposed method is the extension of the original single particle mean-variance mapping optimization by initializing a set of particles. The special feature of the proposed method is a mapping function applied for the mutation based on the mean and variance of n-best population. The proposed $\hbox {MVMO}^{S}$ is tested on various systems and the obtained results are compared to those from many other optimization methods in the literature. Test results have shown that the proposed method can obtain better solution quality than the other methods. Therefore, the proposed $\hbox {MVMO}^{S}$ is a potential method for efficiently solving the convex and nonconvex ED problems in power systems.

1 Introduction

The economic dispatch (ED) is one of the power management tools that is used to determine real power output of thermal generating units to meet required load demand. The ED results in minimum fuel generation cost, minimum transmission power loss while satisfying all units, as well as system constraints [1, 2].

The ED problems may be generally classified into convex and nonconvex optimization problem based on the nature characteristic of the generating units. In the convex ED, the operation cost function is usually approximated by quadratic function. However, the objective function of the ED is more accurate when the cubic function is considered to express the input-output characteristics of thermal generators. Several methods are proposed in the literature for solving ED with cubic fuel cost function such as iterative dynamic programming (DP) [3], Newton approach [4], genetic algorithm (GA) [5] particle swarm optimization (PSO) [6], $\lambda$-logic based algorithm [7, 8] and firefly algorithm (FA) [9]. The ED problem can be represented more exactly by considering various nonconvex elements and nonlinearities in the objective function and constraints such as valve point effects, prohibited operating zones, ramp rate limits and spinning reserve. These effects can cause the input-output curve of thermal generators to become more complicated. For this reason, the practical ED problem should be formulated with a nonconvex objective function which is difficult to find global solution. Many heuristic search approaches are presented in the literature for solving the nonconvex ED problems such as hopfield neural network (HNN) [10–12], genetic algorithm (GA) [13–15], evolutionary programming (EP) [16], evolutionary algorithm (EA) [17], simulated annealing (SA) [18], artificial bee colony (ABC) [19], evolutionary algorithm [17], artificial immune system (AIS) [20], biogeography-based optimization (BBO) [21], and differential evolution (DE) [22, 23], particle swarm optimization (PSO) [24, 25]. Recently, PSO is the most popular method applied for solving the ED problems, especially for nonconvex problems. Several improvements of PSO method are developed for solving the ED problems such as self-organizing hierarchical PSO (SOH_PSO) [26], simulated annealing like particle swarm optimization (SA-PSO) [27], pseudo-gradient based particle swarm optimization (PGPSO) [2], new PSO with local random search (NPSO-LRS) [28], new adaptive particle swarm optimization (NAPSO) [29], Chaotic particle swarm optimization (CPSO) [30]. These improved PSO methods can obtain high quality solutions for the problem. The PSO method is continuously improved for dealing with large-scale and complex problems such as in [31, 32]. Although, heuristic search methods can deal with complex optimization problems, their search ability often provides near global optimal solution. The nonconvex ED problems have been also solved by many hybrid optimization methods such as hybrid approach based on sequential combination of GA and active power optimization (APO) using Newton’s second order approach (GA-APO, NSOA) [33], self-adaptive differential evolution with augmented Lagrange multiplier method (SADE-ALM) [34], integrated artificial intelligence (ETQ) [35], bacterial foraging optimization with Nelder –Mead algorithm (Adaptive BF with NM) [36]. These hybrid methods become powerful search methods for obtaining higher solution quality due to using the advantages of each element method to improve their search ability for the complex problems. However, the hydrid methods may be slower and more complicated than the single methods because of combination of several operations. The nonconvex optimization problem is still a challenge for solution methods. Hence, there is always a need for developing new techniques for solving nonconvex problems.

Recently, Mean-variance mapping optimization (MVMO) is a new meta-heuristic search algorithm which is developed by István Erlich [37]. This algorithm falls into the category of the so-called “population-based stochastic optimization technique”. The similarities between MVMO and the other known stochastic algorithms are in three evolutionary operators including selection, mutation and crossover. The extensions of MVMO is also developed by Rueda & Erlich, which named swarm based mean-variance mapping optimization $(\hbox {MVMO}^{S})$ [38]. Unlike the single particle MVMO, the search process of $\hbox {MVMO}^{S}$ is started with a set of particles. In addition, two parameters of MVMO including the scaling factor and variable increment parameters have been extended to enhance the mapping. Hence, the ability for global search of $(\hbox {MVMO}^{S})$ is more effective than the original version. The $\hbox {MVMO}^{S}$ has been successfully implemented for solving the ED problems [39]. However, the ED was only considered as nonconvex problem which takes into account valve-point effects, multiple fuel options and prohibited operating zones. In this paper, the $\hbox {MVMO}^{S}$ is proposed as a new method for solving the ED problems in general. Both convex and nonconvex ED problems are considered in this study. For convex ED problem, the cubic fuel cost function is considered beside the quadratic fuel cost function which is the basic ED problem. For nonconvex ED problem, besides the formulated ED problems in [39], we have proposed a new problem which combines prohibited operating zones with valve-point loading effects. Moreover, the spinning reserve constraint and large-scale test systems have been proposed for the ED problem with prohibited operating zones which were not mentioned in [39]. The proposed $\hbox {MVMO}^{S}$ is tested on several convex and nonconvex systems and the obtained results are compared to those from many other methods in the literature. The comparisons have shown that the $\hbox {MVMO}^{S}$ method is more effective and provides better solution quality than the other methods in the literature for the problem in terms of optimal solution, especially for large-scale systems. Therefore, the $\hbox {MVMO}^{S}$ is a favorable method for solving the ED problems.

The remaining organization of this paper is as follows. Section 2 presents the formulation of the ED including convex and nonconvex problems. Handling of constraints and implementation of the proposed $\hbox {MVMO}^{S}$ to ED problem are addressed in Sect. 3. Section 4 reports results of the proposed $\hbox {MVMO}^{S}$ method. A number of case studies using standard test systems are used to test the proposed method. The comparisons of results between the proposed method and existing methods are also carried out in this section. The discussion is followed in Sect. 5. After all, the conclusion is given.

2 Problem formulation

2.1 Convex economic dispatch problem

The objective function of the ED problem is to minimize the total production cost, which be written as:

$$\begin{aligned} Minimize \, F_T =\sum _{i=1}^N {F_i } (P_i)\qquad i=1,2,\ldots ,N \end{aligned}$$

(1)

Mathematically, the fuel cost of a thermal generation unit is represented as quadratic function [1]:

$$\begin{aligned} F_i (P_i )=a_i +b_i P_i +c_i P_i^2 \end{aligned}$$

(2)

The solution of ED can be highly improved by introducing higher order generator cost functions. Cubic cost function displays the actual response of thermal generators more accurately. The cubic fuel cost function of a thermal generating unit is represented as follows [4]:

$$\begin{aligned} F_i (P_i )=a_i +b_i P_i +c_i P_i^2 +d_i P_i^3 \end{aligned}$$

(3)

subject to

Real power balance equation The total active power output of generating units must be equal to total power load demand plus power loss:

$$\begin{aligned} \sum _{i=1}^N {P_i } =P_D +P_L \end{aligned}$$

(4)

where the power loss $P_{L}$ is calculated by the below formulation [1]:

$$\begin{aligned} P_L =\sum _{i=1}^N {\sum _{j=1}^N {P_i B_{ij} P_j } } +\sum _{i=1}^N {B_{0i} P_i } +B_{00} \end{aligned}$$

(5)

Generator capacity limits The active power output of generating units must be within the allowed limits:

$$\begin{aligned} P_{i,\min } \le P_i \le P_{i,\max } \end{aligned}$$

(6)

2.2 Nonconvex economic dispatch problems

2.2.1 ED problem with valve point effects

The valve point effects (VPE) is considered as practical operation of thermal generating units. When each steam valve in a turbine of the thermal unit starts to open, produces a rippling effect on the input-output curve. The ripples are shown in Fig. 1. The VPE makes the fuel cost function highly nonlinear and having multiple local optimum. The fuel cost function is described as the superposition of sinusoidal functions and quadratic functions. The model of ED problem with VPE is formulated as follows [2]:

$$\begin{aligned} F_i (P_i )=a_i +b_i P_i +c_i P_i^2 +\left| {e_i \sin (f_i (P_{i,\min } -P_i ))} \right| \end{aligned}$$

(7)

subject to the real power balance constraint in Eq. (4) and generator capacity limits in Eq. (6).

2.2.2 ED problem with prohibited operating zones

The prohibited operating zones (POZ) are the range of output power where the thermal generating unit must avoid operating because it causes undue vibration of the turbine shaft and might bring damage to the shaft and bearings. The cost curve function of units with prohibited zones is described in Fig. 2 [2].

Fig. 1

Fuel cost curve of units with valve-point effects

Fig. 2

Fuel cost curve of units with prohibited zones

The objective function for the ED problem with POZ can be a quadratic function in Eq. (2) or a quadratic function with VPE in Eq. (7). For units without POZ, only the equality constraint in Eq. (4) and inequality constraint in Eq. (6) are considered. As for units operating with POZ, more constraints are added to the constraints mentioned above as follows:

Prohibited operating zone constraint The feasible operating points should be located at one of the sub-regions as follows [2]:

$$\begin{aligned} P_i \in \left\{ {\begin{array}{l} P_{i,\min } \le P_i \le P_{i1}^l \\ P_{ik-1}^u \le P_i \le P_{ik}^l \hbox {, }k=2,\ldots ,n_i \hbox { } \\ P_{in_i }^u \le P_i \le P_{i,\max } \\ \end{array}} \right. \end{aligned}$$

(8)

Spinning reserve constraint The spinning reserve constraint for all units is defined as [17]:

$$\begin{aligned} \sum _{i=1}^N {S_i } \ge S_R \end{aligned}$$

(9)

where the operating margin of each unit Si is determined by:

$$\begin{aligned} S_i= & {} \min \left\{ {P_{i,\max } -P_i ,S_{i,\max } } \right\} ;\hbox { }\forall i\notin \Omega \end{aligned}$$

(10)

$$\begin{aligned} S_i= & {} 0;\quad \forall i\in \Omega \end{aligned}$$

(11)

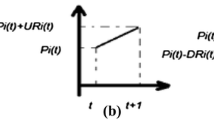
Ramp rate limit constraints The increased or decreased power output of a unit from its initial operating point to the next one should not exceed its ramp up and down rate limits. The ramp rate constraints are determined by [2]:

$$\begin{aligned} P_i -P_{i0} \le UR_i , \hbox {if generation increases}\end{aligned}$$

(12)

$$\begin{aligned} P_{i0} -P_i \le DR_i , \hbox {if generation decreases} \end{aligned}$$

(13)

To handle the ramp rate limits, the highest and lowest possible power outputs of units are determined based on their power output limits, the generator capacity limits in Eq. (6) can be rewritten as follows [2]:

$$\begin{aligned} \max (P_{i,\min } ,P_{i0} -DR)\le P_i \le \min (P_{i,\max } ,P_{i0} +UR) \end{aligned}$$

(14)

3 $\hbox {MVMO}^{S}$ for ED problems

3.1 $\hbox {MVMO}^{S}$

$\hbox {MVMO}^{S}$ is an extension of the original version MVMO. The difference between MVMO and $\hbox {MVMO}^{S}$ is the initial search process with particles. MVMO starts the search with single particle while $\hbox {MVMO}^{S}$ starts the search with a set of particles. MVMO is extended to two parameters: the scaling factor $f_{s}$ and variable increment$\Delta d$parameter to enhance its mapping. Therefore, the global search ability of the $\hbox {MVMO}^{S}$ is strengthened. The detail of $\hbox {MVMO}^{S}$ algorithm is described in [38].

3.2 Calculation of power output for slack unit

Slack variable method is usually used for handling equality constraints in optimization problems where the value of variables is calculated from the others based on the equality constraints [27]. This method is used for calculation of the power output for a slack unit from the power outputs of the remaining units in the system based on the power balance constraint in Eq. (4). The power output of the slack unit is as follows:

$$\begin{aligned} P_s =P_D +P_L -\sum _{\begin{array}{l} i=1 \\ i\ne s \\ \end{array}}^N {P_i } \end{aligned}$$

(15)

Equation (15) represents the calculation of slack unit s which is randomly selected from the available N units and the limit violations of the slack unit will be penalized in the fitness function in Eq. (18). The first unit of all test system is selected as slack unit in this paper.

3.3 Implementation of $\hbox {MVMO}^{S}$ to ED

3.3.1 Initialization of algorithm

The parameters for $\hbox {MVMO}^{S}$ have to be initialized including $iter_{max}$, n_var, n_par, mode, $d_{i}, \Delta d_0^{\mathrm{ini}} , \Delta d_0^{\mathrm{final}}$, archive zize ($n), f_{s\_ini}^*,f_{s\_\mathrm{final}}^*$, n_randomly,n_randomly_min, indep.runs $(m), D_{min.}$.

3.3.2 Normalization and de-normalization of variables

In the proposed $\hbox {MVMO}^{S}$ method, each particle represents a solution. A set of particles is used for finding best solution for the problem. The initial optimization variables are normalized to the [0,1] bound as follows:

$$\begin{aligned} x\_normalized = rand(n\_par, n\_var) \end{aligned}$$

(16)

The search space of the algorithm is always restricted inside the [0,1] range. However, the function evaluation is carried out in the original scales [$P_{i,min}, P_{i,max}$]. The denormalization of the optimization variables is carried as follows:

$$\begin{aligned} P_{i} = P_{i,min}+(P_{i,max} - P_{i,min}). x\_normalized(\iota ,:) \end{aligned}$$

(17)

This initial solution is further checked for POZ violation. If the violation is found, the repairing strategy in [2] is used to move the operating point to a feasible region. After that, the power output for the slack generator is calculated by using Eq. (15). The fitness function includes the objective function in Eq. (1), penalty terms for the slack unit if the generator capacity limits constraint in Eq. (6) is violated and the penalty terms for spinning reserve constraint in Eq. (9). The fitness function $F_{T}$ to be minimized for the considered problem is calculated as follows:

$$\begin{aligned} F_T= & {} \sum _{i=1}^N {F_i (P_i )} + K_s .[ ( {\max (0,P_s -P_{s,\max } )} )\nonumber \\&+\,( {\max (0,P_{s,\min } -P_s )}) ] \nonumber \\&+ \,K_p .\max \left( {0,S_R -\sum _{i=1}^N {S_i } } \right) \end{aligned}$$

(18)

where $K_{s}$ and $K_{p}$ are the penalty factor for the slack unit and spinning reserve constraint, respectively.

$\hbox {MVMO}^{S}$ utilizes swarm implementation to enhance the power of global searching of the classical MVMO by starting the search process with a set of particles, each having its own memory and represented by the corresponding archive and mapping function. At the beginning of the optimization process, each particle performs m steps independently to collect a set of reliable individual solutions. Then, the particles start to communicate and to exchange information. It is worthless when particles are very close to each other since this would entail redundancy. To avoid closeness between particles, the normalized distance of each particle’s local best solution $x^{lbest,i}$ to the global best $x^{gbest}$ is calculated by Eq. (19). This normalized distance is employed to attempt to reduce the swarm size provided. The i-th particle is discarded from the optimization process if the distance $D_{i}$ is less than a certain user defined threshold $D_{min}$ [38]. The information exchange between particles and swarm reduction are aimed at enhancing the global search ability while avoiding redundancy in the search process.

$$\begin{aligned} D_i =\sqrt{\frac{1}{N}\sum _{j=1}^N \left( x_j^{gbest} - x_j^{lbest,i} \right) ^{2}} \end{aligned}$$

(19)

3.3.3 Solution archive

The best fitness and variables are stored in the archive table which is described as Fig. 3. The archive size (n) is taken to be a minimum of two. The table of best individuals is filled up progressively over iterations in a descending order of the fitness. When the table is filled with n members, an update is performed only if the fitness of the new population is better than those in the table.

Fig. 3

The archive is used to store n-best population

Mean ${\bar{x}}_{i }$ and variance $v_i$ are computed from the archive as follows [37]:

$$\begin{aligned} {\bar{x}}_{i }= & {} \frac{1}{n}\sum _{j=1}^n {x_i (j)}\end{aligned}$$

(20)

$$\begin{aligned} v_i= & {} \frac{1}{n}\sum _{j=1}^n {(x_i (j)-{\bar{x}}_{i } } )^{2} \end{aligned}$$

(21)

Where j goes from 1 to n (archive size). At the beginning ${\bar{x}}_{i }$ corresponds with the initialized value of $x_{i}$ and the variance $v_i$ is set to 1.

3.3.4 Offspring creation

The individual with the best fitness, $f_{best}$, and its corresponding optimization values, $x_{best}$, are stored in the memory of the parent population for that iteration. This parent is used for creation of the next offspring. Three common evolutionary operations in offspring creation are: selection, mutation and crossover operators.

Selection

Among N variables of the optimization problem, d variables are selected for mutation operation. There are four strategies which are described in [37] for selecting the variables.

Mutation

For each of the d selected dimension, mutation is used to assign a new value of that variable. Given a uniform random number $x_i^*\in$ [0,1], the transformation of $x_i^*$ to $x_i$ via mapping function is calculated in Eq. (22) and depicted as Fig. 4. The transformation mapping function, h, is calculated by the mean $\bar{x}$ and shape variables $s_{i1}$ and $s_{i2}$ as in Eq. (24) [37]:

$$\begin{aligned} x_i =h_x +(1-h_1 +h_o ).x_i^*-h_o \end{aligned}$$

(22)

where $h_{x}, h_{1}, h_{0}$ are the outputs of transformation mapping function in Eq. (24) based on different inputs given by [37]:

$$\begin{aligned}&h_x =h(x=x_i^*), h_o =h(x=0), h_1 =h(x=1)\end{aligned}$$

(23)

$$\begin{aligned}&h({\bar{x}}_{i },s_{i1} ,s_{i2} ,x)={\bar{x}}_{i } .(1{-}e^{-x.s_{i1} })+(1{-}{\bar{x}}_{i } ).e^{{-}(1-x).s_{i2} } \end{aligned}$$

(24)

where

$$\begin{aligned} s_i =-\ln (v_i ).f_s \end{aligned}$$

(25)

Fig. 4

Variable mapping

The scaling factor $f_{s}$ in Eq. (25) is a MVMO parameter which can be used to change the shape of the function during iteration. In $\hbox {MVMO}^{S}$, this factor is extended due to the need for exploring the search space more globally at the beginning of the iterations. At the end of the iterations, the focus should be on exploitation procedures. In [38], the factor $f_{s}$ is given as follows:

$$\begin{aligned} f_s =f_s^*.\left( {1+rand()} \right) \end{aligned}$$

(26)

where

$$\begin{aligned} f_s^*=f_{s\_\mathrm{ini}}^*+\left( {\frac{i}{i_{\mathrm{final}} }} \right) ^{2}\left( {f_{s\_\mathrm{final}}^*-f_{s\_\mathrm{ini}}^*} \right) \end{aligned}$$

(27)

In Eq. (27), $f_s^*$ denotes the smallest value of $f_{s}$ and the variable i represents the iteration number. $f_{s\_ini}^*$ and $f_{s\_{\mathrm{final}}}^*$ are the initial and final values of $f_s^*$, respectively. The recommended range of $f_{s\_ini}^*$ is from 0.9 to1.0, and range of $f_{s\_{\mathrm{final}}}^*$ is from 1.0 to 3.0. When $f_{s\_{\mathrm{final}}}^*=f_{s\_{\mathrm{ini}}}^*=1$, which means that the option for controlling the $f_{s}$ factor is not used [38]. The shape variables $s_{i1}$ and $s_{i2}$ in Eq. (24) are determined by using the following algorithm[38]:

The above procedure fully exploits the asymmetric characteristic of the mapping function by using different values for $s_{i1}$ and $s_{i2}. \Delta d_0$ is calculated in Eq. (28), this factor is allowed to decrease from 0.4 to 0.01.

$$\begin{aligned} \Delta d_0 =\Delta d_0^{\mathrm{ini}} +\left( {\frac{i}{i_{\mathrm{final}}}} \right) ^{2}\left( {\Delta d_0^{\mathrm{final}} -\Delta d_0^{\mathrm{ini}} } \right) . \end{aligned}$$

(28)

Crossover

The crossover operation is done for the remaining unmutated dimensions where the genes of the parents are inherited. In other words, the values of these unmutated dimensions are clones of the parent. Here, the crossover is done by direct cloning of certain genes. In this way, the offsprings are created by combining the vector $x_{best}$, and vector of d mutated dimensions.

3.3.5 Termination criteria

The algorithm of the proposed $\hbox {MVMO}^{S}$ is terminated when the maximum number of iterations $iter_{max}$ is reached.

3.3.6 Overall procedure

The flowchart of $\hbox {MVMO}^{S}$ is depicted in Fig. 5 [36]:

Fig. 5

The flowchart of $\hbox {MVMO}^{S}$

The steps of procedure of $\hbox {MVMO}^{S}$ for the ED problem are described as follows:

Step 1 :

Setting the parameters for $\hbox {MVMO}^{S}$ including $iter_{max}$, n_var, n_par, mode, $d_{i}, \Delta d_0^{\mathrm{ini}} , \Delta d_0^{\mathrm{final}}$, archive zize, $f_{s\_ini}^*, f_{s\_{\mathrm{final}}}^*$, n_randomly, n_randomly_min, indep.runs(m),$D_{min}$

Set $i = 1, i$ denotes the function evaluation

Step 2 :

Normalizing initial variables to the range [0,1] (i.e. swarm of particles) by using Eq. (16).

Step 3 :

Set $k = 1$, k denotes particle counters.

Step 4 :

De-normalizing variables using Eq. (17), check for POZ violation and repair,calculate power output for the slack generator using Eq. (15), evaluate fitness function in Eq. (18), store $f_{best}$ and $x_{best}$ in archive.

Step 5 :

Increase $i =i+1$. If $i < m$(independent steps), go to Step 6. Otherwise, go to Step 7.

Step 6 :

Check the particles for the global best, collect a set of reliable individual solutions. The i-th particle is discarded from the optimization process if the distance $D_{i}$ is less than a certain user defined threshold $D_{min}$. If the particle is delected, increase $k = k+1, n_{p}= n_{p}$ – 1 and go to step 4. Otherwise, go to Step 7.

Step 7 :

Create offspring generation through three evolutionary operators: selection, mutation and crossover.

Step 8 :

if $k<n_{p},$ increase $k = k+1$ and go to step 4. Otherwise, go to step 9.

Step 9 :

Check termination criteria. If stoping criteria is satisfied, stop. Otherwise, go to step 3. The algorithm of the proposed $\hbox {MVMO}^{S}$ is terminated when the maximum number of iterations $iter_{max}$ is reached.

4 Numerical results

The proposed $\hbox {MVMO}^{S}$ is mplemented to different convex and nonconvex ED problems. The $\hbox {MVMO}^{S}$ is more effective than the original MVMO in term of the global search ability [38]. For this confirmation, the single particle MVMO is also implemented to the ED problems by set the number of particles $n_{p}$ to 1. Different systems corresponding to the formulated problems are used for testing the proposed method. The implementation of the $\hbox {MVMO}^{S}$ is coded in Matlab R2013a platform and executed for 50 independent trials on a core i5-3470 CPU 3.2 GHz PC with 4GB of RAM for each case.

Table 1 Parameter setting of $\hbox {MVMO}^{S}$

4.1 Selection of parameters

Since different parameters of the proposed method have effects on the performance of $\hbox {MVMO}^{S}$. Hence, it is important to determine a set of optimal parameters of the proposed methods for dealing with ED problems. For each problem, the selection of parameters is carried out by varying only one parameter at a time while fixing the others. The parameter is first fixed at the low value and then increased. The obtained result after one run is compared to the previous one. If the obtained result after one run is considerably better than the previous one, their obtained value is chosen as the proper value. Otherwise, their value will be increased. Multiple runs are carried out to choose the suitable set of parameters. By experiments, the set of optimal parameters for each test system are shown in Table 1. The typical parameters are selected as follows:

• $iter_{max}$: maximum number of iterations depend on the scale of test systems and complexity of the problem. The maximum number of iterations is selected in the range from 2000 to 150000 iterations.

• n_var: number of optimization variables. This parameter denotes the number of generating units in system.

• n_par: number of particles is varied from 5, 10, 20, 30, 40 and 50, respectively. The number of particles is chosen by experiments for each case.

• mode : There are four variable selection strategy for offspring creation . Afer all simulations, stragy 4 (mode = 4) is suporior to the other stragy.

• $\Delta d_0^{\mathrm{ini}} , \Delta d_0^{\mathrm{final}} :$ The range of $\Delta d_0$ in Eq. (28) is [0.01 – 0.4]. By experiments, $\Delta d_0^{\mathrm{ini}}$ and $\Delta d_0^{\mathrm{final}}$ is set to 0.25 and 0.02, respectively for all cases.

• $f_{s\_ini}^*, f_{s\_{\mathrm{final}}}^*:$ The range of values of $f_{s\_ini}^*$ is from 0.9 to 1.0 and for values of $f_{s\_\mathrm{final}}^*$ is from 1.0 to 3.0. For all cases, $f_{s\_ini}^*$ is set to 0.95 in the range [0.9, 1.0] and $f_{s\_\mathrm{final}}^*$ is set to 2.5 in the in the range [1.0, 3.0].

• indep.runs(m): The maximum number of independent runs can be selected in the range from 200 to 800.

• $D_{min}$ is set to 0 for all cases.

The penalty factor $K_{s}$ for the slack unit and the penalty factor $K_{p}$ spinning reserve constraint are large enough and set to $10^{3}$ for all systems.

Table 2 Results and comparisons for 20-unit system with quadratic fuel cost function

Table 3 Results and comparisons for 3-unit system with cubic fuel cost function by MVMO and $\hbox {MVMO}^{S}$

4.2 Convex ED problems

The fuel cost function is in turn as the quadratic and cubic form for the convex ED problems.

4.2.1 Case 1: 20-unit test system with quadratic cost function

This system supplies to a total load demand of 2500 MW. The input data of the 20-unit system are from [10] including fuel cost coefficients, generator capacity limits and B loss matrix. The results obtained by the proposed $\hbox {MVMO}^{S}$ are compared to those from lamda-iteration [10], HNN [10], BBO [21] and MVMO in Table 2. The comparison shows that the total cost and power loss obtained by the proposed $\hbox {MVMO}^{S}$ are very close to the other methods in Table 2. It is noted that the $\hbox {MVMO}^{S}$ achieves the optimal solution with a high probability (the standard deviation is 0 %) while the solutions of lamda-iteration and HNN mismatch with the total power demand and power loss.

Table 4 Results and comparisons for 26-unit system with cubic fuel cost function by MVMO and $\hbox {MVMO}^{S}$

Table 5 Results for 6-unit system with VPE by MVMO and $\hbox {MVMO}^{S}$

4.2.2 Case 2: 3-unit test system with cubic cost function

The data information for 3-generating units with cubic cost function are given in [3]. The total power load demand for this system is 1400 MW. The transmission power loss is considered in this case. The B loss matrix for the calculation of power loss is referred from [1]. The obtained results by the MVMO and $\hbox {MVMO}^{S}$ are presented in Table 3 along with the solutions of SA1, SA2 [18] and IGA_MU [13]. The total cost and power loss obtained by the proposed $\hbox {MVMO}^{S}$ are very close to the other methods except SA1. This system has two local optimum (about 6639 and 6642) [13], and SA1 are likely to get stuck in a local solution.

4.2.3 Case 3: 26-unit test system with cubic cost function

The data of the test system including 26 thermal generating units with cubic fuel cost function can be found in [8]. The system load demand for this case is 2000 MW neglecting transmission power loss. The obtained results by the $\hbox {MVMO}^{S}$ are compared to those from GA, PSO [6] and MVMO as given in Table 4. The proposed $\hbox {MVMO}^{S}$ provides the total cost less than GA, PSO and MVMO.

Table 6 Comparisons for 6-unit system with VPE

4.3 Nonconvex ED problems

The proposed method is tested on different nonconvex problem including VPE and POZ characteristics. In order to demonstrate the efficiency of the proposed approach, it is also tested on large-scale systems.

4.3.1 Case 4: ED problem with valve point effects

The proposed $\hbox {MVMO}^{S}$ are applied to IEEE test systems including 30 bus and 6 thermal generating units with VPE. The fuel cost coefficients, generator capacity limits and B loss matrix for this test systems are refered from [33]. The test system here is for 283.4 MW load demand. Table 5 shows the results obtained by the MVMO and $\hbox {MVMO}^{S}$. The comparisons of fuel costs obtained by the proposed $\hbox {MVMO}^{S}$ and other methods are listed in Table 6. The proposed $\hbox {MVMO}^{S}$ can obtain better fuel costs than GA, GA-APSO, NSOA [33], DE [23] and $\lambda$-logic [40], and close to MVMO.

4.3.2 ED problem with prohibited operating zones

(a) Case 5: 15-unit system with POZ

The proposed $\hbox {MVMO}^{S}$ is testes on 15-unit test system [17]. This system consists of 15 thermal generating units, in which four units have POZ. The system supplies to a power load demand of 2650 MW with a system spinning reserve requirement of 200 MW. Power loss and ramp rate constraint are neglected.

In order to show the efficiency of the proposed method, the $\hbox {MVMO}^{S}$ is also tested on a system with some modified units’ data of above 15-unit system. The modifed data system is found in [14]. Table 7 shows the solutions of the MVMO and $\hbox {MVMO}^{S}$ for the original and modified cases.

For the orginal case, the fuel cost of the $\hbox {MVMO}^{S}$ are compared to those of $\lambda -\delta$ iterative method [41], IHNN [11], EHNN [12], EP [42], FCEPA [42], QEA [17], IQEA [17] and MVMO. From the Table 8, the fuel cost of MVMO and $\hbox {MVMO}^{S}$ are less than IHNN and slightly lower than other methods except EHNN. Although the fuel cost from the EHNN is slightly lower than that of the MVMO and $\hbox {MVMO}^{S}$, power balance constraint in the EHNN is not satisfied, where 0.8 MW is not dispatched yet.

For the modified case, the fuel cost obtained by the $\hbox {MVMO}^{S}$ are compared to that of SGA [14], DCGA [14], ETQ [35], CEP [16], FEP [16], IFEP [16] and MVMO. As shown in the Table 9, the cost from the proposed method is slightly lower than that from SGA and DCGA in [14], and close to that from the other methods.

Table 7 Results for 15-unit system with POZ by MVMO and $\hbox {MVMO}^{S}$

The 15-unit test system above includes the ramp rate constraint and neglects spinning reserve required. The power loss is considered for this case. The power load demand for this system is 2630 MW. The fuel cost coefficients, generator capacity limits, prohibited operating zones and B loss matrix are from [24]. Table 10 presents the solutions obtained by the MVMO and $\hbox {MVMO}^{S}$. The solution comparison is shown in Table 11, where the fuel costs of the $\hbox {MVMO}^{S}$ are slightly lower than SA-PSO [27], PGPSO [2], ABC [19], CSA [41] and MVMO, and less than the other methods.

(b) Case 6: Large-scale systems with prohibited operating zones

In order to demonstrate the applicable capability to large-scale systems, the proposed $\hbox {MVMO}^{S}$ is test on 30-unit system, 60-unit system and 90-unit system with POZ. These large-scale systems are built from the basic 15-unit system [17] which supplies to the power load demand of 2650 MW with a required spinning reserve of 200M. The load demand is proportionally adjusted to the size of each large-scale system. Table 12 shows the fuel cost and CPU times obtained by the MVMO and $\hbox {MVMO}^{S}$.

Table 8 Comparisons of best cost for 15-unit system with POZ for original case

Table 9 Comparisons of best cost and CPU time for 15-unit system with modified units’ data neglecting ramp rate constraint and power loss

Table 10 Results for 15-unit system with POZ including ramp rate constraint and power loss by MVMO and $\hbox {MVMO}^{S}$

The $\hbox {MVMO}^{S}$ are compared to the convention GA (CGA), improved GA with multiplier updating method (IGAMUM) [15] and MVMO in term of average total costs and CPU times in Table 13. The comparison shows that the $\hbox {MVMO}^{S}$ can obtain better solution quality than other methods.

4.3.3 Case 7: ED problem with both valve point effects and prohibited operating zones

The test system here is also a large-scale system including 140 generating units which supplies to the power load demand of 49342 MW neglecting transmission power loss. In order to show the efficiency of the proposed $\hbox {MVMO}^{S}$, both nonconvex characteristics including VPE and POZ are consider for this case. The data of this system can be found in [25] where 12 units have VPE and 4 other units have POZ. A comparison of fuel costs and CPU times from the $\hbox {MVMO}^{S}$ and PSO methods [25] is shown in Table 14. The comparison shows that the proposed $\hbox {MVMO}^{S}$ dominates PSO methods including conventional PSO with the constraint treatment strategy (CTPSO), PSO with chaotic sequences (CSPSO), PSO with crossover operation (COPSO) and PSO with both chaotic sequences and crossover operation (CCPSO) in term of optimal solution quality. Note that the maximum fuel cost obtained by $\hbox {MVMO}^{S}$ is even better than the minimum fuel costs obtained by PSO methods. The optimal dispatch solution for 140-unit system is shown in Table 15.

Table 11 Comparisons for 15-unit system with POZ

Table 12 Fuel costs and CPU times for large-scale systems with POZ

Table 13 Comparison of average total costs and CPU times for large-scale systems with POZ

Table 14 Comparisons of fuel costs for 140-unit system with both VPE and POZ

5 Discussion

The proposed $\hbox {MVMO}^{S }$has been implemented to different ED problems including convex and nonconvex characteristics. The issues from the numerical results are given as follows:

5.1 Solution quality

From Tables 2, 3, 4, 6, 8, 9, 11, 13 and 14, the proposed $\hbox {MVMO}^{S}$ provides better total fuel cost than other reported methods. Especially for large-scale system, as seen from Table 14, the proposed $\hbox {MVMO}^{S}$ dominates PSO methods in term of all minimum, average and maximum total fuel cost. Moreover, the power outputs obtained by $\hbox {MVMO}^{S}$ are always between the minimum and maximum generator capacity limits and the total power output of generating units always equals to the power load demand. It is indicated that the equality and inequality constraints always satisfy. Consequently, the $\hbox {MVMO}^{S }$can obtain very good solution quality for ED problems.

5.2 Computational efficiency

In this paper, both the total cost and computational time are used for result comparison. However, it is difficult for the computational time comparison among the methods for optimization problems due to different computer processors and programming languages used. Therefore, the key factor for result comparison is usually the objective function rather than the computational time. The proposed $\hbox {MVMO}^{S}$ has been tested on large-scale systems and the obtained results including total cost and computational time have compared to those from many other methods. The comparison has indicated that the proposed method can obtain better solution quality than other methods. Although the proposed method is not as fast as some methods, it is also faster than many other methods. Moreover, the computational time from the proposed method is not too long compared to the faster methods. In fact, the large-scale and complex optimization problems are always a challenge for solution methods in both global optimal solution and computational time. In future, the proposed method can be further improved for efficiently dealing with different large-scale and complex problems.

5.3 Convergence characteristic

Figures 6, 7, 8, 9 and 10 depict the convergence characteristic of the MVMO and $\hbox {MVMO}^{S}$ for case 1 (ED with quadratic fuel cost function), case 3 (ED with cubic fuel cost function), case 4 (ED with VPE), case 5 (ED with POZ) and case 7 (ED with both VPE and POZ), respectively. All the figures shows that both MVMO and $\hbox {MVMO}^{S}$ provide the solution without premature convergence or trapping in local optima. It indicates their search ability can balance between exploration and exploitation. The MVMO converges faster than the $\hbox {MVMO}^{S}$. This is because the MVMO starts the search process with single particle while $\hbox {MVMO}^{S}$ starts the search process with a set of particles. It makes the $\hbox {MVMO}^{S}$ take more time than the original MVMO to converge. However, from all numerical results, the $\hbox {MVMO}^{S}$ achieves better solution than MVMO. It is confirmed that the global search ability of the $\hbox {MVMO}^{S}$ is better than the MVMO.

Fig. 6

Convergence property of MVMO and $\hbox {MVMO}^{S}$ for case 1 (ED with qudratic fuel cost function)

Fig. 7

Convergence property of MVMO and $\hbox {MVMO}^{S}$ for case 3 (ED with cubic fuel cost function)

Fig. 8

Convergence property of MVMO and $\hbox {MVMO}^{S}$ for case 4 (ED with VPE)

Fig. 9

Convergence property of MVMO and $\hbox {MVMO}^{S}$ for case 5 (original case) ED with POZ

Fig. 10

Convergence property of MVMO and $\hbox {MVMO}^{S}$ for case 7 (ED with both VPE and POZ)

Fig. 11

Distribution of fuel cost of the MVMO and $\hbox {MVMO}^{S}$ for case 2 (3 units with cubic fuel cost function)

Fig. 12

Distribution of fuel cost of the MVMO and $\hbox {MVMO}^{S}$ for case 3 (26 units with cubic fuel cost function)

5.4 Robustness analysis

The MVMO and the $\hbox {MVMO}^{S}$ are run 50 independent trials. The minimum cost, maximum cost, average cost and standard deviation obtained by the MVMO and $\hbox {MVMO}^{S}$ to evaluate the robustness characteristic of the proposed method for ED problems. For case 1, the proposed $\hbox {MVMO}^{S}$ achieves the optimal solution with a high probability (the standard deviation is 0 %). As observed from Tables 1, 6, 11 and 13, the proposed $\hbox {MVMO}^{S}$ robust than most of the other methods in literature. Figures 11, 12, 13 and 14 show the distribution of fuel cost of the MVMO and $\hbox {MVMO}^{S}$ of 50 trials for case 2, 3, 4 and case 5, respectively. All figures show that the $\hbox {MVMO}^{S}$ is more robust than the the MVMO.

Fig. 13

Distribution of fuel cost of the MVMO and $\hbox {MVMO}^{S}$ for case 4 (6 units with VPE)

Fig. 14

Distribution of fuel cost of the MVMO and $\hbox {MVMO}^{S}$ for case 5 (15 units with POZ). a Case 5: original case. b Case 5: modified case. c Case 5: system with poz including ramp rate constraint and power loss

6 Conclusion

In this paper, the proposed $\hbox {MVMO}^{S}$ has been effectively implemented for solving both convex and nonconvex ED problems. For the convex ED problem, the fuel cost function is in turn as the quadratic and cubic form. For the nonconvex ED problem, the nonconvex elements and nonlinearities in objective function and constraints are considered such as valve point effects, prohibited operating zones, ramp rate limits and spinning reserve. The proposed method keeps the concept of the conventional MVMO and starts search process with a set of particles to improve its global search ability and solution quality for optimization problems. The proposed $\hbox {MVMO}^{S}$ has merits of easy implementation, good solutions, robust algorithm and applicable to large-scale systems. The numerical results have shown that the proposed $\hbox {MVMO}^{S}$ has better performance than the other optimization techniques available in the literature in terms of global solution and robustness. Therefore, the proposed $\hbox {MVMO}^{S}$ could be a favorable method for solving the ED problems in power systems.

Appendix

Table 15 Power output of 140-unit system with both VPE and POZ by $\hbox {MVMO}^{S}$