1 Introduction

Suppose we are given a smooth closed (i.e., compact and without boundary) connected n-dimensional manifold M \((n>1)\), equipped with a Riemannian metric, where a smooth closed 1-form c is defined. In what follows, the real and imaginary parts of c will be, respectively, denoted by a and b, and we will write \(c=a+ib.\)

Consider the vector fields

$$\begin{aligned} L_j=\frac{\partial }{\partial t_j}+\frac{\partial C}{\partial t_j}(t)\frac{\partial }{\partial x}, \quad j=1,\ldots ,n, \end{aligned}$$

where \((t_1,\ldots ,t_n)\) are local coordinates on M, x belongs to the unit circle \({\mathbb {S}}^1\), and C is a local primitive of c. They are local generators of the bundle \({\mathcal {V}}\doteq (T')^{\perp }\subset {\mathbb {C}}\otimes T(M\times {\mathbb {S}}^1)\) where \(T'\) is the line sub-bundle of \({\mathbb {C}}\otimes T^*(M\times {\mathbb {S}}^1)\) generated by the 1-form \(dx-c\) (we refer to [11, 20] for details).

Denote by \(\Lambda ^{p,0}\), \(p=0,\ldots ,n\), the sub-bundle of \(\Lambda ^{p}({\mathbb {C}}\otimes T^*(M\times {\mathbb {S}}^1))\) locally generated by \(dt_J=dt_{j_1}\wedge \dots \wedge dt_{j_p}\), if \(J=\{j_1,\ldots \,j_p\}\) and \(1\leqslant j_1< j_2< \cdots <j_p\leqslant n.\)

The focus of this work is the associated differential operator \({\mathbb {L}}: C^\infty (M\times {\mathbb {S}}^1) \rightarrow C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{1,0})\) defined by

$$\begin{aligned} {\mathbb {L}}u=d_tu+c(t)\wedge \partial _x u, \end{aligned}$$
(1.1)

where \(d_t:C^\infty (M\times {\mathbb {S}}^1, \Lambda ^{p,0})\rightarrow C^\infty (M\times {\mathbb {S}}^1, \Lambda ^{p+1,0})\) is the exterior derivative on M.

Any involutive structure defines in a natural way a complex of differential operators which in the case of \({\mathcal {V}}\) is given by (1.1) when acting on functions. Thus, we have a complex

$$\begin{aligned} \begin{aligned}&C^\infty (M\times {\mathbb {S}}^1) {\mathop {\longrightarrow }\limits ^{{\mathbb {L}}}}C^\infty (M\times {\mathbb {S}}^1, \Lambda ^{1,0}){\mathop {\longrightarrow }\limits ^{{\mathbb {L}}^1}}\\&\quad {\mathop {\longrightarrow }\limits ^{{\mathbb {L}}^1}}C^\infty (M\times {\mathbb {S}}^1, \Lambda ^{2,0}) {\mathop {\longrightarrow }\limits ^{{\mathbb {L}}^2}}\cdots {\mathop {\longrightarrow }\limits ^{{\mathbb {L}}^{n-1}}}C^\infty (M\times {\mathbb {S}}^1, \Lambda ^{n,0}) {\mathop {\longrightarrow }\limits ^{{\mathbb {L}}^{n}}}0 \end{aligned} \end{aligned}$$
(1.2)

analogous to the de Rham complex.

Here we will study the smooth global solvability of the equation \({\mathbb {L}}u=f\), i.e., the possibility of finding a globally defined solution \(u\in C^\infty (M\times {\mathbb {S}}^1)\) when f is smooth. Of course, if f is in the range of \({\mathbb {L}}\) it must satisfy two obvious conditions analogous to the fact that an exact form is both closed and orthogonal to the closed cocycles: (i) \({\mathbb {L}}^1f=0\) (a consequence of the involutivity \({\mathbb {L}}^1{\mathbb {L}}=0\)), and (ii) f must be orthogonal to the kernel of the dual operator \({\mathbb {L}}^*.\) They are usually referred to as compatibility conditions for f and may be formulated in equivalent different ways that are chosen to suit best the operator under consideration.

As in [16], we will consider the minimal covering space \(\Pi :{\widetilde{M}}\rightarrow M\) associated with b: a covering space where the pullback \(\Pi ^*b\) is exact, and minimal with respect to such property. A primitive \({\widetilde{B}}\) of \(\Pi ^*b\) can be obtained in \({\widetilde{M}}\) by integration from a point \(t_0\in {\widetilde{M}}.\) Set \(\Omega ^r\doteq \{s\in {\widetilde{M}}: {\widetilde{B}}(s)>r\}\) and \(\Omega _r\doteq \{s\in {\widetilde{M}}: {\widetilde{B}}(s)<r\}\) for the semilevel sets of \({\widetilde{B}}.\) Denote by \({\mathscr {A}}\) the family of the connected components \({{\mathcal {O}}}\) of regular semilevel sets—that is, the sets \(\Omega _r\) and \(\Omega ^r\) when r is a regular value of \({\widetilde{B}}\)—such that \({\widetilde{B}}\) is bounded on \({{\mathcal {O}}}.\) When b is exact we will have \({\widetilde{M}}=M\), and in this case each component of a regular semilevel is in \({\mathscr {A}}\) and M itself is a connected semilevel set for some value of r.

We now state the main result of this work. Denote by \(H_1({\widetilde{M}},{\mathbb {Z}})\) the first homology group of \({\widetilde{M}}\) with coefficients in \({\mathbb {Z}}.\) We will associate to \({{\mathcal {O}}}\in {\mathscr {A}}\) a vector \(I({{\mathcal {O}}})\in {\mathbb {R}}^m\), with \(m=\text {rank\,}i^*(H_1({{\mathcal {O}}},{\mathbb {Z}}))\), where \(i^*:H_1({{\mathcal {O}}},{\mathbb {Z}})\rightarrow H_1({\widetilde{M}},{\mathbb {Z}})\) is the natural homomorphism induced by the inclusion \(i:{{\mathcal {O}}}\hookrightarrow {\widetilde{M}}.\)

Theorem 1.1

Assume that M is a closed orientable surface and that the 1-form \(c=a+ib\) is smooth and closed. The following statements are equivalent:

  1. (I)

    \({\mathbb {L}}\) is globally solvable.

  2. (II)

    One of the two conditions below is satisfied:

    1. (II.1)

      \({\mathscr {A}}=\emptyset \), or, for every \({{\mathcal {O}}}\in {\mathscr {A}}\), \(I({{\mathcal {O}}})\) is neither a rational nor a Liouville vector.

    2. (II.2)

      The form b is exact and the semilevel sets \(\{t\in M: {\widetilde{B}}(t)>r\}\) and \(\{t\in {\widetilde{M}}: {\widetilde{B}}(t)<r\}\) are connected for every \(r\in {\mathbb {R}}\); in addition, a is rational, and if \(q\in {\mathbb {Z}}\) is such that \(qI({{\mathcal {O}}})\in {\mathbb {Z}}^m\) for \({{\mathcal {O}}}\in {\mathscr {A}}\), then qa is integral.

The precise definitions of \({\widetilde{M}}\), of rational and Liouville vectors and forms, and of global solvability are present in [16, 17] and are reviewed in Sect. 2 along with a script of the proof.

When c is smooth and exact, the global solvability of the complex for a smooth closed orientable manifold M was characterized in [12] (in the context of linear self-adjoint operators in a Hilbert space). The consequence is that \({\mathbb {L}}\) is globally solvable if and only if the semilevel sets \(\{t\in M: {\widetilde{B}}>r\}\) and \(\{t\in M: {\widetilde{B}}<r\}\) are connected for every \(r\in {\mathbb {R}}.\) When b is not exact, we point out that \({\mathscr {A}}=\emptyset \) is equivalent to the connectedness of the semilevel sets in \({\widetilde{M}}\) [16].

As for systems of real vector fields, a characterization of the global solvability of the complex is known when \(M={\mathbb {T}}^n\); see [3, 13].

The global solvability of the system when c is real analytic was characterized quite recently by Hounie and Zugliani in [17]. A similar complete characterization for general M and smooth c is only known when b is a Morse form [16, 17]. Conceptually, the proof in the smooth set up and in the real analytic set up is almost identical and the reason why the proof in the first situation is much harder and remains open for higher dimensions \(n>2\) lies on a technical difficulty that can be described as follows. Given a pair of points in a connected semilevel set one may join them by a curve and wishes to estimate the minimal length of such a curve in terms of the distance from the semilevel set boundary to the point of the pair which is closest to this boundary. In the real analytic situation such boundaries are manageable sets (also in the smooth Morse case), while in the general smooth case they can be quite wild. We return to this matter in the Appendix.

The global solvability of systems defined by a smooth closed form has been extensively studied for \(M={\mathbb {T}}^n\), and we mention [2, 6], where a characterization of the global solvability is given when \(M={\mathbb {T}}^2\) and \(a\equiv 0.\) Under particular special hypotheses, other results can be found in [7, 8, 14]. Finally, examples of globally solvable systems when M is a surface can be found in [9, 10].

We point out that some of the results contained in Theorem 1.1 are valid for a general closed manifold. In Sect. 7, we discuss this point further.

A part of this paper was written while the second author was visiting the Department of Mathematics and Statistics at Florida International University. He would like to thank its faculties and staff who provided all that was necessary during the period.

2 Definitions and Proof Strategy

We can construct a covering space \({\widetilde{M}}\) of M with special properties, one of them being that the pullback of b to \({\widetilde{M}}\) is exact. More precisely, take the subgroup H of \(\pi _1(M)\) (basepoints omitted) equal to the kernel of the homomorphism \(T: \pi _1(M) \rightarrow {\mathbb {R}}\) given by

$$\begin{aligned} \gamma \mapsto \int _{\gamma } b. \end{aligned}$$

There exists a covering space \(\Pi :\widetilde{M}\rightarrow M\) such that \(\pi _1(\widetilde{M})\) is isomorphic to H and for each pair of liftings of a point in M to \(\widetilde{M}\) there is a deck transformation mapping one to the other. The covering \(\widetilde{M}\) is called a minimal covering. Moreover, the group \({\mathsf {D}}\) of deck transformations of \(\widetilde{M}\) is \(\pi _1(M)/H\), which is finitely generated.

Thus we may write

$$\begin{aligned} {\widetilde{B}}(\sigma (t))={\widetilde{B}}(t)+b_{\sigma },\quad t\in {\widetilde{M}},\quad \sigma \in {\mathsf {D}}, \end{aligned}$$
(2.1)

where \(b_{\sigma }\) is a constant that is 0 if and only if \(\sigma \) is the identity.

We denote by \(\Omega ^r\doteq \{s\in {\widetilde{M}}: {\widetilde{B}}(s)>r\}\) and \(\Omega _r\doteq \{s\in {\widetilde{M}}: {\widetilde{B}}(s)<r\}\) the semilevel sets of \({\widetilde{B}}.\)

We know that if \({\widetilde{B}}\) is bounded on a component \({{\mathcal {O}}}\) of a semilevel set, then the restriction of \(\Pi \) to \({{\mathcal {O}}}\) is injective (see [16]). Denote by \({\mathscr {A}}\) the family of all the connected components \({{\mathcal {O}}}\) of some regular semilevel set—that is, a component of \(\Omega _r\) or \(\Omega ^r\), where r is some regular value of \({\widetilde{B}}\)—such that \({\widetilde{B}}\) is bounded on \({{\mathcal {O}}}.\)

We define a continuous functional \(T_a\) on the space \(\Gamma ({\widetilde{M}})\) consisting of smooth closed curves in \({\widetilde{M}}.\)

Given \(\gamma \in \Gamma ({\widetilde{M}})\), define

$$\begin{aligned} T_a(\gamma )=\int _{\gamma }\Pi ^*a. \end{aligned}$$

Notice that

  • \(T_a(\gamma )\) depends only on the homotopy class of \(\gamma .\)

  • By the Hurewicz Theorem, \(T_a\) induces a homomorphism on the first homology group \(H_1({\widetilde{M}},{\mathbb {Z}})\) (the class of \(\gamma \) in \(H_1({\widetilde{M}},{\mathbb {Z}})\) will be denoted by \([\gamma ]\)).

Suppose that \({{\mathcal {O}}}\in {\mathscr {A}}.\) Consider the natural homomorphism \(i^*:H_1({{\mathcal {O}}},{\mathbb {Z}})\rightarrow H_1({\widetilde{M}},{\mathbb {Z}})\) induced by the inclusion \(i:{{\mathcal {O}}}\hookrightarrow {\widetilde{M}}.\) As \(i^*(H_1({{\mathcal {O}}}),{\mathbb {Z}}))\) is a subgroup of \(H_1({\widetilde{M}},{\mathbb {Z}})\), it is finitely generated, and we fix a linearly independent set \(\{[\nu _1], \ldots , [\nu _m]\}\) generating its free part F.

We will denote by \(I({{\mathcal {O}}})\) the vector \((2\pi )^{-1}(T_a([\nu _1]),\ldots ,T_a([\nu _m])).\)

Definition 2.1

We say that \(I({{\mathcal {O}}})\) is

  • integral if \(I({{\mathcal {O}}})\in {\mathbb {Z}}^m\);

  • rational if \(I({{\mathcal {O}}})\in {\mathbb {Q}}^m\);

  • Liouville if it is not rational and there exist \(P_j\in {\mathbb {Z}}^m\), \(q_j\in {\mathbb {Z}}^+\), with \(q_j>1\), and \(C>0\) satisfying

    $$\begin{aligned} \left| I({{\mathcal {O}}})-\frac{P_j}{q_j}\right| <\frac{C}{q^j_j} \end{aligned}$$

    for every \(j\in {\mathbb {Z}}^+.\)

It is plain that this definition does not depend on the choice of the generators.

Denote by \({\mathsf {E}}\) the group of deck transformations associated with the universal covering \(\Pi _0:{\mathscr {U}}\rightarrow M.\) This group is isomorphic to \(\pi _1(M).\)

If \(C=A+iB\), where A and B are, respectively, the primitives of the pulled back forms \(\Pi _0^*a\) and \(\Pi _0^*b\), we may write

$$\begin{aligned} C(\sigma ({{\tilde{t}}}))=C({{\tilde{t}}})+c_{\sigma },\quad t\in {\mathscr {U}},\quad \sigma \in {\mathsf {E}}, \end{aligned}$$
(2.2)

where \(c_{\sigma }\) is a constant.

The space of plausible right-hand sides for the equation \({\mathbb {L}}u=f\) will be denoted by \({\mathbb {E}}.\) Set \(F\doteq \Pi _0^*f\) and denote by \(\{\widehat{F}(t,\xi )\}_{\xi \in {\mathbb {Z}}}\) the Fourier coefficients of F with respect to \(x\in {\mathbb {S}}^1.\)

Definition 2.2

(Compatibility conditions) We say that a 1-form \(f\in C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{1,0})\) belongs to \({\mathbb {E}}\) if:

  • for each \(\xi \in {\mathbb {Z}}\) and each smooth curve \(\gamma \) connecting t to \(\sigma (t)\) in \({\mathscr {U}}\) with \(i\xi c_{\sigma }\in 2\pi i{\mathbb {Z}}\),

    $$\begin{aligned} \int _{\gamma }e^{i\xi C(s)}\widehat{F}(s,\xi )=0\text {, and} \end{aligned}$$

  • \(d_t(e^{i\xi C(t)}\widehat{F}(t,\xi ))=0\) for each \(\xi \in {\mathbb {Z}}.\)

To avoid heavy notation, we will keep writing f to denote the pullback of f to \({\widetilde{M}}\) or \({\mathscr {U}}\), except when doing so might lead to confusion.

Definition 2.3

We say that the operator (1.1) is globally solvable if given any 1-form \(f\in {\mathbb {E}}\) there exists \(u\in {\mathscr {D}}'(M\times {\mathbb {S}}^1)\) such that \({\mathbb {L}}u=f.\) If the solution u can be taken in \(C^\infty (M\times {\mathbb {S}}^1)\) we say that \({\mathbb {L}}\) is globally solvable in \(C^\infty .\) We say that the operator (1.1) is globally hypoelliptic if \(u\in C^\infty (M\times {\mathbb {S}}^1)\) whenever \({\mathbb {L}}u\in C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{1,0}).\)

We start by noticing that \({\mathbb {Z}}\ni \xi \mapsto \widehat{f}(t,\xi )\) is rapidly decreasing, i.e., for every \(N\in {\mathbb {Z}}^+\), there is a constant \(C(N)>0\) such that

$$\begin{aligned} |\widehat{f}(t,\xi )|\leqslant \frac{C(N)}{(1+|\xi |)^N} \end{aligned}$$
(2.3)

(and similar estimates hold for the derivatives of f).

We will find the Fourier coefficients \(\widehat{u}(t,\xi )\) of a presumed solution to the system and prove that they satisfy similar convenient bounds. Once this is done, they will determine the smooth function u(x, t) that has these Fourier coefficients proving that \({\mathbb {L}}\) is globally solvable in \(C^\infty .\) Indeed, since the coefficients of a candidate solution to the system satisfy the equation

$$\begin{aligned} d_t\widehat{u}(\cdot ,\xi )+i\xi c(\cdot )\widehat{u}(\cdot ,\xi )=\widehat{f}(\cdot ,\xi ) \end{aligned}$$
(2.4)

in any local chart of M, these coefficients determine initially a continuous function that satisfies the equation \({\mathbb {L}}u=f\) in the weak sense, and to conclude the proof it will remain to be shown that u(t, x) is smooth. This will follow by proving the appropriate decay for the derivatives of the coefficients, which involves an induction argument on the order of the derivatives. This was the approach followed in [16], and we will refer the reader to this paper for details on the computations.

If we integrate the pullback to \({\mathscr {U}}\) of (2.4) from \({{\tilde{t}}}_0 \in {\mathscr {U}}\) to \({{\tilde{t}}}\in {\mathscr {U}}\) for each \(\xi \in {\mathbb {Z}}\), we obtain, with some abuse of notation,

$$\begin{aligned} \widehat{u}({{\tilde{t}}},\xi )=\int _{{{\tilde{t}}}_0}^{{{\tilde{t}}}}\upsilon +Ke^{-i\xi C({{\tilde{t}}})}, \end{aligned}$$

where \(\upsilon (s,\xi )=e^{i\xi [C(s)-C({\tilde{t}})]}\widehat{f}(s,\xi )\) and K is a constant.

In order to find a solution on M we need that \(\widehat{u}(\sigma ({\tilde{t}}),\xi )=\widehat{u}({\tilde{t}},\xi )\), \(\sigma \in {\mathsf {E}}\), which uniquely determines the coefficients of the sought-after solution, when \(i\xi c_{\sigma }\notin 2\pi i{\mathbb {Z}}\), as

$$\begin{aligned} \widehat{u}({\tilde{t}},\xi )=\frac{1}{e^{i\xi c_{\sigma }}-1}\int _{{\tilde{t}}}^{\sigma ({\tilde{t}})}\upsilon , \end{aligned}$$
(2.5)

and

$$\begin{aligned} K=\frac{1}{e^{i\xi c_{\sigma }}-1}\int _{{\tilde{t}}_0}^{\sigma ({\tilde{t}}_0)}e^{i\xi C(s)}\widehat{f}(s,\xi )=e^{i\xi C({\tilde{t}}_0)}\widehat{u}({\tilde{t}}_0,\xi ). \end{aligned}$$

Sometimes we rewrite (2.5) as

$$\begin{aligned} \widehat{u}({\tilde{t}},\xi )=\int _{{\tilde{t}}_0}^{{\tilde{t}}}\upsilon +e^{i\xi [C({\tilde{t}}_0)-C({\tilde{t}})]}\widehat{u}({\tilde{t}}_0,\xi ). \end{aligned}$$
(2.6)

In fact, for each \({\tilde{t}}\in {\mathscr {U}}\) and \(\xi \in {\mathbb {Z}}\), we are free to choose \({\tilde{t}}_0\) and the paths used in (2.5) and (2.6), so the idea is to select them carefully and the choice will vary according to t and \(\xi .\)

Also, in order to prove the estimates, it will be convenient to choose a specific \(\sigma \in {\mathsf {E}}\) that might depend on \({\tilde{t}}\in {\mathscr {U}}\) and \(\xi \in {\mathbb {Z}}\setminus \{0\}.\) As proved in [17], the definition of the coefficients (2.5) is independent of \(\sigma \in {\mathsf {E}}.\)

Lemma 2.4

Let \(\phi ,\sigma \in {\mathsf {E}}.\) If \(f\in {\mathbb {E}}\) and \(i\xi c_{\sigma },i\xi c_{\phi }\notin 2\pi i{\mathbb {Z}}\), then for each \(t\in {\mathscr {U}}\),

$$\begin{aligned} \frac{1}{e^{i\xi c_{\sigma }}-1}\int _{{\tilde{t}}}^{\sigma ({\tilde{t}})}\upsilon =\frac{1}{e^{i\xi c_{\phi }}-1}\int _{{\tilde{t}}}^{\phi ({\tilde{t}})}\upsilon . \end{aligned}$$

Another lemma we import from [17] is

Lemma 2.5

Suppose that \(I({{\mathcal {O}}})\) is neither rational nor Liouville. Then, for every \(\xi \in {\mathbb {Z}}\) with \(\xi \ne 0\), there exists \(l\in \{1,\ldots ,m\}\) such that

$$\begin{aligned} \left| e^{i\xi T_a([\nu _l])}-1\right| \geqslant \frac{K}{|\xi |^s} \end{aligned}$$

for some \(K>0\) and \(s\in {\mathbb {Z}}^+.\)

In the next section, we will start the proof of (II) \(\implies \) (I). The approach will depend on b: in Sects. 3 and 4 we deal with the case in which b is not exact, while in Sect. 5 we assume that b is an exact form.

For the first case, consider the division of the pairs \((t,\xi )\in {\widetilde{M}}\times {\mathbb {Z}}^-\) in two classes. The class (A) consists of the pairs \((t,\xi )\) for which there is \(\sigma \in {\mathsf {D}}\) with \(b_{\sigma }<0\) such that

t and \(\sigma (t)\) are in the same component of \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}\).

As for the pairs in the class (B), for each \(\sigma \in {\mathsf {D}}\) with \(b_{\sigma }<0\),

t and \(\sigma (t)\) are in different components of \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}\).

3 Estimates for the Class (A)

Here it is crucial to work under the assumption that M is a closed orientable surface of genus \(g>0\), shortly \(S_g\)—on which a non-exact 1-form b is defined. Since \(S_g\) is a connected sum of g tori \(T_k\), we can suppose that the set of smooth closed curves representing the canonical generators of \(H_1(S_g,{\mathbb {Z}})\) is \(\{\theta _1,\phi _1,\ldots ,\theta _g,\phi _g\}\), where \(\theta _k,\phi _k\) represent the canonical generators of \(H_1(T_k,{\mathbb {Z}}).\)

We will say that \(M^\dag \subset {\mathbb {R}}^3\) is a surface with boundary if for every point \(p\in M^\dag \), there are a ball \({\mathscr {B}}\ni p\) in \({\mathbb {R}}^3\) and a diffeomorphism between \(M^\dag \cap {\mathscr {B}}\) and an open set of \({\mathscr {Q}}\doteq \{(x,y): x,y\geqslant 0\}.\) The interior points of \(M^\dag \) is the set of points mapped to \({\text {int}}{\mathscr {Q}}.\) The set of points that are mapped to \({\mathscr {Q}}\setminus {\text {int}}{\mathscr {Q}}\) is called the boundary of \(M^\dag \) (denoted by \(\partial M^\dag \)). Note that we depart slightly from the standard definition of boundary since we allow a finite number of corners similar to the vertices of a polygon.

A loop, that is, a smooth simple closed curve \(\alpha \) in the interior of a surface \(M^\dag \) (with or without boundary components) will be called non-trivial if \(M^\dag \setminus \alpha \) is connected.

We would like to join \(t\in {\widetilde{M}}\) to \(t_0\) satisfying the following rules:

  • (i) the term \(-\xi [{\widetilde{B}}(s)-{\widetilde{B}}(t)]\) will remain bounded on each path by a constant independent of \(\xi \);

  • (ii) the length of the path will have polynomial growth with respect to \(|\xi |\); and

  • (iii) the previous bounds do not depend on t.

Condition (i) will be consequence of the connectedness of the semilevel sets in \({\widetilde{M}}.\)

Let us say a few words about condition (ii). The approach in [12]—where b is exact—is to consider a triangulation of a manifold M and the path consists of sides of triangles (recall that \({\widetilde{M}}=M\) in [12], and the solution is given by the integral in (2.6)).

In [2, 6], when \(M={\mathbb {T}}^2\), the approach to obtain the required estimates is to find a compact set in \({\widetilde{M}}\) (which in this case can be \({\mathbb {R}}^2\) or \({\mathbb {R}}\times {\mathbb {S}}^1\)), within which t and a convenient translate of t can be joined by a curve contained in semilevel set.

Here the approach involves a combination of the two cases mentioned above as we describe below. The idea is to find a special compact surface \(M^\sharp \) with boundary where an exact form \(b^\sharp \) is defined. The 1-form \(b^\sharp \) will be related to b and the surface M can be obtained from \(M^\sharp \) after appropriate identifications. A convenient path will then be produced in \(M^\sharp \) and this will grant the required estimates in \({\widetilde{M}}.\) This approach is reminiscent of the method used in [16, 17] for real analytic b where the estimates were obtained first inside a ball centered at t, albeit in the smooth case one must also invoke the technique introduced in [19] that uses triangulations in order to deform the original integration path into one of controllable length. A key technical point is that the boundary \(\partial M^\sharp \) should not contain singular points of \(b^\sharp .\) In [2, 16], the topological results in [1] play an important role and the crucial point is a lemma of Arnold’s that shows the existence of a non-trivial loop in the torus that does not meet the singular set of b. Here we must extend these results to orientable surfaces (see Lemma 3.3).

One decisive tool in the original proof of Arnold’s loop lemma for the torus is a result [1, Lemma 4] that was stated without a complete proof. For the sake of completeness, we offer in the Appendix a more detailed proof of that result for surfaces.

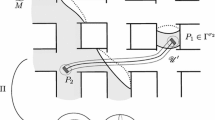
Several times in the sequel we will need a particular construction of covering spaces that we describe now. Suppose that M is the connected sum of a torus \(T={\mathbb {S}}^1\times {\mathbb {S}}^1\) and a surface S through disks D and \(D'\) in the interior of T and S, respectively.

Consider the covering \(\Pi ^{\bullet }:{\mathbb {R}}^2\rightarrow T\) such that \({\mathcal {Q}}\doteq [0,2\pi ]\times [0,2\pi ]\) is a fundamental domain, the y-axis is projected onto \(\theta _1\), the x-axis is projected onto \(\phi _1\), and \(\Pi ^{\bullet }(\partial {\mathcal {Q}})\cap D=\emptyset .\) We will then deal with the covering space \(\Pi _1:{\mathfrak {R}}\rightarrow M\), which is obtained by carrying out, through each pre-image of D, connected sums with copies of S.

In Fig. 1, we illustrate the case when S is another torus.

Fig. 1
figure 1

The covering \({\mathfrak {R}}\)

Full size image

3.1 The Case of Genus 2

Let us describe how to obtain the surface with boundary \(M^\sharp \) from M (cf. the comments made above about \(M^\sharp \)) when M is a bitorus. We consider a non-exact 1-form b defined on a bitorus M and denote by \(\Sigma (b)\) the singular set of b, i.e., the set of zeros of b.

Lemma 3.1

If a non-exact 1-form b is defined on M, there is a non-trivial loop \(\gamma \) in \(M\setminus \Sigma (b).\)

In the proof of this lemma we adapt some ideas from [1] where the analogue result for the case \(M={\mathbb {T}}^2\) was proved.

Proof

We can assume that \(\int _{\theta _1}b\ne 0.\) Construct the covering \({\mathfrak {R}}\) as in Fig. 1. Choose a component \({\mathscr {O}}\) of \({\mathfrak {R}}\setminus \Sigma (\Pi _1^*b)\) intersecting the y-axis. This is possible since \(\int _{\theta _1} b\ne 0.\) We can assume that \({\mathscr {O}}\) does not intersect any of its translates \({\mathscr {O}}+(2\pi r,2\pi s,0)\) with \(r,s\in {\mathbb {Z}}\) (otherwise, we would already have the desired curve). Call \({\mathscr {C}}_m\doteq \{m\}\times {\mathbb {R}}\), \(m\in {\mathbb {Z}}\), and \({\mathfrak {R}}_m\) the closure of region of \({\mathfrak {R}}\) between \({\mathscr {C}}_m\) and \({\mathscr {C}}_{m+1}.\) Write \(\{{\mathscr {O}}^k_m\}_{k\in {\mathbb {Z}}}\) for the components of \({\mathscr {O}}\cap {\mathfrak {R}}_m.\)

According to Lemma A.1 (see Appendix), we have \(\int _{{\mathscr {O}}^k_m\cap {\mathscr {C}}_m}\Pi _1^* b=\int _{{\mathscr {O}}^k_m\cap {\mathscr {C}}_{m+1}}\Pi _1^* b.\) This implies that

$$\begin{aligned} \int _{{\mathscr {O}}\cap {\mathscr {C}}_m}\Pi _1^* b=\int _{{\mathscr {O}}\cap {\mathscr {C}}_{m+1}}\Pi _1^*b. \end{aligned}$$
(3.1)

There are two possibilities: either there is \(n\in {\mathbb {Z}}\) such that \({\mathscr {O}}\cap {\mathscr {C}}_n=\emptyset \) or \({\mathscr {O}}\) intersects \({\mathscr {C}}_m\) for every \(m\in {\mathbb {Z}}.\) Notice that a non-empty intersection between \({\mathscr {O}}^k_m\) and \({\mathscr {C}}_m\) (and \({\mathscr {C}}_{m+1}\)) consists of sets diffeomorphic to open intervals. Also, the projections on \(\theta _1\) of every such interval are pairwise disjoint for every \(k,m\in {\mathbb {Z}}.\)

Hence in both cases, due to (3.1), it must be that \(\int _{\theta _1\cap \Pi _1({\mathscr {O}})}b=0.\) Reasoning in the same manner for every component \({\mathscr {O}}\) of \({\mathfrak {R}}\setminus \Sigma (\Pi _1^*b)\) intersecting the y-axis, the result is that \(\int _{\theta _1}b=0\), a contradiction.

We conclude that there exists such a component \({\mathscr {O}}\) intersecting one of its translates and then we may choose a smooth curve \({{\widetilde{\gamma }}}\) in \({\mathscr {O}}\) joining a point \(Q\in {\mathscr {O}}\) and its translate \(Q+(2\pi r,2\pi s,0).\) By construction, the projection \(\gamma =\Pi _1\circ {{\widetilde{\gamma }}}\) is non-trivial and does not meet \(\Sigma (b).\) \(\square \)

We now can move on to obtain our surface with boundary.

Step 1 There are two possibilities for the loop \(\gamma \) obtained above.

Case 1 Suppose first that \(\int _{\gamma }b=0.\)

Since \(\gamma \) is non-trivial, we can take a loop \(\delta \) on M having intersection number 1 with \(\gamma .\) We call V the union of tubular neighborhoods of \(\gamma \) and \(\delta \) in M, whose closure is a torus with one boundary component. Notice that V is diffeomorphic to the union of tubular neighborhoods of the canonical generators \(\theta _1\) and \(\phi _1\) of a torus \(T_1\) (Figure 2).

Fig. 2
figure 2

Curves \(\gamma \), \(\delta \), and the tubular neighborhoods

Full size image

Hence there is a diffeomorphism \(\varphi \) between M and the connected sum between \(T_1\) and another torus, taking \(\theta _1\) to \(\gamma \) and \(\phi _1\) to \(\delta .\)

Consider the covering space \({\mathfrak {R}}\) and set again \({\mathfrak {R}}_m\) for closure of the region of \({\mathfrak {R}}\) between \({\mathscr {C}}_m\) and \({\mathscr {C}}_{m+1}.\) Notice that \({\mathfrak {R}}_m\) covers a surface \(M_2\) with boundary consisting of two smooth curves and having genus 1 (first picture in Figure 3). We can then define a smooth closed 1-form \(b_2\) as the pushforward to \(M_2\) of the form \((\varphi \circ \Pi _1)^*b\) defined on \({\mathfrak {R}}_m.\)

Case 2 Here \(\int _{\gamma }b\) is not 0.

Claim

Under this condition, there is a loop \(\delta \) on \(M\setminus \Sigma (b)\) whose intersection number with \(\gamma \) is 1.

In fact, we can consider the surface \(M_2\) obtained above, which has two smooth curves \(\eta _1\) and \(\eta _2\) in the boundary. Write \({\mathscr {O}}\) for the component of \(M_2\setminus \Sigma (b_2)\) containing \(\eta _1.\)

If \(\eta _2\) were not contained in \({\mathscr {O}}\), we could apply Lemma A.1 for \({\mathscr {O}}\) and would conclude that \(\int _{{\mathscr {O}}\cap \partial M_2}b_2=\int _{\gamma }b=0.\) Thus \(\eta _2\subset {\mathscr {O}}\), and our claim is proved. \(\square \)

In this framework, we construct again the covering space \({\mathfrak {R}}\), by means of \(\gamma \) and the above \(\delta \), and now \(M_2\) will denote the closure of the region of \({\mathfrak {R}}\) inside \({\mathcal {Q}}\) (second picture in Fig. 3). Further, \(b_2\) will denote the restriction of the pullback \((\varphi \circ \Pi _1)^*b\) to \(M_2.\)

Fig. 3
figure 3

Surfaces \(M_2\) that can be obtained after Step 1

Full size image

Step 2 The result after Step 1 is that we have a closed 1-form \(b_2\) defined on a surface \(M_2\) of genus 1 and with boundary consisting of piecewise smooth curves. Moreover, notice that

figure a

If \(b_2\) is exact, the proof is complete. Otherwise, we have to apply the following version of Lemma 3.1 for \(M_2\) and \(b_2\):

Lemma 3.2

If \(b_2\) is not exact, then there is a non-trivial loop \(\gamma _2\) in the interior of \(M_2\) not intersecting \(\Sigma (b_2).\)

Indeed, we can assume that \(M_2\) is the connected sum of a torus \(T_2\) with a surface \(S_0\), of genus 0 and with boundary components, and that the integral of \(b_2\) along the generator \(\theta _2\) is not 0. The covering \({\mathfrak {R}}\) in this step is constructed after considering again \({\mathbb {R}}^2\), but with the y-axis projecting onto \(\theta _2\), the x-axis is projected onto \(\phi _2\), and by carrying out, in each fundamental domain, a connected sum with copies of \(S_0.\) Now, one can follow the proof of Lemma 3.1. The key point is that Eq. (3.1) remains true for \(b_2\), in view of \((\Diamond ).\)

We then can repeat Step 1, obtaining a closed 1-form \(b^\sharp \) defined on a surface of genus 0 and with boundary consisting of piecewise smooth curves. As \((\Diamond )\) will hold for \(b^\sharp \), it is necessarily an exact form. The possible resulting surfaces are depicted in Fig. 4.

Fig. 4
figure 4

Surfaces that can be obtained after Step 2

Full size image

The conclusion is that we can always find an exact form \(b^\sharp \) defined on a surface \(M^\sharp \) with boundary, and such that \(\Sigma (b^\sharp )\cap \partial M^\sharp =\emptyset .\)

3.2 General Case

Let us turn our attention again for the case when M is a connected sum of g tori \(T_k.\) Motivated by the previous section, a special surface with boundary will be obtained after inductively performing appropriate cuts, reducing the genus until reaching a surface with boundary where an exact form is defined.

Goal

To obtain, from M and b, a surface \(M^\sharp \) with boundary consisting of piecewise smooth curves such that

  • an exact 1-form \(b^\sharp \) is defined on \(M^\sharp \);

  • \(\partial M^\sharp \) does not intersect the singular set of \(b^\sharp .\)

First we state an auxiliary result, analogous to Lemma 3.2.

Lemma 3.3

Suppose that a 1-form \(b^\dag \) is defined on a surface \(M^\dag \) (possibly with boundary components). Assume that the boundary consists of piecewise smooth curves not in the singular set of \(b^\dag \), and that the integral of \(b^\dag \) along them is zero. If \(b^\dag \) is not exact, then there exists a non-trivial loop \(\gamma \) in \(M^\dag \setminus \Sigma (b^\dag ).\)

Indeed, we can assume that \(M^\dag \) is the connected sum of a torus \(T_k\) with a surface \(S^\dag \), of genus \(k-1\) and with boundary components, and that the integral of \(b^\dag \) along the generator \(\theta _k\) is not 0. A covering \({\mathfrak {R}}\) is constructed after considering again \({\mathbb {R}}^2\), but with the y-axis projecting onto \(\theta _k\), the x-axis is projected onto \(\phi _k\), and by carrying out, in each fundamental domain, a connected sum with copies of \(S^\dag .\) As in Lemma 3.2, one follows the proof of Lemma 3.1 and obtains the result.

The goal now can be achieved by induction on the genus. When \(M=S_g\), we proceed as in Sect. 3.1 - Step 1.

Suppose we have obtained a surface \(M_k\) of genus \(0<k<g\), with boundary consisting of piecewise smooth curves, on which a closed 1-form \(b_k\) is defined. Furthermore, suppose that the elements of \(\partial M_k\) do not intersect the singular set of \(b_k.\)

If \(b_k\) is not exact, we will apply Lemma 3.3 for \(M_k\), obtaining \(\gamma _k\) on \(M_k\setminus \Sigma (b_k).\)

Case 1 Suppose first that \(\int _{\gamma _k}b_k= 0.\)

Since \(\gamma _k\) is non-trivial, we can take a loop \(\delta _k\) in the interior of \(M_k\) having intersection number 1 with \(\gamma _k.\) We call V the union of tubular neighborhoods of \(\gamma _k\) and \(\delta _k\) in \(M_k\), whose closure is a torus with one boundary component. Notice that V is diffeomorphic to the union of tubular neighborhoods of the canonical generators \(\theta _k\) and \(\phi _k\) of a torus \(T_k.\)

Hence there is a diffeomorphism \(\varphi \) between \(M_k\) and the connected sum between \(T_k\) and a surface \(S^\dag \), of genus \(k-1\) and with boundary components, taking \(\theta _k\) to \(\gamma _k\) and \(\phi _k\) to \(\delta _k.\)

As above, construct the covering \(\Pi _k:{\mathfrak {R}}\rightarrow M_k\) and set again \({\mathfrak {R}}_m\) for the closure of region of \({\mathfrak {R}}\) between \({\mathscr {C}}_m\) and \({\mathscr {C}}_{m+1}.\) Notice that \({\mathfrak {R}}_m\) covers a surface \(M_{k-1}\) with boundary consisting of two smooth curves and having genus \(k-1.\) We can then define a smooth closed 1-form \(b_{k-1}\) as the pushforward of \((\varphi \circ \Pi _k)^*b_k\) to \(M_{k-1}.\)

Case 2 As for the case when \(\int _{\gamma _k}b_k\ne 0\), we have, as before:

Claim

There is a loop \(\delta _k\) on \(M_k\setminus \Sigma (b_k)\) whose intersection number with \(\gamma _k\) is 1.

Thus we construct again the covering space \({\mathfrak {R}}\), by means of \(\gamma _k\) and the above \(\delta _k\), and now \(M_{k-1}\) will denote the closure of the region of \({\mathfrak {R}}\) inside \({\mathcal {Q}}.\) Further, \(b_{k-1}\) will denote the restriction of \((\varphi \circ \Pi _k)^*b\) to \(M_{k-1}.\)

In any case, we then have a closed 1-form \(b_{k-1}\) defined on a surface \(M_{k-1}\) of genus \(k-1\) and with boundary not intersecting \(\Sigma (b_{k-1}).\) The integral of \(b_{k-1}\) along the boundary components is zero.

If \(b_{k-1}\) is exact, the proof is complete. Otherwise, we apply Lemma 3.3 for \(M_{k-1}\) and \(b_{k-1}\) and, therefore, repeat the process. As the genus of the surface with boundary keeps decreasing each iteration, this process will eventually stop. \(\square \)

Remark 3.4

After the latter proof, we call \(B^\sharp \) a primitive of \(b^\sharp \) defined on \(M^\sharp .\) As in [1], we can assume that the restriction \(B^\sharp \restriction _{\partial M^\sharp }\) has finitely many singular points, which will be indexed by J.

3.3 Obtaining the Estimates

Recall that we have obtained in the previous section a surface with boundary \(M^\sharp \), where an exact form \(b^\sharp \) is defined, and a smooth map from \(M^\sharp \) to M, which we will call \(\Phi .\)

Step 1. Suppose that \(b_{\sigma _0}<0.\) By hypothesis, for every \(\xi <0\), there is a curve \(\gamma (t,\xi )\) connecting t to \(\sigma _0(t)\) inside the sublevel set \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}.\) The projection of such a curve on M is a closed curve denoted by \(\lambda .\) If we follow the path \(\Phi ^{-1}(\lambda )\) from the pre-image \(t'\) of \(\Pi (t)\), there will be a first point p that will intercept the boundary of \(M^\sharp \) (otherwise, \(b^\sharp \) would not be exact).

By the construction of \(\Phi \), we can connect p, through a path \(\tau \) in \(\partial M^\sharp \), to a singular point \(p_j\), \(j\in J\), of the restriction \(B^\sharp \restriction _{\partial M^\sharp }\) such that \(B^\sharp \) is strictly decreasing on \(\tau .\)

Moreover, calling \(\gamma _0(t,\xi )\) the resulting curve connecting \(t'\) to \(p_j\), if \(s\in \gamma _0(t,\xi )\), then

$$\begin{aligned} B^\sharp (s)\leqslant B^\sharp (t')+\frac{1}{1+|\xi |}. \end{aligned}$$
(3.2)

Step 2.

Definition 3.5

By a smooth triangulation of a surface \(M^\dag \), we mean that there is a complex \({\mathcal {K}}\) and a homeomorphism \(h:|{\mathcal {K}}|\rightarrow M^\dag \) such that \(h\restriction _{K}\) is of class \(C^\infty \) for each simplex K of \({\mathcal {K}}.\) We also require that dh(q) be injective in the union of the simplices containing q.

Due to [18], \(M^\sharp \) has a smooth triangulation extending a smooth triangulation of its boundary.

Put \(T_0\doteq \{(x,y)\in {\mathbb {R}}^2: x+y\leqslant 1,\quad x,y\geqslant 0\}.\) Assuming that the two-dimensional simplices are \(K_n\), \(n=1,\ldots , m\), we have that h induces smooth maps \(h_n: T_0 \rightarrow h(K_n).\) Set \({\tilde{C}}\doteq {\text {max}}_n\Vert dh_n\Vert _{\infty }\) and \({\tilde{c}}\doteq {\text {min}}_n\Vert dh_n\Vert _{\infty }\ne 0.\)

For each \(j>0\), we subdivide \(T_0\) into the triangles \(T_0^k\) with vertices \((\frac{r}{2^j},\frac{s}{2^j})\), where r, s are integers in \([0,2^j].\) Therefore, \(M^\sharp \) is the union of N images \(h_n(T_0^k)\) of sub-triangles, where

$$\begin{aligned} N\leqslant \frac{{\text {vol}}(M^\sharp )2^{2j}}{2{\tilde{c}}}. \end{aligned}$$
(3.3)

Replace now \(\gamma _0(t,\xi )\) with \(\gamma _1(t,\xi )\) as follows. First, choose j such that

$$\begin{aligned} 2^{j-1}\leqslant (1+|\xi |)\Vert b^\sharp \Vert _{\infty }\leqslant 2^j. \end{aligned}$$
(3.4)

If T is the image \(h_n(T_0^k)\) of a sub-triangle and \(T\cap \gamma _0(t,\xi )\ne \emptyset \), we connect the first and the last point of \(\gamma _0(t,\xi )\) in T through the image of a segment.

The length of the resulting piecewise smooth curve \(\gamma _1(t,\xi )\) connecting t to \(p_j\) will then satisfy

$$\begin{aligned} |\gamma _1(t,\xi )|\leqslant {\tilde{C}}2^{-j}\sqrt{2} N\leqslant C'(1+|\xi |). \end{aligned}$$
(3.5)

Moreover, (3.2) and the right-hand side inequality of (3.4) allow us to conclude that, if \(s\in \gamma _1(t,\xi )\) and \(s'\in T\cap \gamma _0(t,\xi )\),

$$\begin{aligned} B^\sharp (s)\leqslant |B^\sharp (s)-B^\sharp (s')|+B^\sharp (s') \leqslant B^\sharp (t')+\frac{C''}{1+|\xi |}. \end{aligned}$$
(3.6)

Step 3. The image of \(\gamma _1(t,\xi )\) through \(\Phi \) on M can be lifted to \({\mathscr {U}}.\) Notice that this path will connect t to a point in \(\{\sigma (t_j): \sigma \in {\mathsf {E}},j\in J\}\)—where \(\Pi (t_j)=\Phi (p_j).\) Plugging it in (2.6) and making use of (3.5) and (3.6) yield the estimate

$$\begin{aligned} |\widehat{u}(t,\xi )|\leqslant K(1+|\xi |){\text {sup}}_{M}|{\widehat{f}}(\cdot ,\xi )|+|\widehat{u}(\sigma (t_j),\xi )|. \end{aligned}$$

As \(\sigma (t_j)\) can in turn be connected to \(\sigma _0\sigma (t_j)\) in \(\Omega _{{\widetilde{B}}(\sigma (t_j))+\frac{1}{1+|\xi |}}\), by using (2.5) we have

$$\begin{aligned} |\widehat{u}(\sigma (t_j),\xi )|\leqslant K_{\sigma ,j}{\text {sup}}_{M}|{\widehat{f}}(\cdot ,\xi )|. \end{aligned}$$

Since u is periodic and J is finite, we have the desired decay for \(\xi <0.\)

The proof follows analogously for \(\xi >0.\) \(\square \)

Remark 3.6

It should be noticed that \(\Phi \) is a diffeomorphism between \(M^\sharp \setminus \partial M^\sharp \) and the open subset \(M\setminus X\) of M, where X is a finite collection of loops in M. The plan here was inspired in [16, 17] in the sense that essentially the role of a ball centered at t is played now by a component \({\mathscr {F}}\) of the lift of \(M\setminus X\) to \({\widetilde{M}}.\) Hence, we can connect each of the points in the compact set \(\overline{{\mathscr {F}}}\) (which plays the role of a fundamental domain) to a finite subset of its, through the path above constructed yielding the estimates for the decay of the coefficients.

Remark 3.7

We see from this section that the fact stated in Remark 3.4 is crucial. Although its proof is not elaborated, another way to reach the estimates is to cover the boundary of \(M^\sharp \) with a finite number of closed balls \(\overline{{\mathscr {B}}_j}.\) It is not difficult to extend \(b^\sharp \) to these balls and assume that it has no singular point on them. Call now \(q_j=\min _{\overline{{\mathscr {B}}_j}}B^\sharp .\) We then construct the path \(\gamma _0(t,\xi )\) in Step 1 by connecting \(t'\) to p and p to \(q_j\), if \(p\in {\mathscr {B}}_j.\)

3.4 The Sufficient Part for \({\mathbb {T}}^2\)

We assume here that \(a\equiv 0\), that is, \(c=ib.\) A consequence of the computation obtained above is

Theorem 3.8

Assume that M is a closed orientable surface and that the 1-form b is smooth and closed. The following statements are equivalent:

  1. (1)

    \({\mathbb {L}}^\flat \doteq d_t+ib(t)\partial _x\) is globally solvable.

  2. (2)

    The semilevel sets \(\Omega ^r\doteq \{t\in M: {\widetilde{B}}>r\}\) and \(\Omega _r\doteq \{t\in M: {\widetilde{B}}<r\}\) are connected for every \(r\in {\mathbb {R}}.\)

In fact, the necessity of (2) for the global solvability of \({\mathbb {L}}^\flat \) was already proved in [16] for a closed manifold so we would be only concerned with (2) \(\implies \) (1).

Also, the implication (1) \(\implies \) (2) was proved in [2, 6]. However, since the method of obtaining a special surface with boundary is relatively simple for a torus M, it seems worth to give an alternative proof along these lines.

Suppose that b is not exact. By [1], if follows that there is a non-trivial loop \(\gamma \) on M not intersecting the singular set of b. We can find a loop \(\delta \) whose intersection number with \(\gamma \) is 1.

There is a diffeomorphism \(\varphi \) between M and a torus \(T_1\) taking \(\theta _1\) to \(\gamma \) and \(\phi _1\) to \(\delta .\) Consider here the covering space \({\mathfrak {R}}\) as \({\mathbb {R}}^2\) and set again \({\mathfrak {R}}_m=[m,m+1]\times {\mathbb {R}}.\) Notice that \({\mathfrak {R}}_m\) covers a cylinder \({\mathcal {C}}\doteq [0,2\pi ]\times {\mathbb {S}}^1.\) We can then define a smooth closed 1-form \(b_2\) on \({\mathcal {C}}\) as the pushforward of \((\varphi \circ \Pi _1)^*b\) to \({\mathcal {C}}\) (here \(\Pi _1=\Pi ^\bullet \)).

When \(\int _{\gamma }b=0\), \(b_2\) is exact and nothing else remains to be performed.

When \(\int _{\gamma }b\ne 0\), \(b_2\) is not exact. As previously, due to Lemma A.1, we are able to find a loop \(\delta \) on \(M\setminus \Sigma (b)\) whose intersection number with \(\gamma \) is 1. In this case, we construct again the covering space \({\mathfrak {R}}\), by means of \(\gamma \) and the above \(\delta \), and define a 1-form on the square \({\mathcal {Q}}\) by the restriction of \((\varphi \circ \Pi _1)^*b\) to \({\mathcal {Q}}\), which is exact.

Either way, we have an exact form \(b^\sharp \) defined on a surface \(M^\sharp \) with boundary, and \(\Sigma (b^\sharp )\cap \partial M^\sharp =\emptyset .\) Now the computations in the previous section can be applied for \(M^\sharp \) and \(b^\sharp \) in the same way.

4 Estimates for the Class (B)

The choice of the path connecting \({\tilde{t}}\) to a translate \(\sigma ({\tilde{t}})\) in (2.5) will obey an additional rule to those considered at the beginning of Sect. 3: the term \((e^{i\xi c_{\sigma }}-1)^{-1}\) must have polynomial growth with respect to \(|\xi |\), which will be the contribution of the real part a of the form c.

We can assume that \({\widetilde{B}}\) is bounded on the component of t for pairs in the class (B)—such a component is denoted by \({{\mathcal {O}}}'.\) Consider a component \({{\mathcal {O}}}\) of \(\Omega _r\) inside \({{\mathcal {O}}}'\), with r being a regular value of \({\widetilde{B}}\) and \({\widetilde{B}}(t)<r<{\widetilde{B}}(t)+\frac{1}{2(1+|\xi |)}.\) Our aim is to prove the following

Proposition 4.1

For each pair \((t,\xi )\) in the class (B), there is a piecewise smooth closed curve \(\gamma (t,\xi )\) in \({\widetilde{M}}\) based on t such that

  1. (i)

    \(\gamma (t,\xi )\) is contained in \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}\);

  2. (ii)

    \(|\gamma (t,\xi )|\leqslant C_0(1+|\xi |)\);

  3. (iii)

    \((e^{i\xi T_a(\gamma (t,\xi ))}-1)^{-1}\geqslant {\frac{K}{|\xi |^s}}\) for \(K>0.\)

Proof

Consider a smooth triangulation \({\mathcal {K}}\) for M. Put \(T_0\doteq \{(x,y)\in {\mathbb {R}}^2: x+y\leqslant 1,\quad x,y\geqslant 0\}.\) Assuming that the two-dimensional simplices are \(K_n\), \(n=1,\ldots , m\), we have smooth maps \(h_n: T_0 \rightarrow h(K_n).\) Set \({\tilde{C}}\doteq {\text {max}}_n\Vert dh_n\Vert _{\infty }\) and \({\tilde{c}}\doteq {\text {min}}_n\Vert dh_n\Vert _{\infty }\ne 0.\)

For each \(j>0\), we subdivide \(T_0\) into the triangles \(T_0^k\) with vertices \((\frac{r}{2^j},\frac{s}{2^j})\), where r, s are integers in \([0,2^j].\) Therefore, M is the union of N images \(h_n(T_0^k)\) of sub-triangles, where

$$\begin{aligned} N\leqslant \frac{{\text {vol}}(M)2^{2j}}{2{\tilde{c}}}. \end{aligned}$$
(4.1)

Choose j such that

$$\begin{aligned} 2^{j-1}\leqslant {\tilde{C}}(1+|\xi |)\Vert b\Vert _{\infty }\leqslant 2^{j}. \end{aligned}$$
(4.2)

Notice that a smooth triangulation \({\mathcal {K}}\) for M induces one for \({\widetilde{M}}.\) Consider the union of “triangles” \({\mathcal {T}}\) in \({\widetilde{M}}\) intersecting \({{\mathcal {O}}}.\) Notice that such triangles are in \({{\mathcal {O}}}'.\) In fact, suppose that \(s'\in T\) and \(T\in {\mathcal {T}}.\) If \(s\in {{\mathcal {O}}}\), then

$$\begin{aligned} {\widetilde{B}}(s')<{\widetilde{B}}(s)+{\tilde{C}}2^{-j}\sqrt{2}\Vert b\Vert _{\infty }<{\widetilde{B}}(t)+\frac{1}{1+|\xi |}. \end{aligned}$$

Because \({{\mathcal {O}}}'\) can be projected injectively on M, the number of triangles in \({\mathcal {T}}\) is less or equal to N.

Now notice that the edges and the vertices of the triangles in \({\mathcal {T}}\) define a graph \(\Lambda .\) The fundamental group of \(\Lambda \) is generated by a finite set of piecewise smooth closed curves, called \({\mathscr {C}}\), such that each edge of its appears at most once in every curve [15]. By subdividing a triangle, if necessary, we can assume that \(t\in \Lambda .\)

For each generator \([\nu _l]\) of \(i^*(H_1({{\mathcal {O}}}),{\mathbb {Z}}))\), we have that \(T_a([\nu _l])\) is an integer combination of some \(T_a(\mu _r)\) with \(\mu _r\in {\mathscr {C}}.\) This implies that the vector with entries \((2\pi )^{-1}T_a(\mu _r)\) is neither a rational nor a Liouville vector. Hence, an adaptation of Lemma 2.5 gives us a closed curve denoted by \(\gamma (t,\xi )\) such that

$$\begin{aligned} (e^{i\xi T_a(\gamma (t,\xi ))}-1)^{-1}\geqslant \frac{K}{|\xi |^s}\quad \text {for}\;K>0. \end{aligned}$$

Notice that the length of \(\gamma (t,\xi )\) satisfies

$$\begin{aligned} |\gamma (t,\xi )|\leqslant 3N{\tilde{C}}2^{-j}\sqrt{2}, \end{aligned}$$
(4.3)

and then by (4.1) and the left-hand side of (4.2) the proposition is proved. \(\square \)

The curve \(\gamma (t,\xi )\) can be lifted to \({\mathscr {U}}\) and then plugged in (2.5) in order to yield the desired decay for the Fourier coefficients.

The conclusion after Sections 3 and 4 is the decay for \(\xi <0.\) In order to obtain the decay for \(\xi >0\), we carry out the same proof by using \(\Omega ^{{\widetilde{B}}(t)-\frac{1}{1+|\xi |}}\) and \(\Omega ^r\) with \({\widetilde{B}}(t)-\frac{1}{2(1+|\xi |)}<r<{\widetilde{B}}(t).\)

5 Proof of (II) \(\implies \) (I)—Case When b is Exact

When (II.1) holds, we will reason likewise when b is not exact.

Set \(t_0\doteq {\text {min}}_{s \in M}{\widetilde{B}}(s).\) We divide the pairs \((t,\xi )\in {\widetilde{M}}\times {\mathbb {Z}}^-\) in two classes. The class (A) consists of the pairs \((t,\xi )\) for which

t and \(t_0\) are in the same component of \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}.\)

As for the pairs in the class (B),

t and \(t_0\) are in different components of \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}.\)

For the pairs in the class (A), we make use of the path \(\gamma _0(t,\xi )\), obtained in [12], that connects \(t_0\) to t and satisfies

  • \(\gamma _0(t,\xi )\) is contained in \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}\);

  • \(|\gamma _0(t,\xi )|\leqslant C_0(1+|\xi |)^d\).

The decay follows then from plugging the lift of \(\gamma _0(t,\xi )\) in (2.6).

As for pairs in the class (B), call \({{\mathcal {O}}}'\) the component of \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}\) containing t. Consider a component \({{\mathcal {O}}}\) of \(\Omega _r\) inside \({{\mathcal {O}}}'\), with r being a regular value of \({\widetilde{B}}\) and \({\widetilde{B}}(t)<r<{\widetilde{B}}(t)+\frac{1}{2(1+|\xi |)}.\)

By a proof similar to Proposition 4.1, if (II.1) holds, we have:

Proposition 5.1

For each pair \((t,\xi )\) in the class (B), there is a piecewise smooth closed curve \(\gamma (t,\xi )\) in \({\widetilde{M}}\) based on t such that

  1. (i)

    \(\gamma (t,\xi )\) is contained in \(\Omega _{{\widetilde{B}}(t)+\frac{1}{1+|\xi |}}\);

  2. (ii)

    \(|\gamma (t,\xi )|\leqslant C_0(1+|\xi |)^d\);

  3. (iii)

    \((e^{i\xi T_a(\gamma (t,\xi ))}-1)^{-1}\geqslant \displaystyle {\frac{K}{|\xi |^s}}\) for \(K>0.\)

The curve \(\gamma (t,\xi )\) can be lifted to \({\mathscr {U}}\) and then plugged in (2.5) in order to yield the desired decay for \((t,\xi )\in \) (B).

The conclusion is the decay for \(\xi <0.\) In order to obtain the decay for \(\xi >0\), we carry out the same proof by using \(\Omega ^{{\widetilde{B}}(t)-\frac{1}{1+|\xi |}}\) and \(\Omega ^r\), with \({\widetilde{B}}(t)-\frac{1}{2(1+|\xi |)}<r<{\widetilde{B}}(t).\) This finishes the proof of (II.1) implies (I) when b is exact.

If (II.2) holds, we can define the Fourier coefficients of a candidate to the global solution of the system and prove that they satisfy the required estimates. Denote by q is the smallest positive integer such that qa is integral and set \(J\doteq q{\mathbb {Z}}^-.\)

First we will define the candidate \({\widehat{u}}(p,\xi )\) for \(p\in M\) and \(\xi \in J.\) Define \({\mathscr {D}}'_J\doteq \{u\in {\mathscr {D}}'(M\times {\mathbb {S}}^1): u(t,x)=\sum _{\xi \in J}{\widehat{u}}(t,\xi )e^{i\xi x}\}.\)

Notice that for \(\xi \in J\) the function \(s\mapsto e^{-i\xi A(s)}\) is the lifting of a function defined on M because qa is integral. Consider the isomorphism T of \({\mathscr {D}}'_J\) given by

$$\begin{aligned} T\left( \sum _{\xi \in J}{\widehat{u}}(t,\xi )e^{i\xi x}\right) =\sum _{\xi \in J}{\widehat{u}}(t,\xi )e^{-i\xi A(t)}e^{i\xi x}. \end{aligned}$$

Hence, we have \(T^{-1}{\mathbb {L}} T={\mathbb {L}}^\flat =d_t+ib(t)\partial _x.\) Since the semilevel sets of a primitive \({\widetilde{B}}\) of b are connected, due to the above estimates from [12], it is possible to define the Fourier coefficients of a candidate to the global solution to \({\mathbb {L}}^\flat w=g\)—provided g satisfies the respective compatibility conditions—and prove their uniformly rapid decay. Notice that if \(f\in {\mathbb {E}}\), then \(g=T^{-1}f\) is such that \(e^{-i\xi {\widetilde{B}}(\cdot )}{\widehat{g}}(\cdot ,\xi )\) is exact for every \(\xi \in J.\) We then define \({\widehat{u}}(p,\xi )\doteq \widehat{Tw}(p,\xi )\) for \(\xi \in J.\)

Notice that \(J={\mathbb {Z}}^-\) if a is integral (or, equivalently, if \(q=1\)).

The coefficients \({\widehat{u}}(t,\xi )\) for \(\xi \in {\mathbb {Z}}^-\setminus J\), in turn, will be defined by (2.5), since when \(\xi \notin J\) there exists \(\sigma \in {\mathsf {E}}\) such that \(i\xi c_{\sigma }=i\xi a_{\sigma }\notin 2\pi i{\mathbb {Z}}.\)

In fact, first, given \(t\in M\) and \(\xi <0\), set \({{\mathcal {O}}}\in {\mathscr {A}}\) for the component of \(\Omega _r\) containing t, with \({\widetilde{B}}(t)<r<{\widetilde{B}}(t)+\frac{1}{2(1+|\xi |)}.\) Notice that \(I({{\mathcal {O}}})\) behaves as both a non-rational and a non-Liouville vector with respect to the denominators that are not in J since \(|I({{\mathcal {O}}})-\frac{P}{q}|\geqslant \frac{1}{|q|}\) for every \(P\in {\mathbb {Z}}^{m}\) and \(q\notin J.\) Now apply Proposition 5.1 for \(\xi \notin J.\) We finish plugging the lift of \(\gamma (t,\xi )\) to \({\mathscr {U}}\) in (2.5).

The proof for \(\xi >0\) is analogous.

6 Proof of (I) Implies (II)

In this section, the following lemma will be important (see [17]).

Lemma 6.1

Suppose that \(I({{\mathcal {O}}})\) is a Liouville vector. Then there exist a sequence of real smooth closed 1-forms \(\{P_j\}_{j\in {\mathbb {Z}}^+}\) such that

$$\begin{aligned} T_{P_j}(\gamma ')\in 2\pi {\mathbb {Z}}\quad \text {for every}\;\gamma '\in \Gamma ({{\mathcal {O}}}); \end{aligned}$$

a sequence of integer \(q_j\) with \(q_j>1\); and \(C>0\) satisfying

$$\begin{aligned} \left\| a-\frac{1}{q_j}\cdot P_j\right\| _{\infty }<\frac{C}{q^j_j}. \end{aligned}$$

Now we move on to the proof of the necessity in Theorem 1.1. Assume that neither (II.1) nor (II.2) holds. Hence, we will be in one of the three situations described below that will be labeled as (A), (B) and (C).

(A) There is \({{\mathcal {O}}}\in {\mathscr {A}}\) such that \(I({{\mathcal {O}}})\) is a Liouville vector.

First we will suppose that \(b\not \equiv 0.\) Assuming that \({{\mathcal {O}}}\) is a component of a superlevel set, that is, \({{\mathcal {O}}}\subset \Omega ^{r}\), consider levels \(r_1\) and \(r_2\) both smaller than the maximum K of \({\widetilde{B}}\) on \({{\mathcal {O}}}\) with \(r<r_1<r_2.\) Set \(\Gamma ^{s}\doteq \{t\in {{\mathcal {O}}}: {\widetilde{B}}(t)>s\}.\) We have \(\Gamma ^{r_2}\subset \Gamma ^{r_1}\subset {{\mathcal {O}}}.\)

Let \(\chi :M\rightarrow \{0,1\}\) be the characteristic function of the open set \(\Pi (O)\subset M\):

$$\begin{aligned} \chi (t) = \left\{ \begin{array}{lll} 1, &{} t\in \Pi ({{\mathcal {O}}}), \\ 0, &{} t\notin \Pi ({{\mathcal {O}}}). \end{array} \right. \end{aligned}$$

Next let \(\psi :{\mathbb {R}}\rightarrow [0,1]\) be a smooth non-negative function on \({\mathbb {R}}\) satisfying

  • \(\psi ^{-1}(\{1\})=[r_2,\infty )\);

  • \(\psi ^{-1}(\{0\})=(-\infty ,r_1]\);

As \({{\mathcal {O}}}\) can be projected injectively on M, we can define \(B^\circ \doteq {\widetilde{B}}\circ \Pi ^{-1}\) on \(\Pi ({{\mathcal {O}}}).\)

We then set, for \(t\in M\),

$$\begin{aligned} F(t)=\chi (t)\psi (B^\circ (t)). \end{aligned}$$

Fact 1

  • \(F:M\rightarrow [0,1]\) is smooth;

  • F has support contained in \(\Pi (\overline{\Gamma ^{r_1}}).\)

  • \(B^\circ (t)\leqslant r_2, \quad \forall t\in {\text {supp}}(d_tF).\)

Proof

In order to prove the first assertion, we only have to check that F is smooth at a point \(p\in M\) such that there is a sequence \(\{p_n\}_{n\in {\mathbb {Z}}^+}\) converging to p with \(F(p_n)\ne 0\) and \(F(p)=0.\)

Choose then \({\widetilde{p}}_n\in \overline{\Gamma ^{r_1}}\) with \(\Pi ({\widetilde{p}}_n)=p_n.\) Consider a sufficiently small connected neighborhood N of p evenly covered by \(\Pi \) such that, if \({\widetilde{x}}\) and \({\widetilde{y}}\) belong to a component of \(\Pi ^{-1}(N)\) (thus isometric to N), then \(|{\widetilde{B}}({\widetilde{x}})-{\widetilde{B}}({\widetilde{y}})|<r_1-r.\) This shows that the components of \(\Pi ^{-1}(N)\) which intercept \(\{\widetilde{p_n}\}_{n\in {\mathbb {Z}}^+}\) are in \({{\mathcal {O}}}.\) Hence F is smooth at p.

The remaining items are immediate from the construction of F. \(\square \)

When \(I({{\mathcal {O}}})\) is a Liouville vector, Lemma 6.1 asserts that there exist a sequence of closed forms \(\{P_{j}\}\), \(j\in {\mathbb {Z}}^+\), and integers \(q_{j}>1\) such that \(\{q_{j}^{j}(a-{P_{j}}/{q_{j}})\}\) is bounded (the sequence \(\{q_{j}\}\) can be assumed to go to the infinity).

Also, it says that \(T_{P_j}(\gamma )\in 2\pi {\mathbb {Z}}\) for every closed curve \(\gamma \in C^\infty ([0,1],{{\mathcal {O}}}).\) If we denote by \(A_{j}\) a primitive of \({P_{j}}/{q_{j}}\) on \({\mathscr {U}}\), this allows us to define the functions \(e^{-iq_j A_j(\cdot )}\in C^\infty (\Pi ({{\mathcal {O}}})).\) Finally we set

$$\begin{aligned} v(t,q_{j})\doteq \beta _{j}e^{-iq_j A_{j}(t)}e^{q_j B^\circ (t)}F(t), \end{aligned}$$

and we have

$$\begin{aligned} d_tv(t,q_{j})+iq_{j}c(t)v(t,q_{j})= f(t,q_{j}), \end{aligned}$$
(6.1)

where

$$\begin{aligned} f(t,q_{j})=\beta _{j}e^{-iq_j A_{j}(t)}e^{q_j B^\circ (t)}[iq_j\left( a-\frac{P_j}{q_j}\right) F(t)+d_tF(t)]. \end{aligned}$$

The sequence \(\{\beta _{j}\}\) will be chosen in such a way that \(\{v(t,q_{j})\}\) does not have tempered growth although the \(f(t,q_{j})\) given by (6.1) will be the Fourier coefficients of a smooth 1-form f on M after setting the remaining frequencies (\(\xi \ne q_j\)) equal to zero.

In order to do this, define, for each \(j\in {\mathbb {Z}}^+\), \(\beta _j\doteq {\text {min}}\{e^{q_j\frac{\varepsilon }{2}}e^{-q_jK},q^\frac{j}{2}_je^{-q_jK}\}\), where \(\varepsilon \doteq K-r_2>0.\)

There is a point \(t^*\in \Pi ({{\mathcal {O}}})\) such that \(B^\circ (t^*)=K\) (see [16]). Therefore, we have \(|v(t^*,q_j)|={\text {min}}\{e^{q_j\frac{\varepsilon }{2}},q^\frac{j}{2}_j\}.\) Using that \(I({{\mathcal {O}}})\) is Liouville and Fact 1, we derive that

$$\begin{aligned} |f(t,q_j)|\leqslant C\beta _j\left( \frac{e^{q_jK}}{q^{j-1}_j}+e^{q_j(K-\varepsilon )}\right) \leqslant C\left( \frac{1}{q^{\frac{j}{2}-1}_j}+e^{-q_j\frac{\varepsilon }{2}}\right) , \end{aligned}$$
(6.2)

as desired.

Equations (6.1) and (6.2) also reveal that \(f\in {\mathbb {E}}.\) Moreover, since there is \(\sigma \in {\mathsf {E}}\) such that \(c_{\sigma }\notin 2\pi {\mathbb {Q}}\), by (2.5) the unique solution defined on M to the homogeneous version of the differential equation in (6.1) is null for every Fourier frequency. Hence, any candidate to solve \({\mathbb {L}}u=f\) must have the Fourier coefficients given by \(v(t,q_{j})\) in these respective frequencies. The conclusion is that we cannot have a distribution solving the system.

If \(b\equiv 0\), then \({{\mathcal {O}}}\) is the whole manifold. The above computations can be carried out by defining \(F\equiv 1\) on M in this case.

(B) There exist \({{\mathcal {O}}}\in {\mathscr {A}}\) and \(q\in {\mathbb {Z}}\) such that \(qI({{\mathcal {O}}})\in {\mathbb {Z}}^{m}.\) Further, b is not exact or qa is not integral.

In this case, \(b\not \equiv 0\), and we define F as above once again. Lemma 6.1 says that \(q T_a(\gamma )\in 2\pi {\mathbb {Z}}\) for every closed curve \(\gamma \in C^\infty ([0,1],{{\mathcal {O}}}).\) This allows us to define the functions \(e^{-ijqA(\cdot )}\in C^\infty (\Pi ({{\mathcal {O}}})).\) We again set

$$\begin{aligned} v(t,jq)\doteq \beta _{j}e^{-ijq A(t)}e^{jq B^\circ (t)}F(t). \end{aligned}$$

Thus

$$\begin{aligned} d_tv(t,jq)+ijqc(t)v(t,jq)= f(t,jq), \end{aligned}$$

where

$$\begin{aligned} f(t,jq)=\beta _{j}e^{-ijq A(t)}e^{jq B^\circ (t)}d_tF(t). \end{aligned}$$

We also set \(\beta _{j}\doteq e^{jq\frac{\varepsilon }{2}-jqK}.\) As before, \(\{v(t,jq)\}\) does not have tempered growth and

$$\begin{aligned} |f(t,jq)|\leqslant C\beta _j e^{jq(K-\varepsilon )}\leqslant Ce^{-jq\frac{\varepsilon }{2}}, \end{aligned}$$

which indeed defines an element of \({\mathbb {E}}\) (setting zero for the remaining Fourier frequencies).

As either b is not exact or qa is not integral, there is \(\sigma \in {\mathsf {E}}\) such that \(qc_{\sigma }\notin 2\pi {\mathbb {Z}}.\) Hence, the unique solution defined on M to the homogeneous version of the differential equation is null for each frequency multiple of q, and a candidate to solve \({\mathbb {L}}u=f\) must have the Fourier coefficients given by v(t, jq) in these respective frequencies. Therefore, again we do not have a distribution solving the system.

(C) The 1-forms a and b are, respectively, rational and exact, and there is a disconnected semilevel set of the primitive \({\widetilde{B}}\) of b on M.

First we state a variation of a celebrated lemma of Hörmander’s on a priori estimates. The version presented here is quite similar to the standard one in [19] and need not be proved.

Lemma 6.2

If \({\mathbb {E}}\) is closed linear subspace of \(C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{1,0})\) and \({\mathbb {L}}\) is globally solvable, then there exist constants \(C>0\) and \(m\in {\mathbb {Z}}^+\) such that, for all \(f\in {\mathbb {E}}\) and \(g\in C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{1,0})\),

$$\begin{aligned} \left| \int _{M\times {\mathbb {S}}^1}\langle f, g\rangle \right| \leqslant C \Vert f\Vert _{m}\Vert {\mathbb {L}}^*g\Vert _{m}, \end{aligned}$$

where \({\mathbb {L}}^*\) is the adjoint operator of \({\mathbb {L}}.\)

Here \(\Vert v\Vert _m={\text {sup}}_{M\times {\mathbb {S}}^1}\sum _{|\beta |\leqslant m}|\partial ^{\beta }v(t,x)|\), where \(|\beta |\) denotes the order of a multi-index \(\beta .\)

If there is a disconnected semilevel set of \({\widetilde{B}}\) on M, the operator \({\mathbb {L}}^\flat =d_t+ib(t)\partial _x\) is not globally solvable since (see [12]) there exist 1-forms \(f_0,g_0\) on M, \(f_0\) exact, such that, by setting \(f^\sharp _j(t,x)\doteq e^{j {\widetilde{B}}(t)+ixj}f_0(t)\) and \(g^\sharp _j(t,x)e^{-j {\widetilde{B}}(t)-ixj}g_0(t)\), we have

$$\begin{aligned} I_0\doteq \int _{M\times {\mathbb {S}}^1}\langle f^\sharp _j, g^\sharp _j\rangle \ne 0\text {, and} \\ \Vert f^\sharp _j\Vert _{m}\Vert (\mathbb {L}^\flat )^*(g^{\sharp }_j)\Vert _{m}\rightarrow 0\text { when }j\rightarrow \infty . \end{aligned}$$

Notice that if qa is integral, the function \(s\mapsto e^{-ijq A(s)}\) can be projected on the whole manifold M.

We then consider the smooth 1-forms \(f_j,g_j\) on M having jq-Fourier coefficients equal to \(e^{jq {\widetilde{B}}(t)-ijq A(t)}f_0(t)\) and \(e^{-jq {\widetilde{B}}(t)+ijq A(t)}g_0(t)\), respectively, and equal to zero for the remaining frequencies.

Clearly \(f_j\in {\mathbb {E}}\) and \(f_{j},g_{j}\) jointly violate Lemma 6.2 for the operator \({\mathbb {L}}=d_t+c(t)\partial _x.\)

Remark 6.3

Despite the general result of [12] assumes that M is orientable, at the first level of the complex the inequalities in Lemma 6.2 can be violated in an orientable neighborhood of a certain path (as in [16], for instance), and then the orientability need not be assumed here.

7 Comments

The result in Theorem 1.1 completely characterizes the global solvability at the first level of the complex for tube structures of co-rank 1, with forms defined on orientable surfaces. It completes, for instance, the problem of the global solvability when \(M={\mathbb {T}}^2\), where there were some subclasses (with \(a\not \equiv 0\)) for which it still remained open.

Furthermore, we have seen that some arguments in Theorem 1.1 hold when M is a closed manifold of dimension n. Here we discuss some of the consequences of it.

In fact, the hypotheses on the dimension was essential only in Sect. 3, when proving estimates involving the paths used in the formulae of the solution, for points that can be connected to some of its translates inside a semilevel set. In particular, we can state the next two corollaries.

Corollary 7.1

Assume that M is a closed manifold and that the 1-form c is smooth and closed. If \({\mathbb {L}}\) is globally solvable, then one of the two conditions below is satisfied:

  1. (1)

    \({\mathscr {A}}=\emptyset \), or, for every \({{\mathcal {O}}}\in {\mathscr {A}}\), \(I({{\mathcal {O}}})\) is neither a rational nor a Liouville vector.

  2. (2)

    The form b is exact (\({\widetilde{M}}=M\)) and the semilevel sets \(\{t\in M: {\widetilde{B}}(t)>r\}\) and \(\{t\in M: {\widetilde{B}}(t)<r\}\) are connected for every \(r\in {\mathbb {R}}\); in addition, a is rational, and if \(q\in {\mathbb {Z}}\) is such that \(qI({{\mathcal {O}}})\in {\mathbb {Z}}^m\) for \({{\mathcal {O}}}\in {\mathscr {A}}\), then qa is integral.

Corollary 7.1 was proved in [16] for the case when \(a\equiv 0.\)

When b is exact, we have here made use of the estimates obtained in [12], so we have a proof of

Corollary 7.2

Assume that M is a closed manifold and that the 1-form \(c=a+ib\) is smooth and closed with b exact. The following statements are equivalent:

  1. (I)

    \({\mathbb {L}}\) is globally solvable.

    1. (II.1)

      For every \({{\mathcal {O}}}\in {\mathscr {A}}\), \(I({{\mathcal {O}}})\) is neither a rational nor a Liouville vector.

    2. (II.2)

      The semilevel sets \(\{t\in M: {\widetilde{B}}(t)>r\}\) and \(\{t\in M: {\widetilde{B}}(t)<r\}\) are connected for every \(r\in {\mathbb {R}}\); in addition, a is rational, and if \(q\in {\mathbb {Z}}\) is such that \(qI({{\mathcal {O}}})\in {\mathbb {Z}}^m\) for \({{\mathcal {O}}}\in {\mathscr {A}}\), then qa is integral.

Notice that Corollary 7.2 retrieves [12] when a is exact.

Now, denote by \({\text {rank}}(b)\) the maximal number of elements in \(\{\int _{\delta }b: \delta \in H_1(M,{\mathbb {Z}})\}\) which are linearly independent over \({\mathbb {Z}}\) (for instance, when b is exact, \(r=0\)). In [9], such estimates were proved for the case when \({\text {rank}}(b)=1\), so we also can state:

Corollary 7.3

Assume that M is a closed surface and that the 1-form \(c=a+ib\) is smooth and closed with \({\text {rank}}(b)=1.\) The following statements are equivalent:

  1. (1)

    \({\mathbb {L}}\) is globally solvable.

  2. (2)

    \({\mathscr {A}}=\emptyset \), or, for every \({{\mathcal {O}}}\in {\mathscr {A}}\), \(I({{\mathcal {O}}})\) is neither a rational nor a Liouville vector.

One then might conjecture Theorem 1.1 for a general closed manifold. It is, however, fair to have the impression that, given the nature of the topological tools for dimension 2 used in the proof of the estimates involving the paths, the corresponding proof for higher dimensions is much more involved. In Appendix we raise a question related to it.

We also furnish a result for a special class of examples.

Corollary 7.4

Assume that M is a closed manifold and b has only isolate singular points. The following statements are equivalent:

  1. (I)

    \({\mathbb {L}}\) is globally solvable.

  2. (II)

    One of the two conditions below is satisfied:

    1. (II.1)

      The local primitives of b are open at any singular point.

    2. (II.2)

      The form b is exact, the semilevel sets \(\{t\in M: {\widetilde{B}}(t)>r\}\) and \(\{t\in M: {\widetilde{B}}(t)<r\}\) are connected for every \(r\in {\mathbb {R}}\), and a is integral.

When b is exact, the result is already proved. Otherwise, one can follow the line of the proof of (II.1) \(\implies \) (1). In fact, here it is not necessary to obtain a compact set like \(M^\sharp \), since the approach of finding a path that grants the estimates can be carried out by means of a small ball centered at a singular point and having no singular points at its boundary.

As a remark, Theorem 1.1 and the above corollaries furnish another proof of the result obtained in [17], in the real analytic setup. Indeed, although in the literature this is the first appearance of a vector \(I({{\mathcal {O}}})\) defined for a component of a regular semilevel set, it is the natural generalization of the vector \(I(\Sigma )\) for a component \(\Sigma \) of the singular set (on which b is not open at any of its points), as properties of a on a neighborhood of \(\Sigma \) were analyzed in [17]. Moreover, the mentioned techniques introduced in [19] were so far only applied under the hypothesis of the connectedness of the semilevel sets, and this definition becomes useful to broaden its usage.

Despite that, the estimates for the Fourier coefficients obtained in [17] rely on properties of real analytic functions and, because of it, are more refined.

7.1 Global Hypoellitpticity of \({\mathbb {L}}\) and Global Solvability of \({\mathbb {L}}^{n-1}\)

Likewise in [17], we can summarize a global regularity result for the operator (1.1) as a consequence of the proof of Theorem 1.1, namely

Theorem 7.5

Assume that M is a closed orientable surface and that the 1-form c is smooth and closed. The following statements are equivalent:

  1. (1)

    \({\mathbb {L}}\) is globally hypoelliptic, in the sense of Definition 2.3;

  2. (2)

    \({\mathscr {A}}=\emptyset \), or for every \({{\mathcal {O}}}\in {\mathscr {A}}\), \(I({{\mathcal {O}}})\) is neither a rational nor a Liouville vector.

Indeed, when (2) holds it follows that \({\text {Ker}}{\mathbb {L}}\simeq {\mathbb {C}}.\) If \({\mathbb {L}}u=f\), then \(f\in {\mathbb {E}}\), and by Theorem 1.1 there exists a smooth solution \(u'\) to the system. Hence \(u-u'\) is constant, and one implication is proved. By assuming that (2) does not hold, we are in the situations (A) and (B) described in Sect. 6. It is enough then to take \(\beta _j=1\) there in order to obtain \(u\in {\mathscr {D}}'(M\times {\mathbb {S}}^1)\) not smooth at \((t^*,x)\in \Sigma (b)\times {\mathbb {S}}^1\) and such that \({\mathbb {L}}u=f\in C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{1,0}).\)

Concerning the global solvability of \({\mathbb {L}}^{n-1}\), we can state:

Theorem 7.6

Assume that M is a closed orientable surface and that the 1-form c is smooth and closed. The following statements are equivalent:

  1. (1)

    \({\mathbb {L}}\) is globally solvable, in the sense of Definition 2.3.

  2. (2)

    For every \(f\in C^\infty (M\times {\mathbb {S}}^1,\Lambda ^{2,0})\) orthogonal to the kernel of \({\mathbb {L}}\) there exists \(u\in {\mathscr {D}}'(M\times {\mathbb {S}}^1,\Lambda ^{1,0})\) satisfying \({\mathbb {L}}^{1}u=f.\)

As noticed in [17], one implication can be achieved by following [5], since the technique there consists of violating a priori estimates and it bears on the fact that it is possible to define certain functions in a neighborhood of a component of the singular set (see [5, Lemma 3.2]). Such functions can be replaced by the functions used in Sect. 6. The other implication follows from a general result of functional analysis after proving the global hypoellipticity of \({\mathbb {L}}\), which holds now in view of the above comment.

Analogue versions of these results hold under the conditions of Corollaries 7.2, 7.3, and 7.4.