Bubble Dynamics in Turbulent Duct Flows: Lattice-Boltzmann Simulations and Drop Tower Experiments

Abstract

Lattice-Boltzmann simulations of a turbulent duct flow have been carried out to obtain trajectories of passive tracers in the conditions of a series of microgravity experiments of turbulent bubble suspensions. The statistics of these passive tracers are compared to the corresponding measurements for single-bubble and bubble-pair statistics obtained from particle tracking techniques after the high-speed camera recordings from drop-towers experiments. In the conditions of the present experiments, comparisons indicate that experimental results on bubble velocity fluctuations are not consistent with simulations of passive tracers, which points in the direction of an active role of bubbles. The present analysis illustrates the utility of a recently introduced experimental setup to generate controlled turbulent bubble suspensions in microgravity.

Introduction

Multiphase flows are ubiquitous in technological applications. Specially complex situations correspond to the dispersion of one phase driven by a turbulent flow. In these cases the interaction between the flow and the dispersed phase is complicated by break-up and coalescence phenomena (Colin et al. 2008; Balachandar and Eaton 2010). This problem is most relevant for space technologies such as life support systems and environmental control for life in space (Hurlbert et al. 2010), power generation and propulsion (Meyer et al. 2010) or thermal management (Hill et al. 2010). Therefore there is a strong interest in the study of turbulent bubbly flows under microgravity conditions (Colin 2002).

Whereas there are several studies for the case of normal gravity (Kytömaa 1987; Tryggvason et al. 2006; Mazzitelli et al. 2003), there are few works in microgravity (see for instance Colin et al. 2001). Very recently (Bitlloch et al. 2018) developed a gravity-insensitive method that generates monodisperse, homogeneous bubble suspensions in a turbulent duct flow. One important feature of this method regarding fundamental research in turbulent bubbly flows is the capability of controlling, in an independent way, important characteristics such as the degree of turbulence, the bubble size and also the bubble density.

In a series of microgravity experiments (36 drops of 4.7 s conducted in the ZARM Drop Tower), and by using particle tracking techniques, results on bubble velocity statistics were obtained (Bitlloch et al. 2018). One intriguing result obtained in these experiments was a weak dependence of the relative bubble velocity fluctuations on Reynolds number. Simple scaling arguments of developed turbulence do not predict such dependence. This anomalous scaling could then be either a property of the duct flow in the particular conditions of experiments, or be instead an indication of an active role of the bubbles on the flow.

The main aim of this paper is to obtain precise numerical results on turbulent duct flows in order to elucidate this question. To this end, Lattice-Boltzmann simulations of the flow have been carried out. By using virtual passive tracers, these simulations allowed to compare their statistics with that of the real bubbles. Simulation results also enabled to compare the two-point statistics of passive tracers to that from the particle-tracking of bubble pairs. This gives interesting information on the flow mixing properties and the probability of bubble encounters. In particular we compared the characteristic times of separation between pairs of passive tracers in simulations and pairs of bubbles in the experiments. All these information allowed to obtain an additional and more accurate knowledge of the behavior of turbulent bubbly flows under microgravity conditions.

Lattice-Boltzmann Simulations

In order to characterize the structure and properties of a turbulent flow through a duct of square section we have performed 3D Lattice-Boltzmann simulations. The channel has been discretized into a uniform grid of 320 × 80 × 80 liquid nodes, representing a portion of 400 × 100 × 100 mm³ of the duct, with periodic conditions at its ends. After some tests of various discretizations of the model, we decided for the D3Q15 Lattice Bhatnagar-Gross-Krook (BGK) model with mid-way wall boundary conditions for no-slip walls (Nourgaliev et al. 2003; Bitlloch P 2012).

For the sake of stability, since it is not possible to simulate all scales of turbulence down to the Kolmogorov length, we used the Smagorinsky coefficient for sub-grid scale filtering (Hou et al. 1994). This method is based on the calculation of the local effective viscosity that would dissipate the sub-grid effects generated at each local point. Some remnant numerical instability was controlled by an additional smoothing procedure that preserved mass and momentum (Bitlloch P 2012).

The present code was parallelized and ran in the Mare Nostrum supercomputer at the Barcelona Supercomputing Center (calculating typically with a set of 256 processors) and in a cluster of 16 processors at the Department of Applied Physics of the Polytechnic University of Catalonia (UPC). An overall estimation of the total CPU time used, accounting for checking and optimization of the parallelized code as well as for its subsequent simulations, has been of around 80,000 h.

Code Checkings

In order to check our code, we ran simulations for the same conditions as Pattison et al. (2009). Comparisons showed good agreement in the time-averaged structure of the flow, obtaining the same main longitudinal component of the flow and a reasonable agreement on the residual transversal components associated to the square section of the duct (secondary flow, see below), which was qualitatively correct except for small asymmetries probably due to insufficient temporal averaging.

As an illustrative example, Fig. 1 shows the computed flow in a transversal section of the square duct for both Reynolds numbers of 3800 and 12700. Lines represent the fluctuating component of the flow velocity (u^′ = u −U). Length and color of the lines show the magnitude of each vector in an arbitrary scale. The same comparison is made for the longitudinal section of the flow placed at midway between walls in the z direction is presented in Fig. 2. Higher Reynolds numbers shows a finer and more detailed structure of turbulence that includes smaller eddies.

Fig. 1

Transversal sections of the turbulent flow. Lines and colors represent the direction and magnitude of the fluctuating component of the flow velocity $\mathbf {u}^{\prime }$ in arbitrary scale. (Above): Re = 3800. (Below): Re = 12700. Red indicates values ≥ 5 times those of dark blue

Fig. 2

Velocity fluctuations $\mathbf {u}^{\prime }$ on a longitudinal section of the duct flow (xy plane) at z = 0.5L_c. Flow goes upwards. (Left): Re = 3800. (Right): Re = 12700

As measured by many authors (e.g., Melling and Whitelaw 1976), and in contrast to the case of pipe flow with a circular section, turbulent flow in a square duct generates a weak remnant mean flow contained in the square transversal section of the flow, with pairs of symmetric vortices on each of the four edges of the channel. Those are called secondary flows, as they have a magnitude significantly smaller than the main longitudinal flow, and emerge only after careful time averaging of the transversal flow. Their structure is such that the flow approaches the edges from the bisector of the right angle between walls, then it follows the wall (moving really close to it) until it approaches the bisector of the wall, where it returns to the central part of the section. Figure 3 show the mean secondary flows obtained in our computations for the case of Re = 3800. Lines represent the flow vector (0,U_y,U_z), being the length and color of the lines, the magnitude of the vector in an arbitrary scale. Results have been obtained from averaging over the whole length of the simulation, and over a period of 400,000 iterations (corresponding to 500 s of simulated time for the parameters of our experimental duct) after the simulation had reached the stationary regime. Given the difficulty of observing such secondary flows, they constitute a good test of the numerical simulation.

Fig. 3

Mean secondary flows on a transversal section of the duct (yz plane) for Re = 3800

Analogously, we have done a statistical analysis for the computation with Re = 12700, averaging over a period of 300,000 iterations (corresponding, in our case, to 110 s of simulated time) after reaching the stationary solution of the flow. Comparing the numerical results obtained from both simulations in Fig. 4 we find that the dimensionless profiles of velocity remain essentially unaltered by the change in the degree of turbulence in the flow. This is in agreement with the fact that the main structure of the flow is determined by the largest scales of turbulence, while the smaller ones define the scale of dissipation. The increase of the Reynolds number produces the decrease in size of the smallest scales of turbulence, resulting in the addition of more scales of velocity fluctuations that alter the fine, detailed properties of the flow, while the large scale structure remains unaffected.

Fig. 4

Profiles of mean velocity component $\left < u_{x} \right >$ at different sections y/L_c. Solid lines correspond to Re = 3800, dashed ones to Re = 12700

Figure 5 shows the secondary components of the mean flow velocity for one of the simulations. It is easy to attribute the origin of the apparent asymmetries to the secondary flows of Fig. 3, which would still require further statistical averaging to achieve convergence. Nevertheless, the figure is still interesting in order to realize the order of magnitude of the intensity of the secondary flows in relation to the main flow.

Fig. 5

Profiles of mean velocity components $\left < u_{y} \right >$ and $\left < u_{z} \right >$ for Re = 3800 at the section y/L_c = 0.25

Experimental Details

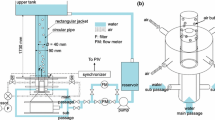
A complete description of the experimental device is presented in Bitlloch et al. (2018), so only a short summary will be made here. The turbulent co-flow is generated by injecting water from nine inlets placed at the base of a vertical duct of square section and dimensions 800 × 100 × 100 mm³, and by using a wire mesh (2.5 mm thick) with square holes of 10 × 10 mm², corresponding to the scale of the most energetic eddies of the duct. The bubble suspension is achieved by injecting into the co-flow a pre-generated slug flow of water and air. This slug flow is formed by combining water and air flows in a T-junction device (Carrera et al. 2008), and is injected into the co-flow by four injectors forming a square. The bubble size is given by the size of the injectors, typically of the order of one millimeter, and can be fine-tuned through the injection parameters (Carrera et al. 2008; Arias et al. 2009; Bitlloch et al. 2015). The resulting Weber numbers are small enough for bubbles injected into the turbulent flow to be roughly spherical. Typical bubble sizes are larger than the dissipative turbulent scales, and therefore they could actively couple to the flow. At the same time bubbles are much smaller than the largest eddies, which are limited by the duct width of 100 mm. Generated void fractions are typically small, of the order of a few percent. For the presented analysis, in order to reduce optical screening between bubbles, we have selected cases in the range from 0.3 to 0.8 void fractions.

This system is insensitive to the gravity level and permits to control the frequency and size of the generated bubbles in a way completely independent from the co-flow characteristics. More details on the setup can be found in Bitlloch et al. (2018). An example of the injection of the bubbles can be seen in Fig. 6, with the resulting turbulent suspension shown in Fig. 7

Fig. 6

Injection in microgravity by using flows of $Q_{l}= 70\frac {\text {ml}}{{\min }}$ and $Q_{g}= 46\frac {\text {ml}}{{\min }}$ ($d_{B} \simeq 1.6$ mm) in each injector, with a co-flow through the duct of Re = 13000

Fig. 7

Bubble suspension far from the injector achieved in microgravity in the same conditions as in Fig. 6

In order to analyze experimental results, images taken by high speed video cameras were processed by particle tracking techniques to reconstruct the bubble trajectories during the experiments. To this aim, after substracting the background, a standard filter was used to highlight the interphase of each bubble. In this way it was possible to identify the trajectories of bubbles by tracking the white area strongly highlighted in their central part, which was surrounded and separated from the rest of bubbles by a clear interphase.

Results

Relative Bubble Velocity Fluctuations

We have analyzed the fluctuations of each component of the relative bubble velocity. Specifically σ_i is defined as the root-mean-square of the fluctuations of the i component of the flow velocity:

$$ \displaystyle \;\; \sigma_{i} = \sqrt{\displaystyle \left< u^{\prime \, 2}_{i} \right>} = \sqrt{\displaystyle \left< {u_{i}^{2}} \right>-\left< u_{i}\right>^{2}} $$

(1)

Previous experimental results, based on particle tracking techniques, concluded that the relative bubble velocity fluctuations of the transversal y-component, σ_y, have a significant decreasing tendency as the Reynolds number increases (Bitlloch et al. 2018). In particular, after relaxing the pseudoturbulence generated by bubbles (due to their relative velocity with respect the co-flow before switching-off gravity), it was found that the ratio σ_y/U_c was 0.13 for Re = 6000 whereas it was 0.08 for Re = 13000 (Bitlloch et al. 2018). For the longitudinal component σ_x, however, the experimental data did not exhibit any conclusive tendency in this respect (σ_x/U_c = 0.10 for Re = 6000 and σ_x/U_c = 0.11 for Re = 13000) (Bitlloch et al. 2018).

To analyze these experimental results we study the profiles of both relative velocity fluctuation by using the present numerical results. Flow data in this case correspond to results that would exhibit passive tracers. Figures 8 and 9 show these profiles taken at depths $\frac {y}{L_{c}}= 0.5$ and 0.25, respectively. We then compare the relative fluctuations on each direction obtained in simulations for different degrees of turbulence. It can be seen that, in both cases, the change of the Reynolds number has no significant effect upon the relative velocity fluctuations. This is a result that coincides with the expectation from simple scaling arguments for fully developed turbulence, but that are not consistent with the mentioned experimental results. According to these results, bubbles do not seem to behave as passive traces of the flow, thus suggesting an active role of bubbles in the turbulence in the conditions of the experiment.

Fig. 8

Profiles of velocity fluctuations σ_i, at the section y/L_c = 0.5. Solid lines correspond to Re = 3800, while dashed ones stand for Re = 12700

Fig. 9

Profiles of velocity fluctuations σ_i, at the section y/L_c = 0.25. Solid lines correspond to Re = 3800 while dashed ones stand for Re = 12700

Behavior of Pairs of Bubbles

In addition, to gain further insight into the dynamics of bubble suspensions in a turbulent flow, we studied the behavior of pairs of bubbles and compared them to numerical predictions. To this aim we evolved by Lattice Boltzmann simulations an initially structured configuration of a large number of tracers (around 40000 tracers distributed in a regular lattice at relative distances of 1.25 mm) for a long period of time, thus reaching a homogeneous distribution. Specifically, the case with Re = 3800 was first evolved during 30000 iterations (corresponding to 37 s of simulated time) and then the statistics was analyzed for the following 20000 iterations (25 s). The statistics of the case Re = 12700 was initiated after 50000 iterations (18.1 s), and spanned another 50000 iterations.

In Fig. 10 we show a transversal coordinate as a function of time, and the projection on the transversal section of four trajectories described by tracers located initially on a close neighborhood. The trajectories clearly show that the tracers remain close to each other for a certain finite time and then they strongly diverge from each other.

Fig. 10

Trajectories described by 4 passive tracers initially separated a distance of 1.25 mm of each other in a flow with Re = 3800 obtained from Lattice-Boltzmann simulations. (Top): transversal coordinate as a function of time; (Bottom): projection on the transversal section

Experimental measurements of bubble pairs have been taken from the trajectories of bubbles previously captured with particle tracking methods. Those located at a distance smaller than 2 mm of another bubble (measured from their centers in the recorded image), have been considered a pair and have been used to calculate the averaged temporal evolution of their separation. In Fig. 11 we display the evolution of the mean distance between pairs of bubbles at different temporal ranges of the microgravity experiments. Noisy signals at the final part of the lines denote a lack of sufficient statistics, caused by the high degree of screening between bubbles in the videos, which makes impossible to follow the trajectory of a bubble for a long period of time. Thus, as time increases, we are losing the track of more bubble pairs and consequently we get poorer statistics. In Fig. 11-top, for the smaller Re = 6000, the slope of the mean separation versus time is steadily reducing in successive time windows. It is important to recall that pseudo-turbulence is decaying during the experiment, as it was observed in Bitlloch et al. (2018). The present results constitute another interesting manifestation of the same phenomena. In Fig. 11-bottom (larger co-flow velocity, with Re = 13000) there are almost no differences in the short times for the first three time windows. In this case the intrinsic turbulence of the co-flow dominates so that the pseudoturbulence relaxation is more difficult to observe (which agrees with relaxation of velocity fluctuations being much weaker in this case as seen in Bitlloch et al. (2018)). The different behavior observed in the last time window is due to the arrival of bubbles already generated in microgravity, and hence generated and transported in different conditions.

Fig. 11

Mean separation of pairs of bubbles. Each line correspond to a temporal range of the experiment in microgravity. (Top): Single experiment (D4) with Re = 6000. (Bottom): Single experiment (D8) with Re = 13000 (see Bitlloch et al. 2018)

Figure 12 plots the mean separation of bubble pairs, measured after the first second of microgravity. Each line corresponds to a different set of injection parameters.

Fig. 12

Mean separation of pairs of bubbles for different parameters of injection. Solid lines correspond to measures from images taken by four video cameras at the indicated drops (see detailed parameters in Bitlloch et al. 2018). In the case of the dark blue line results from two equivalent experiments have been averaged. Dashed lines are fittings (described in Table 1) of the correspondent data. Results have been taken after the first second of microgravity

Namely dark and light red lines correspond to Re = 6000. and dark and light blue lines correspond to Re = 13000. We find that the measurements for equivalent degrees of turbulence share a similar slope once they have reached the linear regime, defining an effective rate of separation.

Dashed lines in Fig. 12 correspond to the linear fittings shown in Table 1. A clear dependence with Reynolds number can be observed on the rate of separation obtained in the fittings. For an increase of Re by a factor ≃2.2, the separation rate is increased by a factor ≃1.6.

Table 1 Linear fittings of the form d_xy = d₀ + v_sep t, for the mean separation in the plane xy between pairs of bubbles, used in Fig. 12

At this point it is important to call the attention upon the fact that the pairs of bubbles defined from experimental images are in many cases only apparent, due to the lack of information about the depth along the visual direction z. A majority of them are separated by distances much larger than the apparent separation and thus will follow rather independent trajectories. If we consider that a pair of bubbles is real when their initial separation Δz₀ in the visual direction is smaller than 1.6 mm, for a homogeneous distribution of bubbles in our duct of width L_y = 100 mm we obtain a proportion of about 3% of real pairs, against 97% of apparent ones. One could think of different strategies to differentiate the two populations of pairs, with the help of a detailed statistical study of tracers in the simulations. However, due to the small statistical significance of the real pairs, the lack of more experiments to increase the amount of data makes any of such attempts virtually hopeless.

Figure 13 shows the evolution of the mean separation between real pairs of tracers, obtained from our simulations for two different degrees of turbulence. The first noticeable observation is that real pairs of tracers, unlike our experimental measures, have an average separation that grows closer to exponentially in time. This rate is defined by an exponent $\mathscr{L}$, which we may assimilate to an effective Lyapunov exponent, that controls the average rate of exponential separation $d(t) = d_{0} e^{\mathscr{L} t}$ of infinitesimally close trajectories in a chaotic dynamical system (Salazar and Collins 2009). Fits in Fig. 13 are shown in Table 2, which adjust nicely to simulations until the finite size effects of the duct section become important and slow down the growth, as can be observed in the figure for the most turbulent case.

Table 2 Exponential fittings of the form $d(t) = d_{0} e^{\mathscr{L} t}$, for the mean separation (in 3D) between pairs of tracers used in Fig. 13

Fig. 13

Mean separation between real pairs of tracers. Distances on logarithmic scale. Fittings in dashed lines described in Table 2

In order to compare the experimental measurements with those of simulations taken in equivalent conditions, we have measured the average separation of apparent pairs of tracers in simulations by selecting only those initially separated a distance smaller than 2 mm in the x–y plane, but larger than 1.5 mm in the z direction. Figure 14 shows the resulting curves, describing a linear growth of the separation, similar to that of the experimental measurements of Fig. 12, until the finite size effects of the duct enter into play. The fits of Fig. 14 are shown in Table 3, which show a dependence of the rate of separation between tracers with Re similar to the experimental case of Table 1. In this case, an increase by a factor ≃3.3 of the Reynolds number causes a factor ≃4.4 in the growth of the separation rate. To allow for a better comparison with experimental results we show in Fig. 15 projected 2D distances for apparent tracers. The linear fittings for these results are also included in Table 3.

Fig. 14

Mean separation between apparent pairs of tracers (i.e., initial Δz₀ > 1.6 mm). Fittings in dashed lines described in Table 3

Table 3 Linear fittings of the form d = d₀ + v_sep t, for the mean separation d (in 3D) between apparent pairs of tracers, used in Fig. 14

Fig. 15

Mean separation separation d_xy (in 2D) between apparent pairs of tracers (i.e., initial Δz₀ > 1.6 mm). Fittings in dashed lines, described in Table 3. For Re = 3800 the fitting has been calculated in the range [0.5,3] s (not shown), where the linear behavior is observed and the fitted line coincides perfectly with the curve

The last aspect we will analyze concerning the dynamics of bubble pairs is the measurement of the statistics of time needed before a pair separates beyond a minimum distance. In the experimental measurements, as well as in the simulations, we have considered the time lapse between the moment the pair reduces its separation to a distance smaller than 2 mm and the moment it surpasses 4 mm, always taken between their respective centers. In Figs. 16 and 17 we show the experimental data and the simulated predictions, respectively.

Fig. 16

Time statistics for experimental bubble pairs. Crosses: Distribution of times for the duration of apparent pairs of bubbles (see text); Circles: number of pairs to which we have lost track, during the given time interval, due to screening effects. (Top) Experiment D4, Re = 6000. (Bottom) Experiment D3, with Re = 13000 (see Bitlloch et al. 2018)

Fig. 17

Normalized probability distribution of duration of pairs of tracers. (Top) Re = 3800. (Bottom) Re = 12700

Results are hard to compare due to the large amount of screening events in the experimental images, that produce an increasing uncertainty in the shape of the curves as the time lapse grows. In simulations, significant differences are observed between the distribution of probability for real pairs of tracers and that of apparent pairs, with much longer life times for real pairs, as a result of the strong correlations of velocities in nearby bubbles, as opposed to the case essentially uncorrelated for distant ones. From the detailed knowledge of the statistics of the time separation of both apparent and real pairs, taken from numerical simulations together with the appropriate characterization of the screening effects, the proper fitting functions could be obtained that would allow to correctly project the experimental data into a reduced set of parameters in order to extract the statistics of real versus apparent bubble pairs, and thus try to detect whether this observable captures some effect not contained in the passive tracer picture. We have not pursued this idea because, as pointed out before, the limited number of experiments available in microgravity prevents from reaching statistically significant conclusions for the minority of the events of interest, namely those corresponding to the real pairs.

Conclusions

Large scale Lattice-Boltzmann simulations have been performed to produce reference states of turbulence with the same conditions of the experiments but without bubbles, to contrast with experimental data in the presence of bubbles, in view of detecting nontrivial couplings between bubble dynamics and turbulence.

This numerical study shows that the relative velocity fluctuations (scaled to its characteristic velocity) of the flow is roughly independent of the degree of turbulence, in accordance with the expectation from simple scaling arguments for fully developed turbulence.

In previous experiments, however, it was observed that the relative velocity fluctuations displayed by bubbles deviated significantly from this scaling, and reflected instead a tendency to decrease with increasing Reynolds number. This suggests an active coupling role of bubbles on the turbulent flow, that would require a more systematic study to be confirmed and quantified more precisely.

By using particle tracking we have studied the space-time statistics of bubble pairs, and compared it with results of passive tracers from Lattice-Boltzmann simulations. In particular we have studied the first-passage time statistics associated to the separation of two-close tracers. We find that the average distance between a pair of tracers increases exponentially with an effective time scale that depends on the degree of turbulence in the flow. For the case of a pair of apparent tracers, though, the average separation between them increases linearly with time. In the analysis of experimental data, we find a similar behavior for the apparent pairs, which dominate the statistics. Real pairs are comparatively rare, and any statistical method to extract the corresponding information for those cases would need a larger number of experiments in microgravity. The conclusions of the present analysis could be, in some sense, limited because only 2D projections of the experimental trajectories are available for comparison with numerical results, but demonstrates the use of the recently introduced experimental setup to generate controlled turbulent bubble suspensions in microgravity.