Introduction

The management and control of two phase flows in microgravity is a key area of research in space technology, due to direct applicability in critical areas such as life support systems, power generation and propulsion, or thermal management with gas-liquid heat exchangers (National Research Council of the National Academies cite.NASA20122012). In the study of dynamics of bubbly flows, a common problem is the difficulty of controlling the characteristics and the regularity of the generation of bubbles when no buoyancy is present. In this respect, Carrera et al. (2008) introduced the strategy of injecting previously-formed liquid-gas slug flows into a liquid cavity, instead of injecting gas directly, with the idea that creating the bubbles prior to injection would allow a better control of the bubble formation mechanism in a gravity-insensitive manner. Specifically, the method consisted of injecting gas into a liquid cross-flow in capillary T-junction, to form a regular slug flow, and then inject the slug flow into a cavity. Indeed, the methods produced very periodic trains of bubbles of a prescribed size, as opposed to direct injection of gas into a liquid cavity, which in the absence of gravity produces in general much more dispersed bubble sizes. Carrera et al. (2008) established the theoretical basis for the mechanism by which bubbles were detached by the drag forces of the liquid crossflow competing with the capillary forces, being buoyancy forces negligible in comparison to the other two. The outcome was then independent of the level of gravity. The size of the bubbles generated with this procedure was typically of the order of the diameter of the capillary tube, but it could be slightly tuned. Altogether with the bubble formation frequency and the bubble-bubble distance, their size could also be modified by adjusting the liquid and gas injection rates into the T-junction. Detailed characterization of the performance of this two-phase T-junction was exhaustively studied by Arias et al. (2009, 2010).

Carrera et al. (2008) also conducted a series of microgravity experiments in the drop tower of ZARM in Bremen, in which this bubble generator was used for the first time in microgravity. They created and injected uniform slug flows into a quiescent cubic cavity. In the absence of buoyancy effects, the injection of the slug flow resulted in the formation of a turbulent jet across the cavity, in which bubbles were dispersed in a roughly conical shape (Fig. 1). While the velocity field of the carrying fluid could not be visualized, the jet region occupied by the bubbles appeared statistically stationary once formed, although the axial symmetry was lost due to the remnants of the flow generated by the rising bubbles at the 1g stage prior to microgravity. Remarkably, with the use of this injection method, the size distribution of the injected bubbles was highly monodisperse and easily controllable even in microgravity. In their paper, Carrera et al. (2008) showed how the experimental mean velocity of bubbles (measured at different points along the axis and at the boundaries of the experimental bubble cones) followed to a large extent the analytical solution for the averaged turbulent flow of a liquid jet without any dispersed phase, as described by Schlichting (1979). This result implied that the presence of bubbles did not affect significantly the mean liquid flow, except for an increase of the total injected momentum. Here we extend and complete the analysis of the same series of microgravity experiments to the statistics of velocity fluctuations to elucidate to what extent and under what conditions the potential two-way interactions between bubbles and turbulence can be quantified and/or possibly neglected. To do so we will introduce an effective stochastic model that neglects such interactions and then confront it to the experimental data. This model includes the finite-size effects of the container and treats the averaged effects of turbulence within k- ε scheme, solving the corresponding transport equations with a finite volume method in a 2D axisymmetric mesh.

Fig. 1
figure 1

Snapshot of a typical experiment of slug bubble injection after 2.5 seconds of microgravity

Full size image

The structure of this paper is as follows. Section “ch::setupAndModelExperi- ch::setupAndModelmental Setup and Theoretical Model” is devoted to the description of the experimental setup and the stochastic model for an ensemble of passive bubbles that fixes the reference to detect possible deviations from this passive behavior in the turbulent jet. In Sections “ch::densityStructureSpatial Structure ch::densityStructureof Bubble Jets” and “ch::velocityStructureVelocity Statistics and Jet Boundaries” we analyze experimental data regarding the spatial structure of the bubble jet and velocity statistics, and compare them to the numerical simulations based on the effective model. While most of the results are consistent with numerical simulations of our effective model within experimental uncertainty, some discrepancies seem to point out to significant bubble-flow interactions in some cases. Finally we present a brief discussion and the main conclusions in Section “Conclusions”.

Experimental Setup and Theoretical Model

Experimental Setup

The experimental setup was already described by Carrera et al. (2008). It consists of a cavity of 100x100x100 mm 3, as sketched in Fig. 2, in which a bubble jet (air in water) is generated through the injection of a slug flow. This slug flow is previously formed in a 1.5 mm diameter T-junction. The bubble diameter depends on the injection parameters but it is roughly of the order of the capillary. In Fig. 2 we also show the structure of a typical mean velocity field obtained numerically in the case of a single-phase flow.

Fig. 2
figure 2

Experimental cell schematics with contour levels of mean velocity (cm/s), as obtained by CFD calculation, for a liquid jet with R e=690. The origin of the coordinated system is located at the entrance of the cavity in the central axis of the jet

Full size image

The analysis of the experimental results will focus on the position and instantaneous velocity of all bubbles for the most typical and well behaved experiments, corresponding to the cases with R e=690 (with parameters of injection Q l =41 ml/min, and Q g =16 ml/min and resulting bubbles of diameter d B ≃1.8mm) and R e=1170 (with Q l =74 ml/min, Q g =18 ml/min and d B ≃1.4mm). The definition of Reynolds number used will be described later in Section “The Mean Velocity Field”. More details on the experimental setup can be found in Carrera et al. (2008).

In order to measure the position and velocity of each bubble during the experiments, all the images taken by the high speed video camera were processed so that an automatic particle tracking software enabled us to identify the paths described by all bubbles. To do so, first it was necessary to homogenize the background of all the frames by subtracting, to each of them, a picture taken by the same camera in the absence of bubbles. After the background correction, we used a standard filter to highlight the interphase of each bubble. Finally we used particle tracking methods to identify and follow the trajectories of all bubbles (Bitlloch 2012).

Since the experimental data is taken from 2D snapshots where the real 3D configuration has been projected, some of the information is lost in the process. In the first place, the component of the velocity of bubbles in the direction z, perpendicular to the plane of the snapshot, cannot be measured. This is not a major issue since the main component of the velocity is u x , in the axial direction x. In addition to this, the properties of the flow in the directions y and z should be statistically equivalent. A more serious limitation is the fact that we cannot measure the depth z at which any bubble is placed, therefore when we conduct a statistical analysis of bubble velocities, we are inevitably mixing velocities that were in fact at different layers of the jet. This fact will be properly incorporated in the statistical analysis.

Description of the Single-Phase Jet

In theoretical framework of the so-called k−ε models, it is assumed that one can decompose the total velocity field of a turbulent flow in two parts, a mean flow component and a fluctuating part. Regarding the first component, it is well known that the spatial structure of the mean flow velocity field of a turbulent single-fluid jet is independent of Re (Schlichting 1979). In these models the fluctuating part of the flow is described in terms of two continuous fields, the local turbulent kinetic energy k of the fluctuating part, and its dissipation rate ε. Closed transport equations for these fields are then postulated. In the case of interest here for the application of this approach, namely the study of turbulent jets, the standard k−ε model it is known to over predict the opening angles of jets (Shih et al. 1995). Being that angle an important point in our study, we have used the improved version that is known to correct this aspect, the so-called realizable k−ε model (Shih et al. 1995), which introduces the transport equations

$$ \frac{\partial (\rho k)}{\partial t} + \nabla \cdot (\rho k {\mathbf{U}}) \,=\, \nabla \cdot \left[ \left( \mu + \frac{\mu_{t}}{\sigma_{k}} \right) \nabla k \right] + 2 \mu_{t} E_{ij} \cdot E_{ij} - \rho \varepsilon \; , $$
(1)
$$ \frac{\partial (\rho \varepsilon)}{\partial t} + \nabla \cdot (\rho \varepsilon {\mathbf{U}}) = \nabla \cdot \left[ \left( \mu + \frac{\mu_{t}}{\sigma_{\varepsilon}} \right) \nabla \varepsilon \right] - \rho C_{2} \frac{\varepsilon^{2}}{k+\sqrt{\nu \varepsilon}} \; , $$
(2)

being U the local mean velocity, ρ the density and E i j the rate-of-strain tensor

$$ E_{ij} = \frac{1}{2} \left( \frac{\partial U_{j}}{\partial x_{i}} + \frac{\partial U_{i}}{\partial x_{j}} \right)~. $$
(3)

μ refers to viscosity and μ t to eddy viscosity, defined by

$$ \mu_{t} = \rho C_{\mu}\frac{k^{2}}{\varepsilon}~, $$
(4)
$$ C_{\mu} = \frac{1}{A_{0}+A_{s} \frac{k U^{(*)}}{\varepsilon}}~, $$
(5)
$$ U^{(*)}=\sqrt{E_{ij}E_{ij}+{\Omega}_{ij} {\Omega}_{ij} } ~, $$
(6)

where

$$ {\Omega}_{ij} = \frac{1}{2} \left( \frac{\partial U_{i}}{\partial x_{j}}-\frac{\partial U_{j}}{\partial x_{i}} \right) $$
(7)

and the other constants, i.e.

$$ A_{0}=4.04, ~,~~~ A_{s}=\sqrt{6}\cos\phi ~, $$
(8)
$$ \phi = \frac{1}{3}\cos^{-1} \left( \sqrt{6}\frac{E_{ij}E_{jk}E_{ki}}{(\sqrt{E_{ij}E_{ij}})^{3}} \right) ~, $$
(9)
$$ C_{2}=1.9, \sigma_{k}=1.0, \sigma_{\epsilon}=1.2 ~, $$
(10)

have been adjusted to the values that offer an optimal performance of the model.

Stochastic Model for the Bubble Jet

Since the experimental results of Carrera et al. (2008) indicated that the local averaged velocities of bubbles coincide to a good extent to the mean flow velocity field of a turbulent single-fluid from the solution of Schlichting (1979), the spreading of the spatial distribution of bubbles must be directly related to the fluctuating part of the flow. In Fig. 3 we can appreciate how the streamlines of the flow that are actually being injected into the cell only suffer a slight opening (of no more than twice its initial separation d T ) after the full length of the jet. It is easy to see how the larger width of the jet is determined by its external layers, that incorporate streamlines from the recirculating flow. In addition, turbulence provides a mechanism that mixes all those layers of mean flow, allowing the dispersion of bubbles through them. Hence, we need to make use of the local characteristics of turbulence in order to properly describe the dispersion of bubbles through the transversal layers of the flow and, at the same time, to confine them inside the boundaries of the jet, preventing them from freely disperse through the whole experimental cell.

Fig. 3
figure 3

Streamlines of the mean flow in the experimental cell, obtained from a simulation with axial symmetry

Full size image

Within the above-mentioned realizable k- ε model of turbulence, we will associate a local diffusivity to bubbles that is inherited from the diffusivity of the kinetic energy of the turbulent component of the flow in the absence of bubbles. The main assumption is thus that bubbles are also passive with respect to the fluctuating component of the flow. As mentioned before, this assumption must be correct in principle sufficiently far downstream, where the bubble suspension becomes more and more dilute and the bubble size becomes negligible compared to the scales of the flow.

Since bubbles are not point-like and the number of them is relatively small, the aim of the model is to formulate an equation for the probability distribution of finding a bubble at a certain location. The model does not intend to be a good description of the individual trajectories of bubbles, which are far from diffusive at small scales of the flow due to strong spatial and temporal correlations of the carrying flow. This implies, for instance, that the model will be inappropriate to describe properties related to the geometry of the bubble trajectories themselves or the correlations between them, such as the probability of bubble encounters and consequently of possible coalescence. Despite this limitation of the model, the assumption of a local diffusivity of the probability of finding bubbles may be reasonably justified to describe the spatial distribution of an ensemble of realizations, provided that coalescence events are rare.

For the purposes of studying the spatial bubble dispersion, the above model pictures the dynamics of bubbles as described by a biased random walk. We write explicitly the instantaneous velocity of a bubble u B as a stochastic (Langevin) equation of the form

$$ \mathbf{u}_{B}(t) = {\mathbf{U}}(\mathbf{s}(t)) + \mathbf{u}^{\prime}(t), $$
(11)

where U(s(t)) is the local mean fluid velocity at the position s(t) of the bubble and \(\mathbf {u}^{\prime }(t)\) is a fluctuating term of zero mean. This fluctuating term is responsible for the diffusivity of bubbles, therefore it should depend on the local properties of the turbulent flow. As mentioned above, we relate this diffusivity to that of the kinetic energy of the turbulent component of the flow without bubbles. Then, both terms of this decomposition (mean and fluctuating velocities) can be obtained from the integration of a k- ε model. In particular, writing the fluctuating term as a Gaussian zero-mean white noise with correlation

$$ \langle \mathbf{u}^{\prime}(t_{1}) \mathbf{u}^{\prime}(t_{2}) \rangle = 2 D_{p} \delta(t_{1}-t_{2}) \; . $$
(12)

The noise intensity D p is taken as proportional to the diffusivity of the turbulent kinetic energy \(\frac {k^{2}}{\varepsilon }\) in the context of the k- ε model

$$ D_{p}=\frac{\mu_{t}}{\rho_{l} \sigma_{p}}=\frac{C_{\mu}}{\sigma_{p}}\frac{k^{2}}{\varepsilon} , $$
(13)

where C μ =0.09 according to the standard model, and σ p is in principle a fitting parameter that connects the diffusivity of P to the eddy viscosity μ t . The prediction of this model regarding the spatial structure of the bubble jet does not seem very sensitive to the parameter σ p , so we take σ p =1 as in the transport equation of k (i.e., σ k =1), considering that both diffusivities must be similar, being both equally originated by the eddy mixing (Versteeg and Malalasekera 1995).

The Langevin equation (11) can be numerically integrated using standard methods, with the result of individual trajectories of single independent bubbles. Examples of such integration are shown later, in the next section. Within this scheme one may easily determine the probability density P(s,t) of finding a bubble in a certain position at any instant of time. This distribution coincides with the concentration of an ensemble of independent bubbles, and is given by the so-called Fokker-Planck equation associated to the stochastic differential Eq. 11. This equation has the form

$$ \frac{\partial P(\mathbf{s},t)}{\partial t} + \nabla \cdot ({\mathbf{U}}P) = \nabla \cdot \left[ D_{p} \nabla P \right] . $$
(14)

In this framework, the concentration of bubbles, proportional to the probability distribution P, diffuses as a passive scalar advected with the mean flow velocity U(s,t), but with a diffusion coefficient D p (s,t) which depends on the local properties of the turbulence through the field \(\frac {k^{2}}{\varepsilon }\).

The Mean Velocity Field

The reported calculations were carried out with the help of the commercial software FLUENT, using a 2D axisymmetric mesh consisting of 56100 cells arranged in a non-uniform distribution, in order to obtain higher density of cells in the critical areas with higher gradients of flow velocity. The volumes for the cells ranged from 3⋅10−13 m 3 up to 2⋅10−7 m 3 (of the total 7.7⋅10−4 m 3). Tests of different meshes with various cell densities were performed without noticeable variations in the outcome.

Taking into account that the presence of bubbles in the injector increases the velocity of the liquid slugs between them, for the simulation of the effective single-phase jet the effective injected momentum J is defined as

$$ J \; = \; \rho_{l} Q_{l} \left< U_{T}\right> \; = \; Q_{l} (Q_{l} + Q_{g}) \frac{\rho_{l}}{A_{T}}, $$
(15)

Q l and Q g being respectively the volumetric flow rates of liquid and gas injected into the T-junction. Note that the effect of the presence of bubbles is here reduced to a modification of the injected momentum, but the medium is treated as an effective continuum, so the intermittent presence of bubbles at any a given point is lost.

The appropriate definition of Reynolds number for the jet will be given by taking the characteristic length L c as the local diameter of the jet at any position, and the characteristic velocity at this same position as given by the injected momentum \(U_{\text {c}} = \sqrt {J/(\rho _{l} A_{\text {c}})}\), with \(A_{\text {c}}=\pi L_{\text {c}}^{2} / 4\), which leads to

$$ \mathit{Re} \; = \; \frac{L_{\text{c}}}{\nu} \sqrt{\frac{J}{\rho_{l} A_{\text{c}}}} \; = \; \frac{4\sqrt{Q_{l}(Q_{l}+Q_{g})}}{\pi \nu d_{T}} \; , $$
(16)

with d T the diameter of the inlet, which coincides in the experiments with that of the T-junction capillary tubes.

It is worth remarking that the effective Reynolds number of the jet, in principle depending on the characteristic scales of length L c and velocity U c whose local values vary with the distance from the injection point, remains constant all along the jet. This can be easily shown (Schlichting 1979) by observing experimentally that the opening angle of a turbulent jet remains constant with the distance, while on the other hand, the flow velocity scale is inversely proportional to the distance. This causes that, to a first approximation, the turbulent flow is statistically self-similar along the jet, under the appropriate rescaling of length and time, i.e. the characteristic eddy velocities are being reduced downstream in the same proportion as their size increases.

Fig. 4
figure 4

Collapse of many curves of U x ⋅(x+x 0) for a jet with R e=690. r is the radial distance in cylindrical coordinates. Dashed lines show the simulation results at various transversal sections of the jet. Solid line corresponds to Schlichting (1979) analytical solution of an infinite single-phase turbulent jet with an infinitely small slit. x 0 has been adjusted to 1.2 cm in order to overlap all the curves from the simulations, due to the finite size of the inlet

Full size image

In Figs. 2 and 3 we show the structure of the mean velocity field for the single-phase turbulent jet as computed within the k- ε model. In these figures it is easy to see how the finite size of the experimental cell plays an important role in the flow structure, specially in the areas with strong recirculation and near the stagnation disk. In Fig. 4 we display the results obtained from the numerical integration of the model for the radial variation of the axial velocity at different positions along the jet axis, and compare with the analytical Schlichting solution for an infinite system. We can observe how the numerical solution of the jet presents a sharper opening angle than the case of the solution for an infinite system, with a significantly higher velocity at the jet axis for the former, given the same injected momentum. Despite this finite-size effect on the opening angle, the jet maintains its velocity decay roughly proportional to \(\frac {1}{x}\), as well as its dependence with the ratio \(\frac {r}{x}\), which is maintained for the internal layers of the jet up to \(\frac {r}{x} \simeq 0.10\). Outside these boundaries, the recirculation due to the finite size conditions become appreciable and, accordingly, the corresponding streamlines differ significantly.

The Bubble-Turbulence Coupling

Since the bubble size is not only monodisperse but preserved through the evolution, while the scales of the turbulent flow increase downstream, the degree of interaction between bubbles and flow is expected to change along the jet. Far downstream the bubbles become effectively point-like and must eventually behave as passive tracers because, since beyond a certain distance from the injector, the smallest eddies will become bigger than the bubbles. On the contrary, the situation is very different at the regions close to the jet inlet, where bubbles are comparable to the jet diameter and to the scale of velocity gradients. In those regions, bubbles will necessarily be active in relation to the liquid flow field.

Measuring the Kolmogorov scales of turbulence (Landau and Lifshitz 1987; Brennen 2005) as well as the Stokes bubble response time (Maxey et al. 1996; Brennen 2005) for the typical parameters of our experiments, we found that bubbles become smaller than the larger scales of turbulence at distances greater than 4 cm, but they should not become passive tracers until distances greater than 80 cm. Being the size of our experimental cell of 10 cm, based on this simple scaling argument bubbles should in principle be active and generate some appreciable back reaction to the flow for most of the jet length. This effect should appear even bigger taking into account that we can only measure velocities of bubbles themselves, since we do not have any other tracer on the flow. However, it is also important to realize that the overall effect of the presence of bubbles on the statistics of turbulence will depend also on the void fraction. For the typically small values of void fraction at hand, their effect may still be quantitatively small. In fact, as already mentioned, the results of Carrera et al. (2008) showed that the mean flow is not significantly affected by the presence of bubbles. Furthermore, as we will see later, the statistical uncertainty of our measurements does not allow us to detect significant deviations from the prediction of the numerical results under the assumption of passive bubbles. We attribute this, in the first place, to the small void fraction, which drops below the 10 % on gas after the first centimeter of jet (once we take into account the initial opening of the jet due to the injector size), and also to the smallness of the effect of wakes created behind bubbles at our small Reynolds numbers.

Spatial Structure of Bubble Jets

Computation of the Spatial Distribution of Bubbles

In order to try to resolve the possible bubble-turbulence coupling in the jet, it is convenient to obtain, as a reference, results for completely passive bubbles, i.e. when bubbles follow the local velocity field without modifying it. To this end we will use a stochastic model in which the bubble velocity is the result of the addition of the local mean flow plus a stochastic diffusive contribution depending on the local intensity of the turbulence.

To visualize the degree of inhomogeneity in the present model regarding the diffusivity of bubbles, we plot in Fig. 5 the quantity \(\frac {k^{2}}{\varepsilon }\), which is in principle proportional to the effective local diffusion coefficient of bubbles. The local diffusivity is remarkably homogeneous in a certain central area and abruptly drops on the sides, defining relatively clear-cut jet boundaries. This drop in diffusivity is larger than one order of magnitude in a relatively narrow layer. This explains the small sensitivity of the results to small changes in σ p on the determination of the diffusion coefficient D P , since bubbles disperse through the whole central region, delimited by this narrow boundary layer. For larger variations of σ p (of around one order of magnitude) we reach the extreme behaviors possible for any scalar transport equation. In the case with \(\sigma _{p} \gtrsim 10\) the advection term predominates over diffusion, impeding a significant dispersion of P over the various layers of the jet. In this case P remains appreciable along the central streamlines of the mean flow, thus strongly underestimating the opening angle of the bubble jet. On the contrary, for \(\sigma _{p} \lesssim 0.1\), diffusion predominates over advection, resulting in an overestimation of the opening angle and unrealistic results near the injector, as a result of an extreme diffusivity.

Fig. 5
figure 5

Contours of constant \(\frac {k^{2}}{\varepsilon }\) (10−1 cm 2/s), as obtained by CFD calculations

Full size image

In Fig. 6 we show the resulting bubble concentration contours, obtained from the numerical integration of Eq. 14. As indicated earlier, bubble spreading is limited by the jet boundaries, and the resulting spatial distributions are similar to those of experiments. Remarkably, this is not the case if a homogeneous diffusivity is used (instead of one locally depending on \(\frac {k^{2}}{\varepsilon }\)). The use of a single value of diffusivity for the whole system results in a distribution of bubbles that either opens in a very small angle (consistent with a scalar transport dominated by advection), or spreads out of the limits of the jet following an unrealistic behavior (corresponding to a transport dominated by diffusion), depending on the value taken for the diffusivity. An example of bubble distribution P in the case of constant diffusivity is shown in Fig. 7. We therefore conclude that, within the k- ε model, an inhomogeneous diffusivity is essential to capture the qualitative shape of the spatial distribution of bubbles.

Fig. 6
figure 6

Contours of mean bubble concentration in an arbitrary scale, corresponding to a local diffusivity proportional to \(\frac {k^{2}}{\varepsilon }\), as obtained by integration of the Fokker Planck equation by using the CFD results

Full size image
Fig. 7
figure 7

Contours of mean bubble concentration in an arbitrary scale, corresponding to a homogeneous bubble diffusivity, as obtained by integration of the Fokker Planck equation. Unrealistic degree of diffusion is present close to the injector

Full size image

Bubble Distribution. Experimental vs Numerical Results

In order to compare the mean superficial density of bubbles ρ b from the experimental snapshots with that from the numerical results, we integrate the probability density of bubbles P over the visual dimension z in the form

$$ \rho_{b} (x,y)= C_{b} {\int}_{-\infty}^{\infty}{P(x,y,z) \; dz} \; . $$
(17)

Since P has been calculated in an arbitrary scale (we have not fixed the frequency of bubble injection), we introduce C b as a constant to fix the density scale in the simulations in order to fit the experimental results. In Fig. 8 we compare the experimental results with the numerical predictions of ρ b for different sections of the jet. The experimental values have been obtained by measuring the mean number of bubbles on small areas of the snapshots, averaged over the whole duration of the microgravity conditions. The constant C b in Eq. 17 has been fixed by imposing the same mean number of bubbles on the section at x=3cm for both numerical and experimental results. This number of bubbles is obtained by calculating the area below the curves in Fig. 8 at that distance.

Fig. 8
figure 8

Superficial density of bubbles at various sections of a jet (x = 1cm, 3cm, 5cm and 7cm) for the cases of jets with R e=690 and R e=1170. Solid lines correspond to simulations and crosses to experimental results

Full size image

As discussed in Carrera et al. (2008), the experimental protocol to generate a uniform slug flow requires to start injecting bubbles some time prior to the microgravity conditions. This is done in order to avoid the relative long transients that precede a stationary generation of a uniform slug flow. The downside of this procedure is that the gas injected during normal gravity conditions is accelerated due to buoyancy forces and drags some of the liquid, producing a weak, residual liquid flow. Although buoyancy forces disappear immediately at the start of the microgravity conditions, a slow relaxation of this residual flow remains, breaking the cylindrical symmetry of the jet and giving it a slight inclination upwards. This can be observed in the small lateral shift of the experimental measures in Fig. 8. Also, the opening angle of the bubble jet seems to be slightly smaller in the simulations, as it can be observed in the figure at high distances from the injection point (i.e., x=5cm and x=7cm), arguably produced by the real effect of the finite size conditions of our experimental cell. With the above disclaimers and taking into account that the statistics of the data is necessarily limited because of the restricted access to the microgravity conditions, the experimental data fit reasonably well with the numerical prediction of our model, in particular in the intermediate range of distances to the inlet, when the prediction of the model is most accurate. At the end of the jet, the cumulative effect of the symmetry-breaking spurious flow associated to the normal-gravity preparation of the initial condition is most pronounced.

In Figs. 9 and 10 we show a 3D representation of the superficial density of bubbles ρ b , but in this case for any point of the projected xy plane, corresponding to all the points where the data can be measured from the experimental snapshots.

Fig. 9
figure 9

Superficial density of bubbles ρ b (cm −2) obtained from a simulation with R e=690, for all points on the projected xy plane

Full size image
Fig. 10
figure 10

Superficial density of bubbles ρ b (cm −2) obtained experimentally in the case of R e=690, for all points on the projected xy plane

Full size image

Velocity Statistics and Jet Boundaries

Mean Velocity. Experimental vs Numerical Results

As before, since we cannot know the z coordinate of the bubbles position, we need to integrate the numerical predictions over that dimension. In this case, one must take into account that not all planes at different depths contribute equally to the statistics. Indeed, layers where there are more bubbles will contribute more significantly. Accordingly, in order to compare the experimental velocity profiles \(\left < u_{x}^{\exp } \right >\) with the numerical results obtained by numerical computations \(\left < u_{x}^{\text {sim}} \right >\), it is necessary to introduce this projection effect into the simulation outcome. The way of achieving this is by integrating the velocity of the flow u x (x,y,z) over the visual dimension z with the help of a weight factor P ⋆(x,y,z) which stands for the proportion of bubbles at each point. P ⋆ corresponds to the probability density of bubbles P(x,y,z) normalized over the visual dimension z in the form

$$ P^{\star}(x,y,z) \equiv \frac{\displaystyle P(x,y,z)}{\displaystyle {\int}_{-\infty}^{\infty} P(x,y,z) \; dz} \; , $$
(18)
$$ {\int}_{-\infty}^{\infty} P^{\star}(x,y,z) \; dz = 1 \; . $$
(19)

Then, the projected mean velocities of the flow, given by the simulations are

$$ \left< \, u_{x}^{\text{sim}} \, \right> = \left< {\int}_{-\infty}^{\infty} dz \;\, P^{\star}(x,y,z) \;\, u_{x}(x,y,z,t) \right> \; , $$
(20)

which, under permutation of the order of the dimensional integration and the statistical mean “<  >”, yields

$$ \left< \, u_{x}^{\text{sim}} \, \right> = {\int}_{-\infty}^{\infty} dz \; P^{\star}(x,y,z) \; \left< \, u_{x}(x,y,z,t) \, \right> $$
(21)

Now, we describe the velocity u x as the sum of a mean velocity U x plus a fluctuating part \(u^{\prime }_{x}\) with zero mean that describes the degree of fluctuations over time.

$$ u_{x}(x,y,z,t) = U_{x}(x,y,z) + u^{\prime}_{x}(x,y,z,t) $$
(22)
$$\begin{array}{@{}rcl@{}} \left< \, u_{x}(x,y,z,t)\, \right> \; &=& \; U_{x}(x,y,z) + \left< \, u^{\prime}_{x}(x,y,z,t) \, \right>\\ \; &=& \; U_{x}(x,y,z) \end{array} $$
(23)

Applying it to Eq. 21 we finally obtain

$$ \left< \, u_{x}^{\text{sim}} \, \right> = {\int}_{-\infty}^{\infty} dz \;\, P^{\star}(x,y,z) \;\, U_{x}(x,y,z) $$
(24)

Due to the inherent uncertainty on the actual Reynolds number injected in the experiments, which may slightly fluctuate and deviate from the nominal value in a rather uncontrolled way, we have left an overall factor on the velocity scale of the simulations as an adjustable parameter. Since the structure of the jet should be equivalent for small injection variations, we scaled the velocity results of the simulations so that the maximum velocity \(\left < u_{x}^{\text {sim}} \right >\) in the section x=3 cm coincide with the experimental measurements, i.e.,

$$ \left< u_{x}^{\text{sim}}(x=3\text{cm}) \right>_{\text{Max}} = \left< u_{x}^{\exp}(x=3\text{cm}) \right>_{\text{Max}} \; . $$
(25)

For the case with R e=690 the simulated velocities have been scaled by a factor 0.69, and the ones of the case with R e=1170 by a factor 0.79. The same factor has been applied to all measured observables corresponding to the same experiment. In Fig. 11 we compare the numerical results with the experimental data from our measurements.

Fig. 11
figure 11

Mean axial velocity at various sections of a jet (x = 1cm, 3cm, 5cm and 7cm) for the cases of jets of R e=690 and R e=1170. Solid lines correspond to simulations \(\left < u_{x}^{\text {sim}} \right >\) and crosses to experimental results \(\left < u_{x}^{\exp } \right >\)

Full size image

Velocity Fluctuations. Experimental vs Numerical Results

For the study of the magnitude of the velocity fluctuations σ sim we will have to follow a similar procedure, but we have no free parameter left for the fitting. This time, for the sake of simplicity of notation, we will not show the dependencies of each variable. In the study of the velocity fluctuations in our projected images, it is important to distinguish the intrinsic fluctuations due to turbulence with respect to the local mean flow, from the apparent velocity variations along the visual direction already contained in the mean flow, which will already give a finite contribution even if the flow is laminar. Starting from the definition of variance

$$ \left( \sigma_{x}^{\text{sim}} \right)^{2} \equiv \left< \, \left( u_{x}^{\text{sim}} \right)^{2} \, \right> - \left< \, u_{x}^{\text{sim}} \, \right>^{2} \; , $$
(26)

and using the relations previously seen in Eqs. 20 and 21, we find

$$ \begin{array}{llllll} & \left( \sigma_{x}^{\text{sim}} \right)^{2} = \left< {\int}_{-\infty}^{\infty} dz \, P^{\star} \, {u_{x}^{2}} \right> - \left< {\int}_{-\infty}^{\infty} dz \, P^{\star} \, u_{x} \right>^{2} \\ & = {\int}_{-\infty}^{\infty} dz \, \!P^{\star} \left<{U_{x}^{2}} \,+\, 2U_{x}u^{\prime}_{x} \,+\, u_{x}^{\prime2} \right> \,-\, \left( {\int}_{-\infty}^{\infty} dz \, P^{\star} \left<U_{x}\,+\,u^{\prime}_{x} \right>\right)^{2} \; \\ & = {\int}_{-\infty}^{\infty} dz \, P^{\star} \left( {U_{x}^{2}} + \left< u_{x}^{\prime2} \right> \right) - \left( {\int}_{-\infty}^{\infty} dz \, P^{\star} \, U_{x} \right)^{2} \; . \end{array} $$
(27)

Knowing that the definition for the kinetic energy of turbulence k is

$$ k=\frac{1}{2}\left( \; \left< u^{\prime2}_{x} \right> + \left< u^{\prime2}_{y} \right> + \left< u^{\prime2}_{z} \right>\; \right) \; , $$
(28)

and assuming for simplicity that turbulence is sufficiently isotropic, we obtain

$$ \left< u^{\prime2}_{x} \right> = \left< u^{\prime2}_{y} \right> = \left< u^{\prime2}_{z} \right> \; , $$
(29)
$$ k=\frac{3}{2} \left< u^{\prime2}_{x} \right> \; , $$
(30)

which, when introduced into Eq. 27 and after rearranging, allow us to express the magnitude of the velocity fluctuations of bubbles \(\sigma _{x}^{\text {sim}}\) as

$$\begin{array}{@{}rcl@{}} \left( \sigma_{x}^{\text{sim}} \right)^{2} &=& {\int}_{-\infty}^{\infty} dz \, P^{\star} \, {U_{x}^{2}} - \left( {\int}_{-\infty}^{\infty} dz \, P^{\star} \, U_{x} \right)^{2}\\ &&+ \frac{2}{3}{\int}_{-\infty}^{\infty} dz \, P^{\star} \, k \; . \end{array} $$
(31)

This equation can actually be expressed as

$$ \left( \sigma_{x}^{\text{sim}} \right)^{2} = {\sigma^{2}_{0}} + {\sigma^{2}_{k}} \; , $$
(32)
$$ {\sigma_{0}^{2}} = \left( {\int}_{-\infty}^{\infty} dy \, P^{\star} \, {U_{x}^{2}} \right) - \left( {\int}_{-\infty}^{\infty} dy \, P^{\star} \, U_{x} \right)^{2} \; , $$
(33)
$$ {\sigma_{k}^{2}} = \frac{2}{3}{\int}_{-\infty}^{\infty} dz \, P^{\star} \, k \; . $$
(34)

In these expressions, σ 0 stands for the magnitude of the apparent fluctuations due to the 3D structure of the jet, already present for the mean flow and which arise from the comparison of mean velocities at layers of different depth along the visual line. On the other hand, σ k stands for the projection of the intrinsic fluctuations of the velocity at the different layers of the jet, that is, those due to turbulence.

In Fig. 12 we compare the velocity fluctuations of the experimental data with the numerical predictions calculated with Eq. 31, with no additional fitting parameter, since the velocity scale has already been fitted using the velocity measurements.

Fig. 12
figure 12

Velocity fluctuations at various sections of a jet (x=1cm, 3cm, 5cm and 7cm) for R e=690 and R e=1170. Solid lines correspond to simulations \(\sigma _{x}^{\text {sim}}\) and crosses to experimental results \(\sigma _{x}^{\exp }\). Dashed red lines correspond to σ k , defined on Eq. 34

Full size image

Dashed lines show the value of σ k as defined in Eq. 34, to illustrate the magnitude of the intrinsic velocity fluctuations due to turbulence in relation to the apparent ones. As for the measurements on the bubble spatial dispersion, for both the measurements of mean values and dispersion of bubbles velocities, the prediction of the k- ε model is also reasonably accurate, within the inherent uncertainties of the experimental data, and taking into account the symmetry breaking of the experimental data to the already mentioned residual flow from the preparation procedure under normal gravity.

Jet Boundaries

Simulations seem to predict slightly smaller opening angles of the bubble jet at large distances from the injection point. It is not clear if this could be attributed to an extra overspreading of bubbles due to the stagnation disk or some other spurious effect of the injection of bubbles in the stage prior to microgravity. In any case, one should take into account that the boundary of the turbulent jet may not be well described within the frame of a k- ε model, because the latter implies a smooth variation of the properties k and ε, whereas in reality at the boundary between the jet and the laminar flow there can be significant changes of local flow characteristics. Moreover the boundary between the turbulent jet and the laminar flow is expected to fluctuate over time, and interactions between bubbles and flow could be important at that fluctuating boundary, for instance ejecting bubbles out of the turbulent part of the jet. Consequently, the average effect on the bubble dispersion and velocity statistics displayed by bubbles near the jet boundary is likely to be missed by our simple model. In fact, when looking at the diffusion coefficient \(\frac {k^{2}}{\varepsilon }\) of the model, plotted in Fig. 5, we find a fast decay of this magnitude in a narrow distance, but this is still a smooth spatial variation and, most importantly, constant in time. It is thus not surprising to find deviations from the prediction of the model in the experimental observation made on the margins of the jet.

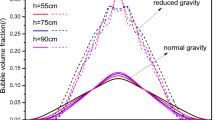
One way to define a the position of the jet boundary is to assume that turbulence effectively vanishes past a certain threshold value of k. In Fig. 13 we show the relative fluctuations of the flow for three simulations with different degrees of turbulence. If we argue that the flow becomes laminar when the relative fluctuations of the flow (k/U 2) drop below a certain value, then we can see on the figure that the tendency is that the radius of the jet (i.e., its opening angle) increases for decreasing Reynolds number. We find the same tendency if we define the boundary of the bubble jet at some intrinsic property of the curve, for instance its inflection point. In this case, in addition, we also find that the relative fluctuations of the velocity at the jet margin as measured by k/U 2 do increase with the Reynolds number.

Fig. 13
figure 13

Profiles of k/U 2 in function of the radial distance, at x=3cm

Full size image

The above predictions of the model seem to be challenged by experimental observations. Indeed, Carrera et al. (2008) reported an opposite dependence of the measured bubble opening angle (although measured very close to the injector), which increased with R e until saturation value for R e≈700. In addition, the effect of Reynolds number on the relative velocity fluctuations at the jet boundary does not appear to be consistent with the model results. For this latter comparison, we have measured velocity fluctuations by carefully choosing bubbles one by one at the apparent jet boundary, at maximal distance from the jet axis, in the projected plane of the images, thus minimizing the possible component along the visual coordinate z. In Fig. 14 we show the relative velocity fluctuations of the bubble velocities measured on the bubbles at the margins of the experimental images. The figure shows a weak decreasing tendency of the relative velocity fluctuations of bubbles at the boundaries when increasing Reynolds number, which would contradict the prediction from the k- ε model defining the jet boundary at the inflection point. Although not fully conclusive, these observations seem to point out a limitation of the model to capture the behavior of bubbles near the jet boundaries, and consequently suggest active bubble-flow interactions in those regions. Much more involved CFD simulations should be invoked to be able to account more precisely for the behavior at that level of detail, a problem that goes much beyond the scope of the present study.

Fig. 14
figure 14

Experimental measures of relative velocity fluctuations at the edges of the bubble jet

Full size image

Conclusions

A stochastic model that captures the essential statistics of bubble spatial dispersion in turbulent bubble jets formed by injection of capillary slug flows is presented. The treatment of bubbles as passive tracers with a local diffusivity associated to the k- ε model seems to reasonably explain the ensemble dynamics of the bubbles. Numerical results obtained with our model compare well with experiments.

Simple scaling analysis comparing the bubble size and the scales of turbulence indicate that the interaction between bubbles and its effect upon the carrying flow cannot be neglected in the regions relatively close to the inlet. However, our analysis shows that, even though potentially important, to the degree of approximation that is consistent with the inherent uncertainty of the experiments, such interactions can be statistically neglected in the cases of the overall spatial distribution of bubbles, their mean velocity and the root-mean-square of their velocity fluctuations. This approximation is expected to be progressively more accurate for increasing distance downstream, since the flow is essentially self-similar with the scale fixed by the jet radius, while the bubbles become relatively smaller (effectively point-like) with respect to the flow scales.

Potential deviations of the effective model from the experimental statistics of bubble dispersion and velocity fluctuations have been detected at the margins of the jets. Indeed we found signs of a weak dependence of the relative velocity fluctuations with Reynolds number that does not seem to be captured by the effective model. Similarly, the weak dependence of the jet opening angle predicted by the model differs from measurements from Carrera et al. (2008). Although the limited statistics of the experiments is not fully conclusive, these observations suggest that the boundaries of the jet are regions where the bubble dynamics is most sensitive, and where inaccuracies of the model may be more apparent, even relatively far downstream. This points to the possible failure of the hypothesis of passive bubbles, assumed in the model, and hence to the relevance of the bubble-flow interactions at the boundaries of the jet.

Our stochastic model works reasonably well to describe the ensemble statistics of many realizations of bubble jets, but cannot provide relevant information contained in the properties of the actual bubble trajectories, for instance to define the probability of bubble encounters, and consequently of potential coalescence events.

A more accurate description of the system should also aim at a more realistic modeling of the bubble trajectories. Diffusive trajectories are indeed too erratic on small scales and overestimate significantly the probability of bubble encounters. Introducing a more realistic tracking of the flow trajectories, even if still as passive tracers, should take into account statistical correlations of the flow which would clearly modify the statistics of bubble encounters. This point has remarkable practical relevance because reducing the degree of bubble coalescence is important to keep the monodispersivity of the suspension, and ultimately the control of the surface-to-volume ratio. Our jets do exhibit a remarkably low degree of bubble coalescence, a point that was already discussed by Carrera et al. (2008). A full description of the dynamics of suspensions of spherical bubbles, including bubble-bubble interactions and bubble-flow interactions could be approached with large scale Lattice-Boltzmann simulations, in the spirit of the work of Yin et al. (2006). In the case of bubble jets, however, the non-homogeneous conditions along the jet makes this analysis very demanding. It is particularly difficult to incorporate correctly the physics of the two-phase flow right at the exit of the injector, where bubbles may significantly deform due to the strong slowing-down as they enter the cavity, and the variations of the flow field are strong at the scale of bubbles. There the problem is that of a turbulent multiply connected free-boundary problem of great numerical difficulty.