1 Introduction

Our purpose in this paper is to study an interesting combination of problems of finding a fixed point of a given nonlinear operator which turns out to solve variational inequalities in real Hilbert spaces. Let C be a nonempty closed convex subset of a real Hilbert space \({\mathcal {H}}\), with inner product \(\langle \cdot , \cdot \rangle \) and an induced norm \(\Vert .\Vert .\) Let \(T: C\rightarrow C\) be nonlinear. The map T has a fixed point if \(Tx=x\) and the set of fixed point of T is denoted by \(F(T):=\lbrace x\in C: Tx=x\rbrace \ne \emptyset .\) The variational inequality problem (VIP) and fixed point problem (FPP)is formulated as:

$$\begin{aligned} \text{ find }\ \ \ x\in C \ \ \text{ such } \text{ that } \ \ \ x\in F(T) \ \ \ \text{ and } \ \ \ \langle f(x), y-x\rangle \ge 0, \ \ \forall y\in C, \end{aligned}$$
(1.1)

where f is a single-valued mapping defined on C.

Let the solution set of (1.1) be denoted by \(\Gamma :=VI(C,f) \cap F(T) \ne \emptyset .\) Problem (1.1) is a generalization of many optimization problems and has been studied by many researchers in different capacities (see, [1, 4, 37, 38] and contained references). Basically, (1.1) includes two remarkable and striking problems:

  1. 1.

    The FPP, which can be defined as follows:

    $$\begin{aligned} \text{ find } \ \ \ x\in C \ \ \ \text{ such } \text{ that } \ \ \ T(x)=x, \end{aligned}$$
    (1.2)

    provided the \(F(T) \ne \emptyset \).

  2. 2.

    Another important problem embeded in problem (1.1) is the well known VIP which has following structure:

    $$\begin{aligned} \text{ find }\ \ \ x\in C \ \ \text{ such } \text{ that } \ \ \ \langle f(x), y-x\rangle \ge 0, \ \ \forall y\in C. \end{aligned}$$
    (1.3)

    Let VIP(C, f) and SOL VIP(C, f) denote problem (1.3) and its solution set, respectively. It is important to note that problem (1.3) is a unifying and an essential modelling tool in many field such as economics, programming, engineering mechanics and many more, for examples see [2, 5, 16] and references contained therein. This concept was introduced and studied by Stampacchia [34], for the purpose of modelling problems in mechanics.

    There are methods for solving (1.3) which include: regularization method and projection method. In what follows, our focus for solving (1.3) is the projection method. This method involves construction of an iterative algorithm of the form:

    $$\begin{aligned} x_{n+1} = P_C(x_n - \lambda f x_n), n\ge 1, \end{aligned}$$
    (1.4)

    where \(\lambda \) is positive and \(P_C\) is a projection onto closed convex subset C. With this method, it is well known that the problem (1.3) is equivalent to the following fixed point problem:

    $$\begin{aligned} \text{ find } \ \ x\in C \ \ \text{ such } \text{ that } \ \ \ x=P_C(x-\lambda f(x)), \end{aligned}$$
    (1.5)

    for an arbitrary positive constant, \(\lambda .\) The basic projection method for solving VIP involves the gradient method, which performs only one iteration onto the feasible set. This method requires that the operators are inverse strongly monotone or strongly monotone (see [12]) for the iterative sequence to converge to the solution set. These conditions are very strong and quite restrictive. To circumvent this challenge, Korpelevich [18] while studying sadle point problems introduced a concept called extragradient method. It was further extended to VIPs for both Euclidean and Hilbert spaces. To be precise, Korpelevich [18] constructed the following algorithm:

    $$\begin{aligned} {\left\{ \begin{array}{ll} x_0 \in C,\\ y_n = P_C(x_n -\mu Ax_n),\\ x_{n+1} = P_C(x_n - \mu Ay_n), \end{array}\right. } \end{aligned}$$
    (1.6)

    where \(\mu \in (0,\frac{1}{L}),\) the singled-valued operator\( A: H\rightarrow H\) is monotone and L-Lipschitz continuous and \(P_C\) is a projection onto C. He proved that the recursive sequence \(\lbrace x_n \rbrace \) generated by (1.6) converged weakly to the solution set SOL VIP(C, A).

Since the the introduction of (1.6), many authors have modified it in various forms (see, [8, 17, 20] and the cited references therein).

In 2006, Nadezhkina and Takahashi [26] used the concept of hybrid and shrinking projection techniques to construct an extragradient based method and obtained a strong convergence. In short, in [31], the following algorithm is presented:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 \in C,\\ y_n = P_C(x_n - \mu Ax_n),\\ z_n = P_C(x_n - \mu A y_n),\\ C_n =\lbrace w\in C: \Vert z_n -w\Vert \le \Vert x_n - w\Vert \rbrace ,\\ Q_n = \lbrace w \in C: \langle x_n -w, x_0 - x_n\rangle \le 0 \rbrace ,\\ x_{n+1} = P_{{C_n} \cap Q_n} x_0. \end{array}\right. } \end{aligned}$$
(1.7)

Observe that the computation of the algorithm (1.6) requires computing two projections per iteration. It is known that projections onto closed convex set \(P_C\) has no closed form of expression. To drop the second \(P_C\) from the algorithm (1.6), Censor et al. [5] introduced a subgradient extragradient method and constructed the following iterative scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 \in H,\\ y_n = P_C(x_n - \mu Ax_n),\\ T_n = \lbrace x \in H:\langle x_n - \mu Ax_n - y_n, x-y_n \rangle \le 0 \rbrace ,\\ x_{n+1} = P_{T_n}(x_n -\mu Ay_n). \end{array}\right. } \end{aligned}$$
(1.8)

The authors of [5] considered a projection onto a half space \(P_{T_n}\) which has a closed form of expression. They proved under some mild conditions that the sequence \(\lbrace x_n \rbrace \) generated by (1.8) converged weakly to the solution. They further modified (1.8), using a hybrid and shrinking projection method as contained in (1.7) and obtained a strong convergence(see, [6]). It is pertinent to mention that Censor et al. [40] extended [5] to Euclidean spaces. Based on this improvement in [6, 26], many researchers have used other techniques to obtain a strong convergence (see [14, 19, 23, 37]).

In recent years, there has been a tremendous interest in developing fast convergence of algorithms, especially for the inertial type extrapolation method which was first proposed by Polyak in [31]. This inertial technique is based on a discrete analogue of a second order dissipative methods. This method was not known until the Nesterov’s acceleration gradient methods was published in 1983 (see, [27]) and by 2009, Beck and Teboulle [3] made it very popular. Recently, some researchers have constructed different fast iterative algorithms by means of inertial extrapolation techniques, for example, inertial Mann algorithm [25], inertial forward-backward splitting algorithm [21], inertial extragradient algorithm [22, 36], inertial projection algorithm [35], and fast iterative shrinkage-thresholding algorithm (FISTA) [3]. Recent results on the use of inertial method can be found in [8, 10, 11, 41,42,43] and contained references

Remark 1.1

We note that the algorithms (1.6)–(1.8) have a major drawback on the stepsize \(\mu \) in the sense that, they heavily rely on the Lipschitz constant of the given operator. This dependence on the Lipschitz constant affects the efficiency of the algorithms. In many practical importance, the Lipschitz constants are not known and in several occasions, difficult to estimate.

Based on Remark 1.1, many researchers have worked and improved the already existing results in various forms. In a recent work published by Gibali [9], he introduced an Armijo-like search rule and remarked that, it is for local approximation of the Lipschitz constant. Although, it does not require the knowledge of Lipschitz constant but might involve additional computation of projection operator. Thong and Hieu [37] presented two parallel iterative algorithms for solving a variational inequality problem and fixed point problem for demicontractive mapping using subgradient extragradient technique. They obtained a strong convergence in both schemes under the assumption that the single-valued operator is monotone and Lipschitz continuous. But, their stepsize was dependent on the Lipschitz constant which was a heavy drawback. To improve on this result, in [36] the authors proposed another two inertial self-adaptive stepsizes for solving variational inequailties and obtained strong convergence results under the assumption that the operator is strongly pseudomonotone, which is also a stronger assumption than being monotone and Lipschitz continuous. Shehu et al. [33] studied an inertial typed subgradient extragradient method with self-adaptive stepsize. Under some mild conditions, the authors obtained a weak convergence. Furthermore, they later considered the operator A to be strongly monotone and Lipschitz continuous and obtanied a strong convergence. More so, Ogwo et al. [29] studied relaxed inertial subgradient extragradient methods for solving variational inequality problems involving quasi-monotone operator and obtained weak convergence. For more results in this direction, see for instance [1, 28,29,30, 38] and cited references. Motivated and inspired by the work of [9, 18, 29, 33, 37], we construct a new inertial algorithm that is simple and efficient for approximating solutions of variational inequlity problems and fixed point problems using subgradient extragradient type method.

Our contributions in this research include the following:

  1. (a)

    A new inertial self-adaptive subgradient extragradient algorithm which does not require the prior knowledge of Lipschitz constant is constructed. The variable stepsize \(\lambda _n\) does not need the \(\lim _{n\rightarrow \infty } \lambda _n=0,\ \text{ or }\ \sum ^{\infty }_{n=1}\lambda _n=0\) as in the case of [36]. It is more applicable than fixed stepsizes.

  2. (b)

    The inertial term we use improves the rate of convergence greatly. It is quite different from the one considered by [10, 11, 19, 23, 24]. It does not also require computing norm difference between \(x_n\) and \(x_{n-1}\) before choosing the inertial factor, \(\theta _n\).

  3. (c)

    We obtain that the iterative sequence \(\lbrace x_n \rbrace \) converges strongly to the solution set. Unlike the weak convergences obtained by [5, 29, 38]. We assume that the single-valued operator A is not required to be strongly monotone as in the case of [33] or strong pseudomonotone used by [36]. These two assumptions are stronger than being monotone and Lipschitz continuous that we consider.

  4. (d)

    The general class of operator called the demicontractive mapping is considered. Many important operators like nonexpansive mapping, pesudocontractivs, k-strictly pseudocontractive, quasi-nonexpansive operators among many others are all embedded in demicontractive mapping (see Remark 2.2 below). It is a more general class of operators than the ones used by [1, 4, 33, 38].

  5. (e)

    Numerical examples are provided which show the general performance of our algorithm.

The rest of the paper is organized as follows: the preliminaries in Sect. 2 deal with basic definitions of the terms and related lemmas, which we state without their proofs. In Sect. 3, we state our algorithm and assumptions for our operators and control sequences. The convergence analysis is given in Sect. 4 while in Sects. 5 and 6 are devoted for numerical illustartions and conclusion, respectively.

2 Preliminaries

We list some basic concepts and lemmas which are useful for constructing and analysing the convergence of our algorithm.

Definition 2.1

Let H be a real Hilbert space and \(\forall x,y \in H, p \in F(T)\). A map \(T: H\rightarrow H\) is called:

  1. (1)

    monotone on H if, \(\langle T(x)-T(y), x-y\rangle \ge 0;\)

  2. (2)

    \(\eta \)-strongly monotone on H if there exists \(\eta > 0\) such that \(\langle T(x) - T(x), x-y\rangle \ge \eta \Vert x-y\Vert ^2; \)

  3. (3)

    Lipschitz continuous on H if, there exists a constant \(L> 0\) such that \(\Vert T(x) - T(y)\Vert \le L\Vert x-y\Vert ;\)

  4. (4)

    a nonexpansive mapping if \(\Vert Tx-Tx\Vert \le \Vert x-y\Vert ;\)

  5. (5)

    a quasi-nonexpansive on H if, \(\Vert T(x)-p\Vert \le \Vert x-p\Vert ;\)

  6. (6)

    \(\kappa \)-strictly pseudo-contractive on H if, \(\Vert Tx-Ty\Vert ^2\le \Vert x-y\Vert ^2 + \kappa \Vert x-y-(Tx-Ty)\Vert ^2\), for some \(\kappa \in [0,1);\)

  7. (7)

    \(\sigma \)-demi-contractive if, there exists \(\sigma \in [0,1)\) such that \(\Vert Tx-p\Vert ^2 \le \Vert x-p\Vert ^2 + \sigma \Vert (I-T)x\Vert ^2;\) or equivalently \(\langle Tx-x,x-p\rangle \le \frac{\sigma -1}{2}\Vert x-Tx\Vert ^2;\) or equivalently \(\langle Tx-p,x-p\rangle \le \Vert x-p\Vert ^2 + \frac{\sigma -1}{2}\Vert x-Tx\Vert ^2.\)

Remark 2.2

We observe that:

  1. (i)

    (7) contains as a special case, nonexpansive mapping, quasi-nonexpansive mapping, \(\kappa \)-strictly pseudo-contractive mapping with a nonempty fixed point.

  2. (ii)

    All nonexpansive operators are \(\kappa \)-strictly pseudo-contractive mapping with a nonempty fixed point.

  3. (iii)

    Also, all quasi-nonexpansive mappings are a subclass of 0-demi-contractive mapping.

  4. (iv)

    Nonexpansive mappings are contained in quasi-nonexpansive mapping.

But the converse of all of these definitions are not necessarily true. To understand this, consider the following examples below.

Example 2.3

[13] We consider a demicontractive mapping which is not neccessarily pseudocontractive or \(\kappa \)-strictly pseudo-contractive. Let \(H={\mathbb {R}}, C= [-1,1]\), let \(T: C \rightarrow C\) be defined by \(Tx = \frac{2}{3}x sin(\frac{1}{x})\) if \(x\ne 0\) and \(T0=0\) otherwise. Observe that the only fixed point of T is zero (0). However, for \(x\in C,\)

$$\begin{aligned} |Tx-0|^2 = |Tx|^2=|\frac{2}{3}x sin(1/x)|^2 \le |2x/3|^2 \le |x|^2 \le |x-0|^2 + \sigma |Tx-x|^2, \end{aligned}$$

for any \(\sigma \in [0,1),\) this shows that T is a demi-contractive.

Let us now show that T is not pseudo-contractive mapping. Let \(x=2/\pi , y=2/3\pi \). Then,

$$\begin{aligned} |Tx-Ty|^2= 256/81 \pi ^2. \end{aligned}$$

‘It follows that

$$\begin{aligned} |x-y|^2 + |(I-T)x-(I-T)y|^2=160/81\pi ^2. \end{aligned}$$

Example 2.4

[38] We consider a case where T is quasi-nonexpansive but fails to be nonexpansive. Let \(Tx=\frac{x}{2}sinx, \ \text{ if }\ x\ne 0\) and \(Tx=x,\) then we have that \(x=\frac{x}{2}sinx,\) which implies that \(sinx =2,\) impossible. Thus, we obtain that \(x=0,\) which means that \(F(T)=\lbrace 0\rbrace .\)

Now, for all \(x \in H,\)

$$\begin{aligned} \Vert Tx-0\Vert =\Vert \frac{x}{2}sinx\Vert \le \Vert \frac{x}{2}\Vert < \Vert x\Vert =\Vert x-0\Vert , \end{aligned}$$

this shows that T is quasi-nonexpansive. However, setting \(x=2\pi \) and \(y=\frac{3\pi }{2},\) we get

$$\begin{aligned} \Vert Tx-Ty\Vert =\Vert \frac{2\pi }{2}sin2\pi -\frac{3\pi }{4}sin \frac{3\pi }{2}\Vert =\frac{3\pi }{4} > \Vert 2\pi -\frac{3\pi }{2}\Vert =\frac{\pi }{2}, \end{aligned}$$

which further means that the operator T is not a nonexpansive mapping.

Example 2.5

[7] We give an example of demi-contractive mapping that is not quasi-nonexpansive and not pseudo-contractive mapping. Let \(f: [-2, 1] \rightarrow [-2, 1]\) be a real-valued function defined by \(f(x)=-x^2-x\). Then, it is demi-contractive on \([-2,1]\) and conitnuous. It is neither quasi-nonexpansive nor pseudo-contractive mapping on \([-2,1]\).

Definition 2.6

The mapping \(P_C: H \rightarrow C\) which assigns to each \(v\in H\), the unique point \(P_C(v)\) such that \(\Vert P_C(v)-v\Vert = \inf \lbrace \Vert w-v\Vert : w\in C\rbrace .\) This is called the projection operator.

The operator \(P_C\) satisfies the following condition:

$$\begin{aligned} \langle x-y, P_Cx - P_C y\rangle \ge \Vert P_C x- P_C y\Vert ^2, \ \ \forall x,y \in H. \end{aligned}$$

Also, for

$$\begin{aligned} P_C x\in H, \langle x-P_C x, P_C x-y\rangle \ge 0, \ \ \forall y \in C. \end{aligned}$$

Further implication is that

$$\begin{aligned} \Vert x-y\Vert ^2\ge \Vert x- P_C x\Vert ^2 + \Vert y-P_C y\Vert ^2, \ \ \forall x \in H, \forall y\in C. \end{aligned}$$

For details on the metric projections, an interested reader is encouraged to consult [44, section 3].

Lemma 2.7

[39] Let H be a Hilbert space and \(S: H \rightarrow H\) be a nonexpansive mapping with a nonempty fixed point. If \(\lbrace x_n \rbrace \) is a sequence in H that converges weakly to a point \(x^*\) and \(\lbrace (I-S)x_n\rbrace \) converges strongly to y, then \((I-S)x^* =y.\)

Lemma 2.8

Let H be a Hilbert space. Then, the following results hold for all \(x,y\in H, \lambda \in {\mathbb {R}}\):

  1. (a)

    \(2\langle x,y\rangle =\Vert x\Vert ^2 + \Vert y\Vert ^2- \Vert x-y\Vert ^2= \Vert x+y\Vert ^2 -\Vert x\Vert ^2 - \Vert y\Vert ^2,\)

  2. (b)

    \(\Vert x-y\Vert ^2 \le \Vert x\Vert ^2 + 2\langle y, x-y\rangle \)

  3. (c)

    \(\Vert \lambda x +(1-\lambda )y\Vert ^2 = \lambda \Vert x\Vert ^2 + (1-\lambda )\Vert y\Vert ^2 -\lambda (1-\lambda )\Vert x-y\Vert ^2.\)

Lemma 2.9

[32] Let \(\lbrace a_n \rbrace \) be a sequence of non-negative real numbers, \(\lbrace \beta _n \rbrace \) be a sequence of real numbers in (0, 1) with condition \(\sum ^{\infty }_{n=1}\beta _n =0,\) and \(\lbrace d_n\rbrace \) be a sequence of real numbers. Assume that

$$\begin{aligned} a_{n+1}\le (1-\beta _n)a_n+ \beta _n d_n, \ \ n\ge 0. \end{aligned}$$

and

  1. (a)

    \(\sum ^{\infty }_{n=0}\alpha _n =\infty \)

  2. (b)

    \(\limsup _{n\rightarrow }d_n\le 0.\)

Then, \(\lim _{n\rightarrow \infty } a_n =0.\)

Lemma 2.10

[24] Let \(\lbrace a_n \rbrace \) be sequence of non-negative real numbers satisfying the following inequality:

$$\begin{aligned} a_{n+1}\le (1-\beta _n)a_n +\delta _n + \gamma _n, n\ge 1, \end{aligned}$$

where \(\lbrace \beta _n \rbrace \) is a sequence in (0, 1) and \(\lbrace \delta _n \rbrace \) is a sequence of real numbers. suppose that \(\sum ^{\infty }_{n=1}\gamma _n < \infty , \) and \(\delta _n \le \beta _n M\) for some \(M> 0.\) Then, \(\lbrace a_n \rbrace \) is a bounded sequence.

Lemma 2.11

[19] Let \(A:H\rightarrow H\) be a monotone and L-Lipschtiz continuous mapping on H. Let \(S=P_C(I-\mu A),\) where \(\mu > 0.\) If \(\lbrace x_n \rbrace \) is a sequence in H satisfying \(x_n \rightharpoonup q\) and \(x_n -Sx_n \rightarrow 0\) then \(q\in VI(C,A)=F(S).\)

Lemma 2.12

[23] Let \(\lbrace a_n\rbrace \) be a sequence of nonnegative real numbers such that there exists a subsequence \(\lbrace a_{n_{j}} \rbrace \) of \(\lbrace a_n\rbrace \) such that \(a_{n_{j}} \le a_{n_{j}+1}\) for all \(j\in {\mathbb {N}}.\) Then, there exists a nondecreasing sequence \(\lbrace m_k \rbrace \) of \({\mathbb {N}}\) such that \(\lim _{k\rightarrow \infty } m_k =\infty \) and the following properties are satisfied by all (sufficiently large) number \(k\in {\mathbb {N}}:\)

$$\begin{aligned} a_{m_{k}}\le a_{m_{k}+1} \quad \ \text{ and } \quad \ a_k \le a_{m_{k}+1}. \end{aligned}$$

That is, \(m_k\) is the largest number n in the set \(\lbrace 1,2,...,k \rbrace \) such that \(a_n \le a_{n+1}.\)

3 The proposed algorithm

We present the proposed algorithm in this section and state the standard assumptions for the control sequences and the operators.

figure a
figure b

Remark 3.4:

  1. i)

    See that Assumption 3.1 (2) requires the operator A to be monotone and Lipschitz continuous.

  2. ii)

    The stepsize \(\lambda _n\) in (3.2) is self-adaptive. It is being generated at each iteration which makes our algorithm easily implemeneted without the prior knowledge of the Lipschitz constant of operator A.

  3. iii)

    The inertial term \(\theta _n (x_n - x_{n-1})\) contains an extra-term like Halpern iterative scheme, this greatly improves the rate of convergence of our proposed Alogrithm.

4 Convergence analysis

To establish the main theorem of this paper, the following lemmas should be stated and proved.

Lemma 4.1

Let \(\lbrace x_n \rbrace \) be the recursive sequence generated by Algorithm 3.3 such that Assumptions 3.1 and 3.2 are satisfied, then \(\lbrace x_n \rbrace \) is bounded.

Proof

Let \(x^* \in \Gamma .\) Then by the definition of variational inequality, we obtain that

$$\begin{aligned} \langle Ax^*, y_n-x^*\rangle \ge 0. \end{aligned}$$

Since A is monotone, we get that

$$\begin{aligned} \langle Ay_n, y_n-x^* \rangle \ge 0. \end{aligned}$$

Thus,

$$\begin{aligned} \langle Ay_n, y_n-x^*+ z_n -z_n\rangle \ge 0. \end{aligned}$$

Hence,

$$\begin{aligned} \langle Ay_n, x^* - z_n\rangle \le \langle Ay_n, y_n-z_n \rangle . \end{aligned}$$
(4.1)

We therefore obtain from the difinition of \(T_n\) that

$$\begin{aligned} \langle w_n -\lambda _nAy_n -y_n, z_n -y_n\rangle \le 0. \end{aligned}$$

It follows that

$$\begin{aligned} \langle w_n - \lambda _n Ay_n, z_n - y_n\rangle= & {} \langle w_n - \lambda _n Aw_n - y_n, z_n - y_n\rangle + \lambda _n \langle Aw_n - Ay_n, z_n-y_n\rangle \nonumber \\\le & {} \lambda _n \langle Aw_n - Ay_n, z_n - y_n\rangle . \end{aligned}$$
(4.2)

Now, using the definition of projection, its characterization and (4.2), we get

$$\begin{aligned} \Vert z_n - x^*\Vert ^2\le & {} \Vert w_n - x^*\Vert ^2-\Vert w_n - y_n\Vert ^2- \Vert y_n -z_n\Vert ^2 + 2 \langle w_n - \lambda _n Ay_n - y_n, z_n - y_n\rangle \nonumber \\\le & {} \Vert w_n - x^*\Vert ^2 - \Vert w_n - y_n \Vert ^2- \Vert y_n - z_n \Vert ^2 + 2\lambda _n \langle Aw_n - Ay_n, z_n - y_n \rangle \nonumber \\\le & {} \Vert w_n - x^*\Vert ^2- \Vert w_n - y_n \Vert ^2 - \Vert y_n - z_n\Vert ^2+ 2\lambda _n \Vert Aw_n - Ay_n\Vert .\Vert z_n -y_n\Vert \nonumber \\\le & {} \Vert w_n - x^*\Vert ^2 - \Vert w_n - y_n\Vert ^2 - \Vert y_n - z_n\Vert ^2 + \frac{2 \mu \lambda _n}{\lambda _{n+1}}\Vert w_n - y_n\Vert .\Vert z_n - y_n\Vert \nonumber \\\le & {} \Vert w_n - x^*\Vert ^2 - \Vert w_n - y_n\Vert ^2-\Vert y_n-z_n\Vert ^2\nonumber \\{} & {} \quad + \frac{\lambda _n}{\lambda _{n+1}} \mu (\Vert w_n - y_n \Vert ^2 + \Vert z_n - y_n\Vert ^2) \nonumber \\= & {} \Vert w_n - x^*\Vert ^2 -\Vert w_n -y_n\Vert ^2 + \frac{\lambda _n}{\lambda _{n+1}}\mu \Vert w_n -y_n \Vert ^2 - \Vert y_n - z_n\Vert ^2\nonumber \\{} & {} \quad +\frac{\lambda _n}{\lambda _{n+1}}\mu \Vert z_n - y_n\Vert ^2 \nonumber \\= & {} \Vert w_n-x^*\Vert ^2 - \left( 1-\frac{\lambda _n}{\lambda _{n+1}}\mu \right) \Vert w_n - y_n\Vert ^2-\left( 1-\frac{\lambda _n}{\lambda _{n+1}}\mu \right) \Vert z_n - y_n\Vert ^2.\nonumber \\ \end{aligned}$$
(4.3)

Observe from (3.2) that \(\lambda _n\) is a monotone nonincreasing sequence. Without loss of generality, we may assume that the \(\lim _{n\rightarrow \infty } \lambda _n = \lambda .\) Therefore,

$$\begin{aligned} \lim _{n\rightarrow \infty } (1-\frac{\lambda _n}{\lambda _{n+1}}\mu )=1-\mu> \epsilon > 0. \end{aligned}$$
(4.4)

It follows from (4.3) and (4.4) that

$$\begin{aligned} \Vert z_n - x^*\Vert ^2 \le \Vert w_n - x^*\Vert ^2. \end{aligned}$$
(4.5)

From the Algorithm 3.3, step 2, using the definition of \(q_n\), condition (d) of Assumption 3.2 and for all \(x^* \in \Gamma ,\) we obtain

$$\begin{aligned} \Vert q_n- x^*\Vert ^2= & {} \Vert (1-\beta _n) (z_n-x^*) + \beta _n( Tz_n - x^*)\Vert ^2 \nonumber \\= & {} (1-\beta _n)^2 \Vert z_n - x^*\Vert ^2 + \beta ^2_n\Vert Tz_n - x^*\Vert ^2 + 2\beta _n(1-\beta _n)\langle Tz_n - x^*, z_n-x^*\rangle \nonumber \\\le & {} (1-\beta _n)^2 \Vert z_n -x^*\Vert ^2 + \beta ^2_n \Vert z_n - x^*\Vert ^2+ \beta ^2_n \sigma \Vert Tz_n - x^*\Vert ^2 \nonumber \\{} & {} \quad + 2\beta _n (1-\beta _n)\left[ \Vert z_n - x^*\Vert ^2-\frac{1-\sigma }{2}\Vert Tz_n -x^*\Vert ^2\right] \nonumber \\= & {} \Vert z_n -x^*\Vert ^2 + \beta _n[\sigma \beta _n - (1-\beta _n)(1-\sigma )\Vert Tz_n - z_n\Vert ^2] \nonumber \\= & {} \Vert z_n - x^*\Vert ^2 + \beta _n[\beta _n - (1-\sigma )]\Vert Tz_n - z_n\Vert ^2 \nonumber \\\le & {} \Vert z_n -x^*\Vert ^2. \end{aligned}$$
(4.6)

Now,

$$\begin{aligned} \Vert w_n -x^*\Vert= & {} \Vert \alpha _n x_0 + (1-\alpha _n)x_n + \theta _n (x_n - x_{n-1})-x^*\Vert \nonumber \\= & {} \Vert \alpha _n (x_0 - x^*)+ (1-\alpha _n)(x_n - x^*) + \theta _n (x_n - x_{n-1})\Vert \nonumber \\\le & {} \alpha _n \Vert x_0 -x^*\Vert + (1-\alpha _n)\Vert x_n - x^*\Vert + \theta _n \Vert x_n - x_{n-1}\Vert \nonumber \\\le & {} \Vert x_n -x^*\Vert +\alpha _n\Vert x_0-x^*\Vert +\theta _n\Vert x_n - x_{n-1}\Vert . \end{aligned}$$
(4.7)

Furthermore

$$\begin{aligned} \Vert x_{n+1} - x^*\Vert= & {} \Vert \tau _n f(w_n) + (1-\tau _n)q_n -x^*\Vert \nonumber \\= & {} \Vert \tau _n(f(w_n)-x^*)+ (1-\tau _n)(q_n - x^*)\Vert \nonumber \\\le & {} \tau _n \Vert f(w_n) - f(x^*)\Vert + \tau _n\Vert f(x^*)-x^*\Vert +(1-\tau _n)\Vert q_n - x^*\Vert \nonumber \\\le & {} \tau _n \rho \Vert w_n - x^*\Vert + \tau _n \Vert f(x^*)-x^*\Vert + (1-\tau _n)\Vert z_n - x^*\Vert \nonumber \\\le & {} \tau _n \rho \Vert w_n -x^*\Vert + (1-\tau _n)\Vert w_n - x^*\Vert +\tau _n \Vert f(x^*)-x^*\Vert \nonumber \\= & {} (\tau _n \rho + 1-\tau _n)\Vert w_n -x^*\Vert + \tau _n \Vert f(x^*)- x^*\Vert \nonumber \\\le & {} (\tau _n \rho + 1-\tau _n)\bigg [\Vert x_n - x^*\Vert + \alpha _n\Vert x_0 -x^*\Vert \nonumber \\{} & {} \quad + \theta _n\Vert x_n - x_{n-1}\Vert \bigg ] + \tau _n\Vert f(x^*)-x^*\Vert \nonumber \\= & {} \bigg [(\tau _n \rho +(1-\tau _n))\bigg ]\Vert x_n - x^*\Vert + \bigg [\tau _n \rho +(1-\tau _n)\bigg ]\alpha _n\Vert x_0-x^*\Vert \nonumber \\{} & {} \quad + \bigg [\tau _n \rho +(1-\tau _n)\bigg ]\theta _n\Vert x_n -x_{n-1}\Vert + \tau _n\Vert f(x^*)-x^*\Vert \nonumber \\\le & {} [1-\tau _n(1-\rho )]\Vert x_n -x^*\Vert +[1-\tau _n(1-\rho )]\alpha _n\Vert x_0-x^*\Vert \nonumber \\{} & {} \quad + (1-\tau _n(1-\rho ))\theta _n\Vert x_n - x_{n-1}\Vert +\tau _n\Vert f(x^*)-x^*\Vert \nonumber \\= & {} [1-\tau _n(1-\rho )]\Vert x_n - x^*\Vert + \alpha _n\Vert x_0-x^*\Vert \nonumber \\{} & {} \quad + \theta _n \Vert x_n-x_{n-1}\Vert + \tau _n \Vert f(x^*) - x^*\Vert \nonumber \\\le & {} [1-\tau _n(1-\rho )]\Vert x_n - x^*\Vert + \tau _n(1-\rho )\Vert x_0 -x^*\Vert \nonumber \\{} & {} \quad + \theta _n \Vert x_n - x_{n-1}\Vert + \tau _n \Vert f(x^*) - x^*\Vert \nonumber \\< & {} [1-\tau _n(1-\rho )]\Vert x_n - x^*\Vert + \tau _n(1-\rho )\Vert x_0-x^*\Vert \nonumber \\{} & {} \quad +\theta _n \Vert x_n - x_{n-1}\Vert + \tau _n \Vert f(x^*) - x^*\Vert \nonumber \\= & {} [1-\tau _n(1-\rho )]\Vert x_n - x^*\Vert + \tau _n(1-\rho )\bigg [\Vert x_0 - x^*\Vert \nonumber \\{} & {} \quad + \tau _n\theta _n\frac{\Vert x_n - x_{n-1}\Vert }{\tau ^2_n(1-\rho )}+ \frac{\Vert f(x^*)-x^*\Vert }{1-\rho }\bigg ]. \end{aligned}$$
(4.8)

Let \(\gamma _n = \tau _n (1-\rho )\) in (4.8). Since, \(\lim _{n\rightarrow \infty }\frac{\theta _n}{\tau ^2_n}\Vert x_n - x_{n-1}\Vert =0,\) set

$$\begin{aligned} M = Sup \bigg \lbrace \Vert x_0 - x^*\Vert , \tau _n\frac{\theta _n \Vert x_n - x_{n-1}\Vert }{\tau ^2_n(1-\rho )}, \frac{\Vert f(x^*)-x^*\Vert }{1-\rho }\bigg \rbrace \end{aligned}$$

and apply Lemma 2.10 in (4.8) to obtain

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert\le & {} (1-\gamma _n)\Vert x_n - x^*\Vert + \gamma _n M \nonumber \\&\vdots&\nonumber \\\le & {} \text{ max }\lbrace \Vert x_1 - x^*\Vert , M\rbrace . \end{aligned}$$
(4.9)

Thus, we conclude from (4.9) and Lemma 2.10 that the sequence, \(\lbrace x_n \rbrace \) is bounded. Consequently, we obtain that \(\lbrace w_n \rbrace , \lbrace y_n \rbrace , \lbrace z_n \rbrace \) and \(\lbrace q_n \rbrace \) are all bounded sequences and this completes the proof of Lemma 4.1. \(\square \)

Lemma 4.2

For all \(x^* \in \Gamma ,\) we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} (1-\zeta _n)\Vert x_n - x^*\Vert ^2 +\zeta _n \bigg (\frac{\tau _n M_0 + \big \langle f(x^*)-x^*, x_{n+1}-x^*\big \rangle }{1-\rho } \bigg ), \end{aligned}$$

where \(\zeta _n=\frac{2\tau _n(1-\rho )}{1-\tau _n \rho }\).

Proof

Let \(x^* \in \Gamma .\) Then,

$$\begin{aligned} \Vert w_n - x^*\Vert ^2= & {} \Vert \alpha _n(x_0-x^*)+(1-\alpha _n)(x_n - x^*)+\theta _n(x_n -x_{n-1})\Vert ^2 \nonumber \\= & {} \Vert \alpha _n(x_0-x^*)+(1-\alpha _n)(x_n - x^*)\Vert ^2+\theta ^2_n\Vert x_n - x_{n-1}\Vert ^2 \nonumber \\{} & {} + 2\theta _n\alpha _n(1-\alpha _n)\langle x_0-x^{*}+x_n -x^{*}, x_n - x_{n-1}\rangle \nonumber \\= & {} \alpha _n\Vert x_0-x^*\Vert ^{2}+(1-\alpha _n)\Vert (x_n - x^*)\Vert ^2-\alpha _n(1-\alpha _n)\Vert x_n -x_0\Vert ^{2}\nonumber \\{} & {} \quad +\theta ^2_n\Vert x_n - x_{n-1}\Vert ^2 \nonumber \\{} & {} \quad + 2\theta _n\alpha _n(1-\alpha _n)\langle x_0-x^{*}+x_n -x^{*}, x_n - x_{n-1}\rangle \nonumber \\\le & {} \alpha _n\Vert x_0-x^*\Vert ^{2}+(1-\alpha _n)\Vert x_n - x^*\Vert ^2+\theta ^2_n\Vert x_n - x_{n-1}\Vert ^2 \nonumber \\{} & {} \quad + 2\theta _n\alpha _n(1-\alpha _n)\big [\langle x_0-x^{*},x_n -x_{n-1}\rangle + \langle x_n-x^*, x_n - x_{n-1}\rangle \big ] \nonumber \\\le & {} \alpha _n\Vert x_0-x^*\Vert ^2 +(1-\alpha _n)\Vert x_n-x^*\Vert ^2 + \theta ^2_n\Vert x_n -x_{n-1}\Vert ^2 \nonumber \\{} & {} \quad +2\theta _n\alpha _n(1-\alpha _n)\bigg [\Vert x_0-x^{*}\Vert \Vert x_n -x_{n-1}\Vert + \Vert x_n-x^*\Vert \Vert x_n - x_{n-1}\Vert \bigg ] \nonumber \\\le & {} (1-\alpha _n)\Vert x_n-x^*\Vert ^2+\alpha _n\Vert x_0-x^*\Vert ^2+ \theta ^2_n\Vert x_n -x_{n-1}\Vert ^2 \nonumber \\{} & {} \quad +\theta _n\alpha _n(1-\alpha _n)\big [\Vert x_0-x^{*}\Vert ^2+\Vert x_n -x_{n-1}\Vert ^2]\nonumber \\{} & {} \quad +\theta _n\alpha _n(1-\alpha _n)[\Vert x_n-x^*\Vert ^2+\Vert x_n - x_{n-1}\Vert ^2\big ]\nonumber \\\le & {} (1-\alpha _n)\Vert x_n-x^*\Vert ^2+\alpha _n\Vert x_0-x^*\Vert ^2+ \theta ^2_n\Vert x_n -x_{n-1}\Vert ^2 \nonumber \\{} & {} \quad +\theta _n\alpha _n\Vert x_0-x^{*}\Vert ^2+ \theta _n\alpha _n \Vert x_n -x_{n-1}\Vert ^2\nonumber \\{} & {} \quad + \theta _n\alpha _n \Vert x_n-x^*\Vert ^2+\theta _n\alpha _n\Vert x_n - x_{n-1}\Vert ^2\nonumber \\\le & {} (1-\alpha _n)\Vert x_n-x^*\Vert ^2+\alpha _n\Vert x_0-x^*\Vert ^2+ \theta _n\Vert x_n -x_{n-1}\Vert ^2 \nonumber \\{} & {} \quad +\alpha _n \Vert x_0-x^*\Vert ^2+\alpha _n\Vert x_n -x^*\Vert ^2+2\alpha _n \theta \Vert x_n -x_{n-1}\Vert ^2 \nonumber \\\le & {} \Vert x_n -x^*\Vert ^2+2\tau ^2_n(1-\rho )\Vert x_0-x^*\Vert ^2+\theta _n\Vert x_n -x_{n-1}\Vert ^2\nonumber \\{} & {} \quad +2\tau ^2_n(1-\delta )\theta _n\Vert x_n-x_{n-1}\Vert ^2 \nonumber \\\le & {} \Vert x_n -x^*\Vert ^2+2\tau ^2_n\Vert x_0-x^*\Vert ^2+\theta _n\Vert x_n -x_{n-1}\Vert ^2+2\tau ^2_n\theta _n\Vert x_n-x_{n-1}\Vert ^2 \nonumber \\= & {} \Vert x_n -x^*\Vert ^2+2\tau ^2_n\Vert x_0-x^*\Vert ^2+\tau ^2_n\frac{\theta _n}{\tau ^2_n}\Vert x_n -x_{n-1}\Vert ^2\nonumber \\{} & {} \quad +2\tau ^4_n\frac{\theta _n}{\tau ^2_n}\Vert x_n-x_{n-1}\Vert ^2. \end{aligned}$$
(4.10)

It follows from (4.10), (3.3) and Lemma 2.8 (b) that

$$\begin{aligned} \Vert x_{n+1} - x^*\Vert ^2\le & {} (1-\tau _n)^2\Vert q_n-x^*\Vert ^2 + 2\tau _n \rho \Vert w_n -x^*\Vert \Vert x_{n+1}-x^*\Vert \nonumber \\{} & {} \quad + 2\tau _n\langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\\le & {} (1-\tau _n)^2\Vert q_n-x^*\Vert ^2 + \tau _n \rho \Vert w_n -x^*\Vert ^2+ \tau _n \rho \Vert x_{n+1}-x^*\Vert ^2 \nonumber \\{} & {} \quad + 2\tau _n\rho \langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\\le & {} (1-\tau _n)^2\Vert z_n-x^*\Vert ^2 + \tau _n \rho \Vert w_n -x^*\Vert ^2+ \tau _n \rho \Vert x_{n+1}-x^*\Vert ^2\nonumber \\{} & {} \quad + 2\tau _n \langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\\le & {} (1-\tau _n)^2\Vert w_n-x^*\Vert ^2 + \tau _n \rho \Vert w_n -x^*\Vert ^2+ \tau _n \rho \Vert x_{n+1}-x^*\Vert ^2 \nonumber \\{} & {} \quad + 2\tau _n \langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\= & {} [(1-\tau _n)^2+\tau _n \rho ]\Vert w_n-x^*\Vert ^2+ \tau _n\rho \Vert x_{n+1}-x^*\Vert ^2\nonumber \\{} & {} \quad +2\tau _n \langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\\le & {} \frac{1}{1-\tau _n\rho }[(1-\tau _n)^2+\tau _n\rho ][\Vert x_n -x^*\Vert ^2+2\tau ^2_n\Vert x_0-x^*\Vert ^2\nonumber \\{} & {} \quad +\tau ^2_n\frac{\theta _n}{\tau ^2_n}\Vert x_n -x_{n-1}\Vert ^2+2\tau ^4_n\frac{\theta _n}{\tau ^2_n}\Vert x_n-x_{n-1}\Vert ^2] \nonumber \\{} & {} \quad +2\tau _n \langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\= & {} \frac{1}{1-\tau _n\rho }[1-2\tau _n+\tau _n\rho ]\Vert x_n -x^*\Vert ^2\nonumber \\{} & {} \quad +\frac{\tau ^2_n}{1-\tau _n\rho }\Vert x_n -x^*\Vert ^2+\frac{2\tau ^2}{1-\tau _n \rho }[(1+\tau _n\rho )\Vert x_0-x^*\Vert ^2\nonumber \\{} & {} \quad +\dfrac{\theta _n}{\tau ^2_n}\Vert x_n-x_{n-1}\Vert ^2+2\tau ^2_n \frac{\theta _n}{\tau ^2_n}\Vert x_n-x_{n-1}\Vert ^2+\frac{\Vert x_n -x^*\Vert ^2}{2}]\nonumber \\{} & {} \quad +\frac{2\tau _n}{1-\tau _n \rho } \langle f(x^*)-x^*, x_{n+1}-x^*\rangle \nonumber \\= & {} (1-\frac{2\tau _n(1-\rho )}{1-\tau _n \rho })\Vert x_n - x^*\Vert ^2\nonumber \\{} & {} \quad +\frac{2\tau _n(1-\rho )}{1-\tau _n \rho }\Bigg [ \frac{\tau _n \bigg [(1+\tau _n \rho )\Vert x_0-x^*\Vert ^2+\frac{\theta _n}{\tau ^2_n}\Vert x_n - x_{n-1}\Vert ^2 \bigg ]}{1-\rho }\Bigg ]\nonumber \\{} & {} \quad +\frac{2\tau _n(1-\rho )}{1-\tau _n\rho } \nonumber \\{} & {} \quad \Bigg [ \tau _n \bigg [ \frac{\frac{\Vert x_n -x^*\Vert ^2}{2\tau _n}+ 2\tau ^2_n\frac{\theta _n}{\tau ^2_n}\Vert x_n-x_{n-1}\Vert ^2+ \langle f(x^*)-x^*, x_{n+1}-x^*\rangle }{1-\rho }\bigg ] \Bigg ]. \nonumber \\ \end{aligned}$$
(4.11)

Letting \(M_0=Sup \bigg \lbrace (1+\tau _n \rho )\Vert x_0-x^*\Vert ^2,\frac{\theta _n}{\tau ^2_n}\Vert x_n-x_{n-1}\Vert ^2,\frac{\Vert x_n-x^*\Vert ^2}{2\tau _n}, 2\tau ^2_n\frac{\theta _n}{\tau ^2_n}\Vert x_n -x_{n-1}\Vert ^2; n\in {\mathbb {N}} \bigg \rbrace \) and in (4.11), we conclude that

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} \bigg (1-\frac{2\tau _n(1-\rho )}{1-\tau _n\rho } \bigg )\Vert x_n -x^*\Vert ^2\nonumber \\{} & {} +\frac{2\tau _n(1-\rho )}{1-\tau _n\rho }\Bigg ( \frac{\tau _n M_0+\langle f(x^*)-x^*, x_{n+1}-x^*\rangle }{1-\rho }\Bigg ). \end{aligned}$$
(4.12)

Putting \(\zeta _n=\frac{2\tau _n(1-\rho )}{1-\tau _n \rho }\) we can re-write (4.12) as follows:

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} (1-\zeta _n)\Vert x_n - x^*\Vert ^2 +\zeta _n \bigg (\frac{\tau _n M_0 +\langle f(x^*)-x^*, x_{n+1}-x^*\rangle }{1-\rho } \bigg ).\nonumber \\ \end{aligned}$$
(4.13)

This completes the proof of Lemma 4.2. \(\square \)

Next, we establish the following important lemma.

Lemma 4.3

We prove that

$$\begin{aligned}{} & {} (1-\tau _n)[(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2+(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2]\\{} & {} \quad \le \Vert x_n -p\Vert ^2 - \Vert x_{n+1} -p\Vert ^2+\tau _n K_0. \end{aligned}$$

Proof

From the algorithm and for all \(x^* \in \Gamma ,\) we get

$$\begin{aligned} \Vert q_n-x^*\Vert ^2= & {} \Vert (1-\beta _n)(z_n-x^*)+\beta _n(Tz_n -x^*)\Vert ^2 \nonumber \\\le & {} (1-\beta _n)\Vert z_n -x^*\Vert ^2 + \beta _n[\Vert z_n -x^*\Vert ^2+\sigma \Vert (I-T)z_n\Vert ^2]\nonumber \\{} & {} \quad -\beta _n(1-\beta _n)\Vert (I-T)z_n\Vert ^2 \nonumber \\\le & {} (1-\beta _n)\Vert z_n -x^*\Vert ^2+\beta _n\Vert z_n -x^*\Vert ^2 +\beta _n \sigma \Vert (I-T)z_n\Vert ^2\nonumber \\= & {} \Vert z_n -x^*\Vert ^2 +\beta _n \sigma \Vert (I-T)z_n\Vert ^2\nonumber \\\le & {} \Vert w_n -x^*\Vert ^2 -(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2-(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2\nonumber \\{} & {} \quad +\beta _n \sigma \Vert (I-T)z_n\Vert ^2\nonumber \\\le & {} \Vert w_n -x^*\Vert ^2 -(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2-(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2 \nonumber \\{} & {} \quad \;\;-\sigma (\lambda -1)(1-\tau _n)\Vert (I-T)z_n\Vert ^2. \nonumber \\ \end{aligned}$$
(4.14)

Furthermore from the Algorithm and for all \( x^* \in \Gamma ,\)

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2\le & {} \tau _n \Vert f(w_n) -x^*\Vert ^2 +(1-\tau _n)\Vert q_n-x^*\Vert ^2 \nonumber \\\le & {} \tau _n\Vert f(w_n)-x^*\Vert ^2 +(1-\tau _n)\nonumber \\{} & {} \quad \bigg \lbrace \Vert w_n -x^*\Vert ^2-(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2-(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2\bigg \rbrace \nonumber \\\le & {} \tau _n \Vert f(w_n)-x^*\Vert ^2+(1-\tau _n)\nonumber \\{} & {} \quad \bigg \lbrace \Vert x_n-x^*\Vert ^2+\alpha _n\Vert x_0-x^*\Vert ^2+\theta _n\Vert x_n-x_{n-1}\Vert ^2 -(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2\nonumber \\{} & {} \quad \;\;-(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2 \bigg \rbrace \nonumber \\= & {} \tau _n \Vert f(w_n)-x^*\Vert ^2+(1-\tau _n)\nonumber \\{} & {} \quad \bigg [\Vert x_n-x^*\Vert ^2+\alpha _n\Vert x_0-x^*\Vert ^2+\theta _n\Vert x_n-x_{n-1}\Vert ^2\bigg ]\nonumber \\{} & {} \quad \;\;-(1-\tau _n)\bigg [(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2-(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2\bigg ] \nonumber \\\le & {} \tau _n \Vert f(w_n)-x^*\Vert ^2+(1-\tau _n)[\Vert x_n-x^*\Vert ^2+\tau ^2_n(1-\delta )\Vert x_0\nonumber \\{} & {} \quad -x^*\Vert ^2+\theta _n\Vert x_n-x_{n-1}\Vert ^2]\nonumber \\{} & {} \quad \;\;-(1-\tau _n)\bigg [(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2+(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2\bigg ]\nonumber \\\le & {} \tau _n \Vert f(w_n)-x^*\Vert ^2+(1-\tau _n)\big [\Vert x_n-x^*\Vert ^2+\tau ^2_n\Vert x_0-x^*\Vert ^2+\theta _n\Vert x_n-x_{n-1}\Vert ^2\big ]\nonumber \\{} & {} \quad \;\;-(1-\tau _n)\bigg [(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2+(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2\bigg ].\nonumber \\ \end{aligned}$$
(4.15)

Thus, it follows from (4.15) that

$$\begin{aligned}{} & {} (1-\tau _n)\bigg [(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert w_n - y_n\Vert ^2+(1-\frac{\lambda _n \mu }{\lambda _{n+1}})\Vert z_n - y_n\Vert ^2\bigg ]\nonumber \\{} & {} \quad \le \Vert x_n -x^*\Vert ^2-\Vert x_{n+1}-x^*\Vert ^2 + \tau _n K_0. \end{aligned}$$
(4.16)

where \(K_0=\sup \bigg \lbrace \Vert f(w_n)-x^*\Vert ^2, \Vert x_n -x^*\Vert ^2,\tau _n\frac{\theta _n}{\tau ^{2}_n}\Vert x_n - x_{n-1}\Vert ^2, \tau _n \Vert x_0-x^*\Vert ^2: n\in {\mathbb {N}}\bigg \rbrace ,\) completing lemma 4.3. \(\square \)

Lemma 4.4

For any \(x^* \in \Gamma \), we obtain

$$\begin{aligned} \sigma (\lambda -1)(1-\tau _n)\Vert z_n -Tz_n\Vert ^2\le & {} \Vert w_n -x^*\Vert ^2-\Vert q_n-x^*\Vert ^2. \end{aligned}$$

Proof

The result follows immediately from Lemma 4.3. \(\square \)

We are now ready to establish the main theorem of this paper.

Theorem 4.5

Let C be a nonempty closed convex subset of a real Hilbert space, H. Let A be a monotone and Lipschitz continuous defined on H and \(T: H \rightarrow H\), be a \(\sigma \)-demi-contractive mapping. Let f be a contraction map defined on H. Assume the solution set \(\Gamma \ne \emptyset .\) If the Assumptions 3.1 and 3.2 are satisfied, then the sequence \(\lbrace x_n \rbrace \) converges strongly to the solution set.

Proof

Since \(P_{\Gamma }f\) is a contraction on H, there exists \(q\in \Gamma \) such that \(q=P_{\Gamma }f(q)\). Thus, we prove that the iterative sequence \(\lbrace x_n \rbrace \) converges strongly to \(q=P_{\Gamma }f(q).\) In order to establish this result, we consider the following two cases.

Case 1: Suppose there is \(n_0 \in {\mathbb {N}}\) such that \(\lbrace \Vert x_n -q\Vert \rbrace ^{\infty }_{n=n_{0}}\) is nonincreasing. Then, \(\lim _{n\rightarrow \infty } \lbrace \Vert x_n -q\Vert \rbrace \) exists. It follows from this fact that

$$\begin{aligned} \lim _{n\rightarrow \infty }(\Vert x_n-q\Vert -\Vert x_{n+1}-q\Vert )=0. \end{aligned}$$

From the Algorithm 3.3, we get

$$\begin{aligned} \Vert w_n - x_n\Vert\le & {} \Vert \alpha _n(x_0-x_n)\Vert +\Vert \theta _n(x_n -x_{n-1})\Vert \nonumber \\= & {} \alpha _n \Vert x_0 - x_n\Vert + \theta _n\Vert x_n-x_{n-1}\Vert \nonumber \\\le & {} \tau ^2_n(1-\rho )\Vert x_0-x_n\Vert +\tau ^2_n\frac{\theta _n}{\tau ^2_n}\Vert x_n - x_{n-1}\Vert . \end{aligned}$$
(4.17)

It follows from (4.17) and the Assumption 3.2(b–c) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n-x_n\Vert =0. \end{aligned}$$
(4.18)

From Lemma 4.3, we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n-y_n\Vert =0=\Vert z_n -y_n\Vert . \end{aligned}$$
(4.19)

It follows from (4.19) that

$$\begin{aligned} \Vert w_n-z_n\Vert \le \Vert w_n -y_n\Vert +\Vert y_n -z_n\Vert . \end{aligned}$$

Subsequently,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n-z_n\Vert =0. \end{aligned}$$
(4.20)

Since the \(\lim _{n\rightarrow \infty }\lbrace \Vert x_n-q\Vert \rbrace \) exists,it follows that

$$\begin{aligned} \lim _{n\rightarrow \infty }(\Vert w_n-p\Vert ^2-\Vert q_n-p\Vert ^2)=0. \end{aligned}$$

That is,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n-p\Vert =\lim _{n\rightarrow \infty }\Vert q_n-p\Vert . \end{aligned}$$
(4.21)

And consequently from the Lemma 4.4, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert z_n-Tz_n\Vert =0. \end{aligned}$$
(4.22)

Using the condition on \(\tau _n\) and definition of \(q_n\), we estimate that

$$\begin{aligned} \Vert q_n-y_n\Vert\le & {} (1-\beta _n)\Vert z_n -y_n\Vert + \beta _n\Vert Tz_n - y_n\Vert \nonumber \\\le & {} \Vert z_n - y_n\Vert +\beta _n\Vert Tz_n -y_n\Vert \nonumber \\= & {} \Vert z_n - y_n\Vert +\tau _n \frac{\beta _n}{\tau _n}\Vert Tz_n -y_n\Vert \rightarrow 0. \end{aligned}$$
(4.23)

It follows from (4.23) and (4.19) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert q_n - y_n\Vert =0. \end{aligned}$$
(4.24)

Now, using the definition of \(q_n\) once again, (4.18), (4.19) and (4.24), we get

$$\begin{aligned} \Vert q_n-x_n\Vert\le & {} \Vert q_n-y_n\Vert +\Vert y_n-w_n\Vert +\Vert w_n-x_n\Vert . \end{aligned}$$
(4.25)

And consequently from (4.25), we conclude that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert q_n - x_n\Vert =0. \end{aligned}$$
(4.26)

Applying the condition on \(\alpha _n\), the Assumption 3.2(b) and the estimate (4.26), we obtain

$$\begin{aligned} \Vert w_n -q_n\Vert\le & {} \alpha _n\Vert x_0-q_n\Vert +(1-\alpha _n)\Vert x_n-q_n\Vert +\theta _n\Vert x_n - x_{n-1}\Vert \nonumber \\\le & {} \tau ^2_n(1-\rho )\Vert x_0-q_n\Vert +\Vert x_n-q_n\Vert +\theta _n\Vert x_n-x_{n-1}\Vert \nonumber \\\le & {} \tau ^2_n\Vert x_0-q_n\Vert +\Vert x_n-q_n\Vert +\theta _n\Vert x_n - x_{n-1}\Vert \nonumber \\= & {} \tau ^2_n\Vert x_0-x^*\Vert +\Vert x_n -q_n\Vert +\frac{\tau ^2\theta _n}{\tau ^2_n}\Vert x_n -x_{n-1}\Vert \rightarrow 0. \end{aligned}$$
(4.27)

Thus, we obtain from (4.27) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n - q_n\Vert =0. \end{aligned}$$
(4.28)

Finally, applying the condition of \(\tau _n\) in the inequality below, using (4.26), we get that

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert\le & {} \tau _n\Vert f(w_n)-x_n\Vert +(1-\tau _n)\Vert q_n -x_n\Vert \rightarrow 0. \end{aligned}$$
(4.29)

Therefore,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{n+1} - x_n\Vert =0. \end{aligned}$$
(4.30)

Because \(\lbrace x_n\rbrace \) is bounded (see Lemma 4.1), there exists a subsequence \(\lbrace x_{n_{k}}\rbrace \) of \(\lbrace x_n\rbrace \) such that \(\lbrace x_{n_{k}}\rbrace \) weakly converges to some q as \(k\rightarrow \infty \) and

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_n - x^*, f(x^*)-x^*\rangle =\lim _{k\rightarrow \infty }\langle x_{n_{k}}-x^*, f(x^*)-x^*\rangle =\langle q-x^*,f(x^*)-x^*\rangle .\nonumber \\ \end{aligned}$$
(4.31)

Since \(x_{n_{k}}\rightharpoonup q\) and \(\Vert w_n - y_n\Vert =\Vert w_n -P_C(w_n -\lambda _n Aw_n)\Vert \rightarrow 0\) by Lemma 2.11, we obtain \(q\in VI(C,A).\) Furthermore, since \(\Vert z_n - x_n\Vert \rightarrow 0\), \(z_{n_{k}}\rightharpoonup q\) and \(\lim _{n\rightarrow \infty }\Vert z_n - Tz_n\Vert =0,\) we get from these facts that \(q\in F(T).\) Therefore, \(q\in VI(C,A)\cap F(T),\) that is, \(q\in \Gamma .\) Also, by \(p=P_{VI(C,A)\cap F(T)}(0)\), we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_n-x^*, f(x^*)-x^*\rangle = \langle q-x^*,f(x^*)-x^*\rangle \le 0. \end{aligned}$$

By our estimate that \(\Vert x_{n+1}-x_n\Vert \rightarrow 0,\) we obtain

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_{n+1}-x^*, f(x^*)-x^*\rangle \le 0. \end{aligned}$$

Therefore, using (4.12), (4.13), (4.31) and Lemma 2.9, we find that the sequence \(\lbrace x_n \rbrace \) converges strongly to q.

Case 2: There exists a subsequence \(\lbrace \Vert x_{n_{k}}-p\Vert ^2\rbrace \) of \(\lbrace \Vert x_n - p\Vert ^2\rbrace \) such that \(\Vert x_{n_{k}}-p\Vert ^2 < \Vert x_{n_{k}+1}-p\Vert ^2\) for all \(k\in {\mathbb {N}}.\) It follows from Lemma 2.12 that there exists a nondecreasing sequence \(\lbrace m_k \rbrace \) of \({\mathbb {N}}\) such that \(\lim _{k\rightarrow \infty }\) and the following inequalities hold for all \(k\in {\mathbb {N}}:\)

$$\begin{aligned} \Vert x_{m_{k}}-p\Vert ^2 \le \Vert x_{m_{k}+1}-p\Vert ^2 \ \ \text{ and }\ \ \Vert x_k-p\Vert ^2 \le \Vert x_{m_{k}+1}-p\Vert ^2. \end{aligned}$$
(4.32)

From Lemma 4.3, we get that

$$\begin{aligned}{} & {} (1-\tau _{m_{k}})[(1-\frac{\lambda _{m_{k}} \mu }{\lambda _{m_{k}+1}})\Vert w_{m_{k}}-y_{m_{k}}\Vert ^2 + (1-\frac{\lambda _{m_{k}}\mu }{\lambda _{m_{k}+1}})\Vert z_{m_{k}}-y_{m_{k}}]\nonumber \\{} & {} \quad \le \Vert x_{m_{k}}-p\Vert ^2 -\Vert x_{m_{k}+1}-p\Vert ^2 +\tau _{m_{k}} K_0 \nonumber \\{} & {} \quad \le \tau _{m_{k}}K_0. \end{aligned}$$
(4.33)

Using (4.33) together with assumptions in \(\lbrace \lambda _n\rbrace \) and \(\lbrace \tau _n \rbrace ,\) it follows that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert w_{m_{k}}-y_{m_{k}}\Vert =0, \lim _{k\rightarrow \infty }\Vert z_{m_{k}}-y_{m_{k}}\Vert =0 \ \ \text{ and }\ \ \lim _{k\rightarrow \infty }\Vert w_{m_{k}}-z_{m_{k}}\Vert =0. \end{aligned}$$
(4.34)

However, from Lemma 4.4, we obtain

$$\begin{aligned} \sigma (\lambda -1)(1-\tau _{m_{k}})\Vert z_{m_{k}}-Tz_{m_{k}}\Vert\le & {} \Vert w_{m_{k}}-p\Vert ^2 -\Vert q_{m_{k}}-p\Vert ^2. \end{aligned}$$
(4.35)

Using Lemma 4.1, it follows from (4.35) that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert z_{m_{k}}-Tz_{m_{k}}\Vert =0. \end{aligned}$$

Furthermore, by the same argument in case 1, we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x_{m_{k}+1}-x^*, f(x^*)-x^*\rangle \le 0. \end{aligned}$$

It follows from (4.12) and (4.32) that

$$\begin{aligned} \Vert x_{m_{k}+1}-x^*\Vert ^2\le & {} (1-\zeta _{m_{k}})\Vert x_{m_{k}}-x^*\Vert ^2 + \zeta _{m_{k}}\bigg (\frac{\tau _{m_{k}+1}M_0 +\langle f(x^*)-x^*, x_{m_{k}+1}-x^*\rangle }{1-\rho } \bigg ) \end{aligned}$$

and hence

$$\begin{aligned} \zeta _{m_{k}}\Vert x_{m_{k}+1}-x^*\Vert ^2\le & {} \zeta _{m_{k}}\bigg (\frac{\tau _{m_{k}+1}M_0 +\langle f(x^*)-x^*, x_{m_{k}+1}-x^*\rangle }{1-\rho } \bigg ). \end{aligned}$$

Since \(\zeta _{m_{k}}>0\) and using (4.32) we get

$$\begin{aligned} \Vert x_k -x^*\Vert ^2\le \Vert x_{m_{k}+1}-x^*\Vert ^2 \le \bigg (\frac{\tau _{m_{k}+1}M_0 +\langle f(x^*)-x^*, x_{m_{k}+1}-x^*\rangle }{1-\rho } \bigg ). \end{aligned}$$

Taking the limit in the above inequality as \(k\rightarrow \infty ,\) we conclude that \(x_k\) converges strongly to \(q=P_{\Gamma }f(q).\) This completes the proof of Theorem 4.5. \(\square \)

5 Numerical illustrations

Let \({H}=\left( l _2({\mathbb {R}}), ~||. ||_{ l _2}\right) \), where \( l _2({\mathbb {R}}):=\{x=(x_1, x_2, x_3, \dots ),~x_i\in {\mathbb {R}}:\sum _{i=1}^\infty |x_i|^2<\infty \}\) and \(||x||_{ l _2}:= \left( \sum _{i=1}^\infty |x_i|^2 \right) ^{\frac{1}{2}},~~\forall x \in l _2({\mathbb {R}}).\) Let \({C}=\{x\in { l _2}({\mathbb {R}}):||x-a||_{{ l _2}}\le r\},\) where \(a=(1, \frac{1}{2}, \frac{1}{3}, \cdots )\), \(r=3\). Then C is a nonempty closed and convex subset of \({ l _2}({\mathbb {R}})\). Thus,

$$\begin{aligned} P_{C}(x) = {\left\{ \begin{array}{ll} x, &{}\text{ if }~~x\in ||x-a||_{{ l _2}}\le r,\\ \frac{x-a}{||x-a||_{{ l _2}}}r +a, &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

Now, define the operators \(A,f,T: { l _2}({\mathbb {R}}) \rightarrow { l _2}({\mathbb {R}})\) by

$$\begin{aligned} Aa:= \left( \frac{a_1+|a_1|}{2}, \frac{a_2+|a_2|}{2},...,\frac{a_i+|a_i|}{2},...\right) ,~~f(a)=\frac{1}{3}a,~~T(a)=\frac{-11}{2}a ~~\forall a\in {\mathfrak {l}}_2. \end{aligned}$$

Then A is Lipschitz continuous and monotone with Lipschitz constant \({L}=1\), f is a contraction with \(\rho =\frac{1}{3}\) and T is a demi-contractive mapping with \(\sigma =\frac{117}{169}\).

Furthermore, we choose \(\lambda _1=1\), \(\mu =0.5\), \(\tau _n=\frac{1}{n+1}\), \(\alpha _n=\frac{2n+3}{50n+100}\), \(\beta _n=\frac{n+1}{100n+2}\) and

$$\begin{aligned} \theta _n:= {\left\{ \begin{array}{ll} \min \left\{ \theta , \frac{e_n}{\Vert x_n-x_{n-1}\Vert }\right\} , &{} \text{ if } ~ x_n \ne x_{n-1}\\ \theta , &{} \text{ otherwise }, \end{array}\right. } \end{aligned}$$

where \(e_n=\frac{1}{n^2}\) and \(\theta =0.3\). Then, we consider the following cases for the numerical experiments.

Case 1: Take \(x_1= (1, \frac{1}{2}, \frac{1}{3}, \cdots ) \) and \(x_0=(\frac{1}{2}, \frac{1}{5}, \frac{1}{10}, \cdots )\).

Case 2: Take \(x_1= (\frac{1}{2}, \frac{1}{5}, \frac{1}{10}, \cdots )\) and \(x_0=(1, \frac{1}{2}, \frac{1}{3}, \cdots )\).

Case 3: Take \(x_1= (1, \frac{1}{4}, \frac{1}{9}, \cdots )\) and \(x_0= (\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \cdots ).\)

The stopping criterion is \(\text{ TOL}_n < 10^{-5}\), where \(\text{ TOL}_n=0.5\Vert x_n - T(PC(x_n - x_n))\Vert ^2\). Note that \(\text{ TOL}_n=0\) implies that \(x_n\) is a solution.

Table 1 Numerical results summarizing the performance of our Algorithm
Full size table
Fig. 1
figure 1

The behavior of \(\text{ TOL}_n\) with \(\varepsilon =10^{-5}\): Top Left: Case 1; Top Right: Case 2; Bottom Right: Case 3

Full size image

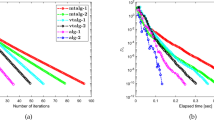
Remark 5.1

The numerical illustration 5 is provided to check the general performance of our Algorithm 3.3. The Table 1 and Fig. 1 show the time it takes and number of iterations it takes for the recursive sequence to converge in the cases 1 to 3 stated above.

6 Conclusion

In the real Hilbert space setting, we have proposed subgradient extragradient methods for approximating a common solution for variational inequality problems and fixed point problems. We obtained a strong convergence under some mild assumptions, that is, the associated single-valued operator A is monotone and Lipschitz continuous. Furthermore, we have adopted self-adaptive stepsize which is generated at each iteration. An appropriate computational experiment is provided to support our theoritical argument. Our algorithm is an improvement to the recent work of [33, 37, 38] among other already announced results in this direction.