1 Introduction

The numerical methods for solving singularly perturbed problems are often concerned and have been developed for decades (see [1,2,3,4,5]). Besides fitted operator numerical methods on the uniform mesh (see [1, 2, 5, 6]), two strategies are commonly used to solve these problems on the non-uniform mesh. One strategy is to use layer-adapted grid methods, i.e., numerical methods on a priori layer-adapted meshes, such as Bakhvalov-type meshes and Shishkin-type meshes (see [1, 2, 4, 5, 7,8,9,10]). Another strategy is to use adaptive grid methods, i.e., numerical methods on adaptive meshes. The application of the adaptive grid gets rid of the limitation of a priori knowledge of the exact solution, only needs to find a monitor function to help optimize the grid continually (see [1, 3, 5, 11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]). The monitor function is defined in terms of the local error (or the local residual) or the arc-length of the solution and so on. Because the construction of the adaptive grid (or the moving mesh) does not depend on the properties of the exact solution, the progresses on the convergence analysis of the adaptive grid method based on the arc-length monitor function have been made gradually almost only for the special cases (see [14,15,16,17,18,19,20,21]), but seldom for the general linear non-conservative case (see [22,23,24,25,26]).

We consider the general linear singularly perturbed convection-reaction-diffusion problem in the non-conservative form:

$$\begin{aligned} \left\{ \begin{array}{ll} Tu(x):=-\varepsilon u''(x)-p(x)u'(x)+q(x)u(x)=f(x), ~ x\in (0,1), \\ u(0)=0, u(1)=0,\\ \end{array}\right. \end{aligned}$$
(1)

where \(0<\varepsilon \ll 1\) is a sufficiently small positive perturbation parameter, p, q and f are sufficiently smooth functions, \(0<\beta \le p(x)\le \beta ^*\), \(|p'(x)| \le C_p\), \(0\le q(x)\le \gamma ^*\) and \(| q'(x)| \le C_q\) for \(x\in [0,1]\), \(\beta , \beta ^*, \gamma ^*, C_p\) and \(C_q\) are constants, and C is a generic positive constant, independent of the perturbation parameter \(\varepsilon \). The problem has a unique solution u that has an exponential boundary layer at \(x=0\).

This problem (1) was solved by the upwind finite difference scheme on the arc-length equidistribution mesh as follows (see [22,23,24,25]):

$$\begin{aligned} \left\{ \begin{array}{l} T^N u_i^N:=-\varepsilon DD^-u_i^N -p_i D^+u_i^N +q_i u_i^N = f_i, i=1,...,N-1,\\ u_0^N=0,~ u_N^N=0,\\ \end{array}\right. \end{aligned}$$
(2)

where \(h_i=x_i-x_{i-1},\quad D^-u_i=\frac{u_i-u_{i-1}}{h_i},\quad D^+u_i=\frac{u_{i+1}-u_i}{h_{i+1}}\) and \(DD^-u_i=\frac{2(D^-u_{i+1}-D^-u_i)}{h_{i+1}+h_{i+1}}\).

The development of related adaptive methods and their convergence analysis are reviewed in the following.

  1. (i)

    In the early days, for the non-conservative homogeneous linear case \(-\varepsilon u'' (x)-p(x) u'(x)=0\), the convergence of the upwind finite difference scheme on the grid equidistributing the monitor function \(M(x, u(x))=|u'(x)|^{1/m}\) and \(\sqrt{1+(u'(x))^2}\) of the exact solution u was obtained by using the a priori truncation error in [11,12,13,14]. For the non-homogeneous case \(-\varepsilon u'' (x)-p(x) u'(x)=f(x)\), the convergence of the upwind finite difference scheme by using \(M(x, u(x))=\alpha + |u''(x)|^{1/m}\) of the exact solution u was obtained by the a priori truncation error in [15]. For the reaction-diffusion case \(-\varepsilon u'' (x)-b(x) u(x)=f(x)\), the convergence of the central finite difference scheme using \(M(x, u(x))=\alpha + |w''(x)|^{1/m}\) (w is the layer component of u) was obtained by the a priori truncation error in [16]. For the conservative quasilinear case \(-\varepsilon u'' (x)-b(x, u)'=f(x)\), the first-order convergence of the simple upwind finite difference scheme using monitor functions based on a priori information of the exact solution was also obtained in [17].

  2. (ii)

    In fact, to devise a rigorous analysis of any adaptive algorithm, the first ingredient one needs is an a posteriori bound on the error of the computed solution (see §I.2.5 in [1]). For the conservative quasilinear case \(-\varepsilon u'' (x)-b(x, u)'=f(x)\), the convergence of the simple upwind finite difference scheme on the adaptive mesh equidistributing the numerical arc-length monitor function \(M(x, u^N(x))=\sqrt{1+((u^N(x))')^2}\) was firstly analyzed by the a posteriori truncation error in [18]. Its uniform first-order error bound was obtained by using the Green’s function, since the conservative equation could easily be reduced to the first-order equation (see [1, 18, 19]). The numerical solution of the above problem was also calculated by equidistributing a monitor function of discrete second-order derivatives in [20].

  3. (iii)

    Afterwards, the special case \(-\varepsilon u'' (x)-p(x) u'(x)=0\) was solved by the simple upwind scheme on the adaptive mesh equidistributing the numerical arc-length monitor function \(M(x, u^N(x))\). By using some techniques developed in [18], the existence of the adaptive solution was proved with a strong grid assumption \(h_i/h_{i+1} \le 1\), and the uniform first-order convergence was obtained by the a posteriori error estimation and using a quadratic interpolation of the numerical solution (see [21]).

  4. (iv)

    However, the uniform first-order convergence of (2) for the general case \(-\varepsilon u''(x)-p(x)u'(x)+q(x)u(x)=f(x)\) was proved in [22] by the a priori truncation error and the grid properties obtained in [14] for the special case \(-\varepsilon u'' (x)-p(x) u'(x)=0\), but not the a posteriori error estimate and not free from the properties of the exact solution. The uniform first-order convergence of (2) for singularly perturbed mixed boundary value problems was derived in [23] also by a priori truncation error, the properties of the exact solution and the grid properties obtained in [14].

  5. (v)

    In the later, by developing the techniques in [21], the existence of the numerical solution of (2) for the general problem (1) on the adaptive mesh equidistributing the numerical arc-length monitor function \(M(x, u^N(x))\) was proved by a slightly weakened grid restriction \(h_i/h_{i+1} \le C\), and the uniform first-order convergence was obtained by the a posteriori error estimation and also the quadratic interpolation of the numerical solution for (1) in [24].

  6. (vi)

    Further, the quadratic interpolation was replaced by a linear interpolation in the error analysis of (2) for (1) in [25] and also of a similar scheme for a singularly perturbed differential difference equation with small delay in [26]. However, the uniform first-order convergence in [25, 26] was obtained by citing [24] and [18, 21] respectively, where the quadratic interpolation and the impractical condition \(h_i/h_{i+1} \le C\) or the conservative equation were used, but without any proof of the existence of numerical solution and the boundedness of the arc-length of the numerical solution.

  7. (vii)

    Recently, for the reaction-diffusion singularly perturbed boundary value problem \(-\varepsilon u'' (x)+a(x) u(x)=f(x)\) of robin-type, the spline difference method on the a posteriori layer adapted mesh by using the monitor function \(M(x, u(x))=\alpha + |w''(x)|^{1/m}\) (see also [16] was discussed in [27]. A posteriori error analyses for the system of reaction-diffusion problems, the nonlinear singularly perturbed system of delay differential equations and the singularly perturbed nonlinear parameterized problem were also discussed in [28,29,30]. The algorithm and its extension for the system of mixed type reaction diffusion problems and several singularly perturbed parabolic problems were developed in [31,32,33,34,35].

The stability of T in (1) was derived in Corollary 4.2 in [24] as follows:

Lemma 1.1

(see [24]) Let \(F(x)=\int _x^1 f(s) d s +c_0\) be a bounded piecewise continuous function. Then, there exists a unique weak solution \(u \in H_0^1(0, 1)\) for the problem (1), such that

$$\begin{aligned} \Vert u\Vert _\infty \le C_1\Vert Tu\Vert _*, \end{aligned}$$
(3)

where \(C_1=C(2 \exp (\gamma ^*/\beta ) + \beta ^*/\beta )/\beta ^2+C\), and

$$\begin{aligned} \Vert u\Vert _{\infty }=\text {ess} \sup _{x\in [0,1]}|u(x)| \quad \text{ and } \quad \Vert u\Vert _{*}=\min _{U:U'=u}\Vert U(x)\Vert _{\infty }. \end{aligned}$$
(4)

Actually, the stability (3) can also be proved under the condition \(q\ge 0\) and \(q+p'\ge 0\) by the derivation for Theorem 1.7 in §I.1.1.2 in [1].

In this paper, we investigate a new upwind finite difference scheme different from (2) on the adaptive mesh equidistributing the numerical arc-length monitor function \(M(x, u^N(x))\) to solve the general non-conservative non-homogeneous convection-reaction-diffusion problem (1). In Section 2, the a posteriori error estimate for the upwind finite difference scheme on an arbitrary mesh is obtained by the stability of T and a linear interpolation of \(u^N\). In Section 3, the adaptive upwind finite difference method is proposed and the existence of the solution is proved by the fixed point theorem without the grid restriction \(h_i/h_{i+1} \le 1\) or C. In Section 4, the boundedness of the arc-length of the numerical solution and then the uniform first-order convergence are derived by using the property of the discrete Green’s function. Finally, in Section 5, the adaptive method is compared with the existing method and shown to be effective and uniformly first-order convergent in the numerical examples.

2 The upwind finite difference scheme and its a posteriori error estimate

For any nodes on interval [0, 1], \(0=x_0<x_1<...< x_n=1\), we investigate a new simple upwind finite difference scheme as follows:

$$\begin{aligned} \left\{ \begin{array}{l} T^N u_i^N:=-\varepsilon D^+(D^-u_i^N) -p_i D^+u_i^N +q_i u_i^N = f_i, i=1,...,N-1, \\ u_0^N=0,~ u_N^N=0,\\ \end{array}\right. \end{aligned}$$
(5)

where \(h_i=x_i-x_{i-1}, D^-u_i=\frac{u_i-u_{i-1}}{h_i}, D^+u_i=\frac{u_{i+1}-u_i}{h_{i+1}}\) and then \(D^+(D^-u_i)\) \(=\frac{D^-u_{i+1}-D^-u_i}{h_{i+1}}\). The simple upwind scheme (5) when \(h_i=h\) gives the simple upwind scheme (2.12) in §I.2.1.2 in [1] and is much similar to the scheme \(-D^+(\varepsilon D^-u_i^N + b(x_i, u^N_i))= f_i \) in [17,18,19,20] and the scheme in [8,9,10], but different from the usually adopted classical simple upwind scheme (2) in [7, 11,12,13,14,15, 21,22,23,24,25,26]. And it is also different from the central difference scheme to avoid oscillations of it, see e.g. the central difference scheme (2.3) in §I.2.1.1 and the discussion in §I.2.1.2 in [1].

Since \(T^N u_i^N = -\frac{\varepsilon }{h_{i}h_{i+1}}u^N_{i-1}+(\frac{\varepsilon }{h_{i}h_{i+1}} +\frac{\varepsilon }{h_{i+1}h_{i+1}}+\frac{p_i}{h_{i+1}}+q_i)u^N_i -(\frac{\varepsilon }{h_{i+1}h_{i+1}}+\frac{p_i}{h_{i+1}})u^N_{i+1}\), the matrix of \(T^{N}\) of the scheme (5) is diagonally dominant and has non-positive off-diagonal entries. Thus, the matrix is an M-matrix. Let \(\Psi ^\pm _i=\frac{1}{\beta }(1-x_i)\Vert T^N u^N_i \Vert _\infty \pm u^N_i \). Then

$$\begin{aligned} T^N \Psi ^\pm _i=\frac{p_i}{\beta }\Vert T^N u^N_i \Vert _\infty +\frac{q_i}{\beta }(1-x_i) \Vert T^N u^N_i \Vert _\infty \pm T^N u^N_i \ge 0, \end{aligned}$$

\(\Psi ^\pm _0\ge 0\) and \(\Psi ^\pm _N\ge 0.\) So, by the discrete comparison principle, \(\Psi ^\pm _i\ge 0\), i.e., \(T^{N}\) is uniformly stable (cf. Lemma 2.11 in §I.2.1 in [1]):

$$\begin{aligned} |u_i^N| \le \frac{1}{\beta } \Vert T^Nu_i^N\Vert _\infty \le \frac{1}{\beta } \Vert f_i\Vert _\infty ,\quad i=0, 1, ..., N. \end{aligned}$$
(6)

For any \( x\in I_{i}=(x_{i},x_{i+1})\), \(i=0,\dots , N-1\), we have a piecewise constant function \(f^N(x)=f_{i}\) and a piecewise linear interpolation

$$\begin{aligned} u^N(x)=\frac{1}{h_{i+1}}(u_{i+1}^N(x-x_{i}) + u_{i}^N(x_{i+1}-x)), \end{aligned}$$
(7)

which satisfies \(u^N(x_i)=u_i^N, u^N(x_{i+1})=u_{i+1}^N\) and \((u^N(x))'=D^+u_i^N\). Alternatively, a quadratic interpolation was used in [21,22,23,24].

For any \( x\in I_{i}=(x_{i},x_{i+1})\), \(i=0,\dots , N-1\), we have

$$\begin{aligned} \begin{array}{cllllll} &{}&{} Tu^N(x)-f^N(x)\\ &{}&{}\quad =-\varepsilon (u^N(x))''-p(x)(u^N(x))'+q(x)u^N(x)\\ &{}&{}\qquad +\varepsilon D^+(D^-u_{i}^N) +p_{i} D^+u_{i}^N -q_{i} u_{i}^N \\ &{}&{}\quad =(-\varepsilon (u^N(x))'+\int _{x}^1 p(t)(u^N(t))'- q(t)u^N(t)dt\\ &{}&{}\qquad -\sum _{j=i+1}^{N-1} \int _{I_{j}} \varepsilon D^+(D^-u_j^N) +p_jD^+u_j^N -q_j u_j^N dt\\ &{}&{}\qquad -\int _{x}^{x_{i+1}} \varepsilon D^+(D^-u_i^N) +p_i D^+u_i^N -q_iu_i^N dt+ \varepsilon D^-u_N^N )'\\ &{}&{}\quad =(-\varepsilon D^+u_i^N+\sum _{j=i+1}^{N-1} \int _{I_{j}} p(t)D^+u_j^N- q(t)u^N(t)dt\\ &{}&{}\qquad +\int _x^{x_{i+1}} p(t)D^+u_j^N- q(t)u^N(t)dt\\ &{}&{}\qquad - \varepsilon D^-u_N^N+\varepsilon D^-u_{i+1}^N -\sum _{j=i+1}^{N-1}\int _{I_{j}}p_jD^+u_j^N -q_j u_j^N dt \\ &{}&{}\qquad +\int _{x}^{x_{i+1}} f_i dt + \varepsilon D^-u_N^N)'\\ &{}&{}\quad =(\sum _{j=i+1}^{N-1}\int _{I_{j}} (p(t)-p_j) D^+u_j^N +(q_ju_j^N- q(t)u^N(t)) dt \\ &{}&{}\qquad +\int _{x}^{x_{i+1}}(p(t)-p_i) D^+u_i^N +(q_iu_i^N -q(t)u^N(t)) \\ &{}&{}\qquad + p_i D^+u_i^N -q_i u_i^N + f_idt)'.\\ \end{array} \end{aligned}$$

And owing to Lemma 1.1, (1) and (4), we have

$$\begin{aligned}\begin{array}{cllllll} &{}&{}\Vert u^N(x)-u(x)\Vert _\infty \le C\Vert Tu^N(x)-Tu(x)\Vert _*\\ &{}&{}\quad = C\Vert Tu^N(x)-f^N(x)+f^N(x)-f(x) \Vert _*\\ &{}&{}\quad \le C\Vert \sum _{j=i+1}^{N-1} \int _{I_{j}} (p(t)-p_j) D^+u_j^N +(q_ju_j^N- q(t)u^N(t)) dt \\ &{}&{}\qquad +\int _{x}^{x_{i+1}} (p(t)-p_i) D^+u_i^N +(q_iu_i^N- q(t)u^N(t))+p_i D^+u_i^N -q_i u_i^N + f_i dt\\ &{}&{}\qquad - \int _{x}^1 f^N-f dt \Vert _\infty \\ &{}&{}\quad \le C \displaystyle {\max _{0\le i \le N-1}} \{ \sum _{j=i}^{N-1} \int _{I_{j}} |(p(t)-p_j) D^+u_j^N|+|(q(t)-q_j)u_j^N| \\ &{}&{}\qquad +|q(t)(u^N(t)-u_j^N)|+|f_j-f| dt+\int _{I_{i}}| p_i D^+u_i^N -q_i u_i^N + f_i|dt \} .\\ \end{array} \end{aligned}$$

Since the items of the right-hand side satisfy:

$$\begin{aligned}{} & {} \int _{I_{j}} |(p(t)-p_j)D^+u_j^N| dt \le C_p \int _{I_j} |(t-x_j)D^+u_j^N| dt \le C h^2_{j+1}|D^+u_j^N|,\\{} & {} \int _{I_{j}} |(q(t)-q_j)u_j^N| dt \le C \int _{I_j} |q(t)-q_j| dt \le C C_q h^2_{j+1},\\{} & {} \int _{I_{j}}| q(t)(u^N(t)-u_j^N)| dt \le \gamma ^* \int _{I_j} |\int ^t_{x_j} (u^N(s))' ds| dt \\{} & {} \quad \le \gamma ^* \int _{I_j} \int ^t_{x_j} |D^+u_j^N| ds dt \le C h^2_{j+1}|D^+u_j^N|,\\{} & {} \int _{I_{j}} |f_j-f(t)| dt\le C h^2_{j+1},\\{} & {} \int _{I_{i}} | p_i D^+u_i^N -q_i u_i^N + f_i| dt \le \beta ^* h_{i+1}|D^+u_i^N|+Ch_{i+1}, \end{aligned}$$

we have

$$\begin{aligned} \Vert u^N(x)-u(x)\Vert _\infty \le C \displaystyle {\max _{0\le i \le N-1}} \{ \sum _{j=i}^{N-1} (h^2_{j+1}|D^+u_j^N|+h^2_{j+1}) + h_{i+1}|D^+u_i^N|+h_{i+1} \}, \end{aligned}$$

and then

$$\begin{aligned} \Vert u^N(x)-u(x)\Vert _\infty \le C \max _{0\le i \le N-1}(h_{i+1}|D^+u_i^N|+h_{i+1}). \end{aligned}$$
(8)

Theorem 2.1

Let u(x) be the solution of (1) and \(u^N_i\) be the solution of (5) on an arbitrary mesh. Then there exists a constant C such that:

$$\begin{aligned} \Vert u_i^N-u(x_i)\Vert _\infty \le C\max _{1\le i \le N} h_i\sqrt{1+(D^- u_i^N )^2}. \end{aligned}$$

Proof

Let \(u^N(x)\) be the piecewise linear interpolation of \(u_i^N\). From (8), we have

$$\begin{aligned} \Vert u_i^N-u(x_i)\Vert _\infty{} & {} \le \Vert u^N(x)-u(x)\Vert _\infty \le C_1\max _{1\le i \le N} (h_i|D^-u_i^N|+h_i)\\{} & {} \le C\max _{1\le i \le N} h_i\sqrt{1+(D^- u_i^N )^2}. \end{aligned}$$

\(\square \)

3 The adaptive upwind FDM and the existence of its solution

The problem (1) is solved iteratively by the adaptive upwind finite difference method:

  1. Step 1.

    Set an initial mesh \(\{x_i^{(0)}\}\), e.g., a uniform mesh \(\{0, \frac{1}{N}, \frac{2}{N},..., 1\}\) or a Shishkin-type mesh.

  2. Step 2.

    For \(k = 0, 1,...\), compute the numerical solution \(\{u_i^{(k)}\}\) by (5) on the current mesh \(\{x_i^{(k)}\}\), and set \(l_i^{(k)}=\sqrt{(x_i^{(k)} - x_{i-1}^{(k)})^2+(u_i^{(k)}-u_{i-1}^{(k)} )^2}\) and \(L^{(k)}=\sum _{j=1}^{N} l_i^{(k)}\).

  3. Step 3.

    Take a user-chosen constant \(C_0 \ge 1\). If the condition

    $$\begin{aligned} \frac{\max _{1\le i \le N} l_i^{(k)}}{L^{(k)}} \le \frac{C_0}{N} \end{aligned}$$
    (9)

    is satisfied, then set \(\{x_i^*\} = \{ x^{(k)}_i \}\), \(u^*= u^{(k)}\) and stop. Otherwise, continue to the next step.

  4. Step 4.

    Set the next mesh \(0 = x_0^{(k+1)}< x_1^{(k+1)}<... < x_N^{(k+1)} = 1\) by equidistributing the arc-length of the polygonal curve of the numerical solution \(u^{(k)}(x)\), such that

    $$\begin{aligned} l_i^{(k+1)}=\sqrt{(x_i^{(k+1)} - x_{i-1}^{(k+1)})^2+(u^{(k)}(x_i^{(k+1)})-u^{(k)}(x_{i-1}^{(k+1)}))^2}=\frac{L^{(k)}}{N}. \end{aligned}$$

    Return to step 2. Similar to the contents in [18, 21, 24,25,26], but the equation (1) is different from those in [18, 21, 26] and the scheme (5) is different from that in [18, 21, 24,25,26], the above adaptive method for (1) constructs a mapping, and its existence theorem also follows the fixed point theorem, which only demands the following newly proved preliminary lemma without using the presupposition \(h_i/h_{i+1} \le 1\) or C used in [21, 24,25,26].

Lemma 3.1

The solution \(\{u^N_i \}\) by (5) for (1) on an arbitrary mesh \(\{x_i \}\) satisfies

$$\begin{aligned} |D^-u^N_i| \le C(N + \varepsilon ^{-1}) \text{ for } i= 1, 2,..., N, \end{aligned}$$

where C a constant independent of \(\varepsilon \) and N.

Proof

From (6), \(|u^N_i| \le C\) for each i. So, \(h_k \ge N^{-1}\) and \(|D^-u_k^N| \le C N\) for some k.

For \(i=k, k+1,..., N-1\), from (5) we have

$$\begin{aligned}{} & {} -\varepsilon (D^+u_j^N-D^-u_j^N) -p_jh_{j+1} D^+u_j^N +q_jh_{j+1} u_j^N =h_{j+1} f_j,\\{} & {} \quad (\varepsilon + p_jh_{j+1}) D^+u_j^N = \varepsilon D^-u_j^N +q_jh_{j+1} u_j^N -h_{j+1} f_j,\\{} & {} \varepsilon |D^+u_j^N| \le \varepsilon |D^-u_j^N| + Ch_{j+1},\\{} & {} \varepsilon (|D^+u_i^N|- |D^-u_k^N|) \le C \sum _{j=k}^{i} h_{j+1} \le C,\\{} & {} |D^-u_{i+1}^N| \le |D^-u_k^N| +C \varepsilon ^{-1} \le C (N+\varepsilon ^{-1}). \end{aligned}$$

For \(i=1, 2,..., k-1\), from (5) we have

$$\begin{aligned}\begin{array}{cllllll} &{}&{}\varepsilon (D^-u_i^N-D^-u_k^N) \\ &{}&{}\quad =\sum _{j=i}^{k-1}\{p_jh_{j+1} D^+u_j^N -q_jh_{j+1} u_j^N +h_{j+1} f_j\}\\ &{}&{}\quad =p_i (u_{i+1}^N- u_i^N)+...+p_{k-1} (u_k^N- u_{k-1}^N)-\sum _{j=i}^{k-1} \{q_jh_{j+1} u_j^N -h_{j+1} f_j\}\\ &{}&{}\quad =-p_i u_i^N+(p_i-p_{i+1}) u_{i+1}^N+...+(p_{k-2}-p_{k-1}) u_{k-1}^N+p_{k-1} u_k^N\\ &{}&{}\qquad -\sum _{j=i}^{k-1} \{q_jh_{j+1} u_j^N -h_{j+1} f_j\},\\ \end{array} \\ \varepsilon |D^-u_i^N| \le \varepsilon |D^-u_k^N| +C+ C C_p \sum _{j=i}^{k-2} h_{j+1}+ C \sum _{j=i}^{k-1} h_{j+1}. \end{aligned}$$

We also have

$$\begin{aligned} \varepsilon |D^-u_i^N| \le \varepsilon CN + C, ~ \text{ i.e., } |D^-u^N_i| \le C(N + \varepsilon ^{-1}). \end{aligned}$$

\(\square \)

We need to prove that there exists a solution by (5) satisfying the equations:

$$\begin{aligned} l_i=\sqrt{(x_i-x_{i-1})^2+(u_i-u_{i-1})^2}=\frac{\sum _{j=1}^{N} l_j}{N}, ~ 1\le i \le N. \end{aligned}$$
(10)

Theorem 3.2

(Existence of a solution of the adaptive upwind FDM) For any \(\varepsilon \in (0, 1)\) and every positive integer N, there exists a mesh equidistributing the arc-length (10) along the piecewise linear interpolation of the solution of (5).

Proof

Let us regard steps 2 and 4 of the algorithm as a mapping: \(\Psi : (h_1, h_2,..., h_N) \rightarrow (\tilde{h}_1, \tilde{h}_2,..., \tilde{h}_N)\), where \(h_i\) and \(\tilde{h}_i\) are of the mesh before and after moving it. Define a set

$$\begin{aligned} S_Q = \{ (h_1, h_2,..., h_N) \in {{\textbf {R}}}^N: h_i \ge Q, 1\le i \le N, \sum _i^N h_i =1 \} \end{aligned}$$

where \(Q = Q(\varepsilon , N)\) satisfies \(0<Q< \frac{1}{N}\). Clearly, \(S_Q\) is not empty. Let \({u^N_i }\) be the numerical solution from (5) on the mesh with the step size \(h_i\) and set \(l_i = h_i\sqrt{1 + |D^-u^N_i|^2}\) \((i=1, 2,..., N)\). From Lemma 3.1 the slope of each segment of \(u^N (x)\) is at most \(C(N + \varepsilon ^{-1})\), so the arc-length of \(u^N (x)\) on each interval of the new mesh with length \(\tilde{h}_i\) for every i is at most \(\tilde{h}_i\sqrt{ 1 + C(N + \varepsilon ^{-1})^2}\). Since the new mesh is taken to split the piecewise linear function \(u^N (x)\) into N pieces, we have

$$\begin{aligned} \tilde{h}_i\sqrt{ 1 + C(N + \varepsilon ^{-1})^2} \ge \frac{\sum _{j=1}^{N} \tilde{l}_j}{N} \ge \frac{\sum _{j=1}^{N} \tilde{h}_j}{N} = \frac{1}{N}, \end{aligned}$$

which leads to

$$\begin{aligned} \tilde{h}_i \ge Q:= \frac{1}{ N \sqrt{ 1 + C(N + \varepsilon ^{-1})^2}}, 1\le i \le N. \end{aligned}$$

Hence \(0< Q < \frac{1}{N}\) and then \(\Psi \) maps \(S_Q\) into itself.

The nonempty set \(S_Q\) is compact and convex, and \(\Psi \) is obviously continuous. So, \(\Psi \) has a fixed point in \(S_Q\) by the Brouwer fixed point theorem, i.e., there is a mesh, as well as a computed solution on it, such that \(l_i = l_j\) for all i and j. \(\square \)

4 The uniform first-order convergence of the adaptive upwind FDM

Define the discrete Green’s function \(G(x_i,x_j)\) of \(T^N\) in (5) as follows:

$$\begin{aligned} T^N G_{i,j}=\delta _{i,j}^N,\quad i=1,2,\dots ,N-1, \end{aligned}$$
(11)

and \(G_{0,j}=G_{N,j}=0,\) for \( j=1, 2, \dots , N-1\), where

$$\begin{aligned} \delta _{i,j}^N=\left\{ \begin{array}{llllll} \frac{1}{h_{i+1}},&{}\quad &{} i=j,\\ 0, &{}\quad &{} \text{ otherwise }. \end{array} \right. \end{aligned}$$

Thus, the numerical solution \(u_i^N\) has the expression

$$\begin{aligned} u_i^N=\sum _{j=1}^{N-1}h_{j+1} G_{i,j} f_j, \end{aligned}$$
(12)

which satisfies (5).

Similar to the property of the discrete Green’s functions in [1, 16, 18, 21, 24], we can prove the following property:

Lemma 4.1

The discrete Green’s function \(G(x_i,x_j)\) in (11) satisfies:

$$\begin{aligned} 0 \le G_{i, j} \le \beta ^{-1}, \text{ for } i,j =0,..., N, \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^{N}|G_{i,j}-G_{i-1,j} |\le \frac{2}{\beta }, \text{ for } j =1, \dots , N-1. \end{aligned}$$
(13)

Proof

Let the barrier function for \(G_{i,j}\) be (see, e.g., [1, 16, 18]):

$$\begin{aligned} B_j^i = \left\{ \begin{array}{cllllll} &{}\beta ^{-1}, &{} \text{ for } i =0, ..., j,\\ &{}\beta ^{-1} \displaystyle {\prod _{k=j+1}^{i}} (1+\frac{\beta h_k}{\varepsilon })^{-1}, &{} \text{ for } i =j+1,...,N. \end{array}\right. \end{aligned}$$

For \(i=1,..., j-1\), we have

$$\begin{aligned} T^{N}B_j^i=q_i\beta ^{-1}\ge 0. \end{aligned}$$

For \(i=j\), we have

$$\begin{aligned} \begin{array}{cllll} T^{N}B_j^j&{}=&{}-\frac{\varepsilon }{h_{j+1}}(\frac{B^{j+1}_j-B^j_j}{h_{j+1}} -\frac{0}{h_{j}})-p_j\frac{B^{j+1}_j-B^j_j}{h_{j+1}}+q_jB^j_j \\ &{}=&{} -(\frac{\varepsilon }{h_{j+1}}+p_j)\frac{B^j_j}{h_{j+1}}[(1+\frac{\beta h_{j+1}}{\varepsilon })^{-1}-1]+q_jB^j_j\\ &{}=&{} \frac{\varepsilon +p_j h_{j+1}}{(\varepsilon +\beta h_{j+1})h_{j+1}}+q_j\beta ^{-1} \ge \frac{1}{h_{j+1}}. \end{array} \end{aligned}$$

For \(i=j+1,..., N-1\), we have

$$\begin{aligned} \begin{array}{cllll} T^{N}B_j^i&{}=&{}-\frac{\varepsilon }{h_{i+1}}(\frac{B^{i+1}_j-B^i_j}{h_{i+1}} -\frac{B^i_{j}-B^{i-1}_j}{h_{i}})-p_i\frac{B^{i+1}_j-B^i_{j}}{h_{i+1}}+q_iB^i_j\\ &{}=&{} \frac{\varepsilon }{h_{i+1}}(\frac{\beta }{\varepsilon +\beta h_{i+1}} -\frac{\beta }{\varepsilon })B^i_{j}+p_i\frac{\beta }{\varepsilon +\beta h_{i+1}}B^i_{j}+q_iB^i_j\\ &{}=&{} \frac{(p_i-\beta )\beta }{\varepsilon +\beta h_{i+1}} B^i_{j}+q_iB^i_j \ge 0. \end{array} \end{aligned}$$

Hence

$$\begin{aligned} T^{N}B_j^i \ge \delta _{i, j}=T^{N}G_{i,j}. \end{aligned}$$

Since \(B_j^0 \ge G_{0, j}\) and \(B_j^N \ge G_{N, j}\), the bounds in the following are established by the discrete comparison principle

$$\begin{aligned} 0 \le G_{i, j} \le B^i_j \le \beta ^{-1}, \text{ for } i,j =0,..., N. \end{aligned}$$

As we know that \(G_{i,j}\) increases for \(i=0,1,\dots ,j\) and \(G_{i,j}\) decreases for \(i=j,j+1,\dots ,N\), we have

$$\begin{aligned} \sum _{i=1}^{N}|G_{i,j}-G_{i-1,j} |=2G_{j,j}\le \frac{2}{\beta }, \text{ for } j =1, \dots , N-1. \end{aligned}$$

\(\square \)

Furthermore,

$$\begin{aligned} {\mathcal {L}}^N=\sum _{i=1}^{N}h_i\sqrt{1+(D^- u_i^N )^2}\le \sum _{i=1}^{N}h_i[1+|D^- u_i^N |]=1+\sum _{i=1}^{N}|u_i^N-u_{i-1}^N |, \end{aligned}$$
(14)

where \({\mathcal {L}}^N\) is the arc length of discrete solution \(\{u_i^N \}\). From (5), (12)-(14), we have

$$\begin{aligned} \begin{array}{cllllll} {\mathcal {L}}^N&{}\le &{} 1+\sum _{i=1}^{N}\sum _{j=1}^{N-1}h_{j+1}|f_j |\cdot |G_{i,j}-G_{i-1,j} |\\ &{}\le &{} 1+\Vert f \Vert _\infty \sum _{j=1}^{N-1}h_{j+1}\sum _{i=1}^{N}|G_{i,j}-G_{i-1,j} | \\ &{}\le &{} 1+\frac{2\Vert f\Vert _\infty }{\beta }. \end{array} \end{aligned}$$
(15)

Theorem 4.2

The solution \({u_i^N }\) of (5) on the grid \(\{x_i \}\) of arc-length equidistribution satisfies:

$$\begin{aligned} \Vert u_i^N-u(x_i)\Vert _\infty \le CN^{-1}, \end{aligned}$$

where C is a constant independent of \(\varepsilon \) and N.

Proof

According to Theorem 2.1, Theorem 3.2, (9) and (15), the solution \({u_i^N }\) of (5) for (1) on the grid \(\{x_i \}\) of arc-length equidistribution satisfies:

$$\begin{aligned} \Vert u_i^N-u(x_i)\Vert _\infty \le C_1\max _{1\le i\le N}h_i\sqrt{1+(D^- u_i^N )^2} \le C_1 C_0 {\mathcal {L}}^N/N \le CN^{-1}. \end{aligned}$$

\(\square \)

Table 1 The numerical results of Ex.1
Full size table

5 Numerical examples

The numerical examples for the problem (1) are solved by the old upwind scheme (2) and new (5) respectively on the uniform mesh and the adaptive mesh. The maximum node errors are denoted as \(e^N_{old}\) and \( e^N_{new}\), respectively. The numerical convergence orders are denoted as \(r^N_{old}\) and \(r^N_{new}\), respectively. The number of iterations are denoted as \(Iter_{old}\) and \(Iter_{new}\), respectively. The numerical convergence order is computed by

$$\begin{aligned} r^N = \log _2 \frac{\max {|u_i-u^N_i|}}{\max {|u_i-u^{2N}_i|}}. \end{aligned}$$

Example 1

Consider the singularly perturbed two-point boundary value problem:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {-\varepsilon u'' (x)-(1+x)u'(x)+u(x)=f(x),\quad x\in {(0,1)}},\\ u(0)=u(1)=0, \end{array}\right. \end{aligned}$$

where f(x) is chosen so that \(u(x)=e^{-\frac{x}{\varepsilon }}-e^x+(e-e^{-\frac{1}{\varepsilon }})x\).

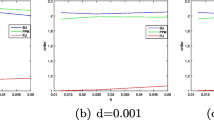
The numerical results are shown in Table 1, Fig. 1 and Fig. 2.

Example 2

Consider the singularly perturbed two-point boundary value problem:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {-\varepsilon u'' (x)-u'(x)+u(x)=0,\quad x\in {(0,1)}},\\ u(0)=0,~u(1)=1. \end{array}\right. \end{aligned}$$

The exact solution is \(u(x)=\frac{\exp (m_1 x)-\exp (m_2x)}{\exp (m_1)-\exp (m_2)}\), where \( m_1=\frac{-1+\sqrt{1+4\varepsilon }}{2\varepsilon },\) \( m_2=\frac{-1-\sqrt{1+4\varepsilon }}{2\varepsilon }.\)

Fig. 1
figure 1

The solutions of Ex. 1 when \(N=32\) for \(\varepsilon =10^{-2}\)

Full size image
Fig. 2
figure 2

The errors of Ex. 1 when \(N=32\) for \(\varepsilon =10^{-2}\)

Full size image

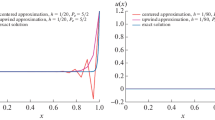
The numerical results are shown in Table 2 and Fig. 3.

Table 2 The numerical results of Ex. 2
Full size table

Example 3

Consider the singularly perturbed two-point boundary value problem:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {-\varepsilon u'' (x)-(1+x(1-x))u'(x)=f(x),\quad x\in {(0,1)}},\\ u(0)=u(1)=0, \end{array}\right. \end{aligned}$$

where f(x) is chosen such that \(u(x)=\frac{1-e^{-\frac{x}{\varepsilon }}}{1-e^{-\frac{1}{\varepsilon }}}-\cos (\frac{\pi }{2}(1-x))\).

The numerical results are shown in Table 3 and Fig. 4.

Fig. 3
figure 3

The errors of Ex. 2 when \(N=32\) for \(\varepsilon =10^{-2}\)

Full size image
Table 3 The numerical results of Ex.3
Full size table

From the rows of iteration numbers, the errors and the numerical convergence orders for each \(\varepsilon \) in the tables, and from the ordinates of errors in the figures, we can see that the two adaptive methods both achieve better accuracy when the mesh is finer and are close to the first-order convergence uniformly with respect to \(\varepsilon \). Moreover, the proposed adaptive upwind finite difference method with new scheme (5) usually uses less iterations to satisfy the iteration tolerance and obtains better precision to resolve the boundary layers than the existing adaptive upwind finite difference method does.

Fig. 4
figure 4

The errors of Ex. 3 when \(N=32\) for \(\varepsilon =10^{-2}\)

Full size image

6 Conclusion

In this work, the rigorous error analysis of the upwind finite difference scheme (5) on the grid that equidistributes the arc-length monitor function \(M(x, u^N(x))=\sqrt{1+((u^N(x))')^2}\) of the numerical solution \(u^N\) to solve the general non-conservative convection-reaction-diffusion problem (1) is finally accomplished through new efforts. By contrast, considering adaptive methods, M(x, u(x)) was of the exact solution u in [11,12,13,14,15,16], the equation was of conservative form in [17,18,19,20], of reaction-diffusion form with no first derivative term in [16, 27, 28, 31,32,33] and of convection-diffusion form with no zero derivative term in [11,12,13,14,15, 21], the a priori truncation error was from a priori knowledge of the exact solution in [22, 23], and the condition \(h_i/h_{i+1} \le 1\) or C was used in [21, 24,25,26]. In fact, the a posteriori error estimate of the upwind finite difference scheme, the existence of the solution of the adaptive upwind finite difference method, and its \(\varepsilon \)-independent first-order convergence are developed step by step with new progresses in this paper. The numerical examples confirm its uniform first-order convergence and show its advantage in precision, too. The works for solving nonlinear singularly perturbed problems, singularly perturbed mixed BVPs, problems having interior layers, systems of singularly perturbed BVPs, singularly perturbed two-dimensional elliptic problems, fractional order integro-parabolic equations and so on are expected to be extended for future study (see e.g. [27,28,29,30,31,32,33,34,35,36,37,38,39]).