1 Introduction

Ordinary and partial differential equations have played a vital role in the mathematical modelling of various real-world phenomena in science and engineering. To make the model more realistic, it is sometimes needed to include past states of the system rather than only the current state. Modelling of such systems leads to delay differential equations (DDEs). These equations arise in many scientific areas such as control theory [33], nonlinear optics [23], neuroscience [35], population dynamics [21], HIV infection models [13], optical feedback [18], and others [15, 38]. Specific examples of delay systems with large delay include semiconductor lasers with two optical feedback loops of different lengths [34], ring-cavity lasers with optical feedback [18], and others [15, 38]. In DDE, however, the evolution of the system at a certain time depends on the past history, the introduction of such delay in the model improves the dynamics of the model but increases the complexity of the system. Therefore, studying this class of differential equations (DE) is important.

When we associate a mathematical model with physical phenomena, we often capture essentials and neglect the minor components, involving small parameters. DE in which the highest-order derivative term is affected by a small parameter \(\varepsilon \) is classified as singularly perturbed problem (SPP). The main characteristics of these problems are the appearance of boundary/interior layer in the solution when \(\varepsilon \rightarrow 0\). Moreover, the presence of delay term makes the problem more challenging. These layers are the small regions, where the solution changes extremely rapidly. Such phenomena cause significant numerical challenges that can only be overcome by employing specially designed numerical methods. While solving SPP, unless specially designed meshes are used, conventional numerical methods fail to reduce error below a certain fixed limit. Such meshes are designed based on prior knowledge of the location of the layers under consideration. To overcome these limitations, many researchers have developed various parameter uniform numerical methods that behave well enough independent of the perturbation parameter.

Many researchers have made efforts to develop parameter uniform numerical methods for singularly delay differential equation (SPDDE) [8, 25]. In [2], the authors discussed a SPDDE with Dirichlet boundary condition. While the authors in [4] studied SPDDE with Robin type boundary condition. In [30], a hybrid difference method is used for parabolic problems with time delay. A stable finite difference scheme for a singularly perturbed problem with delay and advanced term is presented in [29]. In [19], a standard finite difference scheme is presented to solve parabolic SPDDE on an equidistributed mesh. For a time-delayed convection-diffusion problem, a hybrid scheme is given in [14]. While a hybrid difference approach for a parabolic differential equation with delay and advance terms is studied in [20, 36]. A very good amount of literature is available for time delay problems but the study of problems with space delay is still in the initial stage [7, 26, 28, 40].

In the past few years, a growing interest can be seen towards the study of SPDDEs with integral boundary conditions due to their wide applications in science and engineering such as heat conduction, oceanography, electrochemistry, blood flow models, cellular systems, thermodynamics, population dynamics, etc. [1, 5, 10, 11, 16, 17, 22, 24, 42]. For the existence, uniqueness and well-posedness of the solution to such types of problems, the readers are referred to [3, 6, 9] and references therein. The solution of such problems is not known at the boundary points of the domain and the boundary values are associated with the solution at the interior points of the domain. Recently, the interest of researchers for the numerical solution of such class of problems has increased considerably. In [39], the authors studied SPDDE with integral boundary condition using an upwind finite difference method on piecewise uniform Shishkin mesh. In [41], a hybrid difference scheme is used to find the approximate solution for SPDDE with large delay and integral boundary condition. It is proved that the method is almost second-order convergent which is optimal compared to [27]. The theory and numerical approximation for a time-dependent SPDDE with integral boundary condition is little developed. In [40], a parabolic SPDDE of reaction-diffusion type with integral boundary condition is studied. The method presented has almost second order of convergence in space and one in time. In the literature, so far, no one has considered parabolic SPDDE of convection-diffusion type with integral boundary condition. Motivated by the above works, in this article, a parameter uniform numerical method is presented to solve singularly perturbed parabolic DDE with integral boundary condition and having a large delay in space. An implicit numerical scheme comprising the Crank-Nicolson scheme in the time direction and the finite difference scheme in the space direction is used to find an approximate solution. The method presented is parameter uniform and has second order of convergence in time and almost first order in space.

2 The analytical problem

Let \(D=\mu \times \Delta :=(0,2)\times (0,T]\) and consider the following parabolic delay differential equation with integral boundary condition

$$\begin{aligned}&\left. \begin{array}{ll} &{} -\varepsilon y_{ss}(s,t)+p(s)y_s(s,t)+q(s)y(s,t)+r(s)y(s-1,t)+y_t(s,t) =g(s,t)\; \text {in}\; D,\\ &{} y(s,t)=\psi _1(s,t)\;\text {in}\; \Gamma _1:=\{(s,t),\;s\in [-1,0],\;t\in [0,T]\}, \\ &{} y(s,t)=\psi _2(s,t)\; \text {on}\;\Gamma _2:= \{(s,0),\;s\in [0,2]\},\\ &{} {\mathcal {K}} y(s,t)=y(2,t)-\varepsilon \int _{0}^{2} f(s)y(s,t)ds=\psi _3(s,t)\;\text {on}\; \Gamma _3=\{(2,t),\;t\in [0,T]\}, \end{array}\right\} \end{aligned}$$
(2.1)

where \(\varepsilon \ll 1\) is a small positive parameter, g(s, t), p(s), q(s), and r(s) are sufficiently smooth functions. Also, assume that the initial-boundary data \(\psi _1\), \(\psi _2\) and \(\psi _3\) are smooth and bounded functions such that

$$\begin{aligned} \left. \begin{array}{ll} &{}p(s)\ge p_0>p_0^*>0,\;\; q(s)\ge q_0>0,\;\;r(s)\le r_0<0, \\ &{} p_0^*+q_0+r_0>0,\;\;q(s)+r(s)\ge 2\eta >0,\\ &{}y(1^-,t)=y(1^+,t),\;\;y_s(1^-,t)=y_s(1^+,t). \end{array}\right\} \end{aligned}$$
(2.2)

Here, f(s) is non-negative, monotonic function such that \(\displaystyle \int _{0}^{2}f(s)ds<1\). Moreover, the given data satisfies the compatibility conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} \psi _2(0,0)=\psi _1(0,0),\;\;\psi _2(2,0)=\psi _3(2,0),\\ &{}\displaystyle -\varepsilon \frac{\partial ^2\psi _2(0,0)}{\partial s^2}+p(0)\frac{\partial \psi _2(0,0)}{\partial s}+q(0) \psi _2(0,0)+r(0)\psi _1(-1,0)+\frac{\partial \psi _1(0,0)}{\partial t}=g(0,0),\\ &{}\displaystyle -\varepsilon \frac{\partial ^2\psi _2(2,0)}{\partial s^2}+p(2)\frac{\partial \psi _2(2,0)}{\partial s}+q(2) \psi _2(2,0)+r(2)\psi _2(1,0)+\frac{\partial \psi _3(2,0)}{\partial t}=g(2,0). \end{array}\right. } \end{aligned}$$

Rewriting (2.1) as

$$\begin{aligned} {\mathcal {L}}y(s,t)={\mathcal {G}}(s,t), \end{aligned}$$

where

$$\begin{aligned}&{\mathcal {L}}y(s,t)\\&\quad ={\left\{ \begin{array}{ll}-\varepsilon y_{ss}(s,t)+p(s)y_s(s,t)+q(s)y(s,t)+y_t(s,t) \;\;\text {if}\;\; (s,t)\in (0,1]\times [0,T]\\ -\varepsilon y_{ss}(s,t)+p(s)y_s(s,t)+q(s)y(s,t)+r(s)y(s-1,t)+y_t(s,t)\\ \text {if}\;\; (s,t)\in (1,2)\times [0,T] \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\mathcal {G}}(s,t)={\left\{ \begin{array}{ll}g(s,t)-r(s)\psi _1(s-1,t) \;\;&{}\text {if}\;\; (s,t)\in (0,1]\times [0,T]\\ g(s,t)\;\;&{}\text {if}\;\; (s,t)\in (1,2)\times [0,T]. \end{array}\right. } \end{aligned}$$

These assumptions confirms the existence and uniqueness of the solution [2, 31]. The solution of (2.1) exhibits a weak interior layer at \(s=1\) and a strong boundary layer at \(s=2\).

Lemma 2.1

Let \({\mathcal {P}}(s,t)\in C^{2,1}({\bar{D}})\). If \({\mathcal {P}}(0,t)\ge 0\), \({\mathcal {P}}(s,0)\ge 0\), \({{\mathcal {K}}}{{\mathcal {P}}}(2,t)\ge 0\) with \({{\mathcal {L}}}{{\mathcal {P}}}(s,t)\ge 0\) for all \((s,t)\in D\) and \([{\mathcal {P}}_s](1,t)={\mathcal {P}}_s(1^+,t)-{\mathcal {P}}_s(1^-,t)\le 0\). Then \({\mathcal {P}}(s,t)\ge 0\) for all \((s,t)\in {\bar{D}}\).

Proof

Let \((s^k,t^k)\in D\) and \( \displaystyle {\mathcal {P}}(s^k,t^k)=\min \limits _{(s,t)\in {\bar{D}}} {\mathcal {P}}(s,t)\). Consequently,

$$\begin{aligned} {\mathcal {P}}_s(s^k,t^k)=0,\;\;{\mathcal {P}}_t(s^k,t^k)=0 \;\;\text {and}\;\;{\mathcal {P}}_{ss}(s^k,t^k)>0. \end{aligned}$$
(2.3)

Suppose \({\mathcal {P}}(s^k,t^k)<0\), it follows that \((s^k,t^k)\notin \Gamma :=\Gamma _1\cup \Gamma _2\cup \Gamma _3\).

Case I::

If \(s^k\in (0,1)\), then

Case II::

If \(s^k\in (1,2)\), then

Case III::

If \(s^k=1\), then

$$\begin{aligned}{}[{\mathcal {P}}_s](s^k,t^k)={\mathcal {P}}_s(s^{k+},t^k)-{\mathcal {P}}_s(s^{k-},t^k)>0 \text{ since } {\mathcal {P}}(s^k,t^k)<0 . \end{aligned}$$

The result thus follows from a contradiction. \(\square \)

As a consequence of Lemma 2.1, obtaining the following stability estimate is straightforward.

Lemma 2.2

The solution of (2.1) satisfies

$$\begin{aligned} \Vert y\Vert _{\infty ,{\bar{D}}}\le \Vert y\Vert _{\infty , \Gamma }+\frac{1}{\eta }\Vert {\mathcal {G}} \Vert _{\infty , {\bar{D}}}. \end{aligned}$$
(2.4)

Proof

Define \(\theta _{\pm }(s,t)= \displaystyle \Vert y\Vert _{\infty ,\Gamma }+\frac{1}{\eta }\Vert {\mathcal {G}} \Vert _{\infty , {\bar{D}}} \pm y(s,t),\;\;(s,t)\in {\bar{D}}\). For \((s,t)\in \Gamma \), \(\theta _{\pm }(s,t)\ge 0\), and if \((s,t)\in D\), it follows that

$$\begin{aligned} {\mathcal {L}}\theta _\pm (s,t) =(q+r)(s) \left( \Vert y \Vert _\Gamma +\frac{\Vert {\mathcal {G}}\Vert _{{\bar{D}}}}{\eta }\right) \pm {\mathcal {L}}y(s,t) \ge 2\eta \left( \Vert y \Vert _\Gamma +\frac{\Vert {\mathcal {G}}\Vert _{{\bar{D}}}}{\eta }\right) \pm {\mathcal {G}}\ge 0 \end{aligned}$$

and the result follow as a consequence of Lemma 2.1. \(\square \)

Generally, we may take homogeneous boundary data \(\psi _1=\psi _2=\psi _3=0\) by subtracting some appropriate smooth function from y that satisfies the original boundary data [37].

Lemma 2.3

Let y be the solution of (2.1) then there exists a constant C independent of \(\varepsilon \) such that

$$\begin{aligned} \left| \frac{\partial ^i y(s,t)}{\partial t^i}\right| \le C\;\;\text {for all}\;\;(s,t)\in {\bar{D}}\;\;\text { and}\;\;i=0,1,2. \end{aligned}$$

Proof

For \(i=0\), the result follows from Lemma 2.2. The assumption \(\psi _1(s,t)=\psi _3(s,t)=0\) gives \(y=0\) along the left and right hand sides of D, which implies \( y_t=0\) along these sides. Also, \( \psi _2(s,t)=0\) gives \(y=0\) along the line \(t=0\). Thus \(y_{s}=0=y_{ss}\) along the line \(t=0\). Now, put \(t=0\) in (2.1) to obtain

$$\begin{aligned} -\varepsilon y_{ss}(s,0)+p(s)y_s(s,0)+q(s)y(s,0)+r(s)y(s-1,0)+y_t(s,0)=g(s,0) \end{aligned}$$

implying \(y_t(s,0)=g(s,0)\) since \(y_{s}(s,0)=y_{ss}(s,0)=y(s,0)=y(s-1,0)=0\). Thus \(|y_t|\le C\) on \(\Gamma \) as g(s, t) is continuous on \({\bar{D}}\). On applying differential operator \({\mathcal {L}}\) on \(y_t(s,t)\), we get

$$\begin{aligned} {\mathcal {L}}y_t(s,t)=g_t(s,t) \Rightarrow \left| {\mathcal {L}}y_t\right| =\left| g_t\right| \le C. \end{aligned}$$

An application of the Lemma 2.1 yields \(\left| y_t\right| \le C\) on \({\bar{D}}\).

Now \(y_{tt}=0\) on \(\Gamma _1\cup \Gamma _3\) as \(y_t=0\) on \(\Gamma _1\) and \(\Gamma _3\). Differentiating (2.1) with respect to t and put \(t=0\) to obtain

$$\begin{aligned} -\varepsilon y_{sst}(s,0)+p(s) y_{st}(s,0)+q(s) y_t(s,0)&\nonumber \\ +r(s) y_t(s-1,0)+y_{tt}(s,0)= & {} g_t(s,0). \end{aligned}$$
(2.5)

Since \(y_t(s,0)=g(s,0)\),

$$\begin{aligned} y_{st}(s,0)=g_s(s,0),\;\; y_{sst}(s,0)=g_{ss}(s,0) \end{aligned}$$

and by definition

$$\begin{aligned} y_t(s-1,0)=\lim \limits _{\Delta t\rightarrow 0}\frac{y(s-1,\Delta t)-y(s-1,0)}{\Delta t}=0. \end{aligned}$$

From (2.5), we have

$$\begin{aligned} y_{tt}(s,0)=\varepsilon g_{ss}(s,0)-p(s) g_{s}(s,0)-q(s) g_s(s,0)+g_t(s,0). \end{aligned}$$

Since g is continuous on \({\bar{D}}\). Therefore, for significantly large value of C, \(|y_{tt}|\le C\) on \(\Gamma _2\). Hence, \(|y_{tt}|\le C\) on \(\Gamma .\) Moreover, it is easy to verify that

$$\begin{aligned} |{\mathcal {L}}y_{tt}(s,t)|=|g_{tt}(s,t)|\le C \end{aligned}$$

on D and the proof follows from Lemma 2.1. \(\square \)

3 Semi-discretization in time

Let \({{\mathbb {T}}_t}^M=\left\{ t_k=kT/M, k=0:M\right\} \) be a equidistant mesh which partition the domain [0, T] into M number of sub-intervals. Next, we semi-discretize (2.1) using the Crank-Nicholson scheme in the time variable. The resulting semi-discrete problem on \({{\mathbb {T}}_t}^M\) reads

$$\begin{aligned} \left. \begin{array}{ll}\displaystyle \frac{-\varepsilon }{2}Y_{ss}(s,t_{k+1})+\frac{p(s)}{2}Y_s(s,t_{k+1})+l(s)Y(s,t_{k+1})+\frac{r(s)}{2} Y(s-1,t_{k+1}) \\ \displaystyle =\frac{\varepsilon }{2}Y_{ss}(s,t_{k})-\frac{p(s)}{2}Y_s(s,t_{k})+m(s)Y(s,t_{k})-\frac{r(s)}{2} Y(s-1,t_{k})\\ \quad \displaystyle +\frac{g(s,t_{k+1})+g(s,t_k)}{2} \end{array}\right\} \nonumber \\ \end{aligned}$$
(3.1)

where \(s\in [0,2]\) and \(k= 0,1,\ldots , M-1\), such that

$$\begin{aligned} \left. \begin{array}{ll} &{}Y(s,0)=\psi _2(s,0),\;\; 0\le s\le 2,\\ &{} Y(s,t_{k+1})=\psi _1(s,t_{k+1}),\;\;-1\le s\le 0,\;\;-1\le k\le M-1,\\ &{} Y(2,t_{k+1})=\psi _3(2,t_{k+1}),\;\; -1\le k\le M-1. \end{array}\right\} \end{aligned}$$
(3.2)

Here, \(Y(s,t_{k+1})\) denotes a numerical approximation of continuous solution y at \((k+1)\) time step, \(\displaystyle l(s)=\frac{\Delta t q(s)+2}{2\Delta t}\) and \(\displaystyle m(s)=\frac{2-\Delta t q(s)}{2\Delta t}\).

Writing (3.1) as

$$\begin{aligned} {\mathfrak {L}}_{CN}Y(s,t_{k+1})=\hat{{\mathcal {G}}}(s,t_{k+1}) \end{aligned}$$
(3.3)

where

$$\begin{aligned}&{\mathfrak {L}}_{CN}Y\\&\quad = {\left\{ \begin{array}{ll} \displaystyle {\mathfrak {L}}_{CN1}Y= \frac{-\varepsilon }{2}Y_{ss}(s,t_{k+1})+\frac{p(s)}{2}Y_s(s,t_{k+1})+l(s)Y(s,t_{k+1})\;&{}\text {if}\; s\in (0,1],\\ \displaystyle {\mathfrak {L}}_{CN2}Y= \frac{-\varepsilon }{2}Y_{ss}(s,t_{k+1})+\frac{p(s)}{2}Y_s(s,t_{k+1})+l(s)Y(s,t_{k+1})\\ \displaystyle \quad \quad \quad \quad +\frac{r(s)}{2} Y(s-1,t_{k+1})\; &{}\text {if}\; s\in (1,2) \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned}&\hat{{\mathcal {G}}}(s,t_{k+1})\nonumber \\&\quad = {\left\{ \begin{array}{ll} \displaystyle \hat{{\mathcal {G}}}_1=\frac{\varepsilon }{2}Y_{ss}(s,t_{k})-\frac{p(s)}{2}Y_s(s,t_{k})+m(s)Y(s,t_{k})-\frac{r(s)}{2} Y(s-1,t_{k})\\ \displaystyle \quad \quad +\frac{g(s,t_{k+1})+g(s,t_k)}{2} -\frac{r(s)}{2}\psi _1(s-1,t_{k+1})\;\;\text {if}\;\; s\in (0,1],\\ \displaystyle \hat{{\mathcal {G}}}_2= \frac{\varepsilon }{2}Y_{ss}(s,t_{k})-\frac{p(s)}{2}Y_s(s,t_{k})+m(s)Y(s,t_{k})-\frac{r(s)}{2} Y(s-1,t_{k})\\ \displaystyle \quad \quad +\frac{g(s,t_{k+1})+g(s,t_k)}{2}\;\;\text {if}\;\; s\in (1,2]. \end{array}\right. } \end{aligned}$$
(3.4)

Operator \({\mathfrak {L}}_{CN}\) satisfies the following discrete maximum principle.

Lemma 3.1

Let the function \(\chi (s,t_{k+1})\) satisfies \(\chi (s,t_{k+1})\ge 0\) for \(s=0,2\) and \({\mathfrak {L}}_{CN}\chi (s,t_{k+1})\ge 0\) for all \(s\in \mu \). Then \(\chi (s,t_{k+1})\ge 0\) for all \(s\in {\bar{\mu }}\).

Proof

Let \(\chi (\xi ,t_{k+1})=\min \limits _{s\in \mu }\chi (s,t_{k+1})\) for some \(\xi \in \mu \). Then

$$\begin{aligned} \chi _s(\xi ,t_{k+1})=0\quad \mathrm {and}\quad \chi _{ss}(\xi ,t_{k+1})>0. \end{aligned}$$
(3.5)

Suppose \(\chi (\xi ,t_{k+1})<0\), it follows that \((\xi ,t_{k+1})\notin \Gamma \) since \(\chi (\xi ,t_{k+1})\ge 0\) for \(s =0,2\).

Case I::

If \(\chi \in (0,1]\), then

Case II::

If \(\chi \in (1,2)\), then

The required result follows from contradiction. \(\square \)

Lemma 3.2

Let \(Y(s,t_{k+1})\) be the solution of (3.1). Then

$$\begin{aligned} \Vert Y(s,t_{k+1})\Vert _{{\bar{\mu }}}\le \max \left\{ |Y(0,t_{k+1})|,|Y(2,t_{k+1})|,\frac{\Delta t}{\eta \Delta t+1}\Vert \hat{{\mathcal {G}}}\Vert _{{\bar{\mu }}}\right\} . \end{aligned}$$

Proof

Define \(\zeta _{\pm }(s,t_{k+1})=\max \left\{ |Y(0,t_{k+1})|,\frac{\Delta t}{\eta \Delta t+1}\Vert \hat{{\mathcal {G}}}\Vert _{{\bar{\mu }}}\right\} \pm Y(s,t_{k+1})\) for \(s\in [0,1]\). Clearly, \(\zeta _{\pm }(0,t_{k+1})\ge 0\). Moreover, it follows that

Similarly, define \(\displaystyle \zeta _{\pm }(s,t_{k+1})=\max \left\{ |Y(2,t_{k+1})|,\frac{\Delta t}{\eta \Delta t+1}\Vert \hat{{\mathcal {G}}}\Vert _{{\bar{\mu }}}\right\} \pm Y(s,t_{k+1})\) for \(s\in [1,2]\). Clearly, \(\zeta _{\pm }(2,t_{k+1})\ge 0.\) Also, it follows that

An application of Lemma 3.1 yields the desired result. \(\square \)

Next, we compute global errors using local error bounds. From (3.3)

$$\begin{aligned} {\mathcal {L}}_{CN}{\tilde{Y}}(s,t_{k+1})=\tilde{{\mathcal {G}}}(s,t_{k+1}) \end{aligned}$$
(3.6)

where \({\mathcal {L}}_{CN}\) is as defined in (3.3), and

$$\begin{aligned} \tilde{{\mathcal {G}}}={\left\{ \begin{array}{ll} \displaystyle \frac{\varepsilon }{2}y_{ss}(s,t_{k})-\frac{p(s)}{2}y_s(s,t_{k})+m(s)y(s,t_{k})-\frac{r(s)}{2} y(s-1,t_{k})\\ \displaystyle +\frac{g(s,t_{k+1})+g(s,t_k)}{2} -\frac{r(s)}{2}\psi _1(s-1,t_{k+1})\;\;&{}\text {if}\;\; s\in (0,1]\\ \displaystyle \frac{\varepsilon }{2}y_{ss}(s,t_{k})-\frac{p(s)}{2}y_s(s,t_{k})+m(s)y(s,t_{k})-\frac{r(s)}{2} y(s-1,t_{k})\\ \displaystyle +\frac{g(s,t_{k+1})+g(s,t_k)}{2}\;\;&{}\text {if}\;\; s\in (1,2] \end{array}\right. } \end{aligned}$$

with the following boundary conditions

$$\begin{aligned}&{\tilde{Y}}(s,0)=\psi _2(s), s\in [0,2],\\&{\tilde{Y}}(s,t_{k+1})=\psi _1(s,t_{k+1}), -1\le s\le 0, -1\le k\le M-1,\\&{\tilde{Y}}(2,t_{k+1})=\psi _3(t_{k+1}), -1\le k\le M-1. \end{aligned}$$

Lemma 3.3

The local truncation error (LTE) \({\hat{e}}_{k+1}:={\tilde{Y}}(s,t_{k+1})-y(s,t_{k+1})\) at \(k+1\) time step satisfies

$$\begin{aligned} \left\| {\hat{e}}_{k+1}\right\| _{\infty }\le C(\Delta t)^3. \end{aligned}$$

Proof

For proof, see [12]. \(\square \)

Moreover, LTE at each time step contributes to the estimate for global error \(E_k:=y(s,t_k)-Y(s,t_k)\). Then, it follows that

$$\begin{aligned} \left\| E_{k+1}\right\| _{\infty }=\left\| \sum _{i=1}^k{\hat{e}}_i\right\| _{\infty } \le \left\| {\hat{e}}_1 \right\| _{\infty }+\left\| {\hat{e}}_2 \right\| _{\infty }+\ldots +\left\| {\hat{e}}_k\right\| _{\infty } \le C \Delta t^2. \end{aligned}$$
(3.7)

As a result, the time semi-discretization procedure achieves uniform convergence.

The solution \(Y(s,t_{k+1})\) of problem (3.1) admits a decomposition into smooth and singular components [32]. We write

$$\begin{aligned} Y(s,t_{k+1}):=X(s,t_{k+1})+Z(s,t_{k+1}). \end{aligned}$$

Here, the smooth component \(X(s,t_{k+1})\) satisfies

$$\begin{aligned} \left. \begin{array}{ll} &{} {\mathcal {L}}_{CN1}X(s,t_{k+1})=\hat{{\mathcal {G}}}_1(s,t_{k+1}), \\ &{} X(0,t_{k+1})=X_0(0,t_{k+1}),\\ &{} X(1,t_{k+1})=(l(s))^{-1}\hat{{\mathcal {G}}}_1(1,t_{k+1}) \\ \end{array}\right\} \end{aligned}$$
(3.8)

in (0, 1], and in (1, 2) satisfies

$$\begin{aligned} \left. \begin{array}{ll} &{} {\mathcal {L}}_{CN2}X(s,t_{k+1})=\hat{{\mathcal {G}}}_2(s,t_{k+1}), \\ &{} X(1,t_{k+1})=(l(s))^{-1}\left( \hat{{\mathcal {G}}}_2(1,t_{k+1})-\frac{r(1)}{2}X(0,t_{k+1})\right) , \\ &{} X(2,t_{k+1})=X_0(2,t_{k+1})\\ \end{array}\right\} \end{aligned}$$
(3.9)

where \(X_0(s,t_{k+1})\) satisfies the associated reduced problem, and \(Z(s,t_{k+1})\) satisfies

$$\begin{aligned} \left. \begin{array}{ll} &{} {\mathcal {L}}_{CN}Z(s,t_{k+1})=0,\;\;s\in (0,2)\\ &{}Z(0,t_{k+1})=0,\\ &{} Z(2,t_{k+1})=Y(2,t_{k+1})-X(2,t_{k+1}), \\ &{} Z(1^+,t_{k+1})-Z(1^-,t_{k+1})=X(1^-,t_{k+1})-X(1^+,t_{k+1}), \\ &{} Z_s(1^+,t_{k+1})-Z_s(1^-,t_{k+1})=X_s(1^-,t_{k+1})-X_s(1^+,t_{k+1}). \end{array}\right\} \end{aligned}$$
(3.10)

The solution of (2.1) contains a boundary layer at \(s=2\) and an interior layer at \(s=1\). Further, decompose \(Z(s,t_{k+1})\) as \( Z(s,t_{k+1}):=Z_I(s,t_{k+1})+Z_B(s,t_{k+1})\) where \(Z_B(s,t_{k+1})\) and \(Z_I(s,t_{k+1})\) satisfies

$$\begin{aligned} \left. \begin{array}{ll} &{} {\mathcal {L}}_{CN}Z_B(s,t_{k+1})=0,\;\;s\in (0,1)\cup (1,2)\\ &{}Z_B(0,t_{k+1})=0,\\ &{} Z(2,t_{k+1})=Y(2,t_{k+1})-X(2,t_{k+1}) \end{array}\right\} \end{aligned}$$
(3.11)

and

$$\begin{aligned} \left. \begin{array}{ll} &{} {\mathcal {L}}_{CN}Z_I(s,t_{k+1})=0,\;\;s\in (0,1)\cup (1,2)\\ &{}Z_I(0,t_{k+1})=0,\;\; Z_I(2,t_{k+1})=0,\\ &{} \frac{dZ_I}{ds}(1^+,t_{k+1})-\frac{dZ_I}{ds}(1^-,t_{k+1})=\frac{dX}{ds}(1^-,t_{k+1})-\frac{dX}{ds}(1^+,t_{k+1}). \end{array}\right\} \end{aligned}$$
(3.12)

The following lemma provides bounds on the derivatives of smooth component \(X(s,t_{k+1})\) and singular component \(Z(s,t_{k+1})\).

Lemma 3.4

For \(k=0,1,2,3\), the smooth component \(X(s,t_{k+1})\) and singular component \(Z(s,t_{k+1})\) satisfy the following estimates

$$\begin{aligned}&\left| \frac{d^kX(s,t_{k+1})}{ds^k}\right| \le C(1+\varepsilon ^{2-k}) \;\text {for}\; s\in (0,1)\cup (1,2),\\&\left| \frac{d^kZ_B(s,t_{k+1})}{ds^k}\right| \le C\varepsilon ^{-k}\exp \left( \frac{-p_0^*(2-s)}{\varepsilon }\right) \;\text {for}\; s\in (0,1)\cup (1,2), \;\text {and}\\&\left| \frac{d^kZ_I(s,t_{k+1})}{ds^k}\right| \le {\left\{ \begin{array}{ll}C\varepsilon ^{1-k}\exp \left( \frac{-p_0^*(1-s)}{\varepsilon }\right) \; &{}\text {for}\; s\in (0,1] \\ C\varepsilon ^{1-k}\;&{}\text {for}\; s\in (1,2). \end{array}\right. } \end{aligned}$$

Proof

For proof, see [39]. \(\square \)

4 Spatial discretization

The problem’s solution exhibits a strong boundary layer at \(s=2\) and a weak interior layer at \(s=1\). Consequently, to generate a piecewise-uniform mesh \(\bar{{\mathbb {D}}}_s^N\), we partition the given interval [0, 2] into four subintervals as

$$\begin{aligned}{}[0,2]=[0,1-\beta ]\cup [1-\beta ,1]\cup [1,2-\beta ]\cup [2-\beta ,2] \end{aligned}$$

where \(\displaystyle \beta =\min \left\{ 0.5,\frac{2\varepsilon \ln N}{p_0^*}\right\} \) is defined as the mesh transition parameter. Each subinterval contains N/4 mesh elements. Therefore, we may write

$$\begin{aligned} \bar{{\mathbb {D}}}_s^N= \left\{ s_i\right\} _0^N={\left\{ \begin{array}{ll} s_i=0\;\;&{}\text {for}\;\; i=0,\\ s_i=s_{i-1}+h_i \;\;&{}\text {for}\;\;i=1,\ldots , N \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} h_i={\left\{ \begin{array}{ll}\displaystyle \frac{4}{N}(1-\beta )\;\;&{}\text {for}\;\; i=1:N/4,N/2+1:3N/4,\\ \displaystyle \frac{4}{N}\beta \;\;&{}\text {for}\;\; i=N/4+1:N/2,3N/4+1:N. \end{array}\right. } \end{aligned}$$

For \(i\ge 1\), a function \(V_{i,k+1}\) and step size \(h_i\) discretize (3.1) using the difference formula

$$\begin{aligned}&D_s^+V_{i,k+1}=\frac{V_{i+1,k+1}-V_{i,k+1}}{h_{i+1}},\;\\&D_s^-V_{i,k+1}=\frac{V_{i,k+1}-V_{i-1,k+1}}{h_{i}} \text {and}\;\\&\delta _s^2V_{i,k+1}=\frac{2(D_s^+-D_s^-)V_{i,k+1}}{h_i+h_{i+1}}. \end{aligned}$$

The discrete problem on \(\bar{{\mathbb {D}}}_s^N\times {{\mathbb {T}}_t}^M\) thus reads

$$\begin{aligned} {\mathcal {L}}_{CN}^N Y_{i,k+1}=\hat{{\mathcal {G}}}_{i,k+1}, \;i=1,\ldots ,N-1 \end{aligned}$$
(4.1)

where

$$\begin{aligned} {\mathcal {L}}_{CN}^N Y_{i,k+1}={\left\{ \begin{array}{ll}\displaystyle {\mathcal {L}}_{CN1}^N Y_{i,k+1}=\frac{-\varepsilon }{2}\delta _s^2Y_{i,k+1}+\frac{p_i}{2}D_s^-Y_{i,k+1}+l_iY_{i,k+1}\\ \text {for}\; i=1,\ldots , N/2-1,\\ \displaystyle {\mathcal {L}}_{CN2}^N Y_{i,k+1}=\frac{-\varepsilon }{2}\delta _s^2Y_{i,k+1}+\frac{p_i}{2}D_s^-Y_{i,k+1}+l_iY_{i,k+1}+\frac{r_i}{2}Y_{i-N/2,k+1}\\ \text {for}\; i= N/2+1,\ldots ,N-1\end{array}\right. } \end{aligned}$$

and

$$\begin{aligned}&\hat{{\mathcal {G}}}_{i,k+1}\\&\quad ={\left\{ \begin{array}{ll} \displaystyle \hat{{\mathcal {G}}}_1(s_i,t_{k+1})=\frac{\varepsilon }{2}\delta _s^2Y_{i,k}-\frac{p_i}{2}D_s^-Y_{i,k}+m_iY_{i,k}-\frac{r_i}{2}Y_{i-N/2,k}+\frac{1}{2}\left( g_{i,k+1}+g_{i,k}\right) \\ \displaystyle -\frac{r_i}{2}\psi _1(s_{i-N/2},t_{k+1})\;\text {for}\; i=1,\ldots ,N/2-1,\\ \hat{{\mathcal {G}}}_2(s_i,t_{k+1})=\frac{\varepsilon }{2}\delta _s^2Y_{i,k}-\frac{p_i}{2}D_s^-Y_{i,k}+m_iY_{i,k}-\frac{r_i}{2}Y_{i-N/2,k}+\frac{1}{2}\left( g_{i,k+1}+g_{i,k}\right) \\ \displaystyle \text {for}\; i=N/2+1,\ldots , N-1.\end{array}\right. } \end{aligned}$$

Moreover, for \(i=N/2\)

$$\begin{aligned} D_s^+Y_{N/2,k+1}=D_s^-Y_{N/2,k+1} \end{aligned}$$

with

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle Y_{i,0}=\psi _{2,i,0}\;\text {for}\; i=0,\ldots ,N,\nonumber \\ \displaystyle Y_{i,k+1}=\psi _{1,i,k+1}\;\text {for}\; i=-N/2,-N/2+1,\ldots 0,\; k = 0, 1,\ldots ,M-1,\nonumber \\ \displaystyle {\mathcal {K}}^NY_{N,k+1}=Y_{N,k+1}-\varepsilon \sum \limits _{i=1}^{N}\frac{f_{i-1}Y_{i-1,k+1}+f_iY_{i,k+1}}{2}h_i=\psi _{3,N,k+1}\;\text {for}\; k=0,1,\ldots , M-1.\nonumber \end{array}\right. } \end{aligned}$$

The operator \({\mathcal {L}}_{CN}^N\) satisfies the following discrete maximum principle.

Lemma 4.1

Let \(Z_{i,k+1}\ge 0\) for \(i=0,\ldots ,N\), \({\mathcal {L}}_{CN}^N Z_{i,k+1}\ge 0\) for \(i= 1,\ldots ,N/2-1,N/2+1,\ldots ,N\) and \(D_s^+Z_{N/2,k+1}-D_s^-Z_{N/2,k+1}\le 0\). Then \(Z_{i,k+1}\ge 0\) for \(i= 0, 1\ldots ,N\).

Proof

Let \(j^*\in \left\{ 0,1,\ldots ,N\right\} \backslash \{N/2\}\) and \(Z_{j^*,k+1}=\min \limits _{\bar{{\mathbb {D}}}_s^N\times {{\mathbb {T}}_t}^M}{Z_{i,k+1}}\). Assume that \(Z_{j^*,k+1}<0\), it follows that \(j^*\notin \left\{ 0,N\right\} \).

Case I::

For \(j^*\in \left\{ 1,2,\ldots ,N/2-1\right\} \)

$$\begin{aligned} {\mathcal {L}}_{CN1}^N Z_{j^*,k+1}= & {} \frac{-\varepsilon }{2} \delta _s^2Z_{j^*,k+1}+\frac{p_{j^*}}{2} D_s^-Z_{i^*,k+1}+l_{j^*}Z_{j^*,k+1}\\= & {} \frac{-\varepsilon }{{\hat{h}}_{j^*}}\left\{ \frac{Z_{j^*+1,k+1}-Z_{j^*,k+1}}{h_{j^*+1}}-\frac{Z_{j^*,k+1}-Z_{j^*-1,k+1}}{h_{j^*}} \right\} \\&+\frac{p_{j^*}}{2}\left\{ \frac{Z_{j^*,k+1}-Z_{j^*-1,k+1}}{h_{j^*}} \right\} +l_{j^*}Z_{j^*,k+1}\\< & {} 0. \end{aligned}$$
Case II::

For \(j^*\in \left\{ N/2+1,\ldots , N-1\right\} \)

$$\begin{aligned} {\mathcal {L}}_{CN2}^N Z_{j^*,k+1}= & {} \frac{-\varepsilon }{2} \delta _s^2Z_{j^*,k+1}+\frac{p_{j^*}}{2} D_s^-Z_{i^*,k+1}+l_{j^*}Z_{j^*,k+1}+\frac{r_{j^*}}{2}Z_{j^*-N/2,k+1}\\\le & {} \frac{-\varepsilon }{2} \delta _s^2Z_{j^*,k+1}+\frac{p_{j^*}}{2} D_s^-Z_{i^*,k+1}+l_{j^*}Z_{j^*,k+1}+\frac{r_{j^*}}{2}Z_{j^*,k+1}\\= & {} \frac{-\varepsilon }{2} \delta _s^2Z_{j^*,k+1}+\frac{p_{j^*}}{2} D_s^-Z_{i^*,k+1}+(l_{j^*}+r_{j^*})Z_{j^*,k+1}\\= & {} \frac{-\varepsilon }{2} \delta _s^2Z_{j^*,k+1}+\frac{p_{j^*}}{2} D_s^-Z_{i^*,k+1}+\left( \frac{q_{j^*}+r_{j^*}}{2}+\frac{1}{\Delta t}\right) Z_{j^*,k+1}\\\le & {} \frac{-\varepsilon }{2} \delta _s^2Z_{j^*,k+1}+\frac{p_{j^*}}{2} D_s^-Z_{i^*,k+1}+\left( \eta +\frac{1}{\Delta t}\right) Z_{j^*,k+1}\\= & {} \frac{-\varepsilon }{{\hat{h}}_{j^*}}\left\{ \frac{Z_{j^*+1,k+1}-Z_{j^*,k+1}}{h_{j^*+1}}-\frac{Z_{j^*,k+1}-Z_{j^*-1,k+1}}{h_{j^*}} \right\} \\&+\frac{p_{j^*}}{2}\left\{ \frac{Z_{j^*,k+1}-Z_{j^*-1,k+1}}{h_{j^*}} \right\} +\left( \eta +\frac{1}{\Delta t}\right) Z_{j^*,k+1}\\< & {} 0. \end{aligned}$$
Case III::

For \(j^*=N/2\), \(D_s^+Z_{N/2,k+1}-D_s^-\phi _{N/2,k+1}>0\).

The required result follows from contradiction. \(\square \)

Consequently, the following stability estimate of the discrete operator \({\mathcal {L}}_{CN}^N\) can be obtained.

Lemma 4.2

Let \(Z_{i,k+1}\) be the solution of (4.1). Then

$$\begin{aligned} | Z_{i,k+1}|\le \max \left\{ | Z_{0,k+1}|, |Z_{N,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN}^N Z_{i,k+1}\Vert \right\} . \end{aligned}$$

Proof

Let \(\chi _{i,k+1}^{\pm }:=\max \left\{ |Z_{0,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN1}^N Z_{i,k+1}\Vert \right\} \pm Z_{i,k+1}\) for \(i=1,\ldots ,N/2-1\). Clearly, \(\chi _{0,k+1}^{\pm }\ge 0\) and

$$\begin{aligned} {\mathcal {L}}_{CN1}^N\chi _{i,k+1}^\pm= & {} l_i\max \left\{ |Z_{0,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN1}^N Z_{i,k+1}\Vert \right\} \pm {\mathcal {L}}_{CN1}^N Z_{i,k+1}\\= & {} l_i\max \left\{ |Z_{0,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN1}^N Z_{i,k+1}\Vert \right\} \pm \hat{{\mathcal {G}}}_1(s_i,t_{k+1})\\\ge & {} \frac{l_i\Delta t}{\eta \Delta t+1}\Vert \hat{{\mathcal {G}}}_1\Vert \pm \hat{{\mathcal {G}}}_1\\\ge & {} \frac{(q_i+r_i)\Delta t+2}{2\Delta t}\frac{\Delta t}{\eta \Delta t+1}\Vert \hat{{\mathcal {G}}}_1\Vert \pm \hat{{\mathcal {G}}}_1\\\ge & {} \frac{2\eta \Delta t+2}{2\Delta t}\frac{\Delta t}{\eta \Delta t+1}\Vert \hat{{\mathcal {G}}}_1\Vert \pm \hat{{\mathcal {G}}}_1\\\ge & {} 0. \end{aligned}$$

In case, \(i=N/2+1,\ldots ,N-1\), define \(\chi _{i,k+1}^{\pm }=\max \left\{ |Z_{N,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN2}^N Z_{i,k+1}\Vert \right\} \pm Z_{i,k+1}\). Clearly, \(\chi _{N,k+1}^{\pm }\ge 0\) and

$$\begin{aligned} {\mathcal {L}}_{CN2}^N\chi _{i,k+1}^\pm= & {} \left( l_i+\frac{r_i}{2}\right) \max \left\{ |Z_{N,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN2}^N Z_{i,k+1}\Vert \right\} \pm {\mathcal {L}}_{CN2}^N Z_{i,k+1}\\= & {} \left( l_i+\frac{r_i}{2}\right) \max \left\{ |Z_{N,k+1}|,\frac{\Delta t}{\eta \Delta t+1}\Vert {\mathcal {L}}_{CN2}^N Z_{i,k+1}\Vert \right\} \pm \hat{{\mathcal {G}}}_2(s_i,t_{k+1})\\\ge & {} \left( \frac{q_i+r_i}{2}+\frac{1}{\Delta t}\right) \left( \frac{\Delta t}{\eta \Delta t+1}\right) \Vert \hat{{\mathcal {G}}}_2\Vert \pm \hat{{\mathcal {G}}}_2\\\ge & {} \left( \eta +\frac{1}{\Delta t}\right) \left( \frac{\Delta t}{\eta \Delta t+1}\right) \Vert \hat{{\mathcal {G}}}_2\Vert \pm \hat{{\mathcal {G}}}_2\\\ge & {} 0. \end{aligned}$$

Moreover, if \(i=N/2\), \((D_s^+-D_s^-)\chi _{i,k+1}^{\pm }=0.\) Hence, the required result follows from Lemma 4.1. \(\square \)

5 Error analysis

Let us decompose \(Y_{i,k+1}\) into smooth and singular components to obtain a parameter uniform error estimate. We write \(Y_{i,k+1}:=X_{i,k+1}+Z_{i,k+1}\) where the smooth component X and the singular component Z satisfies

$$\begin{aligned} \left. \begin{array}{ll} {\mathcal {L}}_{CN1}^N X_{i,k+1}=\hat{{\mathcal {G}}}_1(s_i,t_{k+1}) \;\text {for}\; i\in \left\{ 1,2,\ldots ,N/2-1\right\} ,\\ X_{0,k+1}=X(0,t_{k+1}),\; X_{N/2-1,k+1}=X(1^-,t_{k+1}),\\ {\mathcal {L}}_{CN2}^N X_{i,k+1}=\hat{{\mathcal {G}}}_2(s_i,t_{k+1}) \;\text {for}\; i\in \left\{ N/2+1,\ldots ,N-1\right\} ,\\ X_{N/2+1,k+1}=X(1^+,t_{k+1}),\;\, X_{N,k+1}=X(2,t_{k+1}), \end{array}\right\} \end{aligned}$$
(5.1)

and

$$\begin{aligned} \left. \begin{array}{ll} {\mathcal {L}}_{CN}^N Z_{i,k+1}=0,\;\text {for}\; i\in \left\{ 1,\ldots ,N-1\right\} \setminus N/2,\\ Z_{0,k+1}=Z(0,t_{k+1}),\; Z_{N,k+1}=Z(2,t_{k+1}),\\ X_{N/2+1,k+1}+Z_{N/2+1,k+1}=X_{N/2-1,k+1}+Z_{N/2-1,k+1},\\ D_s^- X_{N/2,k+1}+D_s^- Z_{N/2,k+1}=D_s^+ X_{N/2,k+1}+D_s^+ Z_{N/2,k+1}. \end{array}\right\} \end{aligned}$$
(5.2)

The error \(e_{i,k+1}\) is given by

$$\begin{aligned} e_{i,k+1}=Y(s_i,t_{k+1})-Y_{i,k+1}=(X(s_i,t_{k+1})-X_{i,k+1})+(Z(s_i,t_{k+1})-Z_{i,k+1}). \end{aligned}$$

Theorem 5.1

Let \(Y(s_i,t_{k+1})\) and \(Y_{i,k+1}\) be the solutions of (3.1) and (4.1), respectively. Then

$$\begin{aligned} \left| Y(s_i,t_{k+1})-Y_{i,k+1}\right| \le CN^{-1}\ln ^2N,\;\text {for} \;0\le i\le N. \end{aligned}$$

Proof

The proof follows on the lines similar to the one presented in [39] for ordinary differential equations. \(\square \)

Finally, we combine (3.7) and Theorem 5.1 to obtain the principle convergence estimate that reads.

Theorem 5.2

Let y and Y be the solutions of the continuous problem (2.1) and the discrete problem (4.1), respectively. Then

$$\begin{aligned} \left| y(s_i,t_{k+1})-Y_{i,k+1}\right| \le C (\Delta t^2+(N^{-1}\ln ^2N)) \end{aligned}$$

for \(0\le i\le N\) and \(0\le k\le M\).

Fig. 1
figure 1

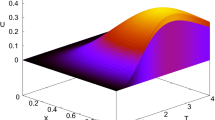
Surface plot of the numerical solution of Example 6.1 with \(M=N=128\) and \(\varepsilon =2^{-4}\)

Full size image
Fig. 2
figure 2

Numerical solutions of Example 6.1 for different values of \(\varepsilon \) at \(t=2\)

Full size image
Fig. 3
figure 3

Surface plot of the numerical solution of Example 6.2 with \(M=N=128\) and \(\varepsilon =2^{-4}\)

Full size image
Fig. 4
figure 4

Numerical solutions of Example 6.2 for different values of \(\varepsilon \) with \(t=2\)

Full size image
Fig. 5
figure 5

Numerical solution of Example 6.1 for different t when \(\varepsilon =2^{-1}\)

Full size image
Fig. 6
figure 6

Numerical solution of Example 6.1 for different t when \(\varepsilon =2^{-4}\)

Full size image
Fig. 7
figure 7

Numerical solution of Example 6.2 for different t when \(\varepsilon =2^{-1}\)

Full size image
Fig. 8
figure 8

Numerical solution of Example 6.2 for different t when \(\varepsilon =2^{-4}\)

Full size image
Table 1 \(E_{N,\bigtriangleup t}\) and \(P_{N,\bigtriangleup t}\) for Example 6.1 with different \(\varepsilon \), M and N
Full size table
Table 2 \(E_{N,\bigtriangleup t}\) and \(P_{N,\bigtriangleup t}\) for Example 6.1 with \(N=512\) and \(\varepsilon =2^{-6}\)
Full size table
Table 3 \(E_{N,\bigtriangleup t}\) and \(P_{N,\bigtriangleup t}\) for Example 6.2 with different \(\varepsilon \), M and N
Full size table
Table 4 \(E_{N,\bigtriangleup t}\) and \(P_{N,\bigtriangleup t}\) for Example 6.2 with \(N=512\) and \(\varepsilon =2^{-6}\)
Full size table
Fig. 9
figure 9

Loglog plot of maximum pointwise error for Example 6.1

Full size image
Fig. 10
figure 10

Loglog plot of maximum pointwise error for Example 6.2

Full size image

6 Numerical experiments

In this section, we consider two model problems, present numerical results using the proposed method, and verify the theoretical estimates numerically.

Example 6.1

Consider the following problem with integral boundary condition

$$\begin{aligned}&[-\varepsilon y_{ss}+(2+s(2-s))y_s+3y+y_t](s,t)-y(s-1,t)\\&\quad =4se^{-t}t^2,\;\; (s,t)\in (0,2)\times (0,2],\\ \displaystyle&y(s,t)=0,\;\;(s,t)\in \Gamma _1,\; y(s,t)=0,\;\;(s,t)\in \Gamma _2,\\ \displaystyle&y(2,t)=\frac{\varepsilon }{6}\int _{0}^{2}y(s,t)ds, (s,t)\in \Gamma _3. \end{aligned}$$

Example 6.2

Consider the following problem with integral boundary condition:

$$\begin{aligned}&[-\varepsilon y_{ss}+3y_s+(s+10)y+y_t](s,t)-y(s-1,t)=2(1+s^2)t^2,\;\; (s,t)\in (0,2)\\&\quad \times (0,2],\\ \displaystyle&y(s,t)=t^2,\;\;(s,t)\in \Gamma _1,\; y(s,t)=0,\;\;(s,t)\in \Gamma _2,\\&\displaystyle y(2,t)=\frac{\varepsilon }{6}\int _{0}^{2}s\sin (s)y(s,t)ds, (s,t)\in \Gamma _3. \end{aligned}$$

The exact solution of the above examples is not known for comparison. Therefore, the double mesh principle [32] is used to estimate the proposed method’s error and rate of convergence. The maximum absolute error \((E_{N,\bigtriangleup t})\) and order of convergence (\(P_{N,\bigtriangleup t}\)) is defined as \( E_{N,\bigtriangleup t}:=\max \left| Y_{N,\bigtriangleup t}(s_i,t_{k+1})-{\tilde{Y}}_{2N,\bigtriangleup t/2}(s_i,t_{k+1})\right| \) and \( P_{N,\bigtriangleup t}:=\displaystyle \log _2\left( \frac{E_{N,\bigtriangleup t}}{E_{2N,\bigtriangleup t/2}}\right) \). Here, \(Y_{N,\bigtriangleup t}(s_i,t_{k+1})\) and \({\tilde{Y}}_{2N,\bigtriangleup t/2}(s_i,t_{k+1})\) denotes the numerical solutions on \(\bar{{\mathbb {D}}}_s^N\times {{\mathbb {T}}_t}^M\) and \(\bar{{\mathbb {D}}}_s^{2N}\times {{\mathbb {T}}_t}^{2M}\), respectively.

The maximum absolute error (\(E_{N,\bigtriangleup t}\)) and corresponding order of convergence (\(P_{N,\bigtriangleup t}\)) for Example 6.1 and Example 6.2 are tabulated for different values of \(\varepsilon \), M, and N in Tables 1 and 3 , respectively. In addition to this Tables 2 and 4 depict the order of convergence in time variable for Examples 6.1 and 6.2 when \(N=512\) and \(\varepsilon =2^{-6}\).

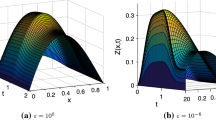
The presence of both interior and a boundary layer is apparent from the surface plots of the numerical solution for Examples 6.1 and 6.2 displayed in Figs. 1 and 3 , respectively. Figures 2 and 4 further illustrates the presence of the layers when \(t=2\) for Example 6.1 and Example 6.2. In contrast, Figs. 5-8 presents the solution for different time t and for different values of \(\varepsilon \) for given examples. It is to observe that as \(\varepsilon \) approaches the limiting value, it attributes the stiffness to the system and leads to the exponential changes across the interior and boundary layers. The log-log plot of errors are given in Figs. 9-10 for Example 6.1 and Example 6.2, respectively. It agrees with the expected convergence rate for the proposed method on the specially generated mesh.

7 Conclusion

A class of singularly perturbed parabolic partial differential equations with a large delay and an integral boundary condition is solved numerically. The proposed method consists of an upwind finite difference scheme on a non-uniform mesh in space and a Crank-Nicolson scheme on a uniform mesh in the time variable. The non-uniform mesh in the spatial direction is chosen so that most of the mesh points remain in the regions with rapid transitions. The method is invested for consistency, stability, and convergence. The error analysis of the proposed method reveals the parameter uniform convergence of first-order in space and second-order in time. Numerical experiments corroborate the theoretical findings.