1 Introduction

In this paper, we consider the differential Sylvester matrix equation (DSE in short) of the form

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{X}(t)=AX(t)+X(t)B+EF^{T}, &{}\quad t\in [t_{0},T_{f}] \\ X(t_{0})=X_{0} &{} \end{array} \right. \end{aligned}$$
(1)

where \(A\in \mathbb {R}^{n\times n}\), \(B\in \mathbb {R}^{p\times p}\), and \(E\in \mathbb {R}^{n\times s}\), \(F\in \mathbb {R}^{p\times s}\), are full rank matrices, with \(s\ll n,p\). The initial condition is given in a factored form as \(X_{0}=Z_{0}\tilde{Z}_{0}^{T}\) and the matrices A and B are assumed to be large and sparse.

Differential Sylvester matrix equations play a fundamental role in many problems in control, filter design theory, model reduction problems, differential equations and robust control problems; see, e.g., [1, 13, 19] and the references therein.

The exact solution of the differential Sylvester matrix Eq. (1) is given by the following result.

Theorem 1

[1] The unique solution of the differential Sylvester equations (1) is defined by

$$\begin{aligned} X(t)=e^{(t-t_{0})A}X_{0}e^{(t-t_{0})B}+\int _{t_{0}}^{t}e^{(t-\tau )A}EF^Te^{(t-\tau )B}d\tau . \end{aligned}$$
(2)

There are several methods for solving small or medium-sized differential Sylvester matrix equations. One can see, for example backward differentiation formula (BDF) and Rosenbrock method [12, 31].

During the last years, there is a large variety of methods to compute the solution of large scale matrix differential equations such as differential Lyapunov matrix equation, differential Sylvester equation and Riccati differential equation. For more details see [4, 5, 7, 18, 19, 26,27,28, 35]. For large-scale problems, the effective methods are based on Krylov subspaces. Some methods have been proposed for solving large matrix equation, see, e.g., [2, 8, 9, 18,19,20, 34]. The main idea employed in these methods is to use a extended Krylov subspace and then apply the Galerkin-type orthogonality condition. In [19], Jbilou and Hached are presented two approaches to solving the large differential Sylvester matrix equation, by using the block extended Krylov subspaces. The main idea in this work is using the extended global Krylov subspaces to solve (1).

The rest of the paper is organized as follows. In the next section, we give expression based on the global Arnoldi process of the unique solution X(t) of the differential Sylvester matrix Eq. (1). In Sect. 3, we recall the extended global Arnoldi algorithm with some of its properties. In Sect. 4, we defined EGA-exp method based on extended global Krylov subspaces and quadrature method to approximate matrix exponential and computing numerical solution of Eq. (1). In Sect. 5, we present a low-rank approximation of solution of differential Eq. (1) using projection onto extended global Krylov subspaces \(\mathcal {K}_{m}^{g}(A,E)\) and \(\mathcal {K}_{m}^{g}(B^T,F)\). Finally, Sect. 6 is devoted to numerical experiments showing effectiveness of proposed methods.

Throughout the paper, we use the following notations. The Frobenius inner product of the matrices X and Y is defined by \(\langle X,Y \rangle _F=tr(X^TY)\), where tr(Z) denotes the trace of a square matrix Z. The associated norm is the Frobenius norm denoted by \(\parallel {\cdot } \parallel _F\). The Kronecker product \(A\otimes B = [a_{i,j} B]\) where \(A=[a_{i,j}]\). This product satisfies the properties: \((A\otimes B)(C\otimes D) = (AC\otimes BD)\) and \((A\otimes B)^T = A^T\otimes B^T\). We also use the matrix product \(\diamond \) defined in [11]. The following proposition gives some properties satisfied by this product.

Proposition 1

Let \(A, \ B, \ C \in \mathbb {R}^{n \times ps}\), \(D \in \mathbb {R}^{n \times n}\), \(L \in \mathbb {R}^{p \times p}\) and \(\alpha \in \mathbb {R}\). Then we have,

  1. 1.

    \((A + B)^T \diamond C = A^T \diamond C + B^T \diamond C\).

  2. 2.

    \( A^T \diamond (B + C) = A^T \diamond B + A^T \diamond C\).

  3. 3.

    \((\alpha A)^T \diamond C = \alpha (A^T \diamond C).\)

  4. 4.

    \((A^T \diamond B)^T = B^T \diamond A.\)

  5. 5.

    \( A^T \diamond (B (L \otimes I_s)) = (A^T \diamond B) L\).

A block matrix \(\mathcal {V}_m = [ V_1, V_2,\ldots , V_m ]\) is F-orthonormal if \(\mathcal {V}_m^T\diamond \mathcal {V}_m =I_m\). We have the following result.

Lemma 1

[24] Let \(\mathcal {V}_m = [ V_1, V_2,\ldots , V_m ]\) be an \(n\times ms\)F-orthonormal block matrix, \(Z\in \mathbb {R}^{m\times s}\) and \(Y\in \mathbb {R}^{ms\times q}\). Then we have

$$\begin{aligned} \Vert \mathcal {V}_m\left( Z\otimes I_s\right) \Vert _F=\Vert Z\Vert _F \quad {\text {and}} \quad \Vert \mathcal {V}_mY\Vert _F\le \Vert Y\Vert _F. \end{aligned}$$

2 Expression of the exact solution of the differential Sylvester equation

In this section we will give the expression of the unique solution X(t) of the differential Sylvester matrix Eq. (1). This expression is based on the global Arnoldi process. The modified global Arnoldi process constructs an F-orthonormal basis \(V_1, \ V_2,\ldots ,V_m\) of the matrix Krylov subspace

$$\begin{aligned} \mathcal {K}_{m}(A,V) = span\left\{ V,AV, A^2V,\ldots ,A^{m-1}V\right\} . \end{aligned}$$
figure a

Let \(\mathcal {V}_m=\left[ V_1, V_2,\ldots , V_m \right] \) and \(\widetilde{H}^A_m \) is the \((m + 1) \times m\) upper Hessenberg matrix whose entries \(h_{i,j}\) are defined by Algorithm 1 and \(H^A_m\) is the \(m \times m\) matrix obtained from \(\widetilde{H}^A_m \) by deleting its last row. We have the following relation

$$\begin{aligned} A\mathcal {V}_m =\mathcal {V}_m\left( H^A_m \otimes I_s\right) +h_{m+1,m}V_{m+1}\left( e_m^T\otimes I_s\right) , \end{aligned}$$

where \(e_m^T=[0,0,\ldots , 0, 1]\).

Let \(P_A\) be the minimal polynomial of A associated to E and \(P_{B^T}\) be the minimal polynomial of \(B^T\) associated to F, q the degree of \(P_A\) and \(q'\) the degree of \(P_{B^T}\). The following result shows that the solution X of (1) can be expressed in terms of the global Arnoldi basis.

Theorem 2

Let \(\mathcal {V}_q=\left[ V_1, V_2,\ldots , V_q \right] \) and \(\mathcal {W}_{q'}=\left[ W_1, W_2,\ldots , W_{q'}\right] \) be the F-orthonormal block matrices obtained by applying simultaneously q and \(q'\) steps of the global Arnoldi algorithm to the pairs (A, E) and \((B^T, F)\) respectively. Then the unique solution X of (1) can be expressed as:

$$\begin{aligned} X(t)=\mathcal {V}_{q}(Y_{qq'}(t)\otimes I_s)\mathcal {W}_{q'}^{T}, \end{aligned}$$
(3)

where \(Y_{qq'}(t)\) is the solution of the low-order differential Sylvester equation

$$\begin{aligned} \dot{Y}_{m}(t)-H^A_{q}Y_{m}(t)-Y_{m}(t)\left( H^B_{q'}\right) ^{T}-\widetilde{E}_{q}\widetilde{F}_{q'}^{T}=0, \end{aligned}$$

with \(\widetilde{E}_{q}=\Vert E\Vert _Fe_1^{(q)}\) and \(\widetilde{F}_{q'}=\Vert F\Vert _Fe_1^{(q')}\).

Proof

Let Z(t) be the matrix defined by \(\mathcal {V}_{q}(Y_{qq'}(t)\otimes I_s)\mathcal {W}_{q'}^{T}\). Then we have,

$$\begin{aligned}&\dot{Z}(t)-AZ(t)-Z(t)B-EF^{T} \\&\quad = \mathcal {V}_{q}(\dot{Y}_{qq'}(t)\otimes I_s)\mathcal {W}_{q'}^{T}{-}A\mathcal {V}_{q}(Y_{qq'}(t)\otimes I_s)\mathcal {W}_{q'}^{T}{-}\mathcal {V}_{q}(Y_{qq'}(t)\otimes I_s) \mathcal {W}_{q'}^{T}B-EF^{T}. \\&\quad = \mathcal {V}_{q}\left[ \left( \dot{Y}_{qq'}(t)-H^A_{q}Y_{qq'}(t)-Y_{qq'}(t)\left( H^B_{q'}\right) ^{T} -\widetilde{E}_{q}\widetilde{F}_{q'}^{T} \right) \otimes I_s\right] \mathcal {W}_{q'}^{T}. \end{aligned}$$

Since \(Y_{qq'}\) is the solution of the lower order differential Sylvester equation then \(\dot{Y}_{qq'}(t)-\mathbb {T}_{q,A}Y_{qq'}(t)-Y_{qq'}(t)\left( H^B_{q'}\right) ^{T}-\widetilde{E}_{q}\widetilde{F}_{q'}^{T}=0\). We get

$$\begin{aligned}\dot{Z}(t)-AZ(t)-Z(t)B-EF^{T}=0.\end{aligned}$$

Therefore, using the fact that the solution of (1) is unique, it follows that \(X(t)= \mathcal {V}_{q}(Y_{qq'}(t)\otimes I_s)\mathcal {W}_{q'}^{T}\). \(\square \)

3 The extended global Arnoldi process

In this section, we recall the extended global Krylov subspace and extended global Arnoldi process. Let V be a matrix of dimension \(n \times s\). Then the extended global Krylov subspace associated to (A, V) is given by

$$\begin{aligned} \mathcal {K}_{m}^{g}(A,V) = { span}\left\{ V,A^{-1}V, AV,A^{-2}V, A^{2}V,\ldots ,A^{m-1}V,A^{-m}V\right\} \end{aligned}$$
(4)

The extended global Arnoldi process constructs an F-orthonormal basis \(\left\{ V_1, \ V_2,\ldots , V_m\right\} \) of the extended global Krylov subspace \(\mathcal {K}_{m}^g(A,V)\) [20]. The algorithm is summarized as follows

figure b

Let \( {\mathbb V}_m = \left[ V_1,V_2,\ldots ,V_m \right] \) with \(V_i\in \mathbb {R}^{n \times 2s}\) and \(2m \times 2m\) upper block Hessenberg matrix

$$\begin{aligned}\mathbb {T}_{m,A}=\mathbb {V}_{m}^{T}\diamond (A\mathbb {V}_{m}).\end{aligned}$$

We have the following relation

$$\begin{aligned} A\mathbb {V}_m= & {} \mathbb {V}_{m+1}(\overline{\mathbb {T}}_{m,A}\otimes I_s) \\= & {} \mathbb {V}_m(\mathbb {T}_{m,A}\otimes I_s)+V_{m+1}(T^A_{m+1,m}E_m^T\otimes I_s), \end{aligned}$$

where \(\overline{\mathbb {T}}_{m,A}=\mathbb {V}_{m+1}^{T}\diamond (A\mathbb {V}_{m})\), and \(E_m^T=[0_{2\times 2(m-1)},I_2]\) is the matrix formed with the last 2 columns of the \(2m\times 2m\) identity matrix \(I_{2m}\).

4 Matrix exponential approximation and Gauss quadrature method

In this section, we compute a approximation of the solution of the large differential Sylvester matrix Eq. (1). Our approach is based on two steps. First approximation of matrix exponential is given using extended global Krylov subspace and then the Gaussian quadrature method is applied.

The exact solution of (1) is given by

$$\begin{aligned} X(t)=e^{(t-t_{0})A}X_{0}e^{(t-t_{0})B}+\int _{t_{0}}^{t}e^{(t-\tau )A}EF^{T}e^{(t-\tau )B}d\tau . \end{aligned}$$
(5)

We use extended global Krylov subspace method to approximate \(e^{(t-\tau )A}E\) and \(e^{(t-\tau )B^T}F\).

By Algorithm 2 we compute \(\mathbb {V}_{m}=[V_{1},\ldots ,V_{m}]\) and \(\mathbb {W}_{m}=[W_{1},\ldots ,W_{m}]\) the F-orthonormal matrices whose columns form an basis of the subspace \(\mathcal {K}_{m}^g(A,E)\) and \(\mathcal {K}_{m}^g(B^T,F)\), respectively.

The approximation \(Z_{m,A}\) of \(Z_A=e^{(t-\tau )A}E\) is obtained by

$$\begin{aligned} Z_{m,A}=\mathbb {V}_{m}\left( e^{(t-\tau )\mathbb {T}_{m,A}}\mathbb {V}_{m}\diamond E\otimes I_s\right) , \end{aligned}$$

where \(\mathbb {T}_{m,A}=\mathbb {V}_{m}^{T}\diamond (A\mathbb {V}_{m})\) (see [32, 33, 36]).

In the same way, an approximation of \(Z_B=e^{(t-\tau )B^T}F\) is given by

$$\begin{aligned} Z_{m,B}=\mathbb {W}_{m}(e^{(t-\tau )\mathbb {T}_{m,B}}\mathbb {W}_{m}\diamond F\otimes I_s), \end{aligned}$$

where \(\mathbb {T}_{m,B}=\mathbb {W}_{m}^{T}\diamond (B^T\mathbb {W}_{m})\).

That leads us to the following approximation

$$\begin{aligned} e^{(t-\tau )A}EF^{T}e^{(t-\tau )B}\approx Z_{m,A}(t)Z_{m,B}^{T}(t). \end{aligned}$$
(6)

Assuming that \(X(t_0) = 0\), then the approximate solution of the differential Sylvester Eq. (1) is obtained by

$$\begin{aligned} X_{m}(t)=\mathbb {V}_{m}(\mathbb {X}_{m}(t)\otimes I_s)\mathbb {W}_{m}^{T}, \end{aligned}$$
(7)

where

$$\begin{aligned} \mathbb {X}_{m}(t)=\int _{t_{0}}^{t}\mathbb {X}_{m,A}(\tau )\mathbb {X}_{m,B}^{T}(\tau )d\tau , \end{aligned}$$
(8)

with

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbb {X}_{m,A}(\tau )=e^{(t-\tau )\mathbb {T}_{m,A}}\mathbb {V}_{m}^{T}\diamond E &{} \\ \mathbb {X}_{m,B}(\tau )=e^{(t-\tau )\mathbb {T}_{m,B}}\mathbb {W}_{m}^{T}\diamond F. &{} \end{array} \right. \end{aligned}$$

Since m is generally very small (\(m<< n\)), the factors \(\mathbb {X}_{m,A}\) and \(\mathbb {X}_{m,B}\) can be computed using the expm function of Matlab, and we calculate the approximation of the integral of (8) by Gauss quadrature formulae.

The next result shows that the \(2m\times 2m\) matrix function \(\mathbb {X}_m(t)\) is solution of a low-order differential Sylvester matrix equation.

Theorem 3

The matrix function \(\mathbb {X}_m(t)\) defined by (8) satisfies the following low-order differential Sylvester matrix equation

$$\begin{aligned} \dot{\mathbb {X}}_{m}(t)=\mathbb {T}_{m,A}\mathbb {X}_{m}(t)+\mathbb {X}_{m}(t)\mathbb {T}_{m,B}^{T}+\widetilde{E}_{m}\widetilde{F}_{m}^{T}, \ \ t\in [t_{0},T_{f}], \end{aligned}$$
(9)

where \(\widetilde{E}_{m}=\mathbb {V}_{m}^{T}\diamond E\) and \(\widetilde{F}_{m}=\mathbb {W}_{m}^{T}\diamond F.\)

Proof

The proof can be easily derived from the expression (8) and the result of Theorem 1. \(\square \)

Let \(R_{m}(t)=\dot{X}_{m}(t)-AX_{m}(t)-X_{m}(t)B-EF^{T}\) be the residual associated to the approximation \(X_m(t)\).

Theorem 4

If \(X_{m}(t)=\mathbb {V}_{m}(\mathbb {X}_{m}(t)\otimes I_s)\mathbb {W}_{m}^{T}\) is the approximation obtained at step m by the extended global Arnoldi algorithm. Then the residual \(R_m(t)\) satisfies the inequality

$$\begin{aligned} \Vert R_{m}(t)\Vert _F^2\le \Vert T^A_{m+1,m}\overline{\mathbb {X}}_{m}(t)\Vert ^2_F+\Vert T^B_{m+1,m}\overline{\mathbb {X}}_{m}(t)\Vert ^2_F, \end{aligned}$$
(10)

for the 2-norm, we have

$$\begin{aligned} \Vert R_{m}(t)\Vert _2\le \max \{\Vert T^A_{m+1,m} \overline{\mathbb {X}}_{m} (t)\Vert _2,\Vert T^B_{m+1,m} \overline{\mathbb {X}}_{m} (t)\Vert _2\}, \end{aligned}$$

where \(\overline{\mathbb {X}}_{m}(t)\) is the \(2\times 2m\) matrix corresponding to the last 2 rows of \(\mathbb {X}_m(t)\).

Proof

We have

$$\begin{aligned}&R_{m}(t)=\dot{X}_{m}(t)-AX_{m}(t)-X_{m}(t)B-EF^{T},\\&\quad \textit{where}\quad X_{m}(t)=\mathbb {V}_{m}(\mathbb {X}_{m}(t)\otimes I_s)\mathbb {W}_{m}^{T}. \end{aligned}$$

Therefore

$$\begin{aligned} R_{m}(t){=}\mathbb {V}_{m}\left( \dot{\mathbb {X}}_{m}(t)\otimes I_s\right) \mathbb {W}_{m}^{T}{-}A\mathbb {V}_{m}\left( \mathbb {X}_{m}(t)\otimes I_s\right) \mathbb {W}_{m}^{T}{-}\mathbb {V}_{m}(\mathbb {X}_{m}(t)\otimes I_s) \mathbb {W}_{m}^{T}B{-}EF^{T}. \end{aligned}$$

We use the following properties

$$\begin{aligned} \left\{ \begin{array}{ll} A\mathbb {V}_{m}=\mathbb {V}_{m+1} \left( \mathbb {\widehat{T}}_{m,A}\otimes I_s\right) , &{} \\ \mathbb {W}^T_{m}B= \left( \mathbb {\widehat{T}}_{m,B}^T\otimes I_s\right) \mathbb {W}_{m+1}^T, &{} \\ \mathbb {V}_{m}=\mathbb {V}_{m+1}\left[ \begin{array}{c} I_{2sm} \\ 0_{2s,2s}\\ \end{array} \right] , &{}\\ \mathbb {W}_{m}^T=\left[ \begin{array}{cc} I_{2sm} &{} 0_{2s,2s} \\ \end{array} \right] \mathbb {W}_{m+1}^T,&\end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbb {\widehat{T}}_{m,A}=\left[ \begin{array}{c} \mathbb {T}_{m,A} \\ T_{m+1,m}^AE^T_m \\ \end{array} \right] , &{} \\ \mathbb {\widehat{T}}_{m,B}^T=\left[ \begin{array}{cc} \mathbb {T}_{m,B}^T &{} E_m(T_{m+1,m}^{B})^{T} \\ \end{array} \right] ,&\end{array} \right. \end{aligned}$$

we obtained

$$\begin{aligned}&R_{m}(t)= \mathbb {V}_{m+1}\left[ \begin{array}{c@{\quad }c} \dot{\mathbb {X}}_{m}(t)\otimes I_s &{} 0 \\ 0 &{} 0 \\ \end{array} \right] \mathbb {W}_{m+1}^{T}-\mathbb {V}_{m+1}\left[ \begin{array}{c@{\quad }c} \mathbb {T}_{m,A}\mathbb {X}_{m}(t)\otimes I_s &{} 0 \\ T^A_{m+1,m}E_m^T\mathbb {X}_{m}(t)\otimes I_s&{} 0 \\ \end{array} \right] \mathbb {W}_{m+1}^{T}\\&~~~~~~~~~~~~~-\mathbb {V}_{m+1}\left[ \begin{array}{c@{\quad }c} \mathbb {X}_{m}(t)\mathbb {T}_{m,B}^T\otimes I_s &{} \mathbb {X}_{m}(t)E_m(T^B_{m+1,m})^T\otimes I_s \\ 0&{} 0 \\ \end{array} \right] \mathbb {W}_{m+1}^{T}\\&~~~~~~~~~~~~~-\mathbb {V}_{m+1}\left[ \begin{array}{c@{\quad }c} \mathbb {V}_{m}^T\diamond EF^{T}\diamond \mathbb {W}_{m} &{} 0 \\ 0&{} 0 \\ \end{array} \right] \mathbb {W}_{m+1}^{T}\\&\mathbb {V}_{m+1}\bigg (\left[ \! \begin{array}{cc} \mathcal {S}_m \left( \mathbb {X}_{m}(t)\right) \!-\!\mathbb {X}_{m} (t)E_m(T^B_{m+1,m})^T \!-\!T^A_{m+1,m}E_m^T\mathbb {X}_{m}(t)0 \end{array} \right] \otimes I_s\bigg ) \mathbb {W}_{m+1}^T, \hbox {where}\nonumber \\&\mathcal {S}_m\left( \mathbb {X}_{m} (t)\right) =\dot{\mathbb {X}}_{m} (t)-\mathbb {T}_{m,A}\mathbb {X}_{m} (t)-\mathbb {X}_{m} (t)\mathbb {T}^T_{m,B}-\widetilde{E}_m \widetilde{F}_m^{T}. \end{aligned}$$

Since \(\mathbb {X}_{m}(t)\) is the exact solution of the equation

$$\begin{aligned} \dot{\mathbb {X}}_{m} (t)=\mathbb {T}_{m,A}\mathbb {X}_{m} (t)+\mathbb {X}_{m} (t)\mathbb {T}^T_{m,B}+\widetilde{E}_m \widetilde{F}_m^{T}. \end{aligned}$$

Then

$$\begin{aligned} R_{m}(t)=\mathbb {V}_{m+1}\bigg (\left[ \begin{array}{c@{\quad }c} 0&{}-\mathbb {X}_{m}(t)E_m(T^B_{m+1,m})^T \\ -T^A_{m+1,m}E_m^T\mathbb {X}_{m}(t)&{} 0\\ \end{array} \right] \otimes I_s\bigg )\mathbb {W}^T_{m+1}. \end{aligned}$$

If \(\overline{\mathbb {X}}_{m}(t)=E_m^T\mathbb {X}_{m}(t)\), then

$$\begin{aligned} \Vert R_{m}(t)\Vert ^2_F\le \Vert T^A_{m+1,m}\overline{\mathbb {X}}_{m}(t)\Vert ^2_F+\Vert T^B_{m+1,m}\overline{\mathbb {X}}_{m}(t)\Vert ^2_F. \end{aligned}$$

The same way for the 2-norm, we have \(\Vert R_{m}(t)\Vert _2\le \max \left\{ \Vert T^A_{m+1,m} \overline{\mathbb {X}}_{m} (t)\Vert _2,\Vert T^B_{m+1,m} \overline{\mathbb {X}}_{m} (t)\Vert _2 \right\} .\)\(\square \)

The following result shows that the approximation \(X_m(t)\) is an exact solution of a perturbed differential Sylvester equation.

Theorem 5

Let \(X_m(t)\) be the approximate solution given by (7). Then we have

$$\begin{aligned} \dot{X}_{m}(t)=(A-F_{m,A})X_{m}(t)+X_{m}(t)(B-F_{m,B})+EF^{T}, \end{aligned}$$
(11)

where

$$\begin{aligned} \left\{ \begin{array}{l} F_{m,A}=V_{m+1}\left( T^A_{m+1,m}E^T_m\otimes I_s\right) \left( \mathbb {V}_m^T\mathbb {V}_m\right) ^{-1}\mathbb {V}_{m}^{T}, \\ F_{m,B}=\mathbb {W}_{m}^T\left( \mathbb {W}_{m}\mathbb {W}_{m}^T \right) ^{-1}\left[ E_m\left( T^B_{m+1,m}\right) ^{T}\otimes I_s\right] W_{m+1}^{T}. \end{array} \right. \end{aligned}$$

Proof

By multiplying (9) on the left by \(\mathbb {V}_{m}\) and on the right by \(\mathbb {W}_{m}^{T}\), we obtained

$$\begin{aligned} \mathbb {V}_m(\dot{\mathbb {X}}_m(t)\otimes I_s)\mathbb {W}_m^T= & {} \mathbb {V}_m(\mathbb {T}_{m,A}\mathbb {X}_{m}(t)\otimes I_s)\mathbb {W}^T_m\\&+\mathbb {V}_m(\mathbb {X}_{m}(t)\mathbb {T}_{m,B}^T\otimes I_s)\mathbb {W}^T_m+\mathbb {V}_m(\widetilde{E}_m\widetilde{F}_m^T\otimes I_s)\mathbb {W}_m^T \\= & {} \mathbb {V}_m(\mathbb {T}_{m,A}\otimes I_s)(\mathbb {X}_{m}(t)\otimes I_s)\mathbb {W}^T_m\\&+\mathbb {V}_m(\mathbb {X}_{m}(t)\otimes I_s)(\mathbb {T}_{m,B}^T\otimes I_s)\mathbb {W}^T_m\\&+\mathbb {V}_m(\widetilde{E}_m\otimes I_s)(\widetilde{F}_m^T\otimes I_s)\mathbb {W}_m^T. \end{aligned}$$

Since

$$\begin{aligned} \left\{ \begin{array}{ll} A\mathbb {V}_{m}=\mathbb {V}_{m}(\mathbb {T}_{m,A}\otimes I_s)+V_{m+1}(T^A_{m+1,m}E^T_m\otimes I_s), &{} \\ \mathbb {W}^T_{m}B=(\mathbb {T}_{m,B}^T\otimes I_s)\mathbb {W}_{m}^T+(E_m(T^B_{m+1,m})^T\otimes I_s)W_{m+1}^T, &{} \\ \end{array} \right. \end{aligned}$$

then

$$\begin{aligned} \dot{X}_m(t)= & {} [A\mathbb {V}_m-V_{m+1}(T^A_{m+1,m}E^T_m\otimes I_s)](\mathbb {X}_{m}(t)\otimes I_s)\mathbb {W}^T_m\\&+\mathbb {V}_m(\mathbb {X}_{m}(t)\otimes I_s)[B\mathbb {W}_m^T-(E_m(T^B_{m+1,m})^T\otimes I_s)W_{m+1}^T]+EF^T \\= & {} [A-V_{m+1}(T^A_{m+1,m}E^T_m\otimes I_s)(\mathbb {V}_m^T\mathbb {V}_m)^{-1}\mathbb {V}_m^T]X_{m}(t)\\&+X_{m}(t)[B-\mathbb {W}_m^T(\mathbb {W}_m\mathbb {W}_m^T)^{-1}(E_m(T^B_{m+1,m})^T\otimes I_s)W_{m+1}^T]+EF^T. \end{aligned}$$

Finally

$$\begin{aligned} \dot{X}_{m}(t)=(A-F_{m,A})X_{m}(t)+X_{m}(t)(B-F_{m,B})+EF^{T}. \end{aligned}$$

\(\square \)

The next result states that the error \(\mathcal {E}_m(t)=X(t)-X_m(t)\) satisfies also a differential Sylvester matrix equation.

Theorem 6

Let X(t) be the exact solution of (1) and let \(X_{m}(t)\) be the approximate solution obtained at step m of Algorithm 2. The error \(\mathcal {E}_m(t)=X(t)-X_m(t)\) satisfies the following equation

$$\begin{aligned} \dot{\mathcal {E}}_{m}(t)=A\mathcal {E}_{m}(t)+\mathcal {E}_{m}(t)B-R_{m}(t), \end{aligned}$$
(12)

Proof

We have

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{X}(t) = AX(t)+X(t)B+EF^T, &{} \\ R_{m}(t)=\dot{X}_{m}(t)-AX_{m}(t)-X_{m}(t)B-EF^{T}, &{} \end{array} \right. \end{aligned}$$

then

$$\begin{aligned} \dot{\mathcal {E}}_{m}(t)= & {} \dot{X}(t)-\dot{X}_{m}(t) \\= & {} AX(t)+X(t)B+EF^T-AX_{m}(t)-X_{m}(t)B-EF^{T}-R_{m}(t)\\= & {} A(X(t)-X_{m}(t))+(X(t)-X_{m}(t))B-R_{m}(t)\\= & {} A\mathcal {E}_{m}(t)+\mathcal {E}_{m}(t)B-R_{m}(t). \end{aligned}$$

\(\square \)

Notice that from Theorem 6, the error \(\mathcal {E}_m(t)\) can be expressed in the integral form as follows

$$\begin{aligned} \mathcal {E}_{m}(t)=e^{(t-t_{0})A}\mathcal {E}_{m,0}e^{(t-t_{0})B}+\int _{t_{0}}^{t}e^{(t-\tau )A}R_{m}(\tau )e^{(t-\tau )B}d\tau , \quad t\in [t_{0},T_{f}]. \end{aligned}$$
(13)

where \(\mathcal {E}_{m,0}=\mathcal {E}_{m}(t_{0}).\)

Next, we give an upper bound for the norm of the error by using the 2-logarithmic norm defined by \(\mu _2(A)=\frac{1}{2}\lambda _{{ max}}(A+A^T).\)

Theorem 7

Assume that the matrices A and B are such that \(\mu _2(A)+\mu _2(B)\ne 0\). Then at step m of the extended global Arnoldi process, we have the following upper bound for the norm of the error \(\mathcal {E}_m(t)\),

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le \Vert \mathcal {E}_{m,0}\Vert _2e^{(t-t_0)(\mu _2(A)+\mu _2(B))}+\alpha _m\frac{e^{(t-t_{0})(\mu _2(A)+\mu _2(B))}-1}{(\mu _2(A)+\mu _2(B))}, \end{aligned}$$
(14)

where

$$\begin{aligned} \alpha _m=\max _{\xi \in [t_0,t]}(\max \{\Vert T^A_{m+1,m}\overline{\mathbb {X}}_{m}(\xi )\Vert _2,\Vert T^B_{m+1,m}\overline{\mathbb {X}}_{m}(\xi )\Vert _2\}). \end{aligned}$$

The matrix \(\overline{\mathbb {X}}_{m}\) is the \(2\times 2m\) matrix corresponding to the last 2 rows of \(\mathbb {X}_{m}(t)\).

Proof

We first point out that \(\Vert e^{tA}\Vert _2\le e^{\mu _{2}(A)t}.\) Using the expression (13) of \(\mathcal {E}_m(t)\), we obtain the following relation

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2=\Vert e^{(t-t_{0})A}\mathcal {E}_{m,0}e^{(t-t_{0})B}\Vert _2+\int _{t_{0}}^{t}\Vert e^{(t-\tau )A}R_{m}(\tau )e^{(t-\tau )B}\Vert _2d\tau . \end{aligned}$$

Therefore, using (13) and the fact that \(\Vert e^{(t-\tau )A}\Vert _2\le e^{(t-\tau )\mu _{2}(A)}\), we get

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le & {} \Vert \mathcal {E}_{m,0}\Vert _2e^{(t-t_{0})(\mu _2(A)+\mu _2(B))}\\&+\max _{\xi \in [t_0,t]}\Vert R_m(\xi )\Vert _2\int _{t_{0}}^{t}e^{(t-\tau )\mu _2(A)}e^{(t-\tau )\mu _2(B)}d\tau \\\le & {} \Vert \mathcal {E}_{m,0}\Vert _2e^{(t-t_{0})(\mu _2(A)+\mu _2(B))}\\&+\max _{\xi \in [t_0,t]}\Vert R_m(\xi )\Vert _2e^{t(\mu _2(A)+\mu _2(B))}\int _{t_{0}}^{t}e^{\tau (\mu _2(A)+\mu _2(B))}d\tau . \\ \end{aligned}$$

Using the result of Theorem 4, we obtain \(\displaystyle {\max _{\xi \in [t_0,t]}}\Vert R_m(\xi )\Vert _2\le \alpha _m\) and then

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le \Vert \mathcal {E}_{m,0}\Vert _2e^{(t-t_0)(\mu _2(A)+\mu _2(B))}+\alpha _m\frac{e^{(t-t_{0})(\mu _2(A)+\mu _2(B))}-1}{(\mu _2(A)+\mu _2(B))}. \end{aligned}$$

Next, we give another upper bound for the norm of the error \(\mathcal {E}_m(t)\). \(\square \)

Theorem 8

The error \(\mathcal {E}_{m}(t)\) satisfies the following inequality

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le \Vert F\Vert _2e^{t\mu _{2}(B)}\varGamma _{1,m}(t)+\Vert \widetilde{E}_m\Vert _2e^{t\mu _{2}(A)}\varGamma _{2,m}(t), \end{aligned}$$
(15)

where

$$\begin{aligned}\left\{ \begin{array}{ll} \varGamma _{1,m}(t)=\int _{t_{0}}^{t}e^{-\tau \mu _{2}(B)}\Vert Z_A(\tau )-Z_{m,A}(\tau )\Vert _2d\tau , &{} \\ \varGamma _{2,m}(t)=\int _{t_{0}}^{t}e^{-\tau \mu _{2}(A)}\Vert Z_B(\tau )-Z_{m,B}(\tau )\Vert _2d\tau . &{} \end{array} \right. \end{aligned}$$

Proof

From the expressions of X(t) and \(X_{m}(t)\), we have

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2= & {} \Vert X(t)-X_{m}(t)\Vert _2\\= & {} \Vert \int _{t_{0}}^{t}\left( Z_A(\tau )Z_B^{T}(\tau )-Z_{m,A}(\tau )Z_{m,B}(\tau )^{T}\right) d\tau \Vert _2 \\= & {} \Vert \int _{t_{0}}^{t}\left( Z_A(\tau )Z^{T}_B(\tau )-Z_{m,A} (\tau )Z^{T}_B(\tau )+Z_{m,A}(\tau )Z_B^{T}(\tau )-Z_{m,A}(\tau )Z^{T}_{m,B}(\tau )\right) d\tau \Vert _2 \\= & {} \Vert \int _{t_{0}}^{t}[(Z_A(\tau )-Z_{m,A}(\tau ))Z_B^{T}(\tau )+Z_{m,A}(\tau )(Z_B(\tau )-Z_{m,B}(\tau ))^{T}]d\tau \Vert _2 \\\le & {} \int _{t_{0}}^{t}\Vert Z_B(\tau )\Vert _2\Vert (Z_A(\tau )-Z_{m,A}(\tau ) )\Vert _2+\Vert Z_{m,A}(\tau )\Vert _2\Vert (Z_B(\tau )-Z_{m,B}(\tau ))\Vert _2d\tau . \end{aligned}$$

Now as

$$\begin{aligned} \mu _{2}(\mathbb {T}_{m,A})= & {} \frac{1}{2}\lambda _{\max } \left( \mathbb {T}_{m,A}+\mathbb {T}_{m,A}^{T}\right) \\\le & {} \frac{1}{2}\lambda _{\max }(A+A^{T}) \\= & {} \mu _{2}(A), \end{aligned}$$

and since

$$\begin{aligned} \left\{ \begin{array}{ll} \Vert Z_B(\tau )\Vert _2\le e^{(t-\tau )\mu _{2}(B)}\Vert F\Vert _2, &{} \\ \Vert Z_{m,A}(\tau )\Vert _2\le e^{(t-\tau )\mu _{2}(\mathbb {T}_{m,A})}\Vert \widetilde{E}_m\Vert _2\le e^{(t-\tau )\mu _{2}(A)}\Vert \widetilde{E}_m\Vert _2, &{} \end{array} \right. \end{aligned}$$

we also have

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le & {} \Vert F\Vert _2e^{t\mu _{2}(B)}\int _{t_{0}}^{t}e^{-\tau \mu _{2}(B)}\Vert Z_A(\tau )-Z_{m,A}(\tau )\Vert _2d\tau \\&+\Vert \widetilde{E}_m\Vert _2e^{t\mu _{2}(A)}\int _{t_{0}}^{t}e^{-\tau \mu _{2}(A)}\Vert Z_B(\tau )-Z_{m,B}(\tau )\Vert _2d\tau .\\ \end{aligned}$$

We get

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le \Vert F\Vert _2e^{t\mu _{2}(B)}\varGamma _{1,m}(t)+\Vert \widetilde{E}_m\Vert _2e^{t\mu _{2}(A)}\varGamma _{2,m}(t). \end{aligned}$$

\(\square \)

One can use some known results [22, 33] to derive upper bounds for \(\Vert Z_A(\tau )-Z_{m,A}(\tau )\Vert _2\), and \(\Vert Z_B(\tau )-Z_{m,B}(\tau )\Vert _2\), when using the extended global Krylov subspaces.

Lemma 2

$$\begin{aligned}&\Vert e_{m,A}(\tau )\Vert _2:=\Vert Z_A(\tau )-Z_{m,A}(\tau )\Vert _2\nonumber \\&\le \Vert V_{m+1}(T^A_{m+1,m}\otimes I_s)\Vert _2\int _0^\tau e^{(u-\tau )\nu _2(A)}\Vert L_{m,A}(u)\Vert _2du, \end{aligned}$$
(16)

where

$$\begin{aligned} \left\{ \begin{array}{ll} L_{m,A}(u)=E_m^T e^{(t-u)\mathbb {T}_{m,A}}\widetilde{E}_m\otimes I_s, &{} \\ \nu _2(A)=\lambda _{\min }\left( \frac{A+A^T}{2}\right) . &{} \end{array} \right. \end{aligned}$$

Proof

We have

$$\begin{aligned}\left\{ \begin{array}{ll} Z_A(\tau )=e^{(t-\tau )A}E, &{} \\ Z_{m,A}(\tau )=\mathbb {V}_{m}\left( e^{(t-\tau ) \mathbb {T}_{m,A}}\widetilde{E}_{m}\otimes I_s\right) , \\ \end{array} \right. \end{aligned}$$

then

$$\begin{aligned} Z'_A(\tau )=-Ae^{(t-\tau )A}E=-AZ_A(\tau ), \end{aligned}$$

and

$$\begin{aligned} Z'_{m,A}(\tau )= & {} -\mathbb {V}_{m}(\mathbb {T}_{m,A}\otimes I_s) \left( e^{(t-\tau )\mathbb {T}_{m,A}}\widetilde{E}_{m}\otimes I_s\right) \\= & {} -\left[ A\mathbb {V}_{m}-V_{m+1}(T^A_{m+1,m}E_{m}^T\otimes I_s) \right] \left( e^{(t-\tau )\mathbb {T}_{m,A}}\widetilde{E}_{m}\otimes I_s\right) \\= & {} -AZ_{m,A}(\tau )+V_{m+1}(T^A_{m+1,m}\otimes I_s)L_{m,A}(\tau ). \end{aligned}$$

Therefore, the error \(e_{m,A}(\tau )=Z_A(\tau )-Z_{m,A}(\tau )\) is such that

$$\begin{aligned} e'_{m,A}(\tau )=-Ae_{m,A}(\tau )-V_{m+1}(T^A_{m+1,m}\otimes I_s)L_{m,A}(\tau ), \end{aligned}$$

which allows to give the following expression of \(e_{m,A}\):

$$\begin{aligned} e_{m,A}(\tau )=-\int _0^\tau e^{(u-\tau )A}V_{m+1}(T^A_{m+1,m}\otimes I_s)L_{m,A}(u)du. \end{aligned}$$
(17)

As \(\tau -u>0\), it follows that

$$\begin{aligned} \Vert e^{(u-\tau )A}\Vert _2\le e^{(\tau -u)\mu _{2}(-A)}=e^{(u-\tau )\nu _{2}(A)}. \end{aligned}$$

Then, we get

$$\begin{aligned} \Vert e_{m,A}(\tau )\Vert _2\le \Vert T^A_{m+1,m}\Vert _2\int _0^\tau e^{(u-\tau )\nu _{2}(A)}\Vert L_{m,A}(u)\Vert _2du. \end{aligned}$$

\(\square \)

Notice that if \(\nu _{2}(A)\) is not known but \(\nu _{2}(A)\ge 0\) (which is the case for positive semidefinite matrices) then we get the upper bound

$$\begin{aligned} \Vert e_{m,A}(\tau )\Vert _2\le \Vert V_{m+1}(T^A_{m+1,m}\otimes I_s)\Vert _2\int _0^\tau \Vert L_{m,A}(u)\Vert _2du. \end{aligned}$$

To define a new upper bound for the norm of the global error \(\mathcal {E}_m(t)\), we can use the upper bounds for the errors \(e_{m,A}\) and \(e_{m,B}\) in the expression (15) stated in Theorem 8 to get

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le & {} \Vert F\Vert _2e^{t\mu _{2}(B)}\int _{t_0}^te^{-\tau \mu _{2}(B)}\Vert e_{m,A}(\tau )\Vert _2d\tau \\&+\Vert \widetilde{E}_m\Vert _2e^{t\mu _{2}(A)}\int _{t_0}^te^{-\tau \mu _{2}(A)}\Vert e_{m,B}(\tau )\Vert _2d\tau ,\\ \end{aligned}$$

and then we obtain

$$\begin{aligned} \Vert \mathcal {E}_{m}(t)\Vert _2\le & {} \Vert F\Vert _2e^{t\mu _{2}(B)}\Vert V_{m+1}(T^A_{m+1,m}\otimes I_s)\Vert _2\int _{t_0}^te^{-\tau \mu _{2}(B)}S_{m,A}(\tau )d\tau \end{aligned}$$
(18)
$$\begin{aligned}&+\Vert \widetilde{E}_m\Vert _2e^{t\mu _{2}(A)}\Vert W_{m+1}(T^B_{m+1,m}\otimes I_s)\Vert _2\int _{t_0}^te^{-\tau \mu _{2}(A)}S_{m,B}(\tau )\Vert _2d\tau ,\nonumber \\ \end{aligned}$$
(19)

where

$$\begin{aligned} \left\{ \begin{array}{ll} S_{m,A}(\tau )=\int _0^\tau e^{(u-\tau )V(A)}\Vert L_{m,A}(u)\Vert _2du, &{} \\ S_{m,B}(\tau )=\int _0^\tau e^{(u-\tau )V(B)}\Vert L_{m,B}(u)\Vert _2du. &{} \end{array} \right. \end{aligned}$$

The approximate solution \(X_m(t)\) could be given as a product of two matrices of low rank. It is possible to decompose it as \(X_m=Z_1\, Z_2^T\) where the matrix \(Z_1\) and \(Z_2\) are of low rank (lower than 2m). Consider the singular value decomposition of the \(2m\times 2m\) matrix

$$\begin{aligned} \mathbb {X}_{m}(t)=\, {\widetilde{G} }_1 \varSigma \, {\widetilde{G} }_2^T, \end{aligned}$$

where \(\varSigma \) is the diagonal matrix of the singular values of \(\mathbb {X}_{m}\) sorted in decreasing order. Let \(\mathbb {X}_{1,l}\) and \(\mathbb {X}_{2,l}\) be the \(2m\times l\) matrices of the first l columns of \( {\widetilde{G} }_1\) and \( {\widetilde{G} }_2\) respectively, corresponding to the l singular values of magnitude greater than some tolerance \(d_{tol}\). We obtain the truncated SVD

$$\begin{aligned} \mathbb {X}_{m}(t) \approx \mathbb {X}_{1,l}\, \varSigma _l\, {\mathbb {X}_{2,l}}^T, \end{aligned}$$

where \(\varSigma _l = \mathrm{diag}[\sigma _1, \ldots , \sigma _l]\). Setting \(Z_{1,m}=\mathbb {V}_{m} \, \left( \mathbb {X}_{1,l}\, \varSigma _l^{1/2}\otimes I_s\right) \) and \(Z_{2,m}=\mathbb {W}_{m} \, \left( \mathbb {X}_{2,l}\, \varSigma _l^{1/2}\otimes I_s\right) \) Leads to

$$\begin{aligned} X_m \approx Z_{1,m}\, Z_{2,m}^T. \end{aligned}$$
(20)

This is very important for large problems when one doesn’t need to compute and store the approximation \(X_m\) at each iteration, see [2, 6, 8].

We summarize the above method for solving large differential Sylvester matrix equations (EGA-exp) in following algorithm.

figure c

5 Low-rank approximate solutions by extended global Arnoldi algorithm

We present in this section an approach that avoid exponential approximation and also avoid quadrature method that we use in previous sections. This approach is based on extended global Krylov projection of the differential Sylvester matrix Eq. (1). For more details on global Krylov projection method for solving large matrix equations see [2, 8, 9, 24].

Recall that when we Apply the extended global Arnoldi algorithm to the pairs (A, E) and \((B^T,F)\), we get F-orthonormal bases \(\left\{ V_1, V_2,\ldots , V_m \right\} \) and \(\left\{ W_1, W_2,\ldots , W_m\right\} \) of extended global Krylov subspaces \(\mathcal {K}_m^g(A,E)\) and \(\mathcal {K}_m^g(B^T,F)\), respectively and we have

$$\begin{aligned} \mathbb {T}_{m,A}=\mathbb {V}_{m}^{T}\diamond (A\mathbb {V}_{m}) \quad \text {and} \quad \mathbb {T}_{m,B}=\mathbb {W}_{m}^{T}\diamond (B^T\mathbb {W}_{m}), \end{aligned}$$

where

$$\begin{aligned} \mathbb {V}_{m}= [V_1, V_2,\ldots , V_m] \quad \text {and} \quad \mathbb {W}_{m} = [W_1, W_2,\ldots , W_m]. \end{aligned}$$

We then consider approximate solution of the large differential Sylvester matrix Eq. (1) that have the low-rank form

$$\begin{aligned} X_{m}(t)=\mathbb {V}_{m}(Y_{m}(t)\otimes I_s)\mathbb {W}_{m}^{T}, \end{aligned}$$
(21)

where \(Y_{m}(t)\) the solution of the reduced differential Sylvester matrix equation

$$\begin{aligned} \dot{Y}_{m}(t)-\mathbb {T}_{m,A}Y_{m}(t)-Y_{m}(t)\mathbb {T}_{m,B}^{T}-\widetilde{E}_{m}\widetilde{F}_{m}^{T}=0. \end{aligned}$$
(22)

with \(\widetilde{E}_{m}=\Vert E\Vert _Fe_1^{(2m)}\) and \(\widetilde{F}_{m}=\Vert F\Vert _Fe_1^{(2m)}\).

The following theorem gives a result that allows us the computation of the norm of the residual.

Theorem 9

The Frobenius norm of the residual \(R_m(t)\) associated to the approximation \(X_{m}(t)\) satisfies the relation

$$\begin{aligned} \Vert R_{m}(t)\Vert _F^2\le \Vert T^A_{m+1,m}\overline{Y}_{m}(t)\Vert ^2_F+\Vert T^B_{m+1,m}\overline{Y}_{m}(t)\Vert ^2_F, \end{aligned}$$
(23)

where \(\overline{Y}_{m}(t)\) is the \(2\times 2m\) matrix corresponding to the last 2 rows of \(Y_m\).

Proof

See Theorem 4. \(\square \)

To solve the reduced order differential Sylvester matrix Eq. (22) one can use Backward Differentiation Formula (BDF) or Rosenbrock method, see [12, 19, 31].

We summarize steps of this approach in the following algorithm

figure d

6 Numerical experiments

In this section, we present some numerical experiments of large and sparse differential Sylvester matrix equations. We compare the two approaches proposed in this work [Algorithm 3 (EGA-exp), Algorithm 4 using BDF (EGA–BDF) and Algorithm 4 using Rosenbrock (EGA–ROS)] whit the extended block Arnoldi (EBA-exp) given in [19]. All the experiments were performed on a laptop with an Intel Core i5 processor and 4 GB of RAM using Matlab2014. The n-by-s matrices E and F are given by random values uniformly distributed on [0, 1].

6.1 Example 1

In this first example, the matrices A and B are obtained from the centered finite difference discretization of the operators:

$$\begin{aligned} L_A(u)= & {} \varDelta u+f_1(x,y)\frac{\partial u}{\partial x}+f_2(x,y)\frac{\partial u}{\partial y}+f(x,y)u\\ L_B(u)= & {} \varDelta u+g_1(x,y)\frac{\partial u}{\partial x}+g_2(x,y)\frac{\partial u}{\partial y}+g(x,y)u \end{aligned}$$

on the unit square \([0,1]\times [0,1]\) with homogeneous Dirichlet boundary conditions. The number of inner grid points in each direction was \(n_0\) and \(p_0\) for the operators \(L_A\) and \(L_B\), respectively. The matrices A and B were obtained from the discretization of the operator \(L_A\) and \(L_B\) with the dimensions \(n = n_0^2\) and \(p=p_0^2\), respectively. The discretization of the operator \(L_A(u)\) and \(L_B(u)\) yields matrices extracted from the Lyapack package [30] using the command fdm_2d_matrix and denoted as \(\mathrm{fdm}(n0,'f\_1(x,y)','f\_2(x,y)','f(x,y)')\). For this experiment, we consider \(A=\mathrm{fdm}(n0,f_1(x,y),f_2(x,y),f(x,y))\) and \(B=\mathrm{fdm}(p0,g_1(x,y),g_2(x,y),g(x,y))\) with \(f_1(x,y)=-e^{xy}\), \(f_2(x,y)=- \sin (xy)\), \(f(x,y)=y^2\), \(g_1(x,y)=-100e^x\), \(g_2(x,y)=-12xy\) and \(g(x,y)=\sqrt{x^2+y^2}\). we used \(s=2\). The time interval considered was [0, 2] and the initial condition \(X_0=X(t_0)\) was \(X_0=Z_0\widetilde{Z}_0^T\), where \(Z_0=0_{n\times 2}\) and \(\widetilde{Z}_0=0_{p\times 2}\). The tolerance was set to \(10^{-7}\) for the stop test on the residual. For the EGA–BDF and Rosenbrock methods, we used a constant timestep \(h=0.1\).

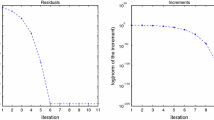
In Fig. 1, we chose a size of \(2500\times 2500\), \(2500\times 2500\) for the matrices A and B, respectively, we plotted the Frobenius norms of the residuals \(\Vert R_m(T_f)\Vert _F\) at final time \(T_f\) versus the number of extended global Arnoldi iterations for the EGA-exp, EGA–BDF and EGA–ROS methods.

Fig. 1
figure 1

Residual norm versus number m of extended global Arnoldi iterations

Full size image

In Fig. 2, the matrices A and B are obtained from the discretisation of the operator \(L_A(u)\) and \(L_B(u)\) with dimensions \(n = 10{,}000\) and \(p = 4900\), respectively. we plotted the Frobenius norms of the residuals \(\Vert R_m(T_f)\Vert _F\) at final time \(T_f\) versus the number of extended global Arnoldi iterations for the EGA-exp, EGA–BDF and EGA–ROS methods.

Fig. 2
figure 2

Residual norm versus number m of extended global Arnoldi iterations

Full size image

6.2 Example 2

For the second set of experiments, we use the matrices add32, pde2961, and \({ thermal}\) from the University of Florida Sparse Matrix Collection [15] and from the Harwell Boeing Collection (http://math.nist.gov/MatrixMarket). The tolerance was set to \(10^{-7}\) for the stop test on the residual. For the EGA–BDF and EGA–ROS methods, we used a constant timestep \(h=0.01\).

In Fig. 3, the matrices \(A={ thermal}\) and \(B=add32\) with dimensions \(n=3456\) and \(p=4960\), respectively, and \(s=3\). we plotted the Frobenius norms of the residuals \(\Vert R_m(T_f)\Vert _F\) at final time \(T_f\) versus the number of extended global Arnoldi iterations for the EGA-exp, EGA–BDF and EGA–ROS methods.

Fig. 3
figure 3

Residual norm versus number m of extended global Arnoldi iterations

Full size image

In Fig. 4, we used the matrices \(A=pde2961\) and \(B=\mathrm{fdm}(90,100e^{x},\sqrt{2x^2+y^2},y^2-x^2)\) with dimensions \(n=2961\) and \(p=8100\), respectively, and \(s=4\). we plotted the Frobenius norms of the residuals \(\Vert R_m(T_f)\Vert _F\) at final time \(T_f\) versus the number of extended global Arnoldi iterations for the EGA-exp, EGA–BDF and EGA–ROS methods.

Fig. 4
figure 4

Residual norm versus number m of extended global Arnoldi iterations

Full size image

6.3 Example 3

In this last example, we compare the performances of the extended global Arnoldi method associated to the different techniques for solving the reduced-order problem and the EBA-exp method given in [19].

In Table 1, we list the Frobenius residual norms at final time \(T_f=2\) and the corresponding CPU time for each method. For this experiment, the algorithms are stopped when the residual norms are smaller than \(10^{-9}\).

Table 1 Runtimes in seconds and the residual norms
Full size table

The numerical results are promising, showing the effectiveness of the global extended exponential method EGA-exp compared with extended block exponential approach EBA-exp given in [19] in terms of precision and computation time.

7 Conclusion

We presented in this paper some iterative methods for computing numerical solutions for large scale differential Sylvester matrix equations with low rank right-hand sides. The first approach arises naturally from the exponential expression of the exact solution and the use of approximation approach of the exponential of a matrix times by extended global Krylov subspaces. The second approach is based on low-rank approximate solutions and extended global algorithm. The approximate solutions are given as products of two low rank matrices and allow for saving memory for large problems. The numerical experiments show that the proposed extended global Krylov based methods are effective for large and sparse problems.