Mathematical analysis of an eco-epidemiological predator–prey model with stage-structure and latency

Abstract

In this paper, an eco-epidemiological predator–prey model with stage structure for the prey and a time delay describing the latent period of the disease is investigated. By analyzing corresponding characteristic equations, the local stability of the trivial equilibrium, the predator-extinction equilibrium, the disease-free equilibrium and the endemic equilibrium is addressed. The existence of Hopf bifurcations at the endemic equilibrium is established. By using Lyapunov functionals and LaSalle’s invariance principle, sufficient conditions are obtained for the global asymptotic stability of the trivial equilibrium, the predator-extinction equilibrium, the disease-free equilibrium and the endemic equilibrium of the model.

1 Introduction

Since the pioneering work of Anderson and May [1], great attention has been paid to developing realistic mathematical models for transmission dynamics of infectious diseases(see, for example [3, 4, 7,8,9,10,11,12, 14, 15, 17,18,19,20]). An increasing number of works are devoted to the study of the relationsips between demographic processes among different populations and diseases. There are many works on dealting with predator–prey models with disease in the predator or the prey (see, for example [3, 10, 11, 13, 14, 17,18,19]). In [17], Zhang et al. considered the following delayed eco-epidemiological predator–prey model:

$$\begin{aligned} \displaystyle \dot{x}(t)= & {} rx(t)-ax^2(t)-a_1x(t)S(t),\nonumber \\ \displaystyle \dot{S}(t)= & {} a_2x(t-\tau )S(t-\tau )-d_3S(t)-\beta S(t)I(t),\\ \displaystyle \dot{I}(t)= & {} \beta S(t)I(t)-d_4I(t),\nonumber \end{aligned}$$

(1.1)

where x(t), S(t) and I(t) represent the densities of the prey, susceptible (sound) predator and infected predator population at time t, respectively. The parameters a, $a_{1}$, $a_{2}$, $d_3$, $d_4$, r and $\beta$ are positive constants(see [17]). In system (1.1), the authors assumed that the infectious predator would die of diseases and only the healthy predator had predation capacity, but once infected with the disease, the predator would not be able to recover.

In most of the liternatures, it was frequently asumed that the disesse incubation is negligible. However, for some disesse, once infected, each susceptible individual becomes infectious instantaneously and later recovers with a permanent acquired immunity. An epidemic model based on these assumptions is called SIR (susceptible, infectious, recovered) model. In [4], Cooke formulated an epidemic model with time delay effect for the spread of a communicable disease carried by a vector by assuming that the force of infection at time t is given by $\beta S(t)I(t-\tau )$, where $\beta$ is the average number of contacts per infective per day and $\tau >0$ is a fixed time during which the infectious agents develop in the vector and it is only after that time that the infected vector can infect a susceptible human. Cooke considered the following model:

$$\begin{aligned} \displaystyle \dot{S}(t)= & {} A-d_1S(t)-\beta S(t)I(t-\,\tau ),\nonumber \\ \displaystyle \dot{I}(t)= & {} \beta S(t)I(t-\tau )-(d_2+\,\gamma )I(t),\\ \displaystyle \dot{R}(t)= & {} \gamma I(t)-d_3 R(t),\nonumber \end{aligned}$$

(1.2)

In system (1.2), S(t) represents the number of individuals who are susceptible to the disease, that is, who are not yet infected at time t; I(t) represents the number of infected individuals who are infectious and are able to spread the disease by contact with susceptible individuals; R(t) represents the number of individuals who have been infected and then removed from the possibility of being infected again or of spreading at time t, respectively. The parameters $d_1, d_2$ and $d_3$ are positive constants representing the death rates of susceptibles, infectives and recovered, respectively. In [7], McCluskey further discussed system (1.2) and completely proved that if the basic reproduction number is greater than unity, the endemic equilibrium is globally stable by constructing a suitable Lyapunov function.

Stage-structure is a natural phenomenon and represents, for example, the division of a population into immature and mature individuals. Predator–prey systems where only immature individuals are consumed by their predator are well known in nature. One example is described in [12], where Chinese fire-bellied newt, which is unable to feed on the mature Rana chensinensis, can only feed on the immature one. Stage-structured models have received great attention in recent years (see, for example, [8, 12, 13, 16]).

Based on above discussions, in this paper, we study the following differential equations

$$\begin{aligned} \displaystyle \dot{x}_1(t)= & {} rx_2(t)-(r_1+d_1)x_1(t)-ax_1^2(t)-a_1x_1(t)S(t),\nonumber \\ \displaystyle \dot{x}_2(t)= & {} r_1x_1(t)-d_2x_2(t),\nonumber \\ \displaystyle \dot{S}(t)= & {} a_2x_1(t)S(t)-bS^2(t)-d_3S(t)-\beta S(t)I(t),\nonumber \\ \displaystyle \dot{I}(t)= & {} \beta e^{-\mu \tau }S(t-\tau )I(t-\tau )-(\mu +\,\gamma )I(t),\nonumber \\ \displaystyle \dot{R}(t)= & {} \gamma I(t)-\mu R(t), \end{aligned}$$

(1.3)

where $x_1(t)$ and $x_2(t)$ represent the densities of the immature and the mature prey population at time t, respectively. The parameters $a, a_1, a_2, b, d_1, d_2, d_3, r, r_1, \beta , \mu$ and $\gamma$ are positive constants, in which r is the birth rate of the prey; a and b are the intra-specific competition rates of the immature prey and susceptible predator , respectively; $d_1$ and $d_2$ are the death rates of the immature prey and mature prey, respectively; $r_1$ is the transformation rate from the immature individuals to mature individuals for the prey; $a_1$ is the capturing rate of the predator, $a_2/a_1$ is the conversion rate of nutrients into the reproduction of the predator. $\tau \ge 0$ represents the latent period of the disease; $\gamma$ is the recovery rate of infectious individuals. In system (1.3), we assume that only the susceptible predators have ability to capture immature prey.

The initial conditions for system (1.3) take the form

$$\begin{aligned}&x_1(\theta )=\varphi _1(\theta )\ge 0,\;\;x_2(\theta )=\varphi _2(\theta )\ge 0,\;\; S(\theta )=\phi _1(\theta )\ge 0,\;\;I(\theta )=\phi _2(\theta )\ge 0,\nonumber \\&R(\theta )=\phi _3(\theta )\ge 0,\;\;\varphi _1(0)>0,\;\;\varphi _2(0)>0,\;\; \phi _1(0)>0,\;\; \phi _2(0)>0,\;\; \phi _3(0)>0,\nonumber \\&(\varphi _1(\theta ),\varphi _2(\theta ), \phi _1(\theta ),\phi _2(\theta ),\phi _3(\theta ))\in {C\left( [-\tau ,0], R_{+0}^5\right) },\;\;\theta \in [-\tau ,0), \end{aligned}$$

(1.4)

where $R_{+0}^5=\{(y_1, y_2, y_3, y_4, y_5): {y_i\ge {0}},i=1,2,3,4,5\}.$

It is well known by the fundamental theory of functional differential equations [5] that system (1.3) has a unique solution $(x_1(t), x_2(t), S(t), I(t), R(t))$ satisfying initial conditions (1.4). It is easy to show that all solutions of system (1.3) with initial conditions (1.4) are defined on $[0, +\,\infty )$ and remain positive for all $t\ge 0$.

The organization of this paper is as follows. In the next section, we show the permanence of solutions of system (1.3) with initial conditions (1.4). In Sect. 3, by using the theory on characteristic equation of delay differential equations with delay-dependent parameters developed by Beretta and Kuang [2], we discuss the local stability of each of feasible equilibria of system (1.3). We establish the existence of Hopf bifurcations at the endemic-coexistence equilibrium. In Sect. 4, by means of Lyaponov functionals and LaSalle’s invariance principle, we obtain sufficient conditions for the global stability of each of feasible equilibria of system (1.3).

2 Permanence

In this section, we give a result on the upper bound of positive solutions of system (1.3) with initial condition (1.4).

Lemma 2.1

Positive solutions of system (1.3) with initial conditions (1.4) are ultimately bounded.

Proof

Let $(x_1(t), x_2(t), S(t), I(t), R(t))$ be any positive solution of system (1.3) with initial conditions (1.4). By the first and second equations of system (1.3), we can obtain

$$\begin{aligned} \dot{x}_1(t)\le & {} rx_2(t)-(r_1+d_1)x_1(t)-ax_1^2(t),\\ \dot{x}_2(t)= & {} {r_1x_1(t)}-d_2x_2(t). \end{aligned}$$

which yields ${\limsup _{t\rightarrow +\,\infty }x_1(t)\le {\frac{|rr_1-d_2(r_1+d_1)|}{ad_2}}:=M_1}$, $\limsup _{t\rightarrow +\,\infty }x_2(t)\le {\frac{r_1}{d_2}M_1}:=M_2$.

By the last three equations of system (1.3), we can obtain

$$\begin{aligned} \dot{S}(t)\le & {} a_2M_1S(t)-bS^2(t)-d_3S(t)-\beta S(t)I(t),\nonumber \\ \dot{I}(t)= & {} \beta e^{-\mu \tau }S(t-\tau )I(t-\tau )-(\mu +\,\gamma )I(t),\\ \dot{R}(t)= & {} \gamma I(t)-\mu R(t).\nonumber \end{aligned}$$

(2.1)

Define

$$\begin{aligned} N(t)=S(t-\tau )+e^{\mu \tau }I(t)+e^{\mu \tau }R(t). \end{aligned}$$

Calculating the derivative of N(t) along positive solutions of system (2.1), it follows that

$$\begin{aligned} \displaystyle \dot{N}(t)\le & {} {-d}N(t)-b\left[ S(t-\tau )-\frac{a_2M_1}{2b}\right] ^2 +\,\frac{(a_2M_1)^2}{4b}\\ \displaystyle\le & {} -dV(t)+\,\frac{(a_2M_1)^2}{4b}, \end{aligned}$$

where $d=\min \{d_3, \mu \}$. If we choose $M_3=(a_2M_1)^2/(4bd)$, then

$$\begin{aligned} \limsup _{t\rightarrow \infty }S(t)\le {M_3}, \;\;\limsup _{t\rightarrow \infty }I(t)\le {e^{-\mu \tau }M_3},\;\; \limsup _{t\rightarrow \infty }R(t)\le {e^{-\mu \tau }M_3}. \end{aligned}$$

This completes the proof. $\square$

Lemma 2.2

For any positive solution $(x_1(t), x_2(t), S(t), I(t), R(t))$ of system (1.3) with initial conditions (1.4), we have

$$\begin{aligned} \displaystyle \liminf _{t\rightarrow +\,\infty }x_1(t)\ge & {} \frac{rr_1-d_2(r_1+d_1+a_1M_3)}{ad_2}:=\underline{x}_1,\\ \liminf _{t\rightarrow +\,\infty }S(t)\ge & {} \frac{a_2\underline{x}_1-(d_3+\,\beta e^{-\mu \tau }M_3)}{b}:=\underline{S}, \end{aligned}$$

where $M_3$ is defined in Lemma 2.1.

Proof

Let $(x_1(t), x_2(t), S(t), I(t), R(t))$ be any positive solution of system (1.3) with initial conditions (1.4). By Lemma 2.1, it follows that $\limsup _{t\rightarrow +\,\infty }S(t)\le M_3, \limsup _{t\rightarrow +\,\infty }I(t)\le e^{-\mu \tau }M_3$. Hence, for $\varepsilon >0$ being sufficiently small, there is a $T_0>0$ such that if $t>T_0$, $S(t)<M_3+\,\varepsilon , I(t)<e^{-\mu \tau }M_3+\,\varepsilon$. Accordingly, for $\varepsilon >0$ being sufficiently small, we derive from the first and the second equations of system (1.3) that, for $t>T_0$,

$$\begin{aligned} \displaystyle \dot{x}_1(t)\ge & {} rx_2(t)-(r_1+d_1)x_1(t) -ax_1^2(t)-a_1(M_3+\,\varepsilon )x_1(t),\nonumber \\ \displaystyle \dot{x}_2(t)= & {} r_1x_1(t)-d_2x_2(t), \end{aligned}$$

(2.2)

which leads to

$$\begin{aligned} \displaystyle {\liminf _{t\rightarrow +\,\infty }x_1(t)\ge \frac{rr_1-d_2(r_1+d_1+a_1M_3)}{ad_2}:=\underline{x}_1.} \end{aligned}$$

(2.3)

By the third equation of system (1.3), we can obtain

$$\begin{aligned} \displaystyle {\dot{S}(t)\ge a_2\underline{x}_1S(t)-bS^2(t) -d_3S(t)-(e^{-\mu \tau }M_3+\,\varepsilon )S(t)}, \end{aligned}$$

(2.4)

By comparison, we have

$$\begin{aligned} \displaystyle {\liminf _{t\rightarrow +\,\infty }S(t)\ge \frac{a_2\underline{x}_1-(d_3+\,\beta e^{-\mu \tau }M_3)}{b}:=\underline{S}.} \end{aligned}$$

(2.5)

This completes the proof. $\square$

3 Local stability and Hopf bifurcations

In this section, we discuss the local stability of each of feasible equilibria of system (1.3) by analyzing the corresponding characteristic equations.

Clearly, system (1.3) always has a trivial equilibrium $E_0(0, 0, 0, 0,0)$. If $rr_1>d_2(r_1+d_1)$, then system (1.3) has a predator-extinction equilibrium $E_1(x_1^0, x_2^0, 0, 0,0)$, where

$$\begin{aligned} \displaystyle x_1^0=\frac{rr_1-d_2(r_1+d_1)}{ad_2},\;\;x_2^0 =\frac{r_1[rr_1-d_2(r_1+d_1)]}{ad_2^2}. \end{aligned}$$

If the following condition holds:

$$\begin{aligned} (H_1)\;\;\displaystyle {\gamma _0=\frac{rr_1-d_2(r_1+d_1)}{ad_2}-\,\frac{d_3}{a_2}>0}, \end{aligned}$$

system (1.3) has a disease-free equilibrium $E_2(x_1^+, x_2^+, S^+, 0, 0)$, where

$$\begin{aligned} \displaystyle {x_1^+=\frac{a_1d_3+abx_1^0}{a_1a_2+ab},\;\;\;\;\;\;x_2^+ =\frac{r_1}{d_2}x_1^+,\;\;\;\;\;\;S^+=\frac{a}{a_1}\left( x_1^0-x_1^+\,\right) }. \end{aligned}$$

Further, if the following condition holds:

$$\begin{aligned} (H_2)\;\;\displaystyle {\gamma _1=\frac{aa_2\beta \gamma _0 e^{-\mu \tau }}{(ab+a_1a_2)(\mu +\,\gamma )}>1}, \end{aligned}$$

then system (1.3) has a unique positive equilibrium $E_*(x_1^*, x_2^*, S^*, I^*, R^*)$, where

$$\begin{aligned} \displaystyle x_1^*= & {} \frac{rr_1-d_2(r_1+d_1)}{ad_2}-\,\frac{a_1(\mu +\,\gamma )}{a\beta }e^{\mu \tau },\;\;\;\;\;\;\;\;\;\;\;x_2^*=\frac{r_1}{d_2}x_1^*,\\ \displaystyle S^*= & {} \frac{(\mu +\,\gamma )e^{\mu \tau }}{\beta },\;\;\;\;\;\;\;\; I^*=\frac{a_2x_1^*-bS^*-d_3}{\beta },\;\;\;\;\;\;\;\;R^*=\frac{\gamma }{\mu }I^*. \end{aligned}$$

Note that the variable R(t) does not appear in the first four equations of system (1.3). Therefore, we first consider the following subsystem of system (1.3):

$$\begin{aligned} \displaystyle \dot{x}_1(t)= & {} rx_2(t)-(r_1+d_1)x_1(t)-ax_1^2(t)-a_1x_1(t)S(t),\nonumber \\ \displaystyle \dot{x}_2(t)= & {} r_1x_1(t)-d_2x_2(t),\\ \displaystyle \dot{S}(t)= & {} a_2x_1(t)S(t)-bS^2(t)-d_3S(t)-\beta S(t)I(t),\nonumber \\ \displaystyle \dot{I}(t)= & {} \beta e^{-\mu \tau }S(t-\tau )I(t-\tau )-(\mu +\,\gamma )I(t).\nonumber \end{aligned}$$

(3.1)

Accordingly, system (3.1) has the equilibria $E_0^1(0, 0, 0, 0)$, $E_1^1(x_1^0, x_2^0, 0,0)$, $E_2^1(x_1^+, x_2^+, S^+, 0)$ and $E_*^1(x_1^*, x_2^*, S^*, I^*)$.

The characteristic equation of system (3.1) at the equilibrium $E_0^1$ takes the form

$$\begin{aligned} (\lambda +d_3)(\lambda +\,\mu +\,\gamma )\left[ \lambda ^2+(r_1+d_1+d_2)\lambda +d_2(r_1+d_1)-rr_1\right] =0, \end{aligned}$$

(3.2)

Clearly, Eq. (3.2) always has two negative real roots: $\lambda _1=-d_3$, $\lambda _2=-(\mu +\,\gamma )$. If $rr_1<d_2(r_1+d_1)$, then all roots of (3.2) are negative. If $rr_1>d_2(r_1+d_1)$, then (3.2) has one positive real root. Hence, $E_0^1$ is locally asymptotically stable when $rr_1<d_2(r_1+d_1)$ and unstable when $rr_1>d_2(r_1+d_1)$.

The characteristic equation of system (3.1) at the equilibrium $E_1^1$ is of the form

$$\begin{aligned}&(\lambda +\,\mu +\,\gamma )\left( \lambda +d_3-a_2x_1^0\right) \left[ \lambda ^2 +\,\left( r_1+d_1+d_2+2ax_1^0\right) \lambda \right. \nonumber \\&\quad \left. +\, rr_1-d_2(r_1+d_1)\right] =0. \end{aligned}$$

(3.3)

Clearly, Eq. (3.3) always has a negative real root $\lambda =-(\mu +\,\gamma )$. All the roots of the following equation

$$\begin{aligned} \lambda ^2+\,\left( r_1+d_1+d_2+2ax_1^0\right) \lambda +rr_1-d_2(r_1+d_1)=0 \end{aligned}$$

are negative as $rr_1>d_2(r_1+d_1)$. The other root of (3.3) is $\lambda =a_2x_1^0-d_3=a_2\gamma _0$. Hence, the equilibrium $E_1^1$ is locally asymptotically stable when $\gamma _0<0$ and unstable when$\gamma _0>0$.

The characteristic equation of system (3.1) at the equilibrium $E_2^1$ takes the form

$$\begin{aligned} \left( \lambda ^3+e_2\lambda ^2+e_1\lambda +e_0\right) \left( \lambda +\,\mu +\,\gamma -\beta S^ +e^{-(\mu +\,\lambda )\tau }\right) =0, \end{aligned}$$

(3.4)

where

$$\begin{aligned} e_2= & {} \frac{rr_1}{d_2}+ax_1^++d_2+bS^+,\\ e_1= & {} (ad_2+a_1a_2)x_1^+S^++bS^+\,\left( \frac{rr_1}{d_2}+ax_1^++d_2\right) , \\ e_0= & {} d_2(ab+a_1 a_2)x_1^+S^+. \end{aligned}$$

We first consider the following equation:

$$\begin{aligned} \lambda ^3+e_2\lambda ^2+e_1\lambda +e_0=0. \end{aligned}$$

(3.5)

A direct calculation shows that

$$\begin{aligned} \Delta _1= & {} e_2>0,\\ \Delta _2= & {} e_1e_2-e_0=\left( \frac{rr_1}{d_2}+ax_1^++d_2+bS^+\right) \left[ ad_2x_1^++bS^+\left( \frac{rr_1}{d_2}+ax_1^+\right) \right] \\&+\,a_1x_1^+a_2S^+\left( \frac{rr_1}{d_2}+ax_1^++bS^+\right) +d_2 bS^+\left( \frac{rr_1}{d_2}+d_2+bS^+\right)>0,\\ \Delta _3= & {} e_0\Delta _2>0. \end{aligned}$$

Hence, by the Routh–Huiwitz criterion, we see that the Eq. (3.5) has no positive roots. Other roots of Eq. (3.4) are determined by the following equation:

$$\begin{aligned} f_1(\lambda ):=\,\lambda +\,\mu +\gamma -\beta S^+e^{-(\mu +\lambda )\tau }=0. \end{aligned}$$

(3.6)

If $\gamma _1>1$, for $\lambda$ real, it is easy to show that,

$$\begin{aligned} f_1(0)=\mu +\gamma -\beta S^+e^{-\mu \tau }=(\mu +\gamma )(1-\gamma _1)<0, \;\;\lim _{\lambda \rightarrow +\infty }f_1(\lambda )=+\infty . \end{aligned}$$

Hence, $f_1(\lambda )=0$ has at least one positive real root in this case. If $\gamma _1<1$, one has

$$\begin{aligned} Re(\lambda )= & {} \beta S^+e^{-\mu \tau }\cos (\tau Im\lambda )-(\mu +\,\gamma )<\beta S^+e^{-\mu \tau }-(\mu +\,\gamma )\\= & {} -(\mu +\,\gamma )(1-\gamma _1)<0. \end{aligned}$$

Accordingly, by Theorem 3.4.1 in Kuang [6], we see that if $\gamma _1<1$, the equilibrium $E_2^1$ is locally asymptotically stable. If $\gamma _1>1$, the equilibrium $E_2^1$ is unstable.

In conclusion, we have the following results.

Theorem 3.1

For system (3.1), we have the following:

• (i) If $rr_1<d_2(r_1+d_1)$, then the equilibrium $E_0^1$ is locally asymptotically stable; if $rr_1>d_2(r_1+d_1)$, then $E_0^1$ is unstable.

• (ii) Assume that $rr_1>d_2(r_1+d_1)$. If $\gamma _0<0$, then the equilibrium $E_1^1$ is locally asymptotically stable; if $\gamma _0>0$, then $E_1^1$ is unstable.

• (iii) Assume that $\gamma _0>0$. If $\gamma _1<1$, then the equilibrium $E_2^1$ is locally asymptotically stable; if $\gamma _1>1$, then $E_2^1$ is unstable.

By Theorem 3.1, for system (1.3), we have the following conclusions.

Corollary 3.1

For system (1.3), we have the following:

• (i) If $rr_1<d_2(r_1+d_1)$, then the equilibrium $E_0$ is locally asymptotically stable; if $rr_1>d_2(r_1+d_1)$, then $E_0$ is unstable.

• (ii) Assume that $rr_1>d_2(r_1+d_1)$. If $\gamma _0<0$, then the equilibrium $E_1$ is locally asymptotically stable; if $\gamma _0>0$, then $E_1$ is unstable.

• (iii) Assume that $\gamma _0>0$. If $\gamma _1<1$, then the equilibrium $E_2$ is locally asymptotically stable; if $\gamma _1>1$, then $E_2$ is unstable.

The characteristic equation of system (3.1) at the endemic-coexistence equilibrium $E_*^1$ is of the form

$$\begin{aligned} \lambda ^4+u_3\lambda ^3+u_2\lambda ^2+u_1\lambda +u_0+\,\left( v_3\lambda ^3 +v_2\lambda ^2+v_1\lambda +v_0\right) e^{-\lambda \tau }=0, \end{aligned}$$

(3.7)

where

$$\begin{aligned} u_3= & {} \mu +\,\gamma +\,\frac{rr_1}{d_2}+ax_1^*+d_2+bS^*,\\ u_2= & {} (\mu +\,\gamma )\left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) +bS^*\left( \mu +\,\gamma +\,\frac{rr_1}{d_2}+ax_1^*+d_2\right) \\&+\,ad_2x_1^*+a_1x_1^*a_2S^*,\\ u_1= & {} (\mu +\,\gamma )(ad_2+a_1a_2S^*)x_1^*+d_2a_1a_2x_1^*S^*+bS^*\left[ (\mu +\,\gamma )\left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) \right. \\&\left. +\,ad_2x_1^*\right] ,\\ u_0= & {} d_2x_1^*S^*(\mu +\,\gamma )(a_1a_2+ab),\\ v_3= & {} -(\mu +\,\gamma ),\\ v_2= & {} -(\mu +\,\gamma )\left( \frac{rr_1}{d_2}+ax_1^*+d_2+bS^*-\beta I^*\right) ,\\ v_1= & {} -(\mu +\,\gamma )\left[ \left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) (bS^*-\beta I^*)+ad_2x_1^* +a_1a_2x_1^*S^*\right] \\ v_0= & {} -d_2x_1^*(\mu +\,\gamma )[a(bS^*-\beta I^*)+a_1a_2S^*]. \end{aligned}$$

When $\tau =0$, Eq. (3.7) becomes

$$\begin{aligned} \lambda ^4+(u_3+v_3)\lambda ^3+(u_2+v_2)\lambda ^2+(u_1+v_1)\lambda +u_0+v_0=0. \end{aligned}$$

(3.8)

By calculation, it follows that

$$\begin{aligned} \triangle _1= & {} u_3+v_3=\frac{rr_1}{d_2}+ax_1^*+d_2+bS^*>0,\\ \triangle _2= & {} (u_3+v_3)(u_2+v_2)-(u_1+v_1)=a_1a_2x_1^*S^* \left( \frac{rr_1}{d_2}+ax_1^*+bS^*\right) \\&+\,ad_2x_1^*\left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) \\&+\,\beta bS^* I^*(\mu +\,\gamma )+bS^*\left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) \left( \frac{rr_1}{d_2}+ax_1^*+d_2+bS^*\right)>0,\\ \triangle _3= & {} (u_1+v_1)\triangle _2-(u_0+v_0)(u_3+v_3)^2=bS^*\left( \frac{rr_1}{d_2} +ax_1^*+d_2\right) [\beta I^*(\mu +\,\gamma )]^2 \\&+\,d_2x_1^*S^*(a_1a_2+ab)\left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) \\&\times \left[ ad_2x_1^*+bS^* \left( \frac{rr_1}{d_2}+ax_1^*+d_2+bS^*\right) \right] \\&+\,a_1x_1^*a_2S^*\left( \frac{rr_1}{d_2}+ax_1^*+bS^*\right) \left[ \beta I^*(\mu +\,\gamma )\right. \\&\times \left. \left( \frac{rr_1}{d_2}+ax_1^*+d_2\right) +d_2x_1^*S^*(a_1a_2+ab)\right] \\&+\,bS^*\beta I^*(\mu +\,\gamma ) \left( \frac{rr_1}{d_2}+ax_1^*+d_2+bS^*\right) \\&\times \left[ \left( \frac{rr_1}{d_2}\right) ^2+2\frac{rr_1}{d_2}\left( ax_1^*+d_2\right) +\,\left( ax_1^*\right) ^2+(d_2)^2\right] \\&+\,\beta I^*d_2x_1^*b(S^*)^2(\mu +\,\gamma )(a_1a_2+2ab)>0,\\ \triangle _4= & {} (u_0+v_0)\triangle _3=ad_2x_1^*\beta ^2I^*(\mu +\,\gamma )\triangle _3>0. \end{aligned}$$

By the Routh–Hurwitz criterion, the equilibrium $E_*^1$ of system (3.1) is locally asymptotically stable when $\tau =0$.

Suppose that Eq. (3.7) has a pair of conjugate purely imaginary roots $\pm i\omega (\omega >0)$. Substituting $\lambda =i\omega$ into (3.7) and separating the real and imaginary parts, one obtains

$$\begin{aligned}&(v_3\omega ^3-v_1\omega )\sin \omega \tau +(v_2\omega ^2-v_0) \cos \omega \tau =\omega ^4-u_2\omega ^2+u_0,\nonumber \\&(v_3\omega ^3-v_1\omega )\cos \omega \tau -(v_2\omega ^2-v_0) \sin \omega \tau =-u_3\omega ^3+u_1\omega . \end{aligned}$$

(3.9)

Squaring and adding the two equations of (3.9), we derive that

$$\begin{aligned} \omega ^8+s_3\omega ^6+s_2\omega ^4+s_1\omega ^2+s_0=0, \end{aligned}$$

(3.10)

where

$$\begin{aligned} s_3= & {} u_3^2-2u_2-v_3^2,\; \;\;\;\;\;\;\;s_2=u_2^2+2u_0-2u_1u_3-v_2^2+2v_1v_3,\\ s_1= & {} u_1^2-2u_0u_2-v_1^2+2v_0v_2,\; \;\;\;s_0=u_0^2-v_0^2. \end{aligned}$$

Let $z=\omega ^2$, then Eq. (3.10) can be rewritten as

$$\begin{aligned} s(z):=z^4+s_3z^3+s_2z^2+s_1z+s_0=0. \end{aligned}$$

(3.11)

If $s_3>0$ and $s_2^2-4s_1s_3<0$, then s(z) has always no positive roots. Hence, under these conditions, Eq. (3.7) has no purely imaginary roots for any $\tau >0$ and accordingly, the equilibrium $E_*^1$ is locally asymptotically stable for all $\tau \ge 0$.

If Eq. (3.11) has at least one positive root, without loss of generality, we assume that (3.11) has four positive roots, namely, $z_1,\;z_2,\;z_3$ and $z_4$, respectively. Accordingly, Eq. (3.10) has four positive roots $\omega _k=\sqrt{z_k}(k=1,2,3,4)$.

For $k=1,2,3,4$, from (3.9) one can get the corresponding $\tau _k^j>0$ such that (3.7) has a pair of purely imaginary roots $\pm i\omega _k$ given by

$$\begin{aligned}&\displaystyle {\tau _k^{j}=\frac{2\pi j}{\omega _k}+\,\frac{1}{\omega _k} \arccos \frac{v_2\omega _k^2\left( \omega _k^4-u_2\omega _k^2+u_0\right) +\,\left( v_3\omega _k^3-v_1\omega _k\right) \left( u_1\omega _k-u_3\omega _k^3\right) }{\left( v_2\omega _k^2\right) ^2 +\,\left( v_3\omega _k^3-v_1\omega _k\right) ^2}},\\&\quad j=0,1,2,\ldots \end{aligned}$$

Differentiating the two sides of (3.7) with respect to $\tau$, it follows that

$$\begin{aligned} \left( \frac{d\lambda }{d\tau }\right) ^{-1}= & {} \displaystyle \frac{4\lambda ^3+3u_3\lambda ^2+2u_2\lambda +u_1}{-\lambda (\lambda ^4 +u_3\lambda ^3+u_2\lambda ^2+u_1\lambda +u_0)}+ \frac{3v_3\lambda ^2+2v_2\lambda +v_1}{\lambda (v_3\lambda ^3+v_2\lambda ^2 +v_1\lambda +v_0)}\\&-\,\frac{\tau }{\lambda }. \end{aligned}$$

After some algebra, one obtains that

$$\begin{aligned}&\displaystyle sign\left\{ \frac{dRe\lambda }{d\tau }\right\} _{\tau =\tau _k^j}={{sign}} \left\{ Re\left( \frac{d\lambda }{d\tau }\right) ^{-1}\right\} _{\tau =\tau _k^j}\\&\quad =\displaystyle sign\left\{ -\frac{\left( u_1-3u_3\omega _k^2\right) \left( u_3\omega _k^2-u_1\right) +2\left( u_2-2\omega _k^2\right) \left( \omega _k^4-u_2\omega _k^2+u_0\right) }{\omega _k^2\left( u_1-u_3\omega _k^2\right) ^2 +\,\left( \omega _k^4-u_2\omega _k^2+u_0\right) ^2}\right. \\&\qquad \displaystyle \left. +\,\frac{\left( v_1-3v_3\omega _k^2\right) \left( v_3\omega _k^2-v_1\right) -2v_2^2\omega _k^2}{(v_2\omega _k)^2+\,\left( v_1\omega _k-v_3\omega _k^3\right) ^2}\right\} \\ \end{aligned}$$

We derive from (3.9) that

$$\begin{aligned} \omega _k^2\left( u_1-u_3\omega _k^2\right) ^2+\,\left( \omega _k^4-u_2\omega _k^2+u_0\right) ^2= (v_2\omega _k)^2+\,\left( v_1\omega _k-v_3\omega _k^3\right) ^2. \end{aligned}$$

Hence, it follows that

$$\begin{aligned} \displaystyle sign\left\{ \frac{dRe\lambda }{d\tau }\right\} _{\tau =\tau _k^j}= & {} sign\left\{ \frac{4\omega _k^6+3s_3\omega _k^4+2s_2\omega _k^2+s_1}{(v_2\omega _k)^2 +\,\left( v_1\omega _k-v_3\omega _k^3\right) ^2}\right\} \\ \displaystyle= & {} sign\left\{ \frac{s'(z_k)}{(v_2\omega _k)^2 +\,\left( v_1\omega _k-v_3\omega _k^3\right) ^2}\right\} . \end{aligned}$$

Based on the theory on characteristic equation of delay differential equations with delay-dependent parameters developed by [6], one can obtain the following result.

Theorem 3.2

Let $\gamma _1>1$ hold. For system (1.3), we have

• (i) If $s_3>0$, and $s_2^2-4s_1s_3<0$, then the coexistence equilibrium $E_*$ is locally asymptotically stable for all $\tau \ge 0$.

• (ii) If $s(z)=0$ has at least one positive root $z_k$, then all roots of (3.7) have negative real parts for $\tau \in [0, \tau _k^0)$, and the equilibrium $E_*$ of system (1.3) is locally asymptotically stable for $\tau \in [0, \tau _k^0)$.

• (iii) If all conditions as stated in (ii) hold true and $s'(z_k)>0$, then system (1.3) undergoes a Hopf bifurcation at $E_*$ when $\tau =\tau _k^j(j=0,1,\ldots )$.

4 Global stability

In this section, we study the global stability of the trivial equilibrium $E_0$, the predator-extinction equilibrium $E_1$, the disease-free equilibrium $E_2$ and the endemic-coexistence equilibrium $E_*$, respectively. The strategy of proofs is to use Lyapunov functions and LaSalle’s invariance principle.

Theorem 4.1

If $rr_1<d_2(r_1+d_1)$, then the trivial equilibrium $E_0(0, 0, 0, 0,0)$ of system (1.3) is globally asymptotically stable.

Proof

By Theorem 3.1, we see that if $rr_1<d_2(r_1+d_1)$, then $E_0$ is locally asymptotically stable. Hence, we only prove that all positive solutions of system (1.3) with initial conditions (1.4) converge to $E_0$. Let $(x_1(t), x_2(t), S(t), I(t), R(t))$ be any positive solution of system (1.3) with initial conditions (1.4). Define

$$\begin{aligned} V_0(t)= & {} \displaystyle x_1(t)+\,\frac{r}{d_2}x_2(t)+\,\frac{a_1}{a_2}S(t) +\,\frac{a_1}{a_2}e^{\mu \tau }I(t)+\,\frac{a_1}{a_2}e^{\mu \tau }R(t)\\&+\,\frac{a_1}{a_2}\beta \int _{t-\tau }^tS(u)I(u)du. \end{aligned}$$

Calculating the derivative of $V_0(t)$ along positive solutions of system (1.3), it follows that

$$\begin{aligned} \displaystyle {\dot{V}_0(t)}= & {} \displaystyle {-\frac{d_2(r_1+d_1) -rr_1}{d_2}x_1(t)-ax_1^2(t)-\,\frac{a_1}{a_2}bS^2(t)-\,\frac{a_1}{a_2}d_3S(t)}\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}e^{\mu \tau }\mu I(t)-\,\frac{a_1}{a_2}e^{\mu \tau }\mu R(t).} \end{aligned}$$

(4.1)

If $rr_1<d_2(r_1+d_1)$, it then follows from (4.1) that $\dot{V}_0(t)\le 0$. By Theorem 5.3.1 in [5], solutions limit to $\Lambda$, the largest invariant subset of $\{\dot{V}_0(t)=0\}$. Clearly, we see from (4.1) that $\dot{V}_0(t)=0$ if and only if $x_1(t)=0, S(t)=0$, $I(t)=0$ and $R(t)=0$. Noting that $\Lambda$ is invariant, for each element in $\Lambda$, we have $x_1(t)=0$. It therefore follows from the first equation of system (1.3) that

$$\begin{aligned} 0=\dot{x}_1(t)=rx_2(t), \end{aligned}$$

which yields $x_2(t)=0$. Hence, $\dot{V}_0(t)=0$ if and only if $(x_1(t), x_2(t), S(t), I(t), R(t))=(0,0,0,0,0)$. Accordingly, the global asymptotic stability of $E_0$ follows from LaSalle’s invariant principle for delay differential systems. $\square$

Theorem 4.2

Assume that $rr_1>d_2(r_1+d_1)$ holds. If $\gamma _0<0$, then the predator-extinction equilibrium $E_1(x_1^0, x_2^0, 0, 0,0)$ of system (1.3) is globally asymptotically stable.

Proof

By Theorem 3.1, we see that if $\gamma _0<0$, then $E_1$ is locally asymptotically stable. Hence, we only prove that all positive solutions of system (1.3) with initial conditions (1.4) converge to $E_1$. Let $(x_1(t), x_2(t), S(t), I(t),R(t))$ be any positive solution of system (1.3) with initial conditions (1.4). System (1.3) can be rewritten as

$$\begin{aligned} \displaystyle \dot{x}_1(t)= & {} \frac{r}{x_1^0}\left[ -x_2(t)\left( x_1(t)-x_1^0\right) \right. \nonumber \\&\left. +x_1(t)\left( x_2(t)-x_2^0\right) \right] +x_1(t)\left[ -a\left( x_1(t)-x_1^0\right) \right] -a_1x_1(t)S(t),\nonumber \\ \displaystyle \dot{x}_2(t)= & {} \frac{r_1}{x_2^0}\left[ -x_1(t)\left( x_2(t)-x_2^0\right) +x_2(t)\left( x_1(t) -x_1^0\right) \right] ,\nonumber \\ \displaystyle \dot{S}(t)= & {} a_2x_1(t)S(t)-bS^2(t)-d_3S(t)-\beta S(t)I(t),\nonumber \\ \displaystyle \dot{I}(t)= & {} \beta e^{-\mu \tau }S(t-\tau )I(t-\tau ) -(\mu +\,\gamma )I(t),\nonumber \\ \displaystyle \dot{R}(t)= & {} \gamma I(t)-\mu R(t). \end{aligned}$$

(4.2)

Define

$$\begin{aligned} \displaystyle V_{11}(t)= & {} x_1-x_1^0-x_1^0\ln \frac{x_1}{x_1^0}+k_1 \left( x_2-x_2^0-x_2^0\ln \frac{x_2}{x_2^0}\right) +\,\frac{a_1}{a_2}S\\&+\,\frac{a_1}{a_2}e^{\mu \tau }I+\,\frac{a_1}{a_2}e^{\mu \tau }R. \end{aligned}$$

where $k_1=rx_2^0/(r_1x_1^0)$. Calculating the derivative of $V_{11}(t)$ along positive solutions of (4.2), it follows that

$$\begin{aligned} \displaystyle {\dot{V}_{11}(t)}= & {} \displaystyle \frac{x_1(t)-x_1^0}{x_1(t)} \dot{x}_1(t)+k_1\frac{x_2(t)-x_2^0}{x_2(t)}\dot{x}_2(t) +\,\frac{a_1}{a_2}\dot{S}(t)\nonumber \\&+\,\frac{a_1}{a_2}e^{\mu \tau }\dot{I}(t) +\,\frac{a_1}{a_2}e^{\mu \tau }\dot{R}(t)\nonumber \\ \displaystyle= & {} -\,\frac{r}{x_1^0}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^0) -\,\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^0)\right) ^2-a\left( x_1(t)-x_1^0\right) ^2\nonumber \\&\displaystyle -\,\frac{a_1}{a_2}bS^2(t)-\,\frac{a_1}{a_2}\left( d_3-a_2x_1^0\right) S(t) -\,\frac{a_1}{a_2}e^{\mu \tau }\mu I(t)-\,\frac{a_1}{a_2}e^{\mu \tau }\mu R(t)\nonumber \\&\displaystyle -\,\frac{a_1}{a_2}\beta S(t)I(t)+\,\frac{a_1}{a_2}\beta S(t-\tau )I(t-\tau ). \end{aligned}$$

(4.3)

Define

$$\begin{aligned} \displaystyle {V_{1}(t)=V_{11}(t)+\,\frac{a_1}{a_2}\beta \int _{t-\tau }^tS(u)I(u)du}. \end{aligned}$$

By calculation, we have that

$$\begin{aligned} \displaystyle \dot{V}_{1}(t)= & {} \displaystyle -\,\frac{r}{x_1^0} \left( \sqrt{\frac{x_2(t)}{x_1(t)}}\left( x_1(t)-x_1^0\right) -\,\sqrt{\frac{x_1(t)}{x_2(t)}} \left( x_2(t)-x_2^0\right) \right) ^2-a\left( x_1(t)-x_1^0\right) ^2\nonumber \\&\displaystyle -\,\frac{a_1}{a_2}bS^2(t)-\,\frac{a_1}{a_2}e^{\mu \tau }\mu I(t) -\,\frac{a_1}{a_2}e^{\mu \tau }\mu R(t)+a_1\gamma _0S(t). \end{aligned}$$

(4.4)

It follows from (4.4) that if $\gamma _0<0$ holds, then $\dot{V}_1(t)\le 0$. By Theorem 5.3.1 in [5], solutions limit to $\Lambda$, the largest invariant subset of $\{\dot{V}_1(t)=0\}$. Clearly, we see from (4.4) that $\dot{V}_1(t)=0$ if and only if $x_1(t)=x_1^0, x_2(t)=x_2^0, S(t)=0, I(t)=0$ and $R(t)=0$. Hence, the only invariant set $\Lambda =\{(x_1^0, x_2^0, 0, 0, 0)\}$. Using LaSalle’s invariant principle for delay differential systems, the global asymptotic stability of $E_1$ follows. $\square$

Theorem 4.3

Let $\gamma _0>0$ hold. If $\gamma _1<1$, then the disease-free equilibrium $E_2(x_1^+, x_2^+, S^+,$ 0, 0) is globally asymptotically stable.

Proof

By Theorem 3.1, we see that if $\gamma _0>0$ and $\gamma _1<1$ hold, then the equilibrium $E_2$ is locally asymptotically stable. Hence, it suffices to show that all positive solutions of system (1.3) with initial conditions (1.4) converge to $E_2$. We achieve this by constructing a global Lyapunov function. Let $(x_1(t), x_2(t), S(t), I(t), R(t))$ be any positive solution of system (1.3) with initial conditions (1.4). System (1.3) can be rewritten as

$$\begin{aligned} \displaystyle \dot{x}_1(t)= & {} \frac{r}{x_1^+}\left[ -x_2(t)\left( x_1(t)-x_1^+\right) +x_1(t)\left( x_2(t)-x_2^+\right) \right] +x_1(t)\left[ -a\left( x_1(t)-x_1^+\right) \right] \nonumber \\&\displaystyle +\,a_1S^+x_1(t)-a_1x_1(t)S(t),\nonumber \\ \displaystyle \dot{x}_2(t)= & {} \frac{r_1}{x_2^+}\left[ -x_1(t)\left( x_2(t)-x_2^+\right) +x_2(t)\left( x_1(t)-x_1^+\right) \right] ,\nonumber \\ \displaystyle \dot{S}(t)= & {} a_2x_1(t)S(t)-bS^2(t)-d_3S(t)-\,\beta S(t)I(t),\nonumber \\ \displaystyle \dot{I}(t)= & {} \beta e^{-\mu \tau }S(t-\tau )I(t-\tau )-(\mu +\,\gamma )I(t),\nonumber \\ \displaystyle \dot{R}(t)= & {} \gamma I(t)-\mu R(t). \end{aligned}$$

(4.5)

Define

$$\begin{aligned} \displaystyle V_{21}(t)= & {} x_1-x_1^+-x_1^+\ln \frac{x_1}{x_1^+}+ k_2\left( x_2-x_2^+-x_2^+\ln \frac{x_2}{x_2^+}\right) \\&+\frac{a_1}{a_2}\left( S-S^+-S^+\ln \frac{S}{S^+}\right) +\,\frac{a_1}{a_2}e^{\mu \tau }I, \end{aligned}$$

where $k_2=rx_2^+/(r_1x_1^+)$. Calculating the derivative of $V_{21}(t)$ along positive solutions of system (4.5), it follows that

$$\begin{aligned} {\displaystyle \dot{V}_{21}(t)}= & {} \displaystyle {\frac{x_1(t)-x_1^+}{x_1(t)} \dot{x}_1(t)+k_2\frac{x_2(t)-x_2^+}{x_2(t)}\dot{x}_2(t) +\,\frac{a_1(S(t)-S^+)}{a_2S(t)}\dot{S}(t) +\,\frac{a_1}{a_2}e^{\mu \tau }\dot{I}(t)}\nonumber \\ \displaystyle= & {} -\,\frac{r}{x_1^+}\left( \sqrt{\frac{x_2(t)}{x_1(t)}} \left( x_1(t)-x_1^+\right) -\,\sqrt{\frac{x_1(t)}{x_2(t)}}\left( x_2(t)-x_2^+\right) \right) ^2 -a\left( x_1(t)-x_1^+\right) ^2\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}b(S(t)-S^+)^2-\,\frac{a_1}{a_2}\beta S(t)I(t) +\,\frac{a_1}{a_2}\beta S(t-\tau )I(t-\tau )}\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}[e^{\mu \tau }(\mu +\gamma )-\beta S^+]I(t)}. \end{aligned}$$

(4.6)

Define

$$\begin{aligned} \displaystyle {V_{2}(t)=V_{21}(t)+\,\frac{a_1}{a_2}\beta \int _{t-\tau }^t S(u)I(u)du}. \end{aligned}$$

By calculation, we have that

$$\begin{aligned} \displaystyle {\dot{V}_{2}(t)}= & {} \displaystyle {-\,\frac{r}{x_1^+}\left[ \sqrt{\frac{x_2(t)}{x_1(t)}}\left( x_1(t)-x_1^+\right) -\sqrt{ \frac{x_1(t)}{x_2(t)}}\left( x_2(t)-x_2^+\right) \right] ^2-a\left( x_1(t)-x_1^+\right) ^2}\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}b(S(t)-S^+)^2-\,\frac{a_1}{a_2} e^{\mu \tau } (\mu +\gamma )(1-\gamma _1)I(t) }. \end{aligned}$$

(4.7)

It follows from (4.7) that if $\gamma _1<1$ holds true, then $\dot{V}_2(t)\le 0$ with equality if and only if $x_1(t)=x_1^+, x_2(t)=x_2^+, S(t)= S^+, I(t)=0$. Hence, the only invariant set in M is $\Lambda =\{(x_1^+, x_2^+, S^+, 0)\}$.

By the fifth equation of system (1.3), it follows that $\lim _{t\rightarrow +\infty }R(t)=0$. Therefore, the global asymptotic stability of the equilibrium $E_2$ of system (1.3) follows from LaSalle’s invariant principle for delay differential systems. $\square$

Theorem 4.4

Assume that $\gamma _1>1$ holds, then the endemic-coexistence equilibrium $E_*(x_1^*, x_2^*, S^*, I^*, R^*)$ of system (1.3) is globally attractive provided

$$\begin{aligned} (H_3)\;\displaystyle {\underline{S}>\frac{\beta }{b}I^*.} \end{aligned}$$

Here, $\underline{S}$ is the persistency constant for S(t) as defined in Lemma 2.2.

Proof

Let $(x_1(t), x_2(t), S(t), I(t), R(t))$ be any positive solution of system (1.3) with initial conditions (1.4). System (1.3) can be rewritten as

$$\begin{aligned} \displaystyle \dot{x}_1(t)= & {} \frac{r}{x_1^*}\left[ -x_2(t)\left( x_1(t)-x_1^*\right) +x_1(t)\left( x_2(t)-x_2^*\right) \right] +x_1(t)\left[ -a\left( x_1(t)-x_1^*\right) \right] \nonumber \\&+\,\displaystyle {a_1S^*x_1(t)-a_1x_1(t)S(t)},\nonumber \\ \displaystyle \dot{x}_2(t)= & {} \frac{r_1}{x_2^*}\left[ -x_1(t)\left( x_2(t)-x_2^*\right) +x_2(t)\left( x_1(t)-x_1^*\right) \right] ,\nonumber \\ \displaystyle \dot{S}(t)= & {} a_2x_1(t)S(t)-bS^2(t)-d_3S(t)-\beta S(t)I(t),\nonumber \\ \displaystyle \dot{I}(t)= & {} \beta e^{-\mu \tau }S(t-\tau )I(t-\tau )-(\mu +\gamma )I(t),\nonumber \\ \displaystyle \dot{R}(t)= & {} \gamma I(t)-\mu R(t). \end{aligned}$$

(4.8)

Define

$$\begin{aligned} \displaystyle V_{31}(t)= & {} x_1-x_1^*-x_1^*\ln \frac{x_1}{x_1^*} +k_3\left( x_2-x_2^*-x_2^*\ln \frac{x_2}{x_2^*}\right) +\,\frac{a_1}{a_2}\left( S-S^*-S^*\ln \frac{S}{S^*}\right) \\&\displaystyle {+\,\frac{a_1}{a_2}e^{\mu \tau }\left( I-I^*-I^*\ln \frac{I}{I^*}\right) }. \end{aligned}$$

where $k_3=rx_2^*/(r_1x_1^*)$.

Calculating the derivative of $V_{31}(t)$ along positive solutions of system (4.8), it follows that

$$\begin{aligned} \displaystyle {\dot{V}_{31}(t)}= & {} \displaystyle \frac{x_1(t)-x_1^*}{x_1(t)} \dot{x}_1(t)+ k_3\frac{x_2(t)-x_2^*}{x_2(t)}\dot{x}_2(t) +\,\frac{a_1}{a_2}\frac{S(t)-S^*}{S(t)}\dot{S}(t)\nonumber \\&+\,\frac{a_1}{a_2}e^{\mu \tau } \frac{I(t)-I^*}{I(t)}\dot{I}(t)\nonumber \\= & {} \displaystyle {-\,\frac{r}{x_1^*}\left[ \sqrt{\frac{x_2(t)}{x_1(t)}} \left( x_1(t)-x_1^*\right) -\,\sqrt{\frac{x_1(t)}{x_2(t)}}\left( x_2(t) -x_2^*\right) \right] ^2-a\left( x_1(t)-x_1^*\right) ^2}\nonumber \\&\displaystyle +\,\frac{a_1}{a_2}\beta I^*(S(t)-S^*)-\,\frac{a_1}{a_2} b(S(t)-S^*)^2-\,\frac{a_1}{a_2}\beta S(t)I(t)\nonumber \\&+\,\frac{a_1}{a_2}\beta S(t-\tau )I(t-\tau )\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}\beta I^*\frac{S(t-\tau )I(t-\tau )}{I(t)} +\,\frac{a_1}{a_2}\beta S^*I^*.} \end{aligned}$$

(4.9)

Define

$$\begin{aligned} \displaystyle {V_{3}(t)=V_{31}(t)+\,\frac{a_1}{a_2}\beta \int _{t-\tau }^t \left[ S(u)I(u)-S^*I^*-S^*I^*\ln \frac{S(u)I(u)}{S^*I^*}\right] du}. \end{aligned}$$

Direct calculation shows that

$$\begin{aligned} \displaystyle {\dot{V}_{3}(t)}= & {} \displaystyle {-\,\frac{r}{x_1^*}\left[ \sqrt{\frac{x_2(t)}{x_1(t)}}\left( x_1(t)-x_1^*\right) -\,\sqrt{\frac{x_1(t)}{x_2(t)}} \left( x_2(t)-x_2^*\right) \right] ^2-a\left( x_1(t)-x_1^*\right) ^2}\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}\beta S^*I^*\left[ \frac{S(t-\tau )I(t-\tau )}{S^*I(t)}-1-\ln \frac{S(t-\tau )I(t-\tau )}{S^*I(t)}\right] }\nonumber \\&\displaystyle {-\,\frac{a_1}{a_2}\beta S^*I^*\left[ \frac{S^*}{S(t)}-1 -\ln \frac{S^*}{S(t)}\right] -\frac{a_1}{a_2}(S(t)-S^*)^2\left[ b -\,\frac{\beta I^*}{S(t)}\right] }.\nonumber \\ \end{aligned}$$

(4.10)

Note that the function $g(x)=x-1-\ln x$ is always non-negative for any $x>0$, and $g(x)=0$ if and only if $x=1$. Hence, if $S(t)>\frac{\beta }{b}I^*$ for $t\ge T$, we have $\dot{V}_{3}(t)\le 0$ with equality if and only if $x_1(t)=x_1^*, x_2(t)=x_2^*, S(t)=S(t-\tau )=S^*$ and $I(t)=I(t-\tau )$. We now look for the invariant subset $\Lambda$ within the set

$$\begin{aligned} M=\left\{ (x_1, x_2, S, I): x_1(t)=x_1^*, x_2(t)=x_2^*, S(t)=S^*, I(t)=I(t-\tau )\right\} . \end{aligned}$$

Since $S(t)=S^*$ on $\Lambda$ and consequently, from the third equation of system (1.3) we obtain

$$\begin{aligned} \displaystyle {0=\dot{S}(t)=a_2x_1^*S^*-b(S^*)^2-d_3S^*-\beta S^*I(t)}. \end{aligned}$$

(4.11)

This yields $I(t)=I^*$. Hence, the only invariant set in M is $\Lambda =\{(x_1^*, x_2^*, S^*, I^*)\}$.

By the fifth equation of system (1.3), it follows that $\lim _{t\rightarrow +\infty }R(t)=R^*$. Therefore, the global attractiveness of $E_*$ follows from LaSalle invariant principle for delay differential systems. This completes the proof. $\square$

5 Conclusion

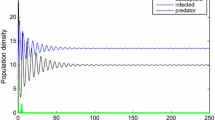
In this paper, we have incorporated the disease for the predator and stage structure for the prey into an eco-epidemiology model. By analyzing the corresponding characteristic equation, the local stability of each of feasible equilibria has been established. It has been shown that, under some conditions, the time delay due to gestation of the predators may destabilize the endemic-coexistence equilibrium of system (1.3) and cause the population to fluctuate. From Theorem 3.2, we see that there is a threshold $\tau _k^0$ for the time delay such that below it the endemic-coexistence equilibrium is stable, but if the delay is greater than the threshold, sustained oscillations arise. By means of Lyapunov functionals and LaSalle’s invariant principle, sufficient conditions were obtained for the global stability of the endemic-coexistence equilibrium, the disease-free equilibrium, the predator-extinction equilibrium and the trivial equilibrium of system (1.2).