1 Introduction

The hibernation of the plants is that the plants stop growing, the bud of a plant or other organ growth came to a halt, only to maintain the weak life period. It is formed during the development of the system, and is a kind of adversity adaptation characteristics. One of the two hibernation state is forced dormancy: due to unfavorable environmental conditions (temperature, drought stress and) temporarily stop growing phenomenon, stress elimination recovery growth. By hibernating, animals can reduce their energy requirements by at least ninety percent and survive for many months while slowly catabolizing body lipid reserves [1]. Hibernation constitutes an effective strategy of animals in order to correspond survive cold environments and limited availability of food [2].

The chemostat is a basic piece of laboratory apparatus. The advantages that certain of the biological parameters assumed to influence the outcomes can be controlled by the experimenters. The chemostat plays an important role in bioprocessing, such as ecology, microbiology, chemical engineering, etc. Smith and Waltman had made discussion about the chemostat model in [3]. The models contain discrete time delays which account for time which laps between uptaked of nutrient and the assimilation of nutrient into viable biomass. Many authors [4–9] discussed various aspects of models with discrete time delay. Especially, Ellermeyer, Hendrix, and Ghoochan [10] did a theoretical and empirical investigation of delayed growth response in the continuous culture of bacteria. Delays occur naturally in biological system by two obvious sources of delays: delays due to the cell cycle; and delays due to the possibility the organism stores the nutrient. Delays appear in a chemostat model in Bush and Cook [11]. They have investigated a model of growth of one organism in the chemostat with a delay in the intrinsic growth rate of the microorganism but with no delay in the substrate equation. Bulert et al. [12] studied a chemostat model with periodic washout rate. Hale and Somolinas [13], Hsu et al. [14], Wolkowicz and Zhao [15] investigated competition in chemostat. Many researchers indicated that it was important to consider models with periodic perturbations, since these models may be quite naturally exposed in many real world phenomena, for instance, food supply, mating habits, cross flooding in rainstorm season. In fact, the perturbations such as cross flooding in rainstorm which are not suitable to be considered with continuity. These perturbations bring sudden changes to the system. Systems with sudden perturbations are involving an impulsive differential equations which have been studied intensively and systematically in [16, 17]. There are few papers [18–22] research the chemostat model with impulsive perturbations on nutrients.

In chemostat’s simplest form, the system approximates conditions for plankton growth in lakes, where the limiting nutrients such as silica and phosphate are supplied from streams draining the watershed. In the lakes, the plankton population movements are subject to many factors, such as currents and turbulent lateral diffusion ( cf. Levin and Segel [23], Mimura [24], Okubo [25], Freedman and Ruan [26], Wang and Wolkowicz [27]), Ruan [28] proposed a diffusive plankton-nutrient interaction model with delayed nutrient recycling and delayed growth response and studied Turing instability and the existence of travelling wave solutions. However, they did not investigate a chemostat model with hibernation and impulsive diffusion on nutrients.

The organizations of the paper are as following. In Sect. 2, we introduce a plankton-nutrient chemostat model with employing impulsive switched systems. In Sect. 3, we present some lemmas. Our main results are stated and proven in Sect. 4. Finally, a brief discussion in Sect. 5.

2 The model

In this section, a plankton-nutrient chemostat model with employing impulsive switched systems is presented:

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{ds_{1}(t)}{dt}=D(s_{1}^{0}-s_{1}(t)), \\ \displaystyle \frac{ds_{2}(t)}{dt}=-Ds_{2}(t)-\frac{m}{k_{1}} \times \frac{s_{2}(t)x(t)}{k+s_{2}(t)},\\ \displaystyle \frac{dx(t)}{dt}=-Dx(t)+\frac{ms_{2}(t)x(t)}{k+s_{2}(t)}, \\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{1}(t)=-ds_{1}(t),\\ \displaystyle \triangle s_{2}(t)=ds_{1}(t) ,\\ \displaystyle \triangle x(t)= 0,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{ds_{1}(t)}{dt}=D(s_{1}^{0}-s_{1}(t)), \\ \displaystyle \frac{ds_{2}(t)}{dt}=-Ds_{2}(t),\\ \displaystyle \frac{dx(t)}{dt}=-d_{1}x(t), \\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{1}(t)=\mu _{1},\\ \displaystyle \triangle s_{2}(t)=\mu _{2},\\ \displaystyle \triangle x(t)= 0,\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(2.1)

It is assumed that System (2.1) is composed of river and reservoir connected by impulsive diffusion. No nutrient input is assumed in the reservoir. Nutrient input is assumed in the river from upper stream. \(s_{1}(t)\) denotes the concentration of the nutrient in the river at time t. \(s_{2}(t)\) denotes the concentration of the nutrient in reservoir at time t. x(t) denotes the concentration of the the plankton in the reservoir at time t. \(s_{1}^{0}\) denotes the input nutrient concentration in the river. D denotes the input rate from the lakes containing the substrate and the wash-out rate of substrate and plankton by products from the reservoir. \(m>0\) is the uptake constants of the nutrient. \(k_{1}>0\) is the yield of plankton per unit mass of nutrient. \( 0 < d< 1\) is diffusive rate from the river to the reservoir unilaterally. \(d_{1}\) is the death rate of the plankton in the intervals of hibernation. It is assumed here that the net exchange from the river \((s_{1}(t))\) to the reservoir \((s_{2}(t))\) is proportional to the difference \(s_{1}(t)-s_{2}(t)\) of concentration of the nutrient. The Michaelis-Menten function \(\frac{s_{2}(t)}{k+s_{2}(t)}\) indicates the consumption rate of nutrient by the plankton, where \(k > 0\) is the half-saturation constant or Michaelis-Menten constant. The impulsive diffusion occurs every \(\tau \) period (\(\tau >0\)), the system evolves from its initial state without being further affected by diffusion until the next pulse appears. \(\triangle s_{i} = s_{i}((n+l)\tau ^{+})-s_{i}((n+l)\tau )(i=1,2),\) and \(s_{1}((n+l)\tau ^{+})\) represents the concentration of the nutrient in the the river immediately after the nth diffusion pulse at time \(t = n\tau \), \(s_{2}((n+l)\tau ^{+})\) represents the concentration of the nutrient in the the reservoir immediately after the nth diffusion pulse at time \(t = n\tau \), while \(s_{1}((n+l)\tau )\) represents the concentration of the nutrient in the river before the nth diffusion pulse at time t, \(s_{2}((n+l)\tau )\) represents the concentration of the nutrient in the reservoir before the nth diffusion pulse at time \(t = (n+l)\tau ,n = 0,1,2,\ldots \). There are two intervals are separated in the period of System (2.1) for the effect climate, that is normal seasons and draught seasons. The plankton is regular growing in the normal seasons, and the plankton is in hibernation in the drought seasons. \(t=(n+l)\tau \) are moments of torrential rain, the nutrient is diffusing between rivers and reservoir in moments of torrential rain. \(t=(n+1)\tau \) are moments of rainy season, the amount of nutrients \(\mu _{1}\) and \(\mu _{2}\) are coming from soil all around in moments of rainy season. The purpose of this paper is to prove that the System (2.1) has a plankton-extinction periodic solution, further, it is globally asymptotically stable, and also prove System (2.1) is permanent.

3 The lemma

The solution of System (2.1), denote by \(X(t)=(s_{1}(t),s_{2}(t),x(t))^{T}\), is a piecewise continuous function X:\(R_{+}\rightarrow R_{+}^{3}\). X(t) is continuous on \((n\tau ,(n+l)\tau ]\) and \(((n+l)\tau ,(n+1)\tau ](n\in Z_{+})\). \(X((n+l)\tau ^{+})=\lim _{t\rightarrow (n+l)\tau ^{+} }X(t)\) and \(X((n+1)\tau ^{+})=\lim _{t\rightarrow (n+1)\tau ^{+} }X(t)\) exist. Obviously the global existence and uniqueness of solutions of (2.1) is guaranteed by the smoothness properties of f, which denotes the mapping defined by right-side of System (2.1) [16].

According to the biological meanings, it is assumed that \(s_{1}(t)\ge 0, s_{2}(t)\ge 0\) and \(x(t)\ge 0\). Now, we will show that all solutions of System (2.1) are uniformly ultimately bounded.

Lemma 3.1

There exists a constant \(M>0\) such that \(s_{1}(t)\le M, s_{2}(t)\le M, x(t)\le M,\) for each solution \((s_{1}(t), s_{2}(t), x(t))\) of (2.1) with all t large enough.

Proof

Define \(V(t)=s_{1}(t)+ s_{2}(t)+\frac{1}{k_{1}} x(t)\) and take \(\lambda =\min \{D,d_{1}\}.\) When \(t\in [n\tau , (n+l)\tau )\), we have

$$\begin{aligned} \frac{dV(t)}{dt}+ \lambda V(t)=D s_{1}^{0}. \end{aligned}$$

When \(t\in [(n+l)\tau , (n+1)\tau ),\) we have

$$\begin{aligned} \frac{dV(t)}{dt}+ \lambda V(t)\le D s_{1}^{0}. \end{aligned}$$

When \(t=(n+l)\tau ,\) we also have

$$\begin{aligned} V(n\tau ^{+})= V(n\tau ). \end{aligned}$$

When \(t=(n+1)\tau ,\) we also have

$$\begin{aligned} V(n\tau ^{+})= V(n\tau )+\mu _{1}+\mu _{2}. \end{aligned}$$

By Lemma 2.3. ( it can been seen in [16]), for \(t\in (n\tau ,(n+1)\tau ]\) , we obtain

$$\begin{aligned}&V(t)\le V(0)\exp (-\lambda t)+\frac{D s_{1}^{0}}{\lambda }(1-e^{-\lambda t}) +(\mu _{1}+\mu _{2})\frac{e^{-\lambda (t-\tau )}}{1-e^{\lambda \tau }}+(\mu _{1}+\mu _{2})\frac{e^{\lambda \tau }}{e^{\lambda \tau }-1}\\&\quad \rightarrow \frac{Ds_{1}^{0}}{\lambda }+(\mu _{1}+\mu _{2})\frac{e^{\lambda \tau }}{e^{\lambda \tau }-1}, \quad as \quad t\rightarrow \infty . \end{aligned}$$

So V(t) is uniformly ultimately bounded. Hence, by the definition of V(t), there exists a constant \(M>0\) such that \(s_{1}(t)\le M, s_{2}(t)\le M, x(t)\le k_{1} M\) for all t large enough. The proof is complete. \(\square \)

If \(x(t)=0\), the subsystem of (2.1) is written as:

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{ds_{1}(t)}{dt}=D(s_{1}^{0}-s_{1}(t)), \\ \displaystyle \frac{ds_{2}(t)}{dt}=-Ds_{2}(t),\\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{1}(t)=-ds_{1}(t),\\ \displaystyle \triangle s_{2}(t)=ds_{1}(t) ,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{ds_{1}(t)}{dt}=D(s_{1}^{0}-s_{1}(t)), \\ \displaystyle \frac{ds_{2}(t)}{dt}=-Ds_{2}(t),\\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{1}(t)=\mu _{1},\\ \displaystyle \triangle s_{2}(t)=\mu _{2},\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(3.1)

Integrating and solving the first two equations of System (3.1) between pulses, we have

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle s_{1}(t)= \left\{ \begin{array}{llc} \displaystyle s^{0}_{1}-[s^{0}_{1}-s_{1}(n\tau ^{+})]e^{-D(t-n\tau )}, \\ \displaystyle s_{2}(n\tau ^{+})e^{-D(t-n\tau )}, \end{array} \right\} n\tau < t\le (n+l)\tau .\\ \displaystyle s_{2}(t)= \left\{ \begin{array}{llc} \displaystyle s^{0}_{1}-[s^{0}_{1}-s_{1}((n+l)\tau ^{+})]e^{-D(t-(n+l)\tau )},\\ \displaystyle s_{2}((n+l)\tau ^{+})e^{-D(t-(n+l)\tau )}, \\ \end{array} \right\} (n+l)\tau < t \le (n+1)\tau . \end{array} \right. \end{aligned}$$
(3.2)

Let \(A=(1-e^{-D(1-l)\tau })+(1-d)e^{-D(1-l)\tau }-(1-d)e^{-D\tau })s^{0}_{1}+\mu _{1},B=ds^{0}_{1}(e^{-D(1-l)\tau }-e^{-D\tau })+\mu _{2}.\) Considering the third,fourth,seventh and eighth equations of System (3.1), we have the stroboscopic map of System (3.1) as following:

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle s_{1}((n+1)\tau ^{+})=(1-d)e^{-D\tau }s_{1}(n\tau ^{+})+A,\\ \displaystyle s_{2}((n+1)\tau ^{+})=de^{-D\tau }s_{1}(n\tau ^{+})+e^{-D\tau }s_{2}(n\tau ^{+})+B.\\ \end{array} \right. \end{aligned}$$
(3.3)

Equation (3.3) are difference equations. They describe the the concentration of the nutrients diffusing from river to reservoir at a pulse in terms of values at the previous pulse. The dynamical behaviors of System (3.3) with Eq. (3.2) determine the dynamical behaviors of System (3.1). So we will devote to investigate System (3.3).

From System (3.3), we can easily have a unique fixed point of System (3.3) as following

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle s_{1}^{*}=\frac{A}{1-(1-d)e^{-D\tau }}>0,\\ \displaystyle s_{2}^{*}=\frac{B[1-(1-d)e^{-D\tau }]+Ade^{-D\tau }}{(1-e^{-D\tau })[1-(1-d)e^{-D\tau }]}>0.\\ \end{array} \right. \end{aligned}$$
(3.4)

To write System (3.3) as a map, we define the map \(F: R^{2}_{+}\rightarrow R^{2}_{+}\):

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle F_{1}(x)=(1-d)e^{-D\tau }x_{1}+A,\\ \displaystyle F_{2}(x)=de^{-D\tau }x_{1}+e^{-D\tau }x_{2}+B.\\ \end{array} \right. \end{aligned}$$
(3.5)

F(x) is the map evaluated at the point \(x=(x_{1},x_{2})\in R^{2}_{+}\). Consequently, in system (3.2), \(F^{n}\) describes the concentration of the nutrients in the time \(n\tau \).

Then we have the following lemmas:

Lemma 3.2

In System (3.3), every point has a bounded orbit.

Proof

For each \(i=1,2\) and each point \(x\in R^{2}_{+}\), we need to show each of the sequence \(\{F^{n}_{i}(x)\}\) is bounded.

From (3.5), if \(x_{1}<x_{2}\), we obtain that

$$\begin{aligned} \max \{F_{1}(x), F_{2}(x)\}\le x_{2}. \end{aligned}$$

On the other hand, if \(x_{1}>x_{2}\), we also obtain that

$$\begin{aligned} \max \{F_{1}(x), F_{2}(x)\}\le x_{1}. \end{aligned}$$

Consequently,

$$\begin{aligned} \max \{F_{1}(x), F_{2}(x)\}\le \max \{x_{1}, x_{2}\}. \end{aligned}$$

Hence, the sequence\(\{F^{n}_{i}(x)\}\) is bounded, that is, for System (3.3), every point has a bounded orbit. \(\square \)

Lemma 3.3

[29] Let \(T: R^{n}_{+}\rightarrow R^{n}_{+}\) be continuous, \(C^{1}\) in \(int(R^{n}_{+})\), and suppose DT(0) exists with \( \lim _{x\rightarrow 0,x>0}DT(x)=DT(0)\). In addition, assume

  1. (a)

    \(DT(x)>0\), if \(x>0\);

  2. (b)

    \(DT(y)<DT(x)\), if \(0<x<y\);

If \(T(0)=0\), Let \(\lambda =\rho (DT(0))\). If \(\lambda \le 1\), for every \(x>0\), \(T^{n}(x)\rightarrow 0\) as \(n\rightarrow \infty \); if \(\lambda \ge 1\), then either \(T^{n}(x)\rightarrow 0\) as \(n\rightarrow \infty \) for every \(x>0\) or there exists a unique nonzero fixed point q of T. In the latter case, \(q>0\) and for every \(x>0\), \(T^{n}(x)\rightarrow q\) as \(n\rightarrow \infty \).

If \(T(0)\ne 0\), then either \(T^{n}(x)\rightarrow 0\) as \(n\rightarrow \infty \) for every \(x>0\) or there exists a unique fixed point q of T. In the latter case, \(q>0\) and for every \(x>0\), \(T^{n}(x)\rightarrow q\) as \(n\rightarrow \infty \).

According to Lemmas 3.2 and 3.3, and doing similarly to Lemma 4.1 [21] and Theorem 4.1 [21], one can easily obtain Lemma 3.4 as the following:

Lemma 3.4

For every point \((x_{1},x_{2})>(0,0)\) of System (3.5), then have

$$\begin{aligned} F^{n}(x)\rightarrow (s_{1}^{*},s_{2}^{*}),\quad as \quad n\rightarrow \infty . \end{aligned}$$

Remark 3.5

Lemma 3.4 implies that the fixed point \((s_{1}^{*},s_{2}^{*})\) of F is globally stable. So all trajectories of (3.1) approach the positive periodic solution \((\widetilde{s_{1}(t)},\widetilde{s_{2}(t)})\) with period \(\tau \), where

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{s_{1}(t)}= \left\{ \begin{array}{llc} \displaystyle s^{0}_{1}-\left[ s^{0}_{1}-s^{*}_{1}\right] e^{-D(t-n\tau )}, n\tau < t\le (n+l)\tau , \\ \displaystyle s^{0}_{1}-\left[ s^{0}_{1}-(1-d)\left( s^{0}_{1}-\left( s^{0}_{1}-s^{*}_{1}\right) e^{-Dl\tau }\right) \right] e^{-D(t-(n+l)\tau )}, (n+l)\tau < t \le (n+1)\tau ,\\ \end{array} \right. \\ \displaystyle \widetilde{s_{2}(t)}= \left\{ \begin{array}{llc} \displaystyle s^{*}_{2}e^{-D(t-n\tau )}, n\tau < t\le (n+l)\tau .\\ \displaystyle \left[ s^{*}_{2}e^{-Dl\tau }+d\left( s^{0}_{1}-\left( s^{0}_{1}-s^{*}_{1}\right) e^{-Dl\tau }\right) \right] e^{-D(t-(n+l)\tau )}, (n+l)\tau < t \le (n+1)\tau \\ \end{array} \right. \end{array} \right. \end{aligned}$$
(3.6)

4 Dynamical behaviors of (2.1)

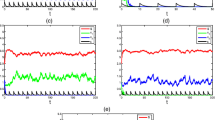
From the above discussion, we know that there exists a plankton-extinction boundary periodic solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) of System (2.1). In this section, we will prove that the plankton-extinction boundary periodic solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) of System (2.1) is globally asymptotically stable.

Theorem 4.1

If

$$\begin{aligned} (1+d)e^{-D\tau }<1, \end{aligned}$$

and

$$\begin{aligned} \frac{m}{D}\ln \frac{k+s_{2}^{*}}{k+s_{2}^{*}e^{-Dl\tau }}<Dl\tau +d_{1}(1-l)\tau , \end{aligned}$$

hold, the plankton-extinction periodic solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) of System (2.1) is globally asymptotically stable.

Proof

First, we prove the local stability of the plankton-extinction solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) of (2.1). Defining \(x_{1}(t)=s_{1}(t)-\widetilde{s_{1}(t)},x_{2}(t)=s_{2}(t)-\widetilde{s_{2}(t)}, x_{3}(t)=x(t),\) then we have the following linearly similar system for system (2.1) which is concerning one periodic solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) to

$$\begin{aligned} \left( \begin{array}{c} \frac{ds_{1}(t)}{dt} \\ \frac{ds_{2}(t)}{dt}\\ \frac{dx(t)}{dt}\\ \end{array} \right) = \left( \begin{array}{ccc} -D &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -D &{}\quad - \frac{m}{k_{1}} \times \frac{\widetilde{s_{2}(t)}}{k+\widetilde{s_{2}(t)}} \\ 0 &{}\quad 0 &{}\quad -D+ \frac{m\widetilde{s_{2}(t)}}{k+\widetilde{s_{2}(t)}}\\ \end{array} \right) \left( \begin{array}{c} s_{1}(t) \\ s_{2}(t)\\ x(t)\\ \end{array} \right) , \quad t \in (n\tau ,(n+l)\tau ], \end{aligned}$$

and

$$\begin{aligned} \left( \begin{array}{c} \frac{ds_{1}(t)}{dt} \\ \frac{ds_{2}(t)}{dt}\\ \frac{dx(t)}{dt}\\ \end{array} \right) = \left( \begin{array}{ccc} -D &{}\quad 0 &{}\quad 0\\ 0&{}\quad -D &{}\quad 0\\ 0&{}\quad 0 &{}\quad -d_{1}\\ \end{array} \right) \left( \begin{array}{c} \frac{ds_{1}(t)}{dt} \\ \frac{ds_{2}(t)}{dt}\\ \frac{dx(t)}{dt}\\ \end{array} \right) , \quad t \in (n\tau ,(n+l)\tau ]. \end{aligned}$$

It is easy to to obtain the fundamental solution matrix

$$\begin{aligned} \Phi (t)=\left( \begin{array}{ccc} \exp (-Dt) &{}\quad *&{}\quad *_{1} \\ 0 &{}\quad \exp (-Dt)&{}\quad *_{2}\\ 0 &{}\quad 0&{}\quad \exp (\int ^{t}_{0}(-D+ \frac{m\widetilde{s_{2}(s)}}{k+\widetilde{s_{2}(s)}})ds)\\ \end{array} \right) , t \in (n\tau ,(n+l)\tau ]. \end{aligned}$$

There is no need to calculate the exact form of \(*,*_{1}\) and \(*_{2}\) as they are not required in the analysis that follows, and

$$\begin{aligned} \Phi (t)=\left( \begin{array}{ccc} \exp (-Dt) &{}\quad 0 &{}\quad 0 \\ 0&{}\quad \exp (-Dt))&{}\quad 0\\ 0&{}\quad 0&{}\quad \exp (-d_{1}t))\\ \end{array} \right) , \quad t \in ((n+l)\tau ,(n+1)\tau ]. \end{aligned}$$

The linearization of the fourth, fifth and sixth equations of (2.1) is

$$\begin{aligned} \left( \begin{array}{c} s_{1}((n+l)\tau ^{+})\\ s_{2}((n+l)\tau ^{+})\\ x((n+l)\tau ^{+})\\ \end{array} \right) = \left( \begin{array}{ccc} 1-d &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1+d &{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} \right) \left( \begin{array}{c} s_{1}((n+l)\tau )\\ s_{2}((n+l)\tau \\ x((n+l)\tau )\\ \end{array} \right) , \quad t \in (n\tau ,(n+l)\tau ], \end{aligned}$$

and the linearization of the tenth,eleventh and twelfth equations of (2.1) is

$$\begin{aligned} \left( \begin{array}{c} s_{1}((n+1)\tau ^{+})\\ s_{2}((n+1)\tau ^{+})\\ x((n+1)\tau ^{+})\\ \end{array} \right) = \left( \begin{array}{ccc} 1&{}\quad 0 &{}\quad 0\\ 0&{}\quad 1 &{}\quad 0\\ 0&{}\quad 0 &{}\quad 1\\ \end{array} \right) \left( \begin{array}{c} s_{1}((n+1)\tau )\\ s_{2}((n+1)\tau )\\ x((n+1)\tau )\\ \end{array} \right) , \quad t\in ((n+l)\tau ,(n+1)\tau ]. \end{aligned}$$

The stability of the periodic solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) is determined by the eigenvalues of

$$\begin{aligned} M=\left( \begin{array}{ccc} 1-d &{}\quad 0 &{}\quad 0\\ 0&{}\quad 1+d &{}\quad 0\\ 0&{}\quad 0 &{}\quad 1\\ \end{array} \right) \left( \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0\\ 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 1\\ \end{array} \right) \Phi (\tau ), \end{aligned}$$

where are

$$\begin{aligned} \lambda _{1}=(1-d)e^{-D\tau }<1, \end{aligned}$$

and

$$\begin{aligned} \lambda _{2}=(1+d)e^{-D\tau }, \end{aligned}$$

and

$$\begin{aligned} \lambda _{3}=e^{\int ^{l\tau }_{0}(-D+\frac{m \widetilde{s_{2}(s)}}{k+\widetilde{s_{2}(s)}})ds-d_{1}(1-l)\tau }. \end{aligned}$$

According to the Floquet theory [21], if \(\mid \lambda _{2}\mid <1\) and \(\mid \lambda _{3}\mid <1\), i.e.

$$\begin{aligned} (1+d)e^{-D\tau }<1, \end{aligned}$$

and

$$\begin{aligned} \frac{m}{D}\ln \frac{k+s_{2}^{*}}{k+s_{2}^{*}e^{-Dl\tau }}<Dl\tau +d_{1}(1-l)\tau , \end{aligned}$$

hold, then \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)},0)\) is locally stable,where \(x^{*}\) is defined as (3.4).

In the following, we will prove the global attraction, choose a \(\varepsilon >0\) such that

$$\begin{aligned} \rho =e^{\int ^{l\tau }_{0}[-D+\frac{m(\widetilde{s_{2}(s)}+\varepsilon )}{k+(\widetilde{s_{2}(s)}+\varepsilon )}]ds -d_{1}(1-l)\tau }<1 \end{aligned}$$

From the second equation of (2.1),  we know that

$$\begin{aligned} \frac{ds_{2}(t)}{dt}\le -Ds_{2}(t). \end{aligned}$$

We consider the comparison impulsive differential equation

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{ds_{11}(t)}{dt}=D(s_{1}^{0}-s_{11}(t)), \\ \displaystyle \frac{ds_{21}(t)}{dt}=-Ds_{21}(t),\\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{11}(t)=-ds_{11}(t),\\ \displaystyle \triangle s_{21}(t)=ds_{11}(t) ,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{ds_{11}(t)}{dt}=D(s_{1}^{0}-s_{11}(t)), \\ \displaystyle \frac{ds_{21}(t)}{dt}=-Ds_{21}(t),\\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{11}(t)=\mu _{1},\\ \displaystyle \triangle s_{21}(t)=\mu _{2},\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(4.1)

From Remark 3.5. and comparison theorem of impulsive equation [21], we have \(s_{1}(t)\le s_{11}(t),s_{2}(t)\le s_{21}(t)\) and \(s_{11}(t)\rightarrow \widetilde{s_{1}(t)},s_{21}(t)\rightarrow \widetilde{s_{2}(t)}\) as \(t\rightarrow \infty \). Then

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle s_{2}(t)\le s_{21}(t)\le \widetilde{s_{2}(t)}+\varepsilon ,\\ \end{array} \right. \end{aligned}$$
(4.2)

for all t large enough. For convenience, we assume (4.2) holds for all \(t\ge 0.\) From (2.1) and (4.2), we get

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \frac{dx(t)}{dt}\le -Dx(t)+\frac{m \widetilde{s_{2}(t)}}{k+\widetilde{s_{2}(t)}}x(t),t\in [n\tau ,(n+l)\tau ),\\ \displaystyle \frac{dx(t)}{dt}= -d_{1}x(t),t\in [(n+l)\tau ,(n+1)\tau ).\\ \end{array} \right. \end{aligned}$$
(4.3)

So

$$\begin{aligned} x((n+1)\tau )\le x(n\tau ^{+})e^{\int ^{(n+l)\tau }_{n\tau }(-D+\frac{m \widetilde{s_{2}(s)}}{k+\widetilde{s_{2}(s)}})ds -d_{1}(1-l)\tau }. \end{aligned}$$

Hence \(x(n\tau )\le x(0^{+})\rho ^{n},\) and \(x(n\tau )\rightarrow 0\) as \(n\rightarrow \infty .\) Therefore \(x(t)\rightarrow 0\) as \(t\rightarrow \infty \).

In the next step, we prove that \(s_{1}(t)\rightarrow \widetilde{s_{1}(t)}, s_{2}(t)\rightarrow \widetilde{s_{2}(t)}\) as \(t\rightarrow \infty .\) For \(\varepsilon >0\) is small enough, there must exist a \(t_{0}>0\) such that \(0<x(t)<\varepsilon \) for all \(t\ge t_{0}.\) Without loss of generality, we assume that \(0<x(t)<\varepsilon \) for all \(t\ge {0}\), then we have

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle -(D+\frac{m\varepsilon }{k_{1}k})s_{2}(t)\le \frac{ds_{2}(t)}{dt}\le -Ds_{2}(t),\\ \end{array} \right. \end{aligned}$$
(4.4)

and \(z_{11}(t)\le s_{1}(t)\le z_{12}(t)\), \(z_{21}(t)\le s_{2}(t)\le z_{22}(t)\) and \(z_{11}(t)\rightarrow \widetilde{z_{11}(t)}\), \(z_{21}(t)\rightarrow \widetilde{z_{21}(t)}\) as \(t\rightarrow \infty \), \(z_{12}(t)\rightarrow \widetilde{s_{1}(t)}\), \(z_{22}(t)\rightarrow \widetilde{s_{2}(t)}\) as \(t\rightarrow \infty ,\) while \((z_{11}(t),z_{12}(t))\) and \((z_{21}(t),z_{22}(t))\) are the solutions of

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dz_{11}(t)}{dt}=D(s_{1}^{0}-z_{11}(t)), \\ \displaystyle \frac{dz_{21}(t)}{dt}=-(D+\frac{m\varepsilon }{k_{1}k})z_{21}(t),\\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle z_{11}(t)=-dz_{11}(t),\\ \displaystyle \triangle z_{21}(t)=dz_{11}(t) ,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{dz_{11}(t)}{dt}=D(s_{1}^{0}-z_{11}(t)), \\ \displaystyle \frac{dz_{21}(t)}{dt}=-Dz_{21}(t),\\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle z_{11}(t)=\mu _{1},\\ \displaystyle \triangle z_{21}(t)=\mu _{2},\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(4.5)

and

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dz_{12}(t)}{dt}=D(s_{1}^{0}-z_{12}(t)), \\ \displaystyle \frac{dz_{22}(t)}{dt}=-Dz_{22}(t),\\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle z_{12}(t)=-dz_{12}(t),\\ \displaystyle \triangle z_{22}(t)=dz_{12}(t) ,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{dz_{12}(t)}{dt}=D(s_{1}^{0}-z_{12}(t)), \\ \displaystyle \frac{dz_{22}(t)}{dt}=-Dz_{22}(t),\\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle z_{12}(t)=\mu _{1},\\ \displaystyle \triangle z_{22}(t)=\mu _{2},\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(4.6)

where \((\widetilde{z_{11}(t)},\widetilde{z_{12}(t)})\) are defined as

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{z_{11}(t)}= \left\{ \begin{array}{llc} \displaystyle s^{0}_{1}-\left[ s^{0}_{1}-z^{*}_{11}\right] e^{-D(t-n\tau )}, n\tau < t\le (n+l)\tau , \\ \displaystyle s^{0}_{1}-\left[ s^{0}_{1}-(1-d)\left( s^{0}_{1}-(s^{0}_{1}-z^{*}_{11})e^{-Dl\tau }\right) \right] e^{-D(t-(n+l)\tau )}, (n+l)\tau < t \le (n+1)\tau ,\\ \end{array} \right. \\ \displaystyle \widetilde{z_{12}(t)}= \left\{ \begin{array}{llc} \displaystyle z^{*}_{12}e^{-(D+\frac{m\varepsilon }{k_{1}k})(t-n\tau )}, n\tau < t\le (n+l)\tau .\\ \displaystyle \left[ z^{*}_{12}e^{-(D+\frac{m\varepsilon }{k_{1}k})l\tau }+d\left( s^{0}_{1}-(s^{0}_{1}-s^{*}_{1})e^{-Dl\tau }\right) \right] e^{-D(t-(n+l)\tau )}, (n+l)\tau < t \le (n+1)\tau \\ \end{array} \right. \end{array} \right. \end{aligned}$$
(4.7)

with

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle z_{11}^{*}=\frac{A_{1}}{1-(1-d)e^{-D\tau }}>0,\\ \displaystyle z_{12}^{*}=\frac{B_{1}[1-(1-d)e^{-D\tau }]+A_{1}de^{-(D+\frac{m\varepsilon }{k_{1}k})\tau }}{(1-e^{-(D+\frac{m\varepsilon }{k_{1}k})\tau })[1-(1-d)e^{-D)\tau }]}>0.\\ \end{array} \right. \end{aligned}$$
(4.8)

and \(A_{1}=(1-e^{-(D+\frac{m\varepsilon }{k_{1}k})(1-l)\tau })+(1-d)e^{-D(1-l)\tau }-(1-d)e^{-D\tau })s^{0}_{1}+\mu _{1},B_{1}=ds^{0}_{1}(e^{-D(1-l)\tau }-e^{-(D+\frac{m\varepsilon }{k_{1}k})\tau })+\mu _{2}.\)

Therefore, for any \(\varepsilon _{1}>0\). there exists a \(t_{1}, t>t_{1}\) such that

$$\begin{aligned} \widetilde{z_{11}(t)}-\varepsilon _{1}<s_{1}(t)<\widetilde{s_{1}(t)}+\varepsilon _{1}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{z_{21}(t)}-\varepsilon _{1}<s_{1}(t)<\widetilde{s_{2}(t)}+\varepsilon _{1}. \end{aligned}$$

Let \(\varepsilon \rightarrow 0\), so we have

$$\begin{aligned} \widetilde{s_{1}(t)}-\varepsilon _{1}<s_{1}(t)<\widetilde{s_{1}(t)}+\varepsilon _{1}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{s_{2}(t)}-\varepsilon _{1}<s_{2}(t)<\widetilde{s_{2}(t)}+\varepsilon _{1}, \end{aligned}$$

for t large enough, which implies \(s_{1}(t)\rightarrow \widetilde{s_{1}(t)}\) and \(s_{2}(t)\rightarrow \widetilde{s_{2}(t)}\) as \(t\rightarrow \infty \). This completes the proof. \(\square \)

Definition 4.2

System (2.1) is said to be permanent, if there are constants \(m,M >0 \) (independent of initial value) and a finite time\(T_{0}\) such that for all solutions \((s_{1}(t),s_{2}(t), x(t))\) with all initial values \(s_{1}(0^{+})>0, s_{2}(0^{+})>0,x(0^{+})>0\), \(m\le s_{1}(t)\le M,m\le s_{2}(t)\le M,\) and \(m\le x(t)\le M\) hold for all \(t\ge T_{0}\). Here \(T_{0}\) may depend on the initial values \((s_{1}(0^{+}),s_{2}(0^{+}), x(0^{+})).\)

Theorem 4.3

Let \((s_{1}(t),s_{2}(t),x(t))\) be any solution of system (2.1), if

$$\begin{aligned} \frac{m}{D}\ln \frac{k+s_{2}^{*}}{k+s_{2}^{*}e^{-Dl\tau }}>Dl\tau +d_{1}(1-l)\tau , \end{aligned}$$

hold, system (2.1) is permanent,where \(s_{2}^{*}\) is defined as (3.4).

Proof

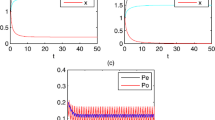
Assume \((s_{1}(t), s_{2}(t), x(t))\) is a solution of system (2.1) with \(s_{1}(0)>0,s_{2}(0)>0, x(0)>0\). By lemma 3.1., we have proved there exists a constant \(M >0\) such that \(s_{1}(t)\le M,s_{2}(t)\le M, x(t)\le M\) for t large enough, we may assume \(s_{1}(t)\le M,s_{2}(t)\le M, x(t)\le M\) for \(t\ge 0\). From theorem 4.1.,  we know \(s_{1}(t)>\widetilde{s_{1}(t)}-\varepsilon _{2}\) and \(s_{2}(t)>\widetilde{s_{2}(t)}-\varepsilon _{2}\) for all t large enough and \(\varepsilon _{2}> 0\), so \(s_{1}(t)\ge s^{0}_{1}-[s^{0}_{1}-s^{*}_{1}]e^{-Dl\tau } +s^{0}_{1}-[s^{0}_{1}-(1-d)(s^{0}_{1}-(s^{0}_{1}-s^{*}_{1})e^{-Dl\tau })]e^{-D(1-l)\tau }-\varepsilon _{2}=m_{2}\) and \(s_{2}(t)\ge s^{*}_{2}e^{-Dl\tau }+ [s^{*}_{2}e^{-Dl\tau }+d(s^{0}_{1}-(s^{0}_{1}-s^{*}_{1})e^{-Dl\tau })]e^{-D(1-l)\tau }-\varepsilon _{2}=m_{3}\) for t large enough. Thus, we only need to find \(m_{1}>0\) such that \(x(t)\ge m_{1}\) for t large enough, we will do it in the following.

By the conditions of this theorem, we can select \(m_{3}>0, \varepsilon _{1}> 0\) small enough such that

$$\begin{aligned} \sigma =\frac{m}{D+\frac{mm_{3}}{kk_{1}}}\ln \frac{k+z_{2}^{*}-\varepsilon _{1}}{k+z_{2}^{*}e^{-(D+\frac{mm_{3}}{kk_{1}})l\tau }-\varepsilon _{1}}-Dl\tau +d_{1}(1-l)\tau >0, \end{aligned}$$

and \(z_{2}^{*}=\frac{B_{2}[1-(1-d)e^{-D\tau }]+A_{2}de^{-(D+\frac{mm_{3}}{k_{1}k})\tau }}{(1-e^{-(D+\frac{mm_{3}}{k_{1}k})\tau })[1-(1-d)e^{-D)\tau }]}>0.\) here \(A_{2}=(1-e^{-(D+\frac{mm_{3}}{k_{1}k})(1-l)\tau })+(1-d)e^{-D(1-l)\tau }-(1-d)e^{-D\tau })s^{0}_{1}+\mu _{1}, B_{2}=ds^{0}_{1}(e^{-D(1-l)\tau }-e^{-(D+\frac{mm_{3}}{k_{1}k})\tau })+\mu _{2}.\) We will prove \(x(t)<m_{3}\) can not hold for \( t\ge 0\). Otherwise,

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{ds_{1}(t)}{dt}=D(s_{1}^{0}-s_{1}(t)), \\ \displaystyle \frac{ds_{2}(t)}{dt}\ge -\left( D+\frac{mm_{3}}{k_{1}k}\right) s_{2}(t),\\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{1}(t)=-ds_{1}(t),\\ \displaystyle \triangle s_{2}(t)=ds_{1}(t) ,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{ds_{1}(t)}{dt}=D(s_{1}^{0}-s_{1}(t)), \\ \displaystyle \frac{ds_{2}(t)}{dt}=-Ds_{2}(t),\\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle s_{1}(t)=\mu _{1},\\ \displaystyle \triangle s_{2}(t)=\mu _{2},\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(4.9)

By Remark 3.5., we have \(s_{1}(t)\ge z_{1}(t),s_{2}(t)\ge z_{2}(t)\) and \(z_{1}(t)\rightarrow \overline{z_{1}(t)}, z_{2}(t)\rightarrow \overline{z_{2}(t)},\) as \(t\rightarrow \infty \), where \((z_{1}(t),z_{2}(t))\) is the solution of

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dz_{1}(t)}{dt}=D(s_{1}^{0}-z_{1}(t)), \\ \displaystyle \frac{dz_{2}(t)}{dt}=-\left( D+\frac{mm_{3}}{k_{1}k}\right) z_{2}(t),\\ \end{array} \right\} t\in (n\tau ,(n+l)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle z_{1}(t)=-dz_{1}(t),\\ \displaystyle \triangle z_{2}(t)=dz_{1}(t) ,\\ \end{array} \right\} t= (n+l)\tau , n= 1,2\ldots ,\\ \left. \begin{array}{llc} \displaystyle \frac{dz_{1}(t)}{dt}=D(s_{1}^{0}-z_{1}(t)), \\ \displaystyle \frac{dz_{2}(t)}{dt}=-Dz_{2}(t),\\ \end{array} \right\} t\in ( (n+l)\tau ,(n+1)\tau ],n= 1,2\ldots , \\ \left. \begin{array}{llc} \displaystyle \triangle z_{1}(t)=\mu _{1},\\ \displaystyle \triangle z_{2}(t)=\mu _{2},\\ \end{array} \right\} t= (n+1)\tau , n= 1,2\ldots ,\\ \end{array} \right. \end{aligned}$$
(4.10)

and

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{z_{1}(t)}= \left\{ \begin{array}{llc} \displaystyle s^{0}_{1}-\left[ s^{0}_{1}-z^{*}_{11}\right] e^{-D(t-n\tau )}, n\tau < t\le (n+l)\tau , \\ \displaystyle s^{0}_{1}-\left[ s^{0}_{1}-(1-d)\left( s^{0}_{1}-\left( s^{0}_{1}-z^{*}_{1}\right) e^{-Dl\tau }\right) \right] e^{-D(t-(n+l)\tau )}, (n+l)\tau < t \le (n+1)\tau ,\\ \end{array} \right. \\ \displaystyle \widetilde{z_{2}(t)}= \left\{ \begin{array}{llc} \displaystyle z^{*}_{2}e^{-(D+\frac{mm_{3}}{k_{1}k})(t-n\tau )}, n\tau < t\le (n+l)\tau .\\ \displaystyle \left[ z^{*}_{2}e^{-(D+\frac{mm_{3}}{k_{1}k})l\tau }+d\left( s^{0}_{1}-\left( s^{0}_{1}-s^{*}_{1}\right) e^{-Dl\tau }\right) \right] e^{-D(t-(n+l)\tau )}, (n+l)\tau < t \le (n+1)\tau \\ \end{array} \right. \end{array} \right. \end{aligned}$$
(4.11)

with

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle z_{1}^{*}=\frac{A_{2}}{1-(1-d)e^{-D\tau }}>0,\\ \displaystyle z_{2}^{*}=\frac{B_{2}[1-(1-d)e^{-D\tau }]+A_{2}de^{-(D+\frac{mm_{3}}{k_{1}k})\tau }}{(1-e^{-(D+\frac{mm_{3}}{k_{1}k})\tau })[1-(1-d)e^{-D)\tau }]}>0.\\ \end{array} \right. \end{aligned}$$
(4.12)

and \(A_{2}=(1-e^{-(D+\frac{mm_{3}}{k_{1}k})(1-l)\tau })+(1-d)e^{-D(1-l)\tau }-(1-d)e^{-D\tau })s^{0}_{1}+\mu _{1}, B_{2}=ds^{0}_{1}(e^{-D(1-l)\tau }-e^{-(D+\frac{mm_{3}}{k_{1}k})\tau })+\mu _{2}.\)

Therefore, exists a \(T_{1}>0\) such that

$$\begin{aligned} s_{1}(t)\ge z_{1}(t)\ge \overline{z_{1}(t)}-\varepsilon _{1}, \end{aligned}$$

and

$$\begin{aligned} s_{2}(t)\ge z_{2}(t)\ge \overline{z_{2}(t)}-\varepsilon _{1}. \end{aligned}$$

Therefore

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \frac{dx(t)}{dt}\ge -Dx(t)+\frac{m (\overline{z_{2}(t)}-\varepsilon _{1})}{k+(\overline{z_{2}(t)}-\varepsilon _{1})}x(t),t\in [n\tau ,(n+l)\tau ),\\ \displaystyle \frac{dx(t)}{dt}= -d_{1}x(t),t\in [(n+l)\tau ,(n+1)\tau ).\\ \end{array} \right. \end{aligned}$$
(4.13)

For \(t\ge T_{1}\), Let \(N_{1}\in N\) and \(N_{1}\tau > T_{1}\), Integrating (4.13) on \((n\tau ,(n+l)\tau ),\) and \(((n+l)\tau ,(n+1)\tau ), n\ge N_{1},\) we have

$$\begin{aligned} x((n+1)\tau )\ge x(n\tau ^{+})e^{\int ^{(n+l)\tau }_{n\tau }(-D+\frac{m \widetilde{s_{2}(s)}}{k+\widetilde{s_{2}(s)}})ds -d_{1}(1-l)\tau }. \end{aligned}$$

Hence \(x(n\tau )\ge x(0^{+})\rho ^{n}\rightarrow +\infty ,\) as \(n\rightarrow \infty \), which is a contradiction to the boundedness of x(t). Hence exists a \(t_{1}>0\) such that \(x(t)\ge m_{1}\). The proof is complete. \(\square \)

Remark 4.4

Let

$$\begin{aligned} f(\tau )= \frac{m}{D}\ln \frac{k+s_{2}^{*}}{k+s_{2}^{*}e^{-Dl\tau }}-Dl\tau -d_{1}(1-l)\tau , \end{aligned}$$

We easily know there exists \(\epsilon >0\) such that \(f(\epsilon )<0,\) and \( f(\tau )\rightarrow -\infty \) as \(\tau \rightarrow +\infty ,\) and \(f''(\tau )<0.\) So \(f(\tau )=0\) has a unique positive root, denoted by \(\tau ^{*}\). From theorem 4.1 and theorem 4.3.,  we know \(\tau ^{*}\) is a threshold. If \(\tau > \tau ^{*}\), then the plankton-extinction boundary periodic solution \((\widetilde{s_{1}(t)},\widetilde{s_{2}(t)},0)\) of system (2.1) is globally asymptotically stable. If \(\tau < \tau ^{*}\) the system(2.1) is permanent.

5 Discussion

In this paper, we investigate a plankton-nutrient chemostat model with employing impulsive switched systems. We analyze that the plankton-extinction periodic solution of System (2.1) is globally asymptotically stable, and we also obtain the permanent condition of System (2.1).

From Theorems 4.1 and 4.3 , we can easily deduce that there must exist a threshold \(d^{*} \). If \(d <d^{*}\), the plankton-extinction periodic solution \((\widetilde{s_{1}(t)}, \widetilde{s_{2}(t)}, 0)\) of System (2.1) is globally asymptotically stable. If \(d >d^{*}\), System (2.1) is permanent. The results show that the impulsive diffusion amount of nutrients plays an important role for the permanence of System (2.1). Our results are valuable for biological resource management in practice.