Dynamics of a Chemostat-Type Model with Impulsive Effects in a Polluted Karst Environment

Abstract

In this paper, we present a chemostat-type model with impulsive effects in a polluted karst environment. The globally asymptotically stable sufficient condition are gained for a microorganism-extinction periodic solution. System permanent condition are also presented. The results are illustrated by simulations.

Supported by NNSFC (No.11791019,11361014), the Science Technology Foundation of Guizhou Education Department (No.QJK[KY]2018019).

1 Introduction

There are wide underground rivers in the underground rock gaps of karst areas. It easy for pollutants and nutrient of soils to come into aquifers for the thin soil layers of karst areas [1]. Many authors [2,3,4] employed SDE,PDE,ODE and IDE to study chemostat systems. References [5, 6] devoted themselves to the effects of toxicants on population. But there are few authors devoted themselves to karst environmental chemostat system with impulsive diffusing and pulse inputting. We mark a notation as $N=nT, N+L=(n+l)T.$

2 The Model

In this paper, we present a chemostat-type model with impulsive effects in a polluted karst environment

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dx_{1}}{dt}=D_{1}(x_{1}^{0}-x_{1}),\\[6pt] \displaystyle \frac{dx_{2}}{dt}=D_{2}(x_{2}^{0}-x_{2})\\[6pt] \displaystyle \quad \qquad -\frac{1}{\delta }\times \frac{\eta x_{2}Y}{\alpha +x_{2}},\\[6pt] \displaystyle \frac{dY}{dt}=-D_{2}\\[6pt] \displaystyle \quad \qquad +\frac{\eta x_{2}Y}{\alpha +x_{2}}-\beta c_{1}Y,\\[6pt] \displaystyle \frac{dc_{1}}{dt}=f_{1}c_{2}-(g_{1}+m_{1})c_{1},\\[6pt] \displaystyle \frac{dc_{2}}{dt}=-h_{1}c_{2},\\[6pt] \end{array} \right\} t\ne (N+L), t\ne (N+1), \\ \left. \begin{array}{llc} \displaystyle x_{1}^{+}=x_{1},\\[6pt] \displaystyle x_{2}^{+}= x_{2},\\[6pt] \displaystyle Y^{+}=Y,\\[6pt] \displaystyle c_{1}^{+}=c_{1},\\[6pt] \displaystyle c_{2}^{+}=(1-\theta _{1}) c_{2},\\[6pt] \end{array} \right\} t= (N+L),\\[6pt] \left. \begin{array}{llc} \displaystyle x_{1}^{+}= (1-d)x_{1}+dx_{2}+\theta _{2},\\[6pt] \displaystyle x_{2}^{+}= dx_{1}(1-d)x_{2},\\[6pt] \displaystyle Y^{+}= Y,\\[6pt] \displaystyle c_{1}^{+}=(1-h_{3}) c_{1},\\[6pt] \displaystyle c_{2}^{+}=c_{2}+\theta ,\\[6pt] \end{array} \right\} t= (N+1),\\ \end{array} \right. \end{aligned}$$

(1)

where system (1) is constructed by two patches, patch (1) is a non-polluted environment and patch (2) is a polluted environment. The meanings of the variables and parameters can be consulted from reference [3,4,5].

3 The Foundation

If $Y=0$, there are two subsystems of system (1) as

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dx_{1}}{dt}=D_{1}(x_{1}^{0}-x_{1}),\\[6pt] \displaystyle \frac{dx_{2}}{dt}=D_{2}(x_{2}^{0}-x_{2}),\\[6pt] \end{array} \right\} t\ne N, \\ \left. \begin{array}{llc} \displaystyle x_{1}^{+}= (1+d)x_{1}+dx_{2}+\theta _{1},\\[6pt] \displaystyle x_{2}^{+}= dx_{1}+(1-d)x_{2},\\[6pt] \end{array} \right\} t= N,\\ \end{array} \right. \end{aligned}$$

(2)

and

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dc_{1}}{dt}=f_{1}c_{2}-(g_{1}+m_{1})c_{1},\\[6pt] \displaystyle \frac{dc_{2}}{dt}=-h_{1}c_{2},\\[6pt] \end{array} \right\} t\ne N, t\ne (N+1),\\[6pt] \left. \begin{array}{llc} \displaystyle \triangle c_{1}=0,\\[6pt] \triangle c_{2}=-\theta _{1}c_{2},\\[6pt] \end{array} \right\} t= (N+L), \\ \left. \begin{array}{llc} \displaystyle \triangle c_{1}=-\theta _{3}c_{1},\\[6pt] \triangle c_{2}=\theta ,\\[6pt] \end{array} \right\} t= (N+1).\\ \end{array} \right. \end{aligned}$$

(3)

i) Integrating on system (2)

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle x_{i}(t)=x^{0}_{i}-[x^{0}_{i}-x_{i}(nT^{+})]e^{-D_{i}(t-nT)}.\\[6pt] \end{array} \right. \end{aligned}$$

(4)

Then,

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle x_{1}((n+1)T^{+})=(1-d)e^{-D_{1}T}x_{1}(nT^{+})+de^{-D_{2}T}x_{2}(nT^{+})\\ \quad \qquad \qquad +(1-d)(1-e^{-D_{1}T})x_{1}^{0}+d(1-e^{-D_{2}T})x_{2}^{0}+\theta _{1},\\[6pt] \displaystyle x_{2}((n+1)T^{+})=de^{-D_{1}T}x_{1}(nT^{+})+(1-d)e^{-D_{2}T}x_{2}(nT^{+})\\ \quad \qquad \qquad +d(1-e^{-D_{1}T})x_{1}^{0}+(1-d)(1-e^{-D_{2}T})x_{2}^{0}.\\[6pt] \end{array} \right. \end{aligned}$$

(5)

From system (5), we gain

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle x_{1}^{*} =\frac{K_{1}+K'_{1}}{K_{2}+K'_{2}},\\[6pt] \displaystyle x_{2}^{*}=\frac{K_{3}+K'_{3} }{K_{4}+K'_{4}},\\[6pt] \end{array} \right. \end{aligned}$$

(6)

where $K_{1}=[(1-d)(1-e^{-D_{1}T})-(1-2d)(1-e^{-D_{2}T})e^{-D_{1}T}]x^{0}_{1} -d(1-e^{-D_{2}T})x^{0}_{2}+(1-e^{-D_{2}T},$ $K'_{1}=de^{-D_{2}T})\theta _{1},$ $K_{2}=1-(1-d)e^{-D_{1}T}-(1-d)e^{-D_{2}T}$ $K'_{2}=-(1-2d)e^{-(D_{1}+D_{2})T},$ $K_{3}=-d(1-e^{-D_{1}T})x^{0}_{1}+[(1-d)(1-e^{-D_{2}T})-(1-2d)(1-e^{-D_{1}T})e^{-D_{2}T}]x^{0}_{2},$ $K'_{3}=de^{-D_{1}T}\theta _{1},$ and $K_{4}=1-(1-d)e^{-D_{2}T}-(1-d)e^{-D_{1}T},$ $K'_{4}=-(1-2d)e^{-(D_{2}+D_{1})T}.$

The map $G: R^{2}_{+}\rightarrow R^{2}_{+}$ coming from system (5) is presented as

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle G_{1}(x)=G_{11}x_{1}+G_{12}x_{2}+G_{13},\\[6pt] \displaystyle G_{2}(x)=G_{21}x_{1}+G_{22}x_{2},\\[6pt] \end{array} \right. \end{aligned}$$

(7)

where $x=(x_{1},x_{2})\in R^{2}_{+}$, and $G_{11}=(1-d)e^{-D_{1}T},G_{12}=de^{-D_{2}T}, G_{13}=(1-d)(1-e^{-D_{1}T})x_{1}^{0}+d(1-e^{-D_{2}T})x_{2}^{0}+\theta _{1}, G_{21}=de^{-D_{1}T}, G_{22}=(1-d)e^{-D_{2}T}, G_{23}=+d(1-e^{-D_{1}T})x_{1}^{0}+(1-d)(1-e^{-D_{2}T})x_{2}^{0}.$

Being similar to reference [7], two lemmas are gotten.

Lemma 1

$G^{n}(x)\rightarrow (x_{1}^{*},x_{2}^{*})$ (as $n\rightarrow \infty$) holds for $(x_{1},x_{2})$ of system (7).

Lemma 2

The solution $(\widetilde{x_{1}},\widetilde{x_{2}})$, which is defined as

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{x_{1}}=x^{0}_{1}-(x^{0}_{1}-x_{1}^{*})e^{-D_{1}(t-nT)}, N< t\le (N+1),\\[6pt] \displaystyle \widetilde{x_{2}}=x^{0}_{2}-(x^{0}_{2}-x_{2}^{*})e^{-D_{2}(t-nT)}, N < t\le (N+1),\\[6pt] \end{array} \right. \end{aligned}$$

(8)

is globally stable.

ii) Integrating on system (3), we have

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle c_{1}((n+1)T^{+})=c_{1}(nT^{+})e^{-(g_{1}+m_{1})T}\\[6pt] \displaystyle \quad \qquad +\frac{ c_{2}(nT^{+})f_{1}(e^{-(g_{1}+m_{1})(1-l)T}-e^{-(h_{1}-g_{1}-m_{1})lT-(g_{1}+m_{1})(1-l)T})}{(h_{1}-g_{1}-m_{1})}\\[6pt] \displaystyle \quad \qquad \qquad +\frac{ (1-\theta _{1})c_{2}(nT^{+})f_{1}(e^{-h_{1}lT}-e^{-(h_{1}-g_{1}-m_{1})T)})}{(h_{1}-g_{1}-m_{1})},\\[6pt] \displaystyle c_{2}((n+1)T^{+})=(1-\theta _{1})e^{-h_{1}T}c_{2}(nT^{+})+\theta .\\[6pt] \end{array} \right. \end{aligned}$$

(9)

From (9), we have $c_{1}^{*}$ and $c_{2}^{*}$ with

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle c_{1}^{*}=\frac{1-\theta _{3}}{1-(1-\theta _{3})e^{-(g_{1}+m_{1})T}}\\[6pt] \displaystyle \quad \qquad \times [\frac{ \theta f_{1}(e^{-(g_{1}+m_{1})(1-l)T}-e^{-(h_{1}-g_{1}-m_{1})lT-(g_{1}+m_{1})(1-l)T})}{(h_{1}-g_{1}-m_{1})(1-(1-\theta _{1}) e^{-h_{1}T})(1-e^{-(g_{1}+m_{1})T})}\\[6pt] \displaystyle \quad \qquad \qquad +\frac{ (1-\theta _{1})\theta f_{1}(e^{-h_{1}lT}-e^{-(h_{1}-g_{1}-m_{1})T)})}{(h_{1}-g_{1}-m_{1})(1-(1-\theta _{1})e^{-h_{1}T})(1-e^{-(g_{1}+m_{1})T})}],\\[6pt] \displaystyle c_{2}^{*}=\frac{\theta }{1-(1-\theta _{1})e^{-h_{1}T}}.\\[6pt] \end{array} \right. \end{aligned}$$

(10)

Obviously, for (9), $(c_{1}^{*},c_{2}^{*})$ is globally asymptotically stable.

Lemma 3

The globally asymptotically stable $(\widetilde{c_{1}},\widetilde{c_{2}})$ of (3) exists. and $\widetilde{c_{1}},\widetilde{c_{2}})$ are in reference [8], $c_{1}^{*}, c_{2}^{*}$ are as (11),  and $c_{1}^{**}=c_{1}^{*}e^{-(g_{1}+m_{1})lT} +\frac{ f_{1}c_{2}^{*}(1-e^{-(h_{1}-g_{1}-m_{1})lT})}{(h_{1}-g_{1}-m_{1})},$ $c_{2}^{**}=(1-\theta _{1})e^{-h_{1}lT}c^{*}_{2}.$

Remark 4

There exist positive constants $m_{0},M_{0},m_{e},M_{e}$, it is easy to get $m_{0}\le c_{o}(t)\le M_{0}$ and $m_{e}\le c_{e}(t)\le M_{e}$.

Similar to reference [7], we can obtain

Lemma 5

There exists a positive constant $\lambda >0$, we can easily have $x_{1}(t)\le [\delta (D_{1} x_{1}^{0}+D_{2} x_{2}^{0})+\frac{\theta \exp (\lambda T)}{\exp (\lambda T)-1}]e^{\lambda T_{1}}$, $x_{2}(t)\le [\delta (D_{1} x_{1}^{0}+D_{2} x_{2}^{0})+\frac{\theta \exp (\lambda T)}{\exp (\lambda T)-1}]e^{\lambda T_{1}}$, $Y(t)\le \delta (D_{1} x_{1}^{0}+D_{2} x_{2}^{0})+\frac{\theta \exp (\lambda T)}{\exp (\lambda T)-1}$, $c_{0}(t)\le \delta (D_{1} x_{1}^{0}+D_{2} x_{2}^{0})+\frac{\theta \exp (\lambda T)}{\exp (\lambda T)-1}$, and $c_{e}(t)\le \delta (D_{1} x_{1}^{0}+D_{2} x_{2}^{0})+\frac{\theta \exp (\lambda T)}{\exp (\lambda T)-1}.$

4 Dynamical Analysis

Theorem 1

Suppose

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle \quad \qquad \qquad d>\frac{1}{2},\\[6pt] \end{array} \right. \end{aligned}$$

(11)

and

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle (\eta -D_{2})T-\frac{\alpha \eta }{D_{2}(\alpha +x^{0}_{2})}\ln \frac{\alpha e^{-D_{2}T}+(e^{-D_{2}T}-1)x^{0}_{2}+x^{*}_{2}}{\alpha +x^{*}_{2}}\\[6pt] \displaystyle \quad +\frac{c^{*}_{1}(1-e^{-(g_{1}+m_{1})lT})}{g_{1}+m_{1}}+\frac{f_{1}c^{*}_{2}lT}{h_{1}-g_{1}-m_{1}} -\frac{f_{1}c^{*}_{2}(1-e^{-(h_{1}-g_{1}-m_{1})lT})}{(h_{1}-g_{1}-m_{1})^{2}}\\[6pt] \displaystyle \quad \qquad +\frac{c^{**}_{1}(e^{-(g_{1}+m_{1})lT}-e^{-(g_{1}+m_{1})T})}{g_{1}+m_{1}}+\frac{f_{1}c^{**}_{2}(1-l)T}{h_{1}-g_{1}-m_{1}}\\[6pt] \displaystyle \quad \qquad \qquad -\frac{fc^{**}_{2}(e^{-(h_{1}-g_{1}-m_{1})lT}-e^{-(h_{1}-g_{1}-m_{1})T})}{(h_{1}-g_{1}-m_{1})^{2}}<0,\\[6pt] \end{array} \right. \end{aligned}$$

(12)

hold, the globally asymptotically stable $(\widetilde{x_{1}},\widetilde{x_{2}},0,\widetilde{c_{1}}, \widetilde{c_{2}})$ exists, and $x^{*}_{2}$, $x^{**}_{2}$ are with (6), and $c^{*}_{1},c^{**}_{1}$,$c^{*}_{2},c^{**}_{2}$ are with in (10).

Proof

Doing it as $y_{1}=x_{1}-\widetilde{x_{1}},y_{2}=x_{2}-\widetilde{x_{2}}, Y=Y, z_{1}=c_{1}-\widetilde{c_{1}},z_{2}=c_{2}-\widetilde{c_{2}}$, then, linear system with considering for one periodic solution $(\widetilde{x_{1}},\widetilde{x_{2}},0,\widetilde{c_{1}},\widetilde{c_{2}})$ is presented as

$$ \left( \begin{array}{c} \frac{dy_{1}}{dt}\\[6pt] \frac{dy_{2}}{dt}\\[6pt] \frac{dY}{dt}\\[6pt] \frac{dz_{1}}{dt}\\[6pt] \frac{dz_{2}}{dt}\\[6pt] \end{array} \right) = \left( \begin{array}{ccccc} -D_{1} &{} 0 &{} 0&{}0&{}0\\[6pt] 0&{} -D_{2} &{} K_{5}&{}0&{}0\\[6pt] 0&{} 0 &{} K'_{5}&{}0&{}0\\[6pt] 0&{} 0 &{} 0&{}-(g_{1}+m_{1})&{}f_{1}\\[6pt] 0&{} 0 &{} 0&{}0&{}-h_{1}\\[6pt] \end{array} \right) \left( \begin{array}{c} y_{1}\\[6pt] y_{2}\\[6pt] Y\\[6pt] z_{1}\\[6pt] z_{2}\\[6pt] \end{array} \right) , $$

where $K_{5}= -\frac{1}{\delta }\times \frac{\eta \widetilde{x_{2}(t)}}{\alpha +\widetilde{x_{2}(t)}},K'_{5}=-[D_{2}+\beta \widetilde{c_{1}(t)}-\frac{\eta \widetilde{x_{2}(t)}}{\alpha +\widetilde{x_{2}(t)}} ].$ Then, the fundamental solution matrix is

$$\varPhi (t)=\left( \begin{array}{ccccc} e^{-D_{1}t} &{} 0 &{} 0&{}0&{}0\\[6pt] 0 &{} e^{-D_{2}t} &{}\dagger &{}0&{}0\\[6pt] 0 &{} 0 &{} K_{6}&{}0&{}0\\[6pt] 0 &{} 0&{} 0&{} K'_{6}&{} \ddagger \\[6pt] 0 &{} 0 &{} 0&{} 0&{} e^{-h_{1}t}\\[6pt] \end{array} \right) , $$

where $K_{6}=e^{\int ^{t}_{0}(-D_{2}+\frac{\eta \widetilde{x_{2}(\xi )}}{\alpha +\widetilde{x_{2}(\xi )}}- \beta \widetilde{c_{1}(\xi )})d\xi },K'_{6}=e^{-(g_{1}+m_{1})t}.$ There is no need for computing $\dagger ,\ddagger$.

When $t=(n+l)T,$ we get

$$ \left( \begin{array}{c} y_{1}(nT^{+})\\[6pt] y_{2}(nT^{+})\\[6pt] Y(nT^{+})\\[6pt] z_{1}(nT^{+})\\[6pt] z_{2}(nT^{+})\\[6pt] \end{array} \right) = \left( \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} 0&{} 0\\[6pt] 0 &{} 1&{} 0&{} 0&{} 0\\[6pt] 0&{} 0&{} 1&{} 0&{} 0\\[6pt] 0&{} 0&{} 0&{} 1&{} 0\\[6pt] 0&{} 0&{} 0&{} 0&{} 1-\theta _{1}\\[6pt] \end{array} \right) \left( \begin{array}{c} y_{1}(nT)\\[6pt] y_{2}(nT)\\[6pt] Y(nT)\\[6pt] z_{1}(nT)\\[6pt] z_{2}(nT)\\[6pt] \end{array} \right) . $$

When $t=(n+1)T,$ we also get

$$ \left( \begin{array}{c} y_{1}(nT^{+})\\[6pt] y_{2}(nT^{+})\\[6pt] Y(nT^{+})\\[6pt] z_{1}(nT^{+})\\[6pt] z_{2}(nT^{+})\\[6pt] \end{array} \right) = \left( \begin{array}{ccccc} 1-d &{} d &{} 0 &{} 0&{} 0\\[6pt] d&{} 1-d&{} 0&{} 0&{} 0\\[6pt] 0&{} 0&{} 1&{} 0&{} 0\\[6pt] 0&{} 0&{} 0&{} 1-\theta _{3}&{} 0\\[6pt] 0&{} 0&{} 0&{} 0&{} 1\\[6pt] \end{array} \right) \left( \begin{array}{c} y_{1}(nT)\\[6pt] y_{2}(nT)\\[6pt] Y(nT)\\[6pt] z_{1}(nT)\\[6pt] z_{2}(nT)\\[6pt] \end{array} \right) . $$

The stability of $(\widetilde{x_{1}},\widetilde{x_{1}},0,\widetilde{c_{1}},\widetilde{c_{2}})$ is decided by eigenvalues of

$$M=\left( \begin{array}{ccccc} 1-d &{} d &{} 0 &{} 0 &{} 0\\[6pt] d &{} 1-d &{} 0 &{} 0 &{} 0\\[6pt] 0 &{} 0 &{} 1 &{} 0 &{} 0\\[6pt] 0 &{} 0 &{} 0 &{} 1-\theta _{3} &{} 0\\[6pt] 0 &{} 0 &{} 0 &{} 0 &{} 1-\theta _{1}\\[6pt] \end{array} \right) \varPhi (\tau ).$$

From condition (12), $e^{-D_{1}\tau }<1$, and $e^{-D_{2}\tau }<1$, the eigenvalues of M are presented as

$$\gamma _{1}=\frac{K_{7}+\sqrt{K'_{7}}}{2}<<1,$$

$$\gamma _{2}=\frac{K_{7}-\sqrt{K'_{7}}}{2}<(1-d)e^{-D_{2}T}<1,$$

$$\gamma _{3}= e^{\int ^{T}_{0}(-D_{2}+\frac{\eta \widetilde{x_{2}(\xi )}}{\alpha +\widetilde{x_{2}(\xi )}}- \beta \widetilde{c_{1}(\xi )})d\xi },$$

$$\gamma _{4}=(1-\theta _{3})e^{-(g_{1}+m_{1})\tau }<1,$$

$$\gamma _{5}=(1-\theta _{1})e^{-h_{1}\tau }<1.$$

where $K_{7}=(1-d)(e^{-D_{1}T}+e^{-D_{2}T}), K'_{7}=(1-d)^{2}(e^{-D_{1}T}+e^{-D_{2}T})^{2}-4(1-2d)e^{-(D_{1}+D_{2})T}.$ For the Floquet theory [6] and condition (14), it is easily to have $\gamma _{3}<1$, then, the locally stable $(\widetilde{x_{1}},\widetilde{x_{2}}, 0, \widetilde{c_{1}}, \widetilde{c_{2}})$ exists.

Choosing $\varepsilon >0$, we have

$$\rho _{1}=\exp [\int ^{\tau }_{0}K_{8}-\beta (\widetilde{c_{1}(t)}-\varepsilon )dt]<1.$$

where $K_{8}=-D_{2}+\frac{\eta (\widetilde{x_{2}}+ \varepsilon )}{\alpha +(\widetilde{x_{2}}+ \varepsilon )}.$ We get $\frac{dx_{2}}{dt}\le D_{2}(x^{0}_{2}-x_{2})$ with considering system (1). So

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dm_{1}}{dt}= D_{1}(x^{0}_{1}-m_{1}),\\[6pt] \displaystyle \frac{dm_{2}}{dt}= D_{2}(x^{0}_{2}-m_{2}),\\[6pt] \end{array} \right\} t\ne (n+1)T,\\[6pt] \left. \begin{array}{llc} \displaystyle \varDelta m_{1}=d(m_{2}-m_{1})+\theta _{2},\\[6pt] \displaystyle \varDelta m_{2}=d(m_{1}-m_{2}),\\[6pt] \end{array} \right\} t=(n+1)T.\\[6pt] \end{array} \right. \end{aligned}$$

(13)

From lemma (2), and [8], we get

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle x_{1}\le m_{1}\le \widetilde{x_{1}}+\varepsilon ,\\[6pt] \displaystyle x_{2}\le m_{2}\le \widetilde{x_{2}}+\varepsilon .\\[6pt] \end{array} \right. \end{aligned}$$

(14)

and

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{c_{1}}-\varepsilon \le c_{1}\le \widetilde{c_{1}}+\varepsilon ,\\[6pt] \displaystyle \widetilde{c_{2}}-\varepsilon \le c_{2}\le \widetilde{c_{2}}+\varepsilon .\\[6pt] \end{array} \right. \end{aligned}$$

(15)

Therefore,

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle \frac{d Y}{dt}\le Y[-D_{2}+\frac{\eta (\widetilde{x_{2}}+\varepsilon )}{\alpha +(\widetilde{x_{2}} +\varepsilon )}-\beta (\widetilde{c_{1}}-\varepsilon )].\\[6pt] \end{array} \right. \end{aligned}$$

(16)

Then, $Y(t)\le Y(0^{+})\exp [\int ^{t}_{0}(-D_{2}+\frac{\eta (\widetilde{x_{2}}+\varepsilon )}{\alpha +(\widetilde{x_{2}} +\varepsilon )}-\beta (\widetilde{c_{1}}-\varepsilon ))ds]$, thus

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle Y((n+1)T)\le Y(nT^{+})\\[6pt] \displaystyle \quad \qquad \times \exp [\int ^{(n+1)T}_{nT}(-D_{2}+\frac{\eta (\widetilde{x_{2}(s)}+\varepsilon )}{\alpha +(\widetilde{x_{2}(s)} +\varepsilon )}-\beta (\widetilde{c_{1}(s)}-\varepsilon ))ds].\\[6pt] \end{array} \right. \end{aligned}$$

(17)

Hence $Y(n\tau )\le Y(0^{+})\rho _{1}^{n}$ and $Y(nT)\rightarrow 0$ as $n\rightarrow \infty$. So $Y(t)\rightarrow 0$ as $t\rightarrow \infty$.

For $\varepsilon >0$, it has a $t_{0}>0$ such that $0<Y<\varepsilon$ for all $t\ge t_{0}$. It is no difficulty to gain

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle \frac{\delta \alpha D_{2}+\eta \varepsilon }{\delta (\alpha +M) }[\frac{\delta (\alpha +M) D_{2}x^{0}_{2}}{\delta (\alpha +M) D_{2}+\eta \varepsilon }-x_{2}]\le \frac{d x_{2}}{dt}\le D_{2}(x^{0}_{2}-x_{2}).\\[6pt] \end{array} \right. \end{aligned}$$

(18)

$(v_{1},v_{2})$, $(n_{1},n_{2})$ are of

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dv_{1}}{dt}=D_{1}(x^{0}_{1}-v_{1}),\\[6pt] \displaystyle \frac{dv_{2}}{dt}= \frac{\delta (\alpha +M) D_{2}+\eta \varepsilon }{\delta (\alpha +M) }[\frac{\delta (\alpha +M) D_{2}x^{0}_{2}}{\delta (\alpha +M) D_{2}+\eta \varepsilon }-v_{2}],\\[6pt] \end{array} \right\} t\ne nT,\\[6pt] \left. \begin{array}{llc} \displaystyle \varDelta v_{1}=d(v_{2}-v_{1})+\theta _{2},\\[6pt] \displaystyle \varDelta v_{2}=d(v_{1}-v_{2}),\\[6pt] \end{array} \right\} t=nT,\\[6pt] \end{array} \right. \end{aligned}$$

(19)

and

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dn_{1}}{dt}= D_{1}(x^{0}_{1}-n_{1}),\\[6pt] \displaystyle \frac{dn_{2}}{dt}= D_{2}(x^{0}_{2}-n_{2}),\\[6pt] \end{array} \right\} t\ne nT,\\[6pt] \left. \begin{array}{llc} \displaystyle \varDelta n_{1}=d(n_{2}-n_{1})+\theta _{2},\\[6pt] \displaystyle \varDelta n_{2}=d(n_{1}-n_{2}),\\[6pt] \end{array} \right\} t=nT,\\[6pt] \end{array} \right. \end{aligned}$$

(20)

respectively, while

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{ v_{1}}=x^{0}_{1}-(x^{0}_{1}-v^{*}_{1})e^{-D_{1}(t-nT)},\\[6pt] \displaystyle \widetilde{v_{2}}=\frac{\delta (\alpha +M) D_{2}x^{0}_{2}}{\delta (\alpha +M) D_{2}+\eta \varepsilon }\\[6pt] \displaystyle \quad \qquad \qquad -(\frac{\delta (\alpha +M) D_{2}x^{0}_{2}}{\delta (\alpha +M) D_{2}+\eta \varepsilon }-v^{*}_{2})e^{-\frac{\delta (\alpha +M) D_{2}+\eta \varepsilon }{\delta (\alpha +M) }(t-nT)},\\[6pt] \end{array} \right. \end{aligned}$$

(21)

with

(22)

For $\varepsilon _{1}>0$, existing a $t_{1}, t>t_{1}$ such that

$$\widetilde{v_{1}}-\varepsilon _{1}<x_{1}<\widetilde{n_{1}}+\varepsilon _{1},$$

and

$$\widetilde{v_{2}}-\varepsilon _{1}<x_{2}<\widetilde{n_{2}}+\varepsilon _{1}.$$

One will gain the followings with considering $\varepsilon \rightarrow 0$,

$$\widetilde{x_{1}}-\varepsilon _{1}<x_{1}<\widetilde{x_{1}}+\varepsilon _{1},$$

and

$$\widetilde{x_{2}}-\varepsilon _{1}<x_{2}<\widetilde{x_{2}}+\varepsilon _{1}.$$

This completes the proofs.

Theorem 2

Suppose

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle \quad \qquad \qquad d>\frac{1}{2},\\[6pt] \end{array} \right. \end{aligned}$$

(23)

and

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle (\eta -D_{2})T-\frac{\alpha \eta }{D_{2}(\alpha +x^{0}_{2})}\ln \frac{\alpha e^{-D_{2}T}+(e^{-D_{2}T}-1)x^{0}_{2}+x^{*}_{2}}{\alpha +x^{*}_{2}}\\[6pt] \displaystyle \quad +\frac{c^{*}_{1}(1-e^{-(g_{1}+m_{1})lT})}{g_{1}+m_{1}}+\frac{f_{1}c^{*}_{2}lT}{h_{1}-g_{1}-m_{1}} -\frac{f_{1}c^{*}_{2}(1-e^{-(h_{1}-g_{1}-m_{1})lT})}{(h_{1}-g_{1}-m_{1})^{2}}\\[6pt] \displaystyle \quad \qquad +\frac{c^{**}_{1}(e^{-(g_{1}+m_{1})lT}-e^{-(g_{1}+m_{1})T})}{g_{1}+m_{1}}+\frac{f_{1}c^{**}_{2}(1-l)T}{h_{1}-g_{1}-m_{1}}\\[6pt] \displaystyle \quad \qquad \qquad -\frac{fc^{**}_{2}(e^{-(h_{1}-g_{1}-m_{1})lT}-e^{-(h_{1}-g_{1}-m_{1})T})}{(h_{1}-g_{1}-m_{1})^{2}}>0,\\[6pt] \end{array} \right. \end{aligned}$$

(24)

hold, system permanence, and $x^{*}_{2}$ and $x^{**}_{2}$ are with (6), $c^{*}_{1},c^{**}_{1}, c^{*}_{2},c^{**}_{2}$ are with (10).

Proof

Owing to remark (4), and lemma (5), we have obtain that $(x_{1},x_{2},Y,$ $c_{1},c_{2})$ is bounded. It can be easily obtained that $c_{1}\ge m_{o}$ and $c_{2}\ge m_{e}$ with considering with remark (4).

Therefore,

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dx_{1}}{dt}=D_{1}(x_{1}^{0}-x_{1}),\\[6pt] \displaystyle \frac{dx_{2}}{dt}\ge D_{2}(x_{2}^{0}-x_{2})-\frac{\eta M}{\delta \alpha }x_{2},\\[6pt] \end{array} \right\} t\ne nT, \\ \left. \begin{array}{llc} \displaystyle \triangle x_{1}= d(-x_{1}+x_{2})+\theta _{2},\\[6pt] \displaystyle \triangle x_{2}= d(x_{1}-x_{2}),\\[6pt] \end{array} \right\} t= nT,\\ \end{array} \right. \end{aligned}$$

(25)

with its comparison system

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dw_{1}}{dt}=D_{1}(x_{1}^{0}-w_{1}),\\[6pt] \displaystyle \frac{dw_{2}}{dt}= \frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }[\frac{\delta \alpha D_{2} x_{2}^{0}}{\delta \alpha D_{2}+\eta M}-w_{2}],\\[6pt] \end{array} \right\} t\ne nT, \\ \left. \begin{array}{llc} \displaystyle \triangle w_{1}= d(w_{2}-w_{1})+\theta _{2},\\[6pt] \displaystyle \triangle w_{2}= d(w_{1}-w_{2}),\\[6pt] \end{array} \right\} t= nT.\\ \end{array} \right. \end{aligned}$$

(26)

With considering (2) and (8), $(\widetilde{w_{1}},\widetilde{w_{2}})$ of (26) is

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \widetilde{w_{1}}=x^{0}_{1}-(x^{0}_{1}-w^{*}_{1})e^{-D_{1}(t-nT)}, nT< t\le (n+1)T,\\[6pt] \displaystyle \widetilde{w_{2}}=\frac{\delta \alpha D_{2} x_{2}^{0}}{\delta \alpha D_{2}+\eta M}-(\frac{\delta \alpha D_{2} x_{2}^{0}}{\delta \alpha D_{2}+\eta M}-w^{*}_{2})e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }(t-nT)},\\[6pt] \displaystyle \qquad \qquad \quad \qquad \qquad nT < t\le (n+1)T,\\[6pt] \end{array} \right. \end{aligned}$$

(27)

with

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle w_{1}^{*}=\frac{[(1-d)(1-e^{-D_{1}T})-(1-2d)(1-e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T})e^{-D_{1}T}]x^{0}_{1} -d(1-e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T})\frac{\delta \alpha D_{2} x_{2}^{0}}{\delta \alpha D_{2}+\eta M}}{1-(1-d)e^{-D_{1} T}-(1-d)e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T}-(1-2d)e^{-(D_{1}+\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha })T}}\\[6pt] \displaystyle \quad \qquad \qquad +\frac{+(1-e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T}+de^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T})\theta _{2}}{1-(1-d)e^{-D_{1}T}-(1-d)e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T}-(1-2d)e^{-(D_{1}+\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha })T}},\\[6pt] \displaystyle w_{2}^{*}=\frac{-d(1-e^{-D_{1}T})x^{0}_{1}+[(1-d)(1-e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T})- (1-2d)(1-e^{-D_{1}\tau })e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T}]\frac{\delta \alpha D_{2} x_{2}^{0}}{\delta \alpha D_{2}+\eta M} }{1-(1-d)e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }T}-(1-d)e^{-D_{1}T}-(1-2d)e^{-(\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }+D_{1})\tau }}\\[6pt] \displaystyle \quad \qquad \qquad +\frac{+de^{-D_{1}\tau }\theta _{2}}{1-(1-d)e^{-\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }\tau }-(1-d)e^{-D_{1}T}-(1-2d)e^{-(\frac{\delta \alpha D_{2}+\eta M}{\delta \alpha }+D_{1})T}}.\\[6pt] \end{array} \right. \end{aligned}$$

(28)

Furthermore, $(\widetilde{w_{1}},\widetilde{w_{2}})$ of (27) is globally asymptotic stable. Then, it exists a $\varepsilon >0$ such that $x_{1}\ge w_{1}\ge \widetilde{w_{1}}-\varepsilon \ge w^{*}_{1}-\varepsilon =k_{1}$ and $x_{2}\ge w_{2}\ge \widetilde{w_{2}}-\varepsilon \ge w^{*}_{2}-\varepsilon =k_{2}$.

Since

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle (\eta -D_{2})T+\frac{\eta \alpha }{D_{2}(\alpha +x^{*}_{2})}\ln \frac{\alpha e^{-D_{2}T}+(e^{-D_{2}T}-1)x^{0}_{2}+x^{*}_{2}}{\alpha +x^{*}_{2}}\\[6pt] \displaystyle \quad +\frac{c^{*}_{1}(1-e^{-(g_{1}+m_{1})l\tau })}{g_{1}+m_{1}}+\frac{fc^{*}_{2}lT}{h_{1}-g_{1}-m_{1}} -\frac{f_{1}c^{*}_{2}(1-e^{-(h_{1}-g_{1}-m_{1})lT})}{(h_{1}-g_{1}-m_{1})^{2}}\\[6pt] \displaystyle +\frac{c^{**}_{1}(e^{-(g_{1}+m_{1})lT}-e^{-(g_{1}+m_{1})T})}{g_{1}+m_{1}}+\frac{f_{1}c^{**}_{2}(1-l)T}{h_{1}-g_{1}-m_{1}}\\[6pt] \displaystyle -\frac{f_{1}c^{**}_{2}(e^{-(h_{2}-g_{2}-m_{2})lT}-e^{-(h_{1}-g_{1}-m_{1})T})}{(h_{1}-g_{1}-m_{1})^{2}}>0,\\[6pt] \end{array} \right. \end{aligned}$$

(29)

$m_{3}>0$ and $\varepsilon _{1}> 0$ can be selected to do as

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle \sigma =(\eta -\frac{\delta \alpha D_{2}+\eta m_{3}}{\delta \alpha }-\varepsilon )T-\frac{\eta \alpha }{D_{2}(\alpha -\varepsilon +\frac{\delta \alpha D_{2}}{\delta \alpha D_{2}+\eta m_{3}}x^{0}_{2})}\\[6pt] \displaystyle \times \ln \frac{(\alpha -\varepsilon +\frac{\delta \alpha D_{2}}{\delta \alpha D_{2}+\eta m_{3}})e^{-\frac{\delta \alpha D_{2}+\eta m_{3}}{\delta \alpha }}-\frac{\delta \alpha D_{2}}{\delta \alpha D_{2}+\eta m_{3}}x^{0}_{2})+k^{*}_{2}}{\alpha -\varepsilon +k^{*}_{2}}\\[6pt] \displaystyle \quad +\frac{c^{*}_{1}(1-e^{-(g_{1}+m_{1})lT})}{g_{1}+m_{1}}+\frac{f_{1}c^{*}_{2}l\tau }{h_{1}-g_{1}-m_{1}} -\frac{f_{1}c^{*}_{2}(1-e^{-(h_{1}-g_{1}-m_{1})lT})}{(h_{1}-g_{1}-m_{1})^{2}}\\[6pt] \displaystyle +\frac{c^{**}_{1}(e^{-(g_{1}+m_{1})lT}-e^{-(g_{1}+m_{1})T})}{g_{1}+m_{1}}+\frac{f_{1}c^{**}_{2}(1-l)T}{h_{1}-g_{1}-m_{1}}\\[6pt] \displaystyle -\frac{f_{1}c^{**}_{2}(e^{-(h_{1}-g_{1}-m_{1})lT}-e^{-(h_{1}-g_{1}-m_{1})T})}{(h_{1}-g_{1}-m_{1})^{2}}>0,\\[6pt] \end{array} \right. \end{aligned}$$

(30)

where $k^{*}_{2}$ is defined as (34)

$Y<m_{3}$ will be proved that it can not be held for $t\ge 0$. Otherwise,

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dx_{1}}{dt}=D_{1}(x_{1}^{0}-x_{1}),\\[6pt] \displaystyle \frac{dx_{2}}{dt}\ge D_{2}(x_{2}^{0}-x_{2}(t))-\frac{\eta m_{3}}{\delta \alpha }x_{2},\\[6pt] \end{array} \right\} t\ne nT, \\ \left. \begin{array}{llc} \displaystyle \triangle x_{1}= d(-x_{1}+x_{2})+\theta _{2},\\[6pt] \displaystyle \triangle x_{2}= d(x_{1}-x_{2}),\\[6pt] \end{array} \right\} t= nT.\\ \end{array} \right. \end{aligned}$$

(31)

with its comparison system

$$\begin{aligned} \left\{ \begin{array}{llc} \left. \begin{array}{llc} \displaystyle \frac{dk_{1}}{dt}=D_{1}(x_{1}^{0}-k_{1}),\\[6pt] \displaystyle \frac{dk_{2}}{dt}\\[6pt] \displaystyle \quad =\frac{\delta \alpha D_{2}+\eta m_{3}}{\delta \alpha }[\frac{\delta \alpha D_{2}}{\delta \alpha D_{2}+\eta m_{3}}x^{0}_{2} -k_{2}], \\[6pt] \end{array} \right\} t\ne nT,\\[6pt] \left. \begin{array}{llc} \displaystyle \triangle k_{1}= d(k_{2}-k_{1})+\mu _{2},\\[6pt] \displaystyle \triangle k_{2}= d(k_{1}-_{2}),\\[6pt] \end{array} \right\} t= nT.\\ \end{array} \right. \end{aligned}$$

(32)

By lemma (2), we gain $x_{1}\ge k_{1}, x_{2}\ge k_{2}$ and $k_{1}\rightarrow \overline{k_{1}},k_{2}(t)\rightarrow \overline{k_{2}},$ as $t\rightarrow \infty$, and

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle \overline{k_{1}}=x^{0}_{1}-[x^{0}_{1}-k^{*}_{1}]e^{-D_{1}(t-nT)},nT< t\le (n+1)T,\\[6pt] \displaystyle \overline{k_{2}} =\frac{\delta \alpha D_{2}}{\delta \alpha D_{2}+\eta m_{3}}x^{0}_{2}-[\frac{\delta \alpha D_{2}}{\delta \alpha D_{2}+\eta m_{3}}x^{0}_{2}-k^{*}_{2}]e^{-\frac{\delta \alpha D_{2}+\eta m_{3}}{\delta \alpha }(t-nT)},\\[6pt] \displaystyle \quad \qquad \qquad \qquad \qquad nT < t\le (n+1)T,\\[6pt] \end{array} \right. \end{aligned}$$

(33)

with

(34)

Therefore,

$$\begin{aligned} \left\{ \begin{array}{llc} \displaystyle x_{1}\ge k_{1}\ge \overline{k_{1}}-\varepsilon _{1},\\[6pt] \displaystyle x_{2}\ge k_{2}\ge \overline{k_{2}}-\varepsilon _{1}.\\[6pt] \end{array} \right. \end{aligned}$$

(35)

For $t\ge T_{1}$

$$\begin{aligned} \left. \begin{array}{llc} \displaystyle \frac{dY}{dt}\ge [-D_{2}+ \frac{\eta (\overline{k_{2}}-\varepsilon _{1})}{\alpha +(\overline{k_{2}}-\varepsilon _{1})}-\beta (\widetilde{c_{1}}+\varepsilon _{1})]Y,\\[6pt] \end{array} \right. \end{aligned}$$

(36)

Let $K_{9}\in N^{+}$ and $K_{9}\tau > T_{1}$, integrating (36) on $(nT,(n+1)T ), n\ge K_{9},$ we have

$$Y((n+1)T)\ge Y(nT^{+})\exp (\int ^{(n+1)T}_{nT}[-D_{2}+ \frac{\eta (\overline{k_{1}}-\varepsilon _{1})}{\alpha +(\overline{k_{1}}-\varepsilon _{1})}-\beta (\overline{k_{2}}+\varepsilon _{1})]dt)$$

$$=x(nT)e^{\sigma },$$

then $Y((K_{9}+k)T)\ge Y(K_{9}T^{+})e^{k\sigma }\rightarrow \infty$, as $k\rightarrow \infty$, it is an illogicality with the bounded Y. Hence $Y\ge m_{3}$.

5 Discussion

In this work, we present a chemostat-type model with impulsive effects in a polluted karst environment. If it is supposed that the variables are shown in the table below:

$x_{1}(0)$	$x_{2}(0)$	Y(0)	$c_{1}(0)$	$c_{2}(0)$	$D_{1}$	$D_{2}$	$x_{1}^{0}$	$x_{2}^{0}$	$\delta$	$\eta$	$\alpha$	$\beta$	$\theta _{1}$	$\theta _{2}$	$\theta _{3}$	$\theta$	$f_{1}$	$g_{1}$	$m_{1}$	$h_{1}$	d	T
2	2	2	0.13	0.15	2	0.2	2	3	1	0.5	2	0.5	0.5	0.8	0.6	0.01	0.4	0.3	0.1	0.4	0.2	1

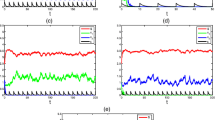
system (1) is permanent (one can see Fig. 1). If it is supposed that another variables are shown in the table below:

$x_{1}(0)$	$x_{2}(0)$	Y(0)	$c_{1}(0)$	$c_{2}(0)$	$D_{1}$	$D_{2}$	$x_{1}^{0}$	$x_{2}^{0}$	$\delta$	$\eta$	$\alpha$	$\beta$	$\theta _{1}$	$\theta _{2}$	$\theta _{3}$	$\theta$	$f_{1}$	$g_{1}$	$m_{1}$	$h_{1}$	d	T
2	2	2	0.13	0.15	2	0.2	2	3	1	0.5	2	0.5	0.5	0.8	0.1	0.01	0.4	0.3	0.1	0.4	0.2	1

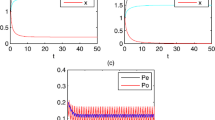
there exists a globally asymptotically stable solution $(\widetilde{x_{1}(t)},\widetilde{x_{2}(t)},0,\widetilde{c_{1}(t)},$ $\widetilde{c_{2}(t)})$ of system (1) (one can see Fig. 2). If it is supposed that another variables are shown in the table below:

$x_{1}(0)$	$x_{2}(0)$	Y(0)	$c_{1}(0)$	$c_{2}(0)$	$D_{1}$	$D_{2}$	$x_{1}^{0}$	$x_{2}^{0}$	$\delta$	$\eta$	$\alpha$	$\beta$	$\theta _{1}$	$\theta _{2}$	$\theta _{3}$	$\theta$	$f_{1}$	$g_{1}$	$m_{1}$	$h_{1}$	d	T
2	2	2	0.13	0.15	2	0.16	2	3	1	0.5	2	0.5	0.5	0.8	0.1	0.01	0.4	0.3	0.1	0.4	0.2	1

then, system (1) is permanent (see Fig. 3).

The simulations show that parameters $0<\theta _{3}<1$ and $D_{2}$ are very important for system (1). The parameters $D_{1}, \theta _{1}, \theta _{2},\theta$ and d of system (1) can also be discussed. The results will guide us how to manage the source of water management in karst areas.

Fig. 1.

The permanence of system (1) with parameters in the first table.

Fig. 2.

The dynamics of the globally asymptotically stable microorganism-extinction with parameters in the second table.

Fig. 3.

The dynamics of the globally asymptotically stable microorganism-extinction with parameters in the third table.