Weight enumerators of some irreducible cyclic codes of odd length

Abstract

Let $n > 1$ be an odd integer, $\kappa (n)$ be the product of all distinct prime divisors of n, and let q be a prime power such that the multiplicative order of q modulo n is a divisor of $\frac{3n}{\kappa (n)}$. In this paper, we obtain weight enumerators of all irreducible cyclic codes of length n over $\mathbb {F}_q$ with the help of their generator polynomials.

1 Introduction

Let n be a positive integer and q be an odd prime such that $gcd(n,q)=1$. Let $\mathbb {F}_q$ be the finite field with q elements. A cyclic code $\mathcal {C}$ of length n over $\mathbb {F}_q$ is an ideal of $\frac{\mathbb {F}_q[x]}{\langle x^n-1\rangle }$. The weight enumerator of $\mathcal {C}$ is defined as $A_0 + A_1 z + \dots + A_{n}z^{n}$, where $A_i$ denotes the number of codewords with weight i, and the sequence $(A_0, A_1, \dots , A_n)$ is called the weight distribution of $\mathcal {C}$ (see [8, Chapters 4 and 7] ).

Further, a minimal ideal in $\frac{\mathbb {F}_q[x]}{\langle x^n-1\rangle }$ is called an irreducible cyclic code of length n over $\mathbb {F}_q$. For any non-negative integer s less than n, the q-cyclotomic coset modulo n containing s is defined by

$$\begin{aligned} \texttt {C}_s^{(n)}=\{ s, sq, \dots , sq^{f_s-1}\}, \end{aligned}$$

where $f_s$ is the least positive integer such that $sq^{f_s} \equiv s \pmod {n}$. It is well known that $\mathcal {M}_s^{(n)}= \langle \frac{x^n-1}{m_s^{(n)}(x)}\rangle$ is an irreducible cyclic code of length n over $\mathbb {F}_q$, where $m_s^{(n)}(x)=\displaystyle \prod _{i \in \texttt {C}_s^{(n)}}(x-\lambda ^i)$ and $\lambda$ denotes a primitive nth root of unity in some extension of $\mathbb {F}_q$. The distinct q-cyclotomic cosets modulo n determine not only the total number of distinct irreducible cyclic codes of length n over $\mathbb {F}_q$ but also the generator polynomials of all such irreducible cyclic codes. For more details, see [13, Chapters 7 and 8].

Cyclic codes have efficient encoding and decoding algorithms (see [2, 6, 14]). This attribute of cyclic codes makes them useful in data transmission technologies, consumer electronics, and communication systems. Note that the weight distribution of a code decides its capability to detect and correct errors. Since cyclic codes constitute a significant subclass of linear codes, thus, finding their weight distributions is a research topic of much interest in Coding Theory. Many researchers have determined the weight distributions of irreducible cyclic codes by adopting different techniques (see [1, 4, 9,10,11, 17, 21, 22, 24]). However, the weight distributions of irreducible cyclic codes of arbitrary length are quite difficult to obtain [4] and are not known in general. In fact, the problem of finding the weight distribution of an irreducible cyclic code is an open problem in many cases [3].

Consequently, many researchers obtained the weight distributions of various families of irreducible cyclic codes by imposing conditions on the choices of n and q. Impressive progress has been made in this direction in the last few decades. For instance, Sharma et al. [20] computed the weight distributions of all $2^m$ length irreducible cyclic codes over $\mathbb {F}_q$, and in [19], the authors have determined the weight distributions of all irreducible cyclic codes of length $p^m$ over $\mathbb {F}_q$ in three cases: when (i) $ord_{p^m}(q)= \phi (p^m)$, (ii) $ord_{p^m}(q)$ is a power of p, and (iii) $ord_{p^m}(q)$ is twice a power of p. Vega [23] generalized the results of [19]. Recently, Riddhi et al. [15] computed the weight distributions of all irreducible cyclic codes of length $n=p_1^{\alpha _1}p_2^{\alpha _2}\dots p_r^{\alpha _r}$ over $\mathbb {F}_l$ for the case when $ord_{p_i^{\alpha _i}}(l)=2p_i^{\alpha _i-1}$ for each $\alpha _i \ge 1$. For more information on the work in this direction, we refer the reader to [5, 7, 12, 16, 18, 25].

Inspired by the earlier work, in this paper, we compute the weight enumerators of irreducible cyclic codes of arbitrary odd length n over $\mathbb {F}_q$, where the multiplicative order of q modulo n, denoted by $ord_n(q)$, is a divisor of $\frac{3n}{\kappa (n)}$. Here, $\kappa (n)$ denotes the product of all distinct prime divisors of n. By our choice of $ord_{n}(q)$, any irreducible cyclic code of length n over $\mathbb {F}_q$ is either m-dimensional or 3m-dimensional, where m is a divisor of $\frac{n}{\kappa (n)}$. Further, we observe that for computing the weight distributions of irreducible cyclic codes of length n, we need weight distributions of 1-dimensional and 3-dimensional irreducible cyclic codes of length u, where $u\mid n$. The weight enumerator of the 1-dimensional cyclic code of length u over $\mathbb {F}_q$ is trivial and is given by the expression: $1+(q-1)z^u$. Moreover, if a 3-dimensional irreducible cyclic code is semi-primitive, then its weight distribution can be obtained from Theorem 3 of [23] (see [23, Example 3]). However, the weight distributions of 3-dimensional irreducible cyclic codes are not known in general. Therefore, in Section 3, we compute the weight distributions of all 3-dimensional irreducible cyclic codes of length u over $\mathbb {F}_q$ from their generator matrices. We find that the weight distribution of a 3-dimensional irreducible cyclic code depends on $gcd(u,q-1)$, and thus, we have two cases: when (i) $gcd(u,q-1)=1$ and (ii) $1< gcd(u,q-1) < u$.

In Section 4, we prove some general results for determining weight enumerators of m-dimensional and $p^*m$-dimensional irreducible cyclic codes of length n over $\mathbb {F}_q$, where m is a divisor of $\frac{n}{\kappa (n)}$ and $p^*$ is an odd prime. We prove that the computation of the weight distribution of $\mathcal {M}_1^{(\frac{n}{v})}$ is enough to determine the weight distribution of $\mathcal {M}_v^{(n)}$, where v is a divisor of n. By writing $n=n_1n_2$, where $n_1$ is such that $ord_{p_i}(q)=p^*$ for every prime divisor $p_i$ of $n_1$ and $n_2$ is such that $ord_{p_i^\prime }(q)=1$ for every prime divisor $p_i^\prime$ of $n_2$, we observe that the weight distribution of $\mathcal {M}_v^{(n)}$ depends on the relation between $n_1$, $n_2$, and v. Therefore, we have three cases: when (i) $n_1 \mid v$, (ii) $n_2 \mid v$, and (iii) neither $n_1 \mid v$ nor $n_2 \mid v$. The above three cases are dealt with in Theorems 15, 16 and 17, respectively. The results obtained in this section are sufficient to compute the weight enumerators of all m-dimensional and 3m-dimensional irreducible cyclic codes of length n over $\mathbb {F}_q$ by choosing $p^*=3$.

2 Preliminaries

Throughout this paper, $n > 1$ is an odd integer, $\kappa (n)$ denotes the product of all distinct prime divisors of n, and q is a prime power such that the multiplicative order of q modulo n is a divisor of $\frac{3n}{\kappa (n)}$. Further, $\mathcal {M}_s^{(k)}$ represents an irreducible cyclic code of length k corresponding to the q-cyclotomic coset containing s (see [13, Chapter 7]).

Let u be a positive integer such that $ord_u(q)=3$. Then $m_1^{(u)}(x)=(x- \lambda )(x- \lambda ^{q})(x-\lambda ^{q^2})$, where $\lambda$ is a fixed primitive uth root of unity in some extension of $\mathbb {F}_q$. Clearly, $\mathcal {M}_1^{(u)}= \langle \frac{x^{u}-1}{m_1^{(u)}(x)} \rangle =\langle g(x) \rangle$ is a 3-dimensional irreducible cyclic code of length u over $\mathbb {F}_q$, where g(x) is its generator polynomial. Let $g(x)=\alpha _0 + \alpha _1 x + \alpha _2 x^2 + \dots +\alpha _{u-3} x^{u-3}$. Therefore, the generator matrix of $\mathcal {M}_1^{(u)}$ is

$$\begin{aligned} G= \begin{pmatrix} \alpha _0 &{} \alpha _1 &{} \alpha _2 &{}\dots &{}\alpha _{u-4} &{}\alpha _{u-3} &{} 0 &{} 0 \\ 0 &{} \alpha _0 &{}\alpha _1 &{} \alpha _2 &{}\dots &{}\alpha _{u-4} &{}\alpha _{u-3} &{} 0 \\ 0 &{} 0 &{} \alpha _0 &{}\alpha _1 &{}\dots &{}\alpha _{u-5} &{} \alpha _{u-4} &{}\alpha _{u-3} \end{pmatrix}. \end{aligned}$$

Definition 1

(Cyclic shift of a matrix) Let $T= \begin{pmatrix} a_{11} &{} a_{12} &{}\dots &{} a_{1,u-1} &{} a_{1u} \\ a_{21} &{} a_{22} &{}\dots &{} a_{2,u-1} &{} a_{2u} \\ a_{31}&{} a_{32} &{} \dots &{} a_{3,u-1} &{}a_{3u} \end{pmatrix}_{3 \times u}$. Rewrite T=$[C_1\,\, \,\,C_2 \,\,\,\,C_3 \,\,\,\, \dots \,\, \,\,C_u]$, where $C_i$ is the ith column of T. For $i=1, 2, \dots , u-1$, define

$$\begin{aligned} T^{(1)}= & {} [C_u\,\, \,\,C_1 \,\,\,\,C_2 \,\,\,\, \dots \,\, \,\,C_{u-1}] \\ T^{(2)}= & {} [C_{u-1}\,\, \,\,C_u \,\,\,\,C_1 \,\,\,\, \dots \,\, \,\,C_{u-2}] \\{} & {} \qquad \qquad \quad \vdots \\ T^{(u-1)}= & {} [C_2\,\, \,\,C_3 \,\,\,\, \dots \,\, \,\,C_{u} \,\,\,\, C_1], \end{aligned}$$

and call $T^{(i)}$ as the ith cyclic shift of T. It can be easily seen that $T^{(u)}=T.$

Definition 2

(Cyclic matrix) A matrix $T_{3 \times u}$ over $\mathbb {F}_q$ is called a cyclic matrix if $[a_1 \,\, b_1 \,\, c_1]T_{3 \times u}$ $=[a \,\, b\,\, c] T_{_{3 \times u}}^{(i)}$ for some $1 \le i \le u-1$, where $[a_1 \,\, b_1 \,\, c_1]$ and $[a \,\, b\,\, c]$ are row matrices over $\mathbb {F}_q$.

Theorem 1

The generator matrix G of $\mathcal {M}_1^{(u)}=\langle g(x) \rangle$ is always a cyclic matrix.

Proof

Let $[a\,\, b\,\,c]$ be a nonzero row matrix over $\mathbb {F}_q$. Clearly,

$$\begin{aligned}{}[a\,\, b\,\,c]G= \left( [a\,\, b\,\,c]C_1,\,\, \,\, [a\,\, b\,\,c]C_2, \,\,\,\, \dots \,\, \,\, ,[a\,\, b\,\,c]C_u \right) \end{aligned}$$

is a codeword in $\mathcal {M}_1^{(u)}$. By the definition of a cyclic code,

$$\begin{aligned} \left( [a\,\, b\,\,c]C_{u-i+1},\,\, [a\,\, b\,\,c]C_{u-i+2}, \,\, \dots \,\,,\,\, [a\,\, b\,\,c]C_{u-i} \right) = [a\,\, b\,\, c]G^{(i)} \end{aligned}$$

is also a codeword in $\mathcal {M}_1^{(u)}$. Since every codeword in $\mathcal {M}_1^{(u)}$ is of the form $[a^\prime \,\, b^\prime \,\,c^\prime ]G$, therefore, there exists some $[a^\prime \,\, b^\prime \,\,c^\prime ]$ over $\mathbb {F}_q$ such that $[a^\prime \,\, b^\prime \,\,c^\prime ]G= [a\,\, b\,\,c]G^{(i)}$. Hence, G is a cyclic matrix. $\square$

3 Weight distributions of 3-dimensional irreducible cyclic codes of length $u$ over $\mathbb {F}_q$

Let u be any positive integer such that $ord_u(q)=3$. In this section, we obtain the weight distributions of 3-dimensional irreducible cyclic codes of length u over $\mathbb {F}_q$. The weight distributions of such codes depend on $gcd(u,q-1)$.

Let $\lambda$ be a fixed primitive uth root of unity in some extension of $\mathbb {F}_q$. Clearly, $\mathcal {M}_1^{(u)}=\langle \frac{x^{u}-1}{m_1^{(u)}(x)} \rangle =\langle g(x) \rangle$ is a 3-dimensional irreducible cyclic code of length u over $\mathbb {F}_q$, where $m_1^{(u)}(x)=(x- \lambda )(x- \lambda ^{q})(x-\lambda ^{q^2})$. By synthetic division, $g(x) = \alpha _0+ \alpha _1 x+ \alpha _2 x^2 + \dots + \alpha _{u-3}x^{u-3}$, where $\alpha _{u-3}=1$, $\alpha _i = \beta _{i+1} + \lambda ^{q^2}\alpha _{i+1}$ for $0 \le i \le u-4$, $\beta _{u-2} =1$, and $\beta _j$ = $\lambda ^{(u-2-j)} \frac{\left( \lambda ^{(q-1)(u-1-j) }-1\right) }{\lambda ^{q-1}-1}$ for $0 \le j \le u-3$. For $\alpha _{u-2} =\alpha _{u-1}=0$, the generator matrix of $\mathcal {M}_1^{(u)}$ can be written as

$$\begin{aligned} G= \begin{pmatrix} \alpha _0 &{} \alpha _1 &{} \alpha _2 &{} \alpha _3 &{}\dots &{}\alpha _{u-4} &{}\alpha _{u-3} &{} \alpha _{u-2} &{} \alpha _{u-1} \\ \alpha _{u-1} &{} \alpha _0 &{}\alpha _1 &{} \alpha _2 &{}\dots &{} \alpha _{u-5} &{} \alpha _{u-4} &{}\alpha _{u-3} &{} \alpha _{u-2} \\ \alpha _{u-2} &{} \alpha _{u-1}&{} \alpha _0 &{}\alpha _1 &{}\dots &{} \alpha _{u-6} &{} \alpha _{u-5} &{} \alpha _{u-4} &{}\alpha _{u-3} \end{pmatrix}. \end{aligned}$$

Since every codeword in $\mathcal {M}_1^{(u)}$ is a linear combination of the rows of G over $\mathbb {F}_q$, therefore, the weight distribution of $\mathcal {M}_1^{(u)}$ depends on the columns of G. For this, we discuss the nature of columns of G. In the following discussion, $C_i$ denotes the ith column of G, where $C_1=\begin{pmatrix} \alpha _{0} \\ \alpha _{u-1} \\ \alpha _{u-2} \end{pmatrix}$, $C_2=\begin{pmatrix} \alpha _{1} \\ \alpha _{0} \\ \alpha _{u-1} \end{pmatrix}$, and for $3\le i \le u$, $C_i=\begin{pmatrix} \alpha _{i-1} \\ \alpha _{i-2} \\ \alpha _{i-3} \end{pmatrix}$. Note that for $1 \le i,j \le u$ and $\eta \in \mathbb {F}_q \setminus \{0\}$, $C_i=\eta C_j$ if and only if $\frac{\alpha _{i-1}}{\alpha _{j-1}} = \frac{\alpha _{i-2}}{\alpha _{j-2}} = \frac{\alpha _{i-3}}{\alpha _{j-3}}$. Since $\frac{\alpha _{i-1}}{\alpha _{j-1}} = \frac{\alpha _{i-2}}{\alpha _{j-2}}$ gives $\frac{\alpha _{i-1}}{\alpha _{j-1}} = \frac{\beta _{i-1}}{\beta _{j-1}}$, and $\frac{\alpha _{i-2}}{\alpha _{j-2}} = \frac{\alpha _{i-3}}{\alpha _{j-3}}$ gives $\frac{\alpha _{i-2}}{\alpha _{j-2}} = \frac{\beta _{i-2}}{\beta _{j-2}}$. This implies $C_i=\eta C_j$ if and only if $\frac{\beta _{i-1}}{\beta _{j-1}} = \frac{\beta _{i-2}}{\beta _{j-2}}$. Further, $\frac{\beta _{i-1}}{\beta _{j-1}} = \frac{\beta _{i-2}}{\beta _{j-2}}$ if and only if $\lambda ^{(q-1)(i-j)} =1$. Therefore, $C_i=\eta C_j$ if and only if $\lambda ^{(q-1)(i-j)} =1$.

Depending on $gcd(u,q-1)$, we have the following two theorems:

Theorem 2

Let u be a positive integer such that $ord_u(q)=3$ and $gcd(u,q-1)=1$. If G is the generator matrix of $\mathcal {M}_1^{(u)}$ over $\mathbb {F}_q$, then the columns of G are pairwise linearly independent.

Proof

From the above discussion, for $1 \le i,j \le u$ and $\eta \in \mathbb {F}_q \setminus \{0\}$, $C_i$=$\eta$ $C_j$ if and only if $\lambda ^{(q-1)(i-j)} =1$. Since $gcd(u,q-1)=1$, therefore, $\lambda ^{(q-1)(i-j)} =1$ if and only if $(i-j) \equiv 0\pmod {u}$. Consequently, the columns of G are pairwise linearly independent. $\square$

Theorem 3

Let u be a positive integer such that $ord_u(q)=3$ and $1< gcd(u,q-1) <u$. If G is the generator matrix of $\mathcal {M}_1^{(u)}$ over $\mathbb {F}_q$, then for each i with $1 \le i \le \frac{u}{gcd(u,q-1)}$, the columns $C_i$ and $C_{i+k^*\frac{u}{gcd(u,q-1)}}$ are linearly dependent, where $1 \le k^* < gcd(u,q-1)$.

Proof

Since $C_i$=$\eta C_j$ if and only if $\lambda ^{(q-1)(i-j)} =1$ and $1< gcd(u,q-1) < u$, therefore, $\lambda ^{(q-1)(i-j)} =1$ if and only if $(i-j)(q-1) \equiv 0 \pmod {u}$. This implies $C_i=\eta C_j$ if and only if $j=i+k^* \frac{u}{gcd(u,q-1)}$, where $1 \le k^* < gcd(u,q-1)$. Therefore, the columns $C_i$ and $C_{i+k^* \frac{u}{gcd(u,q-1)}}$ of G are linearly dependent for $1 \le k^* < gcd(u,q-1)$. $\square$

Now, we obtain the weight distributions of 3-dimensional irreducible cyclic codes of length u over $\mathbb {F}_q$ for the above two cases.

Case I Let $gcd(u,q-1)=1$. For the generator matrix G of $\mathcal {M}_1^{(u)}$, we define $X= \{C_i, 1\le i\le u: C_i\,\, \text {is a column of\,}G \}$. By Theorem 2, all $C_i$’s are linearly independent.

Let $v_{ik}$ be any non-zero vector orthogonal to $C_{i}$. Define a subset of X corresponding to ${v_{ik}}$ as: $X_{v_{ik}}^{(C_i)}=\{C_j : v_{ik}C_j=0\}$. Clearly, $X_{v_{ik}}^{(C_i)} \ne \emptyset$, and $X_{\eta v_{ik}}^{(C_i)}=X_{v_{ik}}^{(C_i)}$ for all $\eta \in \mathbb {F}_q \setminus \{0\}$.

If $X_{v_{11}}^{(C_1)}= \{C_1, C_{j_1}, C_{j_2}, \dots , C_{j_d}\}$, then $v_{11}C_{j_e}=0$ for all $C_{j_e} \in X_{v_{11}}^{(C_1)}$. Clearly, $v_{11}= (0,x,y)$, where $x,y \in \mathbb {F}_q$. Consequently, the following system of equations has a common non-trivial solution:

$$\begin{aligned} \begin{aligned} x\alpha _{j_1-2}&+ y\alpha _{j_1-3}=0 \\ x\alpha _{j_{2}-2}&+ y\alpha _{j_2-3}=0 \\&\vdots \\ x\alpha _{j_d-2}&+ y\alpha _{j_d-3}=0 \end{aligned} \end{aligned}$$

To have a common solution, we must have

$$\begin{aligned} \frac{\alpha _{j_1-2}}{\alpha _{j_1-3}}= \frac{\alpha _{j_2-2}}{\alpha _{j_{2}-3}}= \dots = \frac{\alpha _{j_{d}-2}}{\alpha _{j_{d}-3}}. \end{aligned}$$

Hence, we conclude that if a ratio of elements of the 2nd and 3rd rows of G repeats $r-1$ times, we get a subset $X_{v_{1k}}^{(C_1)}$ of X such that $\mid X_{v_{1k}}^{(C_1)}\mid =r$. Therefore, we can write X as:

$$\begin{aligned} X= X_{v_{11}}^{(C_1)} \cup X_{v_{12}}^{(C_1)} \cup \dots \cup X_{v_{1f}}^{(C_1)} \cup \dots \cup X_{v_{{1(q^2-1)}}}^{(C_1)}. \end{aligned}$$

(1)

Here, f is the number of different ratios of elements of the 2nd and 3rd rows of G except for $\frac{0}{0}$. Clearly, $\mid X_{v_{1k}}^{(C_1)} \mid \ge 2 \,\,\text {for all} \,\,1 \le k \le f$ and $X_{v_{1k}}^{(C_1)} = \{C_1\} \,\,\text {for all} \,\,f+1 \le k \le (q^2-1)$.

Consequently, we have the following result.

Theorem 4

If a ratio of elements of the 2nd and 3rd rows of G repeats $r-1$ times, then the ratio corresponds to a subset of X in (1) of order r.

By Theorem 1, we can always find a vector orthogonal to $C_i$ corresponding to a vector orthogonal to $C_1$. Therefore, the representation of X shown in (1) can be rewritten as:

$$\begin{aligned} X= X_{v_{i1}}^{(C_i)} \cup X_{v_{i2}}^{(C_i)} \cup \dots \cup X_{v_{if}}^{(C_i)} \cup \dots \cup X_{v_{i{(q^2-1)}}}^{(C_i)}, \end{aligned}$$

(2)

As $1 \le i \le u$, therefore, u different representations of X are as follows:

$$\begin{aligned} X= & {} X_{v_{11}}^{(C_1)} \cup X_{v_{12}}^{(C_1)} \cup \dots \cup X_{v_{1f}}^{(C_1)} \cup \dots \cup X_{v_{1{(q^2-1)}}}^{(C_1)}\\ X= & {} X_{v_{21}}^{(C_2)} \cup X_{v_{22}}^{(C_2)} \cup \dots \cup X_{v_{2f}}^{(C_2)} \cup \dots \cup X_{v_{2{(q^2-1)}}}^{(C_2)}\\&\vdots&\\ X= & {} X_{v_{u1}}^{(C_u)} \cup X_{v_{u2}}^{(C_u)} \cup \dots \cup X_{v_{uf}}^{(C_u)} \cup \dots \cup X_{v_{u{(q^2-1)}}}^{(C_u)}. \end{aligned}$$

Clearly, these u representations of X are such that $\mid X_{v_{1j}}^{(C_1)}\mid = \mid X_{v_{ik}}^{(C_i)}\mid$ for some $1 \le j,k \le f$.

Theorem 5

If $X= X_{v_{11}}^{(C_1)} \cup X_{v_{12}}^{(C_1)} \cup \dots \cup X_{v_{1f}}^{(C_1)} \cup \dots \cup X_{v_{1{(q^2-1)}}}^{(C_1)}$ has k different subsets of order r each, then k is a multiple of r.

Proof

Let $X_{v_{11}}^{(C_1)}$ be a subset of order r in

$$\begin{aligned} X= X_{v_{11}}^{(C_1)} \cup X_{v_{12}}^{(C_1)} \cup \dots \cup X_{v_{1f}}^{(C_1)} \cup \dots \cup X_{v_{1{(q^2-1)}}}^{(C_1)} \end{aligned}$$

(3)

By Theorem 1, $X_{v_{11}}^{(C_1)}$ produces r different subsets of order r each in (3). Without loss of generality, let these subsets be $X_{v_{11}}^{(C_1)}, X_{v_{12}}^{(C_1)}, \dots , X_{v_{1r}}^{(C_1)}$ such that $\mid X_{v_{11}}^{(C_1)}\mid =\mid X_{v_{12}}^{(C_1)}\mid =\dots = \mid X_{v_{1r}}^{(C_1)}\mid =r$. Further, let $X_{v_{1,{r+1}}}^{(C_1)}$ be another subset in (3) of order r. Again, by Theorem 1, there will be another r different subsets, $X_{v_{1,{r+1}}}^{(C_1)}, X_{v_{1,{r+2}}}^{(C_1)}, \dots , X_{v_{1,{2r}}}^{(C_1)}$(say) of order r each in (3). Continuing in this manner, the total number of different subsets of order r in (3) is a multiple of r. $\square$

In the following result, we count the total number of different subsets of order r in all u representations of X.

Theorem 6

If $X= X_{v_{11}}^{(C_1)} \cup X_{v_{12}}^{(C_1)} \cup \dots \cup X_{v_{1f}}^{(C_1)} \cup \dots \cup X_{v_{1{(q^2-1)}}}^{(C_1)}$ has k different subsets of order r each, then the number of different subsets of order r in all u representations of X is $\frac{uk}{r}$.

Proof

Let $\mid X_{v_{11}}^{(C_1)}\mid$=r. By Theorem 1, $X_{v_{11}}^{(C_1)}$ produces r different subsets in (3), $X_{v_{11}}^{(C_1)}, X_{v_{12}}^{(C_1)}, \dots , X_{v_{1r}}^{(C_1)}$ (say) such that each has order r. Again by Theorem 1, for each i with $1 \le i \le r$, $X_{v_{1i}}^{(C_1)}$ produces u different subsets of order r each in all u representations of X. Therefore, $X_{v_{11}}^{(C_1)}, X_{v_{12}}^{(C_1)}, \dots , X_{v_{1r}}^{(C_1)}$ collectively produce ur subsets of order r each. This collection of ur subsets includes $X_{v_{11}}^{(C_1)}, X_{v_{21}}^{(C_2)}, \dots , X_{v_{u1}}^{(C_u)}$. By Theorem 1, each $X_{v_{j1}}^{(C_j)}$, $1 \le j \le u$, repeats r times in this collection. Hence, $X_{v_{11}}^{(C_1)}, X_{v_{12}}^{(C_1)}, \dots , X_{v_{1r}}^{(C_1)}$ collectively produce u different subsets of order r each in all u representations of X. In other words, a collection of r subsets of (3) produces u different subsets of order r each. Therefore, if there are k different subsets of order r in (3), then these k subsets will produce $\frac{uk}{r}$ different subsets of order r. By Theorem 5, it will always be an integer. $\square$

Note that a subset of order r in (3) produces codewords of weight $u-r$. The total number of different subsets of order r in (3) can be counted by Theorem 4. Therefore, the total number of codewords in $\mathcal {M}_1^{(u)}$ of weight $u-r$, is given by the following theorem.

Theorem 7

Let $gcd(u,q-1)=1$. If there are k distinct ratios of elements of the 2nd and 3rd rows of G, each repeating $r-1$ times, then $A_{u-r}=\frac{u(q-1)k}{r}$.

Proof

Since $gcd(u,q-1)=1$, by Theorem 2, columns of G are pairwise linearly independent. Clearly, by the fact $X_{\eta v_{ik}}^{(C_i)}=X_{v_{ik}}^{(C_i)}$, Theorems 4 and 6, $A_{u-r}=\frac{u(q-1)k}{r}$. $\square$

Consequently, we have the following result to compute the weight distribution of $\mathcal {M}_1^{(u)}$.

Theorem 8

Let $\mathcal {M}_1^{(u)}=\langle g(x) \rangle$ be an irreducible cyclic code of length u and dimension 3 over $\mathbb {F}_q$ such that $gcd(u,q-1)=1$. Let there be $k_1$ distinct ratios each repeating $r_1-1$ times, $k_2$ distinct ratios each repeating $r_2-1$ times, ..., $k_t$ distinct ratios each repeating $r_t-1$ times in ratios of elements of the 2nd and 3rd rows of G (except for $\frac{0}{0}$). Then the weight distribution of $\mathcal {M}_1^{(u)}$ is given in Table 1.

Table 1 Weight distribution of $\mathcal {M}_1^{(u)}$ when $gcd(u,q-1)=1$

Case II    Let $1< gcd(u,q-1) <u$ and let the generator matrix of $\mathcal {M}_1^{(u)}$ be

$$\begin{aligned} G= \begin{pmatrix} \alpha _0 &{} \alpha _1 &{} \alpha _2 &{}\dots &{}\alpha _{u-4} &{}\alpha _{u-3} &{} 0 &{} 0 \\ 0 &{} \alpha _0 &{}\alpha _1 &{} \alpha _2 &{}\dots &{}\alpha _{u-4} &{}\alpha _{u-3} &{} 0 \\ 0 &{} 0 &{} \alpha _0 &{}\alpha _1 &{}\dots &{}\alpha _{u-5} &{} \alpha _{u-4} &{}\alpha _{u-3} \end{pmatrix}_{3 \times u}. \end{aligned}$$

Then by Theorem 3, we write G as

$$\begin{aligned} G=\begin{pmatrix} B_1&\vline&B_2&\vline&\cdots&\vline&B_{gcd(u,q-1)} \end{pmatrix}_{3 \times u}, \end{aligned}$$

where $B_i$ is a submatrix of order $3 \times \frac{u}{gcd(u,q-1)}$ and for every j, $2 \le j \le gcd(u,q-1)$, there exists some $y \in \mathbb {F}_q \setminus \{0\}$ such that $B_j=yB_1$, where

$$\begin{aligned} B_1= \begin{pmatrix} \alpha _0 &{} \alpha _1 &{} \alpha _2 &{}\dots &{}\alpha _{({u}/{gcd(u,q-1)})-3} &{} 0 &{} 0 \\ 0 &{} \alpha _0 &{} \alpha _1 &{}\dots &{}\alpha _{({u}/{gcd(u,q-1)})-4} &{}\alpha _{({u}/{gcd(u,q-1)})-3} &{} 0 \\ 0 &{} 0 &{} \alpha _0 &{}\dots &{}\alpha _{({u}/{gcd(u,q-1)})-5} &{} \alpha _{({u}/{gcd(u,q-1)})-4} &{}\alpha _{({u}/{gcd(u,q-1)})-3} \end{pmatrix}_{3 \times \frac{u}{gcd(u,q-1)}} \end{aligned}$$

and the columns of $B_1$ are pairwise linearly independent. To compute the weight distribution of $\mathcal {M}_1^{(u)}$, we need to count the number of zeros in $[a\,\, b\,\,c]B_1$, where $[a\,\, b\,\,c]$ is a non-zero row vector over $\mathbb {F}_q$. Since the columns of $B_1$ are pairwise linearly independent, therefore, we proceed as in Case I to count the number of zeros in $[a\,\, b\,\,c]B_1$. For this we consider $X= \{C_i: C_i\,\, \text {is a column of\,}B_1 \}$. By Theorem 4, to count the number of subsets of order r in (1), we need to count the ratios of elements of the 2nd and 3rd rows of $B_1$. Furthermore, by Theorem 3, any subset of order r in (1), produces codewords of weight $u-gcd(u,q-1)r$ in $\mathcal {M}_1^{(u)}$. Therefore, the following theorem gives the total number of codewords of weight $u-gcd(u,q-1)r$ in $\mathcal {M}_1^{(u)}$.

Theorem 9

Let $1<gcd(u,q-1)<u$. If there are k distinct ratios of elements of the 2nd and 3rd rows of $B_1$ each repeating $r-1$ times, then $A_{u-gcd(u,q-1)r}=\frac{u(q-1)k}{gcd(u,q-1)r}$.

Proof

Clearly, by the fact $X_{\eta v_{ik}}^{(C_i)}=X_{v_{ik}}^{(C_i)}$, Theorems 3, 4 and 5, $A_{u-gcd(u,q-1)r}=\frac{u(q-1)k}{gcd(u,q-1)r}$. $\square$

By Theorem 9, we have the following result to compute the weight distribution of $\mathcal {M}_1^{(u)}$.

Theorem 10

Let $\mathcal {M}_1^{(u)}=\langle g(x) \rangle$ be an irreducible cyclic code of length u and dimension 3 over $\mathbb {F}_q$ such that $1<gcd(u,q-1)<u$. In the ratios of elements of the 2nd and 3rd rows of $B_1$ (except for $\frac{0}{0}$), let there be $k_1$ distinct ratios each repeating $r_1-1$ times, $k_2$ distinct ratios each repeating $r_2-1$ times, ..., $k_t$ distinct ratios each repeating $r_t-1$ times. Then the weight distribution of $\mathcal {M}_1^{(u)}$ is given in Table 2.

Table 2 Weight distribution of $\mathcal {M}_1^{(u)}$ when $1<gcd(u,q-1)<u$

Note 1

It should be noted that if $u=3^k$ and $ord_u(q)=3$, then by Lemmas 4 and 6 of [19], $ord_{u/3}(q)=1$. Therefore, weight enumerator of $\mathcal {M}_1^{(u)}$ is: $(1+(q-1)z^{u/3})^3$ (see [23, Theorem 1 (B)]).

4 Weight enumerators of $m$-dimensional and 3$m$-dimensional irreducible cyclic codes of length $n$ over $\mathbb {F}_q$

In this section, we prove some results for any irreducible cyclic code of length n over $\mathbb {F}_q$, where $ord_n(q)$ is a divisor of $\frac{p^*n}{\kappa (n)}$ for any odd prime $p^*$. Recall that $\kappa (n)$ is the product of all distinct prime divisors of n. In Theorems 11 and 13, we prove that the weight enumerators of $p^*m$-dimensional and m-dimensional irreducible cyclic codes of length n can be determined with the help of $p^*$-dimensional and 1-dimensional irreducible cyclic codes, respectively, where m is a divisor of $\frac{n}{\kappa (n)}$. However, the weight distributions of $p^*$-dimensional irreducible cyclic codes are not known in general (see [3, 4]). Note that in Section 3 of this paper, we have obtained the weight distributions of 3-dimensional irreducible cyclic codes. Thus, by choosing $p^*=3$ in the following results, we can compute the weight enumerators of all m-dimensional and 3m-dimensional irreducible cyclic codes of length n over $\mathbb {F}_q$.

Theorem 11

Let $gcd(n,p^*)=1$ and m be a divisor of $\frac{n}{\kappa (n)}$. If $ord_n(q)=p^*m$, then $\mathcal {M}_1^{(n)}=\mathcal {C}_1 \oplus \mathcal {C}_2 \oplus \dots \oplus \mathcal {C}_m$, where $\mathcal {C}_1$, $\mathcal {C}_2$, ..., $\mathcal {C}_m$ are equivalent irreducible cyclic codes such that the weight distribution of each $\mathcal {C}_i$ is the same as the weight distribution of $\mathcal {M}_1^{(n/m)}$ over $\mathbb {F}_q$.

Proof

Since $ord_n(q)\!=\!p^*m$, therefore, the q-cyclotomic coset $\texttt {C}_1^{(n)}\!=\!\{ 1,q, q^2, \dots , q^{p^*m-1}\}$. Let $\mathcal {M}_1^{(n)}=\langle g_1(x) \rangle$. Then $g_1(x)=\frac{x^n-1}{(x-\lambda )(x-\lambda ^q)(x-\lambda ^{q^2})\dots (x-\lambda ^{q^{p^*m-1}})}$, where $\lambda$ is a fixed primitive nth root of unity in some extension of $\mathbb {F}_q$. Note that $(x-\lambda )(x-\lambda ^q)(x-\lambda ^{q^2})\dots (x-\lambda ^{q^{p^*m-1}})=(x^m-\lambda ^m)(x^m-\lambda ^{mq})\dots (x^m-\lambda ^{mq^{p^*-1}})$, therefore,

$$\begin{aligned} g_1(x)=\frac{x^n-1}{(x^m-\lambda ^m)(x^m-\lambda ^{mq})\dots (x^m-\lambda ^{mq^{p^*-1}})} = \frac{y^{{n}/{m}}-1}{(y-\gamma )(y-\gamma ^q)\dots (y-\gamma ^{q^{p^*-1}})}, \end{aligned}$$

(4)

where $x^m=y$ and $\lambda ^m=\gamma$ is a primitive (n/m)th root of unity. By our choice, $ord_{{n}/{m}}(q)=p^*$, therefore by (4), $\mathcal {C}=\langle g(y) \rangle$ is a $p^*$-dimensional cyclic code of length n/m, where $g(y)=\frac{y^{{n}/{m}}-1}{(y-\gamma )(y-\gamma ^q)\dots (y-\gamma ^{q^{p^*-1}})}= \alpha _0 + \alpha _1y+ \cdots + \alpha _{({n}/{m})-p^*}y^{({n}/{m})-p^*}$. Consequently, $g_1(x)=g(x^m)= \alpha _0 + \alpha _1x^m+ \cdots + \alpha _{({n}/{m})-p^*}x^{{n}-p^*m}$. Thus, the generator matrix of $\mathcal {M}_1^{(n)}$ is

$$\begin{aligned} G= \begin{pmatrix} \alpha _0 \,\,\,\, \,\,0\,\,\dots \,\,0 \,\,\,\, \,\, \alpha _1 \,\,\,\, \,\, 0\,\,\dots \,\,0\,\, \,\,\,\, \alpha _2 \,\,\,\, \,\, \dots \,\,\,\, \,\, \alpha _{({n}/{m})-p^*} \,\,\,\, \,\, 0 \,\,\,\, \,\, 0 \,\,\,\, \,\,\dots \,\,\,\, \,\,0\\ 0 \,\,\,\,\,\,\, \,\,\alpha _0 \,\,\,\, \,\,0\,\,\dots \,\,0 \,\,\,\, \,\, \alpha _1 \,\,\,\, \,\, 0\,\,\dots \,\,0\,\, \,\,\,\, \alpha _2 \,\,\,\, \,\, \dots \,\,\,\, \,\, \alpha _{({n}/{m})-p^*} \,\, \,\, 0 \,\,\,\, \,\,\dots \,\,\,\, \,\,0\\ \vdots \,\,\,\,\, \,\,\,\,\,\, \vdots \,\,\,\,\,\,\, \,\,\,\,\, \,\,\,\, \vdots \,\,\,\,\, \,\,\,\, \,\,\,\,\,\,\, \,\,\ \,\,\,\, \,\,\ \vdots \,\, \,\,\, \,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\ \vdots \,\,\,\,\,\, \,\,\, \,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\ \vdots \,\,\,\,\,\, \,\,\, \,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \vdots \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,0 \,\, \dots \,\,0 \,\,\,\,\,\,\, \,\,\ \alpha _0 \,\,\,\, \,\,0\,\,\dots \,\,0 \,\,\,\, \,\, \alpha _1 \,\,\,\, \,\, 0\,\,\dots \,\,0\,\, \,\,\,\, \alpha _2 \,\,\,\, \,\, \dots \,\,\,\, \,\, \alpha _{({n}/{m})-p^*} \end{pmatrix}_{p^* m \times n} \end{aligned}$$

From G, it is clear that

$$\mathcal {M}_1^{(n)}=\mathcal {C}_1 \oplus \mathcal {C}_2 \oplus \dots \oplus \mathcal {C}_m,$$

where $\mathcal {C}_i= \langle x^{i-1}g(x^m), x^{m+i-1}g(x^m), \dots , x^{(p^*-1)m+i-1}g(x^m) \rangle$. Clearly, $\mathcal {C}_1$, $\mathcal {C}_2$, ..., $\mathcal {C}_m$ are equivalent irreducible cyclic codes and have the same weight distribution. From above, $\mathcal {C}_1= \langle g(x^m), x^{m}g(x^m),\dots , x^{(p^*-1)m}g(x^m) \rangle$. Therefore, the weight distribution of $\mathcal {C}_1$ is the same as the weight distribution of the code $\mathcal {M}_1^{(n/m)}=\langle g(x) \rangle$ over $\mathbb {F}_q$. $\square$

By our choice of $ord_{{n}}(q)$ in the above theorem, $\mathcal {M}_1^{(n)}$ is a $p^*m$-dimensional irreducible cyclic code, and the following corollary provides the weight enumerator of any such code.

Corollary 12

If $ord_n(q)=p^*m$, then the weight enumerator of $\mathcal {M}_1^{(n)}$ is $(A(z))^m$, where A(z) is the weight enumerator of $\mathcal {M}_1^{({n}/{m})}$.

Theorem 13

Let m be a divisor of $\frac{n}{\kappa (n)}$. If $ord_n(q)=m$, then $\mathcal {M}_1^{(n)}=\mathcal {C}_1 \oplus \mathcal {C}_2 \oplus \dots \oplus \mathcal {C}_m$, where each $\mathcal {C}_i$ is equivalent to a 1-dimensional irreducible cyclic code of length n/m over $\mathbb {F}_q$.

Proof

Since $ord_n(q)=m$, therefore, the q-cyclotomic coset $\texttt {C}_1^{(n)}=\{ 1,q, q^2, \dots , q^{m-1}\}$. Let $\mathcal {M}_1^{(n)}=\langle g_1(x) \rangle$. Then $g_1(x)=\frac{x^n-1}{(x-\lambda )(x-\lambda ^q)(x-\lambda ^{q^2})\dots (x-\lambda ^{q^{m-1}})}$, where $\lambda$ is a fixed primitive nth root of unity in some extension of $\mathbb {F}_q$. Note that $(x-\lambda )(x-\lambda ^q)(x-\lambda ^{q^2})\dots (x-\lambda ^{q^{m-1}})=(x^m-\lambda ^m)$, therefore,

$$\begin{aligned} g_1(x)=\frac{x^n-1}{(x^m-\lambda ^m)}= \frac{y^{{n}/{m}}-1}{(y-\gamma )}, \end{aligned}$$

where $x^m=y$ and $\lambda ^m=\gamma$ is a primitive (n/m)th root of unity. Let $g(y)=\frac{y^{{n}/{m}}-1}{y-\gamma }= \gamma ^{({n}/{m})-1}+ \gamma ^{({n}/{m})-2}y + \cdots + \gamma ^2y^{({n}/{m})-3}+ \gamma y^{({n}/{m})-2}+ y^{({n}/{m})-1}$. Therefore, $g_1(x)= \gamma ^{({n}/{m})-1}+ \gamma ^{({n}/{m})-2}x^m + \cdots +\gamma x^{n-2m}+ x^{n-m}$. Clearly, $\mathcal {M}_1^{(n)}=\mathcal {C}_1 \oplus \mathcal {C}_2 \oplus \dots \oplus \mathcal {C}_m,$ where each $\mathcal {C}_i$ is a block code such that $\mathcal {C}_i$=$\langle x^{i-1}g(x^m) \rangle$ and is equivalent to a 1-dimensional irreducible cyclic code $\mathcal {C}^\prime$=$\langle g(x) \rangle$. $\square$

In the above theorem, $ord_n(q)=m$ suggests that $\mathcal {M}_1^{(n)}$ is an m-dimensional irreducible cyclic code. The following corollary gives the weight enumerator of any such code.

Corollary 14

If $ord_n(q)=m$, then the weight enumerator of $\mathcal {M}_1^{(n)}$ is $(1+(q-1)z^{{n}/{m}})^m$.

Note that if $ord_n(q)=(p^*)^tm$ and $gcd(n,(p^*)^t)=(p^*)^t$ such that $ord_{n/(p^{*})^{t}m}(q)=1$, then the weight enumerator of $(p^*)^tm$-dimensional codes can also be obtained by Corollary 14 (see Example 1).

Further, let $gcd(n,s)=v$, where $1 \le s \le n$. Then $\mathcal {M}_s^{(n)}$ and $\mathcal {M}_v^{(n)}$ are equivalent codes. We write $n=n_1n_2$, where $n_1$ is such that $ord_{p_i}(q)=p^*$ for every prime divisor $p_i$ of $n_1$ and $n_2$ is such that $ord_{p_i^\prime }(q)=1$ for every prime divisor $p_i^\prime$ of $n_2$. Depending on $n_1$, $n_2$, and v, we have three cases: when (i) $n_1 \mid v$, (ii) $n_2 \mid v$, and (iii) neither $n_1 \mid v$ nor $n_2 \mid v$.

Now, we compute the weight enumerators of $\mathcal {M}_v^{(n)}$ for the above three cases:

Theorem 15

If $n_1 \mid v$, then the weight enumerator of $\mathcal {M}_v^{(n)}$ is $(1+(q-1)z^{{n}/{h}})^h$, where $h=ord_{{n}/{v}}(q)$.

Proof

Let h be the smallest positive integer such that $vq^h \equiv v \pmod {n}$. This implies that $q^h \equiv 1\pmod {\frac{n}{v}}$. Clearly, $h=ord_{{n}/{v}}(q)$. Consequently, $\mathcal {M}_v^{(n)}$ is an h-dimensional irreducible cyclic code of length n. Further, $\texttt {C}_v^{(n)}=\{v,vq, \dots , vq^{h-1}\}$ implies $g_v^{(n)}(x)= \frac{x^n-1}{m_v^{(n)}(x)}= \frac{(x^{{n}/{v}}-1)(1+x^{{n}/{v}}+ \dots + x^{{n(v-1)}/{v}})}{m_v^{(n)}(x)}$, where $m_v^{(n)}(x)$ is the minimal polynomial corresponding to the cyclotomic coset $\texttt {C}_v^{(n)}$.

Let $\mathcal {C}= \langle \frac{x^{{n}/{v}}-1}{m_v^{(n)}(x)} \rangle$. Clearly, the dimension of $\mathcal {C}$ is h, and by Theorem 13, $\mathcal {C}= \mathcal {C}_1 \oplus \mathcal {C}_2 \oplus \dots \oplus \mathcal {C}_{h}$, where $\mathcal {C}_i$’s are equivalent 1-dimensional irreducible cyclic codes. By Corollary 14, the weight enumerator of $\mathcal {C}$ is $(1+(q-1)z^{{n}/{vh}})^h$. Hence, the weight enumerator of $\mathcal {M}_v^{(n)}= \langle g_v^{(n)}(x)\rangle$ is $(1+(q-1)z^{{n}/{h}})^h$. $\square$

Theorem 16

If $n_2\mid v$, then the weight enumerator of $\mathcal {M}_v^{(n)}$ is $(A(z^v))^{{h}/{p^*}}$, where A(z) is the weight enumerator of $\mathcal {M}_1^{({p^*n}/{v{h}})}$ and $h=ord_{{n}/{v}}(q)$.

Proof

Let h be the smallest positive integer such that $vq^h \equiv v \pmod {n}$. This implies that $q^h \equiv 1 \pmod {\frac{n}{v}}$. Clearly, $h=ord_{{n}/{v}}(q)$. Consequently, $\mathcal {M}_v^{(n)}$ is an h-dimensional irreducible cyclic code of length n. Further, $\texttt {C}_v^{(n)}=\{v,vq, \dots , vq^{h-1}\}$ implies $g_v^{(n)}(x)= \frac{x^n-1}{m_v^{(n)}(x)}= \frac{(x^{{n}/{v}}-1)(1+x^{{n}/{v}}+ \dots + x^{{n(v-1)}/{v}})}{m_v^{(n)}(x)}$, where $m_v^{(n)}(x)$ is the minimal polynomial corresponding to the cyclotomic coset $\texttt {C}_v^{(n)}$.

Let $\mathcal {C}= \langle \frac{x^{{n}/{v}}-1}{m_v^{(n)}(x)} \rangle$. Clearly, the dimension of $\mathcal {C}$ is h. By Theorem 11, $\mathcal {C}= \mathcal {C}_1 \oplus \mathcal {C}_2 \oplus \dots \oplus \mathcal {C}_{{h}/{p^*}}$, where $\mathcal {C}_i$’s are equivalent irreducible cyclic codes and the weight distribution of each $\mathcal {C}_i$ is the same as the weight distribution of $\mathcal {M}_1^{(p^*n/vh)}$ over $\mathbb {F}_q$. Evidently, $\mathcal {M}_1^{(p^*n/vh)}$ is a $p^*$-dimensional irreducible cyclic code and $gcd(p^*n/{vh},q-1)=1$. Let A(z) be the weight enumerator of $\mathcal {M}_1^{(p^*n/vh)}$, then by Corollary 12, the weight enumerator of $\mathcal {C}$ is $(A(z))^{{h}/{p^*}}$. Hence, the weight enumerator of $\mathcal {M}_v^{(n)}= \langle g_v^{(n)}(x)\rangle$ is $(A(z^v))^{{h}/{p^*}}$. $\square$

Theorem 17

If v is such that neither $n_1 \mid v$ nor $n_2 \mid v$, then the weight enumerator of $\mathcal {M}_v^{(n)}$ is $(A(z^v))^{{h}/{p^*}}$, where A(z) is the weight enumerator of $\mathcal {M}_1^{(p^*n/vh)}$ and $h=ord_{{n}/{v}}(q)$.

Proof

The proof is similar to that of Theorem 16 and is thus omitted. $\square$

Clearly, if we choose $p^*=3$, then A(z), as mentioned in Theorems 16 and 17, can be obtained from Tables 1 and 2, respectively. The reason we choose $p^*=3$ is as follows:

One can easily observe from the properties of linear codes that the computation of weight distribution of an irreducible cyclic code $\mathcal {M}_1^{(n)}$ over $\mathbb {F}_q$ is directly related to the counting of either all lines $a_1x_1=0$, $a_1x_1+a_2x_2=0$, all planes $a_1x_1+a_2x_2+a_3x_3=0$, ..., or all similar geometric structures $a_1x_1+a_2x_2+a_3x_3 +\cdots +a_nx_n=0$, depending on the dimension of the code. Here, $a_1$, $a_2$, ..., $a_n$ are the coefficients of the generator polynomial of $\mathcal {M}_1^{(n)}$. For $p^*=2$, Riddhi et al. [15] observed that it is sufficient to count the lines of the form $a_1x_1=0$ to compute the weight distribution of an irreducible cyclic code. Similarly, for $p^*=3$, we need to count the lines of the form $a_1x_1+a_2x_2=0$. In Section 3, we have counted all such lines. But for $p^* \ge 4$, it becomes quite tedious to count all geometric structures of the form $a_1x_1+a_2x_2+\dots +a_{p^*-1}x_{p^*-1}=0$. Therefore, in the present paper, we have chosen $p^*=3$, as we can count all the lines explicitly in this case.

5 Some Examples

Example 1

Consider an irreducible cyclic code of length 117 over $\mathbb {F}_{79}$. Here $n=117=9 \cdot 13$ such that $ord_9(79)=3$ and $ord_{13}(79)=1$. Therefore, $ord_{9 \cdot 13}(79)=3$. Consequently, $\mathcal {M}_1^{(117)}$ is a 3-dimensional irreducible cyclic code. Thus, by Corollary 14, its weight enumerator is $(1+78z^{39})^3=1+474552z^{117}+234z^{39}+18252z^{78}$.

Example 2

Consider irreducible cyclic codes of length $n=7 \cdot 5^2$ over $\mathbb {F}_{11}$. It can be easily seen that there are 27 distinct 11-cyclotomic cosets modulo 175. Thus, there are 27 distinct irreducible cyclic codes of length 175 over $\mathbb {F}_{11}$. Note that $ord_7(11)=3$ and $ord_{5}(11)=1$. Therefore, by Lemmas 4 and 6 of [19], $ord_{7 \cdot 5^2}(11)=3\cdot 5$. Clearly, m is a divisor of 5 and has two choices viz. 1 and 5. Consequently, the aforementioned codes are either 1-dimensional, 3-dimensional, 5-dimensional, or 15-dimensional. Since $\mathcal {M}_s^{(n)}$ and $\mathcal {M}_v^{(n)}$ are equivalent codes if $gcd(n,s)=v$, where v is a divisor of 175, therefore, we only need to compute the weight enumerators of $\mathcal {M}_1^{(175)}$, $\mathcal {M}_5^{(175)}$, $\mathcal {M}_7^{(175)}$, $\mathcal {M}_{5^2}^{(175)}$, and $\mathcal {M}_{35}^{(175)}$.

First, we compute the weight enumerator of $\mathcal {M}_1^{(35)}=\langle g(x) \rangle$, where $g(x)=x^{32} + x^{31} + 2x^{30} + 8x^{29} + 4x^{28} + 9x^{25} + 9x^{24} + 7x^{23} + 6x^{22} + 3x^{21} + 4x^{18} + 4x^{17} + 8x^{16} + 10x^{15} + 5x^{14} + 3x^{11} + 3x^{10} + 6x^9 + 2x^8 + x^7 + 5x^4 + 5x^3 + 10x^2 + 7x + 9$. Clearly, by Theorem 10, in the ratios of elements of the 2nd and 3rd rows of $B_1$, there are 6 distinct ratios viz. $\infty , 2,3,6,1$ and 0, each occurring once only. The weight distribution of $\mathcal {M}_1^{(35)}$ is given in Table 3, and thus its weight enumerator, $A(z)=1 + 210z^{25}+420z^{30}+700z^{35}$.

Table 3 Weight distribution of $\mathcal {M}_1^{(35)}$

Next, we consider $\mathcal {M}_1^{(175)}$. Since $ord_{7 \cdot 5^2}(11)=15$, therefore, $\mathcal {M}_1^{(175)}$ is a 15-dimensional code. By Corollary 12, its weight enumerator is: $(A(z))^5= (1 + 210z^{25}+420z^{30}+700z^{35})^5.$

Further, the weight enumerator of $\mathcal {M}_7^{(175)}$ is calculated by Theorem 15. In this case, $v=7$, ${n}/{v}=5^2$ and $ord_{{n}/{v}}(11)=5$ i.e. $h=5$. Thus, the weight enumerator of $\mathcal {M}_7^{(175)}$ is: $(1+10z^{35})^5=1+50z^{35}+1000z^{70}+10,000z^{105}+50,000z^{140}+ 1,00,000z^{175}.$

Similarly, by Theorem 15, the weight enumerator of $\mathcal {M}_{35}^{(175)}$ is: $1+10z^{175}$. By Theorem 16, the weight enumerator of $\mathcal {M}_{5^2}^{(175)}$ is $A^\prime (z^{25})$, where $A^\prime (z)$ is the weight enumerator of $\mathcal {M}_{1}^{(7)}$. Since $gcd(7,10)=1$, therefore, by Theorem 8, its weight distribution is given in Table 4. Consequently, $A^\prime (z)= 1+210z^5+420z^6+700z^7$. Therefore, the weight enumerator of $\mathcal {M}_{5^2}^{(175)}$ is: $1+210z^{125}+ 420z^{150}+ 700 z^{175}$.

Table 4 Weight distribution of $\mathcal {M}_1^{(7)}$

Finally, by Theorem 17, the weight enumerator of $\mathcal {M}_{5}^{(175)}$ is $A(z^5)$, where A(z) is the weight enumerator of $\mathcal {M}_{1}^{(35)}$. Since $A(z)=1 + 210z^{25}+420z^{30}+700z^{35}$, therefore, the weight enumerator of $\mathcal {M}_{5}^{(175)}$ is: $1+210z^{125}+ 420z^{150}+ 700 z^{175}$.

Example 3

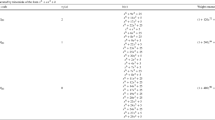
Table 5 gives the weight enumerators of some irreducible cyclic codes of different lengths.

Table 5 Weight enumerators of codes of different lengths

Further, the reader might think about how one can find the pair (n, q) such that the multiplicative order of q modulo n is a divisor of $\frac{3n}{\kappa (n)}$. For finding q for any given length n, we proceed as follows: Let $p_1$, $p_2$, ..., $p_{r-1}$, $p_{r}$, ..., $p_{t}$ be the prime divisors of n. To find q such that

$$\begin{aligned} ord_{p_{i}^{b_i}}(q)={\left\{ \begin{array}{ll} 3 &{} \text {if} \,\,\,\,1 \le i \le r-1;\\ 1 &{} \text {if} \,\,\,\,r\le i \le t\\ \end{array}\right. } \end{aligned}$$

for some integer $b_i$($1 \le i \le t$), we need to compute the common solution of the following congruences:

$$\begin{aligned} x\equiv & {} k_1 \pmod {p_1^{b_1}}\\ x\equiv & {} k_2 \pmod {p_2^{b_2}}\\ \vdots{} & {} \\ x\equiv & {} k_{r-1} \pmod {p_{r-1}^{b_{r-1}}}\\ x\equiv & {} 1 \pmod {p_{r}^{b_r}}\\ \vdots{} & {} \\ x\equiv & {} 1 \pmod {p_{t}^{b_t}}, \end{aligned}$$

where $k_i \equiv \alpha _i^{\frac{\phi (p_i^{b_i})}{3}}\pmod {p_i^{b_i}}$, $1 \le i \le r-1$, $\alpha _i$ is a primitive root modulo $p_i^{b_i}$, and $\phi$ denotes Euler’s Phi function. We can find x by the Chinese Remainder theorem. Let one value of x be k, then all other values will be of the form $p_1^{b_1}p_2^{b_2}\cdots p_{r-1}^{b_{r-1}}p_{r}^{b_r} \cdots p_{t}^{b_t}l+k$, where l is any positive integer. All those values of x that are either a prime or a prime power will be possible choices for q. Also, note that we have not restricted q to be less than n. Our results hold for $q >n$ as well.

Example 4

Let $n=13 \cdot 67\cdot 7$. To obtain q such that $ord_{13}(q)=3$, $ord_{67}(q)=3$, and $ord_{7}(q)=1$, we find $k_1\pmod { 13}$ and $k_2\pmod {67}$. Since 2 and 7 are primitive roots modulo 13 and 67, respectively, therefore, $k_1 \equiv 3 \pmod {13}$ and $k_2 \equiv 29 \pmod {67}$. Next, we find the common solution of the following congruences:

$$\begin{aligned} \begin{aligned} x&\equiv 3 \pmod {13}\\ x&\equiv 29 \pmod {67}\\ x&\equiv 1 \pmod { 7}. \end{aligned} \end{aligned}$$

By the Chinese remainder Theorem, one of the values of x is 29. Since 29 is a prime number, therefore, one choice of q is 29 for given n.

Example 5

Let $n = 3^3\cdot 5 = 135$, and q be such that $ord_{3^3}(q) = 3$ and $ord_{5}(q) = 1$. Since 5 is a primitive root modulo 27, therefore, $k_1 \equiv 19 \pmod {27}$. To find q, we need to obtain the common solution of the following congruences:

$$\begin{aligned} \begin{aligned} x&\equiv 1 9 \pmod {27}\\ x&\equiv 1 \pmod {5}. \end{aligned} \end{aligned}$$

By the Chinese Remainder Theorem, 46 is one of the common solutions of the above congruences and other solutions will be of the form $135l+46$. But 46 is not a prime number. Therefore, we need to find a solution that is either a prime or a prime power. If we take $l=1$, we get 181, which is a prime number. Similarly, for $l=7$, we get another prime 991. Thus, there are many choices of q for $n=135$.

Example 6

Let $n=7^{100}\cdot 11^{101}$, and q be such that $ord_{7^{100}}(q) = 3\cdot 7^{98}$ and $ord_{11^{101}}(q) = 11^{100}$. By Lemmas 4 and 6 of [19], $ord_{7^2}(q) = 3$ and $ord_{11}(q) = 1$. Since 5 is a primitive root modulo 49, therefore, $k_1 \equiv 18 \pmod {49}$. Now, we find the common solution of the following congruences:

$$\begin{aligned} \begin{aligned} x&\equiv 18 \pmod {49}\\ x&\equiv 1 \pmod {11}. \end{aligned} \end{aligned}$$

Clearly, 67 is one such solution. Since 67 is a prime number, therefore, one possible value of q is 67 for given n.

Further, if we fix q, then the prime factorization of $q^3-1$ decides the value of n. In other words, if $q^3-1= 2^ap_1^{\alpha _1}p_2^{\alpha _2}\dots p_t^{\alpha _t}$, then $n=p_1^{\beta _1}p_2^{\beta _2}\dots p_t^{\beta _t}$(because we are studying codes of odd length), where $\beta _i \ge 1$.

Example 7

If we choose $q=5$, then $q^3-1=2^2\cdot 31$ implies that we can obtain the weight enumerators of all irreducible cyclic codes of length $n=31^{\beta _1}$, where $\beta _1 \ge 1$. Similarly, for $q=29$, we can obtain the weight enumerators of all irreducible cyclic codes of length $n=7^{\beta _1} 13^{\beta _2} 67^{\beta _3}$, where at least one of $\beta _i \ge 1$.

6 Conclusion

In this paper, we have obtained the weight enumerators of all m-dimensional and 3m-dimensional irreducible cyclic codes of odd length n over $\mathbb {F}_q$ with the help of the weight enumerators of 1-dimensional and 3-dimensional irreducible cyclic codes of length n/m, respectively. It would be interesting to find: (i) how codes of even length n over $\mathbb {F}_q$ behave (ii) whether the technique used, in this paper, to compute the weight enumerator of any 3-dimensional irreducible cyclic code can be extended to four or higher-dimensional irreducible cyclic codes.