A correction on the determination of the weight enumerator polynomial of some irreducible cyclic codes

Abstract

A classification that shows explicitly all possible weight enumerator polynomials for every irreducible cyclic code of length n over a finite field $\mathbb {F}_q$, in the particular case where each prime divisor of n is also a divisor of $q-1$, was recently given in Brochero Martínez and Giraldo Vergara (Des Codes Cryptogr 78:703–712, 2016). However, as we will see next, such classification is incomplete. Thus, the purpose of this work is to use an already known identity among the weight enumerator polynomials, in order to complete such classification. As we will see later, by means of this identity, we not only complete, in an easier way, this classification, but we also find out the nature of the weight distributions of the class of irreducible cyclic codes studied in Brochero Martínez and Giraldo Vergara (2016).

1 Introduction

Let $\mathbb {F}_9=\mathbb {F}_3(\gamma )$, where $\gamma ^2+\gamma +2=0$. Since $h(x)=x^2+x+2$ is a primitive polynomial over $\mathbb {F}_3$, it should be clear that h(x) is also the parity-check polynomial of a one-weight irreducible cyclic code over $\mathbb {F}_3$, of length $n=8$, and dimension two, whose weight enumerator polynomial is $1+8z^6$. Now, it is quite clear that each prime divisor of n is also a divisor of $q-1$, where $q=3$. However, it is also easy to check that the previous weight enumerator polynomial was excluded from the classification of the weight enumerator polynomials that correspond to the class of irreducible cyclic codes that were recently studied in [1]. In consequence, our counterexample shows that such classification is incomplete. Thus, the purpose of this work is to use an already known identity among the weight enumerator polynomials (see, for example, [3] and [4]), in order to complete such classification. As we will see later, by means of this identity we not only complete, in an easier way, this classification, but we also find out the nature of the weight distributions of the class of irreducible cyclic codes studied in [1].

2 Definitions, notations and preliminary results

First of all, we set, for the rest of this work, the following:

Notation By using p, t, q, n and k, we will denote five positive integers such that p is a prime number, $q = p^t$, $\gcd (q,n)=1$ and $k=\text{ ord }_{n}(q)$, where, as usual, $\text{ ord }_{n}(q)$ denotes the multiplicative order of q modulo n. From now on $\gamma$ will denote a fixed primitive element of $\mathbb {F}_{q^k}$, and for any integer a, the polynomial $h_a(x) \in \mathbb {F}_{q}[x]$ will denote the minimal polynomial of $\gamma ^{-a}$. For any integer y, $\text{ rad }(y)$ will denote the radical of y, that is, if $y=p_1^{e_1} \cdot p_2^{e_2} \cdots p_l^{e_l}$ is the factorization of y in prime factors, then $\text{ rad }(y)=p_1 \cdot p_2 \cdots p_l$.

We now recall the following basic definition (see for example [5]).

Definition 1

Let $h(x) \in \mathbb {F}_q[x]$, be a nonzero polynomial, such that $h(0)\ne 0$. Then, the least positive integer e for which h(x) divides $x^e-1$ is called the order of h(x) and is denoted by $\text{ ord }(h(x))$.

Remark 1

Note that thanks to Part (vi) of Theorem 3.33 in [5], we have that $\text{ ord }(h_a(x))=\frac{n}{\gcd (n,a)}$, for any integer a, such that $\text{ ord }(h_a(x))|n$.

The following simple result will be useful later.

Lemma 1

With our current notation, let u, f and s be positive integers such that $u \ge 2$, $u | (q+1)$, $f=\text{ ord }_{u}(p)$, and $s=(2t)/f$. Then f is even and $p^{f/2} \equiv -1 \pmod {u}$, if $u>2$. In addition, we also have that s is even if and only if $u=2$.

Proof

If $u=2$, clearly $f=1$, and hence, s is even. Suppose now that $u>2$. Since $q=p^t \equiv -1 \pmod {u}$, we take v to be the smallest positive integer such that $p^v \equiv -1 \pmod {u}$. Consequently, $f=2v$ and $t=vw$ for some odd integer w. Therefore f is even, $p^{f/2} \equiv -1 \pmod {u}$, and $s=w$. $\square$

As we will see later, the weight distribution of an irreducible cyclic code, that belongs to the family of codes studied here, can be determined either through the weight distribution of a one-weight irreducible cyclic code or through the weight distribution of a semiprimitive two-weight irreducible cyclic code. Therefore the following characterizations, for those two types of irreducible cyclic codes, are important for this work (see [6, 7]):

Theorem 1

With our current notation, let a be any integer. Also let k, $\varDelta$, u and n be positive integers in such a way that $\varDelta =\frac{q^k-1}{q-1}$, $u=\gcd (\varDelta ,a)$ and $n=\frac{q^k-1}{\gcd (q^k-1,a)}$. Assume that $\deg (h_a(x))=k$. Then, $h_a(x)$ is the parity-check polynomial of an [n, k] one-weight irreducible cyclic code, over $\mathbb {F}_{q}$, whose nonzero weight is $\frac{n}{\varDelta } q^{k-1}$, if and only if $u=1$.

Table 1 Weight distribution of a semiprimitive two-weight code $\mathcal{C}$. Here $s=(k t)/f$, where $f=\text{ ord }_{u}(p)$ and $u=\gcd (\varDelta ,a)$.

Theorem 2

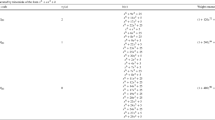
Consider the same notation and assumption as in Theorem 1. Define $f=\text{ ord }_{u}(p)$ (observe that $\gcd (p,u)=1$). Then $h_a(x)$ is the parity-check polynomial of a semiprimitive two-weight irreducible cyclic code, $\mathcal{C}$, if and only if $u=2$ or $u > 2$, f is even and $p^{f/2} \equiv -1 \pmod {u}$. In addition, if $\mathcal{C}$ is a semiprimitive two-weight irreducible cyclic code, then $\mathcal{C}$ is an [n, k] cyclic code over $\mathbb {F}_{q}$, with the weight distribution given in Table 1.

It is already known an identity that relates the weight distributions of some cyclic codes through the powers of their corresponding weight enumerator polynomials. An initial version of this identity was presented in [4] and in [3] (see particularly Lemma 4.5 and Theorem 5.1 in [3]). Since this identity is of main importance for this work, we now recall such a result by means of the following:

Theorem 3

For suitable integers n, k and d, let $\mathcal{C}$ be an [n, k, d] cyclic code, over $\mathbb {F}_{q}$, with parity-check polynomial h(x), and whose weight enumerator polynomial is A(z). Let also r be any positive integer, such that $\gcd (q,r)=1$. Then, the polynomial $h(x^r)$ is the parity-check polynomial of an [nr, kr, d] cyclic code, whose weight enumerator polynomial, B(z), is $B(z)=A(z)^r$.

Now, by considering the previous theorem, and Theorem 3.35 in [5], we now present a new version of the identity in Theorem 3 that considers only the weight enumerator polynomials among irreducible cyclic codes.

Theorem 4

For suitable integers n, k and d, let $\mathcal{C}$ be an [n, k, d] irreducible cyclic code, over $\mathbb {F}_{q}$, with parity-check polynomial h(x), and whose weight enumerator polynomial is given by A(z). Suppose that h(x) has order e, and let $r \ge 2$ be an integer whose prime factors divide e but not $(q^k-1)/e$. Assume also that $q^k \equiv 1 \pmod {4}$, if 4|r. Then $h(x^r)$ will be the parity-check polynomial of an [nr, kr, d] irreducible cyclic code, whose weight enumerator polynomial, B(z), is $B(z)=A(z)^r$.

3 The weight distribution of some irreducible cyclic codes with a particular type of length

In this section we are going to use the characterizations in Theorems 1 and 2, and also the identity in Theorem 4, in order to give the full weight distribution for the class of irreducible cyclic codes, over $\mathbb {F}_q$, whose length n satisfies $\text{ rad }(n) | (q-1)$. As we will see later, our results in this section not only correct the incomplete classification in [1], but also offer a shorter proof for such results which allows us to find out the nature of the weight distributions of the class of irreducible cyclic codes studied in [1]. Thus, we begin our study with the following result that was originally presented in [1] (see Theorem 1 therein).

Theorem 5

With our current notation, suppose that $\text{ rad }(n) | (q-1)$. Thus, if $8 \not \mid n$ or $q \not \equiv 3 \pmod {4}$, then every irreducible cyclic code of length n over $\mathbb {F}_{q}$ is an $[n,r,\frac{n}{r}]$ code where r divides $\frac{n}{\gcd (n,q-1)}$ and its weight enumerator polynomial is $(1+(q-1)z^{\frac{n}{r}})^r$.

Proof

Let $\mathcal{C}$ be an irreducible cyclic code of length n. Thus, thanks to Delsarte’s Theorem (see, for example, [2]), there must exist an integer a such that $h_a(x)$ is the parity-check polynomial of $\mathcal{C}$, and, owing to Remark 1, we have in addition that $\varphi :=\text{ ord }(h_a(x))=\frac{n}{\gcd (n,a)}$. If we take $\mathcal{C'}$ to be the irreducible cyclic code of length $\varphi$ whose parity check polynomial is also $h_a(x)$, then note that the Hamming weights of the codewords of $\mathcal{C}$ and $\mathcal{C'}$ differ just by the constant factor $\frac{n}{\varphi }$. Let $e=\gcd (\varphi ,q-1)$ and $r=\frac{\varphi }{e}=\frac{n}{\gcd (n,(q-1)\gcd (n,a))}$; thus, $r | \frac{n}{\gcd (n,q-1)}$. Since $\gcd (r,\frac{q-1}{e})=1$ and $\text{ rad }(\varphi ) | (q-1)$, observe that if $r \ge 2$ then the prime factors of r divide e but not $(q-1)/e$. In addition, observe that if $8 \not \mid n$, then $4 \not \mid r$. On the other hand, since $e | (q-1)$, we necessarily have $\text{ ord }_{e}(q)=1$. Therefore all the irreducible polynomials, over $\mathbb {F}_{q}$, of order e, must have degree equal to one (see, for example, [5, Theorem 3.5]). Consequently, owing to Theorem 3.35 in [5], there must exist an irreducible polynomial $h(x) \in \mathbb {F}_{q}[x]$ of degree one and order e, such that $h_a(x)=h(x^r)$, and this means that $\deg (h_a(x))=r$. Furthermore, thanks to Theorem 1, we can be sure now that h(x) is the parity-check polynomial of an [e, 1, e] one-weight irreducible cyclic code over $\mathbb {F}_{q}$, whose weight enumerator polynomial is $1+(q-1)z^e$ (in fact, such irreducible cyclic code is equivalent to the repetition code of length e). Now, as a direct application of Theorem 4, $\mathcal{C'}$ is an [er, r, e] irreducible cyclic code, whose weight enumerator polynomial is $(1+(q-1)z^e)^r$. But we already said that the Hamming weights of the codewords of $\mathcal{C}$ and $\mathcal{C'}$ differ just by the constant factor $\frac{n}{er}$, therefore $\mathcal{C}$ is an $[n,r,\frac{n}{r}]$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q-1)z^{\frac{n}{r}})^r$. $\square$

The case in which 8|n and $q \equiv 3 \pmod {4}$ is not covered in Theorem 5, and this is so because this case is somewhat a little more complicated, as we will see below.

Theorem 6

With our current notation suppose that $\text{ rad }(n) | (q-1)$. In addition, suppose that $\mathcal{C}$ is an irreducible cyclic code of length n, whose parity check polynomial is $h_a(x)$ for some suitable integer a. Let $\varphi :=\text{ ord }(h_a(x))=\frac{n}{\gcd (n,a)}$, $e=\gcd (\varphi ,q^2-1)$ and $r=\frac{\varphi }{e}$. If $8 \not \mid e$, then define $b=2$ if 4|e, and $b=1$ otherwise. If 8|e, define $u=\gcd (q+1,\frac{q^2-1}{e})$. Thus, if 8|n and $q \equiv 3 \pmod {4}$, then the following conditional statements are true:

(A) :

If $8 \not \mid e$, then $\mathcal{C}$ is an $[n,rb,\frac{n}{rb}]$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q-1)z^{\frac{n}{rb}})^{rb}$.

(B) :

If 8|e and $u=1$, then $\mathcal{C}$ is an $[n,2r,\frac{qn}{(q+1)r}]$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q^2-1)z^{\frac{qn}{(q+1)r}})^r$.

(C) :

If 8|e and $u \ge 2$, then $\mathcal{C}$ is an $[n,2r,\frac{n}{r}\frac{q+1-u}{q+1}]$ irreducible cyclic code whose weight enumerator polynomial is:

$$\begin{aligned} \left( 1+\frac{(q^2-1)}{u}z^{\frac{n}{r}\frac{q+1-u}{q+1}}+\frac{(q^2-1)(u-1)}{u}z^{\frac{n}{r}} \right) ^r \; . \end{aligned}$$

(1)

Proof

First, we take $\mathcal{C'}$ to be as in the proof of Theorem 5.

Part (A): Let $e'=e/b$ and note that $e'=\gcd (\varphi ,q-1)$ and $rb=\frac{\varphi }{e'}$. Since $\gcd (rb,\frac{q-1}{e'})=1$ and $\text{ rad }(\varphi ) | (q-1)$, observe that if $rb \ge 2$ then the prime factors of rb divide $e'$, but not $(q-1)/e'$. In addition, since $8 \not \mid e$ and $8 | (q^2-1)$, we have $4 \not \mid (rb)$. Now, by following the same arguments as in the proof of Theorem 5, we have that $\mathcal{C'}$ is an $[e'rb,rb,e']$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q-1)z^{e'})^{rb}$. But the codewords of $\mathcal{C}$ and $\mathcal{C'}$ differ just by the constant factor $\frac{n}{e'rb}$, therefore $\mathcal{C}$ is an $[n,rb,\frac{n}{rb}]$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q-1)z^{\frac{n}{rb}})^{rb}$.

Part (B): Since $\gcd (r,\frac{q^2-1}{e})=1$ and $\text{ rad }(\varphi ) | (q^2-1)$, observe that if $r \ge 2$ then the prime factors of r divide e, but not $(q^2-1)/e$. In addition, observe that $q^2 \equiv 1 \pmod {4}$. On the other hand, since $e \not \mid (q-1)$ but $e | (q^2-1)$, we have $\text{ ord }_{e}(q)=2$. Therefore all the irreducible polynomials over $\mathbb {F}_{q}$ of order e must have degree equal to two. Consequently, owing to Theorem 3.35 in [5], there must exist an irreducible polynomial $h(x) \in \mathbb {F}_{q}[x]$ of degree two and order e, such that $h_a(x)=h(x^r)$, and this means that $\deg (h_a(x))=2r$. If $\gamma$ is a primitive element $\mathbb {F}_{q^2}$, then, since h(x) has order e, there must exist an integer $a'$ such that $\gamma ^{-a'}$ is a root of h(x) and $\gcd (q^2-1,a')=\frac{q^2-1}{e}$. That is, $\gcd (\frac{q^2-1}{q-1},a')=\gcd (q+1,\frac{q^2-1}{e})=u=1$. Now, thanks to Theorem 1, we can be sure that h(x) is the parity-check polynomial of an $[e,2,\frac{qe}{q+1}]$ one-weight irreducible cyclic code over $\mathbb {F}_{q}$, whose weight enumerator polynomial is $1+(q-1)z^{\frac{qe}{q+1}}$. Thus, owing to Theorem 4, $\mathcal{C'}$ is an $[er,2r,\frac{qe}{q+1}]$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q-1)z^{\frac{qe}{q+1}})^r$. But the Hamming weights of the codewords of $\mathcal{C}$ and $\mathcal{C'}$ differ just by the constant factor $\frac{n}{er}$, therefore $\mathcal{C}$ is an $[n,2r,\frac{qn}{(q+1)r}]$ irreducible cyclic code whose weight enumerator polynomial is $(1+(q^2-1)z^{\frac{qn}{(q+1)r}})^r$.

Part (C): By following the same arguments as before, we have that there must exist an integer $a'$ and a polynomial $h(x) \in \mathbb {F}_{q}[x]$ of degree two and order e, such that $h_a(x)=h(x^r)$, $\gamma ^{-a'}$ is a root of h(x), and $\gcd (\frac{q^2-1}{q-1},a')=u \ge 2$. Now, thanks to Lemma 1, and owing to Theorem 2, we know that h(x) is the parity-check polynomial of an $[e,2,e\frac{q+1-u}{q+1}]$ semiprimitive two-weight irreducible cyclic code over $\mathbb {F}_{q}$, whose weight enumerator polynomial is $1+\frac{(q^2-1)}{u}z^{e\frac{q+1-u}{q+1}}+\frac{(q^2-1)(u-1)}{u}z^{e}$. Finally, by employing again the same arguments as before, we can conclude that $\mathcal{C}$ is an $[n,2r,\frac{n}{r}\frac{q+1-u}{q+1}]$ irreducible cyclic code whose weight enumerator polynomial is given by (1). $\square$

Example 1

Let $\mathcal{C}$ be a cyclic code over $\mathbb {F}_{7}$ of length $n=576=2^6 3^2$. Suppose that $\varphi =n/2=288=2^5 3^2$, thus, since $q^2-1=48=2^4 3$, we have that $e=48$, $r=6$, 8|e and $u=1$. Then, owing to Part (B) of previous theorem, we can be sure that $\mathcal{C}$ is a [576, 12, 84] irreducible cyclic code whose weight enumerator polynomial is $(1+48z^{84})^6$.

4 Conclusion

In the light of the proofs of Theorems 5 and 6, it should be now clear that the nature of the weight distributions of the codes studied here, is such that these distributions are always obtained through an application of Theorem 4 over a very particular family of irreducible cyclic codes of dimension one or two, and whose length e divides either $q-1$ (Theorem 5), or $q^2-1$ (Theorem 6). In fact, in the cases of Theorem 5, and Part (A) of Theorem 6, such a family is equivalent to the set of repetition codes, while this family corresponds to the set of one-weight irreducible cyclic codes of dimension two, in the case of Part (B), and will corresponds to the set of semiprimitive two-weight irreducible cyclic codes of dimension two, in the case of Part (C). Thus, on the basis of the above, it seems that the family of one-weight irreducible cyclic codes, and the family of semiprimitive two-weight irreducible cyclic codes, are probably a little more important than previously thought.